1 Introduction

Let H be a real Hilbert space with inner product \(\langle \cdot , \cdot \rangle \) and norm \(\|\cdot \|\). Let C be a nonempty, closed and convex subset of H and \(A:H\to H\) be a single-valued operator. The variational inequality problem (shortly, VIP) is formulated as

$$ \text{Find}\quad x^{\dagger }\in C \quad \text{such that}\quad \bigl\langle Ax^{\dagger }, y-x^{\dagger }\bigr\rangle \geq 0,\quad \forall y \in C. $$
(1.1)

We denote the solution set of problem (1.1) \(VI(C,A)\). It is well known that the VIP is a very fundamental problem in nonlinear analysis. It serves as a useful mathematical model which unifies in several ways, many important concepts in applied mathematics such as optimization, equilibrium problem, Nash equilibrium problem, complementarity problem, fixed point problems and system of nonlinear equations; see for instance [19–21, 31, 33]. Moreover, its solutions have been an important part of optimization theory. For these reasons, several researchers have focused on studying iterative methods for approximating the solutions of the VIP (1.1). Two important approaches for solving the VIP are regularized and projection methods. In this paper, we focus on the projection method. The simplest known projection method is the Goldstein gradient projection method [14] which involve a single projection onto the feasible set C per each iteration as follows:

$$ \textstyle\begin{cases} x_{0} \in C \subset \mathbb{R}^{n}, \\ x_{n+1} = P_{C}(x_{n} - \lambda Ax_{n}), \end{cases} $$

where \(\lambda \in (0,\frac{2\eta }{L^{2}} )\), η and L are the strongly monotonicity constant and Lipschitz constant of A, respectively, and \(P_{C}\) is the orthogonal projection onto C. It is well known that the gradient projection method converges weakly to a solution of the VIP if and only if the operator A is strongly monotone and L-Lipschitz continuous. When A is monotone, the gradient projection method fails to converge to solution of the VIP. Korpelevich [28] introduced the following extragradient method (EGM) for solving the VIP when A is monotone and L-Lipschitz continuous:

$$ \textstyle\begin{cases} x_{0} \in C,\qquad \lambda >0, \\ y_{n} = P_{C}(x_{n} - \lambda Ax_{n}), \\ x_{n+1} = P_{C}(y_{n} -\lambda A y_{n}),\quad n \geq 0. \end{cases} $$
(1.2)

Moreover, the sequence \(\{x_{n}\}\) generated by (1.2) converges weakly to a solution of the VIP if the stepsize condition \(\lambda \in (0, \frac{1}{L} )\) is satisfied. It should be noted that in the EGM, one needs to calculate two projections onto the feasible set C in each iteration. If the set C is not so simple, then the EGM become very difficult and its implementation is costly. In order to address such situation, Censor et al. [6, 7] introduced the following subgradient extragradient method (SEGM) which involves a projecting onto a constructible half-space \(T_{n}\):

$$ \textstyle\begin{cases} x_{0} \in C, \lambda >0, \\ y_{n} = P_{C}(x_{n} -\lambda Ax_{n}), \\ T_{n} = \{x\in H: \langle x_{n} -\lambda Ax_{n} - y_{n}, x - y_{n} \rangle \leq 0\}, \\ x_{n+1} = P_{T_{n}}(x_{n} - \lambda Ay_{n}). \end{cases} $$
(1.3)

The authors also proved that the sequence \(\{x_{n}\}\) generated by the SEGM converges weakly to a solution of the VIP (1.1) if the stepsize condition \(\lambda \in (0, \frac{1}{L} )\). Several modifications of the EGM and SEGM have been introduced by many authors; see for instance [12, 22, 24–26, 41–43]. Recently, He [17] modified the EGM and introduced a projection and contraction method (PCM) which requires only a single projection per each iteration as follows:

$$ \textstyle\begin{cases} x_{0} \in H, \\ y_{n} = P_{C}(x_{n} - \lambda Ax_{n}), \\ d(x_{n},y_{n}) = x_{n} -y_{n} - \lambda (Ax_{n} -Ay_{n}), \\ x_{n+1} = x_{n} - \gamma \eta _{n} d(x_{n},y_{n}), \quad \forall n \geq 0 , \end{cases} $$
(1.4)

where \(\gamma \in (0,2)\), \(\lambda \in (0, \frac{1}{L})\) and

$$ \eta _{n} = \frac{\langle x_{n} - y_{n}, d(x_{n},y_{n})\rangle }{ \Vert d(x_{n},y_{n}) \Vert ^{2}}. $$

He proved that the sequence \(\{x_{n}\}\) generated by the PCM converges weakly to a solution of VIP.

On the other hand, the inertial-type algorithm which is a two-step iteration process was introduced by Polyak [38] as a means of accelerating the speed of convergence of iterative algorithms. Recently, many inertial-type algorithms have been introduced by some authors, this includes the inertial proximal method [1, 37], inertial forward–backward method [29], inertial split equilibrium method [23], inertial proximal ADMM [9] and fast iterative shrinkage thresholding algorithm FISTA [5, 8].

In order to accelerate the convergence of the PCM, Dong et al. [11] introduced the following inertial PCM and proved its weak convergence to a solution \(\bar{x} \in VI(C,A) \cap F(T)\), where \(F(T)=\{x\in H: Tx =x\}\) is the set of fixed points of a nonexpansive mapping T:

$$ \textstyle\begin{cases} x_{0},x_{1} \in H, \\ w_{n} = x_{n} + \alpha _{n} (x_{n} -x_{n-1}), \\ y_{n} = P_{C}(w_{n} - \lambda Aw_{n}), \\ d(w_{n},y_{n}) = (w_{n} - y_{n}) - \lambda (Aw_{n} - Ay_{n}), \\ \eta _{n} = \frac{\langle w_{n} - y_{n}, d(w_{n},y_{n})\rangle }{ \Vert d(w_{n},y_{n}) \Vert ^{2}}, \\ x_{n+1} = (1-\tau _{n})w_{n} + \tau _{n}T( w_{n} - \gamma \eta _{n} d(w_{n},y_{n})), \quad n \geq 1, \end{cases} $$
(1.5)

where \(\gamma \in (0,2)\), \(\lambda \in (0, \frac{1}{L} )\), \(\{\alpha _{n}\}\) is a non-decreasing sequence with \(\alpha _{1} = 0\), \(0 \leq \alpha _{n}\leq \alpha <1\) and \(\sigma , \delta >0\) are constants such that

$$ \delta > \frac{\alpha ^{2} (1+\alpha )+\alpha \sigma }{1 - \alpha ^{2}} \quad \text{and}\quad 0 < \underline{\tau } \leq \tau _{n} \leq \frac{[\delta - \alpha ((1+\alpha )+\alpha \delta +\sigma )]}{\delta [1+\alpha (1+\alpha )+\alpha \delta +\sigma ]} = \bar{\tau }. $$

It is important to mention that in solving optimization problems, strong convergence algorithms are more desirable than the weak convergence counterparts (see [3, 15]). Tian and Jiang [45] recently introduced the following hybrid-inertial PCM: \(x_{0}, x_{1} \in H\),

$$ \textstyle\begin{cases} w_{n} = x_{n} + \alpha _{n} (x_{n} -x_{n-1}), \\ y_{n} = P_{C}(w_{n} - \lambda _{n} Aw_{n}), \\ d(w_{n},y_{n}) = (w_{n} - y_{n}) - \lambda (Aw_{n} - Ay_{n}), \\ \eta _{n} = \textstyle\begin{cases} \frac{\langle w_{n} - y_{n}, d(w_{n},y_{n})\rangle }{ \Vert d(w_{n},y_{n}) \Vert ^{2}}, & \text{if } d(w_{n},y_{n}) \neq 0, \\ 0, & \text{otherwise}, \end{cases}\displaystyle \\ z_{n} = w_{n} - \gamma \eta _{n}d(w_{n},y_{n}), \\ C_{n} = \bigl\{ u\in H: \Vert z_{n} - u \Vert ^{2} \leq \Vert x_{n} -u \Vert ^{2} + \alpha _{n}^{2} \Vert x_{n-1}-x_{n} \Vert ^{2} \\ - 2\alpha _{n} \langle x_{n} -u, x_{n-1} -x_{n} \rangle \bigr\} , \\ Q_{n} = \bigl\{ u \in H: \langle u - x_{n}, x_{1} - x_{n} \rangle \leq 0\bigr\} , \\ x_{n+1} = P_{C_{n}\cap Q_{n}}x_{1}. \end{cases} $$
(1.6)

The authors proved that the sequence generated by (1.6) converges strongly to a solution of the VIP with the aid of this stepsize condition: \(0 < a \leq \lambda _{n} \leq b < \frac{1}{L}\). Moreover, other authors have further introduced some strong convergence inertial PCM with certain stepsize conditions in real Hilbert spaces; see e.g. [10, 18, 26, 27, 39, 40, 44]. Note that the stepsize conditions in the above methods restrict the applicability of the methods due to the prior estimate of the Lipschitz constant L. In reality, the Lipschitz constant is very difficult to estimate and even when it is estimated, it is often too small and deteriorates the convergence of the methods. Moreover, the convergence of Algorithm 1.6 involves computing two subsets \(C_{n}\) and \(Q_{n}\), and the projection of \(x_{1}\) onto their intersection \(C_{n} \cap Q_{n}\), which can be very computationally expensive. Hence, it becomes necessary to propose an efficient iterative method which does not depends on the Lipschitz constant and converges strongly to solution of the VIP.

In this paper, we introduce a new self-adaptive inertial projection and contraction method for finding common element in the set of solution of pseudomonotone variational inequalities and the set of fixed points of strictly pseudocontractive mappings in real Hilbert spaces. Our algorithm is designed such that its convergence does not require prior estimate of the Lipschitz constant and we prove a strong convergence result using viscosity approximation method [36]. We also provide some numerical experiments to illustrate the efficiency and accuracy of our proposed method by comparing with other methods in the literature.

2 Preliminaries

Let H be a real Hilbert space and let C be a nonempty, closed and convex subset of H. We use \(x_{n} \to x\) (resp. \(x_{n} \rightharpoonup x\)) to denote that the sequence \(\{x_{n}\}\) converges strongly (resp. weakly) to a point x as \(n \to \infty \).

For each \(x \in H\), there exists a unique nearest point in C, denoted by \(P_{C}x\) satisfying

$$ \Vert x-P_{C}x \Vert \leq \Vert x-y \Vert \quad \forall y \in C. $$

\(P_{C}\) is called the metric projection from H onto C, and it is characterized by the following properties (see, e.g. [13]):

  1. (i)

    For each \(x \in H\) and \(z \in C\),

    $$ z = P_{C}x \quad \Rightarrow\quad \langle x - z, z - y \rangle \geq 0,\quad \forall y \in C. $$
    (2.1)
  2. (ii)

    For any \(x,y \in H\),

    $$ \langle P_{C}x - P_{C}y, x-y \rangle \geq \Vert P_{C}x - P_{C}y \Vert ^{2}. $$
  3. (iii)

    For any \(x \in H\) and \(y \in C\),

    $$ \Vert P_{C}x - y \Vert ^{2} \leq \Vert x-y \Vert ^{2} - \Vert x - P_{C}x \Vert ^{2}. $$
    (2.2)

Definition 2.1

A mapping \(A:H \rightarrow H\) is called

  1. (i)

    η-strongly monotone if there exists a constant \(\eta >0\) such that

    $$ \langle Ax -Ay, x-y \rangle \geq \eta \Vert x-y \Vert ^{2} \quad \forall x,y \in H, $$
  2. (ii)

    α-inverse strongly monotone if there exists a constant \(\alpha >0\) such that

    $$ \langle Ax -Ay, x - y\rangle \geq \alpha \Vert Ax - Ay \Vert ^{2}\quad \forall x,y \in H, $$
  3. (iii)

    monotone if

    $$ \langle Ax - Ay, x- y\rangle \geq 0\quad \forall x,y \in H, $$
  4. (iv)

    pseudomonotone if, for all \(x,y \in H\),

    $$ \langle Ax, y -x \rangle \geq 0\quad \Rightarrow\quad \langle Ay, y -x \rangle \geq 0, $$
  5. (v)

    L- Lipschitz continuous if there exists a constant \(L >0\) such that

    $$ \Vert Ax- Ay \Vert \leq L \Vert x-y \Vert \quad \forall x,y \in H. $$

If A is η-strongly monotone and L-Lipschitz continuous, then A is \(\frac{\eta }{L^{2}}\)-inverse strongly monotone. Also, we note that every monotone operator is pseudomonotone but the converse is not true; see, for instance [25, 26].

Let \(T:H \to H\) be a nonlinear mapping. A point \(x \in H\) is called a fixed point of T if \(Tx = x\). The set of fixed points of T is denoted by \(F(T)\). The mapping \(T:H \to H\) is said to be

  1. (i)

    a contraction, if there exists \(\alpha \in [0,1)\) such that

    $$ \Vert Tx - Ty \Vert \leq \alpha \Vert x-y \Vert \quad \forall x,y \in H. $$

    If \(\alpha =1\), then T is called a nonexpansive mapping,

  2. (ii)

    a κ-strictly pseudocontraction, if there exists \(\kappa \in [0,1)\) such that

    $$ \Vert Tx-Ty \Vert ^{2} \leq \Vert x-y \Vert ^{2} + \kappa \bigl\Vert (I-T)x - (I-T)y \bigr\Vert ^{2}\quad \forall x,y \in H. $$

Remark 2.2

([2])

If T is κ-strictly pseudocontractive, then T has the following important properties:

  1. (a)

    T satisfies Lipschitz condition with Lipschitz constant \(L = \frac{1+\kappa }{1-\kappa }\).

  2. (b)

    \(F(T)\) is closed and convex.

  3. (c)

    \(I-T\) is demiclosed at 0, that is, if \(\{x_{n}\}\) is a sequence in H such that \(x_{n} \rightharpoonup \bar{x}\) and \((I-T)x_{n} \to 0\), then \(\bar{x} \in F(T)\).

Lemma 2.3

([47])

Let H be a real Hilbert space and \(T:H \to H\) be a κ-strictly pseudocontractive mapping with \(\kappa \in [0,1)\). Let \(T_{\alpha }= \alpha I + (1-\alpha )T\) where \(\alpha \in [\kappa ,1)\), then

  1. (i)

    \(F(T_{\alpha }) = F(T)\),

  2. (ii)

    \(T_{\alpha }\) is nonexpansive.

Lemma 2.4

([34, 46])

For all \(x,y,z \in H\), it is well known that

  1. (i)

    \(\|x+y\|^{2} = \|x\|^{2} + 2\langle x,y \rangle + \|y\|^{2}\),

  2. (ii)

    \(\|x+y\|^{2} \leq \|x\|^{2} + 2\langle y,x+y\rangle \),

  3. (iii)

    \(\|tx + (1-t) y\|^{2} = t\|x\|^{2} + (1-t)\|y\|^{2} - t(1-t)\|x-y\|^{2}\), \(\forall t\in [0,1]\).

Lemma 2.5

(see [35])

Consider the Minty variational inequality problem (MVIP) which is defined as finding a point \(x^{\dagger }\in C\) such that

$$\begin{aligned} \bigl\langle Ay, y - x^{\dagger }\bigr\rangle \geq 0,\quad \forall y \in C. \end{aligned}$$
(2.3)

We denote by \(M(C,A)\) the set of solution of (2.3). If a mapping \(h:[0,1] \rightarrow H\) defined as \(h(t) = A(tx + (1-t)y)\) is continuous for all \(x,y \in C\) (i.e., h is hemicontinuous), then \(M(C,A) \subset VI(C,A)\). Moreover, if A is pseudomonotone, then \(VI(C,A)\) is closed, convex and \(VI(C,A) = M(C,A)\).

Lemma 2.6

([30])

Let \(\{\alpha _{n}\}\) and \(\{\delta _{n}\}\) be sequences of nonnegative real numbers such that

$$ \alpha _{n+1} \leq (1-\delta _{n})\alpha _{n} + \beta _{n} + \gamma _{n},\quad n\geq 1, $$

where \(\{\delta _{n}\}\) is a sequence in \((0,1)\) and \(\{\beta _{n}\}\) is a real sequence. Assume that \(\sum_{n=0}^{\infty }\gamma _{n} < \infty \). Then the following results hold:

  1. (i)

    If \(\beta _{n} \leq \delta _{n} M\) for some \(M \geq 0\), then \(\{\alpha _{n}\}\) is a bounded sequence.

  2. (ii)

    If \(\sum_{n=0}^{\infty }\delta _{n} = \infty \) and \(\limsup_{n\rightarrow \infty }\frac{\beta _{n}}{\delta _{n}} \leq 0\), then \(\lim_{n\rightarrow \infty }\alpha _{n} =0\).

Lemma 2.7

([32])

Let \(\{a_{n}\}\) be a sequence of real numbers such that there exists a subsequence \(\{a_{n_{i}}\}\) of \(\{a_{n}\}\) with \(a_{n_{i}} < a_{n_{i}+1}\) for all \(i \in \mathbb{N}\). Consider the integer \(\{m_{k}\}\) defined by

$$\begin{aligned} m_{k} = \max \{j \leq k: a_{j} < a_{j+1}\}. \end{aligned}$$

Then \(\{m_{k}\}\) is a non-decreasing sequence verifying \(\lim_{n \rightarrow \infty }m_{n} = \infty \), and for all \(k \in \mathbb{N}\), the following estimates hold:

$$\begin{aligned} a_{m_{k}} \leq a_{m_{k}+1},\quad \textit{and} \quad a_{k} \leq a_{m_{k}+1}. \end{aligned}$$

3 Main results

In this section, we introduce a new inertial projection and contraction method with a self-adaptive technique for solving the VIP (1.1). The following conditions are assumed throughout the paper.

Assumption 3.1

  1. A.

    The feasible set C is a nonempty, closed and convex subset of a real Hilbert space H,

  2. B.

    the associated operator \(A:H \to H\) is L-Lipschitz continuous, pseudomonotone and weakly sequentially continuous on bounded subset of H, i.e., if for each sequence \(\{x_{n}\}\), we have \(x_{n} \rightharpoonup x\) implies that \(Ax_{n} \rightharpoonup Ax\),

  3. C.

    \(T:H \to H\) is κ-strictly pseudocontractive mapping,

  4. D.

    the solution set \(Sol:=VI(C,A)\cap F(T)\) is nonempty,

  5. E.

    the function \(f: H \to H\) is a contraction with contractive coefficient \(\rho \in (0,1)\),

  6. F.

    the control sequences \(\{\theta _{n}\}\), \(\{\alpha _{n}\}\), \(\{\beta _{n}\}\) and \(\{\delta _{n}\}\) satisfy

    • \(\{\alpha _{n}\} \subset (0,1)\), \(\lim_{n \rightarrow \infty }\alpha _{n} = 0\) and \(\sum_{n=0}^{\infty }\alpha _{n} = \infty \),

    • \(\{\beta _{n}\} \subset (a,1-\alpha _{n}) \) for some \(a >0\),

    • \(\{\theta _{n}\}\subset [0,\theta )\) for some \(\theta >0\) such that \(\lim_{n \rightarrow \infty }\frac{\theta _{n}}{\alpha _{n}}\|x_{n} - x_{n-1}\| = 0\),

    • \(\{\delta _{n}\} \subset (0,1)\) and \(\liminf_{n\to \infty }(\delta _{n} - \kappa )>0\).

Remark 3.2

The inertial parameter \(\theta _{n}\) and \(\alpha _{n}\) can be chosen as follows:

$$ \alpha _{n} = \frac{1}{(n+1)^{p}} \quad \text{and}\quad \theta _{n} = \frac{1}{(n+1)^{1-p}},\quad p \in \biggl(0,\frac{1}{2} \biggr), n \in \mathbb{N}. $$

We now present our Algorithm as follows.

Before proving the convergence of Algorithm 3.3, we provide some key lemmas which will be used in the sequel.

Algorithm 3.3
figure a

Inertial projection and contraction method

Full size image

Lemma 3.4

The stepsize rule defined by (3.1) is well defined and

$$ \min \biggl\{ \sigma ,\frac{\mu l}{L} \biggr\} \leq \lambda _{n} \leq \sigma . $$

Proof

Since A is L-Lipschitz continuous, we have

$$ \bigl\Vert Aw_{n} - A\bigl(P_{C}\bigl(w_{n} - \sigma l^{m_{n}}Aw_{n}\bigr)\bigr) \bigr\Vert \leq L \bigl\Vert w_{n} - P_{C}\bigl(w_{n} - \gamma l^{m_{n}}Aw_{n}\bigr) \bigr\Vert . $$

This is equivalent to

$$\begin{aligned} \frac{\mu }{L} \bigl\Vert Aw_{n} - A\bigl(P_{C} \bigl(w_{n} - \sigma l^{m_{n}}Aw_{n}\bigr)\bigr) \bigr\Vert \leq \mu \bigl\Vert w_{n} - P_{C} \bigl(w_{n} - \gamma l^{m_{n}}Aw_{n}\bigr) \bigr\Vert . \end{aligned}$$

Hence, (3.1) holds for all \(\lambda _{n} \leq \sigma \). If \(\lambda _{n} = \sigma \), then the result follows. On the other hand, if \(\lambda _{n} < \sigma \), then, by the search rule (3.1), \(\frac{\lambda _{n}}{l}\) must violate the inequality (3.1), i.e.,

$$ \biggl\Vert Aw_{n} - A\biggl(P_{C} \biggl(w_{n} - \frac{\lambda _{n}}{l}Aw_{n}\biggr)\biggr) \biggr\Vert > L \biggl\Vert w_{n} - P_{C} \biggl(w_{n} - \frac{\lambda _{n}}{l}Aw_{n}\biggr) \biggr\Vert . $$

Combining this with the fact that A is Lipschitz continuous, we have \(\lambda _{n} > \frac{\mu l}{L}\). Hence \(\min \{ \sigma ,\frac{\mu l}{L} \} \leq \lambda _{n} \leq \sigma \). This completes the proof. □

Lemma 3.5

The sequence \(\{x_{n}\}\) generated by Algorithm 3.3 is bounded. In addition

$$ \xi _{n} \geq \frac{1-\mu }{(1+\mu )^{2}}. $$
(3.4)

Proof

Let \(x^{*} \in VI(C,A)\). Then

$$\begin{aligned} \bigl\Vert z_{n} -x^{*} \bigr\Vert ^{2} =& \bigl\Vert w_{n} -x^{*} - \gamma \xi _{n} d(w_{n},y_{n}) \bigr\Vert ^{2} \\ =& \bigl\Vert w_{n} -x^{*} \bigr\Vert ^{2} - 2\gamma \xi _{n} \bigl\langle w_{n} -x^{*}, d(w_{n},y_{n}) \bigr\rangle + \gamma ^{2} \xi _{n}^{2} \bigl\Vert d(w_{n},y_{n}) \bigr\Vert ^{2} \\ =& \bigl\Vert w_{n} -x^{*} \bigr\Vert ^{2} - 2\gamma \xi _{n} \bigl\langle w_{n} -y_{n}, d(w_{n},y_{n}) \bigr\rangle + \bigl\langle y_{n} -x^{*}, d(w_{n},y_{n}) \bigr\rangle \\ &{} + \gamma ^{2} \xi _{n}^{2} \bigl\Vert d(w_{n},y_{n}) \bigr\Vert ^{2}. \end{aligned}$$
(3.5)

By the definition of \(y_{n}\) and using the variational characterization of the \(P_{C}\), i.e., (2.1), we have

$$ \bigl\langle w_{n} -\lambda _{n} Aw_{n} - y_{n}, y_{n} -x^{*} \bigr\rangle \geq 0. $$
(3.6)

Also since \(x^{*} \in VI(C,A)\) and A is pseudomonotone,

$$ \bigl\langle Ay_{n} , y_{n} -x^{*} \bigr\rangle \geq 0 . $$
(3.7)

Combining (3.6) and (3.7), we have

$$ \bigl\langle d(w_{n},y_{n}), y_{n} -x^{*} \bigr\rangle \geq 0. $$

Therefore, it follows from (3.5) that

$$\begin{aligned} \bigl\Vert z_{n} -x^{*} \bigr\Vert \leq & \bigl\Vert w_{n} - x^{*} \bigr\Vert ^{2} - 2 \gamma \xi _{n} \bigl\langle w_{n} - y_{n}, d(w_{n},y_{n}) \bigr\rangle + \gamma ^{2}\xi _{n}^{2} \bigl\Vert d(w_{n},y_{n}) \bigr\Vert ^{2} \\ =& \bigl\Vert w_{n} - x^{*} \bigr\Vert ^{2} - 2\gamma \xi _{n} \bigl\langle w_{n} - y_{n}, d(w_{n},y_{n}) \bigr\rangle + \gamma ^{2}\xi _{n} \bigl\langle w_{n} - y_{n}, d(w_{n},y_{n}) \bigr\rangle \\ =& \bigl\Vert w_{n} -x^{*} \bigr\Vert ^{2} - \gamma (2 - \gamma ) \xi _{n} \bigl\langle w_{n} - y_{n}, d(w_{n},y_{n}) \bigr\rangle . \end{aligned}$$
(3.8)

However, from the definition of \(z_{n}\) and \(\xi _{n}\), we have

$$\begin{aligned} \xi _{n} \bigl\langle w_{n} - y_{n}, d(w_{n},y_{n})\bigr\rangle =& \bigl\Vert \xi _{n} d(w_{n},y_{n}) \bigr\Vert ^{2} \\ =& \frac{1}{\gamma ^{2}} \Vert z_{n} -w_{n} \Vert ^{2}. \end{aligned}$$
(3.9)

Combining (3.8) and (3.9), we get

$$ \bigl\Vert z_{n} - x^{*} \bigr\Vert ^{2} \leq \bigl\Vert w_{n} -x^{*} \bigr\Vert ^{2} - \frac{2-\gamma }{\gamma } \Vert z_{n} - w_{n} \Vert ^{2}. $$
(3.10)

Since \(\gamma \in (0,2)\), we have

$$ \bigl\Vert z_{n} -x^{*} \bigr\Vert ^{2} \leq \bigl\Vert w_{n} -x^{*} \bigr\Vert ^{2}. $$

Moreover,

$$\begin{aligned} \bigl\Vert w_{n} -x^{*} \bigr\Vert =& \bigl\Vert x_{n} + \theta _{n} (x_{n} -x_{n-1}) - x^{*} \bigr\Vert \\ \leq & \bigl\Vert x_{n} - x^{*} \bigr\Vert + \alpha _{n} \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n} -x_{n-1} \Vert . \end{aligned}$$

Since \(\frac{\theta _{n}}{\alpha _{n}} \|x_{n} -x_{n-1}\| \to 0\), there exists a constant \(M>0\) such that

$$ \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n} -x_{n-1} \Vert \leq M \quad \forall n \geq 1, $$

thus

$$ \bigl\Vert w_{n} -x^{*} \bigr\Vert \leq \bigl\Vert x_{n} -x^{*} \bigr\Vert + \alpha _{n} M. $$

Therefore, it follows from (ii) of Lemma 2.3 that

$$\begin{aligned} \bigl\Vert x_{n+1} - x^{*} \bigr\Vert =& \bigl\Vert \alpha _{n} f(x_{n}) + \beta _{n} x_{n} + (1- \beta _{n} - \alpha _{n})T_{\delta _{n}}z_{n} -x^{*} \bigr\Vert \\ \leq & \alpha _{n} \bigl\Vert f(x_{n}) - x^{*} \bigr\Vert + \beta _{n} \bigl\Vert x_{n} - x^{*} \bigr\Vert + (1-\beta _{n} - \alpha _{n}) \bigl\Vert T_{\delta _{n}}z_{n} -x^{*} \bigr\Vert \\ \leq & \alpha _{n} \bigl\Vert f(x_{n}) - f \bigl(x^{*}\bigr) + f\bigl(x^{*}\bigr) - x^{*} \bigr\Vert + \beta _{n} \bigl\Vert x_{n} - x^{*} \bigr\Vert + (1-\beta _{n} -\alpha _{n}) \bigl\Vert z_{n} -x^{*} \bigr\Vert \\ \leq & \alpha _{n} \rho \bigl\Vert x_{n} - x^{*} \bigr\Vert + \alpha _{n} \bigl\Vert f \bigl(x^{*}\bigr) -x^{*} \bigr\Vert + \beta _{n} \bigl\Vert x^{*} -x^{*} \bigr\Vert \\ &{} + (1-\beta _{n} -\alpha _{n}) \bigl\Vert w_{n} - x^{*} \bigr\Vert \\ \leq & \alpha _{n} \rho \bigl\Vert x_{n} - x^{*} \bigr\Vert + \alpha _{n} \bigl\Vert f \bigl(x^{*}\bigr) -x^{*} \bigr\Vert + \beta _{n} \bigl\Vert x^{*} -x^{*} \bigr\Vert \\ &{} + (1-\beta _{n} -\alpha _{n})\bigl[ \bigl\Vert x_{n} -x^{*} \bigr\Vert + \alpha _{n} M \bigr] \\ \leq & \bigl(1-\alpha _{n} (1-\rho )\bigr) \bigl\Vert x_{n} -x^{*} \bigr\Vert + \alpha _{n} \bigl\Vert f\bigl(x^{*}\bigr) - x^{*} \bigr\Vert + \alpha _{n}M \\ =& \bigl(1-\alpha _{n} (1-\rho )\bigr) \bigl\Vert x_{n} -x^{*} \bigr\Vert + \alpha _{n}(1- \rho ) \biggl[\frac{ \Vert f(x^{*})-x^{*} \Vert +M}{1-\rho } \biggr]. \end{aligned}$$

By induction, we see that \(\{\|x_{n} - x^{*}\|\}\) is bounded. Consequently, \(\{x_{n}\}\) is bounded. Furthermore,

$$\begin{aligned} \bigl\Vert d(w_{n},y_{n}) \bigr\Vert =& \bigl\Vert w_{n} -y_{n} - \lambda _{n} (Aw_{n} - Ay_{n}) \bigr\Vert \\ \leq & \Vert w_{n} -y_{n} \Vert + \lambda _{n} \Vert Aw_{n} - Ay_{n} \Vert \\ \leq & (1-\mu ) \Vert w_{n} - y_{n} \Vert . \end{aligned}$$
(3.11)

Also from (3.1), we have

$$\begin{aligned} \bigl\langle w_{n} - y_{n}, d(w_{n},y_{n}) \bigr\rangle =& \bigl\langle w_{n} -y_{n}, w_{n} -y_{n} - \lambda _{n} (Aw_{n} - Ay_{n}) \bigr\rangle \\ =& \Vert w_{n} -y_{n} \Vert ^{2} - \lambda _{n} \langle w_{n} -y_{n}, Aw_{n} - Ay_{n}\rangle \\ \geq & \Vert w_{n} -y_{n} \Vert ^{2} - \lambda _{n} \Vert w_{n} - y_{n} \Vert \Vert Aw_{n} - Ay_{n} \Vert \\ \geq & \Vert w_{n} -y_{n} \Vert ^{2} - \mu \Vert w_{n} -y_{n} \Vert ^{2} \\ =& (1-\mu ) \Vert w_{n} - y_{n} \Vert ^{2}. \end{aligned}$$
(3.12)

It therefore follows from (3.11) and (3.12) that

$$\begin{aligned} \xi _{n} =& \frac{\langle w_{n} -y_{n}, d(w_{n},y_{n})\rangle }{ \Vert d(w_{n},y_{n}) \Vert ^{2}} \\ \geq & \frac{1-\mu }{(1+\mu )^{2}}. \end{aligned}$$

This completes the proof. □

Lemma 3.6

Let \(x^{*} \in Sol\). Then the sequence \(\{x_{n}\}\) generated by Algorithm 3.3 satisfies the following inequality:

$$ s_{n+1} \leq (1-a_{n})s_{n} + a_{n}b_{n} + c_{n},\quad \forall n \geq 1, $$

where \(s_{n} = \|x_{n} - x^{*}\|^{2}\), \(a_{n} = \frac{2\alpha _{n}(1-\rho )}{1-\alpha _{n}\rho }\), \(b_{n} = \frac{\langle f(x^{*}) - x^{*}, x_{n+1} -x^{*} \rangle }{1-\rho }\), \(c_{n} = \frac{\alpha _{n}^{2}}{1-\alpha _{n}\rho } \|x_{n} -x^{*}\|^{2} + \frac{\theta _{n}}{1-\alpha _{n}\rho }\|x_{n}- x_{n-1}\|M_{2}\) for some \(M_{2}>0\).

Proof

From Lemma 2.4(i), we have

$$\begin{aligned} \bigl\Vert w_{n} -x^{*} \bigr\Vert ^{2} =& \bigl\Vert x_{n} + \theta _{n}(x_{n} -x_{n-1}) - x^{*} \bigr\Vert \\ =& \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + 2\theta _{n}\bigl\langle x_{n} -x^{*}, x_{n} - x_{n-1} \bigr\rangle + \theta _{n}^{2} \Vert x_{n} -x_{n-1} \Vert ^{2} \\ \leq & \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + 2\theta _{n} \bigl\Vert x_{n} -x^{*} \bigr\Vert \Vert x_{n} - x_{n-1} \Vert + \theta _{n}^{2} \Vert x_{n} -x_{n-1} \Vert ^{2} \\ =& \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + \theta _{n} \Vert x_{n} - x_{n-1} \Vert \bigl[2 \bigl\Vert x_{n} -x^{*} \bigr\Vert + \theta _{n} \Vert x_{n} -x_{n-1} \Vert \bigr] \\ \leq & \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + \theta _{n} \Vert x_{n} - x_{n-1} \Vert M_{2}, \end{aligned}$$
(3.13)

where \(M_{2} = \sup_{n\geq 1}\{2\|x_{n} -x^{*}\| + \theta _{n}\|x_{n} -x_{n-1}\| \}\).

Moreover, from Lemma 2.4(iii), we get

$$\begin{aligned} \bigl\Vert T_{\delta _{n}}z_{n} -x^{*} \bigr\Vert ^{2} =& \bigl\Vert \delta _{n} z_{n} + (1- \delta _{n})Tz_{n} - x^{*} \bigr\Vert ^{2} \\ =& \delta _{n} \bigl\Vert z_{n} -x^{*} \bigr\Vert ^{2} + (1-\delta _{n}) \bigl\Vert Tz_{n} - x^{*} \bigr\Vert ^{2} -\delta _{n}(1-\delta _{n}) \Vert z_{n} - Tz_{n} \Vert ^{2} \\ \leq & \delta _{n} \bigl\Vert z_{n} -x^{*} \bigr\Vert ^{2} + (1-\delta _{n}) \bigl[ \bigl\Vert z_{n} -x^{*} \bigr\Vert ^{2} + \kappa \Vert z_{n} - Tz_{n} \Vert ^{2}\bigr] \\ &{}-\delta _{n}(1-\delta _{n}) \Vert z_{n} - Tz_{n} \Vert ^{2} \\ =& \bigl\Vert z_{n} -x^{*} \bigr\Vert ^{2} + (1-\delta _{n}) (\kappa - \delta _{n}) \Vert z_{n} -Tz_{n} \Vert ^{2} \\ \leq & \bigl\Vert z_{n} -x^{*} \bigr\Vert ^{2}. \end{aligned}$$
(3.14)

Also, using Lemma 2.4(ii) and (3.14), we have

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} =& \bigl\Vert \alpha _{n} \bigl(f(x_{n})-x^{*} \bigr) + \beta _{n} \bigl(x_{n}-x^{*}\bigr) + (1 - \beta _{n} - \alpha _{n}) \bigl(T_{\delta _{n}}z_{n} -x^{*}\bigr) \bigr\Vert ^{2} \\ \leq & \bigl\Vert \beta _{n} \bigl(x_{n} -x^{*}\bigr) + (1-\beta _{n} - \alpha _{n}) \bigl(T_{ \delta _{n}}z_{n} -x^{*}\bigr) \bigr\Vert ^{2} + 2\alpha _{n} \bigl\langle f(x_{n}) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \beta _{n}^{2} \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + (1-\beta _{n} - \alpha _{n})^{2} \bigl\Vert T_{ \delta _{n}}z_{n} -x^{*} \bigr\Vert ^{2} \\ &{} + 2\beta _{n}(1- \beta _{n} -\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert \bigl\Vert T_{ \delta _{n}}z_{n}-x^{*} \bigr\Vert \\ & {}+ 2\alpha _{n} \bigl\langle f(x_{n})-f \bigl(x^{*}\bigr), x_{n+1}-x^{*} \bigr\rangle + 2 \alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \beta _{n}^{2} \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + (1-\beta _{n} - \alpha _{n})^{2} \bigl\Vert T_{ \delta _{n}}z_{n} -x^{*} \bigr\Vert ^{2} \\ &{} + \beta _{n}(1-\beta _{n} -\alpha _{n})\bigl[ \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + \bigl\Vert T_{\delta _{n}}z_{n} -x^{*} \bigr\Vert ^{2}\bigr] \\ & {}+ 2\alpha _{n} \rho \bigl\Vert x_{n} - x^{*} \bigr\Vert \bigl\Vert x_{n+1} - x^{*} \bigr\Vert + 2 \alpha _{n} \bigl\langle f \bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \beta _{n}(1-\alpha _{n}) \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + (1-\beta _{n} - \alpha _{n}) (1-\alpha _{n}) \bigl\Vert T_{\delta _{n}}z_{n} - x^{*} \bigr\Vert ^{2} \\ & {}+ \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \beta _{n}(1-\alpha _{n}) \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + (1-\beta _{n} - \alpha _{n}) (1-\alpha _{n}) \bigl\Vert z_{n} - x^{*} \bigr\Vert ^{2} \\ & {}+ \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \beta _{n}(1-\alpha _{n}) \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \\ &{} + (1-\beta _{n} - \alpha _{n}) (1-\alpha _{n}) \biggl[ \bigl\Vert w_{n} -x^{*} \bigr\Vert ^{2} - \frac{2-\gamma }{\gamma } \Vert z_{n} - w_{n} \Vert ^{2} \biggr] \\ & {}+ \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \beta _{n}(1-\alpha _{n}) \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \\ &{} + (1-\beta _{n} - \alpha _{n}) (1-\alpha _{n}) \bigl[ \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + \theta _{n} \Vert x_{n} - x_{n-1} \Vert M_{2} \bigr] \\ & {}+ \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \bigl[(1-2\alpha _{n} + \alpha _{n}\rho )+\alpha _{n}^{2}\bigr] \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \\ &{}+ \theta _{n} \Vert x_{n} - x_{n-1} \Vert M_{2} + \alpha _{n} \rho \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ & {}+ 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle . \end{aligned}$$
(3.15)

Hence

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \leq & \frac{1-2\alpha _{n} + \alpha _{n}\rho }{1-\alpha _{n}\rho } \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + \frac{\alpha _{n}^{2}}{1-\alpha _{n}\rho } \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \\ &{} + \frac{\theta _{n}}{1-\alpha _{n}\rho } \Vert x_{n}- x_{n-1} \Vert M^{2} \\ & {}+ \frac{2\alpha _{n}}{1-\alpha _{n}\rho } \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ =& \biggl[1 - \frac{2\alpha _{n}(1-\rho )}{1-\alpha _{n}\rho } \biggr] \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + \frac{2\alpha _{n}(1-\rho )}{1-\alpha _{n}\rho }\times \frac{\langle f(x^{*}) - x^{*}, x_{n+1} -x^{*} \rangle }{1-\rho } \\ & {}+ \frac{\alpha _{n}^{2}}{1-\alpha _{n}\rho } \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + \frac{\alpha _{n}}{1-\alpha _{n}\rho }\times \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n}- x_{n-1} \Vert M_{2}. \end{aligned}$$

This completes the proof. □

Now we present our strong convergence theorem.

Theorem 3.7

Let \(\{x_{n}\}\) be the sequence generated by Algorithm 3.3 and suppose Assumption 3.1is satisfied. Then \(\{x_{n}\}\) converges strongly to a point \(\bar{x} \in Sol\), where \(\bar{x} = P_{Sol}f(\bar{x})\).

Proof

Let \(x^{*} \in Sol\) and denote \(\|x_{n}-x^{*}\|^{2}\) by \(\Gamma _{n}\) for all \(n \geq 1\). We consider the following two possible cases.

CASE A: Suppose there exists \(n_{0} \in \mathbb{N}\) such that \(\{\Gamma _{n}\}\) is non-increasing for \(N \geq n_{0}\). Since \(\{\Gamma _{n}\}\) is bounded, \(\Gamma _{n}\) converges and thus \(\Gamma _{n} - { \Gamma _{n+1} } \to 0\) as \(n \to \infty \).

First we show that

$$ \lim_{n \rightarrow \infty } \Vert z_{n} - w_{n} \Vert = \lim_{n \rightarrow \infty } \Vert w_{n} - y_{n} \Vert = \lim_{n \rightarrow \infty } \Vert w_{n} -x_{n} \Vert = \lim_{n\to \infty } \Vert x_{n+1} -x_{n} \Vert = 0. $$

From (3.13) and (3.15), we have

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \leq & \beta _{n}(1-\alpha _{n}) \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \\ &{} + (1-\beta _{n} -\alpha _{n}) (1-\alpha _{n}) \biggl[ \bigl\Vert w_{n} -x^{*} \bigr\Vert ^{2} - \frac{2-\gamma }{\gamma } \Vert z_{n} - w_{n} \Vert ^{2} \biggr] \\ & {}+ \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} \\ &{} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \beta _{n}(1-\alpha _{n}) \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \\ &{} + (1-\beta _{n} - \alpha _{n}) (1-\alpha _{n}) \biggl[ \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + \theta _{n} \Vert x_{n} - x_{n-1} \Vert M_{2} \\ &{}- \frac{2-\gamma }{\gamma } \Vert z_{n} - w_{n} \Vert ^{2} \biggr] + \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) \\ &{} + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle . \end{aligned}$$

Since \(\{\beta _{n}\}\subset (1-\alpha _{n})\) and \(\{\alpha _{n}\}\subset (0,1)\), we have

$$\begin{aligned} \frac{2-\gamma }{\gamma } \Vert z_{n} - w_{n} \Vert ^{2} \leq & \bigl(1-2\alpha _{n}+ \alpha _{n}^{2}\bigr) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} + \alpha _{n} \times \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n} - x_{n-1} \Vert M_{2} \\ & {}+ \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ =& \Gamma _{n} - \Gamma _{n+1} -2\alpha _{n} \Gamma _{n} + \alpha _{n}^{2} \Gamma _{n} + \alpha _{n}\rho (\Gamma _{n} + \Gamma _{n+1}) \\ &{} + \alpha _{n} \times \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n} - x_{n-1} \Vert M_{2} \\ & {}+ 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle . \end{aligned}$$

Using the fact that \(\alpha _{n} \to 0\) and \(\frac{\theta _{n}}{\alpha _{n}}\|x_{n} - x_{n-1}\| \to 0\) as \(n\to \infty \), we obtain

$$ \lim_{n \rightarrow \infty }\frac{2-\gamma }{\gamma } \Vert z_{n} - w_{n} \Vert ^{2} = 0, $$

hence

$$ \lim_{n \rightarrow \infty } \Vert z_{n} - w_{n} \Vert = 0. $$
(3.16)

Also from (3.4), (3.9) and the definition of \(z_{n}\), we obtain

$$\begin{aligned} \Vert w_{n} - y_{n} \Vert ^{2} \leq & \frac{(1+\mu )^{2}}{(1-\mu )^{2}\gamma ^{2}} \Vert z_{n} - w_{n} \Vert ^{2}, \end{aligned}$$

Therefore from (3.16), we get

$$ \lim_{n \rightarrow \infty } \Vert w_{n} - y_{n} \Vert = 0. $$
(3.17)

Again from (3.14) and (3.15), we have

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \leq & \beta _{n}(1-\alpha _{n}) \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \\ &{} + (1-\beta _{n} -\alpha _{n}) (1-\alpha _{n}) \bigl[ \bigl\Vert z_{n} -x^{*} \bigr\Vert ^{2} + (1-\delta _{n}) (\kappa - \delta _{n}) \Vert z_{n} - Tz_{n} \Vert ^{2} \bigr] \\ & {}+ \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ \leq & \beta _{n}(1-\alpha _{n}) \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} + (1-\beta _{n} - \alpha _{n}) (1-\alpha _{n})\bigl[ \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \\ &{}+ \theta _{n} \Vert x_{n} - x_{n-1} \Vert M_{2} \\ &{}+ (1-\delta _{n}) (\kappa - \delta _{n}) \Vert z_{n} - Tz_{n} \Vert ^{2}\bigr] + \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) \\ &{}+ 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle . \end{aligned}$$

Then

$$\begin{aligned} (1-\delta _{n}) (\delta _{n}-\kappa ) \Vert z_{n} - Tz_{n} \Vert ^{2} \leq & \bigl(1-2 \alpha _{n}+\alpha _{n}^{2}\bigr) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ &{} + \alpha _{n} \times \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n} - x_{n-1} \Vert M_{2} \\ & {}+ \alpha _{n} \rho \bigl( \bigl\Vert x_{n} - x^{*} \bigr\Vert ^{2} + \bigl\Vert x_{n+1} - x^{*} \bigr\Vert ^{2}\bigr) \\ &{} + 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle \\ =& \Gamma _{n} - \Gamma _{n+1} -2\alpha _{n} \Gamma _{n} + \alpha _{n}^{2} \Gamma _{n} + \alpha _{n}\rho (\Gamma _{n} + \Gamma _{n+1}) \\ &{} + \alpha _{n} \times \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n} - x_{n-1} \Vert M_{2} \\ & {}+ 2\alpha _{n} \bigl\langle f\bigl(x^{*}\bigr) - x^{*}, x_{n+1} -x^{*} \bigr\rangle . \end{aligned}$$

Taking the limit of the above inequality and using the fact that \(\liminf_{n\to \infty } (\delta _{n} - \kappa ) >0\), we have

$$ \lim_{n \rightarrow \infty } \Vert z_{n} - Tz_{n} \Vert = 0. $$
(3.18)

Clearly

$$\begin{aligned} \lim_{n \rightarrow \infty } \Vert w_{n} - x_{n} \Vert = \lim_{n \rightarrow \infty }\alpha _{n} \cdot \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n} - x_{n-1} \Vert = 0. \end{aligned}$$
(3.19)

This implies that

$$ \lim_{n \rightarrow \infty } \Vert z_{n} - x_{n} \Vert = \lim_{n \rightarrow \infty } \Vert y_{n} -x_{n} \Vert = 0. $$

Also

$$\begin{aligned} \lim_{n \rightarrow \infty } \Vert T_{\delta _{n}}z_{n} -z_{n} \Vert = \lim_{n \rightarrow \infty }(1-\delta _{n}) \Vert Tz_{n} - z_{n} \Vert = 0. \end{aligned}$$

On the other hand, it is obvious that

$$\begin{aligned} \Vert x_{n+1} - z_{n} \Vert =& \|\alpha _{n} f(x_{n}) \\ =& \beta _{n} x_{n} + (1- \beta _{n} -\alpha _{n})T_{\delta _{n}}z_{n} - z_{n}\| \\ \leq & \alpha _{n} \bigl\Vert f(x_{n}) - z_{n} \bigr\Vert + \beta _{n} \Vert x_{n} -z_{n} \Vert + (1-\beta _{n} -\alpha _{n}) \Vert T_{\delta _{n}}z_{n} - z_{n} \Vert \\ \to& 0\quad n \to \infty , \end{aligned}$$

hence

$$ \Vert x_{n+1} -x_{n} \Vert \leq \Vert x_{n+1} -z_{n} \Vert + \Vert z_{n} - x_{n} \Vert \to 0\quad n \to \infty . $$

Next, we show that \(\omega _{w}(\{x_{n}\}) \subset Sol\), where \(\omega _{w}(\{x_{n}\})\) is the set of weak accumulation points of \(\{x_{n}\}\). Let \(\{x_{n_{k}}\}\) be a subsequence of \(x_{n}\) such that \(x_{n_{k}} \rightharpoonup p\) as \(k \to \infty \). We need to show that \(p \in Sol\). Since \(\|w_{n_{k}} - x_{n_{k}}\| \to 0\) and \(\|z_{n_{k}} - x_{n_{k}}\| \to 0\), \(w_{n_{k}} \rightharpoonup p\) and \(z_{n_{k}} \rightharpoonup p\), respectively. From the variational characterization of \(P_{C}\) (i.e., (2.1)), we obtain

$$ \langle w_{n_{k}} - \lambda _{n_{k}}Aw_{n_{k}} - y_{n_{k}}, y-y_{n_{k}} \rangle \leq 0\quad \forall y \in C. $$

Hence

$$\begin{aligned} \langle w_{n_{k}} - y_{n_{k}}, y - y_{n_{k}} \rangle \leq & \lambda _{n_{k}} \langle Aw_{n_{k}}, y - y_{n_{k}} \rangle \\ =& \lambda _{n_{k}} \langle Aw_{n_{k}}, w_{n_{k}} - y_{n_{k}} \rangle + \lambda _{n_{k}} \langle Aw_{n_{k}}, y - w_{n_{k}} \rangle . \end{aligned}$$

This implies that

$$ \langle w_{n_{k}} - y_{n_{k}}, y - y_{n_{k}} \rangle + \lambda _{n_{k}} \langle Aw_{n_{k}}, y_{n_{k}} - w_{n_{k}} \rangle \leq \lambda _{n_{k}} \langle Aw_{n_{k}}, y - w_{n_{k}} \rangle \quad \forall y \in C. $$
(3.20)

Fix \(y \in C\) and let \(k \to \infty \) in (3.20). Since \(\|w_{n_{k}} - y_{n_{k}}\|\to 0\) and \(\liminf_{k\to \infty }\lambda _{n_{k}}>0\), we have

$$\begin{aligned} 0 \leq \liminf_{k\to \infty }\langle Aw_{n_{k}}, y - w_{n_{k}} \rangle\quad \forall y \in C. \end{aligned}$$
(3.21)

Now let \(\{\epsilon _{k}\}\) be a sequence of decreasing nonnegative numbers such that \(\epsilon _{k} \to 0\) as \(k \to \infty \). For each \(\epsilon _{k}\), we denote by N the smallest positive integer such that

$$ \langle Aw_{n_{k}}, y - w_{n_{k}} \rangle + \epsilon _{k} \geq 0\quad \forall k \geq N, $$
(3.22)

where the existence of N follows from (3.21). This means that

$$ \langle Aw_{n_{k}}, y + \epsilon _{k}t_{n_{k}} - w_{n_{k}} \rangle \geq 0\quad \forall j \geq N, $$

for some \(t_{n_{k}} \in H\) satisfying \(1 = \langle Aw_{n_{k}}, t_{n_{k}} \rangle \) (since \(Aw_{n_{k}} \neq 0\)). Using the fact that A is pseudomonotone, then we have

$$\begin{aligned} \bigl\langle A(y+\epsilon _{k}t_{n_{k}}), x + \epsilon _{k}t_{n_{k}} - x_{n_{k}} \bigr\rangle \geq 0\quad \forall j \geq N. \end{aligned}$$

Hence

$$\begin{aligned} \langle Ay, y - x_{n_{k}}\rangle \geq \bigl\langle Ay - A(y+\epsilon _{k}t_{n_{k}}), y+\epsilon _{k}t_{n_{k}} - x_{n_{k}} \bigr\rangle - \epsilon _{k}\langle Ay, t_{n_{k}} \rangle\quad \forall k \geq N. \end{aligned}$$
(3.23)

Since \(\epsilon _{k} \to 0\) and A is continuous, the right-hand side of (3.22) tends to zero and thus we obtain

$$ \liminf_{k\to \infty }\langle Ay, y - w_{n_{k}} \rangle \geq 0 \quad \forall y \in C. $$

Hence

$$ \langle Ay, y - p\rangle = \lim_{k\to \infty }\langle Ay, y - w_{n_{k}} \rangle \geq 0 \quad \forall y \in C. $$

Thus from Lemma 2.5, we obtain \(p \in VI(C,A)\). Moreover, since \(\|z_{n_{k}}-Tz_{n_{k}}\|\to 0\), it follows from Remark (2.2)(c) that \(p \in F(T)\). Therefore \(p \in Sol:= VI(C,A)\cap F(T)\).

Now we show that \(\{x_{n}\}\) converges strongly to \(\bar{x} = P_{Sol}f(\bar{x})\). To do this, it suffices to show that

$$ \limsup_{n \rightarrow \infty }\bigl\langle f(\bar{x}) -\bar{x}, x_{n+1}- \bar{x} \bigr\rangle \leq 0. $$

Choose a subsequence \(\{x_{n_{k}}\}\) of \(\{x_{n}\}\) such that

$$ \limsup_{n \rightarrow \infty }\bigl\langle f(\bar{x}) -\bar{x}, x_{n+1} - \bar{x} \bigr\rangle = \lim_{k \rightarrow \infty }\bigl\langle f(\bar{x}) - \bar{x}, x_{n_{k}+1} -\bar{x} \bigr\rangle . $$

Since \(\|x_{n_{k}+1} -x_{n}\| \rightarrow 0\) and \(x_{n_{k}} \rightharpoonup p\), we have from (2.1) that

$$\begin{aligned} \limsup_{n \rightarrow \infty }\bigl\langle f(\bar{x}) -\bar{x},x_{n+1} - \bar{x} \bigr\rangle =& \lim_{k \rightarrow \infty }\bigl\langle f(\bar{x}) - \bar{x}, x_{n_{k}+1} -\bar{x} \bigr\rangle \\ =& \bigl\langle f(\bar{x}) -\bar{x}, p -\bar{x} \bigr\rangle \leq 0. \end{aligned}$$
(3.24)

Hence, putting \(x^{*} = \bar{x}\) in Lemma 3.6 and using Lemma 2.6(ii) and (3.24), we deduce that \(\|x_{n} - \bar{x}\| \rightarrow 0\) as \(n \rightarrow \infty \). This implies that \(\{x_{n}\}\) converges strongly to \(\bar{x} = P_{Sol}f(\bar{x})\).

CASE B: Suppose \(\{\Gamma _{n}\}\) is not eventually decreasing. Hence, we can find a subsequence \(\{\Gamma _{n_{k}}\}\) of \(\{\Gamma _{n}\}\) such that \(\Gamma _{n_{k}} \leq \Gamma _{n_{k}+1}\), for all \(k \geq 1\). Then we can define a subsequence \(\{\Gamma _{{\tau (n)}+1}\}\) as in Lemma 2.7 so that

$$ \max \{\Gamma _{\tau (n)},\Gamma _{n}\} \leq \Gamma _{\tau (n)+1}, \quad \forall n \geq n_{0}. $$

Moreover, \(\{\tau (n)\}\) is a non-decreasing sequence such that \(\tau (n) \to \infty \) as \(n \to \infty \) and \(\Gamma _{\tau (n)} \leq \Gamma _{{\tau (n)}+1}\) for all \(n \geq n_{0}\). Let \(x^{*} \in Sol\), then from Lemma 3.6, we have

$$\begin{aligned} \bigl\Vert x_{{\tau (n)}+1}- x^{*} \bigr\Vert ^{2} \leq & \biggl[1 - \frac{2\alpha _{\tau (n)}(1-\rho )}{1-\alpha _{\tau (n)}\rho } \biggr] \bigl\Vert x_{ \tau (n)} -x^{*} \bigr\Vert ^{2} \\ &{}+ \frac{2\alpha _{\tau (n)}(1-\rho )}{1-\alpha _{\tau (n)}\rho }\times \frac{\langle f(x^{*}) - x^{*}, x_{{\tau (n)}+1} -x^{*} \rangle }{1-\rho } \\ & {}+ \frac{\alpha _{\tau (n)}^{2}}{1-\alpha _{\tau (n)}\rho } \bigl\Vert x_{ \tau (n)} -x^{*} \bigr\Vert ^{2} \\ &{}+ \frac{\alpha _{\tau (n)}}{1-\alpha _{\tau (n)}\rho }\times \frac{\theta _{\tau (n)}}{\alpha _{n}} \Vert x_{\tau (n)}- x_{{\tau (n)}-1} \Vert M, \end{aligned}$$
(3.25)

for some \(M >0\). Following a similar process to CASE A, we have

$$\begin{aligned} \lim_{n \rightarrow \infty } \Vert z_{\tau (n)} -w_{\tau (n)} \Vert =& \lim_{n \rightarrow \infty } \Vert y_{\tau (n)} -w_{\tau (n)} \Vert \\ =& \lim_{n \rightarrow \infty } \Vert w_{\tau (n)} -x_{\tau (n)} \Vert = \lim_{n \rightarrow \infty } \Vert x_{{\tau (n)}+1} -x_{\tau (n)} \Vert =0. \end{aligned}$$

Since \(\{x_{\tau (n)}\}\) is bounded, there exists a subsequence of \(\{x_{\tau (n)}\}\) still denoted by \(\{x_{\tau (n)}\}\) which converges weakly to \(\bar{x} \in C\) and

$$\begin{aligned} \limsup_{n \rightarrow \infty }\bigl\langle f\bigl(x^{*}\bigr) -x^{*}, x_{{\tau (n)}+1} -x^{*} \bigr\rangle =& \lim _{n \rightarrow \infty }\bigl\langle f\bigl(x^{*}\bigr) -x^{*}, x_{\tau (n)+1} -x^{*} \bigr\rangle \\ \leq & \bigl\langle f\bigl(x^{*}\bigr) -x^{*}, \bar{x} -x^{*} \bigr\rangle \leq 0. \end{aligned}$$
(3.26)

Furthermore, since \(\|x_{\tau (n)} -x^{*}\|^{2} \leq \|x_{{\tau (n)}+1} -x^{*}\|^{2}\), from (3.25), we have

$$\begin{aligned} 0 \leq & \biggl[1 - \frac{2\alpha _{\tau (n)}(1-\rho )}{1-\alpha _{\tau (n)}\rho } \biggr] \bigl\Vert x_{ \tau (n)} -x^{*} \bigr\Vert ^{2} + \frac{2\alpha _{\tau (n)}(1-\rho )}{1-\alpha _{\tau (n)}\rho }\times \frac{\langle f(x^{*}) - x^{*}, x_{{\tau (n)}+1} -x^{*} \rangle }{1-\rho } \\ & {}+ \frac{\alpha _{\tau (n)}^{2}}{1-\alpha _{\tau (n)}\rho } \bigl\Vert x_{ \tau (n)} -x^{*} \bigr\Vert ^{2} + \frac{\alpha _{\tau (n)}}{1-\alpha _{\tau (n)}\rho }\times \frac{\theta _{\tau (n)}}{\alpha _{n}} \Vert x_{\tau (n)}- x_{{\tau (n)}-1} \Vert M - \bigl\Vert x_{\tau (n)} -x^{*} \bigr\Vert ^{2}. \end{aligned}$$

Hence

$$\begin{aligned} \frac{2(1-\rho )}{1-\alpha _{\tau (n)}\rho } \bigl\Vert x_{\tau (n)} -x^{*} \bigr\Vert ^{2} \leq & \frac{2(1-\rho )}{1-\alpha _{\tau (n)}\rho }\times \frac{\langle f(x^{*}) - x^{*}, x_{{\tau (n)}+1} -x^{*} \rangle }{1-\rho } \\ &{}+ \frac{\alpha _{\tau (n)}}{1-\alpha _{\tau (n)}\rho } \bigl\Vert x_{\tau (n)} -x^{*} \bigr\Vert ^{2} \\ & {}+ \frac{1}{1-\alpha _{\tau (n)}\rho }\times \frac{\theta _{\tau (n)}}{\alpha _{n}} \Vert x_{\tau (n)}- x_{{\tau (n)}-1} \Vert M. \end{aligned}$$

Therefore from (3.26), we have

$$\begin{aligned} \lim_{n \rightarrow \infty } \bigl\Vert x_{\tau (n)} -x^{*} \bigr\Vert = 0. \end{aligned}$$

As a consequence, we obtain, for all \(n \geq n_{0}\),

$$ 0 \leq \bigl\Vert x_{n} -x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x_{\tau (n)+1}-x^{*} \bigr\Vert ^{2}, $$

hence \(\lim_{n \rightarrow \infty }\|x_{n} -x^{*}\| =0\). This implies that \(\{x_{n}\}\) converges to \(x^{*}\). This completes the proof. □

Remark 3.8

  1. (a)

    We emphasize here that the assumption that A is pseudomonotone is more general than the monotone condition used by [11, 17, 41, 44] for PCM.

  2. (b)

    Also, the convergence result is proved without any prior condition on the stepsize. This improves the results of [10, 11, 44, 45] and many other results in this direction.

  3. (c)

    The strong convergence result proved in this paper is more desirable in optimization theory than the weak convergence counterparts; see [3].

4 Numerical experiments

In this section, we will test the numerical efficiency of the proposed Algorithm 3.3 by solving some variational inequality problems. We shall compare our method Algorithm 3.3 with other inertial projection contraction methods proposed in [10, 11, 44]. Our interest is to investigate how the line search process improve the numerical efficiency of Algorithm 3.3. It should be noted that the methods proposed in [10, 11, 44] required prior estimate of the Lipschitz constant of the cost operator. Moreover, the methods in [11, 44] converge for monotone variational inequalities, thus may not be applied for pseudomonotone variational inequalities. All numerical computations are carried out using a Lenovo PC with the following specification: Intel(R)core i7-600, CPU 2.48GHz, RAM 8.0GB, MATLAB version 9.5 (R2019b).

Example 4.1

We consider the variational inequality problem given in [16] which is a HP-hard model in finite dimensional space. The cost operator \(A:\mathbb{R}^{m} \to \mathbb{R}^{m}\) is defined by \(A(x) = Mx + q\), with \(M = BB^{T}+S+D\) where \(B,S,D \in \mathbb{R}^{m \times m}\) are randomly generated matrices such that S is skew symmetric, D is a positive definite diagonal matrix and \(q=0\). In this case, the operator A is monotone and Lipschitz continuous with \(L = \max (eig(BB^{T}+S+D))\). The feasible set is described as linear constraints \(Qx \leq b\) for some \(Q \in \mathbb{R}^{k\times m}\) and a random vector \(b \in \mathbb{R}^{k}\) with nonnegative entries. We also define the mapping \(T:\mathbb{R}^{m} \to \mathbb{R}^{m}\) by \(Tx = (\frac{-3x_{1}}{2},\frac{-3x_{2}}{2},\dots , \frac{-3x_{m}}{2} )\), which is \(\frac{1}{5}\)-strictly pseudocontractive and \(F(T) = \{0\}\). It is easy to see that \(Sol = \{0\}\). We compare the performance of Algorithm 3.3 with Algorithm 1.5 of [11], Algorithm 3.1 of Cholamjiak et al. [10] and Algorithm 1 of Thong et al. [44] which are also versions of projection and contraction method. To validate the convergence of all the algorithms, we use \(\|x_{n+1}-x_{n}\| < 10^{-5}\) as stopping criterion. We choose the following parameters for Algorithm 3.3: \(\theta _{n} =\frac{1}{5n+2}\), \(\alpha _{n} = \frac{1}{\sqrt{5n+2}}\), \(\beta _{n} = \frac{1}{2}-\frac{1}{\sqrt{5n+2}}\), \(\delta _{n} = \frac{1}{5}+\frac{2n}{5n+2}\), \(\gamma =0.85\), \(l = 0.5\), \(\sigma =2\), \(\mu = 0.1\). The projection onto C is easily solved by using the FMINCON Optimization solver in MATLAB Optimization Toolbox. Since the other algorithms require prior estimate of the Lipschitz constant, we choose the following parameters for the algorithms:

  • for Algorithm 1.5 of Dong et al. [11], we take \(\alpha _{n} = \frac{1}{5n+2}\), \(\lambda = \frac{1}{2L}\), \(\gamma = 0.85\), and \(\tau _{n} = \frac{1}{2}\),

  • for Algorithm 3.1 in Cholamjiak et al. [10], we take \(\alpha _{n} = \frac{1}{5n+2}\), \(\lambda = \frac{1}{2L}\), \(\gamma = 0.85\), \(\theta _{n} = \frac{1}{2} - \frac{1}{(5n+2)^{0.5}}\) and \(\beta _{n} = \frac{1}{(5n+2)^{0.5}}\),

  • for Algorithm 1 in Thong et al. [44], we take \(\alpha _{n} = \frac{1}{5n+2}\), \(\lambda = \frac{1}{2L}\), \(\gamma = 0.85\), \(\beta _{n} =\frac{1}{(5n+2)^{0.5}}\) and \(f(x) = \frac{x}{2}\).

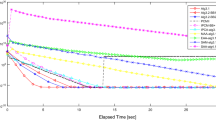
The numerical results are presented in Table 1 and Fig. 1.

Figure 1
figure 1

Example 4.1, Top Left: Case I; Top Right: Case II; Bottom Left: Case III; Bottom Right: Case IV

Full size image
Table 1 Computation result for Example 4.1
Full size table

From the numerical results, it is clear that our Algorithm 3.3 solves the HP-hard problem with a smaller number of iterations and CPU-time (second). This shows the advantage of using a line search process for selecting the stepsize in Algorithm 3.3 rather than a fixed stepsize which depends on the estimate of the Lipschitz constant as used in [10, 11, 44].

Example 4.2

In this example, we consider a variational inequality problem in an infinite dimensional space where A is a pseudomonotone and Lipschitz continuous operator but not monotone. We only compare our Algorithm 3.3 with Algorithm 3.1 of Cholamjiak et al. [10] which is strongly convergent and also solves the pseudomonotone variational inequality problem.

Let \(H=L_{2}([0,1])\) endowed with inner product \(\langle x,y \rangle = \int _{0}^{1}x(t)y(t)\,dt\) for all \(x,y \in L_{2}([0,1])\) and norm \(\|x\| = (\int _{0}^{1}|x(t)|^{2}\,dt )^{\frac{1}{2}}\) for all \(x \in L_{2}([0,1])\). Let

$$ C = \bigl\{ x \in L_{2}\bigl([0,1]\bigr):\langle y,x\rangle \leq a \bigr\} , $$

where \(y= 3t^{2}+9\) and \(a =1\). Then we can define the projection \(P_{C}\) as

$$ P_{C}(x) = \textstyle\begin{cases} \frac{a-\langle y,x\rangle }{ \Vert y \Vert ^{2}} &\text{if } \langle y,x \rangle >a, \\ x, & \text{otherwise}. \end{cases} $$

Define the operator \(B:C \rightarrow \mathbb{R}\) by \(B(u) = \frac{1}{1+\|u\|^{2}}\) and \(F: L^{2}([0,1]) \rightarrow L^{2}([0,1])\) as the Volterra integral operator defined by \(F(u)(t) = \int _{0}^{t} u (s)\,ds\) for all \(u \in L^{2}([0,1])\) and \(t\in [0,1]\). F is bounded, linear and monotone with \(L = \frac{\pi }{2}\) (cf. Exercise 20.12 in [4]). Let \(A: L^{2}([0,1])\rightarrow L^{2}([0,1])\) be defined by

$$ A(u) (t) = \bigl(B(u)F(u)\bigr) (t). $$

Suppose \(\langle Au, v-u \rangle \geq 0\) for all \(u,v \in C\), then \(\langle Fu, v-u \rangle \geq 0\). Hence

$$\begin{aligned} \langle Av,v-u \rangle =& \langle BvFv, v-u \rangle \\ =& Bv \langle Fv, v-u \rangle \\ \geq & Bv\bigl(\langle Fv, v-u \rangle - \langle Fu, v-u \rangle \bigr) \\ =& Bv\langle Fv - Fu, v-u \rangle \geq 0. \end{aligned}$$
(4.1)

Thus, A is pseudomonotone. To see that A is not monotone, choose \(v =1\) and \(u =2\), then

$$ \langle Av - Au,v- u \rangle = -\frac{1}{10} < 0. $$

Now consider the VIP in which the underlying operator A is as defined above. Let \(T:L^{2}([0,1]) \to L^{2}([0,1])\) be defined by \(Tx(t) = x(t)\) which is 0-strictly pseudocontractive. Clearly, \(Sol = \{0\}\). We choose the following parameters for Algorithm 3.3: \(\alpha _{n} = \frac{1}{n+4}\), \(\theta _{n} =\alpha _{n}^{2}\), \(\beta _{n} = \frac{n+1}{n+4}\), \(\delta _{n} = \frac{2n}{4n+1}\), \(l = 0.28\), \(\mu = 0.57\), \(\sigma = 2\), \(\gamma =1\). We take \(\beta _{n} =\frac{1}{n+4}\), \(\alpha _{n} = \alpha _{n}^{2}\), \(\lambda = \frac{1}{2\pi }\), \(\gamma = 1\) and \(f(x) = x\) in Algorithm 3.1 of Cholamjiak et al. [10]. Using \(\|x_{n+1} -x_{n}\|<10^{-5}\) as stopping criterion, we plot the graphs of \(\|x_{n+1}-x_{n}\|\) against number of iterations with the following initial points:

Case I::

\(x_{0} = \frac{\exp (2t)}{9}\), \(x_{1}= \frac{\exp (3t)}{7}\),

Case II::

\(x_{0} = \sin (2t)\), \(x_{1}= \cos (5t)\),

Case III::

\(x_{0} =\exp (2t)\), \(x_{1} = \sin (7t)\),

Case IV::

\(x_{0} = t^{2} +3t-1\), \(x_{1} = (2t+1)^{2}\).

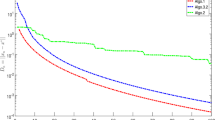
The numerical results can be found in Table 2 and Fig. 2. The numerical results also show that Algorithm 3.3 performs better in terms of number of iterations and CPU time taken for computation than Algorithm 3.1 of [10]. This also signifies the advantage of using dynamic stepsize rather than a fixed stepsize which depends on an estimate of the Lipschitz constant.

Figure 2
figure 2

Example 4.2, Top Left: Case I; Top Right: Case II; Bottom Left: Case III; Bottom Right: Case IV

Full size image
Table 2 Computation result for Example 4.2
Full size table

5 Conclusion

In this paper, we introduced a new self-adaptive inertial projection and contraction method for approximating solutions of variational inequalities which are also fixed points of a strictly pseudocontarctive mapping in real Hilbert space. A strong convergence result is proved without prior estimate of the Lipschitz constant of the cost operator for the variational inequality problem. This is very important in the case where the Lipschitz constant cannot be estimated or very difficult to estimate. Furthermore, we provided some numerical examples to show the accuracy and efficiency of the proposed method. This result improves and extends the corresponding results of [11, 17, 26, 41, 42, 44, 45] and other important results in the literature.