1 Introduction

The well known Hermite–Hadamard inequality for a convex function \(\varPsi : U\rightarrow \mathbb{R}\) on an interval U of real numbers, with \({\phi ,\varphi }\in U\) and \(\phi <\varphi \) is given by

$$ \varPsi \biggl(\frac{\phi +\varphi }{2} \biggr)\leq \frac{1}{\varphi -\phi } \int _{\phi }^{\varphi }\varPsi (\xi )\,d\xi \leq \frac{\varPsi (\phi )+\varPsi (\varphi )}{2}. $$
(1.1)

Numerous scientists examined this inequality and published various generalizations and extensions by using fractional integrals and derivatives [5, 8, 15, 16, 18, 19, 23, 25–29, 32, 33]. The theories of k- and \((k,s)\)-fractional operators are the more generalized way to express fractional calculus operators (see [21, 22, 24]). The classical fractional operators become special cases of such theories. Considering late developments in the theory of differential and integral equations, it is getting very hard to ignore the existence of integral inequalities that help determine the bounds on unknown functions. Applications of integral inequalities are important in various fields of science, like mathematics, physics, engineering, among others, we especially notice initial-value problems, the stability of linear transformation, integral differential equations, and impulse equations. We refer the readers [1, 3, 4, 6, 7, 12, 13, 20] for such applications in several branches of mathematics and the references therein. Firstly, we give some key definitions and mathematical fundamentals of the theory of fractional calculus which are utilized in this paper.

Definition 1.1

([14])

A function \(\psi :[\phi ,\varphi ]\to \mathbb{R}\) is called convex if the following inequality holds on an interval \([\phi ,\varphi ]\subseteq \mathbb{R}\):

$$ \psi \bigl(\nu l+(1-\nu )r\bigr)\leq \nu \psi (l)+(1-\nu )\psi (r), $$

where \(l,r \in [\phi ,\varphi ]\), and \(\nu \in [0,1]\).

Definition 1.2

([24])

Let ψ be a continuous function on a finite interval \([\phi ,\varphi ]\). Then the left and right \((k,s)\)-Riemann–Liouville fractional integrals of order \(\chi >0\) are defined by

$$\begin{aligned} F_{\phi ^{+},k}^{\chi ,s}\psi (\tau )= \frac{(s+1)^{1-\frac{\chi }{k}}}{k\varGamma _{k}(\chi )} \int _{ \phi }^{\tau } \bigl(\tau ^{s+1}-\wp ^{s+1}\bigr)^{\frac{\chi }{k}-1}\wp ^{s}\psi ( \wp )\,d\wp , \end{aligned}$$

and

$$\begin{aligned} F_{\varphi ^{-},k}^{\chi ,s}\psi (\tau )= \frac{(s+1)^{1-\frac{\chi }{k}}}{k\varGamma _{k}(\chi )} \int _{ \tau }^{\varphi } \bigl(\wp ^{s+1}-\tau ^{s+1}\bigr)^{\frac{\chi }{k}-1}\wp ^{s} \psi (\wp )\,d\wp , \end{aligned}$$

respectively, where \(k>0\), \(s\in \mathbb{R}\setminus \{-1\}\).

Definition 1.3

([10])

The left and right conformable fractional integral operators \(\mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\) and \(\mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\) of order \(\beta \in \mathbb{C}\), such that \(\mathfrak{Re}(\beta )>0\) and \(0<\chi \leq 1\), for \(\psi \in L_{1}[\phi ,\varphi ]\) are defined by

$$ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\psi (\wp ) = \frac{1}{\varGamma (\beta )} \int _{\phi }^{\wp } \biggl( \frac{(\wp -\phi )^{\chi }-(\nu -\phi )^{\chi }}{\chi } \biggr)^{\beta -1}( \nu -\phi )^{\chi -1}\psi (\nu )\,d\nu $$

and

$$ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\wp ) = \frac{1}{\varGamma (\beta )} \int _{\wp }^{\varphi } \biggl( \frac{(\varphi -\wp )^{\chi }-(\varphi -\nu )^{\chi }}{\chi } \biggr)^{ \beta -1} (\varphi -\nu )^{\chi -1}\psi (\nu )\,d\nu , $$

respectively, where Γ is the Euler gamma function.

Definition 1.4

([21])

The generalized left and right k-conformable fractional integral operators \(\mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\) and \(\mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\) of order \(\beta \in \mathbb{C}\), \(\mathfrak{Re}(\beta )>0\), \(k>0\) and \(0<\chi \leq 1\), for \(\psi \in L_{1,\chi }[\phi ,\varphi ]\) are defined by

$$ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\psi (\wp ) = \frac{1}{k\varGamma _{k}(\beta )} \int _{\phi }^{\wp } \biggl( \frac{(\wp -\phi )^{\frac{\chi }{k}}-(\nu -\phi )^{\frac{\chi }{k}}}{\chi } \biggr)^{\frac{\beta }{k}-1}(\nu -\phi )^{\frac{\chi }{k}-1}\psi ( \nu )\,d\nu $$

and

$$ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\wp ) = \frac{1}{k\varGamma _{k}(\beta )} \int _{\wp }^{\varphi } \biggl( \frac{(\varphi -\wp )^{\frac{\chi }{k}} -(\varphi -\nu )^{\frac{\chi }{k}}}{\chi } \biggr)^{\frac{\beta }{k}-1}( \varphi -\nu )^{\frac{\chi }{k}-1}\psi (\nu )\,d\nu , $$

respectively.

Definition 1.5

([11])

A function \(\psi :D\subset \mathbb{R^{+}}\to \mathbb{R^{+}}\) is called geometric–arithmetically s-convex on D if \(s\in (0,1]\), \(\forall \phi ,\varphi \in D\) and \(\nu \in [0,1]\), we have

$$ \psi \bigl(\phi ^{\nu }\varphi ^{1-\nu }\bigr)\leq \nu ^{s}\psi (\phi )+(1-\nu )^{s} \psi (\varphi ). $$

We use the following notations in our upcoming results:

  • \(SX(h,D)\)—class of h-convex functions;

  • \(SV(h,D)\)—class of h-concave functions;

  • \(K_{s}^{2}\)—s-convex functions in the second sense;

  • \(P(I)\)—quasiconvex functions.

Sanja Varošanec presented the class of convex functions in [31] as follows:

Definition 1.6

Let \(h:D\subset \mathbb{R}\rightarrow \mathbb{R}\) be a positive function. We say that \(\psi : D\subset \mathbb{R}\rightarrow \mathbb{R}\) is h-convex, if ψ is nonnegative and \(\forall \phi ,\varphi \in D\), \(\nu \in (0,1)\), we have

$$ \psi \bigl(\nu \phi + (1-\nu )\varphi \bigr)\leq h(\nu )\psi (\phi ) + h(1-\nu ) \psi (\varphi ) . $$
(1.2)

If the inequality in (1.2) is reversed, then ψ will be h-concave, i.e., \(\psi \in SV(h,D)\). If \(h(\nu )=\nu \), then all nonnegative convex functions belong to \(SX(h,D)\) and all nonnegative concave functions belong to \(SV(h,D)\); if \(h(\nu )=1\), then \(SX(h,D)\supseteq P(D)\) and if \(h(\nu )=\nu ^{s}\), where \(s\in (0,1)\), then \(SX(h,D)\supseteq K_{s}^{2}\).

The formal definition of the beta function given in [2] is stated as follows:

Definition 1.7

The classical beta function, also called the Euler integral of the first kind, is a special function defined by

$$\begin{aligned} \textbf{B}(x,y)= \int _{0}^{1}t^{x-1}(1-t)^{y-1} \,dt,\quad \mathfrak{R}(x)>0, \mathfrak{R}(y)>0. \end{aligned}$$
(1.3)

Definition 1.8

([17])

The integral form of the hypergeometric function is given as

$$ \mathfrak{_{2}F}_{1}(u,v;c;z)=\frac{1}{\mathbf{B}(v,c-v)} \int _{0}^{1}\wp ^{v-1}(1-\wp )^{c-v-1}(1-z\wp )^{-u}\,d\wp , $$

for \(|z|<1\), \(\mathbb{R}(c)> \mathbb{R}(v)>0\).

Definition 1.9

([9])

Consider an interval \(J \subset (0,\infty )=\mathbb{R+}\) and \((s+1)\in \mathbb{R}\setminus \{0\}\). A function \(\psi : J\rightarrow \mathbb{R}\) is called \((s+1)\)-convex if

$$ \psi \bigl(\bigl[\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1} \bigr]^{\frac{1}{s+1}}\bigr)\leq \wp \psi (\phi )+(1-\wp )\psi (\varphi ), $$

for all \(\phi , \varphi \in J\) and \(\wp \in [0,1]\).

Lemma 1.10

([30])

Let \(\psi : [\phi ,\varphi ] \rightarrow \mathbb{R}\)be a differentiable function on \((\phi ,\varphi )\)with \(\phi < \varphi \)and \(\psi \in L_{1}[\phi ,\varphi ]\). Then the following equality for fractional conformable integrals holds:

$$\begin{aligned} & \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\beta }\varGamma (\beta +1)}{2(\varphi -\phi )^{\chi \beta }} \bigl[\mathfrak{J}^{\chi ,\beta }_{\phi ^{+}} \psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr] \\ &\quad =\frac{(\varphi -\phi )}{2} \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{ \beta }-\bigl(1-(1-\wp )^{\chi } \bigr)^{\beta } \bigr]\psi ^{\prime }\bigl(\wp \phi +(1-\wp ) \varphi \bigr)\,d\wp . \end{aligned}$$

2 Inequalities involving \((k,s)\)-Riemann–Liouville fractional integral

This section includes mean-type inequalities for \((k,s)\)-Riemann–Liouville fractional integral operators of order \(\chi >0\).

Theorem 2.1

Let \(\psi : [\phi ,\varphi ]\subset (0,\infty )\rightarrow \mathbb{R}\)be an \((s+1)\)-convex function such that \(\psi \in L[\phi ,\varphi ]\). Then

  1. (i)

    for \(s > -1\), we have

    $$\begin{aligned} \psi \biggl( \biggl[\frac{\phi ^{s+1}+\varphi ^{s+1}}{2} \biggr]^{ \frac{1}{s+1}} \biggr)&\leq \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s}\psi ( \varphi )+F_{\varphi ^{-},k}^{ \chi ,s}\psi (\phi ) \bigr] \\ &\leq \frac{\psi (\phi )+\psi (\varphi )}{2}, \end{aligned}$$
    (2.1)

    and

  2. (ii)

    for \(s < -1\), we have

    $$\begin{aligned} \psi \biggl( \biggl[\frac{\phi ^{s+1}+\varphi ^{s+1}}{2} \biggr]^{ \frac{1}{s+1}} \biggr) &\leq \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\phi ^{s+1}-\varphi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s}\psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s}\psi (\phi ) \bigr] \\ &\leq \frac{\psi (\phi )+\psi (\varphi )}{2}. \end{aligned}$$

Proof

(i) Since ψ is an \((s+1)\)-convex function, we can write

$$\begin{aligned}& \psi \bigl(\bigl[\nu x^{s+1}+(1-\nu )y^{s+1} \bigr]^{\frac{1}{s+1}}\bigr)\leq \nu \psi (x)+(1- \nu )\psi (y), \end{aligned}$$
(2.2)
$$\begin{aligned}& \psi \bigl(\bigl[(1-\nu ) x^{s+1}+\nu y^{s+1}\bigr]^{\frac{1}{s+1}}\bigr)\leq (1-\nu ) \psi (x)+\nu \psi (y). \end{aligned}$$
(2.3)

Let \(\nu =\frac{1}{2}\), then

$$\begin{aligned} \psi \biggl(\biggl[\frac{x^{s+1}+y^{s+1}}{2}\biggr]^{\frac{1}{s+1}}\biggr) \leq \frac{\psi (x)+\psi (y)}{2}. \end{aligned}$$

Assume \(x^{s+1}=\nu \phi ^{s+1}+(1-\nu )\varphi ^{s+1}\) and \(y^{s+1}=(1-\nu )\phi ^{s+1}+\nu \varphi ^{s+1}\), then we have

$$\begin{aligned} &\psi \biggl(\biggl[\frac{\phi ^{s+1}+\varphi ^{s+1}}{2}\biggr]^{\frac{1}{s+1}}\biggr) \\ &\quad \leq \frac{1}{2}\bigl[\psi \bigl(\bigl[\nu \phi ^{s+1}+(1-\nu ) \varphi ^{s+1}\bigr]^{ \frac{1}{s+1}}\bigr)+\psi \bigl(\bigl[\phi ^{s+1}(1-\nu )+\nu \varphi ^{s+1}\bigr]^{ \frac{1}{s+1}} \bigr)\bigr]. \end{aligned}$$

Multiplying the above inequality by \(\nu ^{\frac{\chi }{k}-1}\) and then integrating with respect to ν over \([0,1]\), we get

$$\begin{aligned} & \frac{k}{\chi }\psi \biggl(\biggl[\frac{\phi ^{s+1}+\varphi ^{s+1}}{2} \biggr]^{ \frac{1}{s+1}}\biggr) \\ &\quad \leq \frac{1}{2} \biggl[ \int _{0}^{1}\nu ^{\frac{\chi }{k}-1}\bigl[ \psi \bigl(\bigl[\nu \phi ^{s+1}+(1-\nu )\varphi ^{s+1} \bigr]^{\frac{1}{s+1}}\bigr)\bigr]\,d\nu \\ &\qquad {}+ \int _{0}^{1}\nu ^{\frac{\chi }{k}-1}\bigl[\psi \bigl(\bigl[\phi ^{s+1}(1- \nu )+\nu \varphi ^{s+1} \bigr]^{\frac{1}{s+1}}\bigr)\bigr]\,d\nu \biggr]. \end{aligned}$$
(2.4)

Now, let \(\nu \phi ^{s+1}+(1-\nu )\varphi ^{s+1}=u^{s+1}\) and \((1-\nu )\phi ^{s+1}+\nu \varphi ^{s+1}=v^{s+1}\), then (2.4) becomes

$$ \psi \biggl(\biggl[\frac{\phi ^{s+1}+\varphi ^{s+1}}{2}\biggr]^{\frac{1}{s+1}} \biggr) \leq \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s}\psi ( \varphi )+F_{\varphi ^{-},k}^{ \chi ,s}\psi (\phi ) \bigr]. $$
(2.5)

Now, by replacing \(x=\phi \), \(y=\varphi \) in (2.2) and (2.3), respectively, then adding, we have

$$ \psi \bigl(\bigl[\nu \phi ^{s+1}+(1-\nu )\varphi ^{s+1}\bigr]^{\frac{1}{s+1}}\bigr)+\psi \bigl(\bigl[(1- \nu )\phi ^{s+1}+\nu \varphi ^{s+1}\bigr]^{\frac{1}{s+1}}\bigr) \leq \bigl[\psi ( \phi )+\psi (\varphi )\bigr]. $$
(2.6)

Multiplying (2.6) by \(\nu ^{\frac{\chi }{k}-1}\) and then integrating over \([0,1]\), we have

$$ \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s} \psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s}\psi (\phi ) \bigr] \leq \frac{\psi (\phi )+\psi (\varphi )}{2}. $$
(2.7)

Now, from (2.5) and (2.7), we get the desired result. This completes the proof of (i).

(ii) The proof of (ii) is similar to (i), so is omitted. Thus, the proof of the theorem is completed. □

Example 2.2

By plotting the graphs of (2.1) for a convex function \(\psi (\wp )= e^{\wp }\), we check that both inequalities are valid. It is known that the \((k,s)\)-Riemann–Liouville fractional integrals of this function for \(s=0\) are given by

$$\begin{aligned} F_{\phi ^{+},k}^{\chi ,0}e^{\varphi }= \frac{1}{k\varGamma _{k}(\chi )} \int _{\phi }^{\varphi } (\varphi -\wp )^{\frac{\chi }{k}-1}e^{ \wp } \,d\wp \end{aligned}$$
(2.8)

and

$$\begin{aligned} F_{\varphi ^{-},k}^{\chi ,0}e^{\phi }= \frac{1}{k\varGamma _{k}(\chi )} \int _{\phi }^{\varphi } (\wp -\phi )^{\frac{\chi }{k}-1}e^{\wp } \,d\wp . \end{aligned}$$
(2.9)

By utilizing these expressions in the double inequality (2.1), we get

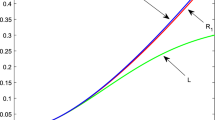
$$\begin{aligned} & 2e^{\frac{\phi +\varphi }{2}} \leq \frac{\chi }{k(\varphi -\phi )^{\frac{\chi }{k}}} \int _{0}^{1}\bigl[( \varphi -\wp )^{\frac{\chi }{k}-1}+(\wp -\phi )^{\frac{\chi }{k}-1}\bigr]e^{ \wp }\,d\wp \leq e^{\phi }+e^{\varphi }. \end{aligned}$$
(2.10)

The three functions given by the left, middle, and right sides of the double inequality (2.10) are plotted in Fig. 1 against \(\chi \in (0,1]\). The graphs of the functions show the validity of dual inequality.

Figure 1
figure 1

The graphs illustrate the validity of the double inequality (2.10) for the case \(\phi = 0\), \(\varphi = 1\), and \(k=1\)

Full size image

Theorem 2.3

Let \(\psi : [\phi ,\varphi ]\subset (0,\infty )\rightarrow \mathbb{R}\)be a differentiable function on \((\phi ,\varphi )\)with \(\phi <\varphi \), \(s\in \mathbb{R}\setminus \{-1\}\)such that \(\psi {'}\in L[\phi ,\varphi ]\), then

  1. (i)

    for \(s>-1\), we have

    $$\begin{aligned} & \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s} \psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s}\psi (\phi ) \bigr] \\ &\quad =\frac{(\varphi ^{s+1}-\phi ^{s+1})}{2(s+1)} \\ &\qquad {}\times \int _{0}^{1} \bigl[(1-\wp )^{\frac{\chi }{k}}-( \wp )^{\frac{\chi }{k}} \bigr] N^{ \frac{1}{s+1}-1}\psi ^{\prime }\bigl[\bigl( \wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1}\bigr)^{\frac{1}{s+1}} \bigr]\,d\wp , \end{aligned}$$

    where \(N=(\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1})\);

  2. (ii)

    for \(s <-1\), we can write

    $$\begin{aligned} & \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\phi ^{s+1}-\varphi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s} \psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s}\psi (\phi ) \bigr] \\ &\quad =\frac{(\phi ^{s+1}-\varphi ^{s+1})}{2(s+1)} \\ &\qquad {}\times \int _{0}^{1} \bigl[(1-\wp )^{\frac{\chi }{k}}-( \wp )^{\frac{\chi }{k}} \bigr] M^{ \frac{1}{s+1}-1}\psi ^{\prime }\bigl[\bigl( \wp \varphi ^{s+1}+(1-\wp )\phi ^{s+1}\bigr)^{\frac{1}{s+1}} \bigr]\,d\wp , \end{aligned}$$

    where \(M=(\wp \varphi ^{s+1}+(1-\wp )\phi ^{s+1})\).

Proof

(i) Consider

$$\begin{aligned} I={}& \int _{0}^{1} \bigl[(1-\wp )^{\frac{\chi }{k}}-( \wp )^{ \frac{\chi }{k}} \bigr] N^{\frac{1}{s+1}-1}\psi ^{\prime }\bigl[\bigl( \wp \phi ^{s+1}+(1- \wp )\varphi ^{s+1}\bigr)^{\frac{1}{s+1}} \bigr]\,d\wp \\ ={}& \int _{0}^{1}(1-\wp )^{\frac{\chi }{k}} N^{\frac{1}{s+1}-1} \psi ^{\prime }\bigl[\bigl(\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1}\bigr)^{\frac{1}{s+1}}\bigr]\,d \wp \\ &{}- \int _{0}^{1}\wp ^{\frac{\chi }{k}} N^{\frac{1}{s+1}-1}\psi ^{\prime }\bigl[\bigl( \wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1}\bigr)^{\frac{1}{s+1}}\bigr]\,d \wp \\ ={}&I_{1}-I_{2} . \end{aligned}$$
(2.11)

Integrating \(I_{1}\) by parts, we get

$$\begin{aligned} I_{1}={}&\frac{s+1}{\varphi ^{s+1}-\phi ^{s+1}}\psi ( \varphi ) \\ &{}-\frac{\chi (s+1)}{k(\varphi ^{s+1}-\phi ^{s+1})} \int _{0}^{1}(1- \wp )^{\frac{\chi }{k}-1}\psi \bigl(\bigl(\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1} \bigr)^{ \frac{1}{s+1}}\bigr)\,d\wp . \end{aligned}$$
(2.12)

Let \(\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1}=u^{s+1}\), then (2.12) becomes

$$\begin{aligned} I_{1}&=\frac{s+1}{\varphi ^{s+1}-\phi ^{s+1}}\psi (\varphi )- \frac{\chi (s+1)^{2}}{k(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}+1}} \int _{\phi }^{\varphi }\bigl(u^{s+1}-\phi ^{s+1}\bigr)^{\frac{\chi }{k}-1}u^{s} \psi (u)\,du \\ &=\frac{s+1}{\varphi ^{s+1}-\phi ^{s+1}}\psi (\varphi )- \frac{(s+1)^{\frac{\chi }{k}+1}\varGamma _{k}(\chi +k)}{(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}+1}} F_{\varphi ^{-},k}^{\chi ,s}\psi (\phi ). \end{aligned}$$

Now, integrating \(I_{2}\) by parts, we have the equation

$$\begin{aligned} I_{2}={}&-\frac{s+1}{\varphi ^{s+1}-\phi ^{s+1}}\psi (\phi ) \\ &{}+\frac{\chi (s+1)}{k(\varphi ^{s+1}-\phi ^{s+1})} \int _{0}^{1} \wp ^{\frac{\chi }{k}-1}\psi \bigl( \bigl(\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1} \bigr)^{ \frac{1}{s+1}}\bigr)\,d\wp . \end{aligned}$$
(2.13)

Let \(\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1}=u^{s+1}\), then (2.13) becomes

$$\begin{aligned} I_{2}&=-\frac{s+1}{\varphi ^{s+1}-\phi ^{s+1}}\psi (\phi )+ \frac{\chi (s+1)^{2}}{k(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}+1}} \int _{\phi }^{\varphi }\bigl(\varphi ^{s+1}-u^{s+1} \bigr)^{ \frac{\chi }{k}-1}u^{s}\psi (u)\,du \\ &=-\frac{s+1}{\varphi ^{s+1}-\phi ^{s+1}}\psi (\phi )+ \frac{(s+1)^{\frac{\chi }{k}+1}\varGamma _{k}(\chi +k)}{(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}+1}} F_{\phi ^{+},k}^{\chi ,s} \psi (\varphi ). \end{aligned}$$

Now, by using the values of \(I_{1}\) and \(I_{2}\) in (2.11), we get

$$\begin{aligned} I={}&\frac{s+1}{\varphi ^{s+1}-\phi ^{s+1}}\psi (\varphi )- \frac{(s+1)^{\frac{\chi }{k}+1}\varGamma _{k}(\chi +k)}{(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}+1}} F_{\varphi ^{-},k}^{\chi ,s}\psi (\phi ) \\ &{}+\frac{s+1}{\varphi ^{s+1}-\phi ^{s+1}}\psi (\phi )- \frac{(s+1)^{\frac{\chi }{k}+1}\varGamma _{k}(\chi +k)}{(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}+1}} F_{\phi ^{+},k}^{\chi ,s} \psi (\varphi ) \\ ={}& \frac{(s+1)(\psi (\phi )+\psi (\varphi ))}{\varphi ^{s+1}-\phi ^{s+1}}- \frac{(s+1)^{\frac{\chi }{k}+1}\varGamma _{k}(\chi +k)}{(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}+1}} \bigl[F_{\phi ^{+},k}^{\chi ,s} \psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s}\psi (\phi ) \bigr], \end{aligned}$$

which gives

$$\begin{aligned} & \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s} \psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s}\psi (\phi ) \bigr] \\ &\quad =\frac{(\varphi ^{s+1}-\phi ^{s+1})}{2(s+1)} \int _{0}^{1} \bigl[(1-\wp )^{\frac{\chi }{k}}-( \wp )^{\frac{\chi }{k}} \bigr] N^{ \frac{1}{s+1}-1}\psi ^{\prime }\bigl[\bigl( \wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1}\bigr)^{\frac{1}{s+1}} \bigr]\,d\wp . \end{aligned}$$

This completes the proof of (i)

(ii) The proof of (ii) is similar to (i), so is omitted. Thus, the proof of the theorem is completed. □

Theorem 2.4

Let \(\psi : [\phi ,\varphi ]\subset (0,\infty )\rightarrow \mathbb{R}\)be a differentiable function on \((\phi ,\varphi )\), \(\phi < \varphi \), such that \(\psi {'}\in L[\phi ,\varphi ]\). If \(|\psi {'}|^{g}\), where \(g > 1\), is \((s+1)\)-convex, then

  1. (i)

    for \(s > -1\),

    $$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s}\psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s} \psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{(\varphi ^{s+1}-\phi ^{s+1})}{2(s+1)} \biggl\{ \varphi ^{-s} \mathfrak{_{2}F_{1}} \biggl(\frac{s}{s+1},1;2;1- \frac{\phi ^{s+1}}{\varphi ^{s+1}} \biggr) \biggr\} ^{1-\frac{1}{g}} \biggl[ \biggl( \frac{1}{\frac{\chi }{k}+1} \biggr) \\ &\qquad {}\times \bigl[ \bigl\vert \psi {'}(\phi ) \bigr\vert ^{g}+ \bigl\vert \psi {'}(\varphi ) \bigr\vert ^{g} \bigr] \biggr]^{\frac{1}{g}}, \end{aligned}$$
    (2.14)
  2. (ii)

    for \(s < -1\),

    $$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s}\psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s} \psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{(\phi ^{s+1}-\varphi ^{s+1})}{2(s+1)} \biggl\{ \phi ^{-s} \mathfrak{_{2}F_{1}} \biggl(\frac{s}{s+1},1;2;1- \frac{\varphi ^{s+1}}{\phi ^{s+1}} \biggr) \biggr\} ^{1-\frac{1}{g}} \biggl[ \biggl(\frac{1}{\frac{\chi }{k}+1} \biggr) \\ &\qquad {}\times \bigl[ \bigl\vert \psi {'}(\phi ) \bigr\vert ^{g}+ \bigl\vert \psi {'}(\varphi ) \bigr\vert ^{g} \bigr] \biggr]^{\frac{1}{g}}. \end{aligned}$$

Proof

(i) Applying Theorem 2.3, modulus property, Hölder’s inequality, and \((s+1)\)-convexity of \(|\psi {'}|^{g}\), we get

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{(s+1)^{\frac{\chi }{k}}\varGamma _{k}(\chi +k)}{2(\varphi ^{s+1}-\phi ^{s+1})^{\frac{\chi }{k}}} \bigl[F_{\phi ^{+},k}^{\chi ,s}\psi (\varphi )+F_{\varphi ^{-},k}^{ \chi ,s} \psi (\phi ) \bigr] \biggr\vert \\ &\quad = \biggl\vert \frac{(\varphi ^{s+1}-\phi ^{s+1})}{2(s+1)} \int _{0}^{1} \bigl[(1-\wp )^{\frac{\chi }{k}}-( \wp )^{\frac{\chi }{k}} \bigr] N^{ \frac{1}{s+1}-1}\psi {'}\bigl[ \bigl(\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1} \bigr)^{\frac{1}{s+1}}\bigr]\,d\wp \biggr\vert \\ &\quad \leq \biggl\vert \frac{(\varphi ^{s+1}-\phi ^{s+1})}{2(s+1)} \int _{0}^{1} \bigl[(1-\wp )^{\frac{\chi }{k}}+( \wp )^{\frac{\chi }{k}} \bigr] N^{ \frac{1}{s+1}-1}\psi {'}\bigl[ \bigl(\wp \phi ^{s+1}+(1-\wp )\varphi ^{s+1} \bigr)^{\frac{1}{s+1}}\bigr]\,d\wp \biggr\vert \\ &\quad \leq \frac{(\varphi ^{s+1}-\phi ^{s+1})}{2(s+1)} \biggl( \int _{0}^{1}N^{ \frac{1}{s+1}-1}\,d\wp \biggr)^{1-\frac{1}{g}} \\ &\qquad {}\times \biggl( \int _{0}^{1} \bigl[(1-\wp )^{\frac{\chi }{k}}+( \wp )^{\frac{\chi }{k}} \bigr]|\psi {'}[\bigl(\wp \phi ^{s+1}+(1-\wp ) \varphi ^{s+1}\bigr)^{\frac{1}{s+1}}|^{g} \,d\wp \biggr)^{\frac{1}{g}} \\ &\quad \leq \frac{(\varphi ^{s+1}-\phi ^{s+1})}{2(s+1)} \biggl( \int _{0}^{1}N^{ \frac{1}{s+1}-1}\,d\wp \biggr)^{1-\frac{1}{g}} \\ &\qquad {}\times \biggl( \int _{0}^{1} \bigl[(1-\wp )^{\frac{\chi }{k}}+( \wp )^{\frac{\chi }{k}} \bigr] \bigl[\wp \bigl\vert \psi {'}( \phi ) \bigr\vert ^{g}+(1-\wp ) \bigl\vert \psi {'}(\varphi ) \bigr\vert ^{g} \bigr]\,d\wp \biggr)^{\frac{1}{g}} \\ &\quad =\frac{(\varphi ^{s+1}-\phi ^{s+1})}{2(s+1)} \biggl\{ \varphi ^{-s} \mathfrak{_{2}F_{1}} \biggl(\frac{s}{s+1},1;2;1- \frac{\phi ^{s+1}}{\varphi ^{s+1}} \biggr) \biggr\} ^{1-\frac{1}{g}} \biggl[ \biggl(\frac{1}{\frac{\chi }{k}+1} \biggr) \\ &\qquad {}\times \bigl[ \bigl\vert \psi {'}(\phi ) \bigr\vert ^{g}+ \bigl\vert \psi {'}(\varphi ) \bigr\vert ^{g} \bigr] \biggr]^{\frac{1}{g}}. \end{aligned}$$

This completes the proof of (i).

(ii) The proof of (ii) is similar to (i), so is omitted. Thus, the proof of the theorem is completed. □

Example 2.5

By plotting the graphs of inequalities of Theorem 2.4 for the convex function \(\psi (\wp )= \wp ^{2}\) and \(g=2\), we prove the validity of the results. Substitution of (2.8) and (2.9) into inequality (2.14) gives

$$\begin{aligned} &\biggl\vert \frac{\phi ^{2}+\varphi ^{2}}{2}- \frac{\chi }{2k(\varphi -\phi )^{\frac{\chi }{k}}} \int _{0}^{1}\bigl[( \varphi -\wp )^{\frac{\chi }{k}-1}+(\wp -\phi )^{\frac{\chi }{k}-1}\bigr]x^{2}\,d\wp \biggr\vert \\ &\quad \leq (\varphi -\phi ) \biggl(\frac{k}{\chi +k} \biggr)^{ \frac{1}{2}}\bigl(\phi ^{2}+\varphi ^{2} \bigr)^{\frac{1}{2}}. \end{aligned}$$
(2.15)

The three functions given by the left, middle and right sides of the double inequality (2.15) are plotted in Fig. 2 against \(\chi \in (0,1]\). The graphs of the functions illustrate the validity of both inequalities.

Figure 2
figure 2

The graphs illustrate the result of the double inequality given by (2.15) for the case \(\phi = 0\), \(\varphi = 1\), and \(k=1\)

Full size image

3 Inequalities involving conformable fractional integral operator

This section contains mean-type inequalities for conformable fractional integral operators by using h-convexity.

Theorem 3.1

Let \(\mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\)and \(\mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\)be the left- and right-sided generalized conformable fractional integrals operators of order \(\beta \in \mathbb{C}\), \(\mathfrak{Re}(\beta )>0\)and \(0<\chi \leq 1\). Let \(\psi :[\phi ,\varphi ]\rightarrow \mathbb{R}\)be a positive mapping with \(\psi \in L_{1}[\phi ,\varphi ]\)and \(0\leq \phi <\varphi \). If ψ is h-convex on \([\phi ,\varphi ]\), then

$$\begin{aligned} & \psi \biggl(\frac{\phi +\varphi }{2} \biggr) \\ &\quad \leq \frac{h(\frac{1}{2})\chi ^{\beta }\varGamma (\beta +1)}{(\varphi -\phi )^{\chi \beta }} \bigl[\mathfrak{J}^{\chi ,\beta }_{\phi ^{+}} \psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr] \\ &\quad \leq \chi \beta h \biggl(\frac{1}{2} \biggr) \bigl[\psi (\phi )+\psi ( \varphi ) \bigr] \\ &\qquad {}\times \int _{0}^{1} \bigl(1-\nu ^{\chi } \bigr)^{\beta -1}\nu ^{\chi -1} \bigl[h(\nu )+h(1- \nu ) \bigr]\,d\nu . \end{aligned}$$
(3.1)

Proof

Since ψ is h-convex function, we can write

$$ \psi \bigl(\nu x+(1-\nu )y\bigr)\leq h(\nu )\psi (x)+h(1-\nu ) \psi (y) $$
(3.2)

and

$$ \psi \bigl((1-\nu )x+\nu y\bigr)\leq h(1-\nu )\psi (x)+h(\nu ) \psi (y). $$
(3.3)

Let \(\nu =\frac{1}{2}\), then

$$\begin{aligned} \psi \biggl(\frac{x+y}{2}\biggr) \leq h\biggl(\frac{1}{2} \biggr)\psi (x)+h\biggl(\frac{1}{2}\biggr)\psi (y) = h\biggl( \frac{1}{2}\biggr)\bigl[\psi (x)+\psi (y)\bigr]. \end{aligned}$$

Assume \(x=\nu \phi +(1-\nu )\varphi \) and \(y=\phi (1-\nu )+\varphi \nu \), then we have

$$ \psi \biggl(\frac{\phi +\varphi }{2}\biggr)\leq h\biggl(\frac{1}{2} \biggr)\bigl[\psi \bigl(\nu \phi +(1- \nu )\varphi \bigr)+\psi \bigl(\phi (1-\nu )+\nu \varphi \bigr)\bigr]. $$

Multiplying the above inequality by \((1-\nu ^{\chi })^{\beta -1}\nu ^{\chi -1}\) and then integrating with respect to ν over \([0,1]\), we get

$$\begin{aligned} & \psi \biggl(\frac{\phi +\varphi }{2} \biggr) \int _{0}^{1}\bigl(1- \nu ^{\chi } \bigr)^{\beta -1} \nu ^{\chi -1}\,dt \\ &\quad \leq h\biggl(\frac{1}{2}\biggr) \biggl[ \int _{0}^{1}\bigl(1-\nu ^{\chi } \bigr)^{ \beta -1} \nu ^{\chi -1} \psi \bigl(\nu \phi +(1-\nu )\varphi \bigr)\,d\nu \\ &\qquad {}+ \int _{0}^{1} \bigl(1-\nu ^{\chi } \bigr)^{\beta -1}\nu ^{\chi -1} \psi \bigl((1-\nu )\phi +\nu \varphi \bigr)\,d\nu \biggr], \end{aligned}$$

which can also be written as

$$\begin{aligned} & \frac{1}{\chi \beta }\psi \biggl(\frac{\phi +\varphi }{2}\biggr) \\ &\quad \leq h\biggl(\frac{1}{2}\biggr) \biggl[ \int _{0}^{1} \bigl(1-\nu ^{\chi } \bigr)^{ \beta -1}\nu ^{\chi -1} \psi \bigl(\nu \phi + (1-\nu )\varphi \bigr)\,d\nu \biggr] \\ &\qquad {}+ h\biggl(\frac{1}{2}\biggr) \biggl[ \int _{0}^{1} \bigl(1-\nu ^{\chi } \bigr)^{\beta -1} \nu ^{\chi -1} \psi \bigl((1-\nu )\phi +\nu \varphi \bigr)\,d\nu \biggr]. \end{aligned}$$
(3.4)

Now, let \(\nu \phi +(1-\nu )\varphi =u\) and \((1-\nu )\phi +\nu \varphi =v\), then (3.4) becomes

$$\begin{aligned} & \frac{1}{\chi \beta }\psi \biggl(\frac{\phi +\varphi }{2}\biggr) \\ &\quad \leq \frac{h(\frac{1}{2})\chi ^{\beta -1}\varGamma (\beta )}{(\varphi -\phi )^{\chi \beta }} \biggl[\frac{\chi ^{1-\beta }}{\varGamma (\beta )} \int _{\phi }^{ \varphi } \bigl((\varphi -\phi )^{\chi }-(\varphi -u)^{\chi }\bigr)^{\beta -1}( \varphi -u)^{\chi -1}\psi (u)\,du \\ &\qquad {}+\frac{\chi ^{1-\beta }}{\varGamma (\beta )} \int _{\phi }^{ \varphi } \bigl((\varphi -\phi )^{\chi }-(v-\phi )^{\chi }\bigr)^{\beta -1}(v- \phi )^{\chi -1}\psi (v)\,dv \biggr], \end{aligned}$$

which can be written as

$$ \psi \biggl(\frac{\phi +\varphi }{2} \biggr)\leq \frac{h(\frac{1}{2})\chi ^{\beta }\varGamma (\beta +1)}{(\varphi -\phi )^{\chi \beta }} \bigl[\mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\psi ( \varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr]. $$
(3.5)

Now, by replacing \(x=\phi \), \(y=\varphi \) in (3.2) and (3.3), respectively, then adding we have

$$ \psi \bigl(\nu \phi +(1-\nu )\varphi \bigr)+\psi \bigl((1-\nu ) \phi +\nu \varphi \bigr) \leq \bigl[h(\nu )+h(1-\nu )\bigr] \bigl[\psi (\phi )+ \psi (\varphi )\bigr]. $$
(3.6)

Multiplying (3.6) by \((1-\nu ^{\chi })^{\beta -1}\nu ^{\chi -1}\) and then integrating over \([0,1]\), we have

$$\begin{aligned} & \frac{h(\frac{1}{2})\chi ^{\beta }\varGamma (\beta +1)}{(\varphi -\phi )^{\chi \beta }} \bigl[\mathfrak{J}^{\chi ,\beta }_{\phi ^{+}} \psi (\varphi ) + \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr] \\ &\quad \leq \chi \beta h\biggl(\frac{1}{2}\biggr)\bigl[\psi (\phi )+\psi ( \varphi )\bigr] \int _{0}^{1}\bigl(1-\nu ^{\chi } \bigr)^{\beta -1} \nu ^{\chi -1}\bigl[h(\nu )+h(1- \nu )\bigr]\,d\nu . \end{aligned}$$
(3.7)

Now, from (3.5) and (3.7), we get the desired result. □

Example 3.2

We verify the result of Theorem 3.1 for the convex function \(\psi (\wp )= e^{2\wp }\) and \(h(\nu )=\nu \). It is known that the conformable fractional integrals of this function for \(\beta =1\) are given by

$$ \mathfrak{J}^{\chi ,1}_{\phi ^{+}}\psi (\varphi ) = \int _{ \phi }^{\varphi }(\nu -\phi )^{\chi -1}e^{2\nu } \,d\nu $$
(3.8)

and

$$ \mathfrak{J}^{\chi ,1}_{\varphi ^{-}}\psi (\phi ) = \int _{ \phi }^{\varphi }(\varphi -\nu )^{\chi -1}e^{2\nu } \,d\nu . $$
(3.9)

Substituting these expressions into inequality (3.1), we get

$$\begin{aligned} & 2e^{(\phi +\varphi )}\leq \frac{\chi }{(\varphi -\phi )^{\chi }} \int _{0}^{1}\bigl[(\varphi -\nu )^{\chi -1}+(\nu -\phi )^{\chi -1}\bigr]e^{2 \nu }\,d\nu \leq \bigl[e^{2\phi }+e^{2\varphi }\bigr]. \end{aligned}$$
(3.10)

The three functions given by the left, middle, and right sides of this double inequality are plotted in Fig. 3 against \(\chi \in (0,1]\) to show clearly that both inequalities are valid.

Figure 3
figure 3

The graphs illustrate the validity of the dual inequality (3.10) for the case \(\phi = 0\) and \(\varphi = 1\)

Full size image

Theorem 3.3

Let \(\psi : [\phi ,\varphi ] \rightarrow \mathbb{R}\)be a differentiable function on \((\phi ,\varphi )\)with \(\psi {'}\in L_{1}[\phi ,\varphi ]\). If \(|\psi {'}|\)is an h-convex function on \([\phi ,\varphi ]\), then the following inequality for fractional conformable integrals holds:

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\beta }\varGamma (\beta +1)}{2(\varphi -\phi )^{\chi \beta }} \bigl[\mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{\varphi -\phi }{2} \biggl[ \bigl\vert \psi {'}(\phi ) \bigr\vert \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{\beta }+\bigl(1-(1-\wp )^{\chi } \bigr)^{\beta } \bigr]h(\wp )\,d\wp \\ &\qquad {}+ \bigl\vert \psi {'}(\varphi ) \bigr\vert \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{ \beta }+\bigl(1-(1-\wp )^{\chi } \bigr)^{\beta } \bigr]h(1-\wp )\,d\wp \biggr]. \end{aligned}$$
(3.11)

Proof

By using Lemma 1.10, modulus property, and h-convexity, we have

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\beta }\varGamma (\beta +1)}{2(\varphi -\phi )^{\chi \beta }} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr] \biggr\vert \\ &\quad = \biggl\vert \frac{(\varphi -\phi )}{2} \int _{0}^{1} \bigl[\bigl(1-\wp ^{ \chi }\bigr)^{\beta }-\bigl(1-(1-\wp )^{\chi } \bigr)^{\beta } \bigr]\psi {'}\bigl(\wp \phi +(1- \wp ) \varphi \bigr)\,d\wp \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{2} \biggl\vert \int _{0}^{1} \bigl[\bigl(1- \wp ^{\chi }\bigr)^{\beta }+\bigl(1-(1-\wp )^{\chi } \bigr)^{\beta } \bigr]\psi {'}\bigl(\wp \phi +(1-\wp ) \varphi \bigr)\,d\wp \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{2} \int _{0}^{1} \bigl[\bigl(1-\wp ^{ \chi }\bigr)^{\beta }+\bigl(1-(1-\wp )^{\chi } \bigr)^{\beta } \bigr] \bigl[h(\wp ) \bigl\vert \psi {'}( \phi ) \bigr\vert +h(1-\wp ) \bigl\vert \psi {'}(\varphi ) \bigr\vert \bigr]\,d\wp \\ &\quad =\frac{(\varphi -\phi )}{2} \biggl[ \bigl\vert \psi {'}(\phi ) \bigr\vert \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{\beta }+\bigl(1-(1-\wp )^{\chi } \bigr)^{\beta } \bigr]h(\wp )\,d\wp \\ &\qquad {}+ \bigl\vert \psi {'}(\varphi ) \bigr\vert \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{ \beta }+\bigl(1-(1-\wp )^{\chi } \bigr)^{\beta } \bigr]h(1-\wp )\,d\wp \biggr], \end{aligned}$$

which completes the proof. □

Example 3.4

We verify the result of Theorem 3.3 for the convex function \(\psi (\nu )= e^{\nu }\), \(\beta =1\), and \(h(\nu )=\nu \). In this case, inequality (3.11) is given by

$$ -\frac{\chi (1+e)}{1+\chi } \leq (1+e)-\chi \int _{0}^{1}\bigl[( \nu -\phi )^{\chi -1}+(\varphi -\nu )^{\chi -1}\bigr]e^{\nu }\,d\nu \leq \frac{\chi (1+e)}{1+\chi }. $$
(3.12)

The three functions given by the left, middle, and right sides of this double inequality are plotted in Fig. 4 against \(\chi \in (0,1]\) to show that both inequalities are valid.

Figure 4
figure 4

The graphs illustrate validity of the double inequality given by (3.12) for the case \(\phi = 0\), \(\varphi = 1\), and \(0<\chi \leq 1\)

Full size image

Corollary 3.5

If we take \(h(\wp )=1\)in Theorem 3.3, then we get the result:

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\beta }\varGamma (\beta +1)}{2(\varphi -\phi )^{\chi \beta }} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{\chi } \bigl[ \bigl\vert \psi {'}(\phi ) \bigr\vert + \bigl\vert \psi {'}( \varphi ) \bigr\vert \bigr]\mathbf{B} \biggl(\frac{1}{\chi },\beta +1 \biggr), \end{aligned}$$

where B denotes the usual beta function.

Corollary 3.6

If we take \(h(\wp )=\wp \)in Theorem 3.3, then we get the result for simple convex function presented below:

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\beta }\varGamma (\beta +1)}{2(\varphi -\phi )^{\chi \beta }} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{\chi } \biggl[ \frac{ \vert \psi {'}(\phi ) \vert + \vert \psi {'}(\varphi ) \vert }{2} \biggr]\mathbf{B} \biggl( \frac{1}{\chi },\beta +1 \biggr). \end{aligned}$$

Corollary 3.7

If we take \(h(\wp )=\wp ^{s}\)in Theorem 3.3, where \(s\in (0,1)\), then the result for geometric–arithmetically s-convex functions is as follows:

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\beta }\varGamma (\beta +1)}{2(\varphi -\phi )^{\chi \beta }} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+}}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-}}\psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{\chi } \biggl[ \frac{ \vert \psi {'}(\phi ) \vert + \vert \psi {'}(\varphi ) \vert }{2} \biggr] \biggl[ \mathbf{B} \biggl(\frac{s+1}{\chi },\beta +1 \biggr) \\ & \qquad {}+\mathbf{B} \biggl(\frac{1}{\chi },\beta +1 \biggr) \mathfrak{_{2}F_{1}} \biggl(-s,\frac{1}{\chi }; \frac{\chi +\chi \beta +1}{\chi };u^{\frac{1}{\chi }-1} \biggr) \biggr]. \end{aligned}$$

4 Inequalities involving generalized k-conformable fractional integral operators

In this section, mean-type inequalities for k-conformable fractional integral operator by using h-convexity are established.

Theorem 4.1

Let \(\mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\)and \(\mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\)be the left- and right-sided generalized k-conformable fractional integrals operators of order \(k>0\), \(\mathfrak{Re}(\beta )>0\)and \(0<\chi \leq 1\). Let \(\psi :[\phi ,\varphi ]\rightarrow \mathbb{R}\)be a positive mapping with \(\psi \in L_{1}[\phi ,\varphi ]\)and \(0\leq \phi <\varphi \). If ψ is h-convex on \([\phi ,\varphi ]\), then

$$\begin{aligned} \psi \biggl(\frac{\phi +\varphi }{2} \biggr) \leq &\frac{h(\frac{1}{2})\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{(\varphi -\phi )^{{\chi \beta }{k}}} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr] \\ \leq &\frac{\chi \beta }{k} h \biggl(\frac{1}{2} \biggr) \bigl[\psi ( \phi )+ \psi (\varphi ) \bigr] \int _{0}^{1} \bigl(1-\nu ^{\chi } \bigr)^{\frac{\beta }{k}-1} \nu ^{\chi -1} \bigl[h(\nu )+h(1-\nu ) \bigr]\,d\nu . \end{aligned}$$

Proof

Since ψ is an h-convex function, we can write

$$ \psi \bigl(\nu x+(1-\nu )y\bigr)\leq h(\nu )\psi (x)+h(1-\nu ) \psi (y) $$
(4.1)

and

$$ \psi \bigl((1-\nu )x+\nu y\bigr)\leq h(1-\nu )\psi (x)+h(\nu ) \psi (y). $$
(4.2)

Let \(\nu =\frac{1}{2}\), then

$$\begin{aligned} \psi \biggl(\frac{x+y}{2}\biggr) \leq h\biggl(\frac{1}{2} \biggr)\psi (x)+h\biggl(\frac{1}{2}\biggr)\psi (y) = h\biggl( \frac{1}{2}\biggr)\bigl[\psi (x)+\psi (y)\bigr]. \end{aligned}$$

Assume \(x=\nu \phi +(1-\nu )\varphi \) and \(y=\phi (1-\nu )+\varphi \nu \), then we have

$$ \psi \biggl(\frac{\phi +\varphi }{2}\biggr)\leq h\biggl(\frac{1}{2} \biggr)\bigl[\psi \bigl(\nu \phi +(1- \nu )\varphi \bigr)+\psi \bigl(\phi (1-\nu )+\nu \varphi \bigr)\bigr]. $$

Multiplying the above inequality by \((1-\nu ^{\chi })^{\frac{\beta }{k}-1}\nu ^{\chi -1}\) and then integrating with respect to ν over \([0,1]\), we get

$$\begin{aligned} \frac{k}{\chi \beta }\psi \biggl(\frac{\phi +\varphi }{2}\biggr) \leq{}& h\biggl(\frac{1}{2}\biggr) \biggl[ \int _{0}^{1} \bigl(1-\nu ^{\chi } \bigr)^{ \frac{\beta }{k}-1}\nu ^{\chi -1} \psi \bigl(\nu \phi +(1-\nu )\varphi \bigr)\,d\nu \\ & {}+ \int _{0}^{1} \bigl(1-\nu ^{\chi } \bigr)^{\frac{\beta }{k}-1}\nu ^{ \chi -1} \psi \bigl((1-\nu )\phi +\nu \varphi \bigr)\,d\nu \biggr]. \end{aligned}$$
(4.3)

Now, let \(\nu \phi +(1-\nu )\varphi =u\) and \((1-\nu )\phi +\nu \varphi =v\), then (4.3) becomes

$$\begin{aligned} & \frac{k}{\chi \beta }\psi \biggl(\frac{\phi +\varphi }{2}\biggr) \\ &\quad \leq \frac{h(\frac{1}{2})\chi ^{\frac{\beta }{k}-1}\varGamma _{k}(\beta )}{(\varphi -\phi )^{\frac{\chi \beta }{k}}} \biggl[\frac{\chi ^{1-\frac{\beta }{k}}}{\varGamma _{k}(\beta )} \int _{\phi }^{\varphi } \bigl((\varphi -\phi )^{\chi }-(\varphi -u)^{\chi }\bigr)^{ \frac{\beta }{k}-1}(\varphi -u)^{\chi -1}\psi (u)\,du \\ &\qquad {}+\frac{\chi ^{1-\frac{\beta }{k}}}{\varGamma _{k}(\beta )} \int _{ \phi }^{\varphi } \bigl((\varphi -\phi )^{\chi }-(v-\phi )^{\chi }\bigr)^{ \frac{\beta }{k}-1}(v-\phi )^{\chi -1}\psi (v)\,dv \biggr], \end{aligned}$$

which can be written as

$$ \psi \biggl(\frac{\phi +\varphi }{2} \biggr)\leq \frac{h(\frac{1}{2})\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{(\varphi -\phi )^{\frac{\chi \beta }{k}}} \bigl[\mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\psi ( \varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr]. $$
(4.4)

Now, by replacing \(x=\phi \), \(y=\varphi \) in (4.1) and (4.2), respectively, then adding we have

$$ \psi \bigl(\nu \phi +(1-\nu )\varphi \bigr)+\psi \bigl((1-\nu ) \phi +\nu \varphi \bigr) \leq \bigl[h(\nu )+h(1-\nu )\bigr] \bigl[\psi (\phi )+ \psi (\varphi )\bigr]. $$
(4.5)

Multiplying (4.5) by \((1-\nu ^{\chi })^{\frac{\beta }{k}-1}\nu ^{\chi -1}\) and then integrating over \([0,1]\), we have

$$\begin{aligned} & \frac{h(\frac{1}{2})\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{(\varphi -\phi )^{\frac{\chi \beta }{k}}} \bigl[\mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k} \psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr] \\ &\quad \leq \frac{\chi \beta }{k} h\biggl(\frac{1}{2}\biggr)\bigl[\psi (\phi )+\psi (\varphi )\bigr] \int _{0}^{1}\bigl(1-\nu ^{\chi } \bigr)^{\frac{\beta }{k}-1} \nu ^{\chi -1}\bigl[h( \nu )+h(1-\nu )\bigr]\,d\nu . \end{aligned}$$
(4.6)

Now, from (4.4) and (4.6), we get the desired result. □

Theorem 4.2

Let \(\psi : [\phi ,\varphi ] \rightarrow \mathbb{R}\)be a differentiable function on \((\phi ,\varphi )\)with \(\phi < \varphi \)and \(\psi \in L_{1}[\phi ,\varphi ]\). Then the following equality for k-conformable fractional integral holds:

$$\begin{aligned} & \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{2(\varphi -\phi )^{\frac{\chi \beta }{k}}} \bigl[\mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k} \psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr] \\ &\quad =\frac{(\varphi -\phi )}{2} \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{ \frac{\beta }{k}}-\bigl(1-(1-\wp )^{\chi } \bigr)^{\frac{\beta }{k}} \bigr]\psi {'}\bigl( \wp \phi +(1-\wp ) \varphi \bigr)\,d\wp . \end{aligned}$$

Proof

Consider

$$\begin{aligned} I={}& \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{\frac{\beta }{k}}-\bigl(1-(1- \wp )^{\chi } \bigr)^{\frac{\beta }{k}} \bigr]\psi {'}\bigl(\wp \phi +(1-\wp ) \varphi \bigr)\,d\wp \\ ={}& \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{\frac{\beta }{k}} \bigr] \psi {'}\bigl(\wp \phi +(1-\wp )\varphi \bigr)\,d\wp \\ &{}- \int _{0}^{1} \bigl[\bigl(1-(1-\wp )^{\chi }\bigr)^{\frac{\beta }{k}} \bigr]\psi {'}\bigl(\wp \phi +(1-\wp )\varphi \bigr)\,d\wp \\ ={}&I_{1}-I_{2}. \end{aligned}$$
(4.7)

Integrating by parts and using substitution \(u=\wp \phi +(1-\wp )\varphi \), we have

$$\begin{aligned} I_{1}&= \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{\frac{\beta }{k}} \bigr]\psi {'}\bigl(\wp \phi +(1-\wp )\varphi \bigr)\,d\wp \\ &=\frac{\psi (\varphi )}{\varphi -\phi }- \frac{\beta \chi }{k(\varphi -\phi )} \int _{0}^{1}\bigl(1-\wp ^{ \chi } \bigr)^{\frac{\beta }{k}-1}\wp ^{\chi -1}\psi \bigl(\wp \phi +(1-\wp ) \varphi \bigr)\,d\wp \\ &=\frac{\psi (\varphi )}{\varphi -\phi }- \frac{\beta \chi }{k(\varphi -\phi )^{\frac{\chi \beta }{k}+1}} \int _{\phi }^{\varphi } \bigl((\varphi -\phi )^{\chi }-(\varphi -u)^{ \chi } \bigr)^{\frac{\beta }{k}-1}(\varphi -u)^{\chi -1}\psi (u)\,du \\ &=\frac{\psi (\varphi )}{\varphi -\phi }- \frac{\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{(\varphi -\phi )^{\frac{\chi \beta }{k}+1}}\mathfrak{J}^{\chi ,\beta }_{ \varphi ^{-},k} \psi (\phi ). \end{aligned}$$

Also, we have

$$\begin{aligned} I_{2}&= \int _{0}^{1} \bigl[\bigl(1-(1-\wp )^{\chi }\bigr)^{ \frac{\beta }{k}} \bigr]\psi {'}\bigl(\wp \phi +(1-\wp )\varphi \bigr)\,d\wp \\ &=\frac{-\psi (\phi )}{\varphi -\phi }+ \frac{\beta \chi }{k(\varphi -\phi )} \int _{0}^{1}\bigl(1-(1-\wp )^{ \chi } \bigr)^{\frac{\beta }{k}-1}(1-\wp )^{\chi -1}\psi \bigl(\wp \phi +(1-\wp ) \varphi \bigr)\,d\wp \\ &=\frac{-\psi (\phi )}{\varphi -\phi }+ \frac{\beta \chi }{k(\varphi -\phi )^{\frac{\chi \beta }{k}+1}} \int _{\phi }^{\varphi } \bigl((\varphi -\phi )^{\chi }-(u-\phi )^{ \chi } \bigr)^{\frac{\beta }{k}-1}(u-\phi )^{\chi -1}\psi (u)\,du \\ &=\frac{-\psi (\phi )}{\varphi -\phi }+ \frac{\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{(\varphi -\phi )^{\frac{\chi \beta }{k}+1}} \mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k} \psi (\varphi ). \end{aligned}$$

By using the obtained values of \(I_{1}\) and \(I_{2}\) in (4.7) and then multiplying the result by \(\frac{\varphi -\phi }{2}\), we get the desired result. □

Theorem 4.3

Let \(\psi : [\phi ,\varphi ] \rightarrow \mathbb{R}\)be a differentiable function on \((\phi ,\varphi )\)with \(\psi {'}\in L_{1}[\phi ,\varphi ]\). If \(|\psi {'}|\)is an h-convex function on \([\phi ,\varphi ]\), then the following inequality for fractional conformable integral holds:

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{2(\varphi -\phi )^{\frac{\chi \beta }{k}}} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{\varphi -\phi }{2} \biggl[ \bigl\vert \psi {'}(\phi ) \bigr\vert \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{\frac{\beta }{k}}+\bigl(1-(1-\wp )^{\chi } \bigr)^{ \frac{\beta }{k}} \bigr]h(\wp )\,d\wp \\ &\qquad {}+ \bigl\vert \psi {'}(\varphi ) \bigr\vert \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{ \frac{\beta }{k}}+\bigl(1-(1-\wp )^{\chi } \bigr)^{\frac{\beta }{k}} \bigr]h(1-\wp )\,d\wp \biggr]. \end{aligned}$$

Proof

By using Lemma 4.2, modulus property, and h-convexity, we have

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{2(\varphi -\phi )^{\frac{\chi \beta }{k}}} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr] \biggr\vert \\ &\quad = \biggl\vert \frac{(\varphi -\phi )}{2} \int _{0}^{1} \bigl[\bigl(1-\wp ^{ \chi }\bigr)^{\frac{\beta }{k}}-\bigl(1-(1-\wp )^{\chi } \bigr)^{\frac{\beta }{k}} \bigr] \psi {'}\bigl(\wp \phi +(1-\wp ) \varphi \bigr)\,d\wp \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{2} \biggl\vert \int _{0}^{1} \bigl[\bigl(1- \wp ^{\chi }\bigr)^{\frac{\beta }{k}}+\bigl(1-(1-\wp )^{\chi } \bigr)^{\frac{\beta }{k}} \bigr]\psi {'}\bigl(\wp \phi +(1-\wp ) \varphi \bigr)\,d\wp \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{2} \int _{0}^{1} \bigl[\bigl(1-\wp ^{ \chi }\bigr)^{\frac{\beta }{k}}+\bigl(1-(1-\wp )^{\chi } \bigr)^{\frac{\beta }{k}} \bigr] \bigl[h(\wp ) \bigl\vert \psi {'}(\phi ) \bigr\vert +h(1-\wp ) \bigl\vert \psi {'}(\varphi ) \bigr\vert \bigr]\,d\wp \\ &\quad =\frac{(\varphi -\phi )}{2} \biggl[ \bigl\vert \psi {'}(\phi ) \bigr\vert \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{\frac{\beta }{k}}+\bigl(1-(1-\wp )^{\chi } \bigr)^{ \frac{\beta }{k}} \bigr]h(\wp )\,d\wp \\ &\qquad {}+ \bigl\vert \psi {'}(\varphi ) \bigr\vert \int _{0}^{1} \bigl[\bigl(1-\wp ^{\chi }\bigr)^{ \frac{\beta }{k}}+\bigl(1-(1-\wp )^{\chi } \bigr)^{\frac{\beta }{k}} \bigr]h(1-\wp )\,d\wp \biggr], \end{aligned}$$

which completes the proof. □

Corollary 4.4

If we take \(h(\wp )=1\)in Theorem 4.3, then we get the result presented below:

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{2(\varphi -\phi )^{\frac{\chi \beta }{k}}} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{\chi } \bigl[ \bigl\vert \psi ^{\prime }(\phi ) \bigr\vert + \bigl\vert \psi ^{\prime }( \varphi ) \bigr\vert \bigr] \mathbf{B} \biggl(\frac{1}{\chi },\frac{\beta }{k}+1 \biggr), \end{aligned}$$

where B denotes the usual beta function.

Corollary 4.5

If we take \(h(\wp )=\wp \)in Theorem 4.3, then we get the result for simple convex function presented below.

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{2(\varphi -\phi )^{\frac{\chi \beta }{k}}} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{\chi } \biggl[ \frac{ \vert \psi {'}(\phi ) \vert + \vert \psi {'}(\varphi ) \vert }{2} \biggr]\mathbf{B} \biggl( \frac{1}{\chi },\frac{\beta }{k}+1 \biggr). \end{aligned}$$

Corollary 4.6

If we take \(h(\wp )=\wp ^{s}\)in Theorem 4.3, where \(s\in (0,1)\), then the result for geometric–arithmetically s-convex functions is as follows:

$$\begin{aligned} & \biggl\vert \frac{\psi (\phi )+\psi (\varphi )}{2}- \frac{\chi ^{\frac{\beta }{k}}\varGamma _{k}(\beta +k)}{2(\varphi -\phi )^{\frac{\chi \beta }{k}}} \bigl[ \mathfrak{J}^{\chi ,\beta }_{\phi ^{+},k}\psi (\varphi )+ \mathfrak{J}^{\chi ,\beta }_{\varphi ^{-},k}\psi (\phi ) \bigr] \biggr\vert \\ &\quad \leq \frac{(\varphi -\phi )}{\chi } \biggl[ \frac{ \vert \psi {'}(\phi ) \vert + \vert \psi {'}(\varphi ) \vert }{2} \biggr] \biggl[ \mathbf{B} \biggl(\frac{s+1}{\chi },\frac{\beta }{k}+1 \biggr) \\ &\qquad {}+\mathbf{B} \biggl(\frac{1}{\chi },\frac{\beta }{k}+1 \biggr) \mathfrak{_{2}F_{1}} \biggl(-s,\frac{1}{\chi }; \frac{\chi k+\chi \beta +k}{\chi k};u^{\frac{1}{\chi }-1} \biggr) \biggr]. \end{aligned}$$

5 Applications to quadrature formulae

This section consists some particular inequalities which generalize some classical results like the trapezoid inequality. Also Hadamard’s inequality can be observed.

Proposition 5.1

(Hadamard’s inequality)

By using the assumptions of Theorem 2.1with \(\chi =1\), \(s=0\), and \(k=1\), we get the following Hadamard’s inequality:

$$\begin{aligned} & \psi \biggl(\frac{\phi +\varphi }{2}\biggr) \leq \frac{1}{\varphi -\phi } \int _{\phi }^{\varphi }\psi (\nu )\,d\nu \leq \frac{\psi (\phi )+\psi (\varphi )}{2}. \end{aligned}$$
(5.1)

Proposition 5.2

By using the assumptions of Theorem 3.1with \(\chi =1\), \(\beta =1\), and \(h(\nu )=\nu \), we get the Hadamard’s inequality (5.1).

Proposition 5.3

By utilizing the assumptions of Corollary 3.5with \(\chi =1\)and \(\beta =1\), we get the following “trapezoid inequality”:

$$\begin{aligned} & \biggl\vert (\varphi -\phi )\frac{\psi (\phi )+\psi (\varphi )}{2}- \int _{\phi }^{\varphi }\psi (\nu )\,d\nu \biggr\vert \leq \frac{(\varphi -\phi )^{2}}{2} \bigl[ \bigl\vert \psi {'}(\phi ) \bigr\vert + \bigl\vert \psi {'}( \varphi ) \bigr\vert \bigr]. \end{aligned}$$

Proposition 5.4

By utilizing the assumptions of Corollary 3.6with \(\chi =1\)and \(\beta =1\), we get the following “trapezoid inequality”:

$$\begin{aligned} & \biggl\vert (\varphi -\phi )\frac{\psi (\phi )+\psi (\varphi )}{2}- \int _{\phi }^{\varphi }\psi (\nu )\,d\nu \biggr\vert \leq \frac{(\varphi -\phi )^{2}}{6} \bigl[ \bigl\vert \psi {'}(\phi ) \bigr\vert + \bigl\vert \psi {'}( \varphi ) \bigr\vert \bigr]. \end{aligned}$$

Proposition 5.5

By using the assumptions of Theorem 2.4with \(\chi =1\), \(k=1\), and \(s=0\), we get the following “trapezoid inequality”:

$$\begin{aligned} & \biggl\vert (\varphi -\phi )\frac{\psi (\phi )+\psi (\varphi )}{2}- \int _{\phi }^{\varphi }\psi (\nu )\,d\nu \biggr\vert \leq \frac{(\varphi -\phi )^{2}}{2} \biggl( \frac{ \vert \psi {'}(\phi ) \vert ^{g}+ \vert \psi {'}(\varphi ) \vert ^{g}}{2} \biggr)^{ \frac{1}{g}}. \end{aligned}$$

6 Conclusions

In the current article, we presented generalizations of some mean-type inequalities for fractional integrals of \((k,s)\)-Riemann and conformable type. For this purpose, we utilized the \((s+1)\)- and h-convex mappings. This work includes equalities so that we can make progress in finding more inequalities by using different functions. The validity of the results is illustrated by considering different convex functions and then by plotting graphs. The presented work includes quadrature formulas as bounds of novel inequalities. The findings of this investigation complement those of previous studies. Simply, the recent study confirms the earlier results and plays an additional role by making generalizations.