Time-delayed local feedback control for a chaotic finance system

Abstract

In this paper, we consider the local control problem for a chaotic finance system via the time-delayed feedback. Using the Lyapunov–Krasovskii stability theorem, the quadratic system theory, some integral inequalities, and rigorous mathematical analysis, we obtain a local stabilization condition by means of linear matrix inequalities. Then we discuss the estimate of the region of asymptotic stability and give the corresponding optimization problem. Also, we address the local control problem under the nondelayed feedback. Finally, we present numerical simulations to show the effectiveness of the proposed results.

1 Introduction

In the past several decades, the dynamical behaviors have attracted significant research attention for various kinds of nonlinear finance systems [1–6]. It has been widely identified that the chaotic behavior is encountered in financial/economic systems. Moreover, it has been well acknowledged that the existence of the chaotic phenomenon in financial/economic systems will lead to a possible uncertainty in the macroeconomic operation. Hence it is important to investigate stabilization and synchronization problems for various kinds of chaotic finance systems [7–12]. For example, the stabilization problem has been studied in [9] for an uncertain fractional-order finance system via the adaptive sliding-mode strategy, and in [11] the stabilization and synchronization problems have been addressed for an uncertain financial hyperchaotic system by using the impulsive control approach. In [12] the adaptive control scheme has been used to control a novel finance system.

In [13, 14] the time-delayed feedback control (TDFC) has been recognized as an effective method for controlling chaos in nonlinear dynamical systems. Compared with some other control schemes, the TDFC is more convenient to be implemented in practice since it does not require the reference signal that corresponds to the unstable periodic orbit. Over the past more than a decade, the TDFC has been extensively utilized to control the nonlinear finance systems [15–19]. For example, the minimum entropy algorithm has been applied in [16] for controlling chaos in the Behrens–Feichtinger model through TDFC, and in [18] the dynamical behavior has been studied for a nonlinear finance system under TDFC by using the characteristic equation of the linearized model. In [19] the $H_{\infty }$ control problem has been addressed for a finance system with external disturbance via TDFC.

Nevertheless, it should be pointed out that the results in [16, 17] are mainly based on the numerical simulations, and the discussions in [15, 18] are based on the characteristic equations of the corresponding linearized models. It is obvious that the theoretical analysis in [16, 17] is absent, and the application ranges of the results in [15, 18] are unknown. In addition, it is worth mentioning that all unstable equilibrium points in [19] are controlled by a unified delayed feedback controller, and this makes the resultant design condition a bit rigorous.

The finance systems discussed in the existing literature are essentially nonlinear quadratic systems. The stability analysis and control design for quadratic systems have also received wide investigations in the past more than a decade [20–25]. In particular, in [23–25] the time delay is incorporated in the considered models. However, note that the results in [23–25] are concerned with models with a single state delay and cannot be applied to the finance system subject to TDFC. Moreover, the analysis approaches used in [23–25] are somewhat conservative.

Motivated by these discussions, this paper is concerned with the TDFC problem for a chaotic finance system by using the quadratic system theory. By incorporating an augmented Lyapunov–Krasovskii (L–K) functional, some integral inequalities, and rigorous mathematical analysis the local control design conditions are first obtained in the context of linear matrix inequalities (LMIs). Then the paper discusses the estimate of the stability region and proposes the corresponding optimization problems. Finally, numerical simulations demonstrate the effectiveness of the obtained results. The main contributions of this paper are as follows: (1) a new local stabilization condition is established for a typical finance system under the TDFC strategy, and (2) the estimate of the region of asymptotic stability is discussed for the first time, and the corresponding optimization problem is formulated.

Notation. The superscript ``T” is the transpose of a matrix. For a matrix P, $P>0$$(P\geq 0)$ means that P is symmetric and positive definite (positive semidefinite). By $\|\cdot \|$ we denote the 2-norm of a vector and by $\lambda (\cdot )_{M}$ the maximum eigenvalue value of a matrix. The symmetric terms in a matrix are denoted by ∗.

2 Problem formulation

In [1, 2] the finance model composed of four subblocks (i.e., production, money, stock, and labor force) has been purified and simplified as follows:

$$\begin{aligned} \textstyle\begin{cases} \dot{\mathbf{x}}(t)=f_{1}(\mathbf{y}(t)-{\mathrm{SV}})\mathbf{x}(t)+f_{2} \mathbf{z}(t), \\ \dot{\mathbf{y}}(t)=f_{3}({\mathrm{BEN}}-\alpha \mathbf{y}(t)-\beta \mathbf{x}^{2}(t)), \\ \dot{\mathbf{z}}(t)=-f_{4}\mathbf{z}(t)-f_{5}\mathbf{x}(t), \end{cases}\displaystyle \end{aligned}$$

(1)

where $\mathbf{x}(t)$, $\mathbf{y}(t)$, $\mathbf{z}(t)$, SV, and BEN denote, respectively, the interest rate, the investment demand, the price index, the amount of savings, and the benefit rate of investment; α, β, and $f_{i}$ ($i=1,2,\ldots,5$) are all constants. Model (1) is obtained through careful analysis and many experiments. We see that nine independent parameters are involved in the model. By choosing an appropriate coordinate system and setting an appropriate dimension to every state variable, model (1) has been further simplified for convenience of analysis [1, 2]. The further simplified model contains only three most important parameters and is described as

$$\begin{aligned} \textstyle\begin{cases} \dot{x}_{1}(t)=x_{3}(t)+(x_{2}(t)-a)x_{1}(t), \\ \dot{x}_{2}(t)=1-bx_{2}(t)-x_{1}^{2}(t), \\ \dot{x}_{3}(t)=-x_{1}(t)-cx_{3}(t), \end{cases}\displaystyle \end{aligned}$$

(2)

where a, b, and c are some positive scalars representing, respectively, the saving amount, the cost per investment, and the demand elasticity of commercial markets.

Denote $\Delta \triangleq c-b-abc$. It is easy to see that if $\Delta <0$, then model (2) has a unique fixed point $(0,1/b,0)$, and if $\Delta >0$, then model (2) has three fixed points

$$\begin{aligned} (0,1/b,0), \quad\bigl(\pm \sqrt{\Delta /c},(ac+1)/c,\mp \sqrt{\Delta /c^{3}}\bigr). \end{aligned}$$

For the finance model (2), it has been verified that the dynamic behaviors are highly correlated with parameters a, b, and c. In many cases the fixed points of system (2) are unstable. For example, when we choose $a=3$, $b=0.1$, and $c=1$ or $a=2.5$, $b=0.2$, and $c=1.2$, a chaotic behavior occurs in system (2).

Letting $x(t)\triangleq [x_{1}(t) x_{2}(t) x_{3}(t)]^{T}$ and

$$\begin{aligned} A\triangleq \begin{bmatrix} -a&0&1 \\ 0&-b&0 \\ -1&0&-c \end{bmatrix},\qquad f\bigl(x(t)\bigr)\triangleq \begin{bmatrix} x_{1}(t)x_{2}(t) \\ 1-x_{1}^{2}(t) \\ 0 \end{bmatrix}, \end{aligned}$$

the chaotic finance system (2) can be read as follows:

$$\begin{aligned} \dot{x}(t)=Ax(t)+f\bigl(x(t)\bigr)+u(t). \end{aligned}$$

(3)

In this paper, we apply the TDFC scheme

$$\begin{aligned} u(t)=K\bigl(x(t)-x(t-\tau )\bigr), \end{aligned}$$

(4)

where K is the controller gain matrix.

Denoting a fixed point by $x^{\ast }$, we see that

$$\begin{aligned} Ax^{*}+f\bigl(x^{*}\bigr)=0. \end{aligned}$$

(5)

Denoting $e(t)\triangleq x(t)-x^{*}$ and using (3)–(5), we have the closed-loop dynamics

$$\begin{aligned} \dot{e}(t)=&(A+K)e(t)-Ke(t-\tau )+f\bigl(x(t)\bigr)-f\bigl(x^{*} \bigr). \end{aligned}$$

(6)

Note that $f(x(t))-f(x^{*})=Fe(t)+g(e(t))$, where

$$\begin{aligned} F=& \begin{bmatrix} x_{2}^{*}&x_{1}^{*}&0 \\ -2x_{1}^{*}&0&0 \\ 0&0&0 \end{bmatrix},\qquad g(e)= \begin{bmatrix} e_{1}e_{2} \\ -e_{1}^{2} \\ 0 \end{bmatrix}= \begin{bmatrix} e^{T}B_{1} \\ e^{T}B_{2} \\ e^{T}B_{3} \end{bmatrix}e \triangleq B(e)e \end{aligned}$$

with

$$\begin{aligned} &B_{1}= \begin{bmatrix} 0&1/2&0 \\ 1/2&0&0 \\ 0&0&0 \end{bmatrix},\qquad B_{2}= \begin{bmatrix} -1&0&0 \\ 0&0&0 \\ 0&0&0 \end{bmatrix},\qquad B_{3}=0_{3\times 3}. \end{aligned}$$

Then we obtain the following closed-loop dynamics:

$$\begin{aligned} \dot{e}(t)=&\bigl[A+F+K+B(e)\bigr]e(t)-Ke(t-\tau ). \end{aligned}$$

(7)

The initial condition associated with system (7) is denoted by $e(s)=\phi (s)$, $s\in [-\tau,0)$. Moreover, it is reasonable to assume that the initial condition $\phi (s)$ ($s\in [-\tau,0)$) satisfies the open-loop dynamics $\dot{\phi }(s)=[A+F+B(\phi )]\phi (s)$.

In this paper, we assume that the initial condition $\phi (s)$ ($s \in [-\tau,0)$) of the closed-loop dynamics (7) belongs to a set of the following form:

$$\begin{aligned} X_{\rho }= \bigl\{ \phi (s)\in C^{1}[-\tau,0]: \mathop{\operatorname{max}}_{s\in [- \tau,0]} \bigl\Vert \phi (s) \bigr\Vert \leq \rho \bigr\} , \end{aligned}$$

(8)

where $\rho >0$ is a scalar to be maximized.

For system (2), it is almost impossible to design the controller (4) such that the closed-loop dynamics (7) is globally asymptotically stable. The main aim of this paper designing the time-delayed feedback controller (4) such that the closed-loop error dynamics (7) is locally asymptotically stable. Meanwhile, we would like to obtain an estimate (of the form $X_{\rho }$) of the asymptotic stability region.

For the local analysis of dynamics (7), we introduce the box

$$\begin{aligned} \mathcal{X}=[-\bar{e}_{1},\bar{e}_{1}]\times [- \bar{e}_{2},\bar{e}_{2}] \times [-\bar{e}_{3}, \bar{e}_{3}], \end{aligned}$$

(9)

which can be equivalently written as follows:

$$\begin{aligned} \mathcal{X}=\operatorname{Co}\{v_{1},v_{2}, \ldots,v_{8}\} = \bigl\{ e\in \mathbb{R}^{3}: \vert h_{i}e \vert \leq \bar{e}_{i},i=1,2,3 \bigr\} , \end{aligned}$$

(10)

where “Co” is the convex hull, and $v_{i}$, $h_{j}$$(i=1,2,\ldots,8,j=1,2,3)$ are given as

$$\begin{array}{rl}& v_1={[\begin{array}{ccc}-{\overline{e}}_1& -{\overline{e}}_2& -{\overline{e}}_3\end{array}]}^T,v_2={[\begin{array}{ccc}-{\overline{e}}_1& -{\overline{e}}_2& {\overline{e}}_3\end{array}]}^T,\\ & v_3={[\begin{array}{ccc}-{\overline{e}}_1& {\overline{e}}_2& -{\overline{e}}_3\end{array}]}^T,v_4={[\begin{array}{ccc}-{\overline{e}}_1& {\overline{e}}_2& {\overline{e}}_3\end{array}]}^T,\\ & v_5={[\begin{array}{ccc}{\overline{e}}_1& -{\overline{e}}_2& -{\overline{e}}_3\end{array}]}^T,v_6={[\begin{array}{ccc}{\overline{e}}_1& -{\overline{e}}_2& {\overline{e}}_3\end{array}]}^T,\\ & v_7={[\begin{array}{ccc}{\overline{e}}_1& {\overline{e}}_2& -{\overline{e}}_3\end{array}]}^T,v_8={[\begin{array}{ccc}{\overline{e}}_1& {\overline{e}}_2& {\overline{e}}_3\end{array}]}^T,\\ & h_1=[\begin{array}{ccc}1& 0& 0\end{array}],h_2=[\begin{array}{ccc}0& 1& 0\end{array}],h_3=[\begin{array}{ccc}0& 0& 1\end{array}].\end{array}$$

Next, we introduce several indispensable integral inequalities.

Lemma 1

([26, 27])

For a given$n\times n$matrix$Z>0$, two scalarsaandbsatisfying$b>a$and a differentiable vector function$\omega (t) \in \mathbb{R}^{n}$, we have the following integral inequalities:

$$\begin{aligned} &(1) \quad (b-a) \int ^{b}_{a}\omega ^{T}(s)Z\rho (s) \, \mathrm{d}s \\ &\phantom{(1) \quad}\quad\geq \biggl( \int ^{b}_{a}\omega (s) \,\mathrm{d}s \biggr)^{T} Z \biggl( \int ^{b}_{a}\rho (s) \,\mathrm{d}s \biggr)+3 \varOmega _{1}^{T}Z\varOmega _{1}, \\ &(2) \quad (b-a) \int ^{b}_{a}\omega ^{T}(s)Z\omega (s) \, \mathrm{d}s\geq \biggl( \int ^{b}_{a}\omega (s) \,\mathrm{d}s \biggr)^{T} \\ &\phantom{(2) \quad}\qquad{}\times Z \biggl( \int ^{b}_{a}\omega (s) \,\mathrm{d}s \biggr)+3 \varOmega _{1}^{T}Z \varOmega _{1}+5\varOmega _{2}^{T}Z\varOmega _{2}, \\ & (3)\quad \frac{(b-a)^{2}}{2} \int ^{b}_{a} \int ^{b}_{\theta }\omega (s) \,\mathrm{d}s\,\mathrm{d} \theta \geq \biggl( \int ^{b}_{a} \int ^{b}_{ \theta }\omega (s) \,\mathrm{d}s\,\mathrm{d} \theta \biggr)^{T} \\ &\phantom{(1) \quad}\qquad{}\times Z \biggl( \int ^{b}_{a} \int ^{b}_{\theta }\omega (s) \,\mathrm{d}s \,\mathrm{d} \theta \biggr)+8\varOmega _{3}^{T}Z\varOmega _{3}, \end{aligned}$$

where

$$\begin{aligned} \varOmega _{1}={}& \int ^{b}_{a}\omega (s) \,\mathrm{d}s- \frac{2}{b-a} \int ^{b}_{a} \int ^{b}_{\theta }\omega (s) \,\mathrm{d}s\,\mathrm{d} \theta, \\ \varOmega _{2}={}& \int ^{b}_{a}\omega (s) \,\mathrm{d}s- \frac{6}{b-a} \int ^{b}_{a} \int ^{b}_{\theta }\omega (s) \,\mathrm{d}s\,\mathrm{d} \theta \\ &{}+\frac{12}{(b-a)^{2}} \int ^{b}_{a} \int ^{b}_{\lambda } \int ^{b}_{ \theta }\omega (s) \,\mathrm{d}s\,\mathrm{d} \theta \,\mathrm{d}\lambda, \\ \varOmega _{3}={}& \int ^{b}_{a} \int ^{b}_{\theta }\omega (s) \,\mathrm{d}s \,\mathrm{d} \theta -\frac{3}{b-a} \int ^{b}_{a} \int ^{b}_{\lambda } \int ^{b}_{ \theta }\omega (s) \,\mathrm{d}s\,\mathrm{d} \theta \,\mathrm{d}\lambda. \end{aligned}$$

3 Main results

In this section, we first consider the local stabilization problem by using the L–K stability theory and the quadratic system theory in the context of LMIs.

For presentation convenience, we denote

$$\begin{aligned} &\vartheta _{1}(t)\triangleq \int ^{t}_{t-\tau }e(s)\,\mathrm{d}s, \qquad\vartheta _{2}(t)\triangleq \int ^{0}_{-\tau } \int ^{t}_{t+\theta }e(s) \,\mathrm{d}s\,\mathrm{d}\theta, \\ &\mathcal{E}(R,1)\triangleq \bigl\{ e\in \mathbb{R}^{3}: e^{T}\operatorname{Re}\leq 1, R>0 \bigr\} ,\qquad \mathcal{D}(\kappa ) \triangleq \bigl\{ e\in \mathbb{R}^{3}: \Vert e \Vert ^{2} \leq \kappa ^{2} \bigr\} . \end{aligned}$$

Theorem 1

Let$\bar{e}_{1}>0$, $\bar{e}_{2}>0$, $\bar{e}_{3}>0$, $\delta >0$, and$\tau >0$be given scalars. The closed-loop dynamics (7) is locally asymptotically stable if there exist$9\times 9$-dimensional symmetric matrix$P=(P_{ij})_{3\times 3}$and$3\times 3$-dimensional matrices$Q>0$, $Z>0$, $R>0$, X, andYsuch that the following LMIs hold:

$$\begin{aligned} & \begin{bmatrix} \varPhi _{11}^{v_{i}}&\varPhi _{12}&\varPhi _{13}&\varPhi _{14}&\varPhi _{15}^{v_{i}} \\ *&\varPhi _{22}&\varPhi _{23}&\varPhi _{24}&-\delta Y^{T} \\ *&*&\varPhi _{33}&\varPhi _{34}&P_{12}^{T} \\ *&*&*&\varPhi _{44}&P_{13}^{T} \\ *&*&*&*&\varPhi _{55} \end{bmatrix}< 0,\quad i=1,2,\ldots,8, \end{aligned}$$

(11)

$$\begin{aligned} &P+ \begin{bmatrix} \varPi _{11}&6Z&-24Z/\tau \\ *&\varPi _{22}&\varPi _{23} \\ *&*&\varPi _{33} \end{bmatrix}\geq 0, \end{aligned}$$

(12)

$$\begin{aligned} &h_{1}^{T}h_{1}\leq \bar{e}_{1}^{2}R,\qquad h_{2}^{T}h_{2}\leq \bar{e}_{2}^{2}R,\qquad h_{3}^{T}h_{3} \leq \bar{e}_{3}^{2}R, \end{aligned}$$

(13)

where$P_{ij}$, $1\leq i\leq j\leq 3$, are$3\times 3$-dimensional, and

$$\begin{aligned} \varPhi _{11}^{v_{i}}={}&X\bigl[A+F+B(v_{i})\bigr]+ \bigl[A+F+B(v_{i})\bigr]^{T}X^{T}+Y \\ &{}+Y^{T}+P_{12}+P_{12}^{T}+\tau \bigl(P_{13}+P_{13}^{T}\bigr)+Q-9Z, \\ \varPhi _{12}={}&3Z-Y-P_{12}, \qquad \varPhi _{13}=P_{22}-P_{13}+ \tau P_{23}^{T}-24Z/ \tau, \\ \varPhi _{14}={}&P_{23}+\tau P_{33}+60Z/\bigl(\tau ^{2}\bigr),\qquad \varPhi _{22}=-Q-9Z, \\ \varPhi _{15}^{v_{i}}={}&-X+\delta \bigl[A+F+B(v_{i} \bigr]^{T}X^{T}+\delta Y^{T}+P_{11}, \\ \varPhi _{23}={}&-P_{22}+36Z/\tau,\qquad \varPhi _{24}=-P_{23}-60Z/\bigl(\tau ^{2}\bigr), \\ \varPhi _{33}={}&-P_{23}-P_{23}^{T}-192Z/ \bigl(\tau ^{2}\bigr), \qquad \varPhi _{44}=-720Z/\bigl( \tau ^{4}\bigr), \\ \varPhi _{34}={}&-P_{33}+360Z/\bigl(\tau ^{3}\bigr),\qquad \varPhi _{55}=\tau ^{2}Z-\delta (X+X)^{T}, \\ \varPi _{11}={}&{-}R+6\tau Z,\qquad \varPi _{22}=(4Q+18Z)/\tau, \\ \varPi _{23}={}&{-}6(Q+8Z)/\bigl(\tau ^{2}\bigr),\qquad \varPi _{33}=12(Q+12Z)/\bigl(\tau ^{3}\bigr). \end{aligned}$$

Moreover, if there exists feasible solutions, then the controller gain is given by the matrix$K=X^{-1}Y$.

Proof

Choose the following augmented L–K functional:

$$\begin{aligned} V(t)=&\eta ^{T}(t)P\eta (t)+ \int ^{t}_{t-\tau }e^{T}(s)Qe(s) \,\mathrm{d}s +\tau \int ^{0}_{-\tau } \int ^{t}_{t+\theta }\dot{e}^{T}(s)Z \dot{e}(s)\, \mathrm{d}s\,\mathrm{d}\theta, \end{aligned}$$

(14)

where $\eta (t)={[\begin{array}{ccc}{e}^T(t)& {\vartheta }_1^T(t)& {\vartheta }_2^T(t)\end{array}]}^T$.

Through some direct calculations, we can obtain that

$$\begin{aligned} \dot{V}(t)={}&2\eta ^{T}(t)P\dot{\eta }(t)+e^{T}(t)Qe(t)-e^{T}(t- \tau )Qe(t- \tau ) \\ &{}+\tau ^{2}\dot{e}^{T}(t)Z\dot{e}(t)-\tau \int ^{t}_{t-\tau }\dot{e}^{T}(s)Z \dot{e}(s)\, \mathrm{d}s. \end{aligned}$$

(15)

Using the second inequality in Lemma 1, we see that

$$\begin{aligned} &-\tau \int ^{t}_{t-\tau }\dot{e}^{T}(s)Z\dot{e}(s)\, \mathrm{d}s \leq - \begin{bmatrix} \xi _{1}(t) \\ \xi _{2}(t) \\ \xi _{3}(t) \end{bmatrix}^{T} \begin{bmatrix} Z&0&0 \\ 0&3Z&0 \\ 0&0&5Z \end{bmatrix} \begin{bmatrix} \xi _{1}(t) \\ \xi _{2}(t) \\ \xi _{3}(t) \end{bmatrix}, \end{aligned}$$

(16)

where

$$\begin{aligned} &\xi _{1}(t)=e(t)-e(t-\tau ),\qquad \xi _{2}(t)=e(t)+e(t-\tau )-(2/\tau ) \vartheta _{1}(t), \\ &\xi _{3}(t)=e(t)-e(t-\tau )+(6/\tau )\vartheta _{1}(t)- \bigl(12/\tau ^{2}\bigr) \vartheta _{2}(t). \end{aligned}$$

Denoting $\tilde{A}(e)\triangleq A+F+K+B(e)$, from (7) it follows that

$$\begin{aligned} 2\bigl[e^{T}(t)+\delta \dot{e}^{T}(t)\bigr]X\bigl[ \tilde{A}(e)e(t)-Ke(t-\tau )- \dot{e}(t)\bigr]=0. \end{aligned}$$

(17)

Adding the left side of (17) to $\dot{V}(t)$ and using (16) yield that

$$\begin{aligned} \dot{V}(t)\leq \zeta ^{T}(t)\varPhi (e)\zeta (t), \end{aligned}$$

(18)

where $\zeta (t)={[\begin{array}{ccccc}{e}^T(t)& e^T(t-\tau )& {\vartheta }_1^T(t)& {\vartheta }_2^T(t)& {\dot{e}}^T(t)\end{array}]}^T$, and

$$\begin{aligned} \varPhi (e)= \begin{bmatrix} \varPhi _{11}(e)&\tilde{\varPhi }_{12}&\varPhi _{13}&\varPhi _{14}&\varPhi _{15}(e) \\ *&\varPhi _{22}&\varPhi _{23}&\varPhi _{24}&-\delta K^{T}X^{T} \\ *&*&\varPhi _{33}&\varPhi _{34}&P_{12}^{T} \\ *&*&*&\varPhi _{44}&P_{13}^{T} \\ *&*&*&*&\varPhi _{55} \end{bmatrix} \end{aligned}$$

with

$$\begin{aligned} \varPhi _{11}(e)={}&X\bigl[A+F+B(e)+K\bigr]+\bigl[A+F+B(e)+K \bigr]^{T}X^{T}+P_{12} \\ &{} +P_{12}^{T}+\tau \bigl(P_{13}+P_{13}^{T} \bigr)+Q-9Z, \tilde{\varPhi }_{12}=3Z-K^{T}X^{T}-P_{12}, \\ \varPhi _{15}(e)={}&{-}X+\delta \bigl[A+F+B(e)+K\bigr]^{T}X^{T}+P_{11}. \end{aligned}$$

Let $Y\triangleq XK$ and note that $\varPhi (e)$ is affine with respect to $e_{1}$, $e_{2}$, and $e_{3}$. Hence, if LMIs (11) were true, then the inequality $\varPhi (e)<0$ could be ensured on $\mathcal{X}$. Then we have

$$\begin{aligned} \dot{V}(t)< 0 \end{aligned}$$

(19)

on the box $\mathcal{X}$, which implies that

$$\begin{aligned} V(t)\leq V(0), \quad t\geq 0. \end{aligned}$$

(20)

On the other hand, using the inequalities (1) and (3) in Lemma 1, we have [28, 29]

$$\begin{aligned} V(t)\geq {}&\eta ^{T}(t)P\eta (t)+(1/\tau )\vartheta _{1}^{T}(t)Q \vartheta _{1}(t)+(3/\tau )\bigl[ \vartheta _{1}(t)-(2/\tau )\vartheta _{2}(t) \bigr]^{T} \\ &{}\times Q\bigl[\vartheta _{1}(t)-(2/\tau )\vartheta _{2}(t) \bigr]+(2/\tau )\bigl[ \tau e(t)-\vartheta _{1}(t)\bigr]^{T} \\ &{}\times Z\bigl[\tau e(t)-\vartheta _{1}(t)\bigr]+(4/\tau )\bigl[\tau e(t)+2 \vartheta _{1}(t)-(6/\tau )\vartheta _{2}(t) \bigr]^{T} \\ &{}\times Z\bigl[\tau e(t)+2\vartheta _{1}(t)-(6/\tau )\vartheta _{2}(t)\bigr]= \eta ^{T}(t) (P+\varPi )\eta (t), \end{aligned}$$

(21)

where

$$\begin{aligned} &\varPi = \begin{bmatrix} 6\tau Z&6Z&-24Z/\tau \\ *&\varPi _{22}&\varPi _{23} \\ *&*&\varPi _{33} \end{bmatrix}. \end{aligned}$$

By (12) and (21) it follows that

$$\begin{aligned} V(t)\geq e^{T}(t)\operatorname{Re}(t), \end{aligned}$$

(22)

which shows that the L–K functional $V(t)$ is positive definite.

In addition, from (13) we can infer that

$$\begin{aligned} \mathcal{E}(R,1)\subseteq \mathcal{X}. \end{aligned}$$

(23)

For all initial conditions $\phi (s)\in X_{\rho }$ satisfying $V(0)\leq 1$, we can see from (20) and (22) that all trajectories $e(t)$ are contained in the set $\mathcal{E}(R,1)$. By (19) and (23) we conclude that the closed-loop dynamics (7) is asymptotically stable for all $\phi (s)$ satisfying $V(0)\leq 1$ [20, 24], and this completes the proof. □

Remark 1

The finance model (2) is essentially a particular kind of quadratic system [20–25]. However, it is worth pointing out that the existing results concerning quadratic systems cannot be directly applied to the finance system (2) subject to TDFC. Moreover, differently from the results in [23–25], the augmented L–K functional and the advanced integral inequalities are utilized in this paper. In addition, it is worth mentioning that the matrix P in Theorem 1 is not required to be positive definite.

Remark 2

Model (2) considered in this paper is simple yet typical. In fact, several recent finance models are derived from model (2), such as the hyperchaotic finance system [5], the delayed finance system [6], and fractional-order economic system [7]. The proposed results in this paper can be readily extended to the finance systems discussed in [5, 6] and model (1) in this paper.

If we employ the nondelayed feedback

$$\begin{aligned} u(t)=K\bigl(x(t)-x^{*}\bigr), \end{aligned}$$

(24)

then the closed-loop dynamics (7) becomes

$$\begin{aligned} \dot{e}(t)=\bigl[A+F+K+B(e)\bigr]e(t). \end{aligned}$$

(25)

Correspondingly, we easily obtain the following condition.

Corollary 1

Let$\bar{e}_{1}>0$, $\bar{e}_{2}>0$, $\bar{e}_{3}>0$, and$\delta >0$be given scalars. The chaotic finance system (2) can be locally asymptotically stabilized by the feedback controller (24) with$K=X^{-1}Y$if there exist$3\times 3$-dimensional matrices$P>0$, X, andYsuch that the following LMIs hold:

$$\begin{aligned} & \begin{bmatrix} \varPsi _{1}^{v_{i}}&\varPsi _{2}^{v_{i}} \\ *&-\delta (X+X)^{T} \end{bmatrix}< 0, \quad i=1,2,\ldots,8, \end{aligned}$$

(26)

$$\begin{aligned} &h_{1}^{T}h_{1}\leq \bar{e}_{1}^{2}P,\qquad h_{2}^{T}h_{2}\leq \bar{e}_{2}^{2}P,\qquad h_{3}^{T}h_{3} \leq \bar{e}_{3}^{2}P, \end{aligned}$$

(27)

where

$$\begin{aligned} &\varPsi _{1}^{v_{i}}=X\bigl[A+F+B(v_{i})\bigr]+ \bigl[A+F+B(v_{i})\bigr]^{T}X^{T}+Y+Y^{T}, \\ &\varPsi _{2}^{v_{i}}=-X+\delta \bigl[A+F+B(v_{i} \bigr]^{T}X^{T}+\delta Y^{T}+P. \end{aligned}$$

We further consider the estimate of the asymptotic stability region involved in Theorem 1 and Corollary 1. To this end, we introduce the inequalities

$$\begin{aligned} \textstyle\begin{cases} P\leq \operatorname{diag}\{P_{1},P_{2},P_{3}\},\quad P_{1}\leq p_{1}I, \\ P_{2}\leq p_{2}I,\qquad P_{3}\leq p_{3}I,\qquad Q\leq qI, \qquad Z\leq zI, \end{cases}\displaystyle \end{aligned}$$

(28)

where $P_{i}>0$, $p_{i}>0$$(i=1,2,3)$, $q>0$, and $z>0$.

Using (28) and the Jensen integral inequalities [30], it follows that

$$\begin{aligned} V(0)\leq {}&\lambda _{1}\mathop{\operatorname{max}}_{s\in [-\tau,0]} \bigl\Vert \phi (s) \bigr\Vert ^{2}+ \lambda _{2}{\operatorname{max}}_{s\in [-\tau,0]} \bigl\Vert \dot{\phi }(s) \bigr\Vert ^{2} \\ \leq {}&\tilde{\lambda }_{1}\mathop{\operatorname{max}}_{s\in [-\tau,0]} \bigl\Vert \phi (s) \bigr\Vert ^{2}+\tilde{\lambda }_{2} \mathop{\operatorname{max}}_{s\in [-\tau,0]} \bigl\Vert \dot{\phi }(s) \bigr\Vert ^{2}, \end{aligned}$$

(29)

where

$$\begin{aligned} &\lambda _{1}=\bigl[\lambda _{M}(P_{1})+\tau ^{2}\lambda _{M}(P_{2})+\bigl( \tau ^{4}/4\bigr)\lambda _{M}(P_{3})+\tau \lambda _{M}(Q)\bigr], \\ &\lambda _{2}=\bigl(\tau ^{3}/2\bigr)\lambda _{M}(Z), \qquad\tilde{\lambda }_{1}=p_{1}+ \tau ^{2}p_{2}+\bigl(\tau ^{4}/4\bigr)p_{3}+ \tau q, \qquad \tilde{\lambda }_{2}=\bigl(\tau ^{3}/2\bigr)z. \end{aligned}$$

Then the maximization of the estimate of the asymptotic stability region in Theorem 1 can be formulated as follows.

Problem 1

$\min _{P,P_{1},P_{2},P_{3},Q,Z,X,Y,p_{1},p_{2},p_{3},q,z} ( \tilde{\lambda }_{1}+\tilde{\lambda }_{2})$ s.t. LMIs (11)–(13) and (28). hold.

By solving Problem 1 we can obtain the scalars $\lambda _{1}$ and $\lambda _{2}$. Recalling that the initial condition $\phi (s)$ satisfies $V(0)\leq 1$, by (29) we can require $\phi (s)$ to satisfy

$$\begin{aligned} \lambda _{1}\mathop{\operatorname{max}}_{s\in [-\tau,0]} \bigl\Vert \phi (s) \bigr\Vert ^{2}+ \lambda _{2}\mathop{\operatorname{max}}_{s\in [-\tau,0]} \bigl\Vert \dot{\phi }(s) \bigr\Vert ^{2} \leq 1. \end{aligned}$$

(30)

From (30) we see that $\|\phi (s)\|_{c}^{2}\leq 1/\rho _{1}$, which shows that all admissible $\phi (s)$ are contained in the ball $\mathcal{D}(\sqrt{1/\lambda _{1}})$. Let us choose a box $\tilde{\mathcal{X}}=[-\omega,\omega ]\times [-\omega,\omega ] \times [-\omega,\omega ]$ such that the ball $\mathcal{D}(\sqrt{1/\lambda _{1}})$ is contained in $\tilde{\mathcal{X}}$, that is, $\mathcal{D}(\sqrt{1/\lambda _{1}})\subseteq \tilde{\mathcal{X}}$. Recalling that $\dot{\phi }(s)=[A+F+B(\phi )]\phi (s)$, we see that the matrix inequality

$$\begin{aligned} \bigl[A+F+B(\phi )\bigr]^{T}\bigl[A+F+B(\phi )\bigr]\leq \gamma I \end{aligned}$$

(31)

can ensure that $\dot{\phi }^{T}(s)\dot{\phi }(s)\leq \gamma \phi ^{T}(s)\phi (s)$. Noting that $\phi \in \mathcal{D}(\sqrt{1/\lambda _{1}})$, it follows that the matrix inequality (31) can be ensured by the LMIs

$$\begin{aligned} & \begin{bmatrix} \gamma I&[A+F+B(\tilde{v}_{i})]^{T} \\ *&I \end{bmatrix}\geq 0,\quad i=1,2, \ldots,8, \end{aligned}$$

(32)

where $\tilde{v}_{i}$$(i=1,2,\ldots,8)$ are the vertices of the box $\tilde{\mathcal{X}}$.

By solving LMIs (32) can readily obtain the minimum γ. Furthermore, from (29) and (31) we see that the maximum admissible bound of the initial condition set $X_{\rho }$ involved in Theorem 1 can be given by $\rho =1/\sqrt{(\lambda _{1}+\gamma \lambda _{2})}$.

In Corollary 1 the ellipsoid $\mathcal{E}(P,1)$ can be seen as an estimate of the asymptotic stability region. The corresponding optimization problem can be written as

Problem 2

$\min_{P,X,Y,p} p$ s.t. LMIs (26)–(27) and $P\leq pI$ hold.

Remark 3

In the past more than a decade the TDFC strategy has been widely applied for controlling chaos in nonlinear finance systems [15–19]. Unlike most existing results, our obtained results are based on the rigorous mathematical theories such as the L–K theorem and the quadratic systems theory. Moreover, the results in this paper are based on the finance system itself, not on its linearized mode. In addition, it is worth mentioning that the estimate $X_{\rho }$ and its maximization of the asymptotic stability region have been discussed in this paper. It is obvious that our proposed results are indispensable supplements of the existing ones.

Remark 4

The obtained results in this paper are expressed by means of LMIs, which can be conveniently solved by Matlab LMI Control Toolbox.

4 Numerical simulations

In this section, we illustrate the effectiveness of our proposed results via numerical simulations. Choosing $a=2.5$, $b=0.2$, and $c=1.2$, we easily verify that system (2) has three unstable fixed points

$$\begin{aligned} \mathbb{P}_{1}^{*}\triangleq (\nu _{1},\nu _{2},-\nu _{3}), \qquad \mathbb{P}_{2}^{*} \triangleq (-\nu _{1},\nu _{2},\nu _{3}),\qquad \mathbb{P}_{3}^{*}\triangleq (0,5,0), \end{aligned}$$

where $\nu _{1}=0.5774$, $\nu _{2}=3.3333$, and $\nu _{3}=0.4811$.

First, we address the local stabilization problem via the time-delayed feedback controller (4). For the fixed point $\mathbb{P}_{1}^{*}$, by solving the Problem 1 with $\tau =0.5$, $\bar{e}_{1}=0.46$, $\bar{e}_{2}=0.46$, $\bar{e}_{3}=1$, and $\delta =0.33$, we obtain $\lambda _{1}=19.0787$ and $\lambda _{2}=0.3153$ and the following controller gain:

$$\begin{aligned} K= \begin{bmatrix} -1.6647&2.0298&0.7061 \\ -1.2980&-3.2695&0.1205 \\ 0.5648&-0.1501&-0.1977 \end{bmatrix} \bigl(\mathbb{P}_{1}^{*} \bigr). \end{aligned}$$

Choosing $\omega =0.2290$ such that $\mathcal{D}(\sqrt{1/\lambda _{1}})\subseteq \tilde{\mathcal{X}}$ and applying LMIs (32), we get the minimum $\gamma =5.6445$. Then we obtain the bound $\rho =0.2190$ of the initial condition set $X_{\rho }$. Similarly, for the fixed point $\mathbb{P}_{2}^{*}$, we have $\rho =0.2190$ and

$$\begin{aligned} K= \begin{bmatrix} -1.6646&-2.0300&0.7064 \\ 1.2980&-3.2693&-0.1204 \\ 0.5646&0.1504&-0.1981 \end{bmatrix} \bigl(\mathbb{P}_{2}^{*} \bigr). \end{aligned}$$

Next, we consider the local stabilization problem via the nondelayed feedback controller (24). Choosing $\bar{e}_{1}=\bar{e}_{2}=5$, $\bar{e}_{3}=10$, and $\delta =1$ and then solving Problem 2, we obtain the ellipsoid $\mathcal{E}(P,1)$ and the corresponding controller gains with

$$\begin{aligned} &P= \begin{bmatrix} 0.0400&0.0000&-0.0000 \\ 0.0000&0.0400&-0.0000 \\ -0.0000&-0.0000&0.0370 \end{bmatrix} \bigl(\mathbb{P}_{1}^{*}, \mathbb{P}_{2}^{*}, \mathbb{P}_{3}^{*} \bigr), \\ &K= \begin{bmatrix} -9.9927&-0.5774&-1.0000 \\ 1.1548&-17.2375&-0.0000 \\ 1.0000&-0.0000&0.2000 \end{bmatrix} \bigl(\mathbb{P}_{1}^{*} \bigr), \\ &K= \begin{bmatrix} -10.0146&0.5774&-1.0000 \\ -1.1548&-17.1628&-0.0000 \\ 1.0000&0.0000&0.2000 \end{bmatrix} \bigl(\mathbb{P}_{2}^{*} \bigr), \\ &K= \begin{bmatrix} -11.6791&0.0000&-1.0000 \\ -0.0000&-17.1725&0.0000 \\ 1.0000&0.0000&0.2000 \end{bmatrix} \bigl(\mathbb{P}_{3}^{*} \bigr). \end{aligned}$$

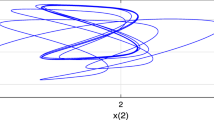
Using the obtained controller gains, we plotted the state responses of the closed-loop dynamics in Figs. 1–5, from which it is clear that our proposed control strategy is really effective in controlling the chaotic finance system (2).

Figure 1

State responses of the closed-loop dynamics (7) ($\mathbb{P}_{1}^{*}$)

Figure 2

State responses of the closed-loop dynamics (7) ($\mathbb{P}_{2}^{*}$)

Figure 3

State responses of the closed-loop dynamics (25) ($\mathbb{P}_{1}^{*}$)

Figure 4

State responses of the closed-loop dynamics (25) ($\mathbb{P}_{2}^{*}$)

Figure 5

State responses of the closed-loop dynamics (25) ($\mathbb{P}_{3}^{*}$)

5 Conclusions

In this paper, we have considered the local control problem for a chaotic finance system via TDFC scheme. By using an augmented L–K functional, the quadratic system theory, and rigorous mathematical analysis, we have established the local stabilization conditions in terms of LMIs. Subsequently, we discussed the estimate and its maximization of the asymptotic stability region. Finally, by simulation results we demonstrated the effectiveness of the obtained conditions. The techniques developed in this paper can be employed to investigate the synchronization problem [8, 11, 31] and the $H_{\infty }$ control problem [19, 32, 33]. In addition, it is worth pointing out that there exists conservatism in our results. By utilizing the recently developed integral inequalities [34] and L–K functionals [35, 36] we can establish less conservative results, which is our further work.