1 Introduction

Let n be a positive integer, \(n\geq 2\) and \(N=\{1,2,\ldots ,n\}\). \(\mathbb{C}\) (or, respectively, \(\mathbb{R}\)) denotes the set of all complex (or, respectively, real) numbers, \(\mathbb{C}^{n\times n}\) (or, respectively, \(\mathbb{R}^{n\times n}\)) denotes the set of all \({n\times n}\) complex (or, respectively, real) matrices and I stands for the identity matrix. Let \(A=[a_{ij}]\in \mathbb{C}^{n\times n}\) and \(\sigma (A)\) be the set of all eigenvalues of A. Eigenvalue problems of matrices has a wide range of practical applications, such as image restoration [1], linear and multilinear algebra [2], higher order Markov chains [3], etc. In order to locate all eigenvalues of matrices, the authors in [4,5,6,7,8,9,10,11,12,13] found some regions including all eigenvalues of matrices in the complex plane. The first work is due to Geršgorin, who presented such a region called the Geršgorin disk theorem [5], which consists of n disks centered at the diagonal elements of the matrix.

Theorem 1

([5, Geršgorin set])

Let \(A=[a_{ij}]\in \mathbb{C}^{n\times n}\). Then

$$\begin{aligned}& \sigma (A) \subseteq \varGamma (A) = \bigcup_{i\in N} \varGamma _{i}(A), \end{aligned}$$

where

$$\begin{aligned}& \varGamma _{i}(A)= \bigl\{ z\in \mathbb{C}: \vert z-a_{ii} \vert \leq r_{i}(A) \bigr\} \end{aligned}$$

and

$$\begin{aligned}& r_{i}(A)=\sum_{j\in N, j\neq i} \vert a_{ij} \vert . \end{aligned}$$

Although Geršgorin set is concise, its result is not accurate enough. Hence, tighter sets than \(\varGamma (A)\) are conjectured till now. The Dashnic–Zusmanovich localization set, which is tighter than Geršgorin set, provided by Dashnic–Zusmanovich (DZ) [14], is described as follows.

Theorem 2

([14, DZ set])

Let \(A=[a_{ij}]\in {\mathbb{C}} ^{n\times n}\). Then

$$\begin{aligned}& \sigma (A)\subseteq D(A)=\bigcap_{i\in N}\bigcup _{j\in N, j\neq i} D _{ij}(A), \end{aligned}$$

where

$$\begin{aligned}& D_{ij}(A)=\bigl\{ z\in \mathbb{C}: \vert z-a_{ii} \vert \bigl( \vert z-a_{jj} \vert -r^{i}_{j}(A) \bigr)\leq r _{i}(A) \vert a_{ji} \vert \bigr\} \end{aligned}$$

and

$$\begin{aligned}& r_{j}^{i}(A)=r_{j}(A)- \vert a_{ji} \vert . \end{aligned}$$

It is generally accepted that an eigenvalue localization set is connected with one kind of non-singular matrices [7, 8]. The non-singularity criterions for matrices derived from the Geršgorin set in Theorem 1 and DZ set in Theorem 2 are as follows.

Theorem 3

([7])

If \(A=[a_{ij}]\in {\mathbb{C}} ^{n\times n}\) is an SDD matrix, i.e., for each \(i\in N\), we have

$$\begin{aligned}& \vert a_{ii} \vert >r_{i}(A), \end{aligned}$$

then it is non-singular.

Theorem 4

([7])

If \(A=[a_{ij}]\in {\mathbb{C}} ^{n\times n}\) is a DZ matrix, i.e., there exists an index \(i\in N\), for all \(j\in N\), \(j\neq i\),

$$\begin{aligned}& \vert a_{ii} \vert \bigl( \vert a_{jj} \vert -r_{j}^{i}(A)\bigr)>r_{i}(A) \vert a_{ji} \vert , \end{aligned}$$

then it is non-singular.

By excluding some proper subsets that contain no eigenvalues of matrices from some existing eigenvalue localization sets, the authors in [15,16,17,18] obtained some tighter sets and some sufficient conditions for non-singularity of matrices. Inspired by these effective results, we in this paper first present a new eigenvalue localization set by excluding some proper subsets from DZ set, and we obtain a new sufficient condition for non-singularity of matrices. In order to precisely locate all eigenvalues of matrices, we in Sect. 3 present another set which includes two positive integers s and k, and show by an example that, by adjusting the parameters s and k, one can locate all eigenvalues and judge the non-singularity of matrices accurately.

2 Exclusion sets in Dashnic–Zusmanovich localization sets

In this section, we present a new eigenvalue inclusion set by excluding some proper subsets that contain no eigenvalues of matrices from DZ sets, and, as an application, we provide a sufficient condition to judge the non-singularity of matrices.

Theorem 5

Let \(A=[a_{ij}]\in \mathbb{C}^{n\times n}\). Then

$$\begin{aligned}& \sigma (A)\subseteq \varOmega (A)=\bigcap_{i\in N} \bigcup_{j\in N, j \neq i} \bigl(D_{ij}(A)\setminus \varOmega _{ij}(A) \bigr), \end{aligned}$$

where

$$\begin{aligned}& \varOmega _{ij}(A)=\bigl\{ z\in \mathbb{C}: \vert z-a_{ii} \vert \bigl( \vert z-a_{jj} \vert +r_{j}^{i}(A)\bigr)< \bigl(2 \vert a _{ij} \vert -r_{i}(A)\bigr) \vert a_{ji} \vert \bigr\} . \end{aligned}$$

Proof

Let λ be an eigenvalue of A and \(x=(x_{1},\ldots ,x_{n})^{T} \in \mathbb{C}^{n}\setminus \{0\}\) be its eigenvector. Then

$$\begin{aligned}& Ax=\lambda x. \end{aligned}$$
(1)

Let \(|x_{p}|=\max _{j\in N}|x_{j}|\). Obviously, \(|x_{p}|>0\). For any \(i\in N\), \(i\neq p\), the pth formula of (1) can be written as

$$\begin{aligned}& (\lambda -a_{pp})x_{p}=\sum _{s\neq p,i}a_{ps}x_{s}+a_{pi}x_{i}. \end{aligned}$$
(2)

Taking the absolute value of (2) and using the triangle inequality, we have

$$ \vert \lambda -a_{pp} \vert \vert x_{p} \vert \leq \sum_{s\neq p,i} \vert a_{ps} \vert \vert x_{s} \vert + \vert a_{pi} \vert \vert x _{i} \vert \leq r_{p}^{i}(A) \vert x_{p} \vert + \vert a_{pi} \vert \vert x_{i} \vert , $$

i.e.,

$$ \bigl( \vert \lambda -a_{pp} \vert -r_{p}^{i}(A)\bigr) \vert x_{p} \vert \leq \vert a_{pi} \vert \vert x_{i} \vert . $$
(3)

If \(|x_{i}|>0\), then from the ith formula of (1), i.e.,

$$\begin{aligned}& (\lambda -a_{ii})x_{i}=\sum _{t\neq i}a_{it}x_{t}, \end{aligned}$$
(4)

we have

$$\begin{aligned}& \vert \lambda -a_{ii} \vert \vert x_{i} \vert \leq r_{i}(A) \vert x_{p} \vert . \end{aligned}$$
(5)

Multiplying (3) and (5) and noting that \(|x_{p}||x_{i}|>0\), we have

$$\begin{aligned}& \vert \lambda -a_{ii} \vert \bigl( \vert \lambda -a_{pp} \vert -r_{p}^{i}(A)\bigr) \leq r_{i}(A) \vert a_{pi} \vert . \end{aligned}$$
(6)

If \(|x_{i}|=0\) in (3), then \(|\lambda -a_{pp}|-r _{p}^{i}(A)\leq 0\) as \(|x_{p}|>0\), which implies that (6) also holds. Therefore, \(\lambda \in D_{ip}(A)\). On the other hand, from (2) and (4), we have

$$\begin{aligned}& a_{pi}x_{i}=(\lambda -a_{pp})x_{p}- \sum_{s\neq p,i}a_{ps}x_{s} \end{aligned}$$

and

$$\begin{aligned}& a_{ip}x_{p}=(\lambda -a_{ii})x_{i}- \sum_{t\neq i,p}a_{it}x_{t}, \end{aligned}$$

which leads to

$$\begin{aligned} \vert a_{pi} \vert \vert x_{i} \vert \leq & \vert \lambda -a_{pp} \vert \vert x_{p} \vert +\sum_{s\neq p,i} \vert a _{ps} \vert \vert x_{s} \vert \leq \vert \lambda -a_{pp} \vert \vert x_{p} \vert +\sum _{s\neq p,i} \vert a_{ps} \vert \vert x _{p} \vert \\ =&\bigl( \vert \lambda -a_{pp} \vert +r_{p}^{i}(A)\bigr) \vert x_{p} \vert \end{aligned}$$
(7)

and

$$\begin{aligned}& \vert a_{ip} \vert \vert x_{p} \vert \leq \vert \lambda -a_{ii} \vert \vert x_{i} \vert + \sum_{t\neq i,p} \vert a_{it} \vert \vert x _{t} \vert \leq \vert \lambda -a_{ii} \vert \vert x_{i} \vert +r_{i}^{p}(A)) \vert x_{p} \vert , \end{aligned}$$

i.e.,

$$\begin{aligned}& \bigl( \vert a_{ip} \vert -r_{i}^{p}(A) \bigr) \vert x_{p} \vert \leq \vert \lambda -a_{ii} \vert \vert x_{i} \vert . \end{aligned}$$
(8)

By (7) and (8), we have

$$\begin{aligned}& \vert a_{pi} \vert \bigl(2 \vert a_{ip} \vert -r_{i}(A)\bigr)\leq \vert \lambda -a_{ii} \vert \bigl( \vert \lambda -a_{pp} \vert +r _{p}^{i}(A) \bigr), \end{aligned}$$

which implies that \(\lambda \notin \varOmega _{ip}(A)\). Hence, \(\lambda \in (D_{ip}(A)\setminus \varOmega _{ip}(A) )\).

For some certain \(i\in N\), \(i\neq p\), since we do not know which p is appropriate to λ, we can only conclude that

$$\begin{aligned}& \lambda \in \bigcup_{p\in N, i \neq p} \bigl(D_{ip}(A) \setminus \varOmega _{ip}(A) \bigr). \end{aligned}$$

Furthermore, by the arbitrariness of i, we have

$$\begin{aligned}& \lambda \in \bigcap_{i\in N}\bigcup _{j\in N, j\neq i} \bigl(D_{ij}(A) \setminus \varOmega _{ij}(A) \bigr). \end{aligned}$$

The conclusion follows. □

Now, a comparison theorem for Theorems 1, 2 and 5 is obtained.

Theorem 6

Let \(A=[a_{ij}]\in \mathbb{C}^{n\times n}\). Then

$$\begin{aligned}& \varOmega (A)\subseteq D(A)\subseteq \varGamma (A). \end{aligned}$$

Proof

It is showed in Theorem 7 of [19] that \(D(A)\subseteq \varGamma (A)\). For any \(i,j\in N\), \(j\neq i\), by \((D_{ij}(A)\setminus \varOmega _{ij}(A)) \subseteq D_{ij}(A)\), obviously,

$$\begin{aligned}& \bigcap_{i\in N}\bigcup_{j\in N, i\neq j} \bigl(D_{ij}(A)\setminus \varOmega _{ij}(A)\bigr)\subseteq \bigcap_{i\in N}\bigcup_{j\in N, i\neq j}D_{ij}(A). \end{aligned}$$

Hence, \(\varOmega (A)\subseteq D(A)\) holds. □

Next, based on the fact that \(\det (A)=0\) if and only if \(0\in \sigma (A)\) for a matrix A, we can obtain the following condition for judging the non-singularity of matrices.

Corollary 1

Let \(A=[a_{ij}]\in \mathbb{C}^{n\times n}\). If there exists \(i\in N\), for any \(j\in N\), \(j\neq i\), either

$$\begin{aligned}& \vert a_{ii} \vert \bigl( \vert a_{jj} \vert -r_{j}^{i}(A) \bigr)>r_{i}(A) \vert a_{ji} \vert , \end{aligned}$$
(9)

or

$$\begin{aligned}& \vert a_{ii} \vert \bigl( \vert a_{jj} \vert +r_{j}^{i}(A)\bigr)< \bigl(2 \vert a_{ij} \vert -r_{i}(A)\bigr) \vert a_{ji} \vert , \end{aligned}$$
(10)

then A is non-singular.

Proof

Let \(0\in \sigma (A)\). By Theorem 5, we have \(0\in \varOmega (A)\), i.e., for each \(i\in N\), there exists \(j\in N\), \(j \neq i\), such that

$$\begin{aligned}& \vert a_{ii} \vert \bigl( \vert a_{jj} \vert -r_{j}^{i}(A)\bigr)\leq r_{i}(A) \vert a_{ji} \vert \end{aligned}$$

and

$$\begin{aligned}& \vert a_{ii} \vert \bigl( \vert a_{jj} \vert +r_{j}^{i}(A)\bigr)\geq \bigl(2 \vert a_{ij} \vert -r_{i}(A)\bigr) \vert a_{ji} \vert . \end{aligned}$$

This contradicts (9) and (10). Consequently, \(0\notin \sigma (A)\), that is, A is non-singular. □

Remark 1

(i) Let i and j be any two elements of N, and \(i\neq j\). If \((2|a_{ij}|-r_{i}(A))|a_{ji}|>0\), then, by \(|a_{ij}|\leq r_{i}(A)\), we have \(0<2|a_{ij}|-r_{i}(A)\leq r_{i}(A)\) and

$$\begin{aligned} \vert z-a_{ii} \vert \bigl( \vert z-a_{jj} \vert -r^{i}_{j}(A)\bigr) \leq & \vert z-a_{ii} \vert \bigl( \vert z-a_{jj} \vert +r ^{i}_{j}(A) \bigr) \\ < &\bigl(2 \vert a_{ij} \vert -r_{i}(A)\bigr) \vert a_{ji} \vert \\ \leq & r_{i}(A) \vert a_{ji} \vert , \end{aligned}$$

which implies that

$$\begin{aligned}& \varOmega _{ij}(A)\subseteq D_{ij}(A) \quad \mbox{and}\quad \bigl(D_{ij}(A)\setminus \varOmega _{ij}(A) \bigr)\subseteq D_{ij}(A). \end{aligned}$$
(11)

That is to say, \(\varOmega _{ij}(A)\) is well defined. If \((2|a_{ij}|-r _{i}(A))|a_{ji}|\leq 0\), then \(\varOmega _{ij}(A)=\emptyset \). Obviously, (11) also holds. Here, \(\varOmega _{ij}(A)\) is called the exclusion set of \(D_{ij}(A)\).

(ii) As has been shown in [7, 8], the wider the class of non-singular matrices is, the tighter eigenvalue localization set it will lead to. Obviously, this conclusion, in turn, holds true. By Corollary 1, one can conclude that the conditions of Corollary 1 for judging the non-singularity of matrices are weaker than those in Theorems 3 and 4.

Next, an example is given to show that \(\varOmega (A)\) can catch all eigenvalues of a matrix A more precisely than \(\varGamma (A)\) and \(D(A)\), and that Theorems 3 and 4 cannot be used to judge the non-singularity of A in some cases, but Corollary 1 works better.

Example 1

Let

$$A=\begin{bmatrix} 11&4+\mathbf{{i}}&0&15-\mathbf{{i}} \\ -2-\mathbf{{i}}&10&5-\mathbf{{i}}&0 \\ 0&6&12+\mathbf{{i}}&4 \\ 16&2&0&11 \end{bmatrix}. $$

By computations, all eigenvalues of \(\mathcal{A}\) are \(26.4293-0.7552\mathbf{{i}}\), \(-4.4930+0.6450\mathbf{{i}}\), \(16.0853+0.0217\mathbf{{i}}\), \(5.9784+1.0885\mathbf{{i}}\). Next, the eigenvalue location and the determination of non-singularity for A are considered.

(I) Eigenvalue inclusion sets for A.

From Theorem 1, we have

$$\begin{aligned}& \varGamma (A)= \bigl\{ z\in \mathbb{C}: \vert z-11 \vert \leq 19.1564 \bigr\} . \end{aligned}$$

From Theorem 2, we have

$$\begin{aligned}& D(A)=D_{24}(A)= \bigl\{ z\in \mathbb{C}: \vert z-10 \vert \bigl( \vert z-11 \vert -16 \bigr)\leq 15.0662 \bigr\} . \end{aligned}$$

From Theorem 5, we have

$$\begin{aligned}& \varOmega (A)= \bigl[D_{12}(A)\cup D_{13}(A) \cup \bigl(D_{24}(A)\setminus \varOmega _{41}(A)\bigr) \cup \bigl(D_{43}(A)\cap \varOmega _{14}(A)\bigr)\bigr], \end{aligned}$$

where

$$\begin{aligned}& D_{12}(A)= \bigl\{ z\in \mathbb{C}: \vert z-11 \vert \bigl( \vert z-10 \vert -5.0990 \bigr)\leq 42.8356 \bigr\} , \\& D_{13}(A)= \bigl\{ z\in \mathbb{C}: \vert z-11 \vert \bigl( \vert z-12-\mathbf{{i}} \vert -10 \bigr)\leq 0 \bigr\} , \\& D_{43}(A)= \bigl\{ z\in \mathbb{C}: \vert z-11 \vert \bigl( \vert z-12-\mathbf{{i}} \vert -18 \bigr)\leq 72 \bigr\} , \\& \varOmega _{14}(A)= \bigl\{ z\in \mathbb{C}: \vert z-11 \vert \bigl( \vert z-11 \vert +2 \bigr)\leq 175.568 \bigr\} , \\& \varOmega _{41}(A)= \bigl\{ z\in \mathbb{C}: \vert z-11 \vert \bigl( \vert z-11 \vert +4.1231 \bigr)\leq 210.4662 \bigr\} . \end{aligned}$$

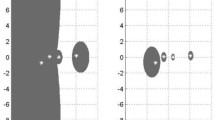
The eigenvalue localization sets \(\varGamma (A)\), \(D(A)\) and \(\varOmega (A)\) are drawn in Fig. 1, respectively, as red boundary, black boundary and yellow zones, and all eigenvalues are plotted as red asterisks. It is obvious that

$$\begin{aligned} \sigma (A)\subseteq \varOmega (A)\subseteq D(A)\subset \varGamma (A), \end{aligned}$$

another way of stating it is, \(\varOmega (A)\) can capture all eigenvalues of A more precisely than \(D(A)\) and \(\varGamma (A)\).

Figure 1
figure 1

Comparisons of \(\varOmega (A)\), \(D(A)\) and \(\varGamma (A)\)

Full size image

(II) The determination for non-singularity of A.

From Fig. 1, one can see that \(0\in \varGamma (A)\) and \(0\in D(A)\), but \(0\notin \varOmega (A)\), that is, the sets \(\varGamma (A)\) and \(D(A)\) cannot be used to judge the non-singularity of A. However, by \(0\notin \varOmega (A)\), one can conclude that A is non-singular.

Furthermore, as

$$\begin{aligned} \vert a_{11} \vert =11< 19.1564= r_{1}(A) \end{aligned}$$

and

$$\begin{aligned}& \vert a_{11} \vert \bigl( \vert a_{44} \vert -r_{4}^{1}(A) \bigr)=99.0000 < 306.5024=r_{1}(A) \vert a _{41} \vert , \\& \vert a_{22} \vert \bigl( \vert a_{44} \vert -r_{4}^{2}(A) \bigr)=-50.0000 < 14.6702=r_{2}(A) \vert a _{42} \vert , \\& \vert a_{33} \vert \bigl( \vert a_{44} \vert -r_{4}^{3}(A) \bigr)=-84.2912 < 0=r_{3}(A) \vert a _{43} \vert , \\& \vert a_{44} \vert \bigl( \vert a_{33} \vert -r_{3}^{4}(A) \bigr)= 66.4575 < 72.0000 =r _{4}(A) \vert a_{34} \vert , \end{aligned}$$

we know that the conditions in Theorems 3 and 4 do not hold, that is, Theorems 3 and 4 do not work. However, by

$$\begin{aligned}& \vert a_{11} \vert \bigl( \vert a_{22} \vert -r_{2}^{1}(A) \bigr)=53.9108 > 42.8350=r_{1}(A) \vert a _{21} \vert , \\& \vert a_{11} \vert \bigl( \vert a_{33} \vert -r_{3}^{1}(A) \bigr)=22.4575 > 0= r_{1}(A) \vert a _{31} \vert , \\& \vert a_{11} \vert \bigl( \vert a_{44} \vert +r_{4}^{1}(A) \bigr)=143.0000 < 174.5631=\bigl(2 \vert a _{14} \vert - r_{1}(A)\bigr) \vert a_{41} \vert , \end{aligned}$$

we know that there exists an index \(i=1\), for \(j=2,3,4\), either (9) or (10) holds. Then we can conclude the non-singularity of A by Corollary 1.

3 An eigenvalue localization set with parameters

In this section, an eigenvalue localization set with parameters and its applications is considered.

Theorem 7

Let \(A=sI-B\in \mathbb{C}^{n\times n}\) and \(s\in \mathbb{C}\). Given an arbitrary positive integer k, then

$$\begin{aligned} \sigma (A)\subseteq \varOmega _{k}^{s}(A)=\bigcap _{i\in N} \bigcup_{j\in N , j\neq i} \bigl(D^{s}_{ij}\bigl(B^{k}\bigr)\setminus \varOmega ^{s} _{ij}\bigl(B^{k}\bigr) \bigr), \end{aligned}$$

where

$$\begin{aligned} D^{s}_{ij}\bigl(B^{k}\bigr)= \bigl\{ z\in \mathbb{C}: \bigl\vert (s-z)^{k}-\bigl(B^{k} \bigr)_{ii} \bigr\vert \bigl( \bigl\vert (s-z)^{k}- \bigl(B ^{k}\bigr)_{jj} \bigr\vert -r_{j}^{i} \bigl(B^{k}\bigr)\bigr)\leq r_{i}\bigl(B^{k} \bigr) \bigl\vert \bigl(B^{k}\bigr)_{ji} \bigr\vert \bigr\} \end{aligned}$$

and

$$\begin{aligned} \varOmega ^{s}_{ij}\bigl(B^{k}\bigr) =& \bigl\{ z\in \mathbb{C}: \bigl\vert (s-z)^{k}-\bigl(B^{k} \bigr)_{ii} \bigr\vert \bigl( \bigl\vert (s-z)^{k}- \bigl(B ^{k}\bigr)_{jj} \bigr\vert +r_{j}^{i} \bigl(B^{k}\bigr)\bigr) \\ &{}< \bigl(2 \bigl\vert \bigl(B^{k}\bigr)_{ij} \bigr\vert -r_{i}\bigl(B^{k}\bigr)\bigr) \bigl\vert \bigl(B^{k}\bigr)_{ji} \bigr\vert \bigr\} . \end{aligned}$$

Proof

Let \(\lambda \in \sigma (A)\). Given an arbitrary positive integer k, suppose that \(\lambda \notin \varOmega _{k}^{s}(A)\). Then there exists \(i\in N\), for all \(j\in N\), \(j\neq i\), \(\lambda \notin (D^{s}_{ij}(B ^{k})\setminus \varOmega ^{s}_{ij}(B^{k}) )\), that is, \(\lambda \notin D^{s}_{ij}(B^{k})\) or \(\lambda \in \varOmega ^{s}_{ij}(B^{k})\), i.e.,

$$\begin{aligned} \bigl\vert (s-\lambda )^{k}-\bigl(B^{k} \bigr)_{ii} \bigr\vert \bigl( \bigl\vert (s-\lambda )^{k}-\bigl(B^{k}\bigr)_{jj} \bigr\vert -r_{j} ^{i}\bigl(B^{k}\bigr)\bigr)> r_{i}\bigl(B^{k}\bigr) \bigl\vert \bigl(B^{k}\bigr)_{ji} \bigr\vert , \end{aligned}$$

or

$$\begin{aligned} \bigl\vert (s-\lambda )^{k}-\bigl(B^{k} \bigr)_{ii} \bigr\vert \bigl( \bigl\vert (s-\lambda )^{k}-\bigl(B^{k}\bigr)_{jj} \bigr\vert +r_{j} ^{i}\bigl(B^{k}\bigr)\bigr)< \bigl(2 \bigl\vert \bigl(B^{k}\bigr)_{ij} \bigr\vert -r_{i}\bigl(B^{k}\bigr)\bigr) \bigl\vert \bigl(B^{k}\bigr)_{ji} \bigr\vert . \end{aligned}$$

By Corollary 1, \((s-\lambda )^{k}I-B^{k}\) is non-singular, which implies that \((s-\lambda )^{k}\) is not an eigenvalue of \(B^{k}\).

On the other hand, let x be an eigenvector corresponding to λ, i.e., \(Ax=\lambda x\), which leads to that \(Bx=(s-\lambda )x\). Furthermore, we have \(B^{k}x=(s-\lambda )^{k}x\), which implies that \((s -\lambda )^{k}\) is an eigenvalue of \(B^{k}\). This is a contradiction. Hence, \(\lambda \in \varOmega _{k}^{s}(A)\). □

By Theorem 7, the following general method for non-singularity of matrices is obtained.

Corollary 2

Let \(A=sI-B\in \mathbb{C}^{n\times n}\) and \(s\in \mathbb{C}\). Given an arbitrary positive integer k, if there exists an index i, for all \(j\in N\), \(j\neq i\), either

$$\begin{aligned} \bigl( \bigl\vert s^{k}-\bigl(B^{k} \bigr)_{ii} \bigr\vert -r_{i}^{j} \bigl(B^{k}\bigr)\bigr) \bigl\vert s^{k}- \bigl(B^{k}\bigr)_{jj} \bigr\vert > \bigl\vert \bigl(B^{k}\bigr)_{ij} \bigr\vert r _{j} \bigl(B^{k}\bigr), \end{aligned}$$
(12)

or

$$\begin{aligned} \bigl( \bigl\vert s^{k}-\bigl(B^{k} \bigr)_{ii} \bigr\vert +r_{i}^{j} \bigl(B^{k}\bigr)\bigr) \bigl\vert s^{k}- \bigl(B^{k}\bigr)_{jj} \bigr\vert < \bigl\vert \bigl(B^{k}\bigr)_{ij} \bigr\vert \bigl(2 \bigl\vert \bigl(B ^{k}\bigr)_{ji} \bigr\vert -r_{j} \bigl(B^{k}\bigr)\bigr), \end{aligned}$$
(13)

then A is non-singular.

Remark 2

Taking \(k=1\) and arbitrary complex number s in Theorem 7 and Corollary 2, then they degenerate, respectively, into Theorem 5 and Corollary 1. Hence, Theorem 7 and Corollary 2 can be viewed as generalizations of Theorem 5 and Corollary 1. Furthermore, by selecting appropriate parameters s and k, one may locate all eigenvalues and judge the non-singularity of matrices precisely.

Example 2

Consider again the matrix A in Example 1. Taking \(s=11\) and \(k=2\), the sets \(\varOmega (A)\) and \(\varOmega _{2}^{11}(A)\) are drawn in Fig. 2, respectively, as yellow zones and blue zones. All eigenvalues are plotted as red asterisks. It can be seen from Fig. 2 that the set \(\varOmega _{2}^{11}(A)\) can be used to more precisely locate all eigenvalues of A and judge the non-singularity of A.

Figure 2
figure 2

Comparisons of \(\varOmega (A)\) and \(\varOmega _{2}^{11}(A)\)

Full size image

4 Conclusions

In this paper, we present a new eigenvalue inclusion set \(\varOmega (A)\) by excluding some proper subsets that contain no eigenvalues of matrices from Dashnic–Zusmanovich localization sets \(D(A)\), and we prove that \(\varOmega (A)\) is tighter than \(D(A)\) for a matrix A. After that, by the set \(\varOmega (A)\), we obtain a sufficient condition for judging the non-singularity of matrices. To catch all eigenvalues of matrices precisely, we put forward another eigenvalue inclusion set \(\varOmega _{k}^{s}(A)\) including two parameters s and k. By selecting these two positive integer s and k appropriately, one can locate all eigenvalues of matrices and judge the non-singularity of matrices precisely. However, how to choose s and k to make \(\varOmega _{k}^{s}(A)\) works better? This question at present is far from being solved.