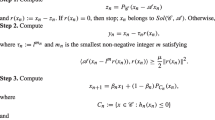Abstract
In this paper, we introduce the Orlicz space corresponding to the Young function and, by virtue of the equivalent theorem between the modified K-functional and modulus of smoothness, establish the direct, inverse, and equivalent theorems for linear combination of the Jacobi weighted Baskakov–Kantorovich operators in the Orlicz spaces.
Similar content being viewed by others
1 Motivations and main results
In recent years, since the Orlicz spaces are more general than the classical \(L_{p}\) spaces, which are composed of measurable functions \(f(x)\) such that \(|f(x)|^{p}\) are integrable, there is growing interest in problems of approximation in Orlicz spaces.
For proceeding smoothly, we recall from [22] some definitions and related results.
A continuous convex function \(\varPhi(t)\) on \([0,\infty)\) is called a Young function if
For a Young function \(\varPhi(t)\), its complementary Young function is denoted by \(\varPsi(t)\).
It is clear that the convexity of \(\varPhi(t)\) leads to \(\varPhi (\alpha t) \le\alpha\varPhi(t)\) for \(\alpha\in[0,1]\). In particular, we have \(\varPhi(\alpha t)<\alpha\varPhi(t)\) for \(\alpha\in(0,1)\).
A Young function \(\varPhi(t)\) is said to satisfy the \(\Delta_{2}\)-condition, denoted by \(\varPhi\in\Delta_{2}\), if there exist \(t_{0}>0\) and \(C\ge1\) such that \(\varPhi(2t)\le C\varPhi(t)\) for \(t\ge t_{0}\).
Let \(\varPhi(t)\) be a Young function. We define the Orlicz class \(L_{\varPhi}[0,\infty)\) as the collection of all Lebesgue-measurable functions \(u(x)\) on \([0,\infty)\). Since the integral
is finite, we define the Orlicz space \(L_{\varPhi}^{*}[0,\infty)\) as the linear hull of \(L_{\varPhi}[0,\infty)\) under the Luxembourg norm
The Orlicz norm, which is equivalent to the Luxembourg norm on \(L_{\varPhi}^{*}[0,\infty)\), is given by
and satisfies
Throughout this paper, we use C to denote a constant independent of n and x, which may be not necessarily the same in different cases.
Let \(f\in L_{\varPhi}^{*}[0,\infty)\) and \(r\in\mathbb{N}\). Then the weighted K-functional \(K_{r,\varphi}(f,t^{r})_{w,\varPhi}\), the weighted modified K-functional \(\bar{K}_{r,\varphi}(f,t^{r})_{w, \varPhi}\), and the weighted modulus of smoothness \(\omega_{{r,\varphi }}(f,t)_{w,\varPhi}\) are given respectively by
and
where
for \(a,b\in\mathbb{R}\) is the Jacobi weight function, and \(g^{(r-1)} \in AC_{\mathrm{loc}}\) means that g is \(r-1\) times differentiable and \(g^{(r-1)}\) is absolutely continuous in every closed finite interval \([c,d]\subset[0,\infty)\).
Between the weighted modulus of smoothness and the weighted modified K̄-functional, there are the following equivalent theorems.
Theorem A
([13])
Let \(f\in L_{\varPhi}^{*}[0,\infty)\) and \(r\in\mathbb{N}\). Then there exist constants C and \(t_{0}\) such that
for \(0< t\le t_{0}\).
Theorem B
([12])
Let \(f\in L_{\varPhi}^{*}[0,\infty)\) and \(r\in\mathbb{N}\). Then there exist constants C and \(t_{0}\) such that
for \(0< t\le t_{0}\).
For \(f\in C([0,\infty))\), the classical Baskakov operators are defined in [3] as
where \(v_{n,k}(x)=\binom{n+k-1 }{k}\frac{x^{k}}{(1+x)^{n+k}}\), \(k, n\in\mathbb{N}\). To approximate functions in the \(L_{p}\)-norm, Ditzian and Totik [5] defined the Kantorovich modifications
and obtained the direct inequality
and the week converse inequality
for \(\alpha<2\), where \(f\in L_{p}[0,\infty)\), \(1\le p<\infty\), and \(\varphi(x)=\sqrt{x(1+x)}\).
There are many approximation results on operators of the Baskakov type in the space \(C[0,\infty)\) or \(L_{p}[0,\infty)\). See [1,2,3,4,5,6,7,8,9,10,11,12, 14,15,16,17,18,19,20,21, 23, 24, 28, 29] and closely related references therein. Gupta and Acu [10] discussed a uniform estimate and established a quantitative result for the modified Baskakov–Szász–Mirakyan operators. Kumar and Acar [14] introduced a modification of generalized Baskakov–Durrmeyer operators of the Stancu type and studied their approximation properties. Goyal and Agrawal [8] introduced the Bézier variant of the generalized Baskakov–Kantorovich operators, established a direct approximation theorem with the aid of the Ditzian–Totik modulus of smoothness, and studied the rate of convergence for the functions having the derivatives of bounded variation for these operators. Zhang and Zhu [29] studied preservation properties, such as monotonicity, convexity, and smoothness, as well as those under the average, of the Baskakov–Kantorovich operators. Gadjev [7] studied the approximation of functions by the Baskakov–Kantorovich operator in the space \(L_{p}[0,\infty)\) and obtained the double inequality
for \(\ell\in\mathbb{N}\) with \(\ell\ge C_{1}n\), where \(C_{1}\) is a positive constant, and
is a K-functional.
For \(n, r\in\mathbb{N}\) such that \(n\geq2r\), the linear combinations of the Baskakov–Kantorovich operator are defined as
where the coefficients \(c_{i}(n,r)\) only dependent of n, r and satisfy the following conditions:
There are few results on the linear combinations of the Baskakov–Kantorovich operators. In [11], we obtained approximation properties for linear combinations of modified summation operators of integral type in the Orlicz space. Basing on these conclusions, we discover in this paper approximation properties for linear combinations of the Baskakov–Kantorovich operators.
Our main results in this paper can be stated as the following three theorems.
Theorem 1.1
(Direct theorem)
Let \(f\in L_{\varPhi}^{*}[0,\infty)\), \(\varPsi\in\Delta_{2}\), \(\varphi(x)=\sqrt{x(1+x)} \), \(n,a,b\in\mathbb{N}\), and \(0\le a,b< n-1\). Then
Theorem 1.2
(Inverse theorem)
Let \(f\in L_{\varPhi}^{*}[0,\infty)\), \(n\ge2r\), \(\varphi(x)= \sqrt{x(1+x)} \), \(a,b\in\mathbb{N}\), and \(0\le a,b< n-1\). Then
Theorem 1.3
(Equivalence theorem)
Let \(f\in L_{\varPhi}^{*}[0,\infty)\), \(n\ge2r\), \(\varphi(x)= \sqrt{x(1+x)} \), \(\varPsi\in\Delta_{2}\), \(a,b\in\mathbb{N}\), and \(0\le a,b< n-1\). Then
These main results are stronger than the results mentioned before.
2 Proof of the direct theorem
To prove the direct theorem, we need several lemmas.
Lemma 2.1
The operators \(\tilde{V}_{n}(f;x)\) defined in (1.4) satisfy
where \(\delta_{n}^{2r}(x)=\max \{\varphi^{2r}(x), \frac{1}{n^{r}} \}\), \(\varphi(x)=\sqrt{x(1+x)} \), \(r\in \mathbb{N}\), and C is a positive constant.
Proof
This follows from simple calculation. □
Lemma 2.2
([5])
If t locates between x and u, then
Lemma 2.3
([5])
For \(w(x)=x^{a}(1+x)^{b}\) and \(a,b\in\mathbb{R}\), we have
Lemma 2.4
Let \(f\in L_{\varPhi}^{*}[0,\infty)\), \(w(x)=x^{a}(1+x)^{b}\), \(a,b\in\mathbb{N}\), and \(0\le a,b< n-1\). Then
Proof
By Lemma 2.3 we can write
Using (1.1) and Jensen’s inequality gives
Similarly, we have
Consequently, we arrive at
Combining (1.5), (1.6), and (2.1), it follows that
The proof of Lemma 2.4 is complete. □
Lemma 2.5
([13])
For \(f\in L_{\varPhi}^{*}[0,\infty)\) and \(\varPsi\in\Delta_{2}\), we have
where
is the Hardy–Littlewood function of \(f(x)\).
We now in a position to prove Theorem 1.1.
Proof of Theorem 1.1
Let
Taylor’s formula with integral remainder of \(g\in U\) gives
where
From (1.7) it follows that
and
We now estimate \(|w(x)\tilde{V}_{n}(R_{2r}(g;u,x);x) |\). As \(x\in[\frac{1}{n},\infty)\), we have \(\delta_{n}^{2r}(x)=\varphi^{2r}(x)\). Applying Lemma 2.2 leads to
From Cauchy’s integral inequality [25, 26] and Lemma 2.1 it follows that
where
Similarly, we can also obtain
Now we estimate \(J_{3}\). By Cauchy’s integral inequality [25, 26] and Lemma 2.1 we derive that
where \(w_{1}(x)=x^{a}(1+x)^{b+1}\).
Finally, we estimate \(J_{4}\). Applying Cauchy’s integral inequality [25, 26] and Lemma 2.1 yields
where
From the previous inequalities and Lemma 2.5 it follows that
For \(x\in [0,\frac{1}{n} )\), we have \(\delta_{n}^{2r}(x)=\frac{1}{n ^{r}}\). Accordingly,
Using Cauchy’s integral inequality [25, 26] and Lemma 2.1 yields
and
Therefore we have
and
Hence, by virtue of (2.3) and (2.4), we derive
and, consequently,
Combining this inequality with (1.2), (2.2), and Lemma 2.4 results in
The proof of the direct theorem is complete. □
3 Proofs of the inverse and equivalence theorems
We first prepare several lemmas for proving Theorems 1.2 and 1.3.
Lemma 3.1
If \(f\in L_{\varPhi}^{*}[0,\infty)\), \(n\ge2r\), \(a,b\in\mathbb{N}\), and \(0\le a,b< n-1\), then
Proof
From [7, Eq. (16)] it follows that
where
By Lemma 2.3 it follows that
where
and, similarly,
Employing inequalities between (3.1) and (3.2) yields
Combining this inequality with (1.5) and (1.6) results in
The proof of Lemma 3.1 is complete. □
Lemma 3.2
Let \(f\in L_{\varPhi}^{*}[0,\infty)\), \(n\ge2r\), \(a,b\in\mathbb {N}\), and \(0\le a,b< n-1\). Then
Proof
Since
we obtain
where
and, by Jensen’s inequality,
where \(C_{1}\ge1\). Similarly, we have
Consequently, it follows that
Combining this inequality with (1.5) and (1.6) yields
The proof of Lemma 3.2 is complete. □
We now in a position to prove Theorems 1.2 and 1.3.
Proof of Theorem 1.2
From Lemmas 3.1 and 3.2 and [27, Theorem 2.2] we obtain
Application of inequality (1.3) concludes the inverse theorem. □
Proof of Theorem 1.3
Using the so-called order function \(\psi(t)=t^{\alpha}|\ln t|^{ \beta}e^{|\ln t|^{\gamma}}\) for \(0<\alpha<1\), \(\beta\in \mathbb{R}\), and \(\gamma<1\) and combining Theorems 1.1 and 1.2 conclude the equivalence theorem. □
References
Acu, A.M., Gupta, V.: Direct results for certain summation-integral type Baskakov–Szász operators. Results Math. 72(3), 1161–1180 (2017). https://doi.org/10.1007/s00025-016-0603-2
Agrawal, P.N., Gupta, V., Sathish Kumar, A.: Generalized Baskakov–Durrmeyer type operators. Rend. Circ. Mat. Palermo (2) 63(2), 193–209 (2014). https://doi.org/10.1007/s12215-014-0152-z
Baskakov, V.A.: An instance of a sequence of linear positive operators in the space of continuous functions. Dokl. Akad. Nauk SSSR (N. S.) 113, 249–251 (1957) (Russian)
Cao, F., Ding, C.: \(L^{p}\) approximation by multivariate Baskakov–Kantorovich operators. J. Math. Anal. Appl. 348(2), 856–861 (2008). https://doi.org/10.1016/j.jmaa.2008.05.049
Ditzian, Z., Totik, V.: Moduli of Smoothness. Springer Series in Computational Mathematics, vol. 9. Springer, New York (1987). https://doi.org/10.1007/978-1-4612-4778-4.
Erençin, A.: Durrmeyer type modification of generalized Baskakov operators. Appl. Math. Comput. 218(8), 4384–4390 (2011). https://doi.org/10.1016/j.amc.2011.10.014
Gadjev, I.: Approximation of functions by Baskakov–Kantorovich operator. Results Math. 70(3–4), 385–400 (2016). https://doi.org/10.1007/s00025-016-0554-7
Goyal, M., Agrawal, P.N.: Bézier variant of the generalized Baskakov Kantorovich operators. Boll. Unione Mat. Ital. 8(4), 229–238 (2016). https://doi.org/10.1007/s40574-015-0040-2
Guo, S., Qi, Q., Liu, G.: The central approximation theorems for Baskakov Bézier operators. J. Approx. Theory 147(1), 112–124 (2007). https://doi.org/10.1016/j.jat.2005.02.010
Gupta, V., Acu, A.M.: On Baskakov–Szász–Mirakyan-type operators preserving exponential type functions. Positivity 22(3), 919–929 (2018). https://doi.org/10.1007/s11117-018-0553-x
Han, L.-X., Qi, F.: On approximation by linear combinations of modified summation operators of integral type in Orlicz spaces. Mathematics 7(1) (2019) Article ID 6. https://doi.org/10.3390/math7010006
Han, L.-X., Wu, G.: Strong converse inequality of weighted simultaneous approximation for gamma operators in Orlicz spaces \(L^{*}_{\varPhi}(0,\infty)\). Appl. Math. J. Chin. Univ. Ser. A 31(3), 366–378 (2016) (Chinese)
Han, L.-X., Wu, G.: Equivalent theorems of approximation by weighted Szász–Kantorovich–Bézier operators in Orlicz spaces. Adv. Math. (China) 47(5), 719–734 (2018)
Kumar, A.S., Acar, T.: Approximation by generalized Baskakov–Durrmeyer–Stancu type operators. Rend. Circ. Mat. Palermo (2) 65(3), 411–424 (2016). https://doi.org/10.1007/s12215-016-0242-1
Milovanović, G.V., Mursaleen, M., Nasiruzzaman, Md.: Modified Stancu type Dunkl generalization of Szász–Kantorovich operators. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 112(1), 135–151 (2018). https://doi.org/10.1007/s13398-016-0369-0
Mursaleen, M., Al-Abied, A.A.H., Ansari, K.J.: On approximation properties of Baskakov–Schurer–Szász–Stancu operators based on q-integers. Filomat 32(4), 1359–1378 (2018). https://doi.org/10.2298/fil1804359m
Mursaleen, M., Ansari, K.J., Khan, A.: Approximation by Kantorovich type q-Bernstein–Stancu operators. Complex Anal. Oper. Theory 11(1), 85–107 (2017). https://doi.org/10.1007/s11785-016-0572-1
Mursaleen, M., Nasiruzzaman, Md.: Dunkl generalization of Kantorovich type Szász–Mirakjan operators via q-calculus. Asian-Eur. J. Math. 10(4), 1750077 (2017). https://doi.org/10.1142/S1793557117500772
Mursaleen, M., Rahman, S., Ansari, K.J.: Approximation by generalized Stancu type integral operators involving Sheffer polynomials. Carpath. J. Math. 34(2), 215–228 (2018)
Mursaleen, M., Rahman, S., Ansari, K.J.: On the approximation by Bézier–Păltănea operators based on Gould–Hopper polynomials. Math. Commun. 24(2), 147–164 (2019)
Nasiruzzaman, Md., Rao, N., Wazir, S., Kumar, R.: Approximation on parametric extension of Baskakov–Durrmeyer operators on weighted spaces. J. Inequal. Appl. 2019, 103 (2019). https://doi.org/10.1186/s13660-019-2055-1
Rao, M.M., Ren, Z.D.: Theory of Orlicz Space. Monographs and Textbooks in Pure and Applied Mathematics, vol. 146. Marcel Dekker, Inc., New York (1991)
Rao, N., Wafi, A.: Stancu-variant of generalized Baskakov operators. Filomat 31(9), 2625–2632 (2017). https://doi.org/10.2298/fil1709625r
Srivastava, H.M., Mursaleen, M., Nasiruzzaman, Md.: Approximation by a class of q-beta operators of the second kind via the Dunkl-type generalization on weighted spaces. Complex Anal. Oper. Theory 13(3), 1537–1556 (2019). https://doi.org/10.1007/s11785-019-00901-6
Tian, J.-F., Ha, M.-H.: Properties of generalized sharp Hölder’s inequalities. J. Math. Inequal. 11(2), 511–525 (2017). https://doi.org/10.7153/jmi-11-42
Tian, J.-F., Ha, M.-H., Wang, C.: Improvements of generalized Hölder’s inequalities and their applications. J. Math. Inequal. 12(2), 459–471 (2018). https://doi.org/10.7153/jmi-2018-12-34
van Wickeren, E.: Weak-type inequalities for Kantorovitch polynomials and related operators. Nederl. Akad. Wetensch. Indag. Math. 49(1), 111–120 (1987). https://doi.org/10.1016/s1385-7258(87)80011-2
Verma, D.K., Gupta, V., Agrawal, P.N.: Some approximation properties of Baskakov–Durrmeyer–Stancu operators. Appl. Math. Comput. 218(11), 6549–6556 (2012). https://doi.org/10.1016/j.amc.2011.12.031
Zhang, C., Zhu, Z.: Preservation properties of the Baskakov–Kantorovich operators. Comput. Math. Appl. 57(9), 1450–1455 (2009). https://doi.org/10.1016/j.camwa.2009.01.027
Acknowledgements
The authors appreciate the anonymous referees for their careful corrections to and valuable comments on the original version of this paper.
Availability of data and materials
Not applicable.
Funding
The first author was partially supported by NSFC (Grant No. 11461052) and by IMNSFC (Grant No. 2016MS0118).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the manuscript and read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Han, LX., Guo, BN. & Qi, F. Equivalent theorem of approximation by linear combination of weighted Baskakov–Kantorovich operators in Orlicz spaces. J Inequal Appl 2019, 223 (2019). https://doi.org/10.1186/s13660-019-2174-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-019-2174-8