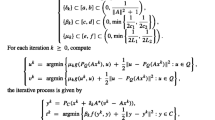A new extragradient algorithm for split equilibrium problems and fixed point problems

Abstract

In this paper, we present a new extragradient algorithm for approximating a solution of the split equilibrium problems and split fixed point problems. The strong convergence theorems are proved in the framework of Hilbert spaces under some mild conditions. We apply the obtained main result for the problem of finding a solution of split variational inequality problems and split fixed point problems and a numerical example and computational results are also provided.

1 Introduction

Let C and D be nonempty closed and convex subsets of real Hilbert spaces $H_{1}$ and $H_{2}$, respectively, and let $H_{1}$ and $H_{2}$ be endowed with an inner product $\langle \cdot , \cdot \rangle$ and the corresponding norm $\|\cdot \|$. By → and ⇀, we denote strong convergence and weak convergence, respectively. Suppose that $f\colon C\times C\rightarrow \mathbb{R}$ be a bifunction. The equilibrium problem (EP) is to find $z\in C$ such that

$$ f(z,x)\geq 0, \quad \forall x\in C. $$

(1.1)

The solution set of the equilibrium problem is denoted by $\operatorname{EP} (f)$. The equilibrium problem is a generalization of many mathematical models such as variational inequalities, fixed point problems, and optimization problems; see [6, 14, 17, 18, 20, 35]. In 2013, Anh [2] introduced an extragradient algorithm for finding a common element of fixed point set of a nonexpansive mapping and solution set of an equilibrium problem on pseudomonotone and Lipschitz-type continuous bifunction in real Hilbert space. The author proved the strong convergence of the generated sequence under some condition on it. Since then, many authors considered the EP and related problems and proved weak and strong convergence. See, for example [1,2,3,4, 11, 21, 26, 41].

Moudafi [32] (see also He [25]) introduced the split equilibrium problem (SEP) which is to find $z\in C$ such that

$$ z\in \operatorname{EP}(f)\cap L^{-1}\bigl( \operatorname{EP}(g)\bigr), $$

(1.2)

where $L\colon H_{1}\rightarrow H_{2}$ is a bounded linear operator and $g\colon D\times D\rightarrow \mathbb{R}$ be another bifunction. It is well known that SEP is a generalization of equilibrium problem by considering $g=0$ and $D=H_{2}$.

He [25] used the proximal method and introduced an iterative method and showed that the generated sequence converges weakly to a solution of SEP under suitable conditions on parameters provided that f, g are monotone bifunctions on C and D, respectively.

Problem SEP is an extension of many mathematical models which have been considered and studied intensively by several authors recently: split variational inequality problems [12], split common fixed point problems [7, 13, 16, 19, 28, 31, 36, 38,39,40], and the split feasibility problems which have been used for studying medical image reconstruction, sensor networks, intensity modulated radiation therapy, and data compression; see [5, 8,9,10] and the references quoted therein.

In this paper, motivated and inspired by the above literature, we consider a new extragradient algorithm for finding a common solution of split equilibrium problem of pseudomonotone and Lipschitz-type continuous bifunctions and split fixed point problem of nonexpansive mappings in real Hilbert space. That is, we are interested in considering the following problem: let $H_{1}$ and $H_{2}$ be real Hilbert spaces and C and D be nonempty closed and convex subsets of $H_{1}$ and $H_{2}$, respectively. Let $f\colon C\times C\rightarrow \mathbb{R}$ and $g\colon D\times D\rightarrow \mathbb{R}$ be pseudomonotone and Lipschitz-type continuous bifunctions, $T\colon C \rightarrow C$ and $S\colon D\rightarrow D$ be nonexpansive mappings and $L\colon H_{1}\rightarrow H_{2}$ be a bounded linear operator, we consider the problem of finding a solution $p\in C$ such that

$$ p\in \bigl( \operatorname{EP}(f)\cap F(T) \bigr)\cap L^{-1} \bigl( \operatorname{EP}(g)\cap F(S) \bigr)=: \varOmega , $$

(1.3)

where $F(T)$ is the fixed points set of T and $\varOmega \neq \emptyset$. Under some mild conditions, the strong convergence theorem will be provided.

The paper is organized as follows. Section 2 gathers some definitions and lemmas of geometry of real Hilbert spaces and monotone bifunctions, which will be needed in the remaining sections. In Sect. 3, we prepare a new extragradient algorithm and prove the strong convergence theorem. In Sect. 4, the results of Sect. 3 are applied to solve split variational inequality problems and split fixed point problem of nonexpansive mappings. Finally, in Sect. 5, the numerical experiments are showed and discussed.

2 Preliminaries

We now provide some basic concepts, definitions and lemmas which will be used in the sequel. Let C be a closed and convex subset of a real Hilbert space H. The operator $P_{C}$ is called a metric projection operator if it assigns to each $x\in H$ its nearest point $y\in C$ such that

$$ \Vert x-y \Vert = \min \bigl\{ \Vert x-z \Vert : z \in C\bigr\} . $$

An element y is called the metric projection of x onto C and denoted by $P_{C}x$. It exists and is unique at any point of the real Hilbert space. It is well known that the metric projection operator $P_{C}$ is continuous.

Lemma 2.1

Let H is a real Hilbert space and C is a nonempty, closed and convex subset of H. Then, for all $x\in H$, the element $z=P_{C}x$ if and only if

$$ \langle x-z, z-y\rangle \geq 0, \quad \forall y\in C. $$

The metric projection satisfies in the following inequality:

$$ \Vert P_{C}x-P_{C}y \Vert ^{2} \leq \langle P_{C}x-P_{C}y, x-y\rangle , \quad \forall x,y \in H, $$

(2.1)

therefore the metric projection is firmly nonexpansive operator in H. For more information concerning the metric projection, please see Sect. 3 of [24].

Lemma 2.2

([23])

Let H be a real Hilbert space and $T:H\rightarrow H$ be a nonexpansive mapping with $F(T)\neq \emptyset$. Then the mapping $I -T$ is demiclosed at zero, that is, if $\{x_{n}\}$ is a sequence in H such that $x_{n}\rightharpoonup x$ and $\|x_{n} -Tx_{n}\|\rightarrow 0$, then $x \in F(T)$.

Lemma 2.3

([42])

Assume that $\{a_{n}\}$ is a sequence of nonnegative numbers such that

$$ a_{n+1}\leq (1-\gamma _{n})a_{n}+\gamma _{n}\delta _{n},\quad \forall n\in \mathbb{N}, $$

where $\{\gamma _{n}\}$ is a sequence in $(0,1)$ and $\{\delta _{n}\}$ is a sequence in $\mathbb{R}$ such that

• (i) $\lim_{n\rightarrow \infty }\gamma _{n}=0$, $\sum^{\infty }_{n=1}\gamma _{n}=\infty$,

• (ii) $\limsup_{n\rightarrow \infty }{\delta _{n} } \leq 0$.

Then $\lim_{n\rightarrow \infty }a_{n}=0$.

Lemma 2.4

([30])

Let $\{a_{n}\}$ be a sequence of real numbers such that there exists a subsequence $\{n_{i}\}$ of $\{n\}$ such that $a_{n_{i}}< a_{n_{i}+1}$ for all $i\in \mathbb{N}$. Then there exists a nondecreasing sequence $\{m_{k}\}\subset \mathbb{N}$ such that $m_{k}\rightarrow \infty$ as $k\rightarrow \infty$ and the following properties are satisfied by all (sufficiently large) numbers $k\in \mathbb{N}$:

$$ a_{m_{k}}\leq a_{m_{k}+1}\quad \textit{and}\quad a_{k}\leq a_{m_{k}+1}. $$

In fact, $m_{k} = \max \{ j\leq k : a_{j} < a_{j+1}\}$.

Definition 2.5

A bifunction $f\colon C\times C\rightarrow \mathbb{R}$ is said to be

• monotone on C if

  $$ f(x,y)+f(y,x)\leq 0, \quad \forall x, y\in C; $$

• pseudomonotone on C if

  $$ f(x,y) \geq 0\quad \Longrightarrow\quad f(y,x)\leq 0,\quad \forall x, y\in C; $$

• Lipschitz-type continuous on C if there exist two positive constants $c_{1}$ and $c_{2}$ such that

  $$ f(x,y)+ f(y,z)\geq f(x,z)-c_{1} \Vert x-y \Vert ^{2} -c_{2} \Vert y-z \Vert ^{2},\quad \forall x, y,z\in C. $$

Let C be a nonempty closed and convex subset of a real Hilbert space H and $f : C\times C \rightarrow \mathbb{R}$ be a bifunction, we will assume the following conditions:

• (A1) f is pseudomonotone on C and $f(x,x)=0$ for all $x\in C$;

• (A2) f is weakly continuous on $C\times C$ in the sense that if $x,y\in C$ and $\{x_{n}\}, \{y_{n}\}\subset C$ converge weakly to x and y, respectively, then $f(x_{n},y_{n})\rightarrow f(x,y)$ as $n\rightarrow \infty$;

• (A3) $f(x, \cdot )$ is convex and subdifferentiable on C for every fixed $x\in C$;

• (A4) f is Lipschitz-type continuous on C with two positive constants $c_{1}$ and $c_{2}$.

It is easy to show that under assumptions (A1)–(A3), the solution set $\operatorname{EP}(f)$ is closed and convex (see, for instance [34]).

We need the following lemma to prove our main results.

Lemma 2.6

([2])

Assume that f satisfies (A1), (A3), (A4) such that $\operatorname{EP}(f)$ is nonempty and $0 < \rho _{0} < \min \{\frac{1}{2c_{1}},\frac{1}{2c_{2}}\}$. If $x_{0} \in C$, and $y_{0}$, $z_{0}$ are defined by

$$ \textstyle\begin{cases} y_{0} = \operatorname{arg}\operatorname{min} \{ \rho _{0} f(x_{0}, y) + \frac{1}{2} \Vert y-x _{0} \Vert ^{2} : y \in C \}, \\ z_{0} = \operatorname{arg}\operatorname{min} \{ \rho _{0} f(y_{0}, y) + \frac{1}{2} \Vert y-x _{0} \Vert ^{2} : y \in C \}, \end{cases} $$

then

• (i) $\rho _{0}$ $[f(x_{0},y) - f(x_{0},y_{0})] \geq \langle y _{0} - x_{0},y_{0} - y \rangle$, $\forall y \in C$;

• (ii) $\|z_{0} - p\|^{2}$ $\leq \|x_{0} - p\|^{2} - (1 - 2\rho _{0}c_{1})\|x_{0} - y_{0}\|^{2} - (1 - 2\rho _{0}c_{2})\|y_{0} - z_{0} \|^{2}$, $\forall p \in \operatorname{EP}(f)$.

3 Main results

In this section, we present our main algorithm and show the strong convergence theorem for finding a common solution of split equilibrium problem of pseudomonotone and Lipschitz-type continuous bifunctions and split fixed point problem of nonexpansive mappings in real Hilbert space.

Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces and C and D be nonempty closed and convex subsets of $H_{1}$ and $H_{2}$, respectively. Suppose that $f\colon C\times C\rightarrow \mathbb{R}$ and $g\colon D \times D\rightarrow \mathbb{R}$ be bifunctions. Let $L\colon H_{1} \rightarrow H_{2}$ be a bounded linear operator with its adjoint $L^{*}$, $T\colon C\rightarrow C$ and $S\colon D\rightarrow D$ be nonexpansive mappings and $h \colon C\rightarrow C$ be a ρ-contraction mapping. We introduce the following extragradient algorithm for solving the split equilibrium problem and fixed point problem.

Algorithm 3.1

Choose $x_{1}\in H_{1}$. The control parameters $\lambda _{n}$, $\mu _{n}$, $\alpha _{n}$, $\beta _{n}$, $\delta _{n}$ satisfy the following conditions:

$$\begin{aligned}& 0< \underline{\lambda } \leq \lambda _{n} \leq \overline{\lambda } < \min \biggl\lbrace \frac{1}{2c_{1}},\frac{1}{2c_{2}} \biggr\rbrace ,\qquad 0< \underline{\mu } \leq \mu _{n} \leq \overline{\mu } < \min \biggl\lbrace \frac{1}{2d _{1}},\frac{1}{2d_{2}} \biggr\rbrace , \\& \beta _{n}\in (0,1),\qquad 0< \liminf_{n\rightarrow \infty } \beta _{n}\leq \limsup_{n\rightarrow \infty } \beta _{n}< 1, \qquad 0< \underline{ \delta } \leq \delta _{n}\leq \overline{\delta }< \frac{1}{ \Vert L \Vert ^{2}}, \\& \alpha _{n}\in \biggl(0,\frac{1}{2-\rho }\biggr),\qquad \lim _{n\rightarrow \infty }\alpha _{n}=0,\qquad \sum ^{\infty }_{n=1} \alpha _{n}=\infty . \end{aligned}$$

Let $\{x_{n}\}$ be a sequence generated by

$$ \textstyle\begin{cases} u_{n}=\operatorname{arg}\operatorname{min} \lbrace \mu _{n} g(P_{D}(Lx_{n}),u)+ \frac{1}{2} \Vert u-P_{D}(Lx_{n}) \Vert ^{2}\colon u\in D \rbrace , \\ v_{n}=\operatorname{arg}\operatorname{min} \lbrace \mu _{n} g(u_{n},u)+\frac{1}{2} \Vert u-P _{D}(Lx_{n}) \Vert ^{2}\colon u\in D \rbrace , \\ y_{n}=P_{C} (x_{n}+\delta _{n}L^{*} (Sv_{n}-Lx_{n} ) ), \\ t_{n}=\operatorname{arg}\operatorname{min} \lbrace \lambda _{n} f(y_{n},y)+ \frac{1}{2} \Vert y-y_{n} \Vert ^{2}\colon y\in C \rbrace , \\ z_{n}=\operatorname{arg}\operatorname{min} \lbrace \lambda _{n} f(t_{n},y)+ \frac{1}{2} \Vert y-y_{n} \Vert ^{2}\colon y\in C \rbrace , \\ x_{n+1}=\alpha _{n}h(x_{n})+(1-\alpha _{n})(\beta _{n}x_{n}+(1-\beta _{n})Tz _{n}). \end{cases} $$

Theorem 3.2

Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces and C and D be nonempty closed and convex subsets of $H_{1}$ and $H_{2}$, respectively. Suppose that $f\colon C\times C\rightarrow \mathbb{R}$ and $g\colon D \times D\rightarrow \mathbb{R}$ be bifunctions which satisfy (A1)–(A4) with some positive constants $\{c_{1}, c_{2} \}$ and $\{d_{1}, d_{2} \}$, respectively. Let $L\colon H_{1}\rightarrow H_{2}$ be a bounded linear operator with its adjoint $L^{*}$, $T\colon C\rightarrow C$ and $S\colon D\rightarrow D$ be nonexpansive mappings, $h \colon C\rightarrow C$ be a ρ-contraction mapping and $\varOmega \neq \emptyset$. Then the sequence $\{x_{n}\}$ generated by Algorithm 3.1 converges strongly to $q=P_{\varOmega }h(q)$.

Proof

Let $p\in \varOmega$. So, $p\in \operatorname{EP}(f)\cap F(T)\subset C$ and $Lp\in \operatorname{EP}(g) \cap F(S)\subset D$. Since $P_{D}$ is firmly nonexpansive, we get

$$\begin{aligned} \bigl\Vert P_{D}(Lx_{n})-Lp \bigr\Vert ^{2} =& \bigl\Vert P_{D}(Lx_{n})-P_{D}(Lp) \bigr\Vert ^{2} \\ \leq &\bigl\langle P_{D}(Lx_{n})-P_{D}(Lp), Lx_{n}-Lp\bigr\rangle \\ =&\bigl\langle P_{D}(Lx_{n})-Lp, Lx_{n}-Lp \bigr\rangle \\ =&\frac{1}{2} \bigl[ \bigl\Vert P_{D}(Lx_{n})-Lp \bigr\Vert ^{2}+ \Vert Lx_{n}-Lp \Vert ^{2}- \bigl\Vert P _{D}(Lx_{n})-Lx_{n} \bigr\Vert ^{2} \bigr], \end{aligned}$$

and hence

$$ \bigl\Vert P_{D}(Lx_{n})-Lp \bigr\Vert ^{2}\leq \Vert Lx_{n}-Lp \Vert ^{2}- \bigl\Vert P_{D}(Lx_{n})-Lx_{n} \bigr\Vert ^{2}. $$

(3.1)

Since S is nonexpansive, $Lp\in F(S)$ and using Lemma 2.6 and the definition of $u_{n}$ and $v_{n}$, we have

$$\begin{aligned} \Vert Sv_{n}-Lp \Vert ^{2} =& \bigl\Vert Sv_{n}-S(Lp) \bigr\Vert ^{2} \\ \leq & \Vert v_{n}-Lp \Vert ^{2} \\ \leq & \bigl\Vert P_{D}(Lx_{n})-Lp \bigr\Vert ^{2}-(1-2\mu _{n}d_{1}) \bigl\Vert P_{D}(Lx_{n})-u _{n} \bigr\Vert ^{2} \\ &{}-(1-2\mu _{n}d_{2}) \Vert u_{n}-v_{n} \Vert ^{2}, \end{aligned}$$

(3.2)

for each $n\in \mathbb{N}$. From (3.1), (3.2) and the assumptions, we obtain

$$ \Vert Sv_{n}-Lp \Vert ^{2}\leq \Vert Lx_{n}-Lp \Vert ^{2}- \bigl\Vert P_{D}(Lx_{n})-Lx_{n} \bigr\Vert ^{2}. $$

(3.3)

By (3.3), we get

$$\begin{aligned} \bigl\langle L(x_{n}-p),Sv_{n}-Lx_{n}\bigr\rangle =&\langle Sv_{n}-Lp, Sv_{n}-Lx _{n} \rangle - \Vert Sv_{n}-Lx_{n} \Vert ^{2} \\ =&\frac{1}{2} \bigl[ \Vert Sv_{n}-Lp \Vert ^{2}- \Vert Lx_{n}-Lp \Vert ^{2}- \Vert Sv_{n}-Lx _{n} \Vert ^{2} \bigr] \\ \leq &-\frac{1}{2} \bigl\Vert P_{D}(Lx_{n})-Lx_{n} \bigr\Vert ^{2}-\frac{1}{2} \Vert Sv_{n}-Lx _{n} \Vert ^{2}. \end{aligned}$$

This implies that

$$\begin{aligned} 2\delta _{n} \bigl\langle L(x_{n}-p),Sv_{n}-Lx_{n} \bigr\rangle \leq & -\delta _{n} \bigl\Vert P_{D}(Lx_{n})-Lx_{n} \bigr\Vert ^{2} \\ &{}-\delta _{n} \Vert Sv_{n}-Lx_{n} \Vert ^{2}. \end{aligned}$$

(3.4)

Since $P_{C}$ is nonexpansive and by (3.4), we obtain

$$\begin{aligned} \Vert y_{n}-p \Vert ^{2} =& \bigl\Vert P_{C} \bigl(x_{n}+\delta _{n}L^{*} (Sv_{n}-Lx _{n} ) \bigr)-P_{C}(p) \bigr\Vert ^{2} \\ \leq & \bigl\Vert (x_{n}-p)+\delta _{n}L^{*} (Sv_{n}-Lx_{n} ) \bigr\Vert ^{2} \\ =& \Vert x_{n}-p \Vert ^{2}+\delta _{n}^{2} \bigl\Vert L^{*} (Sv_{n}-Lx_{n} ) \bigr\Vert ^{2}+2\delta _{n}\bigl\langle x_{n}-p,L^{*} (Sv_{n}-Lx_{n} ) \bigr\rangle \\ \leq & \Vert x_{n}-p \Vert ^{2}+\delta _{n}^{2} \Vert L \Vert ^{2} \Vert Sv_{n}-Lx_{n} \Vert ^{2}- \delta _{n} \bigl\Vert P_{D}(Lx_{n})-Lx_{n} \bigr\Vert ^{2}-\delta _{n} \Vert Sv_{n}-Lx_{n} \Vert ^{2} \\ =& \Vert x_{n}-p \Vert ^{2}-\delta _{n} \bigl(1-\delta _{n} \Vert L \Vert ^{2}\bigr) \Vert Sv_{n}-Lx_{n} \Vert ^{2}-\delta _{n} \bigl\Vert P_{D}(Lx_{n})-Lx_{n} \bigr\Vert ^{2}, \end{aligned}$$

(3.5)

then we obtain

$$ \Vert y_{n}-p \Vert \leq \Vert x_{n}-p \Vert . $$

(3.6)

By Lemma 2.6, the definition of $t_{n}$ and $z_{n}$ and the assumptions we have

$$ \Vert z_{n}-p \Vert \leq \Vert y_{n}-p \Vert , $$

(3.7)

for each $n\in \mathbb{N}$. From (3.6) and (3.7), we get

$$ \Vert z_{n}-p \Vert \leq \Vert x_{n}-p \Vert . $$

(3.8)

Set $q_{n}=\beta _{n}x_{n}+(1-\beta _{n})Tz_{n}$. It follows from (3.8) that

$$\begin{aligned} \Vert q_{n}-p \Vert \leq &\beta _{n} \Vert x_{n}-p \Vert + (1-\beta _{n}) \Vert Tz_{n}-p \Vert \\ \leq &\beta _{n} \Vert x_{n}-p \Vert + (1-\beta _{n}) \Vert z_{n}-p \Vert \\ \leq & \Vert x_{n}-p \Vert . \end{aligned}$$

(3.9)

By the definition of $x_{n+1}$ and (3.9), we obtain

$$\begin{aligned} \Vert x_{n+1}-p \Vert \leq &\alpha _{n} \bigl\Vert h(x_{n})-p \bigr\Vert + (1-\alpha _{n}) \Vert q_{n}-p \Vert \\ \leq &\alpha _{n} \bigl\Vert h(x_{n})-h(p) \bigr\Vert +\alpha _{n} \bigl\Vert h(p)-p \bigr\Vert + (1-\alpha _{n}) \Vert x_{n}-p \Vert \\ \leq &\alpha _{n}\rho \Vert x_{n}-p \Vert +\alpha _{n} \bigl\Vert h(p)-p \bigr\Vert + (1-\alpha _{n}) \Vert x_{n}-p \Vert \\ \leq &\bigl(1-\alpha _{n}(1-\rho )\bigr) \Vert x_{n}-p \Vert +\alpha _{n}(1-\rho )\frac{ \Vert h(p)-p \Vert }{1-\rho } \\ \leq &\max \biggl\lbrace \Vert x_{n}-p \Vert , \frac{ \Vert h(p)-p \Vert }{1-\rho } \biggr\rbrace \\ \vdots & \\ \leq &\max \biggl\lbrace \Vert x_{1}-p \Vert , \frac{ \Vert h(p)-p \Vert }{1-\rho } \biggr\rbrace . \end{aligned}$$

This implies that the sequence $\{x_{n}\}$ is bounded. By (3.6) and (3.8), the sequences $\{y_{n}\}$ and $\{z_{n}\}$ are bounded too.

By Lemma 2.6, (3.6), the definition of $q_{n}$ and assumptions on $\beta _{n}$ and $\delta _{n}$, we get

$$\begin{aligned} \Vert q_{n}-p \Vert ^{2} \leq &\beta _{n} \Vert x_{n}-p \Vert ^{2}+ (1-\beta _{n}) \Vert Tz _{n}-p \Vert ^{2} \\ \leq &\beta _{n} \Vert x_{n}-p \Vert ^{2}+ (1-\beta _{n}) \Vert z_{n}-p \Vert ^{2} \\ \leq &\beta _{n} \Vert x_{n}-p \Vert ^{2}+ (1-\beta _{n}) \\ &{}\times\bigl[ \Vert y_{n}-p \Vert ^{2}-(1-2 \lambda _{n}c_{1}) \Vert y_{n}-t_{n} \Vert ^{2}-(1-2\lambda _{n}c_{2}) \Vert t_{n}-z _{n} \Vert ^{2} \bigr] \\ \leq &\beta _{n} \Vert x_{n}-p \Vert ^{2}+ (1-\beta _{n}) \\ &{}\times\bigl[ \Vert x_{n}-p \Vert ^{2}-(1-2 \lambda _{n}c_{1}) \Vert y_{n}-t_{n} \Vert ^{2}-(1-2\lambda _{n}c_{2}) \Vert t_{n}-z _{n} \Vert ^{2} \bigr] \\ =& \Vert x_{n}-p \Vert ^{2}- (1-\beta _{n}) \bigl[(1-2\lambda _{n}c_{1}) \Vert y_{n}-t _{n} \Vert ^{2}+(1-2\lambda _{n}c_{2}) \Vert t_{n}-z_{n} \Vert ^{2} \bigr]. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} \leq & \alpha _{n} \bigl\Vert h(x_{n})-p \bigr\Vert ^{2}+ (1-\alpha _{n}) \Vert q_{n}-p \Vert ^{2} \\ \leq &\alpha _{n} \bigl\Vert h(x_{n})-p \bigr\Vert ^{2}+ (1-\alpha _{n})\bigl\{ \Vert x_{n}-p \Vert ^{2} -(1-\beta _{n})\bigl[(1-2\lambda _{n}c_{1}) \Vert y_{n}-t_{n} \Vert ^{2} \\ &{}+(1-2\lambda _{n}c_{2}) \Vert t_{n}-z_{n} \Vert ^{2}\bigr] \bigr\} , \end{aligned}$$

and hence

$$\begin{aligned}& (1-\beta _{n}) \bigl[(1-2\lambda _{n}c_{1}) \Vert y_{n}-t_{n} \Vert ^{2}+(1-2 \lambda _{n}c_{2}) \Vert t_{n}-z_{n} \Vert ^{2} \bigr] \\& \quad \leq \Vert x_{n}-p \Vert ^{2} - \Vert x_{n+1}-p \Vert ^{2} +\alpha _{n}M, \end{aligned}$$

(3.10)

where

$$\begin{aligned} M =& \sup \bigl\{ \bigl\vert \bigl\Vert h(x_{n})-p \bigr\Vert ^{2}- \Vert x_{n}-p \Vert ^{2} \bigr\vert +(1-\beta _{n})\bigl[(1-2\lambda _{n}c_{1}) \Vert y_{n}-t_{n} \Vert ^{2} \\ &{}+(1-2\lambda _{n}c_{2}) \Vert t_{n}-z_{n} \Vert ^{2}\bigr], n\in \mathbb{N}\bigr\} . \end{aligned}$$

By (3.9), we have

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} =& \bigl\Vert \alpha _{n} \bigl(h(x_{n})-p\bigr)+ (1-\alpha _{n}) (q_{n}-p) \bigr\Vert ^{2} \\ \leq &(1-\alpha _{n})^{2} \Vert q_{n}-p \Vert ^{2}+2 \alpha _{n}\bigl\langle h(x_{n})-p,x _{n+1}-p\bigr\rangle \\ \leq &(1-\alpha _{n})^{2} \Vert x_{n}-p \Vert ^{2}+2 \alpha _{n}\bigl\langle h(x_{n})-h(p),x _{n+1}-p\bigr\rangle +2 \alpha _{n}\bigl\langle h(p)-p,x_{n+1}-p\bigr\rangle \\ \leq &(1-\alpha _{n})^{2} \Vert x_{n}-p \Vert ^{2}+2 \alpha _{n}\rho \Vert x_{n}-p \Vert \Vert x_{n+1}-p \Vert +2 \alpha _{n}\bigl\langle h(p)-p,x_{n+1}-p\bigr\rangle \\ \leq &(1-\alpha _{n})^{2} \Vert x_{n}-p \Vert ^{2}+ \alpha _{n}\rho \bigl( \Vert x _{n}-p \Vert ^{2}+ \Vert x_{n+1}-p \Vert ^{2} \bigr) \\ &{}+2 \alpha _{n}\bigl\langle h(p)-p,x _{n+1}-p\bigr\rangle \\ =& \bigl((1-\alpha _{n})^{2}+ \alpha _{n}\rho \bigr) \Vert x_{n}-p \Vert ^{2}+ \alpha _{n} \rho \Vert x_{n+1}-p \Vert ^{2} \\ &{}+2 \alpha _{n} \bigl\langle h(p)-p,x_{n+1}-p \bigr\rangle . \end{aligned}$$

(3.11)

So, we get

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} \leq & \biggl(1-\frac{2(1-\rho )\alpha _{n}}{1-\alpha _{n}\rho } \biggr) \Vert x_{n}-p \Vert ^{2} \\ &{}+\frac{2(1-\rho )\alpha _{n}}{1-\alpha _{n}\rho } \biggl(\frac{\alpha _{n}M_{0}}{2(1-\rho )}+\frac{1}{(1-\rho )}\bigl\langle h(p)-p,x_{n+1}-p \bigr\rangle \biggr) \\ =&(1-\gamma _{n} ) \Vert x_{n}-p \Vert ^{2} \\ &{}+\gamma _{n} \biggl(\frac{\alpha _{n}M_{0}}{2(1-\rho )}+\frac{1}{(1- \rho )}\bigl\langle h(p)-p,x_{n+1}-p\bigr\rangle \biggr), \end{aligned}$$

(3.12)

where $M_{0}=\sup \lbrace \|x_{n}-p\|^{2}, n\in \mathbb{N} \rbrace$, put $\gamma _{n}=\frac{2(1-\rho )\alpha _{n}}{1-\alpha _{n}\rho }$ for each $n\in \mathbb{N}$. By the assumptions on $\alpha _{n}$, we have

$$ \lim_{n\rightarrow \infty }\gamma _{n}=0,\qquad \sum ^{\infty } _{n=1}\gamma _{n}=\infty . $$

(3.13)

Since $P_{\varOmega }h$ is a contraction on C, there exists $q\in \varOmega$ such that $q=P_{\varOmega }h(q)$. We prove that the sequence $\{x_{n}\}$ converges strongly to $q=P_{\varOmega }h(q)$. In order to prove it, let us consider two cases.

Case 1. Suppose that there exists $n_{0}\in \mathbb{N}$ such that $\{\|x_{n}-q\|\}_{n=n_{0}}^{\infty }$ is nonincreasing. In this case, the limit of $\{\|x_{n}-q\|\}$ exists. This together with the assumptions on $\{\alpha _{n}\}$, $\{\beta _{n}\}$, $\{\lambda _{n}\}$ and (3.10) implies that

$$ \lim_{n\rightarrow \infty } \Vert y_{n}-t_{n} \Vert =\lim_{n\rightarrow \infty } \Vert t_{n}-z_{n} \Vert =0. $$

(3.14)

On the other hands, from the definition of $x_{n+1}$ and (3.8), we get

$$\begin{aligned} \Vert x_{n+1}-q \Vert ^{2} \leq &\alpha _{n} \bigl\Vert h(x_{n})-q \bigr\Vert ^{2}+ (1-\alpha _{n}) \bigl\Vert \beta _{n}x_{n}+(1-\beta _{n})Tz_{n}-q \bigr\Vert ^{2} \\ =&\alpha _{n} \bigl\Vert h(x_{n})-q \bigr\Vert ^{2}+ (1-\alpha _{n}) \\ &{}\times\bigl[\beta _{n} \Vert x _{n}-q \Vert ^{2}+(1-\beta _{n}) \Vert Tz_{n}-q \Vert ^{2}-\beta _{n}(1-\beta _{n}) \Vert x _{n}-Tz_{n} \Vert ^{2} \bigr] \\ \leq &\alpha _{n} \bigl\Vert h(x_{n})-q \bigr\Vert ^{2}+ (1-\alpha _{n}) \\ &{}\times\bigl[\beta _{n} \Vert x_{n}-q \Vert ^{2}+(1-\beta _{n}) \Vert x_{n}-q \Vert ^{2}-\beta _{n}(1-\beta _{n}) \Vert x _{n}-Tz_{n} \Vert ^{2} \bigr] \\ =&\alpha _{n} \bigl\Vert h(x_{n})-q \bigr\Vert ^{2}+ (1-\alpha _{n}) \bigl[ \Vert x_{n}-q \Vert ^{2}-\beta _{n}(1-\beta _{n}) \Vert x_{n}-Tz_{n} \Vert ^{2} \bigr], \end{aligned}$$

and hence

$$\begin{aligned} \beta _{n}(1-\beta _{n}) (1-\alpha _{n}) \Vert x_{n}-Tz_{n} \Vert ^{2} \leq & \alpha _{n} \bigl\Vert h(x_{n})-q \bigr\Vert ^{2}+ \Vert x_{n}-q \Vert ^{2} \\ &{}- \Vert x_{n+1}-q \Vert ^{2}. \end{aligned}$$

(3.15)

Since the limit of $\{\|x_{n}-q\|\}$ exists and by the assumptions on $\{\alpha _{n}\}$ and $\{\beta _{n}\}$, we obtain

$$ \lim_{n\rightarrow \infty } \Vert x_{n}-Tz_{n} \Vert =0. $$

(3.16)

From (3.9) and (3.11), we have

$$\begin{aligned} \Vert x_{n+1}-q \Vert ^{2}- \Vert x_{n}-q \Vert ^{2}-2 \alpha _{n}\bigl\langle h(x_{n})-q,x _{n+1}-q\bigr\rangle \leq & \Vert q_{n}-q \Vert ^{2}- \Vert x_{n}-q \Vert ^{2} \\ \leq & 0. \end{aligned}$$

(3.17)

Again, since the limit of $\{\|x_{n}-q\|\}$ exists and $\alpha _{n} \rightarrow 0$, it follows that

$$ \lim_{n\rightarrow \infty } \bigl( \Vert q_{n}-q \Vert ^{2}- \Vert x_{n}-q \Vert ^{2} \bigr)= 0 $$

and hence

$$ \lim_{n\rightarrow \infty } \Vert q_{n}-q \Vert = \lim_{n\rightarrow \infty } \Vert x_{n}-q \Vert , $$

and by (3.9), we get

$$ \lim_{n\rightarrow \infty } \Vert x_{n}-q \Vert = \lim_{n\rightarrow \infty } \Vert z_{n}-q \Vert . $$

(3.18)

We also get from (3.6), (3.7) and (3.18)

$$ \lim_{n\rightarrow \infty } \Vert x_{n}-q \Vert = \lim_{n\rightarrow \infty } \Vert y_{n}-q \Vert . $$

(3.19)

By (3.5) and (3.19),

$$ \lim_{n\rightarrow \infty } \Vert Sv_{n}-Lx_{n} \Vert =\lim_{n\rightarrow \infty } \bigl\Vert P_{D}(Lx_{n})-Lx_{n} \bigr\Vert =0, $$

(3.20)

which implies that

$$ \lim_{n\rightarrow \infty } \bigl\Vert Sv_{n}-P_{D}(Lx_{n}) \bigr\Vert =0. $$

(3.21)

It follows from (3.2) that

$$\begin{aligned}& (1-2\mu _{n}d_{1}) \bigl\Vert P_{D}(Lx_{n})-u_{n} \bigr\Vert ^{2}+(1-2\mu _{n}d_{2}) \Vert u _{n}-v_{n} \Vert ^{2} \\& \quad \leq \bigl\Vert P_{D}(Lx_{n})-Lp \bigr\Vert ^{2}- \Vert Sv_{n}-Lp \Vert ^{2} \\& \quad = \bigl( \bigl\Vert P_{D}(Lx_{n})-Lp \bigr\Vert + \Vert Sv_{n}-Lp \Vert \bigr) \bigl( \bigl\Vert P_{D}(Lx _{n})-Lp \bigr\Vert - \Vert Sv_{n}-Lp \Vert \bigr) \\& \quad = \bigl( \bigl\Vert P_{D}(Lx_{n})-Lp \bigr\Vert + \Vert Sv_{n}-Lp \Vert \bigr) \bigl\Vert P_{D}(Lx_{n})-Sv _{n} \bigr\Vert . \end{aligned}$$

So,

$$ \lim_{n\rightarrow \infty } \bigl\Vert P_{D}(Lx_{n})-u_{n} \bigr\Vert =\lim_{n\rightarrow \infty } \Vert u_{n}-v_{n} \Vert =0, $$

(3.22)

and hence

$$ \lim_{n\rightarrow \infty } \bigl\Vert P_{D}(Lx_{n})-v_{n} \bigr\Vert =0. $$

(3.23)

From (3.20) and (3.23), we get

$$ \lim_{n\rightarrow \infty } \Vert Lx_{n}-v_{n} \Vert =0. $$

(3.24)

It follows from $x_{n}\in C$, the definition of $y_{n}$ and (3.20) that

$$\begin{aligned} \Vert y_{n}-x_{n} \Vert =& \bigl\Vert P_{C} \bigl(x_{n}+\delta _{n}L^{*} (Sv_{n}-Lx _{n} ) \bigr)-P_{C}(x_{n}) \bigr\Vert \\ \leq & \bigl\Vert x_{n}+\delta _{n}L^{*} (Sv_{n}-Lx_{n} )-x_{n} \bigr\Vert \\ \leq & \delta _{n} \Vert L \Vert \Vert Sv_{n}-Lx_{n} \Vert \rightarrow 0. \end{aligned}$$

(3.25)

Because $\{x_{n}\}$ is bounded, there exists a subsequence $\{x_{n _{k}}\}$ of $\{x_{n}\}$ such that $\{x_{n_{k}}\}$ converges weakly to some x̄, as $k\rightarrow \infty$ and

$$\begin{aligned} \limsup_{n\rightarrow \infty }\bigl\langle x_{n}-q,h(q)-q\bigr\rangle =& \lim_{k\rightarrow \infty }\bigl\langle x_{n_{k}}-q,h(q)-q \bigr\rangle \\ =&\bigl\langle \bar{x}-q,h(q)-q\bigr\rangle . \end{aligned}$$

(3.26)

Consequently $\{Lx_{n_{k}}\}$ converges weakly to Lx̄. By (3.24), $\{v_{n_{k}}\}$ converges weakly to Lx̄. We show that $\bar{x}\in \varOmega$. We know that $x_{n}\in C$ and $v_{n}\in D$, for each $n\in \mathbb{N}$. Since C and D are closed and convex sets, so C and D are weakly closed, therefore, $\bar{x}\in C$ and $L\bar{x}\in D$. From (3.25) and (3.14), we see that $\{y_{n_{k}}\}$, $\{t_{n_{k}}\}$ and $\{z_{n_{k}}\}$ converge weakly to x̄. By (3.22) and (3.23), we also see that $\{u_{n_{k}}\}$ and $\{P_{D}(Lx_{n_{k}})\}$ converge weakly to Lx̄. Algorithm 3.1 and assertion (i) in Lemma 2.6 imply that

$$\begin{aligned} \lambda _{n_{k}} \bigl(f(y_{n_{k}},y)-f(y_{n_{k}},t_{n_{k}}) \bigr) \geq & \langle t_{n_{k}}-y_{n_{k}},t_{n_{k}}-y \rangle \\ \geq & - \Vert t_{n_{k}}-y_{n_{k}} \Vert \Vert t_{n_{k}}-y \Vert , \quad \forall y\in C, \end{aligned}$$

and

$$\begin{aligned} \mu _{n_{k}} \bigl(g\bigl(P_{D}(Lx_{n_{k}}),u\bigr)-g \bigl(P_{D}(Lx_{n_{k}}),u_{n _{k}}\bigr) \bigr) \geq & \bigl\langle u_{n_{k}}-P_{D}(Lx_{n_{k}}),u_{n_{k}}-u \bigr\rangle \\ \geq &- \bigl\Vert u_{n_{k}}-P_{D}(Lx_{n_{k}}) \bigr\Vert \Vert u_{n_{k}}-u \Vert ,\quad \forall u \in D. \end{aligned}$$

Hence, it follows that

$$ f(y_{n_{k}},y)-f(y_{n_{k}},t_{n_{k}})+\frac{1}{\lambda _{n_{k}}} \Vert t _{n_{k}}-y_{n_{k}} \Vert \Vert t_{n_{k}}-y \Vert \geq 0,\quad \forall y\in C, $$

and

$$ g\bigl(P_{D}(Lx_{n_{k}}),u\bigr)-g\bigl(P_{D}(Lx_{n_{k}}),u_{n_{k}} \bigr)+\frac{1}{\mu _{n_{k}}} \bigl\Vert u_{n_{k}}-P_{D}(Lx_{n_{k}}) \bigr\Vert \Vert u_{n_{k}}-u \Vert \geq 0,\quad \forall u\in D. $$

Letting $k\rightarrow \infty$, by the hypothesis on $\{\lambda _{n}\}$, $\{\mu _{n}\}$, (3.14), (3.22) and the weak continuity of f and g (condition (A2)), we obtain

$$ f(\bar{x},y)\geq 0, \quad \forall y\in C \quad \text{and}\quad g(L\bar{x},u)\geq 0,\quad \forall u\in D. $$

This means that $\bar{x}\in \operatorname{EP}(f)$ and $L\bar{x}\in \operatorname{EP}(g)$. It follows from (3.14), (3.16) and (3.25) that

$$ \Vert z_{n}-Tz_{n} \Vert \leq \Vert z_{n}-t_{n} \Vert + \Vert t_{n}-y_{n} \Vert + \Vert y_{n}-x_{n} \Vert + \Vert x_{n}-Tz_{n} \Vert \rightarrow 0. $$

This together with Lemma 2.2 implies that $\bar{x}\in F(T)$. On the other hand, from (3.21) and (3.23), we get

$$ \Vert v_{n}-Sv_{n} \Vert \leq \bigl\Vert v_{n}-P_{D}(Lx_{n}) \bigr\Vert + \bigl\Vert P_{D}(Lx_{n})-Sv_{n} \bigr\Vert \rightarrow 0, $$

and using again Lemma 2.2, we obtain $L\bar{x}\in F(S)$. Then we proved that $\bar{x}\in \operatorname{EP}(f)\cap F(T)$ and $L\bar{x}\in \operatorname{EP}(g) \cap F(S)$, that is, $\bar{x}\in \varOmega$. By Lemma 2.1, $\bar{x}\in \varOmega$ and (3.26), we get

$$ \limsup_{n\rightarrow \infty }\bigl\langle x_{n}-q,h(q)-q \bigr\rangle = \bigl\langle \bar{x}-q,h(q)-q\bigr\rangle \leq 0. $$

(3.27)

Finally, from (3.12), (3.13), (3.27) and Lemma 2.3, we find that the sequence $\{x_{n}\}$ converges strongly to q.

Case 2. Suppose that there exists a subsequence $\{n_{i}\}$ of $\{n\}$ such that

$$ \Vert x_{n_{i}}-q \Vert < \Vert x_{{n_{i}}+1}-q \Vert , \quad \forall i\in \mathbb{N}. $$

According to Lemma 2.4, there exists a nondecreasing sequence $\{m_{k}\}\subset \mathbb{N}$ such that $m_{k}\rightarrow \infty$,

$$ \Vert x_{m_{k}}-q \Vert \leq \Vert x_{{m_{k}}+1}-q \Vert \quad \text{and}\quad \Vert x_{k}-q \Vert \leq \Vert x_{{m_{k}}+1}-q \Vert , \quad \forall k\in \mathbb{N}. $$

(3.28)

From this and (3.10), we get

$$\begin{aligned}& (1-\beta _{m_{k}}) \bigl[(1-2\lambda _{m_{k}}c_{1}) \Vert y_{m_{k}}-t_{m _{k}} \Vert ^{2}+(1-2\lambda _{m_{k}}c_{2}) \Vert t_{m_{k}}-z_{m_{k}} \Vert ^{2} \bigr] \\& \quad \leq \alpha _{m_{k}}M+ \Vert x_{m_{k}}-q \Vert ^{2}- \Vert x_{{m_{k}}+1}-q \Vert ^{2} \\& \quad \leq \alpha _{m_{k}}M. \end{aligned}$$

This together with the assumptions on $\{\alpha _{n}\}$, $\{\beta _{n} \}$ and $\{\lambda _{n}\}$ implies that

$$ \lim_{k\rightarrow \infty } \Vert y_{m_{k}}-t_{m_{k}} \Vert =0,\qquad \lim_{k\rightarrow \infty } \Vert t_{m_{k}}-z_{m_{k}} \Vert =0 \quad \text{and}\quad \lim_{k\rightarrow \infty } \Vert y_{m_{k}}-z_{m_{k}} \Vert =0. $$

From (3.15), we have

$$\begin{aligned} \beta _{m_{k}}(1-\beta _{m_{k}}) (1-\alpha _{m_{k}}) \Vert x_{m_{k}}-Tz_{m_{k}} \Vert ^{2} \leq & \alpha _{m_{k}} \bigl\Vert h(x_{m_{k}})-q \bigr\Vert ^{2}+ \Vert x_{m_{k}}-q \Vert ^{2}- \Vert x_{{m_{k}}+1}-q \Vert ^{2} \\ \leq & \alpha _{m_{k}} \bigl\Vert h(x_{m_{k}})-q \bigr\Vert ^{2}. \end{aligned}$$

By the hypothesis on $\{\alpha _{n}\}$ and $\{\beta _{n}\}$, we have

$$ \lim_{k\rightarrow \infty } \Vert x_{m_{k}}-Tz_{m_{k}} \Vert =0. $$

By (3.17), we get

$$\begin{aligned} -2 \alpha _{m_{k}}\bigl\langle h(x_{m_{k}})-q,x_{{m_{k}}+1}-q \bigr\rangle \leq & \Vert x_{{m_{k}}+1}-q \Vert ^{2}- \Vert x_{m_{k}}-q \Vert ^{2} \\ &{}-2 \alpha _{m_{k}} \bigl\langle h(x_{m_{k}})-q,x_{{m_{k}}+1}-q\bigr\rangle \\ \leq & \Vert q_{m_{k}}-q \Vert ^{2}- \Vert x_{m_{k}}-q \Vert ^{2}\leq 0. \end{aligned}$$

Since the sequence $\{x_{n}\}$ is bounded and $\alpha _{n}\rightarrow 0$, we obtain

$$ \lim_{k\rightarrow \infty } \Vert q_{m_{k}}-q \Vert =\lim _{k\rightarrow \infty } \Vert x_{m_{k}}-q \Vert . $$

By the same argument as Case 1, we have

$$ \limsup_{k\rightarrow \infty }\bigl\langle x_{m_{k}}-q,h(q)-q\bigr\rangle \leq 0. $$

It follows from (3.12) and (3.28) that

$$\begin{aligned} \Vert x_{{m_{k}}+1}-q \Vert ^{2} \leq &(1-\gamma _{m_{k}} ) \Vert x_{m_{k}}-q \Vert ^{2}+ \gamma _{m_{k}} \biggl(\frac{\alpha _{m_{k}}M_{0}}{2(1-\rho )}+\frac{1}{(1- \rho )}\bigl\langle h(q)-q,x_{{m_{k}}+1}-q\bigr\rangle \biggr) \\ \leq &(1-\gamma _{m_{k}}) \Vert x_{{m_{k}}+1}-q \Vert ^{2}+\gamma _{m_{k}} \biggl(\frac{ \alpha _{m_{k}}M_{0}}{2(1-\rho )}+ \frac{1}{(1-\rho )}\bigl\langle h(q)-q,x _{{m_{k}}+1}-q\bigr\rangle \biggr), \end{aligned}$$

and hence

$$ \gamma _{m_{k}} \Vert x_{{m_{k}}+1}-q \Vert ^{2} \leq \gamma _{m_{k}} \biggl(\frac{ \alpha _{m_{k}}M_{0}}{2(1-\rho )}+\frac{1}{(1-\rho )}\bigl\langle h(q)-q,x _{{m_{k}}+1}-q\bigr\rangle \biggr). $$

Since $\gamma _{m_{k}}>0$ and using (3.28) we get

$$ \Vert x_{k}-q \Vert ^{2}\leq \Vert x_{{m_{k}}+1}-q \Vert ^{2} \leq \biggl(\frac{ \alpha _{m_{k}}M_{0}}{2(1-\rho )}+\frac{1}{(1-\rho )}\bigl\langle h(q)-q,x _{{m_{k}}+1}-q\bigr\rangle \biggr). $$

Taking the limit in the above inequality as $k\rightarrow \infty$, we conclude that $x_{k}$ converges strongly to $q=P_{\varOmega }h(q)$. □

4 Application to variational inequality problems

In this section, we apply Theorem 3.2 for finding a solution of a variational inequality problems for a monotone and Lipschitz-type continuous mapping. Let H be a real Hilbert space, C be a nonempty and convex subset of H and $A\colon C\rightarrow C$ be a nonlinear operator. The mapping A is said to be

• monotone on C if

  $$ \langle Ax-Ay,x-y\rangle \geq 0,\quad \forall x, y\in C; $$

• pseudomonotone on C if

  $$ \langle Ax,y-x\rangle \geq 0\quad \Longrightarrow\quad \langle Ay,x-y\rangle \leq 0,\quad \forall x, y\in C; $$

• L-Lipschitz continuous on C if there exists a positive constant L such that

  $$ \Vert Ax-Ay \Vert \leq L \Vert x-y \Vert ,\quad \forall x, y\in C. $$

The variational inequality problem is to find $x^{*}\in C$ such that

$$ \bigl\langle Ax^{*},x-x^{*}\bigr\rangle \geq 0, \quad \forall x\in C. $$

(4.1)

For each $x,y\in C$, we define $f(x,y)=\langle Ax,y-x\rangle$, then the equilibrium problem (1.1) become the variational inequality problem (4.1). We denote the set of solutions of the problem (4.1) by $\operatorname{VI}(C,A)$. We assume that A satisfies the following conditions:

• (B1) A is pseudomonotone on C;

• (B2) A is weak to strong continuous on C that is, $Ax_{n}\rightarrow Ax$ for each sequence $\{x_{n}\}\subset C$ converging weakly to x;

• (B3) A is $\mathrm{L}_{1}$-Lipschitz continuous on C for some positive constant $\mathrm{L}_{1}>0$.

Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces and C and D be nonempty closed and convex subsets of $H_{1}$ and $H_{2}$, respectively. Suppose that $A\colon C\rightarrow C$ and $B\colon D\rightarrow D$ are $\mathrm{L}_{1}$ and $\mathrm{L}_{2}$-Lipschitz continuous on C and D, respectively. Let $L\colon H_{1}\rightarrow H_{2}$ be a bounded linear operator with its adjoint $L^{*}$, $T\colon C\rightarrow C$ and $S\colon D\rightarrow D$ be nonexpansive mappings and $h \colon C \rightarrow C$ be a ρ-contraction mapping. We consider the following extragradient algorithm for solving the split variational inequality problems and fixed point problems.

Algorithm 4.1

Choose $x_{1}\in H_{1}$. The control parameters $\lambda _{n}$, $\mu _{n}$, $\alpha _{n}$, $\beta _{n}$, $\delta _{n}$ satisfy the following conditions:

$$\begin{aligned}& 0< \underline{\lambda } \leq \lambda _{n} \leq \overline{\lambda } < L _{1},\qquad 0< \underline{\mu } \leq \mu _{n} \leq \overline{\mu } < L_{2}, \qquad \beta _{n}\in (0,1), \\& 0< \liminf _{n\rightarrow \infty } \beta _{n}\leq\limsup_{n\rightarrow \infty } \beta _{n}< 1, \qquad 0< \underline{ \delta } \leq \delta _{n}\leq \overline{\delta }< \frac{1}{ \Vert L \Vert ^{2}}, \\& \alpha _{n}\in \biggl(0,\frac{1}{2-\rho }\biggr),\qquad \lim _{n\rightarrow \infty }\alpha _{n}=0,\qquad \sum ^{\infty }_{n=1}\alpha _{n}=\infty . \end{aligned}$$

Let $\{x_{n}\}$ be a sequence generated by

$$ \textstyle\begin{cases} u_{n}=P_{D} ( P_{D}(Lx_{n})-\mu _{n} B (P_{D}(Lx_{n}) ) ), \\ v_{n}=P_{D} ( P_{D}(Lx_{n})-\mu _{n} B (u_{n}) ) ), \\ y_{n}=P_{C} (x_{n}+\delta _{n}L^{*} (Sv_{n}-Lx_{n} ) ), \\ t_{n}=P_{C} ( y_{n}-\lambda _{n} Ay_{n} ), \\ z_{n}=P_{C} ( y_{n}-\lambda _{n} At_{n} ), \\ x_{n+1}=\alpha _{n}h(x_{n})+(1-\alpha _{n})(\beta _{n}x_{n}+(1-\beta _{n})Tz _{n}). \end{cases} $$

Theorem 4.2

Let $A\colon C\rightarrow C$ and $B\colon D\rightarrow D$ be mappings such that assumptions (B1)–(B3) hold with some positive constants $\mathrm{L}_{1}>0$ and $\mathrm{L}_{2}>0$, respectively and $\varOmega := \{p\in \operatorname{VI}(C,A)\cap F(T), Lp\in \operatorname{VI}(D,B)\cap F(S)\} \neq \emptyset$. Then the sequence $\{x_{n}\}$ generated by Algorithm 4.1 converges strongly to $q=P_{\varOmega }h(q)$.

Proof

Since the mapping A is satisfied the assumptions (B1)–(B3), it is easy to check that the bifunction $f(x,y)=\langle Ax,y-x\rangle$ satisfies conditions (A1)–(A3). Moreover, since A is $\mathrm{L} _{1}$-Lipschitz continuous on C, it follows that

$$\begin{aligned} f(x,y)+ f(y,z)-f(x,z) =&\langle Ax-Ay,y-z\rangle \\ \geq & - \Vert Ax-Ay \Vert \Vert y-z \Vert \\ \geq & -L_{1} \Vert x-y \Vert \Vert y-z \Vert \\ \geq &-\frac{L_{1}}{2} \Vert x-y \Vert ^{2}-\frac{L_{1}}{2} \Vert y-z \Vert ^{2}, \quad \forall x, y,z\in C. \end{aligned}$$

Then f is Lipschitz-type continuous on C with $c_{1}=c_{2}=\frac{L _{1}}{2}$, and hence f satisfies condition (A4).

It follows from the definitions of f and $y_{n}$ that

$$\begin{aligned} t_{n} =&\operatorname{arg}\operatorname{min} \biggl\lbrace \lambda _{n} \langle Ay_{n},y-y _{n}\rangle + \frac{1}{2} \Vert y-y_{n} \Vert ^{2}\colon y\in C \biggr\rbrace \\ =&\operatorname{arg}\operatorname{min} \biggl\lbrace \frac{1}{2} \bigl\Vert y-(y_{n}-\lambda _{n}Ay _{n}) \bigr\Vert ^{2}\colon y\in C \biggr\rbrace \\ =&P_{C}(y_{n}-\lambda _{n}Ay_{n}), \end{aligned}$$

and similarly, we can get $u_{n}=P_{D} ( P_{D}(Lx_{n})-\mu _{n} B (P_{D}(Lx_{n}) ) )$, $v_{n}=P_{D} ( P_{D}(Lx _{n})-\mu _{n} B (u_{n}) )$, and $z_{n}=P_{C} ( y_{n}-\lambda _{n} At_{n} )$. Then the extragradient Algorithm 3.1 reduces to the Algorithm 4.1 and we get the conclusion from and Theorem 3.2. □

5 Numerical experiments

In this section, we give examples and numerical results to support Theorem 3.2. In addition, we compare the introduced algorithm with the parallel extragradient algorithm, which was presented in [27].

We consider the bifunctions f and g which are given in the form of Nash–Cournot oligopolistic equilibrium models of electricity markets [15, 34],

$$\begin{aligned}& f(x,y) = (Px + Qy)^{T} (y - x), \quad \forall x, y \in \mathbb{R} ^{k}, \end{aligned}$$

(5.1)

$$\begin{aligned}& g(u,v) = (Uu + Vv)^{T} (v - u),\quad \forall u, v \in \mathbb{R} ^{m}, \end{aligned}$$

(5.2)

where $P, Q \in \mathbb{R}^{k\times k}$ and $U, V \in \mathbb{R} ^{m\times m}$ are symmetric positive semidefinite matrices such that $P - Q$ and $U - V$ are positive semidefinite matrices. The bifunctions f and g satisfy conditions (A1)–(A4) (see [37]). Indeed, f and g are Lipshitz-type continuous with constants $c_{1} = c _{2} = \frac{1}{2}\|P-Q\|$ and $d_{1} = d_{2} = \frac{1}{2}\|U-V\|$, respectively. Notice that, if $b_{1} = \max \{c_{1}, d_{1}\}$ and $b_{2} = \max \{c_{2}, d_{2}\}$, then both bifunctions f and g are Lipshitz-type continuous with constants $b_{1}$ and $b_{2}$.

The following numerical experiments are written in Matlab R2015b and performed on a Desktop with Intel(R) Core(TM) i3 CPU M 390 @ 2.67 GHz 2.67 GHz and RAM 4.00 GB.

Example 5.1

Let the bifunctions f and g be given as (5.1) and (5.2), respectively. We will be concerned with the following boxes: $C = \prod_{i=1}^{k} [-5,5]$, $D = \prod_{j=1}^{m} [-20,20]$, $\overline{C} = \prod_{i=1}^{k} [-3,3]$ and $\overline{D} = \prod_{j=1}^{m} [-10,10]$. The nonexpansive mappings $T : C\rightarrow C$ and $S : D\rightarrow D$ are given by $T =P_{\overline{C}}$ and $S =P_{\overline{D}}$, respectively. The contraction mapping $h : C \rightarrow C$ is a $k \times k$ matrix such that $\| h \| < 1$, while the linear operator $L : \mathbb{R}^{k} \rightarrow \mathbb{R} ^{m}$ is a $m \times k$ matrix.

In this numerical experiment, the matrices P, Q, U, and V are randomly generated in the interval $[-5,5]$ such that they satisfy above required properties. Besides, the matrices h and L are randomly generated in the interval $(0,\frac{1}{k})$ and $[-2,2]$, respectively. We randomly generated starting point $x_{1} \in \mathbb{R}^{k}$ in the interval $[-20,20]$ with the following control parameters: $\delta _{n} = \frac{1}{2 \|L\|^{2}}$, $\alpha _{n} = \frac{1}{n+2}$ and $\mu _{n} = \lambda _{n} = \frac{1}{4\max \{b_{1},b_{2}\}}$. The following three cases of the control parameter $\beta _{n}$ are considered:

• Case 1. $\beta _{n} = 10^{-10} + \frac{1}{n+1}$.

• Case 2. $\beta _{n} = 0.5$.

• Case 3. $\beta _{n} = 0.99 - \frac{1}{n+1}$.

Note that to obtain the vector $u_{n}$, in the Algorithm 3.1, we need to solve the optimization problem

$$ \operatorname{arg}\operatorname{min} \biggl\lbrace \mu _{n} g \bigl(P_{D}(Lx_{n}),u\bigr)+ \frac{1}{2} \bigl\Vert u-P_{D}(Lx_{n}) \bigr\Vert ^{2}\colon u\in D \biggr\rbrace , $$

which is equivalent to the following convex quadratic problem:

$$ {\operatorname{arg}\operatorname{min}} \biggl\lbrace \frac{1}{2}u^{T} J u + K^{T}u\colon u\in D \biggr\rbrace , $$

(5.3)

where $J = 2\mu _{n} V + I_{m}$ and $K = \mu _{n} UP_{D}(Lx_{n}) - \mu _{n} VP_{D}(Lx_{n}) - P_{D}(Lx_{n})$ (see [27]).

On the other hand, in order to obtain the vector $v_{n}$, we need to solve the following convex quadratic problem:

$$ \operatorname{arg}\operatorname{min} \biggl\lbrace \frac{1}{2}u^{T} \overline{J} u + \overline{K}^{T}u \colon u\in D \biggr\rbrace , $$

(5.4)

where $\overline{J} = J$ and $\overline{K} = \mu _{n} Uu_{n} - \mu _{n} Vu_{n} - P_{D}(Lx_{n})$. Similarly, to obtain the vectors $t_{n}$ and $z_{n}$, we have to consider the convex quadratic problems in the same way as in (5.3) and (5.4), respectively. We use the Matlab Optimization Toolbox to solve vectors $u_{n}$, $v_{n}$, $t_{n}$ and $z_{n}$. The Algorithm 3.1 is tested by using the stopping criterion $\|x_{n+1}-x_{n}\| < 10^{-3}$. In Table 1, we randomly take 10 starting points and the presented results are in average.

Table 1 The numerical results for different parameter $\beta _{n}$ of Example 5.1

From Table 1, we may suggest that a smallest size of parameter $\beta _{n}$, as $\beta _{n} = 10^{-10} + \frac{1}{n+1}$, provides less computational times and iterations than other cases.

Example 5.2

We consider the problem (1.3) when $T = I_{\mathbb{R}^{k}}$ and $S = I_{\mathbb{R}^{m}}$ are identity mappings on $\mathbb{R}^{k}$ and $\mathbb{R}^{m}$, respectively. It follows that the problem (1.3) becomes the split equilibrium problem which was considered in [27]. In this case, we compare the Algorithm 3.1 with the parallel extragradient algorithm (PEA), which was in [27, Corollary 3.1]. For this numerical experiment, we consider the problem setting and the control parameters as in Example 5.1, but only for the case of parameter $\beta _{n}$ is $10^{-10} + \frac{1}{n+1}$. The starting point $x_{1} \in \mathbb{R} ^{k}$ is randomly generated in the interval $[-5,5]$. We compare Algorithm 3.1 with PEA by using the stopping criterion $\|x_{n+1}-x_{n}\| < 10^{-3}$. In Table 2, we randomly take 10 starting points and the presented results are in average.

Table 2 The numerical results for the split equilibrium problem of Example 5.2

From Table 2, we see that both computational times and iterations of Algorithm 3.1 are less than those of PEA.

6 Conclusions

We introduce a new extragradient algorithm and its convergence theorem for the split equilibrium problems and split fixed point problems. We also apply the main result to the problem of split variational inequality problems and split fixed point problems. Some numerical example and computational results are provided for discussing the possible usefulness of the results which are presented in this paper. We would like to note that this paper convinces us to consider the future research directions, for example, to consider the convergence analysis and the more general cases of the problem (like the non-convex case) directions; one may see [22, 29, 33] for more inspiration.