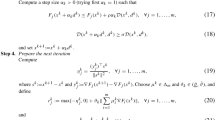Abstract
In this paper, the algorithm for large-scale nonlinear equations is designed by the following steps: (i) a conjugate gradient (CG) algorithm is designed as a sub-algorithm to obtain the initial points of the main algorithm, where the sub-algorithm’s initial point does not have any restrictions; (ii) a quasi-Newton algorithm with the initial points given by sub-algorithm is defined as main algorithm, where a new nonmonotone line search technique is presented to get the step length \(\alpha_{k}\). The given nonmonotone line search technique can avoid computing the Jacobian matrix. The global convergence and the \(1+q\)-order convergent rate of the main algorithm are established under suitable conditions. Numerical results show that the proposed method is competitive with a similar method for large-scale problems.
Similar content being viewed by others
1 Introduction
Consider the following nonlinear equations:
Here \(e:\Re^{n} \rightarrow\Re^{n}\) is continuously differentiable and n denotes large-scale dimension. The large-scale nonlinear equations are difficult to solve since the relations of the variables x are complex and the dimension is larger. Problem (1.1) can model many real-life problems, such as engineering problems, dimensions of mechanical linkages, concentrations of chemical species, cross-sectional properties of structural elements, etc. If the Jacobian \(\nabla e(x)\) of e is symmetric, then problem (1.1) is called a system of symmetric nonlinear equations. Let p be the norm function with \(p(x)=\frac{1}{2}\Vert e(x)\Vert ^{2}\), where \(\Vert \cdot \Vert \) is the Euclidean norm. Then (1.1) is equivalent to the following global optimization models:
In fact, there are many actual problems that can convert to the above problems (1.2) (see [1–9] etc.) and have similar models (see [10–27] etc.). The iterative formula for (1.1) is
where \(\alpha_{k}\) is a step length and \(d_{k}\) is a search direction. Now let us review some methods for \(\alpha_{k}\) and \(d_{k}\), respectively:
(i) Li and Fukashima [28] proposed an approximately monotone technique for \(\alpha_{k}\):
where \(e_{k}=e(x_{k})\), \(\delta_{1}>0, \delta_{2}>0\) are positive constants, \(\alpha_{k}=r^{i_{k}}, r\in(0,1), i_{k}\) is the smallest nonnegative integer i satisfying (1.3) and \(\epsilon_{k}\) such that
(ii) Gu et al. [29] presented a descent line search technique:
(iii) Brown and Saad [30] gave the following technique to obtain \(\alpha_{k}\):
where \(\beta\in(0,1)\) and \(\nabla p(x_{k})=\nabla e(x_{k}) e(x_{k})\).
(iv) Based on this technique, Zhu [31] proposed a nonmonotone technique:
\(p(x_{l(k)})=\max_{0\leq j\leq m(k)}\{p(x_{k-j})\}\), \(m(0)=0\), and \(m(k)= \min\{m(k-1)+1,M\}\), \(k\geq 1\), and M is a nonnegative integer.
(v) Yuan and Lu [32] gave a new technique:
and some convergence results are obtained.
Next we present some techniques for the calculation of \(d_{k}\). At present, there exist many well-known methods for \(d_{k}\), such as the Newton method, the trust region method, and the quasi-Newton method, etc.
(i) The Newton method has the following form to get \(d_{k}\):
This method is regarded as one of the most effective methods. However, its efficiency largely depends on the possibility to efficiently solve (1.9) at each iteration. Moreover, the exact solution of the system (1.9) could be too burdensome when the iterative point \(x_{k}\) is far from the exact solution [33]. In order to overcome this drawback, inexact quasi-Newton methods are often used.
(ii) The quasi-Newton method is of the form
where \(B_{k}\) is generated by a quasi-Newton update formula, where the BFGS (Broyden-Fletcher-Goldfarb-Shanno) update formula is one of the well-known quasi-Newton formulas with
where \(s_{k}=x_{k+1}-x_{k}, y_{k}=e_{k+1}-e_{k}\), and \(e_{k+1}=e(x_{k+1})\). Set \(H_{k}\) to be the inverse of \(B_{k}\), then the inverse formula of (1.11) has the following form:
There exist many quasi-Newton methods (see [31, 32, 34–39]) representing the basic approach underlying most of the Newton-type large-scale algorithms.
The earliest nonmonotone line search framework was developed by Grippo, Lampariello, and Lucidi in [40] for Newton’s methods. Many subsequent papers have exploited nonmonotone line search techniques of this nature (see [41–44] etc.), which shows that the nonmonotone technique works well in many cases. Considering these points, Zhu [31] proposed the nonmonotone line search (1.7). From (1.7), we can see that the Jacobian matrix \(\nabla e(x)\) must be computed at every iteration. Computing the Jacobian matrix \(\nabla e(x)\) may be expensive if n is large and for any n at every iteration. Thus, one might prefer to remove the matrix, leading to a new nonmonotone technique.
Inspired by the above observations, we make a study of inexact quasi-Newton methods with a new nonmonotone technique for solving smooth nonlinear equations. In the kth iteration of our algorithm, the following new nonmonotone technique is used to obtain \(\alpha_{k}\):
where \(\sigma\in(0,1)\) is a constant and \(d_{k}\) is a solution of (1.10). Comparing with (1.7), the new technique (1.13) does not compute the Jacobian matrix \(\nabla e(x)\). Then the storage and workload can be saved in theory. In Section 3, we will state the technique (1.13) is well defined.
It is well known that the initial point plays an important role in an algorithm. For example, the local superlinear convergence needs the iteration point x lies in the neighborhood of the optimal solution \(x^{*}\), if the choice of the point x is correct then the Newton method can get the optimal solution \(x^{*}\) just need one step, moreover, the correct initial point can speed up the efficiency of an algorithm. The nonlinear conjugate gradient method is one of the most effective line search methods for unconstrained optimization problems due to its simplicity and low memory requirement, especially for large-scale problems. Many scholars have made many studies and obtained lots of achievements on the CG methods or other similar new methods (see [45–49] etc.), where the results of [46] are especially interesting. It has been proved that the numerical performance of the CG methods is very interesting for large-scale problems in different application fields. These considerations prompt us to design a CG algorithm (sub-algorithm) for solving large-scale nonlinear equations, where the terminated iteration point of the CG algorithm was used as the initial point of the given algorithm (main algorithm). Then there exist two advantages from this process: one is that we can use the CG’s characteristic to get a better initial point and another is that the good convergent results of the main algorithm can be preserved. The main attributes of this paper are stated as follows:
-
A sub-algorithm is designed to get the initial point of the main algorithm.
-
A new nonmonotone line search technique is presented, moreover, the Jacobian matrix \(\nabla e_{k}\) must not be computed at every iteration.
-
The given method possesses the sufficient descent property for the normal function \(p(x)\).
-
The global convergence and the \(1+q\)-order convergent rate of the new method are established under suitable conditions.
-
Numerical results show that this method is more effective than other similar methods.
We organize the paper as follows. In Section 2, the algorithms are stated. Convergent results are established in Section 3 and numerical results are reported in Section 4. In the last section, our conclusion is given. Throughout this paper, we use these notations: \(\Vert \cdot \Vert \) is the Euclidean norm, \(e(x_{k})\) and \(g(x_{k+1})\) are replaced by \(e_{k}\) and \(g_{k+1}\), respectively.
2 Algorithm
In this section, we will design a sub-algorithm and the main algorithm, respectively. These two algorithms are listed as follows.
Initial point algorithm (sub-algorithm)
-
Step 0:
Given any \(x_{0} \in\Re^{n}, \delta_{1},\delta_{2} \in(0,1), \epsilon_{k}>0\), \(r \in(0,1), \epsilon\in[0,1)\), let \(k:=0\).
-
Step 1:
If \(\Vert e_{k}\Vert \leq\epsilon\), stop. Otherwise let \(d_{k}=-e_{k}\) and go to next step.
-
Step 2:
Choose \(\epsilon_{k+1}\) satisfies (1.4) and let \(\alpha_{k}=1,r,r^{2},r^{3},\ldots \) until (1.3) holds.
-
Step 3:
Let \(x_{k+1}=x_{k} +\alpha_{k} d_{k}\).
-
Step 4:
If \(\Vert e_{k+1}\Vert \leq\epsilon\), stop.
-
Step 5:
Compute \(d_{k+1}=-e_{k+1}+\beta_{k}d_{k}\), set \(k=k+1\) and go to Step 2.
Remark
(i) \(\beta_{k}\) of Step 5 is a scalar and different \(\beta_{k}\) will determine different CG methods.
(ii) From Step 2 and [28], it is easy to deduce that there exists \(\alpha_{k}\) such that (1.3). Thus, this sub-algorithm is well defined.
In the following, we will state the main algorithm. First, assume that the terminated point of sub-algorithm is \(x_{sup}\), then the given algorithm is defined as follows.
Algorithm 1
Main algorithm
Step 0: Choose \(x_{sup} \in\Re^{n}\) as the initial point, an initial symmetric positive definite matrix \(B_{0}\in\Re^{n\times n}\), and constants \(r, \sigma\in(0,1), \epsilon_{\mathrm{main}}<\epsilon\), a positive integer \(M>0\), \(m(k)=0\), let \(k:=0\);
-
Step 1:
Stop if \(\Vert e_{k}\Vert \leq\epsilon_{\mathrm{main}}\). Otherwise solve (1.10) to get \(d_{k}\).
-
Step 2:
Let \(\alpha_{k}=1,r,r^{2},r^{3},\ldots \) until (1.13) holds.
-
Step 3:
Let the next iterative be \(x_{k+1}=x_{k}+\alpha_{k}d_{k}\).
-
Step 4:
Update \(B_{k}\) by quasi-Newton update formula and ensure the update matrix \(B_{k+1}\) is positive definite.
-
Step 5:
Let \(k:=k+1\). Go to Step 1.
Remark
Step 4 of Algorithm 1 can ensure that \(B_{k}\) is always positive definite. This means that (1.10) has a unique solution \(d_{k}\). By positive definiteness of \(B_{k}\), it is easy to obtain \(e_{k}^{T}d_{k}<0\). In the following sections, we only concentrate to the convergence of the main algorithm.
3 Convergence analysis
Let Ω be the level set with
Similar to [31, 32, 50], the following assumptions are needed to prove the global convergence of Algorithm 1.
Assumption A
(i) e is continuously differentiable on an open convex set \(\Omega_{1}\) containing Ω.
(ii) The Jacobian of e is symmetric, bounded, and positive definite on \(\Omega_{1}\), i.e., there exist positive constants \(M^{*}\geq m_{*}>0\) such that
and
Assumption B
\(B_{k}\) is a good approximation to \(\nabla e_{k}\), i.e.,
where \(\epsilon_{*}\in(0,1)\) is a small quantity.
Considering Assumption B and using the von Neumann lemma, we deduce that \(B_{k}\) is also bounded (see [31]).
Lemma 3.1
Let Assumption B hold. Then \(d_{k}\) is a descent direction of \(p(x)\) at \(x_{k}\), i.e.,
Proof
By using (1.10), we get
Thus, we have
It follows from (3.4) that
The proof is complete. □
The following lemma shows that the line search technique (1.13) is reasonable, then Algorithm 1 is well defined.
Lemma 3.2
Let Assumptions A and B hold. Then Algorithm 1 will produce an iteration \(x_{k+1}=x_{k}+\alpha_{k}d_{k}\) in a finite number of backtracking steps.
Proof
From Lemma 3.5 in [32] we have in a finite number of backtracking steps
from which, in view of the definition of \(p(x_{l(k)})=\max_{0\leq j\leq m(k)}\{p(x_{k-j})\}\geq p(x_{k})\), we obtain (1.13). Thus we conclude the result of this lemma. The proof is complete. □
Now we establish the global convergence theorem of Algorithm 1.
Theorem 3.1
Let Assumptions A and B hold, and \(\{\alpha_{k}, d_{k}, x_{k+1}, e_{k+1}\}\) be generated by Algorithm 1. Then
Proof
By the acceptance rule (1.13), we have
Using \(m(k+1)\leq m(k)+1\) and \(p(x_{k+1})\leq p(x_{l(k)})\), we obtain
This means that the sequence \(\{p(x_{l(k)})\}\) is decreasing for all k. Then \(\{p(x_{l(k)})\}\) is convergent. Based on Assumptions A and B, similar to Lemma 3.4 in [32], it is not difficult to deduce that there exist constants \(b_{1}\geq b_{2}>0\) such that
By (1.13) and (3.10), for all \(k>M\), we get
Since \(\{p(x_{l(k)})\}\) is convergent, from the above inequality, we have
This implies that either
or
If (3.12) holds, following [40], by induction we can prove that
and
for any positive integer j. As \(k\geq l(k)\geq k-M\) and M is a positive constant, by
and (3.14), it can be derived that
According to (3.10) and the rule for accepting the step \(\alpha_{k}d_{k}\),
This means
which implies that
or
If equation (3.18) holds, since \(B_{k}\) is bounded, then \(\Vert e_{k}\Vert =\Vert B_{k}d_{k}\Vert \leq \Vert B_{k}\Vert \Vert d_{k}\Vert \rightarrow0\) holds. The conclusion of this lemma holds. If (3.17) holds. Then acceptance rule (1.13) means that, for all large enough k, \(\alpha_{k}'=\frac{\alpha_{k}}{r}\) such that
Since
Using (3.19) and (3.20) in [32], we have
where \(\delta^{*} >0\) is a constant and \(\sigma< \delta^{*}\). So we get
Note that \(\delta^{*}-\sigma>0\) and \(e_{k}^{T}d_{k}<0\), we have from dividing (3.21) by \(\alpha_{k}'\Vert d_{k}\Vert \)
By (3.10), we have
Consider \(\Vert e_{k}\Vert =\Vert B_{k}d_{k}\Vert \leq \Vert B_{k}\Vert \Vert d_{k}\Vert \) and the bounded \(B_{k}\) again, we complete the proof. □
Lemma 3.3
see Lemma 4.1 in [31]
Let e be continuously differentiable, and \(\nabla e(x)\) be nonsingular at \(x^{*}\) which satisfies \(e(x^{*})=0\). Let
If \(\Vert x_{k}-x^{*}\Vert \) sufficiently small, then the inequality
holds.
Theorem 3.2
Let the assumptions in Lemma 3.3 hold. Assume that there exists a sufficiently small \(\varepsilon_{0}>0\) such that \(\Vert B_{k}-\nabla e(x_{k})\Vert \leq\varepsilon_{0}\) for each k. Then the sequence \(\{x_{k}\}\) converges to \(x^{*}\) superlinearly for \(\alpha_{k}=1\). Moreover, if e is q-order smooth at \(x^{*}\) and there is a neighborhood U of \(x^{*}\) satisfying for any \(x_{k}\in U\),
then \(x_{k}\rightarrow x^{*}\) with order at least \(1+q\), where η is a constant.
Proof
Since g is continuously differentiable and \(\nabla e(x)\) is nonsingular at \(x^{*}\), there exists a constant \(\gamma>0\) and a neighborhood U of \(x^{*}\) satisfying
where \(\nabla e(y)\) is nonsingular for any \(y\in U\). Consider the following equality when \(\alpha_{k}=1\):
the second term and the third term are \(o(\Vert x_{k}-x^{*}\Vert )\). By the von Neumann lemma, and considering that \(\nabla e(x_{k})\) is nonsingular, \(B_{k}\) is also nonsingular. For any \(y\in U\) and \(\nabla e(y)\) being nonsingular and \(\max\{\Vert \nabla e(y)\Vert ,\Vert \nabla e(y)^{-1}\Vert \}\leq\gamma\), then we obtain from Lemma 3.3
this means that the sequence \(\{x_{k}\}\) converges to \(x^{*}\) superlinearly for \(\alpha_{k}=1\).
If e is q-order smooth at \(x^{*}\), then we get
Consider the second term of (3.27) as \(x_{k}\rightarrow x^{*}\), and use (3.26), we can deduce that the second term of (3.27) is also \(O(\Vert x_{k}-x^{*}\Vert ^{q+1})\). Therefore, we have
The proof is complete. □
4 Numerical results
In this section, we report results of some numerical experiments with the proposed method. The test functions have the following form:
where these functions have the associated initial guess \(x_{0}\). These functions are stated as follows.
Function 1
Exponential function 2
Initial guess: \(x_{0}=(\frac{1}{n^{2}},\frac{1}{n^{2}},\ldots,\frac{1}{n^{2}})^{T}\).
Function 2
Trigonometric function
Initial guess: \(x_{0}=(\frac{101}{100n},\frac{101}{100n},\ldots,\frac {101}{100n})^{T}\).
Function 3
Logarithmic function
Initial guess: \(x_{0}=(1,1,\ldots,1)^{T}\).
Function 4
Broyden tridiagonal function [[51], pp. 471-472]
Initial guess: \(x_{0}=(-1,-1,\ldots,-1)^{T}\).
Function 5
Trigexp function [[51], p. 473]
Initial guess: \(x_{0}=(0,0,\ldots,0)^{T}\).
Function 6
Strictly convex function 1 [[52], p. 29]. \(e(x)\) is the gradient of \(h(x)=\sum_{i=1}^{n}(e^{x_{i}}-x_{i})\).
Initial guess: \(x_{0}=(\frac{1}{n},\frac{2}{n},\ldots,1)^{T}\).
Function 7
Strictly convex function 2 [[52], p. 30]
\(e(x)\) is the gradient of \(h(x)=\sum_{i=1}^{n}\frac{i}{10}(e^{x_{i}}-x_{i})\).
Initial guess: \(x_{0}=(1,1,\ldots,1)^{T}\).
Function 8
Variable dimensioned function
Initial guess: \(x_{0}=(1-\frac{1}{n},1-\frac{2}{n},\ldots,0)^{T}\).
Function 9
Discrete boundary value problem [53].
Initial guess: \(x_{0}=(h(h-1),h(2h-1),\ldots,h(nh-1))\).
Function 10
The discretized two-point boundary value problem similar to the problem in [53]
when A is the \(n\times n\) tridiagonal matrix given by
and \(F(x)=(F_{1}(x),F_{2}(x),\ldots,F_{n}(x))^{T}\) with \(F_{i}(x)=\sin x_{i} -1, i=1,2,\ldots,n\), and \(x_{0}=(50,0, 50,0,\ldots)\).
In the experiments, all codes were written in MATLAB r2009a and run on a PC with G1620T@2.40 GHz CPU processor and 4.0 GB memory and Windows XP operation system. In order to compare the performance the given algorithm with CG’s initial points (called new method with CG), we also do the experiment with only the main algorithm with initial points \(x_{0}\) (called the normal method). Aslam Noor et al. [54] presented a variational iteration technique for nonlinear equations, where the so-called VIM1 method has the better numerical performance. The VIM1 method has the following iteration form:
where \(\beta_{i}\in(0,1)\) for \(i=1,2,\ldots,n\). In their paper, only low dimension problems (two variables) are tested. In this experiment, we also give the numerical results of this method for large-scale nonlinear equations to compare with our proposed algorithm.
The parameters were chosen as \(r=0.1\), \(\sigma=0.9, M=12,\epsilon=10^{-4}\), and \(\epsilon_{\mathrm{main}}=10^{-5}\). In order to ensure the positive definiteness of \(B_{k}\), in Step 4 of the main algorithm: if \(y_{k}^{T}s_{k}>0\), update \(B_{k}\) by (1.11), otherwise let \(B_{k+1}=B_{k}\). This program will also be stopped if the iteration number of main algorithm is larger than 200. Since the line search cannot always ensure these descent conditions \(d_{k}^{T}e_{k}<0\) and \(d_{k}^{T}\nabla e(x_{k}) e_{k}<0\), an uphill search direction may occur in numerical experiments. In this case, the line search rule maybe fails. In order to avoid this case, the stepsize \(\alpha_{k}\) will be accepted if the searching time is larger than six in the inner circle for the test problems.
In the sub-algorithm, the CG formula is used by the following Polak-Ribière-Polyak (PRP) method [55, 56]
For the line search technique, (1.3) is used and the largest search number of times is ten, where \(\delta_{1}=\delta_{2}=10^{-7}\), and \(\epsilon_{k}=\frac{1}{NI^{2}}\) (NI is the iteration number). The sub-algorithm will also stopped if the iteration number is larger than 150. The iteration number, the function evaluations, and the CPU time of the sub-algorithm are added to the main algorithm for new method with CG. The meaning of the items of the columns of Table 1 is:
Dim: the dimension.
NI: the number of iterations.
NG: the number of function evaluations.
cpu time: the cpu time in seconds.
GF: the final norm function evaluations \(p(x)\) when the program is stopped.
GD: the final norm evaluations of search direction \(d_{k}\).
fails: fails to find the final values of \(p(x)\) when the program is stopped.
From Tables 1-2, it is easy to see that the number of iterations and the number of function evaluations of the new method with CG are less than those of the normal method for these test problems. Moreover, the cpu time and the final function norm evaluations of the new method with CG are more competitive than those of the normal method. For the VIM1 method, the results of Problems 1-7 are very interesting, but it fails for Problems 8-10. Moreover, it is not difficult to find that more CUP time is needed for this method. The main reason maybe lies in the computation of the Jacobian matrix at every iteration.
The tool of Dolan and Moré [57] is used to analyze the efficiency of these three algorithms.
Figures 1-3 show that the performance of these methods are relative to NI, NG, and cpu time of Tables 1-2, respectively. The numerical results indicate that the proposed method performs best among these three methods. To this end, we think that the enhancement of this proposed method is noticeable.
5 Conclusion
In this paper, we focus on two algorithms solved a class of large-scale nonlinear equations. At the first step, a CG algorithm, called a sub-algorithm, was used as the initial points of the main algorithm. Then a quasi-Newton algorithm with the initial points done by a CG sub-algorithm was defined as the main algorithm. In order to avoid computing the Jacobian matrix, a nonmonotone line search technique was used in the algorithms. The convergence results are established and numerical results are reported.
According to the numerical performance, it is clear that the CG technique is very effective for large-scale nonlinear equations. This observation inspires us to design the CG methods to directly solve nonlinear equations in the future.
References
Chen, B, Shu, H, Coatrieux, G, Chen, G, Sun, X, Coatrieux, J: Color image analysis by quaternion-type moments. J. Math. Imaging Vis. 51, 124-144 (2015)
Fu, Z, Ren, K, Shu, J, Sun, X, Huang, F: Enabling personalized search over encrypted outsourced data with efficiency improvement. IEEE Trans. Parallel Distrib. Syst. (2015). doi:10.1109/TPDS.2015.2506573
Gu, B, Sheng, VS: A robust regularization path algorithm for ν-support vector classification. IEEE Trans. Neural Netw. Learn. Syst. (2016). doi:10.1109/TNNLS.2016.2527796
Gu, B, Sheng, VS, Tay, KY, Romano, W, Li, S: Incremental support vector learning for ordinal regression. IEEE Trans. Neural Netw. Learn. Syst. 26, 1403-1416 (2015)
Guo, P, Wang, J, Li, B, Lee, S: A variable threshold-value authentication architecture for wireless mesh networks. J. Internet Technol. 15, 929-936 (2014)
Li, J, Li, X, Yang, B, Sun, X: Segmentation-based image copy-move forgery detection scheme. IEEE Trans. Inf. Forensics Secur. 10, 507-518 (2015)
Pan, Z, Zhang, Y, Kwong, S: Efficient motion and disparity estimation optimization for low complexity multiview video coding. IEEE Trans. Broadcast. 61, 166-176 (2015)
Shen, J, Tan, H, Wang, J, Wang, J, Lee, S: A novel routing protocol providing good transmission reliability in underwater sensor networks. J. Internet Technol. 16, 171-178 (2015)
Xia, Z, Wang, X, Sun, X, Wang, Q: A secure and dynamic multi-keyword ranked search scheme over encrypted cloud data. IEEE Trans. Parallel Distrib. Syst. 27, 340-352 (2015)
Fu, Z, Wu, X, Guan, C, Sun, X, Ren, K: Towards efficient multi-keyword fuzzy search over encrypted outsourced data with accuracy improvement. IEEE Trans. Inf. Forensics Secur. (2016). doi:10.1109/TIFS.2016.2596138
Gu, B, Sun, X, Sheng, VS: Structural minimax probability machine. IEEE Trans. Neural Netw. Learn. Syst. (2016). doi:10.1109/TNNLS.2016.2544779
Ma, T, Zhou, J, Tang, M, Tian, Y, Al-Dhelaan, A, Al-Rodhaan, M, Lee, S: Social network and tag sources based augmenting collaborative recommender system. IEICE Trans. Inf. Syst. 98, 902-910 (2015)
Ren, Y, Shen, J, Wang, JN, Han, J, Lee, S: Mutual verifiable provable data auditing in public cloud storage. J. Internet Technol. 16, 317-323 (2015)
Yuan, G: Modified nonlinear conjugate gradient methods with sufficient descent property for large-scale optimization problems. Optim. Lett. 3, 11-21 (2009)
Yuan, G, Duan, X, Liu, W, Wang, X, et al.: Two new PRP conjugate gradient algorithms for minimization optimization models. PLoS ONE 10, e0140071 (2015)
Yuan, G, Lu, X: A modified PRP conjugate gradient method. Ann. Oper. Res. 166, 73-90 (2009)
Yuan, G, Lu, X, Wei, Z: A conjugate gradient method with descent direction for unconstrained optimization. J. Comput. Appl. Math. 233, 519-530 (2009)
Yuan, G, Wei, Z: New line search methods for unconstrained optimization. J. Korean Stat. Soc. 38, 29-39 (2009)
Yuan, G, Wei, Z: The superlinear convergence analysis of a nonmonotone BFGS algorithm on convex objective functions. Acta Math. Sin. Engl. Ser. 24(1), 35-42 (2008)
Yuan, G, Wei, Z: Convergence analysis of a modified BFGS method on convex minimizations. Comput. Optim. Appl. 47, 237-255 (2010)
Yuan, G, Wei, Z: A trust region algorithm with conjugate gradient technique for optimization problems. Numer. Funct. Anal. Optim. 32, 212-232 (2011)
Yuan, G, Wei, Z: The Barzilai and Borwein gradient method with nonmonotone line search for nonsmooth convex optimization problems. Math. Model. Anal. 17, 203-216 (2012)
Yuan, G, Wei, Z, Wang, Z: Gradient trust region algorithm with limited memory BFGS update for nonsmooth convex minimization. Comput. Optim. Appl. 54, 45-64 (2013)
Yuan, G, Wei, Z, Wu, Y: Modified limited memory BFGS method with nonmonotone line search for unconstrained optimization. J. Korean Math. Soc. 47, 767-788 (2010)
Yuan, G, Wei, Z, Zhao, Q: A modified Polak-Ribière-Polyak conjugate gradient algorithm for large-scale optimization problems. IIE Trans. 46, 397-413 (2014)
Yuan, G, Zhang, M: A modified Hestenes-Stiefel conjugate gradient algorithm for large-scale optimization. Numer. Funct. Anal. Optim. 34, 914-937 (2013)
Zhang, Y, Sun, X, Baowei, W: Efficient algorithm for K-barrier coverage based on integer linear programming. China Communications 13, 16-23 (2016)
Li, D, Fukushima, M: A global and superlinear convergent Gauss-Newton-based BFGS method for symmetric nonlinear equations. SIAM J. Numer. Anal. 37, 152-172 (1999)
Gu, G, Li, D, Qi, L, Zhou, S: Descent directions of quasi-Newton methods for symmetric nonlinear equations. SIAM J. Numer. Anal. 40, 1763-1774 (2002)
Brown, PN, Saad, Y: Convergence theory of nonlinear Newton-Krylov algorithms. SIAM J. Optim. 4, 297-330 (1994)
Zhu, D: Nonmonotone backtracking inexact quasi-Newton algorithms for solving smooth nonlinear equations. Appl. Math. Comput. 161, 875-895 (2005)
Yuan, G, Lu, X: A new backtracking inexact BFGS method for symmetric nonlinear equations. Comput. Math. Appl. 55, 116-129 (2008)
Nash, SG: A surey of truncated-Newton matrices. J. Comput. Appl. Math. 124, 45-59 (2000)
Dembao, RS, Eisenstat, SC, Steinaug, T: Inexact Newton methods. SIAM J. Numer. Anal. 19, 400-408 (1982)
Griewank, A: The ’global’ convergence of Broyden-like methods with a suitable line search. J. Aust. Math. Soc. Ser. B, Appl. Math 28, 75-92 (1986)
Ypma, T: Local convergence of inexact Newton methods. SIAM J. Numer. Anal. 21, 583-590 (1984)
Yuan, G, Wei, Z, Lu, X: A BFGS trust-region method for nonlinear equations. Computing 92, 317-333 (2011)
Yuan, G, Wei, Z, Lu, S: Limited memory BFGS method with backtracking for symmetric nonlinear equations. Math. Comput. Model. 54, 367-377 (2011)
Yuan, G, Yao, S: A BFGS algorithm for solving symmetric nonlinear equations. Optimization 62, 82-95 (2013)
Grippo, L, Lampariello, F, Lucidi, S: A nonmonotone line search technique for Newton’s method. SIAM J. Numer. Anal. 23, 707-716 (1986)
Birgin, EG, Martinez, JM, Raydan, M: Nonmonotone spectral projected gradient methods on convex sets. SIAM J. Optim. 10, 1196-1211 (2000)
Han, J, Liu, G: Global convergence analysis of a new nonmonotone BFGS algorithm on convex objective functions. Comput. Optim. Appl. 7, 277-289 (1997)
Liu, G, Peng, J: The convergence properties of a nonmonotonic algorithm. J. Comput. Math. 1, 65-71 (1992)
Zhou, J, Tits, A: Nonmonotone line search for minimax problem. J. Optim. Theory Appl. 76, 455-476 (1993)
Yuan, G: A new method with descent property for symmetric nonlinear equations. Numer. Funct. Anal. Optim. 31, 974-987 (2010)
Yuan, G, Meng, Z, Li, Y: A modified Hestenes and Stiefel conjugate gradient algorithm for large-scale nonsmooth minimizations and nonlinear equations. J. Optim. Theory Appl. 168, 129-152 (2016)
Yuan, G, Lu, S, Wei, Z: A new trust-region method with line search for solving symmetric nonlinear equations. Int. J. Comput. Math. 88, 2109-2123 (2011)
Yuan, G, Wei, Z, Li, G: A modified Polak-Ribière-Polyak conjugate gradient algorithm for nonsmooth convex programs. J. Comput. Appl. Math. 255, 86-96 (2014)
Yuan, G, Zhang, M: A three-terms Polak-Ribière-Polyak conjugate gradient algorithm for large-scale nonlinear equations. J. Comput. Appl. Math. 286, 186-195 (2015)
Yuan, G, Lu, X, Wei, Z: BFGS trust-region method for symmetric nonlinear equations. J. Comput. Appl. Math. 230, 44-58 (2009)
Gomez-Ruggiero, M, Martinez, J, Moretti, A: Comparing algorithms for solving sparse nonlinear systems of equations. SIAM J. Sci. Comput. 23, 459-483 (1992)
Raydan, M: The Barzilai and Borwein gradient method for the large scale unconstrained minimization problem. SIAM J. Optim. 7, 26-33 (1997)
Moré, J, Garbow, B, Hillström, K: Testing unconstrained optimization software. ACM Trans. Math. Softw. 7, 17-41 (1981)
Aslam Noor, M, Waseem, M, Inayat Noor, K, Al-Said, E: Variational iteration technique for solving a system of nonlinear equations. Optim. Lett. 7, 991-1007 (2013)
Polak, E, Ribière, G: Note sur la convergence de directions conjugees. Rev. Franaise Informat. Recherche Opérationnelle 3, 35-43 (1969)
Polyak, E: The conjugate gradient method in extremal problems. USSR Comput. Math. Math. Phys. 9, 94-112 (1969)
Dolan, ED, Moré, JJ: Benchmarking optimization software with performance profiles. Math. Program. 91, 201-213 (2002)
Acknowledgements
Only the author contributed in writing this paper. The author thanks the referees and the Editor for their valuable comments, which greatly improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares to have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Huang, L. A quasi-Newton algorithm for large-scale nonlinear equations. J Inequal Appl 2017, 35 (2017). https://doi.org/10.1186/s13660-017-1301-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-017-1301-7