1 Introduction

Let H be a real Hilbert space whose inner product and norm are denoted by \(\langle\cdot,\cdot\rangle\) and \(\Vert \cdot \Vert \), respectively, C be a nonempty, closed, and convex subset of H. It is well known that for any \(x\in H\), there exists a unique point \(y_{0}\in C\) such that

$$ \Vert x-y_{0}\Vert =\inf\bigl\{ \Vert x-y\Vert :y\in C \bigr\} . $$

Here, \(y_{0}\) is denoted by \(P_{C}x\), where \(P_{C}\) is called the metric projection of H onto C.

Let us recall some kinds of nonlinear mappings as follows, which are needed in the next sections. A mapping \(T:C\rightarrow H\) is called L-Lipschitzian if there exists a constant \(L>0\) such that \(\Vert Tx-Ty\Vert \leq L\Vert x-y\Vert \), \(\forall x,y\in C\). In particular, if \(L\in {}[0,1)\), then T is said to be a contraction; if \(L=1\), then T is called a nonexpansive mapping. Let us fix a sequence \(\{a_{n}\}\) in \([0,\infty ) \) with \(a_{n}\rightarrow0\). If the inequality \(\Vert T^{n}x-T^{n}y\Vert \leq \Vert x-y\Vert +a_{n}\) holds for all \(x,y\in C\) and \(n\geq1\), then T is said to be nearly nonexpansive [1, 2] with respect to \(\{a_{n}\}\). Let \(\{ T_{n} \} \) be a sequence of mappings from C into H. Then the sequence \(\{ T_{n} \} \) is called a sequence of nearly nonexpansive mappings [3, 4] with respect to a sequence \(\{a_{n}\}\) if

$$ \Vert T_{n}x-T_{n}y\Vert \leq \Vert x-y\Vert +a_{n}, \quad\forall x,y\in C, \forall n\geq1. $$
(1.1)

It is obvious that the sequence of nearly nonexpansive mappings is a wider class of sequence of nonexpansive mappings. A mapping \(A:C\rightarrow H\) is called α-inverse strongly monotone if there exists a positive real number \(\alpha>0\) such that

$$ \langle Ax-Ay,x-y \rangle\geq\alpha \Vert Ax-Ay\Vert ^{2},\quad \forall x,y\in C, $$

and a mapping \(F:C\rightarrow H\) is called η-strongly monotone if there exists a constant \(\eta\geq0\) such that

$$ \langle Fx-Fy,x-y \rangle\geq\eta \Vert x-y\Vert ^{2},\quad\forall x,y\in C. $$

In particular, if \(\eta=0\), then F is said to be monotone.

Let \(G:C\times C\rightarrow \mathbb{R} \) be a bifunction and B be a nonlinear mapping. The generalized equilibrium problem, denoted by GEP, is to find a point \(x\in C\) such that

$$ G ( x,y ) + \langle Bx,y-x \rangle\geq0 $$
(1.2)

for all \(y\in C\), and the solution of the problem (1.2) is denoted by \(\operatorname {GEP}( G ) \), i.e.,

$$ \operatorname {GEP}( G ) = \bigl\{ x\in C:G ( x,y ) + \langle Bx,y-x \rangle\geq0, \ \forall y\in C \bigr\} . $$

If \(B=0\), then the GEP is reduced to equilibrium problem, denoted by EP, which is to find a point \(x\in C\) such that

$$ G ( x,y ) \geq0 $$

for all \(y\in C\). The set of solutions of EP is denoted by \(\operatorname {EP}(G)\). In the case of \(G=0\), then GEP is equivalent to find a \(x\in C\) such that

$$ \langle Bx,y-x \rangle\geq0 $$
(1.3)

for all \(y\in C\). The problem (1.3) is called variational inequality problem, denoted by \(VI ( C,B ) \), and the solution of \(VI ( C,B ) \) is denoted by Ω, i.e.,

$$ \Omega= \bigl\{ x\in C: \langle Bx,y-x \rangle\geq0, \ \forall y \in C \bigr\} . $$

The generalized equilibrium problem includes, as special cases, the optimization problem, the variational inequality problem, the fixed point problem, the nonlinear complementarity, the Nash equilibrium problem in noncooperative games, the vector optimization problem, etc. Hence, the existence of solutions of generalized equilibrium problems has been extensively studied by many authors in the literature (see, e.g., [5–9]).

Let \(S:C\rightarrow H\) be a nonexpansive mapping. The following problem is called a hierarchical fixed point problem: Finding \(x^{\ast}\in \operatorname {Fix}(T)\) such that

$$ \bigl\langle x^{\ast}-Sx^{\ast},x-x^{\ast} \bigr\rangle \geq0, \quad x\in \operatorname {Fix}(T), $$
(1.4)

where \(\operatorname {Fix}( T ) \) is the set of fixed points of T, i.e., \(\operatorname {Fix}( T ) = \{ x\in C:Tx=x \} \). The problem (1.4) is equivalent to the following fixed point problem: Finding an \(x^{\ast }\in C\) that satisfies \(x^{\ast}=P_{\operatorname {Fix}(T)}Sx^{\ast}\). Since \(\operatorname {Fix}(T)\) is closed and convex, the metric projection \(P_{\operatorname {Fix}(T)}\) is well defined.

It is well known that the hierarchical fixed point problem (1.4) links with some monotone variational inequalities and convex programming problems; see [10–15]. Therefore, there exist various methods to solve the hierarchical fixed point problem; see Yao and Liou in [16], Xu in [17], Marino and Xu in [18] and Bnouhachem and Noor in [19].

Now, we give some iteration schemes which are related with the problems (1.2), (1.3), and (1.4). In 2011, Ceng et al. [25] investigated the following iterative method:

$$ x_{n+1}=P_{C} \bigl[ \alpha_{n}\rho Vx_{n}+ ( 1-\alpha_{n}\mu F ) Tx_{n} \bigr] ,\quad \forall n\geq0, $$
(1.5)

where F is a L-Lipschitzian and η-strongly monotone operator with constants \(L,\eta>0\) andV is a γ-Lipschitzian (possibly non-self-)mapping with constant \(\gamma\geq0\) such that \(0<\mu <\frac {2\eta}{L^{2}}\) and \(0\leq\rho\gamma<1-\sqrt{1-\mu( 2\eta-\mu L^{2} ) }\). They proved that under some approximate assumptions on the operators and parameters, the sequence \(\{x_{n}\}\) generated by (1.5) converges strongly to the unique solution of the variational inequality

$$ \bigl\langle ( \rho V-\mu F ) x^{\ast},x-x^{\ast} \bigr\rangle \leq0, \quad\forall x\in \operatorname {Fix}(T). $$
(1.6)

Recently, in 2013, Sahu et al. [26] introduced the following iterative process for the sequence of nearly nonexpansive mappings \(\{ T_{n} \} \) defined by (1.1):

$$ \begin{cases} y_{n}= ( 1-\beta_{n} ) x_{n}+\beta_{n}S_{n}x_{n}, \\ x_{n+1}=P_{C} [ \alpha_{n}fx_{n}+\sum_{i=1}^{n} ( \alpha _{i-1}-\alpha_{i} ) T_{i}y_{n} ] ,\quad\forall n\geq1,\end{cases} $$
(1.7)

where f is a contraction and \(\{ S_{n} \} \) is a sequence of nonexpansive mappings from C into itself. They proved that the sequence \(\{x_{n}\}\) generated by (1.7) converges strongly to the unique solution of the following variational inequality:

$$ \biggl\langle \frac{1}{\tau} ( I-f ) x^{\ast}+ ( I-S ) x^{\ast},x-x^{\ast} \biggr\rangle \geq0, \quad \forall x\in\bigcap _{i=1}^{\infty} \operatorname {Fix}( T_{n} ). $$

In the same year, Bnouhachem and Noor [19] introduced a new iterative scheme to find a common solution of a variational inequality, a generalized equilibrium problem and a hierarchical fixed point problem. Their scheme is as follows:

$$ \begin{cases} G ( u_{n},y ) + \langle Bx,y-u_{n} \rangle+\frac {1}{r_{n}}\langle y-u_{n},u_{n}-x_{n} \rangle\geq0, \quad \forall y\in C, \\ z_{n}=P_{C} ( u_{n}-\lambda_{n}Au_{n} ), \\ y_{n}=P_{C} ( \beta_{n}Sx_{n}+ ( 1-\beta_{n} ) z_{n} ), \\ x_{n+1}=P_{C} ( \alpha_{n}fx_{n}+\sum_{i=1}^{n} ( \alpha _{i-1}-\alpha_{i} ) V_{i}y_{n} ), \quad \forall n\geq1, \end{cases} $$
(1.8)

where \(V_{i}=k_{i}I+ ( 1-k_{i} ) T_{i}\), \(0\leq k_{i}<1\), \(\{ T_{i} \} _{i=1}^{\infty}:C\rightarrow C\) is a countable family of \(k_{i}\)-strict pseudo-contraction mappings, A and B are inverse strongly monotone mappings. They proved that the sequence \(\{ x_{n} \} \) generated by (1.8) converges strongly to a point \(z\in P_{\Omega \cap \operatorname {GEP}( G ) \cap \operatorname {Fix}( T ) }f ( z ) \) which is the unique solution of the following variational inequality:

$$ \bigl\langle ( I-f ) z,x-z \bigr\rangle \geq0, \quad \forall x\in\Omega \cap \operatorname {GEP}( G ) \cap \operatorname {Fix}( T ), $$

where \(\operatorname {Fix}( T ) =\bigcap_{i=1}^{\infty} \operatorname {Fix}( T_{i} ) \).

In 2014, Bnouhachem and Chen [20] introduced the following iterative method:

$$ \begin{cases} F_{1} ( u_{n},y ) + \langle Dx_{n},y-u_{n} \rangle +\varphi( y ) -\varphi( u_{n} ) +\frac{1}{r_{n}}\langle y-u_{n},u_{n}-x_{n} \rangle\geq0, \quad \forall y\in C; \\ z_{n}=P_{C} ( u_{n}-\lambda_{n}Au_{n} ); \\ y_{n}=\beta_{n}Sx_{n}+ ( 1-\beta_{n} ) z_{n}; \\ x_{n+1}=P_{C} [ \alpha_{n}\rho Ux_{n}+\gamma_{n}x_{n}+ ( ( 1-\gamma_{n} ) I-\alpha_{n}\mu F ) ( T ( y_{n} ) ) ] ,\quad\forall n\geq0,\end{cases} $$
(1.9)

where \(D,A:C\rightarrow H\) are inverse strongly monotone mappings, \(F_{1}:C\times C\rightarrow \mathbb{R} \) is a bifunction, \(\varphi:C\rightarrow \mathbb{R} \) is a proper lower semicontinuous and convex function, \(S,T:C\rightarrow C\) are nonexpansive mappings, \(F:C\rightarrow C\) is Lipschitzian and a strongly monotone mapping and \(U:C\rightarrow C\) is a Lipschitzian mapping. The authors proved the strong convergence of the sequence generated by (1.9) to a common solution of a variational inequality, a generalized mixed equilibrium problem, and a hierarchical fixed point problem.

In addition to all these papers, similar problems are considered in several papers; see, e.g., [21–24].

In this paper, motivated by the above works and by the recent work going in this direction, we introduce an iterative projection method and prove a strong convergence theorem based on this method for computing an approximate element of the common set of solution of a generalized equilibrium problem, a variational inequality problem and a fixed point problem for a sequence of nearly nonexpansive mappings defined by (1.1). The proposed method improves and extends many known results; see, e.g., [4, 11, 25, 27, 28] and the references therein.

2 Preliminaries

Let \(\{ x_{n} \} \) be a sequence in a Hilbert space H and \(x\in H \). Throughout this paper, \(x_{n}\rightarrow x\) denotes the strong convergence of \(\{ x_{n} \} \) to x and \(x_{n}\rightharpoonup x\) denotes the weak convergence. Let C be a nonempty subset of a real Hilbert space H. For solving an equilibrium problem for a bifunction \(G:C\times C\rightarrow \mathbb{R} \), let us assume that G satisfies the following conditions:

  1. (A1)

    \(G ( x,x ) =0\), \(\forall x\in C\),

  2. (A2)

    G is monotone, i.e. \(G ( x,y ) +G ( y,x ) \leq0\), \(\forall x,y\in C\),

  3. (A3)

    \(\forall x,y,z\in C\),

    $$ \lim_{t\rightarrow0^{+}}G \bigl( tz+ ( 1-t ) x,y \bigr) \leq G ( x,y ), $$
  4. (A4)

    \(\forall x\in C\), \(y\longmapsto G ( x,y ) \) is convex and lower semicontinuous.

Lemma 1

[29]

Let C be a nonempty, closed, and convex subset of H, and let G be a bifunction from \(C\times C\) into ℝ satisfying (A1)-(A4). Let \(r>0\) and \(x\in H\). Then there exists \(z\in C\) such that

$$ G ( z,y ) +\frac{1}{r} \langle y-z,z-x \rangle\geq0 $$
(2.1)

for all \(x\in C\).

Lemma 2

[30]

Suppose that \(G:C\times C\rightarrow \mathbb{R}\) satisfies (A1)-(A4). For \(r>0\) and \(x\in H\), define a mapping \(T_{r}:H\rightarrow C\) as follows:

$$ T_{r} ( x ) = \biggl\{ z\in C:G ( z,y ) +\frac{1}{r}\langle y-z,z-x \rangle\geq0,\ \forall y\in C \biggr\} $$

for all \(z\in H\). Then the following hold:

  1. (1)

    \(T_{r}\) is single valued,

  2. (2)

    \(T_{r}\) is firmly nonexpansive i.e.

    $$ \Vert T_{r}x-T_{r}y\Vert ^{2}\leq\langle T_{r}x-T_{r}y,x-y \rangle,\quad\forall x,y\in H, $$
  3. (3)

    \(\operatorname {Fix}( T_{r} ) =\operatorname {EP}( G ) \),

  4. (4)

    \(\operatorname {EP}( G ) \) is closed and convex.

Let \(T_{1},T_{2}:C\rightarrow H\) be two mappings. We denote \(\mathcal{B} ( C ) \), the collection of all bounded subsets of C. The deviation between \(T_{1}\) and \(T_{2}\) on \(B\in \mathcal{B} ( C ) \), denoted by \(\mathfrak{D}_{B} ( T_{1},T_{2} ) \), is defined by

$$ \mathfrak{D}_{B} ( T_{1},T_{2} ) =\sup\bigl\{ \Vert T_{1}x-T_{2}x\Vert :x\in B \bigr\} . $$

The following lemmas will be used in the next section.

Lemma 3

[3]

Let C be a nonempty, closed, and bounded subset of a Banach space X and \(\{T_{n}\}\) be a sequence of nearly nonexpansive self-mappings on C with a sequence \(\{a_{n}\}\) such that \(\mathfrak{D} _{C} ( T_{n},T_{n+1} ) <\infty\). Then, for each \(x\in C\), \(\{T_{n}x\}\) converges strongly to some point of C. Moreover, if T is a mapping from C into itself defined by \(Tz=\lim_{n\rightarrow\infty }T_{n}z \) for all \(z\in C\), then T is nonexpansive and \(\lim _{n\rightarrow \infty}\mathfrak{D}_{C} ( T_{n},T ) =0\).

Lemma 4

[25]

Let \(V:C\rightarrow H\) be a γ-Lipschitzian mapping with a constant \(\gamma\geq0\) and let \(F:C\rightarrow H\) be a L-Lipschitzian and η-strongly monotone operator with constants \(L,\eta >0\). Then for \(0\leq\rho\gamma<\mu\eta\),

$$ \bigl\langle ( \mu F-\rho V ) x- ( \mu F-\rho V ) y,x-y \bigr\rangle \geq( \mu \eta-\rho\gamma) \Vert x-y\Vert ^{2},\quad\forall x,y\in C. $$

That is, \(\mu F-\rho V\) is strongly monotone with coefficient \(\mu\eta -\rho\gamma\).

Lemma 5

[31]

Let C be a nonempty subset of a real Hilbert space H. Suppose that \(\lambda\in( 0,1 ) \) and \(\mu>0\). Let \(F:C\rightarrow H\) be a L-Lipschitzian and η-strongly monotone operator on C. Define the mapping \(G:C\rightarrow H\) by

$$ Gx=x-\lambda\mu Fx,\quad \forall x\in C. $$

Then G is a contraction that provided \(\mu<\frac{2\eta}{L^{2}}\). More precisely, for \(\mu\in( 0,\frac{2\eta}{L^{2}} ) \),

$$ \Vert Gx-Gy\Vert \leq( 1-\lambda\nu) \Vert x-y\Vert ,\quad \forall x,y\in C, $$

where \(\nu=1-\sqrt{1-\mu( 2\eta-\mu L^{2} ) }\).

Lemma 6

[32]

Let C be a nonempty, closed, and convex subset of a real Hilbert space H, and T be a nonexpansive self-mapping on C. If \(\operatorname {Fix}( T ) \neq\emptyset\), then \(I-T\) is demiclosed; that is whenever \(\{ x_{n} \} \) is a sequence in C weakly converging to some \(x\in C\) and the sequence \(\{ ( I-T ) x_{n} \} \) strongly converges to some y, it follows that \(( I-T ) x=y\). Here I is the identity operator of H.

Lemma 7

[33]

Assume that \(\{ x_{n} \} \) is a sequence of nonnegative real numbers satisfying the conditions

$$ x_{n+1}\leq( 1-\alpha_{n} ) x_{n}+ \alpha_{n}\beta_{n},\quad \forall n\geq1, $$

where \(\{ \alpha_{n} \} \) and \(\{ \beta_{n} \} \) are sequences of real numbers such that

$$\begin{aligned} \mbox{(i)}& \quad \{ \alpha_{n} \} \subset[ 0,1 ] \quad \textit{and}\quad \sum _{n=1}^{\infty}\alpha_{n}=\infty, \\ \mbox{(ii)}&\quad \limsup_{n\rightarrow\infty}\beta_{n}\leq0. \end{aligned}$$

Then \(\lim_{n\rightarrow\infty}x_{n}=0\).

3 Main results

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let \(A,B:C\rightarrow H\) be α, θ-inverse strongly monotone mappings, respectively. Let \(G:C\times C\rightarrow \mathbb{R} \) be a bifunction satisfying assumptions (A1)-(A4), \(S:C\rightarrow H\) be a nonexpansive mapping and \(\{ T_{n} \} \) be a sequence of nearly nonexpansive mappings with the sequence \(\{ a_{n} \} \) such that \(\mathcal {F}:=\operatorname {Fix}( T ) \cap\Omega\cap \operatorname {GEP}( G ) \neq \emptyset\) where \(Tx=\lim_{n\rightarrow\infty}T_{n}x\) for all \(x\in C\) and \(\operatorname {Fix}( T ) =\bigcap_{n=1}^{\infty} \operatorname {Fix}( T_{n} ) \). It is clear that the mapping T is nonexpansive. Let \(V:C\rightarrow H\) be a γ-Lipschitzian mapping, \(F:C\rightarrow H\) be a L-Lipschitzian and η-strongly monotone operator such that these coefficients satisfy \(0<\mu<\frac{2\eta}{L^{2}}\), \(0\leq\rho\gamma<\nu\), where \(\nu =1-\sqrt{1-\mu( 2\eta-\mu L^{2} ) }\). For an arbitrarily initial value \(x_{1}\), define the sequence \(\{ x_{n} \} \) in C generated by

$$ \begin{cases} G ( u_{n},y ) + \langle Bx_{n},y-u_{n} \rangle+\frac {1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq0,\quad \forall y\in C, \\ z_{n}=P_{C} ( u_{n}-\lambda_{n}Au_{n} ), \\ y_{n}=P_{C} [ \beta_{n}Sx_{n}+ ( 1-\beta_{n} ) z_{n} ] ,\\ x_{n+1}=P_{C} [ \alpha_{n}\rho Vx_{n}+ ( I-\alpha_{n}\mu F ) T_{n}y_{n} ] ,\quad n\geq1,\end{cases} $$
(3.1)

where \(\{ \lambda_{n} \} \subset( 0,2\alpha) \), \(\{ r_{n} \} \subset( 0,2\theta) \), \(\{ \alpha _{n} \} \) and \(\{ \beta_{n} \} \) are sequences in \([ 0,1] \).

As can be seen, the convergence of the sequence \(\{ x_{n} \} \) generated by (3.1) depends on the choice of the control sequences and mappings. We list the following hypotheses on them:

$$\begin{aligned} \mbox{(C1)}&\quad \lim_{n\rightarrow\infty}\alpha_{n}=0\quad \text{and}\quad \sum_{n=1}^{\infty}\alpha_{n}=\infty; \\ \mbox{(C2)}&\quad \lim_{n\rightarrow\infty}\frac{a_{n}}{\alpha_{n}}=0, \hspace{15pt} \lim_{n\rightarrow\infty}\frac{\beta_{n}}{\alpha_{n}}=0,\hspace{15pt} \lim_{n\rightarrow\infty}\frac{\vert\alpha_{n}-\alpha_{n-1}\vert}{\alpha_{n}}=0,\hspace{15pt} \lim_{n\rightarrow\infty} \frac{\vert\lambda_{n}-\lambda_{n-1}\vert}{\alpha_{n}}=0; \\ &\quad \lim_{n\rightarrow\infty}\frac{\vert\beta_{n}-\beta _{n-1}\vert}{\alpha_{n}}=0,\quad \text{and}\quad \lim _{n\rightarrow \infty}\frac{\vert r_{n}-r_{n-1}\vert}{\alpha_{n}}=0; \\ \mbox{(C3)}&\quad \lim_{n\rightarrow\infty}\mathfrak{D}_{B} ( T_{n},T_{n+1} ) =0\quad \text{and}\quad \lim_{n\rightarrow\infty} \frac{\mathfrak{D}_{B} ( T_{n},T_{n+1} ) }{\alpha_{n}}=0\quad \text{for each }B\in\mathcal{B} ( C ). \end{aligned}$$

Now, we need the following lemmas to prove our main theorem.

Lemma 8

Assume that the conditions (C1), (C2) hold and \(p\in \mathcal {F}\). Then the sequences \(\{ x_{n} \} \), \(\{ y_{n} \} \), \(\{ z_{n} \} \), and \(\{ u_{n} \} \) generated by (3.1) are bounded.

Proof

It is easy to see that the mapping \(I-r_{n}B\) is nonexpansive, so the mapping \(I-\lambda_{n}A\) is also nonexpansive. From Lemma 2, we have \(u_{n}=T_{r_{n}} ( x_{n}-r_{n}Bx_{n} ) \). Let \(p\in \mathcal {F}\). So, we get \(p=T_{r_{n}} ( p-r_{n}Bp ) \). Then we obtain

$$\begin{aligned} \Vert u_{n}-p\Vert ^{2} =&\bigl\Vert T_{r_{n}} ( x_{n}-r_{n}Bx_{n} ) -T_{r_{n}} ( p-r_{n}Bp ) \bigr\Vert ^{2} \\ \leq&\bigl\Vert ( x_{n}-r_{n}Bx_{n} ) - ( p-r_{n}Bp ) \bigr\Vert ^{2} \\ =&\Vert x_{n}-p\Vert ^{2}-2r_{n} \langle x_{n}-p,Bx_{n}-Bp \rangle+r_{n}^{2} \Vert Bx_{n}-Bp\Vert ^{2} \\ \leq&\Vert x_{n}-p\Vert ^{2}-r_{n} ( 2\theta -r_{n} ) \Vert Bx_{n}-Bp\Vert ^{2} \\ \leq&\Vert x_{n}-p\Vert ^{2}. \end{aligned}$$
(3.2)

From (3.2), we get

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2} =&\bigl\Vert P_{C} ( u_{n}-\lambda_{n}Au_{n} ) -P_{C} ( p- \lambda_{n}Ap ) \bigr\Vert ^{2} \\ \leq&\bigl\Vert u_{n}-p-\lambda_{n} ( Au_{n}-Ap ) \bigr\Vert ^{2} \\ \leq&\Vert u_{n}-p\Vert ^{2}-\lambda_{n} ( 2 \alpha-\lambda_{n} ) \Vert Au_{n}-Ap\Vert ^{2} \\ \leq&\Vert u_{n}-p\Vert ^{2} \\ \leq&\Vert x_{n}-p\Vert ^{2}. \end{aligned}$$
(3.3)

It follows from (3.3) that

$$\begin{aligned} \Vert y_{n}-p\Vert =&\bigl\Vert P_{C} \bigl[ \beta _{n}Sx_{n}+ ( 1-\beta_{n} ) x_{n} \bigr] -P_{C}p\bigr\Vert \\ \leq&\bigl\Vert \beta_{n}Sx_{n}+ ( 1-\beta_{n} ) z_{n}-p\bigr\Vert \\ \leq& ( 1-\beta_{n} ) \Vert z_{n}-p\Vert +\beta _{n}\Vert Sx_{n}-p\Vert \\ \leq& ( 1-\beta_{n} ) \Vert x_{n}-p\Vert +\beta _{n}\Vert Sx_{n}-Sp\Vert +\beta_{n}\Vert Sp-p \Vert \\ \leq&\Vert x_{n}-p\Vert +\beta_{n}\Vert Sp-p\Vert . \end{aligned}$$
(3.4)

Since \(\lim_{n\rightarrow\infty}\frac{\beta_{n}}{\alpha_{n}}=0\), without loss of generality, we can assume that \(\beta_{n}\leq\alpha_{n}\), for all \(n\geq1\). This gives us \(\lim_{n\rightarrow\infty}\beta_{n}=0\).

Let \(t_{n}=\alpha_{n}\rho Vx_{n}+ ( I-\alpha_{n}\mu F ) T_{n}y_{n} \). Then we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert =&\Vert P_{C}t_{n}-P_{C}p \Vert \\ \leq&\Vert t_{n}-p\Vert \\ =&\bigl\Vert \alpha_{n}\rho Vx_{n}+ ( I- \alpha_{n}\mu F ) T_{n}y_{n}-p\bigr\Vert \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert +\bigl\Vert ( I-\alpha_{n}\mu F ) T_{n}y_{n}- ( I- \alpha_{n}\mu F ) T_{n}p\bigr\Vert \\ \leq&\alpha_{n}\rho\gamma \Vert x_{n}-p\Vert +\alpha _{n}\Vert \rho Vp-\mu Fp\Vert \\ &{}+ ( 1-\alpha_{n}\nu) \bigl( \Vert y_{n}-p\Vert +a_{n} \bigr). \end{aligned}$$
(3.5)

From (3.4) and (3.5), we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert \leq&\alpha_{n}\rho\gamma \Vert x_{n}-p\Vert +\alpha_{n}\Vert \rho Vp-\mu Fp\Vert \\ &{}+ ( 1-\alpha_{n}\nu) \bigl( \Vert x_{n}-p\Vert + \beta_{n}\Vert Sp-p\Vert +a_{n} \bigr) \\ \leq& \bigl( 1-\alpha_{n} ( \nu-\rho\gamma) \bigr) \Vert x_{n}-p\Vert \\ &{}+\alpha_{n} \biggl( \Vert \rho Vp-\mu Fp\Vert +\Vert Sp-p \Vert +\frac{a_{n}}{\alpha_{n}} \biggr) \\ \leq& \bigl( 1-\alpha_{n} ( \nu-\rho\gamma) \bigr) \Vert x_{n}-p\Vert \\ &{}+\alpha_{n} ( \nu-\rho\gamma) \biggl[ \frac{1}{ ( \nu -\rho\gamma) } \biggl( \Vert \rho Vp-\mu Fp\Vert +\Vert Sp-p\Vert +\frac {a_{n}}{\alpha_{n}} \biggr) \biggr] . \end{aligned}$$
(3.6)

From condition (C2), there exists a constant \(M_{1}>0\) such that

$$ \Vert \rho Vp-\mu Fp\Vert +\Vert Sp-p\Vert +\frac {a_{n}}{\alpha_{n}}\leq M_{1}, \quad \forall n\geq1. $$

Thus, from (3.6) we have

$$ \Vert x_{n+1}-p\Vert \leq\bigl( 1-\alpha_{n} ( \nu-\rho \gamma) \bigr) \Vert x_{n}-p\Vert +\alpha_{n} ( \nu- \rho\gamma) \frac{M_{1}}{ ( \nu-\rho\gamma) }. $$

By induction, we get

$$ \Vert x_{n+1}-p\Vert \leq\max\biggl\{ \Vert x_{1}-p \Vert ,\frac{M_{1}}{ ( \nu-\rho\gamma) } \biggr\} . $$

Hence, we find that \(\{ x_{n} \} \) is bounded. So, the sequences \(\{ y_{n} \} \), \(\{ z_{n} \} \), and \(\{ u_{n} \} \) are bounded. □

Lemma 9

Assume that (C1)-(C3) hold. Let \(p\in \mathcal {F}\) and \(\{ x_{n} \} \) be the sequence generated by (3.1). Then the follow hold:

  1. (i)

    \(\lim_{n\rightarrow\infty} \Vert x_{n+1}-x_{n}\Vert =0\).

  2. (ii)

    \(w_{w} ( x_{n} ) \subset \operatorname {Fix}( T ) \) where \(w_{w} ( x_{n} ) \) is the weak w-limit set of \(\{ x_{n} \} \), i.e., \(w_{w} ( x_{n} ) = \{ x:x_{n_{i}}\rightharpoonup x \} \).

Proof

(i) Since the mappings \(P_{C}\) and \(( I-\lambda_{n}A ) \) are nonexpansive, we get

$$\begin{aligned} \Vert z_{n}-z_{n-1}\Vert =&\bigl\Vert P_{C} ( u_{n}-\lambda_{n}Au_{n} ) -P_{C} ( u_{n-1}-\lambda_{n-1}Au_{n-1} ) \bigr\Vert \\ \leq&\bigl\Vert ( u_{n}-\lambda_{n}Au_{n} ) - ( u_{n-1}-\lambda_{n-1}Au_{n-1} ) \bigr\Vert \\ =&\bigl\Vert u_{n}-u_{n-1}-\lambda_{n} ( Au_{n}-Au_{n-1} ) - ( \lambda_{n}- \lambda_{n-1} ) Au_{n-1}\bigr\Vert \\ \leq&\bigl\Vert u_{n}-u_{n-1}-\lambda_{n} ( Au_{n}-Au_{n-1} ) \bigr\Vert +\vert\lambda_{n}- \lambda_{n-1}\vert \Vert Au_{n-1}\Vert \\ \leq&\Vert u_{n}-u_{n-1}\Vert +\vert\lambda _{n}-\lambda_{n-1}\vert \Vert Au_{n-1}\Vert , \end{aligned}$$
(3.7)

and so

$$\begin{aligned} \Vert y_{n}-y_{n-1}\Vert =&\bigl\Vert P_{C} \bigl[ \beta_{n}Sx_{n}+ ( 1-\beta_{n} ) z_{n} \bigr] \\ & {}-P_{C} \bigl[ \beta_{n-1}Sx_{n-1}- ( 1- \beta_{n-1} ) z_{n-1} \bigr] \bigr\Vert \\ \leq&\bigl\Vert \beta_{n}Sx_{n}+ ( 1-\beta_{n} ) z_{n}-\beta_{n-1}Sx_{n-1}+ ( 1- \beta_{n-1} ) z_{n-1}\bigr\Vert \\ \leq&\bigl\Vert \beta_{n} ( Sx_{n}-Sx_{n-1} ) + ( \beta_{n}-\beta_{n-1} ) Sx_{n-1} \\ & {}+ ( 1-\beta_{n} ) ( z_{n}-z_{n-1} ) + ( \beta_{n-1}-\beta_{n} ) z_{n-1}\bigr\Vert \\ \leq&\beta_{n}\Vert x_{n}-x_{n-1}\Vert + ( 1- \beta_{n} ) \Vert z_{n}-z_{n-1}\Vert \\ &{}+\vert\beta_{n}-\beta_{n-1}\vert\bigl( \Vert Sx_{n-1}\Vert +\Vert z_{n-1}\Vert \bigr) \\ \leq&\beta_{n}\Vert x_{n}-x_{n-1}\Vert + ( 1- \beta_{n} ) \bigl[ \Vert u_{n}-u_{n-1}\Vert \\ & {}+\vert\lambda_{n}-\lambda_{n-1}\vert \Vert Au_{n-1}\Vert \bigr] \\ &{}+\vert\beta_{n}-\beta_{n-1}\vert\bigl( \Vert Sx_{n-1}\Vert +\Vert z_{n-1}\Vert \bigr). \end{aligned}$$
(3.8)

On the other hand, since \(u_{n}=T_{r_{n}} ( x_{n}-r_{n}Bx_{n} ) \) and \(u_{n-1}=T_{r_{n-1}} ( x_{n-1}-r_{n-1}Bx_{n-1} ) \), we have

$$ G ( u_{n},y ) + \langle Bx_{n},y-u_{n} \rangle+ \frac {1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq0, \quad \forall y\in C, $$
(3.9)

and

$$\begin{aligned} &G ( u_{n-1},y ) + \langle Bx_{n-1},y-u_{n-1} \rangle \\ &\quad {}+\frac{1}{r_{n-1}} \langle y-u_{n-1},u_{n-1}-x_{n-1} \rangle\geq0, \quad \forall y\in C. \end{aligned}$$
(3.10)

If we take \(y=u_{n-1}\) and \(y=u_{n}\) in (3.9) and (3.10), respectively, then we get

$$ G ( u_{n},u_{n-1} ) + \langle Bx_{n},u_{n-1}-u_{n} \rangle+\frac{1}{r_{n}} \langle u_{n-1}-u_{n},u_{n}-x_{n} \rangle\geq0$$
(3.11)

and

$$\begin{aligned} &G ( u_{n-1},u_{n} ) + \langle Bx_{n-1},u_{n}-u_{n-1} \rangle \\ &\quad {}+\frac{1}{r_{n-1}} \langle u_{n}-u_{n-1},u_{n-1}-x_{n-1} \rangle\geq0. \end{aligned}$$
(3.12)

It follows from (3.11), (3.12), and monotonicity of the function G that

$$ \langle Bx_{n-1}-Bx_{n},u_{n}-u_{n-1} \rangle+ \biggl\langle u_{n}-u_{n-1},\frac{u_{n-1}-x_{n-1}}{r_{n-1}}- \frac{u_{n}-x_{n}}{r_{n}}\biggr\rangle \geq0. $$

The last inequality implies that

$$\begin{aligned} 0 \leq& \biggl\langle u_{n}-u_{n-1},r_{n} ( Bx_{n-1}-Bx_{n} ) + \frac{r_{n}}{r_{n-1}} ( u_{n-1}-x_{n-1} ) - ( u_{n}-x_{n} ) \biggr\rangle \\ =& \biggl\langle u_{n-1}-u_{n},u_{n}-u_{n-1}+ \biggl( 1-\frac {r_{n}}{r_{n-1}}\biggr) u_{n-1} \\ &{} + ( x_{n-1}-r_{n}Bx_{n-1} ) - ( x_{n}-r_{n}Bx_{n} ) -x_{n-1}+ \frac{r_{n}}{r_{n-1}}x_{n-1} \biggr\rangle \\ =& \biggl\langle u_{n-1}-u_{n}, \biggl( 1-\frac{r_{n}}{r_{n-1}} \biggr) u_{n-1}+ ( x_{n-1}-r_{n}Bx_{n-1} ) \\ &{} - ( x_{n}-r_{n}Bx_{n} ) -x_{n-1}+\frac{r_{n}}{r_{n-1}} x_{n-1} \biggr\rangle - \Vert u_{n}-u_{n-1}\Vert ^{2} \\ =& \biggl\langle u_{n-1}-u_{n}, \biggl( 1-\frac{r_{n}}{r_{n-1}} \biggr) ( u_{n-1}-x_{n-1} ) \\ & {}+ ( x_{n-1}-r_{n}Bx_{n-1} ) - ( x_{n}-r_{n}Bx_{n} ) \biggr\rangle -\Vert u_{n}-u_{n-1}\Vert ^{2} \\ \leq&\Vert u_{n-1}-u_{n}\Vert \biggl\{ \biggl\vert 1- \frac {r_{n}}{r_{n-1}}\biggr\vert \Vert u_{n-1}-x_{n-1}\Vert \\ &{} +\bigl\Vert ( x_{n-1}-r_{n}Bx_{n-1} ) - ( x_{n}-r_{n}Bx_{n} ) \bigr\Vert \biggr\} - \Vert u_{n}-u_{n-1}\Vert ^{2} \\ \leq&\Vert u_{n-1}-u_{n}\Vert \biggl\{ \biggl\vert 1- \frac {r_{n}}{r_{n-1}}\biggr\vert \Vert u_{n-1}-x_{n-1}\Vert \\ &{} +\Vert x_{n-1}-x_{n}\Vert \biggr\} -\Vert u_{n}-u_{n-1}\Vert ^{2}. \end{aligned}$$
(3.13)

From (3.13), we have

$$ \Vert u_{n-1}-u_{n}\Vert \leq\biggl\vert 1- \frac {r_{n}}{r_{n-1}}\biggr\vert \Vert u_{n-1}-x_{n-1} \Vert +\Vert x_{n-1}-x_{n}\Vert . $$

Without loss of generality, we can assume that there exists a real number μ such that \(r_{n}>\mu>0\) for all positive integers n. Then we obtain

$$ \Vert u_{n-1}-u_{n}\Vert \leq \Vert x_{n-1}-x_{n} \Vert +\frac{1}{\mu}\vert r_{n-1}-r_{n}\vert \Vert u_{n-1}-x_{n-1}\Vert . $$
(3.14)

From (3.8) and (3.14), we get

$$\begin{aligned} \Vert y_{n}-y_{n-1}\Vert \leq&\beta_{n}\Vert x_{n}-x_{n-1}\Vert \\ &{}+ ( 1-\beta_{n} ) \biggl[ \Vert x_{n-1}-x_{n} \Vert +\frac{1}{\mu}\vert r_{n-1}-r_{n} \vert \Vert u_{n-1}-x_{n-1}\Vert \\ & {}+\vert\lambda_{n}-\lambda_{n-1}\vert \Vert Au_{n-1}\Vert \biggr] +\vert\beta_{n}- \beta_{n-1}\vert\bigl( \Vert Sx_{n-1}\Vert +\Vert z_{n-1}\Vert \bigr) \\ =&\Vert x_{n}-x_{n-1}\Vert + ( 1-\beta_{n} ) \biggl[ \frac{1}{\mu}\vert r_{n-1}-r_{n}\vert \Vert u_{n-1}-x_{n-1}\Vert \\ & {}+\vert\lambda_{n}-\lambda_{n-1}\vert \Vert Au_{n-1}\Vert \biggr] +\vert\beta_{n}- \beta_{n-1}\vert\bigl( \Vert Sx_{n-1}\Vert +\Vert z_{n-1}\Vert \bigr). \end{aligned}$$

Then we have

$$\begin{aligned} \Vert x_{n+1}-x_{n}\Vert =&\Vert P_{C}t_{n}-P_{C}t_{n-1} \Vert \\ \leq&\Vert t_{n}-t_{n-1}\Vert \\ =&\bigl\Vert \alpha_{n}\rho Vx_{n}+ ( I- \alpha_{n}\mu F ) T_{n}y_{n} \\ &{} -\alpha_{n-1}\rho Vx_{n-1}+ ( I- \alpha_{n-1}\mu F ) T_{n-1}y_{n-1}\bigr\Vert \\ \leq&\bigl\Vert \alpha_{n}\rho V ( x_{n}-x_{n-1} ) + ( \alpha_{n}-\alpha_{n-1} ) \rho Vx_{n-1} \\ &{}+ ( I-\alpha_{n}\mu F ) T_{n}y_{n}- ( I- \alpha_{n}\mu F ) T_{n}y_{n-1} \\ &{}+T_{n}y_{n-1}-T_{n-1}y_{n-1} \\ & {}+\alpha_{n-1}\mu FT_{n-1}y_{n-1}- \alpha_{n}\mu FT_{n}y_{n-1}\bigr\Vert \\ \leq&\alpha_{n}\rho\gamma \Vert x_{n}-x_{n-1} \Vert +\gamma\vert\alpha_{n}-\alpha_{n-1}\vert \Vert Vx_{n-1}\Vert \\ &{}+ ( 1-\alpha_{n}\nu) \Vert T_{n}y_{n}-T_{n}y_{n-1} \Vert +\Vert T_{n}y_{n-1}-T_{n-1}y_{n-1} \Vert \\ &{}+\mu \Vert \alpha_{n-1}FT_{n-1}y_{n-1}-\alpha _{n}FT_{n}y_{n-1}\Vert \\ \leq&\alpha_{n}\rho\gamma \Vert x_{n}-x_{n-1} \Vert +\gamma\vert\alpha_{n}-\alpha_{n-1}\vert \Vert Vx_{n-1}\Vert \\ &{}+ ( 1-\alpha_{n}\nu) \bigl[ \Vert y_{n}-y_{n-1} \Vert +a_{n} \bigr] +\Vert T_{n}y_{n-1}-T_{n-1}y_{n-1} \Vert \\ &{}+\mu\bigl\Vert \alpha_{n-1} ( FT_{n-1}y_{n-1}-FT_{n}y_{n-1} ) - ( \alpha_{n}-\alpha_{n-1} ) FT_{n}y_{n-1} \bigr\Vert \\ \leq&\alpha_{n}\rho\gamma \Vert x_{n}-x_{n-1} \Vert +\gamma\vert\alpha_{n}-\alpha_{n-1}\vert \Vert Vx_{n-1}\Vert \\ &{}+ ( 1-\alpha_{n}\nu) \biggl\{ \Vert x_{n}-x_{n-1} \Vert \\ &{}+ ( 1-\beta_{n} ) \biggl[ \frac{1}{\mu}\vert r_{n-1}-r_{n}\vert \Vert u_{n-1}-x_{n-1} \Vert +\vert\lambda_{n}-\lambda_{n-1}\vert \Vert Au_{n-1}\Vert \biggr] \\ & {}+\vert\beta_{n}-\beta_{n-1}\vert\bigl( \Vert Sx_{n-1}\Vert +\Vert z_{n-1}\Vert \bigr) \biggr\} \\ &{}+ ( 1-\alpha_{n}\nu) a_{n}+\mathfrak{D}_{B} ( T_{n},T_{n-1} ) \\ &{}+\mu\alpha_{n-1}L\mathfrak{D}_{B} ( T_{n},T_{n-1} ) +\vert\alpha_{n}-\alpha_{n-1}\vert \Vert FT_{n}y_{n-1}\Vert \\ \leq& \bigl( 1-\alpha_{n} ( \nu-\rho\gamma) \bigr) \Vert x_{n}-x_{n-1}\Vert \\ &{}+\vert\alpha_{n}-\alpha_{n-1}\vert\bigl( \gamma \Vert Vx_{n-1}\Vert +\Vert FT_{n}y_{n-1}\Vert \bigr) \\ &{}+ ( 1+\mu\alpha_{n-1}L ) \mathfrak{D}_{B} ( T_{n},T_{n-1} ) +a_{n} \\ &{}+\frac{1}{\mu}\vert r_{n-1}-r_{n}\vert \Vert u_{n-1}-x_{n-1}\Vert +\vert\lambda_{n}-\lambda _{n-1}\vert \Vert Au_{n-1}\Vert \\ &{}+\vert\beta_{n}-\beta_{n-1}\vert\bigl( \Vert Sx_{n-1}\Vert +\Vert z_{n-1}\Vert \bigr) \\ \leq& \bigl( 1-\alpha_{n} ( \nu-\rho\gamma) \bigr) \Vert x_{n}-x_{n-1}\Vert + ( 1+\mu\alpha_{n-1}L ) \mathfrak{D}_{B} ( T_{n},T_{n-1} ) \\ &{}+M_{2} \biggl( \vert\alpha_{n}-\alpha_{n-1} \vert+\frac {1}{\mu }\vert r_{n-1}-r_{n}\vert \\ &{} +\vert\lambda_{n}-\lambda_{n-1}\vert+\vert \beta_{n}-\beta_{n-1}\vert\biggr) +a_{n}, \end{aligned}$$
(3.15)

where

$$\begin{aligned} M_{2} =&\max\Bigl\{ \sup_{n\geq1} \bigl( \gamma \Vert Vx_{n-1}\Vert +\Vert FT_{n}y_{n-1}\Vert \bigr), \sup_{n\geq1}\Vert u_{n-1}-x_{n-1}\Vert , \\ &{} \sup_{n\geq1}\Vert Au_{n-1}\Vert , \sup_{n\geq 1} \bigl( \Vert Sx_{n-1}\Vert +\Vert z_{n-1}\Vert \bigr) \Bigr\} . \end{aligned}$$

Hence, we write

$$ \Vert x_{n+1}-x_{n}\Vert \leq\bigl( 1- \alpha_{n} ( \nu-\rho\gamma) \bigr) \Vert x_{n}-x_{n-1} \Vert +\alpha_{n} ( \nu-\rho\gamma) \delta_{n}, $$
(3.16)

where

$$\begin{aligned} \delta_{n} =&\frac{1}{ ( \nu-\rho\gamma) } \biggl[ ( 1+\mu \alpha_{n-1}L ) \frac{\mathfrak{D}_{B} ( T_{n},T_{n-1} ) }{\alpha_{n}} \\ &{}+\frac{a_{n}}{\alpha_{n}}+M_{2} \biggl( \frac{\vert\alpha _{n}-\alpha _{n-1}\vert}{\alpha_{n}}+ \frac{1}{\mu}\frac{\vert r_{n-1}-r_{n}\vert}{\alpha_{n}} + \frac{\vert\lambda_{n}-\lambda_{n-1}\vert}{\alpha_{n}}+\frac{\vert\beta_{n}-\beta_{n-1}\vert }{\alpha _{n}} \biggr) \biggr] . \end{aligned}$$

From conditions (C2) and (C3), we get

$$ \limsup_{n\rightarrow\infty}\delta_{n}\leq0. $$
(3.17)

So, it follows from (3.16), (3.17), and Lemma 7 that

$$ \lim_{n\rightarrow\infty} \Vert x_{n+1}-x_{n}\Vert =0. $$
(3.18)

(ii) First, we show that \(\lim_{n\rightarrow\infty} \Vert u_{n}-x_{n}\Vert =0\). Since \(p\in \mathcal {F}\), from (3.2) and (3.3), we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^{2} \leq&\Vert t_{n}-p \Vert ^{2} \\ =&\bigl\Vert \alpha_{n}\rho Vx_{n}+ ( I- \alpha_{n}\mu F ) T_{n}y_{n}-p\bigr\Vert ^{2} \\ =&\bigl\Vert \alpha_{n}\rho Vx_{n}-\alpha_{n} \mu Fp+ ( I-\alpha_{n}\mu F ) T_{n}y_{n}- ( I- \alpha_{n}\mu F ) T_{n}p\bigr\Vert ^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1-\alpha_{n}\nu) \bigl( \Vert y_{n}-p \Vert +a_{n} \bigr) ^{2} \\ =&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2} \\ &{}+ ( 1-\alpha_{n}\nu) \bigl( \Vert y_{n}-p\Vert ^{2}+2a_{n}\Vert y_{n}-p\Vert +a_{n}^{2} \bigr) \\ =&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1-\alpha_{n}\nu) \Vert y_{n}-p\Vert ^{2} \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1-\alpha_{n}\nu) \bigl[ \beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &{}+ ( 1-\beta_{n} ) \Vert z_{n}-p\Vert ^{2} \bigr] +2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p\Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ =&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1-\alpha_{n}\nu) \beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &{}+ ( 1-\alpha_{n}\nu) ( 1-\beta_{n} ) \Vert z_{n}-p\Vert ^{2} \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1-\alpha_{n}\nu) \beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &{}+ ( 1-\alpha_{n}\nu) ( 1-\beta_{n} ) \bigl[ \Vert x_{n}-p\Vert ^{2}-r_{n} ( 2\theta-r_{n} ) \Vert Bx_{n}-Bp\Vert ^{2} \\ & {}-\lambda_{n} ( 2\alpha-\lambda_{n} ) \Vert Au_{n}-Ap\Vert ^{2} \bigr] \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2}+\Vert x_{n}-p\Vert ^{2} \\ &{}- ( 1-\alpha_{n}\nu) ( 1-\beta_{n} ) \bigl[ r_{n} ( 2\theta-r_{n} ) \Vert Bx_{n}-Bp\Vert ^{2} \\ &{}+ \lambda_{n} ( 2\alpha-\lambda_{n} ) \Vert Au_{n}-Ap\Vert ^{2} \bigr] \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2}. \end{aligned}$$
(3.19)

Then, from (3.19), we get

$$\begin{aligned} & ( 1-\alpha_{n}\nu) ( 1-\beta_{n} ) \bigl\{ r_{n} ( 2\theta-r_{n} ) \Vert Bx_{n}-Bp\Vert ^{2}+\lambda_{n} ( 2\alpha-\lambda_{n} ) \Vert Au_{n}-Ap\Vert ^{2} \bigr\} \\ &\quad \leq \alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2}+\Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1}-p\Vert ^{2} \\ &\qquad {}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ &\quad \leq \alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2}+ \bigl( \Vert x_{n}-p\Vert +\Vert x_{n+1}-p\Vert \bigr) \Vert x_{n+1}-p\Vert \\ &\qquad {}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2}. \end{aligned}$$

It follows from (3.18) and from conditions (C1) and (C2) that \(\lim_{n\rightarrow\infty} \Vert Bx_{n}-Bp\Vert =0\) and \(\lim_{n\rightarrow\infty} \Vert Au_{n}-Ap\Vert =0\).

Since \(T_{r_{n}}\) is firmly nonexpansive mapping, we have

$$\begin{aligned} \Vert u_{n}-p\Vert ^{2} =&\bigl\Vert T_{r_{n}} ( x_{n}-r_{n}Bx_{n} ) -T_{r_{n}} ( p-r_{n}Bp ) \bigr\Vert ^{2} \\ \leq& \bigl\langle u_{n}-p, ( x_{n}-r_{n}Bx_{n} ) - ( p-r_{n}Bp ) \bigr\rangle \\ =&\frac{1}{2} \bigl\{ \Vert u_{n}-p\Vert ^{2}+ \bigl\Vert ( x_{n}-r_{n}Bx_{n} ) - ( p-r_{n}Bp ) \bigr\Vert ^{2} \\ &{}- \bigl\Vert u_{n}-p- \bigl[ ( x_{n}-r_{n}Bx_{n} ) - ( p-r_{n}Bp ) \bigr] \bigr\Vert ^{2} \bigr\} . \end{aligned}$$

Therefore, we get

$$\begin{aligned} \Vert u_{n}-p\Vert ^{2} \leq&\bigl\Vert ( x_{n}-r_{n}Bx_{n} ) - ( p-r_{n}Bp ) \bigr\Vert ^{2} \\ &{}-\bigl\Vert u_{n}-x_{n}-r_{n} ( Bx_{n}-Bp ) \bigr\Vert ^{2} \\ \leq&\Vert x_{n}-p\Vert ^{2}-\bigl\Vert u_{n}-x_{n}-r_{n} ( Bx_{n}-Bp ) \bigr\Vert ^{2} \\ \leq&\Vert x_{n}-p\Vert ^{2}-\Vert u_{n}-x_{n}\Vert ^{2} \\ &{}+2r_{n}\Vert u_{n}-x_{n}\Vert \Vert Bx_{n}-Bp\Vert . \end{aligned}$$
(3.20)

Then, from (3.3), (3.19), and (3.20), we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^{2} \leq&\alpha_{n} \Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1- \alpha_{n}\nu) \bigl[ \beta_{n}\Vert Sx_{n}-p \Vert ^{2} \\ &{}+ ( 1-\beta_{n} ) \Vert z_{n}-p\Vert ^{2} \bigr] +2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p\Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1-\alpha_{n}\nu) \bigl[ \beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &{}+ ( 1-\beta_{n} ) \Vert u_{n}-p\Vert ^{2} \bigr] +2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p\Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1-\alpha_{n}\nu) \bigl[ \beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &{}+ ( 1-\beta_{n} ) \bigl( \Vert x_{n}-p\Vert ^{2}-\Vert u_{n}-x_{n}\Vert ^{2} \\ &{}+ 2r_{n}\Vert u_{n}-x_{n} \Vert \Vert Bx_{n}-Bp\Vert \bigr) \bigr] \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2}+\Vert x_{n}-p\Vert ^{2} \\ &{}- ( 1-\alpha_{n}\nu) ( 1-\beta_{n} ) \Vert u_{n}-x_{n}\Vert ^{2}+2r_{n}\Vert u_{n}-x_{n}\Vert \Vert Bx_{n}-Bp\Vert \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2}. \end{aligned}$$

The last inequality implies that

$$\begin{aligned} & ( 1-\alpha_{n}\nu) ( 1-\beta_{n} ) \Vert u_{n}-x_{n}\Vert ^{2} \\ &\quad \leq\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &\qquad {}+\Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1}-p \Vert ^{2}+2r_{n}\Vert u_{n}-x_{n} \Vert \Vert Bx_{n}-Bp\Vert \\ &\qquad {}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ &\quad \leq\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &\qquad {}+ \bigl( \Vert x_{n}-p\Vert +\Vert x_{n+1}-p\Vert \bigr) \Vert x_{n+1}-x_{n}\Vert \\ &\qquad {}+2r_{n}\Vert u_{n}-x_{n}\Vert \Vert Bx_{n}-Bp\Vert \\ &\qquad {}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2}. \end{aligned}$$

Since \(\lim_{n\rightarrow\infty} \Vert Bx_{n}-Bp\Vert =0\) and \(\{ \Vert y_{n}-p\Vert \} \) is a bounded sequence, by using (3.18) and conditions (C1), (C2), we obtain

$$ \lim_{n\rightarrow\infty} \Vert u_{n}-x_{n}\Vert =0. $$
(3.21)

On the other hand, since a metric projection \(P_{C}\) satisfies

$$ \langle u-v,P_{C}u-P_{C}v \rangle\geq \Vert P_{C}u-P_{C}v\Vert ^{2}, $$

we write

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2} =&\bigl\Vert P_{C} ( u_{n}-\lambda_{n}Au_{n} ) -P_{C} ( p- \lambda_{n}Ap ) \bigr\Vert ^{2} \\ \leq& \bigl\langle z_{n}-p, ( u_{n}-\lambda_{n}Au_{n} ) - ( p-\lambda_{n}Ap ) \bigr\rangle \\ =&\frac{1}{2} \bigl\{ \Vert z_{n}-p\Vert ^{2}+ \bigl\Vert u_{n}-p ( Au_{n}-Ap ) \bigr\Vert ^{2} \\ &{}- \bigl\Vert u_{n}-p-\lambda_{n} ( Au_{n}-Ap ) - ( z_{n}-p ) \bigr\Vert ^{2} \bigr\} \\ \leq&\frac{1}{2} \bigl\{ \Vert z_{n}-p\Vert ^{2}+\Vert u_{n}-p\Vert ^{2} \\ &{}- \bigl\Vert u_{n}-z_{n}-\lambda_{n} ( Au_{n}-Ap ) \bigr\Vert ^{2} \bigr\} \\ \leq&\frac{1}{2} \bigl\{ \Vert z_{n}-p\Vert ^{2}+\Vert u_{n}-p\Vert ^{2} \\ &{}- \Vert u_{n}-z_{n}\Vert ^{2}+2 \lambda_{n} \langle u_{n}-z_{n},Au_{n}-Ap \rangle\bigr\} \\ \leq&\frac{1}{2} \bigl\{ \Vert z_{n}-p\Vert ^{2}+\Vert u_{n}-p\Vert ^{2}-\Vert u_{n}-z_{n}\Vert ^{2} \\ &{}+ 2\lambda_{n}\Vert u_{n}-z_{n}\Vert \Vert Au_{n}-Ap\Vert \bigr\} . \end{aligned}$$

So, we get

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2} \leq&\Vert u_{n}-p \Vert ^{2}-\Vert u_{n}-z_{n}\Vert ^{2} \\ &{}+2\lambda_{n}\Vert u_{n}-z_{n}\Vert \Vert Au_{n}-Ap\Vert \\ \leq&\Vert x_{n}-p\Vert ^{2}-\Vert u_{n}-z_{n}\Vert ^{2} \\ &{}+2\lambda_{n}\Vert u_{n}-z_{n}\Vert \Vert Au_{n}-Ap\Vert . \end{aligned}$$
(3.22)

By using (3.19) and (3.22), we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^{2} \leq&\alpha_{n} \Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1- \alpha_{n}\nu) \bigl[ \beta_{n}\Vert Sx_{n}-p \Vert ^{2} \\ &{}+ ( 1-\beta_{n} ) \Vert z_{n}-p\Vert ^{2} \bigr] +2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p\Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+ ( 1-\alpha_{n}\nu) \bigl[ \beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &{}+ ( 1-\beta_{n} ) \bigl( \Vert x_{n}-p\Vert ^{2}-\Vert u_{n}-z_{n}\Vert ^{2} \\ &{}+ 2\lambda_{n}\Vert u_{n}-z_{n} \Vert \Vert Au_{n}-Ap\Vert \bigr) \bigr] \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2}+\Vert x_{n}-p\Vert ^{2} \\ &{}- ( 1-\alpha_{n}\nu) \beta_{n}\Vert u_{n}-z_{n}\Vert ^{2}+2\lambda_{n} \Vert u_{n}-z_{n}\Vert \Vert Au_{n}-Ap\Vert \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2}. \end{aligned}$$

Therefore, we get

$$\begin{aligned} ( 1-\alpha_{n}\nu) \beta_{n}\Vert u_{n}-z_{n} \Vert ^{2} \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &{}+\Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1}-p \Vert ^{2} \\ &{}+2\lambda_{n}\Vert u_{n}-z_{n}\Vert \Vert Au_{n}-Ap\Vert \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2} \\ \leq&\alpha_{n}\Vert \rho Vx_{n}-\mu Fp\Vert ^{2}+\beta_{n}\Vert Sx_{n}-p\Vert ^{2} \\ &{}+ \bigl( \Vert x_{n}-p\Vert +\Vert x_{n+1}-p\Vert \bigr) \Vert x_{n+1}-x_{n}\Vert \\ &{}+2\lambda_{n}\Vert u_{n}-z_{n}\Vert \Vert Au_{n}-Ap\Vert \\ &{}+2 ( 1-\alpha_{n}\nu) a_{n}\Vert y_{n}-p \Vert + ( 1-\alpha_{n}\nu) a_{n}^{2}. \end{aligned}$$

Since \(\lim_{n\rightarrow\infty} \Vert Au_{n}-Ap\Vert =0\) and \(\{ \Vert y_{n}-p\Vert \} \) is a bounded sequence, by using (3.18) and conditions (C1), (C2), we obtain

$$ \lim_{n\rightarrow\infty} \Vert u_{n}-z_{n}\Vert =0. $$
(3.23)

Also, from (3.21) and (3.23), we have

$$ \lim_{n\rightarrow\infty} \Vert x_{n}-z_{n}\Vert =0. $$
(3.24)

On the other hand, we get

$$\begin{aligned} \Vert x_{n}-y_{n}\Vert \leq&\Vert x_{n}-u_{n}\Vert +\Vert u_{n}-z_{n} \Vert +\Vert z_{n}-y_{n}\Vert \\ =&\Vert x_{n}-u_{n}\Vert +\Vert u_{n}-z_{n} \Vert +\beta_{n} ( Sx_{n}-z_{n} ). \end{aligned}$$

Since \(\lim_{n\rightarrow\infty}\beta_{n}=0\), again from (3.21) and (3.23), we obtain

$$ \lim_{n\rightarrow\infty} \Vert x_{n}-y_{n}\Vert =0. $$
(3.25)

Now, we show that \(\lim_{n\rightarrow\infty} \Vert x_{n}-Tx_{n}\Vert =0\). Before that we need to show that \(\lim_{n\rightarrow\infty} \Vert x_{n}-T_{n}x_{n}\Vert =0\):

$$\begin{aligned} \Vert x_{n}-T_{n}x_{n}\Vert \leq&\Vert x_{n}-x_{n+1}\Vert +\Vert x_{n+1}-T_{n}x_{n} \Vert \\ \leq&\Vert x_{n}-x_{n+1}\Vert +\Vert P_{C}t_{n}-P_{C}T_{n}x_{n} \Vert \\ \leq&\Vert x_{n}-x_{n+1}\Vert +\bigl\Vert \alpha_{n}\rho Vx_{n}+ ( I-\alpha_{n}\mu F ) T_{n}y_{n}-T_{n}x_{n}\bigr\Vert \\ \leq&\Vert x_{n}-x_{n+1}\Vert +\bigl\Vert \alpha_{n} ( \rho Vx_{n}-\mu FT_{n}y_{n} ) +T_{n}y_{n}-T_{n}x_{n}\bigr\Vert \\ \leq&\Vert x_{n}-x_{n+1}\Vert +\alpha_{n} \Vert \rho Vx_{n}-\mu FT_{n}y_{n}\Vert +\Vert y_{n}-x_{n}\Vert +a_{n}. \end{aligned}$$

Since \(a_{n}\rightarrow0\), by using (3.18), (3.25), and condition (C1), we obtain

$$ \lim_{n\rightarrow\infty} \Vert x_{n}-T_{n}x_{n} \Vert =0. $$
(3.26)

Hence, from (3.26) and condition (C3), we have

$$\begin{aligned} \Vert x_{n}-Tx_{n}\Vert \leq&\Vert x_{n}-T_{n}x_{n}\Vert +\Vert T_{n}x_{n}-Tx_{n}\Vert \\ \leq&\Vert x_{n}-T_{n}x_{n}\Vert + \mathfrak{D}_{B} ( T_{n},T ) \rightarrow0\quad \text{as }n \rightarrow\infty. \end{aligned}$$

Since \(\{ x_{n} \} \) is bounded, there exists a weak convergent subsequence \(\{ x_{n_{k}} \} \) of \(\{ x_{n} \} \). Let \(x_{n_{k}}\rightharpoonup w\) as \(k\rightarrow\infty\). From the Opial condition, we get \(x_{n}\rightharpoonup w\). So, it follows from Lemma 6 that \(w\in \operatorname {Fix}( T ) \). Therefore, \(w_{w} ( x_{n} ) \subset \operatorname {Fix}( T ) \). □

Theorem 1

Assume that (C1)-(C3) hold. Then the sequence \(\{ x_{n} \} \) generated by (3.1) converges strongly to \(x^{\ast }\in \mathcal {F}\), which is the unique solution of the variational inequality

$$ \bigl\langle ( \rho V-\mu F ) x^{\ast},x-x^{\ast} \bigr\rangle \leq0,\quad\forall x\in \mathcal {F}. $$
(3.27)

Proof

Since the mapping T is defined by \(Tx=\lim_{n\rightarrow\infty}T_{n}x\) for all \(x\in C\), by Lemma 3, T is a nonexpansive mapping, and \(\operatorname {Fix}( T ) \neq\emptyset\). Moreover, since the operator \(\mu F-\rho V\) is \(( \mu\eta-\rho\gamma) \)-strongly monotone by Lemma 4, we get the uniqueness of the solution of the variational inequality (3.27). Let us denote this solution by \(x^{\ast}\in \operatorname {Fix}( T ) =\mathcal {F}\).

Now, we divide our proof into three steps.

Step 1. From Lemma 8, since \(\{ x_{n} \} \) is bounded, there exists an element w such that \(x_{n}\rightharpoonup w\). First, we show that \(w\in \mathcal {F}=\operatorname {Fix}( T ) \cap\Omega \cap \operatorname {GEP}( G ) \). It follows from Lemma 9 that \(w\in \operatorname {Fix}( T ) =\bigcap_{n=1}^{\infty} \operatorname {Fix}( T_{n} ) \). Next we show that \(w\in\Omega\). Let \(N_{C}v\) be the normal cone to C at \(v\in C\), i.e.,

$$ N_{C}v= \bigl\{ w\in H: \langle v-u,w \rangle\geq0,\ \forall u\in C \bigr\} . $$

Let

$$ Hv= \begin{cases} Av+N_{C}v,&v\in C, \\ \emptyset,&v\notin C.\end{cases} $$

Then H is maximal monotone mapping. Let \(( v,u ) \in G ( H ) \). Since \(u-Av\in N_{C}v\) and \(z_{n}\in C\), we get

$$ \langle v-z_{n},u-Av \rangle\geq0. $$
(3.28)

On the other hand, from the definition of \(z_{n}\), we have

$$ \langle v-z_{n},z_{n}-u_{n}-\lambda_{n}Au_{n} \rangle\geq0 $$

and hence,

$$ \biggl\langle v-z_{n},\frac{z_{n}-u_{n}}{\lambda_{n}}+Au_{n} \biggr\rangle \geq0. $$

Therefore, using (3.28), we get

$$\begin{aligned} \langle v-z_{n_{i}},u \rangle \geq& \langle v-z_{n_{i}},Av \rangle \\ \geq& \langle v-z_{n_{i}},Av \rangle- \biggl\langle v-z_{n_{i}},\frac{z_{n_{i}}-u_{n_{i}}}{\lambda_{n_{i}}}+Au_{n_{i}} \biggr\rangle \\ =& \biggl\langle v-z_{n_{i}},Av-Au_{n_{i}}-\frac {z_{n_{i}}-u_{n_{i}}}{\lambda _{n_{i}}} \biggr\rangle \\ =& \langle v-z_{n_{i}},Av-Az_{n_{i}} \rangle+ \langle v-z_{n_{i}},Az_{n_{i}}-Au_{n_{i}} \rangle - \biggl\langle v-z_{n_{i}},\frac{z_{n_{i}}-u_{n_{i}}}{\lambda _{n_{i}}} \biggr\rangle \\ \geq& \langle v-z_{n_{i}},Az_{n_{i}}-Au_{n_{i}} \rangle- \biggl\langle v-z_{n_{i}},\frac{z_{n_{i}}-u_{n_{i}}}{\lambda_{n_{i}}} \biggr\rangle . \end{aligned}$$
(3.29)

By using (3.21), (3.23), and (3.24), we get \(u_{n_{i}}\rightharpoonup w\) and \(z_{n_{i}}\rightharpoonup w\) for \(i\rightarrow\infty\). Hence, from (3.29) we have

$$ \langle v-w,u \rangle\geq0. $$

Since H is maximal monotone, we have \(w\in H^{-1}0\) and hence \(w\in \Omega \).

Finally, we show that \(w\in \operatorname {GEP}( G ) \). By using \(u_{n}=T_{r_{n}} ( x_{n}-r_{n}Bx_{n} ) \), we get

$$ G ( u_{n},y ) + \langle Bx_{n},y-u_{n} \rangle+ \frac {1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq0,\quad \forall y\in C. $$

Also, from the monotonicity of G, we have

$$ \langle Bx_{n},y-u_{n} \rangle+\frac{1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq G ( y,u_{n} ), \quad \forall y\in C, $$

and

$$ \langle Bx_{n_{k}},y-u_{n_{k}} \rangle+ \biggl\langle y-u_{n_{k}},\frac{u_{n_{k}}-x_{n_{k}}}{r_{n_{k}}} \biggr\rangle \geq G ( y,u_{n_{k}} ), \quad \forall y\in C. $$
(3.30)

Let \(y\in C\) and \(y_{t}=ty+ ( 1-t ) w\), for \(t\in( 0,1 ] \). Then \(y_{t}\in C\). From (3.30), we get

$$\begin{aligned} \langle By_{t},y_{t}-u_{n_{k}} \rangle \geq& \langle By_{t},y_{t}-u_{n_{k}} \rangle- \langle Bx_{n_{k}},y_{t}-u_{n_{k}} \rangle \\ &{}- \biggl\langle y_{t}-u_{n_{k}},\frac {u_{n_{k}}-x_{n_{k}}}{r_{n_{k}}}\biggr\rangle +G ( y_{t},u_{n_{k}} ) \\ =& \langle By_{t}-Bx_{n_{k}},y_{t}-u_{n_{k}} \rangle+ \langle Bu_{n_{k}}-Bx_{n_{k}},y_{t}-u_{n_{k}} \rangle \\ &{}- \biggl\langle y_{t}-u_{n_{k}},\frac {u_{n_{k}}-x_{n_{k}}}{r_{n_{k}}}\biggr\rangle +G ( y_{t},u_{n_{k}} ). \end{aligned}$$
(3.31)

Since B is Lipschitz continuous, using (3.21) we obtain \(\lim_{k\rightarrow\infty} \Vert Bu_{n_{k}}-Bx_{n_{k}}\Vert =0\). It follows from (3.31), \(u_{n_{k}}\rightharpoonup w\) and the monotonicity of B that

$$ \langle By_{t},y_{t}-w \rangle\geq G ( y_{t},w ). $$
(3.32)

Therefore, from assumptions (A1)-(A4) and (3.32), we have

$$\begin{aligned} 0 =&G ( y_{t},y_{t} ) \leq tG ( y_{t},y ) + ( 1-t ) G ( y_{t},w ) \\ \leq&tG ( y_{t},y ) + ( 1-t ) \langle By_{t},y_{t}-w \rangle \\ \leq&tG ( y_{t},y ) + ( 1-t ) t \langle By_{t},y-w \rangle. \end{aligned}$$

The last inequality implies that

$$ G ( y_{t},y ) + ( 1-t ) \langle By_{t},y-w \rangle\geq0. $$

If we take the limit \(t\rightarrow0^{+}\), we get

$$ G ( w,y ) + \langle Bw,y-w \rangle\geq0,\quad \forall y\in C. $$

Hence, we have \(w\in \operatorname {GEP}( G ) \). Thus, we obtain \(w\in \mathcal {F}=\operatorname {Fix}( T ) \cap\Omega\cap \operatorname {GEP}( G ) \).

Step 2. We show that \(\limsup_{n\rightarrow\infty} \langle ( \rho V-\mu F ) x^{\ast},x_{n}-x^{\ast} \rangle\leq0\), where \(x^{\ast}\) is the unique solution of variational inequality (3.27). Since the sequence \(\{ x_{n} \} \) is bounded, it has a weak convergent subsequence \(\{ x_{n_{k}} \} \) such that

$$ \limsup_{n\rightarrow\infty} \bigl\langle ( \rho V-\mu F ) x^{\ast},x_{n}-x^{\ast} \bigr\rangle =\limsup _{k\rightarrow\infty } \bigl\langle ( \rho V-\mu F ) x^{\ast},x_{n_{k}}-x^{\ast } \bigr\rangle . $$

Let \(x_{n_{k}}\rightharpoonup w\), as \(k\rightarrow\infty\). It follows from Step 1 that \(w\in \mathcal {F}\). Hence

$$ \limsup_{n\rightarrow\infty} \bigl\langle ( \rho V-\mu F ) x^{\ast},x_{n}-x^{\ast} \bigr\rangle = \bigl\langle ( \rho V-\mu F ) x^{\ast},w-x^{\ast} \bigr\rangle \leq0. $$

Step 3. Finally, we show that the sequence \(\{ x_{n} \} \) generated by (3.1) converges strongly to the point \(x^{\ast}\). By using the iteration (3.1), we have

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert ^{2} =& \bigl\langle P_{C}t_{n}-x^{\ast},x_{n+1}-x^{\ast} \bigr\rangle \\ =& \bigl\langle P_{C}t_{n}-t_{n},x_{n+1}-x^{\ast} \bigr\rangle + \bigl\langle t_{n}-x^{\ast},x_{n+1}-x^{\ast} \bigr\rangle . \end{aligned}$$
(3.33)

Since the metric projection \(P_{C}\) satisfies the inequality

$$ \langle x-P_{C}x,y-P_{C}x \rangle\leq0,\quad \forall x \in H, y\in C, $$

from (3.33), we get

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert ^{2} \leq& \bigl\langle t_{n}-x^{\ast},x_{n+1}-x^{\ast} \bigr\rangle \\ =& \bigl\langle \alpha_{n}\rho Vx_{n}+ ( I- \alpha_{n}\mu F ) T_{n}y_{n}-x^{\ast},x_{n+1}-x^{\ast} \bigr\rangle \\ =& \bigl\langle \alpha_{n} \bigl( \rho Vx_{n}-\mu Fx^{\ast} \bigr) + ( I-\alpha_{n}\mu F ) T_{n}y_{n} \\ &{} - ( I-\alpha_{n}\mu F ) T_{n}x^{\ast },x_{n+1}-x^{\ast } \bigr\rangle \\ =&\alpha_{n}\rho\bigl\langle Vx_{n}-Vx^{\ast},x_{n+1}-x^{\ast } \bigr\rangle +\alpha_{n} \bigl\langle \rho Vx^{\ast}-\mu Fx^{\ast },x_{n+1}-x^{\ast} \bigr\rangle \\ &{}+ \bigl\langle ( I-\alpha_{n}\mu F ) T_{n}y_{n}- ( I-\alpha_{n}\mu F ) T_{n}x^{\ast},x_{n+1}-x^{\ast} \bigr\rangle . \end{aligned}$$

Hence, from Lemma 5, we obtain

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert ^{2} \leq& \alpha_{n}\rho\gamma\bigl\Vert x_{n}-x^{\ast}\bigr\Vert \bigl\Vert x_{n+1}-x^{\ast }\bigr\Vert + \alpha_{n} \bigl\langle \rho Vx^{\ast}-\mu Fx^{\ast },x_{n+1}-x^{\ast} \bigr\rangle \\ &{}+ ( 1-\alpha_{n}\nu) \bigl( \bigl\Vert y_{n}-x^{\ast } \bigr\Vert +a_{n} \bigr) \bigl\Vert x_{n+1}-x^{\ast} \bigr\Vert \\ \leq&\alpha_{n}\rho\gamma\bigl\Vert x_{n}-x^{\ast} \bigr\Vert \bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert + \alpha_{n} \bigl\langle \rho Vx^{\ast}-\mu Fx^{\ast },x_{n+1}-x^{\ast} \bigr\rangle \\ &{}+ ( 1-\alpha_{n}\nu) \bigl( \beta_{n}\bigl\Vert x_{n}-x^{\ast }\bigr\Vert +\beta_{n}\bigl\Vert Sx^{\ast}-x^{\ast}\bigr\Vert \\ &{}+ ( 1-\beta_{n} ) \bigl\Vert z_{n}-x^{\ast} \bigr\Vert +a_{n} \bigr) \bigl\Vert x_{n+1}-x^{\ast} \bigr\Vert \\ \leq&\alpha_{n}\rho\gamma\bigl\Vert x_{n}-x^{\ast} \bigr\Vert \bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert + \alpha_{n} \bigl\langle \rho Vx^{\ast}-\mu Fx^{\ast },x_{n+1}-x^{\ast} \bigr\rangle \\ &{}+ ( 1-\alpha_{n}\nu) \bigl( \beta_{n}\bigl\Vert x_{n}-x^{\ast }\bigr\Vert +\beta_{n}\bigl\Vert Sx^{\ast}-x^{\ast}\bigr\Vert \\ &{}+ ( 1-\beta_{n} ) \bigl\Vert x_{n}-x^{\ast} \bigr\Vert +a_{n} \bigr) \bigl\Vert x_{n+1}-x^{\ast} \bigr\Vert \\ \leq& \bigl( 1-\alpha_{n} ( \nu-\rho\gamma) \bigr) \bigl\Vert x_{n}-x^{\ast}\bigr\Vert \bigl\Vert x_{n+1}-x^{\ast} \bigr\Vert \\ &{}+\alpha_{n} \bigl\langle \rho Vx^{\ast}-\mu Fx^{\ast },x_{n+1}-x^{\ast } \bigr\rangle \\ &{}+ ( 1-\alpha_{n}\nu) \beta_{n}\bigl\Vert Sx^{\ast }-x^{\ast }\bigr\Vert \bigl\Vert x_{n+1}-x^{\ast} \bigr\Vert \\ &{}+ ( 1-\alpha_{n}\nu) a_{n}\bigl\Vert x_{n+1}-x^{\ast }\bigr\Vert \\ \leq&\frac{ ( 1-\alpha_{n} ( \nu-\rho\gamma) ) }{2}\bigl( \bigl\Vert x_{n}-x^{\ast} \bigr\Vert ^{2}+\bigl\Vert x_{n+1}-x^{\ast }\bigr\Vert ^{2} \bigr) \\ &{}+\alpha_{n} \bigl\langle \rho Vx^{\ast}-\mu Fx^{\ast },x_{n+1}-x^{\ast } \bigr\rangle \\ &{}+ ( 1-\alpha_{n}\nu) \beta_{n}\bigl\Vert Sx^{\ast }-x^{\ast }\bigr\Vert \bigl\Vert x_{n+1}-x^{\ast} \bigr\Vert \\ &{}+ ( 1-\alpha_{n}\nu) a_{n}\bigl\Vert x_{n+1}-x^{\ast }\bigr\Vert . \end{aligned}$$

The last inequality implies that

$$\begin{aligned}& \begin{aligned} \bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert ^{2} \leq{}& \frac{ ( 1-\alpha _{n} ( \nu-\rho\gamma) ) }{ ( 1+\alpha_{n} ( \nu -\rho\gamma) ) }\bigl\Vert x_{n}-x^{\ast}\bigr\Vert ^{2} \\ &{}+\frac{2\alpha_{n}}{ ( 1+\alpha_{n} ( \nu-\rho\gamma ) ) } \bigl\langle \rho Vx^{\ast}-\mu Fx^{\ast},x_{n+1}-x^{\ast } \bigr\rangle \\ &{}+\frac{2\beta_{n}}{ ( 1+\alpha_{n} ( -\rho\gamma) ) }\bigl\Vert Sx^{\ast}-x^{\ast}\bigr\Vert \bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert \\ &{}+\frac{2a_{n}}{ ( 1+\alpha_{n} ( \nu-\rho\gamma) ) }\bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert \\ \leq{}& \bigl( 1-\alpha_{n} ( \nu-\rho\gamma) \bigr) \bigl\Vert x_{n}-x^{\ast}\bigr\Vert ^{2}+\alpha_{n} ( \nu-\rho\gamma) \theta_{n}, \end{aligned} \\& \theta_{n}=\frac{2}{ ( 1+\alpha_{n} ( \nu-\rho\gamma) ) ( \nu-\rho\gamma) } \biggl[ \bigl\langle \rho Vx^{\ast}-\mu Fx^{\ast},x_{n+1}-x^{\ast} \bigr\rangle +\frac{\beta_{n}}{\alpha_{n}}M_{3} +\frac{a_{n}}{\alpha_{n}}\bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert \biggr] , \end{aligned}$$

and

$$ \sup_{n\geq1} \bigl\{ \bigl\Vert Sx^{\ast}-x^{\ast} \bigr\Vert \bigl\Vert x_{n+1}-x^{\ast}\bigr\Vert \bigr\} \leq M_{3}. $$

Since \(\frac{\beta_{n}}{\alpha_{n}}\rightarrow0\) and \(\frac {a_{n}}{\alpha _{n}}\rightarrow0\), we get

$$ \limsup_{n\rightarrow\infty}\theta_{n}\leq0. $$

So, it follows from Lemma 7 that the sequence \(\{ x_{n} \} \) generated by (3.1) converges strongly to \(x^{\ast}\in \mathcal {F}\) which is the unique solution of variational inequality (3.27). □

Putting \(A=0\) in Theorem 1, we have the following corollary.

Corollary 1

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let \(B:C\rightarrow H\) be θ-inverse strongly monotone mapping, \(G:C\times C\rightarrow \mathbb{R} \) be a bifunction satisfying assumptions (A1)-(A4), \(S:C\rightarrow H\) be a nonexpansive mapping and \(\{ T_{n} \} \) be a sequence of nearly nonexpansive mappings with the sequence \(\{ a_{n} \} \) such that \(\mathcal {F}:=\operatorname {Fix}( T ) \cap\Omega\cap \operatorname {GEP}( G ) \neq \emptyset\) where \(Tx=\lim_{n\rightarrow\infty}T_{n}x\) for all \(x\in C\) and \(\operatorname {Fix}( T ) =\bigcap_{n=1}^{\infty} \operatorname {Fix}( T_{n} ) \). Let \(V:C\rightarrow H\) be a γ-Lipschitzian mapping, \(F:C\rightarrow H \) be a L-Lipschitzian and η-strongly monotone operator such that these coefficients satisfy \(0<\mu<\frac{2\eta}{L^{2}}\), \(0\leq\rho \gamma <\nu\), where \(\nu=1-\sqrt{1-\mu( 2\eta-\mu L^{2} ) }\). For an arbitrarily initial value \(x_{1}\in C\), consider the sequence \(\{ x_{n} \} \) in C generated by

$$ \begin{cases} G ( u_{n},y ) + \langle Bx_{n},y-u_{n} \rangle+\frac {1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq0, \quad \forall y\in C, \\ y_{n}=P_{C} [ \beta_{n}Sx_{n}+ ( 1-\beta_{n} ) u_{n} ] ,\\ x_{n+1}=P_{C} [ \alpha_{n}\rho Vx_{n}+ ( I-\alpha_{n}\mu F ) T_{n}y_{n} ] ,\quad n\geq1,\end{cases} $$
(3.34)

where \(\{ r_{n} \} \subset( 0,2\theta) \), \(\{ \alpha_{n} \} \) and \(\{ \beta_{n} \} \) are sequences in \([ 0,1 ] \) satisfying the conditions (C1)-(C3) except the condition \(\lim_{n\rightarrow\infty}\frac{\vert\lambda _{n}-\lambda _{n-1}\vert}{\alpha_{n}}=0\). Then the sequence \(\{ x_{n} \} \) generated by (3.34) converges strongly to \(x^{\ast }\in \mathcal {F}\), where \(x^{\ast}\) is the unique solution of variational inequality (3.27).

In Theorem 1, if we take \(A=0\) and \(\beta_{n}=0\) for all \(n\geq1\), then we have the following corollary.

Corollary 2

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let \(B:C\rightarrow H\) be θ-inverse strongly monotone mapping, \(G:C\times C\rightarrow \mathbb{R} \) be a bifunction satisfying assumptions (A1)-(A4), \(\{ T_{n} \} \) be a sequence of nearly nonexpansive mappings with the sequence \(\{ a_{n} \} \) such that \(\mathcal {F}:=\operatorname {Fix}( T ) \cap\Omega \cap \operatorname {GEP}( G ) \neq\emptyset\) where \(Tx=\lim_{n\rightarrow\infty }T_{n}x\) for all \(x\in C\) and \(\operatorname {Fix}( T ) =\bigcap_{n=1}^{\infty }\operatorname {Fix}( T_{n} ) \). Let \(V:C\rightarrow H\) be a γ-Lipschitzian mapping, \(F:C\rightarrow H\) be a L-Lipschitzian and η-strongly monotone operator such that these coefficients satisfy \(0<\mu <\frac{2\eta}{L^{2}}\), \(0\leq\rho\gamma<\nu\), where \(\nu=1-\sqrt {1-\mu ( 2\eta-\mu L^{2} ) }\). For an arbitrarily initial value \(x_{1}\in C\), consider the sequence \(\{ x_{n} \} \) in C generated by

$$ \begin{cases} G ( u_{n},y ) + \langle Bx_{n},y-u_{n} \rangle+\frac {1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq0, \quad \forall y\in C, \\ x_{n+1}=P_{C} [ \alpha_{n}\rho Vx_{n}+ ( I-\alpha_{n}\mu F ) T_{n}u_{n} ] ,\quad n\geq1,\end{cases} $$
(3.35)

where \(\{ r_{n} \} \subset( 0,2\theta) \), \(\{ \alpha_{n} \} \) is a sequence in \([ 0,1 ] \) satisfying the conditions (C1)-(C3) except the conditions \(\lim_{n\rightarrow \infty}\frac{\beta_{n}}{\alpha_{n}}=0\), \(\lim_{n\rightarrow\infty}\frac{ \vert\lambda_{n}-\lambda_{n-1}\vert}{\alpha_{n}}=0\) and \(\lim_{n\rightarrow\infty}\frac{\vert\beta_{n}-\beta _{n-1}\vert}{\alpha_{n}}=0\). Then the sequence \(\{ x_{n} \} \) generated by (3.35) converges strongly to \(x^{\ast }\in \bigcap_{n=1}^{\infty} \operatorname {Fix}( T_{n} ) \cap\Omega\cap \operatorname {GEP}( G ) \), where \(x^{\ast}\) is the unique solution of variational inequality (3.27).

Putting \(A=0\) and \(B=0\), we have the following corollary, which gives us an iterative scheme to find a common solution of an equilibrium problem and a hierarchical fixed point problem.

Corollary 3

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let \(G:C\times C\rightarrow \mathbb{R} \) be a bifunction satisfying assumptions (A1)-(A4), \(S:C\rightarrow H\) be a nonexpansive mapping and \(\{ T_{n} \} \) be a sequence of nearly nonexpansive mappings with the sequence \(\{ a_{n} \} \) such that \(\mathcal {F}:=\operatorname {Fix}( T ) \cap\Omega\cap \operatorname {GEP}( G ) \neq \emptyset\) where \(Tx=\lim_{n\rightarrow\infty}T_{n}x\) for all \(x\in C\) and \(\operatorname {Fix}( T ) =\bigcap_{n=1}^{\infty} \operatorname {Fix}( T_{n} ) \). Let \(V:C\rightarrow H\) be a γ-Lipschitzian mapping, \(F:C\rightarrow H \) be a L-Lipschitzian and η-strongly monotone operator such that these coefficients satisfy \(0<\mu<\frac{2\eta}{L^{2}}\), \(0\leq\rho \gamma <\nu\), where \(\nu=1-\sqrt{1-\mu( 2\eta-\mu L^{2} ) }\). For an arbitrarily initial value \(x_{1}\), define the sequence \(\{ x_{n} \} \) in C generated by

$$ \begin{cases} G ( u_{n},y ) +\frac{1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq0,\quad \forall y\in C, \\ y_{n}=P_{C} [ \beta_{n}Sx_{n}+ ( 1-\beta_{n} ) u_{n} ] ,\\ x_{n+1}=P_{C} [ \alpha_{n}\rho Vx_{n}+ ( I-\alpha_{n}\mu F ) T_{n}y_{n} ] ,\quad n\geq1,\end{cases} $$
(3.36)

where \(\{ r_{n} \} \subset( 0,\infty) \), \(\{ \alpha_{n} \} \) and \(\{ \beta_{n} \} \) are sequences in \([ 0,1 ] \) satisfying the conditions (C1)-(C3) except the condition \(\lim_{n\rightarrow\infty}\frac{\vert\lambda _{n}-\lambda _{n-1}\vert}{\alpha_{n}}=0\). Then the sequence \(\{ x_{n} \} \) generated by (3.36) converges strongly to \(x^{\ast }\in \bigcap_{n=1}^{\infty} \operatorname {Fix}( T_{n} ) \cap \operatorname {EP}( G ) \), where \(x^{\ast}\) is the unique solution of variational inequality (3.27).

Corollary 4

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let \(A,B:C\rightarrow H\) be α, θ-inverse strongly monotone mappings, respectively. \(G:C\times C\rightarrow \mathbb{R} \) be a bifunction satisfying assumptions (A1)-(A4), \(S:C\rightarrow H\) be a nonexpansive mapping and \(\{ T_{n} \} \) be a sequence of nonexpansive mappings such that \(\mathcal {F}:=\operatorname {Fix}( T ) \cap \Omega\cap \operatorname {GEP}( G ) \neq\emptyset\) where \(Tx=\lim_{n\rightarrow \infty}T_{n}x\) for all \(x\in C\) and \(\operatorname {Fix}( T ) =\bigcap_{n=1}^{\infty} \operatorname {Fix}( T_{n} ) \). Let \(V:C\rightarrow H\) be a γ-Lipschitzian mapping, \(F:C\rightarrow H\) be a L-Lipschitzian and η-strongly monotone operator such that these coefficients satisfy \(0<\mu<\frac{2\eta}{L^{2}}\), \(0\leq\rho\gamma<\nu\), where \(\nu =1-\sqrt{1-\mu( 2\eta-\mu L^{2} ) }\). For an arbitrarily initial value \(x_{1}\in C\), consider the sequence \(\{ x_{n} \} \) in C generated by (3.1) where \(\{ \lambda_{n} \} \subset( 0,2\alpha ) \), \(\{ r_{n} \} \subset( 0,2\theta) \), \(\{ \alpha_{n} \} \) and \(\{ \beta_{n} \} \) are sequences in \([ 0,1 ] \) satisfying the conditions (C1)-(C3) of Theorem  1 except the condition \(\lim_{n\rightarrow\infty }\frac {a_{n}}{\alpha_{n}}=0\). Then the sequence \(\{ x_{n} \} \) converges strongly to \(x^{\ast}\in \mathcal {F}\), where \(x^{\ast}\) is the unique solution of variational inequality (3.27).

Remark 1

Our results can be reduced to some corresponding results in the following ways:

  1. (1)

    In our iterative process (3.35), if we take \(G ( x,y ) =0\) for all \(x,y\in C\), \(B=0\), and \(r_{n}=1\) for all \(n\geq1\), then we derive the iterative process

    $$ x_{n+1}=P_{C} \bigl[ \alpha_{n}\rho Vx_{n}+ ( I-\alpha_{n}\mu F ) T_{n}x_{n} \bigr] ,\quad n\geq1, $$

    which is studied by Sahu et al. [4]. Therefore, Theorem 1 generalizes the main result of Sahu et al. [4, Theorem 3.1]. So, our results extend the corresponding results of Ceng et al. [25] and of many other authors.

  2. (2)

    If we take S as a nonexpansive self-mapping on C and \(T_{n}=T\) for all \(n\geq1\) such that T is a nonexpansive mapping in (3.1), then it is clear that our iterative process generalizes the iterative process of Wang and Xu [28]. Hence, Theorem 1 generalizes the main result of Wang and Xu [28, Theorem 3.1]. So, our results extend and improve the corresponding results of [11, 27].

  3. (3)

    The problem of finding the solution of variational inequality (3.27) is equivalent to finding the solutions of hierarchical fixed point problem

    $$ \bigl\langle ( I-S ) x^{\ast},x^{\ast}-x \bigr\rangle \leq0,\quad \forall x\in \mathcal {F}, $$

    where S= \(I- ( \rho V-\mu F ) \).

Example 1

Let \(H=\mathbb{R} \) and \(C= [ 0,1 ] \). Let \(G:C\times C\rightarrow \mathbb{R} \), \(G ( x,y ) =y^{2}+xy-2x^{2}\), \(S=I\), \(A:C\rightarrow H\), \(Ax=2x\), \(B:C\rightarrow H\), \(Bx=3x-1\), \(Vx=4x+2\), \(Fx=5x\), and

$$ T_{n}x= \begin{cases} 1-x, & \text{if }x\in[ 0,1 ),\\ a_{n}, & \text{if }x=1,\end{cases} $$

for all \(x\in C\). It is clear that \(G ( x,y ) \) is a bifunction satisfying the assumptions (A1)-(A4), S is nonexpansive mapping, A is \(\frac{1}{4}\)-inverse strongly monotone mapping, B is \(\frac{1}{6}\)-inverse strongly monotone mapping, V is γ-Lipschitzian mapping with \(\gamma=4\), F is L-Lipschitzian and η-strongly monotone operator with \(L=\eta=5\) and \(\{ T_{n} \} \) is a sequence of nearly nonexpansive mappings with respect to the sequence \(a_{n}=\frac {1}{2n^{2}-1}\). Define sequences \(\{ \alpha_{n} \} \) and \(\{ \beta _{n} \} \) in \([ 0,1 ] \) by \(\alpha_{n}=\frac{1}{n}\) and \(\beta_{n}=\frac{1}{n^{2}+2}\) for all \(n\geq1\) and take \(\mu=\rho =\frac{1}{5}\), \(\nu=1\), \(r_{n}=\frac{1}{n+3}\), and \(\lambda_{n}=\frac {1}{n+2}\). It is easy to see that all conditions of Theorem 1 are satisfied. First, we find the sequence \(\{ u_{n} \} \) which satisfies the following generalized equilibrium problem for all \(y\in C\):

$$ G ( u_{n},y ) + \langle Bx_{n},y-u_{n} \rangle+ \frac {1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq0. $$

For all \(n\geq1\), we get

$$\begin{aligned} &G ( u_{n},y ) + \langle Bx_{n},y-u_{n} \rangle+\frac {1}{r_{n}} \langle y-u_{n},u_{n}-x_{n} \rangle\geq0 \\ &\quad \Rightarrow \quad y^{2}+u_{n}y-2u_{n}^{2}+ ( 3x_{n}-1 ) ( y-u_{n} ) +\frac{1}{r_{n}} ( y-u_{n} ) ( u_{n}-x_{n} ) \geq0 \\ &\quad \Rightarrow \quad y^{2}r_{n}+y ( u_{n}r+3x_{n}r_{n}+u_{n}-r_{n}-x_{n} ) -2u_{n}^{2}r_{n}-3x_{n}u_{n}r_{n}+u_{n}r_{n} -u_{n}^{2}+u_{n}x_{n} \geq0. \end{aligned}$$

Put \(K ( y ) =y^{2}r_{n}+y ( u_{n}r+3x_{n}r_{n}+u_{n}-r_{n}-x_{n} ) -2u_{n}^{2}r_{n}-3x_{n}u_{n}r_{n}+u_{n}r_{n}-u_{n}^{2}+u_{n}x_{n}\). Then K is a quadratic function of y with coefficients \(a=r_{n}\), \(b=u_{n}r_{n}+3x_{n}r_{n}+u_{n}-r_{n}-x_{n}\), and \(c=-2u_{n}^{2}r_{n}-3x_{n}u_{n}r_{n}+u_{n}r_{n}-u_{n}^{2}+u_{n}x_{n}\). Next, we compute the discriminant Δ of K as follows:

$$\begin{aligned} \Delta =&b^{2}-4ac \\ =& ( u_{n}r+3x_{n}r_{n}+u_{n}-r_{n}-x_{n} ) ^{2} \\ &{}-4r_{n} \bigl( -2u_{n}^{2}r_{n}-3x_{n}u_{n}r_{n}+u_{n}r_{n}-u_{n}^{2}+u_{n}x_{n} \bigr) \\ =& ( u_{n}-r_{n}-x_{n}+3r_{n}u_{n}+3r_{n}x_{n} ) ^{2}. \end{aligned}$$

We know that \(K ( y ) \geq0\) for all \(y\in C= [ 0,1 ] \). If it has most one solution in \([ 0,1 ] \), so \(\Delta\leq0\) and hence \(u_{n}=\frac{r_{n}+x_{n} ( 1-3r_{n} ) }{1+3r_{n}}=\frac{1+nx_{n}}{n+6}\). By using this equation, the sequence \(\{ x_{n} \} \) generated by the iterative scheme (3.1) becomes

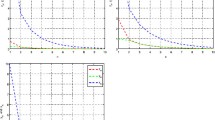
$$ \begin{cases} y^{2}+u_{n}y-2u_{n}^{2}+ ( 3x_{n}-1 ) ( y-u_{n} ) + ( n+3 ) ( y-u_{n} ) ( u_{n}-x_{n} ) \geq0, \quad \forall y\in C ,\\ z_{n}=u_{n}-\frac{2}{n+2}u_{n},\\ y_{n}=\frac{1}{n^{2}+2}x_{n}+ ( 1-\frac{1}{n^{2}+2} ) z_{n}, \\ x_{n+1}=\frac{1}{5n}(4x_{n}+2)+ ( 1-\frac{1}{n} ) ( 1-y_{n} ),\quad \forall n\geq1,\end{cases} $$
(3.37)

for all \(n\geq1\), and it converges strongly to \(x^{\ast}=0.5\) which is the unique common fixed point of the sequence \(\{ T_{n} \} \) and the unique solution of the variational inequality (1.6) over \(\bigcap_{n=1}^{\infty} \operatorname {Fix}( T_{n} ) \). Some of the values of the iterative scheme (3.37) for the different initial values \(x_{1}=0.1\), \(x_{1}=0.4\), and \(x_{1}=0.7\) are as in Table 1.

Table 1 Some of the values of the iterative scheme ( 3.37 )
Full size table