1 Introduction

The need for mobile internet access is dramatically increasing as the number of smartphone users, Internet of Things (IoT) devices, and machine-to-machine (M2M) connections grows. This is resulting in great demand for radio spectrum access. Traditional spectrum access and sharing techniques no longer cope with that great demand. Cognitive radio (CR) is a promising technology that enables opportunistic spectrum access based on spectrum sensing [1, 2]. Primary users (PUs) are not utilizing their licensed spectrum all the time, giving secondary users (SUs) the opportunity to sense the spectrum and search for spectrum holes to utilize for their transmission. To enable SUs to sense a wideband spectrum, a high-rate analog-to-digital converter (ADC) is needed to sample the received signal at the Nyquist rate.

Compressive sensing (CS) has been considered a more suitable solution for sampling a wideband signal at a sub-Nyquist rate, taking advantage of the sparse nature of the wideband spectrum. Measurement campaigns have shown that the wideband spectrum is underutilized most of the time [3]. This made it possible to recover the wideband spectrum at the SUs by a small number of measurements using CS recovery algorithms [4]. In [5], the authors proposed a compressive spectrum sensing (CSS) approach using an analog-to-information converter (AIC) for the reconstruction of the power spectral density (PSD) of a sparse wideband spectrum with few compressed measurements. Cooperative CSS was proposed to take advantage of spatial diversity, in which measurements from the SUs are sent to a fusion center to obtain the final spectrum sensing decision [6]. This approach can mitigate the effects of interference and multipath fading.

For enhancing spectrum sensing performance, various approaches have been proposed. These approaches include modeling PU behavior in time, frequency, and spatial domains [7]. This helps in simulating and designing CR networks and a better selection of channels to be utilized by SUs. Another approach proposed is transmitting PU information to SUs using pilot signals [8]. However, this approach requires modifications to legacy PU systems and signaling overhead. Using geo-locational databases to provide SUs with information about PU systems and spectrum utilization was proposed in [9]. However, this approach requires frequent updating of the databases and imposes communication overhead on SU terminals.

Recently, deep learning (DL) techniques have been integrated into spectrum sensing, enabling CRs to detect the presence of primary signals in noisy environments. By being trained on large spectral datasets, DL algorithms can detect signals with different modulation types and spectral patterns with high accuracy and speed. This enhances spectrum management and facilitates the optimization of scarce spectral resources. The authors in [10] repurposed AlexNet, which is an existing convolutional neural network (CNN), to perform spectrum sensing by sensing the spectrum energy using a small training set. The performance of the CNN detector outperforms traditional energy detectors in the existence of interference or noise. In [11], the authors proposed a deep neural network (DNN) that captures the temporal correlations by treating the received signal as time series data. The proposed DNN model detects various types of modulated primary signals even in low signal-to-noise ratio (SNR). Since SUs have limited hardware capabilities, authors in [12] proposed a collaborative spectrum sensing approach. A DNN is used to detect the wideband spectrum utilization using the observations obtained from SUs sensing different narrowband parts of the spectrum.

This paper is organized as follows. In Sect. , we discuss the related work concerning our research problem. In Sect. , we summarize our motivations and contributions. In Sect. , we describe our system model. In Sect. , we discuss our proposed weighted sequential approach. In Sect. , the simulation and results are explained. The paper is finally concluded in Sect. .

2 Related work

Although CSS served well in reducing the number of measurements required for spectrum recovery, we still need to further reduce the number of measurements. This is due to the limited capabilities of smart devices such as (IoT devices, smart gadgets, wearables, etc.), which rely on batteries and have limited hardware.

Weighted CS has been proposed where a sparse signal can be recovered from a fewer number of compressive measurements by introducing prior knowledge about the sensed signal as weights to the recovery algorithm. This prior knowledge can be for example the probability of signal elements being non-zero. In [13], the authors proposed a recovery algorithm based on solving weighted \(l_{1}\) minimization, where the entries of the unknown signal were divided into two sets with different probabilities of the each set having non-zero elements. They computed the optimal weights utilizing the probability of each set and showed that their weighted \(l_{1}\) minimization performed better than the traditional \(l_{1}\) minimization. In [14], the authors considered a heterogeneous wideband spectrum where similar applications are assigned to the same frequency block. The block-like structure of the spectrum was exploited to assign different weights for each block according to the block’s occupancy level. However, the aforementioned approaches divide the unknown signal into only two sets which is not enough to model a wideband spectrum with a variety of spectrum usage levels. In [15], the authors proposed to assign a different weight to each channel of the wideband spectrum. They proposed a weighted \(l_{1}\) approach where the weight is related to the channel’s duty cycle. Their weighted approach provided the best detection performance among the aforementioned approaches. However, incorporating prior knowledge of PUs behavior either require modifications to the primary systems or communication overhead on the SUs. Also, the accuracy of spectrum occupancy information or its source were not discussed in the scope of weighted CS studies.

To solve these problems, Researchers proposed that the SU can estimate information about the behavior of PUs and spectrum occupancy utilizing spectrum sensing decisions. In [16], the authors utilized prior knowledge about the PU’s average idle and busy times to estimate the duty cycle of a single channel utilizing average estimators as well as maximum likelihood estimation (MLE). In [17], the authors compared the performance of sampling the spectrum using uniform and random sampling on the estimation of the mean idle and busy times. They found that random sampling provides better estimation performance for a fixed sensing window. However, in both [16, 17] the PU activity periods were assumed to follow the exponential distribution which has been proved to be an imperfect fit in [18]. The authors of [19, 20] proposed to estimate the distribution of idle and busy times of a single channel utilizing spectrum sensing decisions by using the modified method of moments (MMoM). The idle and busy periods were assumed to follow the Generalized Pareto (GP) distribution [21] which was considered a good fit in practical scenarios, and they also provided a hardware experiment to confirm their findings. In [22], we investigated the effects of compressive sensing parameters on the estimation of PU behavior based on MMoM and showed that we can accurately estimate PU statistics under certain conditions of CS parameters. In another approach, the authors of [23] proposed an adaptive algorithm to sense the spectrum without the requirement of any prior knowledge of the spectrum sparsity.

In traditional as well as weighted CS, the number of the non-zero elements (denoted as sparsity order) of the sparse signal is needed as prior knowledge to calculate the number of compressive measurements [24]. The number of compressive measurements is usually optimistically (more than required) calculated based on the sparsity order. The sparsity order of a wideband signal can be estimated by long-term monitoring of the spectrum. However, using a fixed number of measurements calculated at the maximum sparsity order is a waste of the CR memory and power resources as the sparsity of a wideband spectrum is always changing.

Sequential CS was proposed to adapt the acquisition of compressive measurements [25]. In this approach, the measurements are acquired step by step until a satisfactory recovery of the spectrum is achieved. The authors proposed to stop measurement acquisition when two consecutive recoveries with a different number of measurements are the same. In [26], the authors proposed using the coherence between two consecutive spectrum decisions as the sopping rule for measurement acquisition. Authors of [27], proposed dividing the total sensing time into smaller time slots and in each time slot some measurements are taken. The acquired measurements are then divided into a training set and a testing set, and then cross-validation is used to check if the spectrum is recovered accurately to stop measurement acquisition. The rest of the time slots can be used by the SU for signal transmission. However, the number of measurements in the testing set which is used to validate the spectrum recovery needs to be larger than the number of measurements in the training set which is used to actually recover the spectrum. In [28], the authors proposed using the Euclidean distance between the measurements taken from the sensed signal and measurements taken from the signal after recovery to evaluate the accuracy of the recovery. However, for that approach to be usable, the number of measurements taken in each time slot must exceed a certain bound. A summary and comparison of the related work can be found in Table 1.

Table 1 Summary and comparison of related work
Full size table

3 Motivations and contributions

Motivated by the need to sense the wideband spectrum with fewer measurements due to the limited hardware capabilities of IoT and smart devices, we proposed an approach that both adapts and reduces the number of measurements needed for CS recovery. The contributions of this paper can be summarized as follows:

  1. (1)

    We proposed estimating duty cycles of the channels of a wideband spectrum using the periodically obtained spectral decisions.

  2. (2)

    The estimated duty cycles of the channels are incorporated as weights in the CS recovery algorithm.

  3. (3)

    We proposed an adaptive CSS approach based on both sequential and weighted CS techniques. The proposed approach acquires measurements from the sensed signal in a step-by-step fashion until a satisfactory recovery of the spectrum is achieved. No prior knowledge about spectrum sparsity is required.

  4. (4)

    The coherence between the consecutive obtained spectral decisions is used as a halting condition of measurement acquisition. This approach reduced the number of measurements required for the validation of the recovery accuracy compared to the related work.

  5. (5)

    Our algorithm could reduce the number of measurements needed for spectrum recovery by approximately 50% on average while not sacrificing the Receiver Operating Characteristics (ROC) performance.

4 Methods

4.1 System model

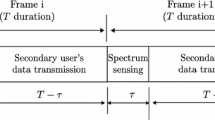
Let us consider a CR network where a single SU periodically senses a sparse wideband frequency spectrum to detect PUs as illustrated in Fig. 1. The sparse spectrum has N non-overlapping channels. The channel between the SU and each of the operating PUs is considered an Additive White Gaussian Noise (AWGN) channel. We assume a dynamic spectrum where the number of active PUs at a given time is randomly changing; while, the power transmitted by each PU is unknown. The wideband signal received by the SU unit as transmitted from L active PUs is denoted by \(s_{i}(t)\) where \(i \in [1, L]\), and can be represented mathematically as follows

$$\begin{aligned} x(t) = \sum _{i=1}^{L} s_{i}(t) + w(t) \end{aligned}$$
(1)

where w(t) is the AWGN.

Fig. 1
figure 1

An illustration of the proposed cognitive radio network

Full size image

To obtain the spectrum received at the SU, we can apply Discrete Fourier Transform (DFT) to Eq. (1) as follows

$$\begin{aligned} X = S + W \end{aligned}$$
(2)

where S, X, and W are all N x 1 vectors representing the spectra of the transmitted, received, and noise signals, respectively

The SU has to compressively sample the signal, then a CS recovery algorithm is used to reconstruct the original signal and then the spectrum can be obtained. An AIC can be used to sample the received signal at a sub-Nyquist rate. As the number of active channels L is much lower than the total number of channels N, the SU can collect only M number of measurements where (\(L< M < N\)). The \(M \times 1\) measurement vector can be represented as follows

$$\begin{aligned} y = \Phi x = \Phi F^{-1} X \end{aligned}$$
(3)

where \(\Phi \) is the \(M\times N\) measurement matrix and \(F^{-1} \) is the \(N\times N\) inverse DFT matrix. To ensure perfect recovery of the \(N \times 1\) signal vector from the M compressive measurements, the measurement matrix \(\Phi \) must satisfy the restricted isometry property (RIP) [29] which states that if there exists an isometry constant \(\delta _{s}\) where \(0< \delta _{s} <1\) the measurement matrix must satisfy the following inequality [29]

$$\begin{aligned} (1- \delta _{s}) \left\Vert {x}\right\Vert _2^2 \le \left\Vert {\Phi x}\right\Vert _2^2 \le (1+ \delta _{s}) \left\Vert {x}\right\Vert _2^2 \end{aligned}$$
(4)

where \(\left\Vert {.}\right\Vert _{2}\) denotes the \(l_{2}\)-norm.

To achieve the RIP condition, the number of measurements or the number of rows of the measurements matrix M must be in the order of \(C \hspace{0.25em} L \hspace{0.25em} log(N/L)\) where C is a constant [30]. A measurement matrix where its elements are interdependently and identically distributed (i.i.d) from Gaussian distribution achieves RIP condition with a high probability. CS recovery is done by solving the system of equations described in Eq. (3). However, this system of equations is an under-determined system as M is less than N which results in an infinite number of solutions. Fortunately, we are only interested in the sparsest solution. The desired solution can be obtained through an optimization problem such as \(l_{0}\)-norm minimization; however, it is considered as an NP-hard problem. Instead, \(l_{1}\)-norm minimization is considered a more convenient solution which can be represented as follows [31]

$$\begin{aligned} \begin{aligned} \min _{x} \quad&\left\Vert {x}\right\Vert _{1} \\ \text { s.t.} \quad&y = \Phi x \\ \end{aligned} \end{aligned}$$
(5)

Solving the optimization problem in (5) can be done using several algorithms such as Greedy algorithms like matching pursuit (MP) [32], orthogonal matching pursuit (OMP) [33], and Compressive sampling matching pursuit (CoSaMP) [34], or convex relaxation approaches such as Basis Pursuit (BP) [35] and Basis Pursuit Denoising (BPDN) [36].

4.2 Modeling of PU behavior

The wideband spectrum of N channels modeled in the paper is divided into j groups of channels having similar duty cycles, and each channel has a duty cycle \(\Psi _{n}\) where \(\Psi _{n} \in \{\Psi _{1}, \Psi _{2}, \Psi _{3},..., \Psi _{j}\}\), and n is the channel index. The average duty cycle \(\bar{\Psi }= \frac{1}{N} \sum _{n=1}^{N} \Psi _{n}\) is set to a low value to reproduce a sparse domain. In order to model the PU’s behavior for each channel, the Continuous-Time Semi-Markov Chain (CTSMC) model was used. According to this model the time index is continuous, and the activity of the PU is modeled as staying in an activity state (idle/busy) for a random period of time called (state holding time) and then switching to the other state for another random period of time. The state holding times in the CTSMC model can follow any arbitrary distribution on the contrary to the Continuous-Time Markov Chain where the state holding times can only follow the exponential distribution. Monitoring the spectrum for the purpose of estimating the activity of PUs can be done by either sampling at high sampling rate, or a relatively lower sampling rate. High sampling rate or (high-resolution modeling) can be used to accurately characterize the spectrum utilization but only for a short time scale due to the huge amount of samples to be stored and processed. However, a relatively lower sampling rate or (low-resolution modeling) can be used to model how a CR unit can monitor the spectrum. It was found that in low-resolution modeling, the idle/busy periods of a channel follow the GP distribution over a wide range of radio technologies [21]. The cumulative distribution function (CDF) of GP distribution is as follows [7]:

$$\begin{aligned} F_{GP} (T;\mu ,\lambda ,\alpha ) = 1 - \Big [1 + \frac{\alpha (T-\mu )}{\lambda } \Big ]^{-1/\alpha } \end{aligned}$$
(6)

where T represents time period length and \(\mu ,\lambda ,\alpha \) are location, scale and shape parameters, respectively. The GP parameters satisfy these conditions:

$$\begin{aligned} T\ge \mu \hbox { for } \alpha>0 \\ \mu \le T \le \mu - \frac{\lambda }{\alpha } \hbox { for }\alpha<0 \\ \mu>0,\lambda >0 \hbox { and } \alpha < 1/2 \end{aligned}$$

The mean \(\mathbb {E} \{T\}\) and the variance \(\mathbb {V} \{T\}\) are given by [7]:

$$\begin{aligned} \mathbb {E} \{T\}= & {} \mu + \frac{\lambda }{1-\alpha } \end{aligned}$$
(7)
$$\begin{aligned} \mathbb {V} \{T\}= & {} \frac{\lambda ^{2}}{(1-\alpha )^2 (1-2\alpha )} \end{aligned}$$
(8)

The channel’s duty cycle (DC) is a simple yet an important parameter to characterize the usage of a channel and the PU’s behavior. The duty cycle is a commonly used parameter in time domain models which describes the average occupancy of a channel, or the probability of finding a channel in busy state as being utilized by a PU. The DC is denoted by \(\Psi \) and can be expressed mathematically as [7]

$$\begin{aligned} \Psi = \frac{\mathbb {E} \{T_{busy}\}}{\mathbb {E} \{T_{busy}\} + \mathbb {E} \{T_{idle}\} } \end{aligned}$$
(9)

where \(\mathbb {E} \{T_{busy}\}\) is the mean value of busy periods and \(\mathbb {E} \{T_{idle}\}\) is the mean of idle periods.

5 The proposed system

In this section of the paper, we discuss our proposed approach. We aim to design a spectrum sensing algorithm that can learn the spectrum utilization information and utilize it to reduce the consumption of CR resources. To achieve this goal, we first estimate the occupancy level of the N channels through the periodically obtained spectrum sensing decisions. Then we use the estimated information to solve a weighted compressive spectrum sensing problem that recovers the spectrum using a few number of compressive measurements. We use a sequential method for measurement acquisition so that we can stop the process once a satisfactory spectrum recovery is achieved. The block diagram of the system is shown in Fig. 2.

Fig. 2
figure 2

Block diagram of the proposed system

Full size image

5.1 Signal recovery

For the SU to be able to recover the sensed wideband spectrum and detect the presence of PUs, a CS recovery algorithm is required. Since we assume an AWGN channel between the SU and the PUs, we use BPDN as the recovery algorithm as it can recover the spectrum from noisy measurements. The optimization problem BPDN is given by [36]:

$$\begin{aligned} \begin{aligned} \min _{x} \quad&\left\Vert {x}\right\Vert _{1} \\ \text {s.t.} \quad&\left\Vert {y-\Phi x}\right\Vert _2^2 < \epsilon \\ \end{aligned} \end{aligned}$$
(10)

where \(\epsilon \) is the amount of noise in the measurements. To balance between the minimization of signal recovery error due to the noise effect and finding the sparsest solution, a penalty parameter \(\lambda \) is used. Therefore, the optimization problem given in (10) can be solved as an unconstrained minimization problem given as:

$$\begin{aligned} \min _{x} \quad \left\Vert {y-\Phi x}\right\Vert _2^2 + \lambda \left\Vert {x}\right\Vert _{1} \end{aligned}$$
(11)

The spectrum decision is then acquired by comparing the PSD level of each channel in the recovered spectrum with a threshold as follows

$$\begin{aligned} \hat{D}_{n} = \left\{ \begin{array}{ll} 1 &{} \hspace{0.35cm} \text {if} \hspace{0.35cm} |\hat{X}_{n}| > \rho ,\hspace{0.25cm} \text {where} \hspace{0.25cm} n \in [1,N] \\ 0 &{} \hspace{0.35cm} \text {if} \hspace{0.35cm} |\hat{X}_{n}| < \rho ,\hspace{0.25cm} \text {where} \hspace{0.25cm} n \in [1,N] \end{array} \right. \end{aligned}$$
(12)

where \(\hat{D} \in \mathbb {R}^{N}\) is the spectrum decision vector, and \(\rho \) is a threshold chosen according to the noise level.

5.2 Estimation of channels’ duty cycles

The binary spectrum sensing decisions (or the obtained states of the channels) denoted as \(\hat{D}\) are used to reconstruct the lengths of the idle and busy periods as illustrated in Fig. 3, where \(S_{0}\) and \(S_{1}\) are idle and busy states of a channel, respectively. The time taken by a channel to flip from one state to another (denoted by \(T_{i}\)) is considered as an estimate of the original activity period, where \(i=1\) represents a busy period and \(i=0\) represents an idle period. Hence, the activity (idle/busy) periods of a PU in a certain channel can be estimated as integer multiple of the sensing period \(T_{s}\) which is defined as the time between two sensing events (i.e., \({\hat{T}_{i,n} }=K T_{s}\) or \( (K+1) T_{s}\) relative to the position where the sensing of a period started with respect to the original period, where ’K’ is an integer representing the number of consecutive binary decisions of the same channel state, and ’n’ represents the index of the periods.

There are three ways to reconstruct an activity (idle/busy) period. For example we can estimate the idle period denoted as \(T_{0}\) in Fig. 3 as the following:

  1. (1)

    \(\hat{T}_{0}=t_{b}-t_{a}\), where the estimated period would be an underestimation of the actual period.

  2. (2)

    \(\hat{T}_{0}=t_{y}-t_{x}\), where the estimated period would be an overestimation of the actual period.

  3. (3)

    \(\hat{T}_{0}=\frac{(t_{b}-t_{a}) + (t_{y}-t_{x})}{2}\), where the estimated period would be a more accurate estimation of the actual period which is used in this paper.

Fig. 3
figure 3

Reconstruction of activity periods from binary spectrum sensing decisions. \(S_{1}\), \(S_{0}\) are busy and idle channel states, respectively, while \(T_{s}\) is the sensing period, and \(T_{0}\) represent an actual idle period

Full size image

Using the method above we can reconstruct the activity periods for all the N channels. Then to estimate the duty cycles \(\Psi \) (average occupancy) of the channels, we need to firstly estimate the mean of the reconstructed activity periods as follows:

$$\begin{aligned} \mathbb {E} (\hat{T}_{i}) = \frac{1}{N_{p}} \sum _{n=1}^{N_{p}} \hat{T}_{i,n} \end{aligned}$$
(13)

where \(N_{p}\) denotes the number of reconstructed periods.

The duty cycle of any channel is estimated as:

$$\begin{aligned} \hat{\Psi }_{n} = \frac{ \mathbb {E} (\hat{T}_{1})}{\mathbb {E} (\hat{T}_{0}) + \mathbb {E} (\hat{T}_{1})} \end{aligned}$$
(14)

where n is the channel index.

5.3 The proposed weighted sequential approach

5.3.1 Weighted CSS model

The weighted CSS approach incorporates prior knowledge about spectrum utilization (PU behavior statistics) into the CS problem. This is done by multiplying the elements of the wideband spectrum denoted here by \(X \in \mathbb {R}^{N}\) by a weights vector w to refine the search space of the CS recovery algorithm and help it to find the sparsest solution. It is wanted to give lower weights to the part of the spectrum where it is more likely to be occupied, and higher weights to the part where it is more sparse. The question is how to assign those weights.

Let a sparse signal x has a support denoted by \(x_{T}\) which contains the non-zero elements of the signal. If the support \(x_{T}\) is known or can be easily estimated, researchers proposed using the following weighted \(l_{1}\) minimization to solve the problem [37]

$$\begin{aligned} \begin{aligned} \min _{x} \quad \left\Vert {x}\right\Vert _{w1} = \min _{x} \quad \sum _{n=1}^{N} w_{n} x_{n} \hspace{0.2cm} \\ \text {with} \hspace{0.2cm} w_{n} = \left\{ \begin{array}{ll} 1 &{} \hspace{0.02cm} n \in x_{T}^{c} \\ w &{} \hspace{0.02cm} n \in x_{T} \end{array} \right. \end{aligned} \end{aligned}$$
(15)

where \(x_{T}^{c}\) is the support complement, and \(0 \le w \le 1\).

However, in a wideband radio spectrum the support which determines the active channels cannot be easily estimated or be known as prior information due to the highly dynamic change of PUs behavior. So, it was proposed to divide the spectrum frequency channels into two different groups according to their average level of sparsity, and each group is assigned different weights related to the inverse of the sparsity level as in [14]. But, dividing the channels into two groups is not enough to give accurate weights for each channel according to its unique sparsity level.

In our work, we used the weighted model proposed in [15] which was found to give more accurate weights related to each channel’s sparsity level. The weights in this model are assigned according to the duty cycle \(\Psi \) of the channel. In this paper, we will use the estimated duty cycles to assign those weights as

$$\begin{aligned} w_{n} = 1 - \hat{ \Psi }_{n} \end{aligned}$$
(16)

where \(\hat{\Psi }_{n}\) is the estimated duty cycle of the \(\textit{n}\)-th channel.

Note that in traditional BPDN the weights vector is assumed to be only ones by default as all the elements of x are treated equally in CS recovery. The weighted CSS recovery problem using BPDN to recover the spectrum then can be described as

$$\begin{aligned} \min _{x} \quad \left\Vert {y-\Phi x}\right\Vert _2^2 + \lambda \left\Vert {x}\right\Vert _{w1} \end{aligned}$$
(17)

5.3.2 Sequential CSS model

In traditional compressive spectrum sensing, the number of compressed measurements needed to accurately recover the spectrum should be in the order of \(C \hspace{0.25em} L_{max} \hspace{0.25em} log(N/L_{max})\) [30], where C is a constant that is chosen optimistically to ensure that enough measurements are acquired for proper spectrum recovery, and \(L_{max}\) is the maximum sparsity level (maximum number of active channels) that can be estimated by long-term monitoring of the spectrum through measurement campaigns.

However, this approach tends to require a large number of compressed measurements to ensure accurate recovery of the spectrum at the maximum sparsity level which is not always the case. This results in acquiring an excessively unnecessary number of measurements, which results in wasting the sampling effort of the sampler, and utilizing unneeded sensing time and consumed power by the hardware.

On the other hand, using a technique that acquires the compressive measurements sequentially while adapting the number of measurements to the actual sparsity level can significantly save the sampling effort, the required sensing time, and the power consumed by the hardware.

In sequential CSS, the sensing time \(\tau \) which is the time required by the hardware to acquire the compressed measurements, is divided into p time slots where \(p \in [1,P]\). The employed sensing time used by the CR should be smaller than the channel coherence time and the dynamic change in the PU behavior, so that the spectrum holes pointed out in the spectrum recovery decision can be used by the SU before the spectrum occupancy states change. This enables us to assume that the spectrum is block stationary during the sensing process, and the spectrum occupancy does not change during the sensing time. In each time slot, \(\Delta M\) measurements are taken to give a spectrum recovery denoted as \(\hat{X}\), and the sequential acquisition of measurements does not stop until a satisfactory recovery of the sparse spectrum is achieved.

This sequential approach does not require the CR to sense the spectrum for the whole sensing time, which enables the CR to obtain spectrum decisions faster and the remaining of sensing time can be utilized for transmission by the SU. The spectrum recovery error defined as \(e = \left\Vert {X - \hat{X}}\right\Vert _{2}\) cannot be used to stop measurement acquisition in practice as the actual spectrum X is unknown to the CR. Hence, the research field is still open to finding an appropriate stopping condition to be able to stop acquiring the measurements sequentially when an accurate spectrum recovery is achieved.

5.3.3 The proposed weighted sequential model

Here we describe the proposed algorithm to recover the spectrum using a weighted sequential approach as shown in Algorithm 1. The SU will acquire the compressive measurements sequentially followed by a spectral recovery in each time slot to obtain a spectrum sensing decision denoted as \(\hat{D}_{p}\), where p is the index of the time slot. At the end of each time slot a measurement vector \(y_{p}\) is acquired by concatenating the \(\Delta M\) measurements taken in each time slot where \(\Delta M = M_{p} - M_{p-1}\) and \(M_{1}< M_{2}< \dots < M_{P}\). This can be modeled mathematically as the following:

$$\begin{aligned} y_{p} = \Delta \Phi _{1} x_{1} + \Delta \Phi _{2} x_{2} + \dots + \Delta \Phi _{p} x_{p} \end{aligned}$$
(18)

and spectrum recovery \(\hat{X_{p}}\) is done in each time slot after signal recovery using weighted BPDN as the following:

$$\begin{aligned} \min _{x_{p}} \quad \left\Vert {y_{p}- \Delta \Phi _{p} x_{p}}\right\Vert _2^2 + \lambda \left\Vert {x_{p}}\right\Vert _{w1} \end{aligned}$$
(19)

where \(X_{p}\) is the Fourier transform of \(x_{p}\), then spectrum sensing decision is obtained by comparing the PSD level of each channel to a certain threshold \(\rho \) as the following:

$$\begin{aligned} \hat{D_{p}} = | \hat{X_{P}} | > \rho \end{aligned}$$
(20)

The weights vector w in Eq. (19) is assumed to equal ones at the beginning of the execution of the algorithm which is equivalent to using the traditional non-weighted BPDN algorithm. That is because we cannot incorporate the weights in the recovery algorithm until we reach some confidence level of the estimated weights. This issue will be discussed at the end of this section.

Algorithm 1
figure a

Weighted Sequential Compressive Spectrum Sensing With Coherence as Stopping Condition

Full size image

After that the coherence between each two consecutive spectrum decisions which are obtained using different number of measurements is calculated. If the coherence reaches 1, measurement acquisition stops and a final spectral recovery is declared. If not, measurements acquisition continues until a satisfactory spectral recovery is achieved. The coherence between consecutive spectral decisions is calculated as

$$\begin{aligned} Coh_{p} = \quad \frac{<\hat{D_{p}}, \hat{D}_{p-1} >}{\left\Vert {\hat{D_{p}}}\right\Vert _{2} \hspace{0.5em} \left\Vert {\hat{D}_{p-1}}\right\Vert _{2}} \end{aligned}$$
(21)

where \(<\varvec{\cdot }>\) denotes dot product. As the recovery algorithm is the main contributor to the computational complexity in CSS, Table 2 shows the computational complexity of the CS recovery algorithms used in our proposed approach compared to the work done in related work. Our approach proposes to reduce and adapt the acquired compressive measurements but at the cost of having a higher computational complexity compared to the other approaches. The advances made in the manufacturing of microprocessors with more computational power and even less power consumption can allow us to use higher computational complexity algorithms to guarantee the best accuracy for spectrum recovery.

Table 2 Comparison of computational complexity
Full size table

Now comes the question of when to incorporate the weights. Since the weights are based on the estimated duty cycles and duty cycles represent the average occupancy level of the channels, we need to wait until we have an accurate estimation. If duty cycles are incorporated as weights; while, the estimation error is high or not saturated, this will lead to faulty spectrum sensing decisions at the output of the recovery algorithm. To measure the accuracy of the estimated duty cycles we used the Root Mean Square Error (RMSE) and showed that when enough measurements are considered in the CS recovery, we can estimate the duty cycles accurately and that the estimation error saturates in [22]. However, in practical implementation, we cannot measure the RMSE to know when we can incorporate the weights in CS recovery as we do not know the real values of duty cycles. So we proposed to use the \(\ell _{2}\)-norm distance between each of two consecutive estimated weights vectors denoted as \(w_{d}\) to know when the estimated weights have converged and we have confident weights. This is valid if the spectral recovery is at a desired level of accuracy, so no estimation errors are to be assumed due to excessive miss-detection or false alarm which is what we assume in this paper.

Fig. 4
figure 4

RMSE of duty cycle estimation v.s. the weights distance \(w_{d}\)

Full size image

The weights distance \(w_{d}\) is shown against time instances in Fig. 4, and is calculated as:

$$\begin{aligned} w_{d}(J) = \left\Vert {w_{J} - w_{J-1}}\right\Vert _{2} \end{aligned}$$
(22)

where J is the time instance index.

Fig. 5
figure 5

A flowchart illustrating the steps of the proposed approach

Full size image

It can be seen in Fig. 4, that both RMSE of duty cycle estimation and \(w_{d}\) decrease with time as more activity periods are reconstructed resulting in a more accurate estimation of the periods’ expected values. So we can incorporate the weights in the recovery algorithm when the weights distance is below a certain threshold \(w_{d_{thr}}\). A flowchart of the proposed approach is shown in Fig. 5.

6 Results and discussion

In this section, we discuss the benefits of using our proposed weighted sequential compressive spectrum sensing approach on the measurements and the sensing time. In our simulation we considered an SU observing a wideband frequency spectrum of N equals 128 non-overlapping channels. The channels were divided into 7 groups, where each channel had a duty cycle \(\Psi _{n}\) where \(\Psi _{n} \in \{0.01, 0.05, 0.1, 0.3, 0.5, 0.7, 0.9\}\). The number of channels per group was selected to give an overall average duty cycle \(\bar{\Psi } = 0.1\) to represent a sparse spectrum.

In order to model the behavior of a PU in each channel, idle and busy periods were randomly drawn from the GP distribution, and the parameters were chosen as in Table 3 to reproduce the channels’ duty cycles by using Eqs. (7) and (9). The parameters were chosen to provide a PU behavior compared to what was done in [19], and to simulate a PU behavior similar to a real spectrum scenario with the parameters found in [7]. The received signal at the SU was assumed to have an SNR of 30 dB. The SU sensed the spectrum every \(T_{s}\) seconds to obtain the spectrum decision \(\hat{D}\), where \(T_{s}\) must be less than or equal to the minimum activity period to achieve an accurate estimation as shown in [22]. Here the minimum period which is equal to the location parameter \(\mu _{i}\) is 0.5 s, so \(T_{s}\) is also set to equal 0.5 s.

Table 3 GP parameters used in the simulation
Full size table

The binary spectrum decisions were then used to estimate the lengths of idle and busy periods of the PU in each channel. After that, the duty cycle was estimated to calculate the weights. In Algorithm 1, the total permitted number of measurements \(M_{P}\) was calculated as \(1.7 \times L_{max} \hspace{0.25em} log(N/L_{max} + 1)\) [24] to equal 75 for recovering the signal at \(L_{max}\) plus the additional \(\Delta M\) of 5 measurements for validation. The sensing time was divided into P = 16 time slots; while, \(\Delta M = M_{P}/P\) was to equal 5. You can freely choose the value of \(\Delta M\), but choosing a very low value can result in taking more time slots to achieve the appropriate number of measurements to recover the spectrum which means high computational processing due to the excessive spectrum recoveries, and choosing a larger value can result in faster time to decision (less time slots) but leads to use extra unwanted measurements. The weights distance threshold \(w_{d_{thr}}\) was set to 0.001 to ensure we have accurate weights.

Firstly, we investigate the effect of using the weighted sequential approach introduced in Algorithm 1 on the needed number of measurements to reconstruct the spectrum in two conditions. The first is when no weights are incorporated which we will call ‘Non-weighted Sequential BPDN’, and the second is after incorporation of the weights which we will call ‘Weighted Sequential BPDN’. Figure 6 shows that by using the proposed approach we can adapt the number of measurements needed to recover the spectrum with the actual number of active PUs (sparsity order) compared to the traditional technique which requires a fixed number of measurements for any sparsity order. We can see that when the weights are incorporated the proposed sequential approach significantly saves the CR from taking unnecessary additional measurements. As the measurements are an integer multiple of the time slots, similar results for the average time slots are to be expected.

Fig. 6
figure 6

Average number of compressed measurements against the number of active channels, at \(\Delta M = 5\)

Full size image

Secondly, in Fig. 7 we show the saving in the measurements and the sensing time using the proposed weighted sequential approach over the traditional BPDN approach. The saving percentage is calculated as \(Saving = \frac{M_{tr} - M_{pr}}{M_{tr}} \times 100 = \frac{Time slots_{tr} - Time slots_{pr}}{Time slots_{tr}} \times 100\), where \(M_{tr}\), and \(M_{pr}\) are the average number of measurements for each sparsity order in traditional BPDN and the proposed weighted sequential BPDN, respectively, and \(Time slots_{tr}\), and \(Time slots_{pr}\) are the average number of time slots for each sparsity order for BPDN and the proposed weighted sequential BPDN, respectively. Note that \(M_{tr}\) is always 75 measurements for all sparsity orders, and \(Time slots_{tr}\) is always 16 for all sparsity orders. It is obvious that the proposed weighted sequential BPDN reduces both the measurements and sensing time requirements for spectrum sensing which saves the CR resources. The difference between the two saving curves is due to the fact that traditional BPDN takes 75 measurements in 16 time slots; while, our system is designed to take up to 80 measurements in 16 time slots as an extra time slot is always needed to validate spectrum recovery before ceasing measurements acquisition.

Finally, we evaluate the performance of the proposed weighted sequential BPDN and traditional BPDN. We are interested in the ability to detect the presence of the PU, so in Fig. 8 we show the ROC curve for the two approaches averaged over 1000 time instances, where \(P_{d}\) is the probability of detection, and \(P_{f}\) is the probability of false alarm. We can see that both approaches have a very close performance in the case of \(\Delta M = 5\). Our approach can achieve a slightly better performance than the traditional approach at \(P_{f}\) of 0.1 with a \(P_{d}\) of approximately 100% which is compatible with spectrum sensing standards. It is commonly desired in spectrum sensing to have a probability of detection above or equal to 0.9 with a false alarm probability not exceeding 0.1 such as in the IEEE 802.22 [38].

Using our proposed weighted sequential approach can significantly reduce both the number of measurements and the sensing time needed for spectrum recovery, by adapting to the actual number of active channels in the sensed spectrum, while achieving a similar detection performance compared to the traditional approach. This enables sensing the spectrum efficiently and reduces the consumption of the CR resources especially the power consumed in sampling the spectrum repeatedly, and the memory required to store and process the acquired measurements. Also, the time required for the CR to sense the spectrum is reduced which enables faster detection of spectrum holes. For future work, we would consider using DL techniques to predict PU behavior. This would adapt the measurements directly to the spectrum utilization levels and significantly reduce the number of iterations in our approach.

Fig. 7
figure 7

Saving in the measurements and the sensing time achieved using weighted sequential BPDN over traditional BPDN

Full size image
Fig. 8
figure 8

ROC comparison of the traditional BPDN and the proposed weighted sequential BPDN, at SNR = 5 dB

Full size image

7 Conclusions

We proposed a weighted sequential compressive spectrum sensing algorithm in this paper. Our algorithm recovers the spectrum by adapting compressed measurements to dynamic changes in the number of active channels of the underutilized wideband spectrum. Furthermore, it can reduce the amount of time required for spectrum sensing, resulting in faster spectrum decisions and more time available for secondary user transmission. It also incorporates its estimated knowledge of the primary user’s presence to help further reduce measurements and sensing time. It can reduce CR resource consumption, such as the power consumed by the hardware to sample the wideband spectrum, which is critical for low-cost and battery-powered devices, as well as the memory requirement to store and process the measurements. It also reduces the required sensing time required to obtain a spectrum sensing decision resulting in faster utilization of spectrum holes. In noisy measurements, we demonstrated that our proposed algorithm could maintain the same ROC performance as traditional compressive sensing techniques.