1 Introduction

The development of cellular communication technology has entered the fifth generation (5G) which has specifications for high data rates (throughput), low latency, high connection users per square-km, high-capacity mobility, and low power consumption [1]. One of the key technologies that support the high-speed 5G network is the support from antenna capabilities that have multiple-input multiple-output (MIMO) specifications, large number of elements, beamforming capabilities, and wide bandwidth [2, 3].

MIMO capability supports 5G network performance because it can increase signal transmission paths which will improve signal-to-noise ratio (SNR) [4]. Thus, the MIMO antenna design is one of the basic requirements in the development of 5G antenna technology [5].

In the development of MIMO antennas for 5G applications, microstrip antennas are the most widely chosen because of their low profile, easy placement, and compact size. However, microstrip antennas are inseparable from various limitations, such as narrow bandwidth and low gain [6], especially for the development of MIMO antennas that have massive elements, the emergence of a high mutual coupling effect between adjacent elements [7]. The mutual coupling effect causes a decrease in the quality of the antenna parameters due to electromagnetic interference from two or more antennas that are too close together. The mutual coupling effect is kept to a minimum because it affects the performance of each MIMO antenna. This has become one of the main focuses and issues in the development of MIMO antennas, especially microstrip antennas which have a surface wave effect on the substrate.

The results of studies related to the development of massive MIMO antennas have been submitted previously in a few studies and antenna designs, but further studies are still needed to find better performance solutions and meet 5G technology specifications [7, 8]. A few techniques and analysis of 5G MIMO antenna design have been proposed previously, such as tapered-slot technique [9], dual-slant method [10], substrate integrated waveguide (SIW) technique [11], printed array clutched application [12], and studies about the defected ground structure (DGS) [13]. The results of this study have shown that the performance of the MIMO antenna is sufficient to meet the standard, but not yet in the application of a larger number of elements. Massive MIMO antenna design with many elements will certainly cause radiation interference between elements. For this reason, a solution is needed to increase the isolation between elements [14, 15]. Several studies to improve the isolation of massive MIMO antennas have been proposed previously, such as the development of a dielectric resonator antenna (DRA) [16,17,18,19,20,21], using a frequency selective surface wall [22, 23], using parasitic elements [24], using an antenna filtering method [25], and adding stacked patch antenna design [7]. Besides, it is also proposed a combination of dielectric resonator design with shielded metasurface [26], fractal design techniques to increase radiation efficiency [27,28,29,30], and decoupling technique to improve isolation between elements to improve antenna performance [31,32,33,34,35].

The results of these studies show that performance is in accordance with the standard, but still needs to be improved to achieve better performance, such as lower ECC parameters for many elements and higher gain. Thus, the 5G MIMO antenna that is designed can support greater data transmission capabilities. For this reason, this study will be further investigated through a combination of several existing techniques such as decoupling and dielectric resonator techniques by adding electromagnetic bandgap (EBG) and DGS approaches. This effort is expected to be able to further suppress the mutual coupling effect between MIMO antenna elements, which has an impact on lower ECC parameter performance and significantly increased antenna gain.

The presentation of this paper consists of the background and problems in the first section, then an explanation of the research method in the second section, continued with the proposed design in the third section, the results and discussion in the fourth section, and conclusions and recommendations in the fifth section as a closing.

2 Method and experiment

The flow of the implementation of this study begins with studying the design methods of DRA, EBG, and DGS on the development of massive MIMO antennas. Furthermore, the CST microwave studio software simulation was carried out to obtain the results and performance of the combination of the three methods of changing the structure of the microstrip antenna. The simulation is continued repeatedly with various optimizations if the results have not reached the desired performance. After obtaining improved results, fabrication and measurements are carried out to ensure the results meet the expected performance. This flow is as shown in Fig. 1.

Fig. 1
figure 1

Design method of massive MIMO DRA-EBG-DGS

Full size image

3 Proposed design

To determine the effect of the use of DRA-EBG-DGS on the performance of the massive MIMO antenna, this study was conducted by comparing several parameters of the massive MIMO antenna without the use of DRA-EBG-DGS with the performance of the use of DRA-EBG-DGS on the 8 × 8 massive MIMO antenna.

3.1 8 × 8 MIMO design without DRA-EBG-DGS

MIMO antenna design begins with a single patch antenna following the general equation in designing a microstrip antenna using a transmission line approach [36] with an equation approach:

$$W_{p} = \frac{c}{{2f_{r} \sqrt {\frac{{\varepsilon_{r} + 1}}{2}} }}$$
(1)
$$\varepsilon_{{{\text{eff}}}} = \frac{{\varepsilon_{r} + 1}}{2} + \frac{{\varepsilon_{r} - 1}}{2}\left( {\frac{1}{{\sqrt {1 + 12\frac{h}{{W_{p} }}} }}} \right)$$
(2)
$$L_{{{\text{eff}}}} = \frac{c}{{2f_{r} \sqrt {\varepsilon_{{{\text{eff}}}} } }}$$
(3)
$$\Delta L = 0.412h\frac{{\left( {\varepsilon_{{{\text{eff}}}} + 0.3} \right)\left( {\frac{{W_{p} }}{h} + 0.264} \right)}}{{\left( {\varepsilon_{{{\text{eff}}}} - 0.258} \right)\left( {\frac{{W_{p} }}{h} + 0.8} \right)}}$$
(4)
$$L_{p} = L_{{{\text{eff}}}} - 2\Delta L$$
(5)
$${W}_{g}=6h+{W}_{p}$$
(6)
$${L}_{g}=6h+{L}_{p}$$
(7)

\({L}_{p}\) is the length of patch antenna element, \({W}_{p}\) is the width of patch antenna element, and h is the height of patch antenna element. \({W}_{g}\) is the width of the ground plane, \({\varepsilon }_{r}\) is the permittivity relative, and \({L}_{g}\) is the length of the ground plane. In this study, the substrate material is Epoxy FR-4 with \({\varepsilon }_{r}\) = 4.3 and the antenna frequency is 3.5 GHz as one of the 5G C-band frequency bands under 6 GHz. Dimensions of the design results are shown in Table 1.

Table 1 Dimension of patch antenna
Full size table

Then proceed with designing an 8 × 8 array configuration with 8 elements in the \(x\)-axis direction and 8 elements in the \(y\)-axis direction with a distance between elements λ/2. The design results are as in Fig. 2.

Fig. 2
figure 2

Design of 8 × 8 massive MIMO antenna without DRA-EBG-DGS

Full size image

3.2 8 × 8 MIMO design using DRA-EBG-DGS

The proposed design using this DRA-EBG-DGS combination is to place a dielectric resonator on the patch antenna and add an EBG structure between the MIMO antenna elements. Then do the arrangement of the DGS structure on the ground plane structure. The design stage using a dielectric resonator begins with the calculation of the diameter and height. The dimensional design approach follows equation [37]:

$$F_{r} = \frac{c}{{2\pi r \sqrt {\varepsilon_{{{\text{DRA}}}} } }}\left[ {1.71 t \frac{r}{h} + 0,1578 \left( {\frac{{r^{2} }}{h}} \right) } \right]$$
(8)

where \(c\) is the speed of light, \(r\) is radius, \(h\) is the height, \(t\) is the width of the microstrip, and \({\epsilon }_{DRA}\) is coefficient which value 9.9% for alumina ceramic material. The calculation and design results are shown in Table 2 and Fig. 3.

Table 2 Dimension of DRA
Full size table
Fig. 3
figure 3

Design of DRA

Full size image

Furthermore, for the EBG design approach using the mushroom form using the following equation approach [38]:

$$L= {\mu }_{0}h$$
(9)
$$C= \frac{W {\varepsilon }_{0} (1+{\varepsilon }_{0})}{\pi }\mathrm{cos}h \frac{(2W+g)}{g}$$
(10)

\(h\) is the substrate thickness, \({\mu }_{0}\) is the permeability of free space, \(W\) is the EBG patch width, \({\varepsilon }_{0}\) is the permittivity of free space, and \(g\) is the gap between two EBG cell. The results of the design and optimization are shown in Table 3 and Fig. 4.

Table 3 Dimension of EBG
Full size table
Fig. 4
figure 4

Design of EBG

Full size image

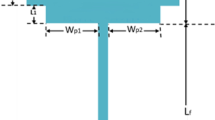
Furthermore, DGS is designed using a microstrip line approach [39] by optimizing the length, width, and distance between the microstrip lines. The results of the DGS design are shown in Table 4 and Fig. 5.

Table 4 Dimension of DGS
Full size table
Fig. 5
figure 5

Design of DGS

Full size image

Thus, the use of DRA-EBG-DGS can be developed in the 8 × 8 massive MIMO antenna configuration as shown in Fig. 6.

Fig. 6
figure 6

Design of 8 × 8 massive MIMO antenna using DRA-EBG-DGS

Full size image

4 Result and discussion

The simulation results in this study use CST Microwave Studio simulation software to obtain results and comparisons of massive MIMO antennas using DRA-EBG-DGS with conventional massive MIMO antennas without using DRA-EBG-DGS. The comparison of S-parameters can be seen in Fig. 7.

Fig. 7
figure 7

Simulation result of S-parameter

Full size image

These results indicate that the effect of using DRA-EBG-DGS can widen the bandwidth of the massive MIMO 8 × 8 antenna to 246 MHz. This result is quite significant without using DRA-EBG-DGS which only has a bandwidth of 145.4 MHz.

The next simulation is a two-dimensional (2D) radiation pattern. The simulation results of this radiation pattern are shown in Fig. 8. We used the beam direction from \(-\)60° to 60°. These results indicate that the massive MIMO design using DRA-EBG-DGS can increase the gain to 24.7 dB compared to 19.5 dB without using DRA-EBG-DGS. This result is significant and proves that this proposed design can increase the antenna gain to a higher level.

Fig. 8
figure 8

Simulation result of 2D radiation pattern

Full size image

The next simulation result is a comparison of the 360° polar radiation pattern from the CST simulation software. These results confirm the direction of the massive MIMO 8 × 8 antenna radiation beam in all directions and show the resulting beamwidth. The simulation results of the 360° radiation pattern are shown in Fig. 9.

Fig. 9
figure 9

Simulation result of 360° radiation pattern

Full size image

These results show a comparison of the 360° radiation pattern of the massive MIMO 8 × 8 antenna using DRA-EBG-DGS and without using DRA-EBG-DGS, where there is an increase in the beamwidth of the massive MIMO antenna using DRA-EBG-DGS to be 8.4° wider than without. DRA-EBG-DGS is only 5.4° (Fig. 9).

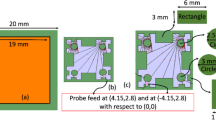
Furthermore, to verify the simulation results, we fabricated a massive MIMO antenna using DRA-EBG-DGS. For the fabrication sample, we only do a comparison using a 4 × 4 MIMO configuration which is assumed to be representative for a larger number of arrays as show in Fig. 10.

Fig. 10
figure 10

Fabrication antenna massive MIMO 4 × 4

Full size image

Figure 11 shows the comparison of the S-parameter massive MIMO antenna 4 × 4 simulation results and measurements. These results show that there is no significant difference between the simulation results and measurements. The difference is only due to the measurement installation factor which has an additional loss so that the measurement results slightly decrease.

Fig. 11
figure 11

Comparison of S-parameter 4 × 4 massive MIMO antenna

Full size image

Figure 12 shows a comparison of the 2D radiation pattern between the simulation results and measurements of the 4 × 4 massive MIMO antenna. Similar to the results of the S-parameter comparison, the comparison of simulation results and measurements of 2D radiation patterns also does not show a significant difference, the difference is only due to not ideal measurement conditions, and there are several loss factors for antenna measurement installations.

Fig. 12
figure 12

Comparison of 2D radiation pattern 4 × 4 massive MIMO antenna

Full size image

As the result in this study, we observe the effect of using DRA-EBG-DGS on the performance of the ECC parameter which is the benchmark for MIMO antenna performance. The simulation results of the comparison of the effect of using DRA-EBG-DGS on ECC parameters are shown in Table 5.

Table 5 Comparison of ECC parameter
Full size table

Table 5 shows that the use of DRA-EBG-DGS in the massive MIMO antenna design can suppress the mutual coupling effect and improve the ECC parameters. The results show a significant improvement in the ECC parameter so that it can prove that the DRA-EBG-DGS design is effective in the design of the massive MIMO antenna.

5 Conclusions

Massive MIMO antenna design using the DRA-EBG-DRS combination for 5G C-band applications has been described. The simulation and measurement results show a significant improvement in the performance of the massive antenna when using the DRA-EBG-DGS combination. The results of this study show an improvement in the value of the antenna bandwidth and an increase in antenna gain and slightly widen the antenna beamwidth. The most important result is the improvement of the ECC parameter which is an important indicator of the performance of a massive MIMO antenna which has many elements, where a lower ECC parameter will support the overall network performance.

The results of this study are a basic proposal that can be the foundation for the development of a massive MIMO antenna design for 5G applications. In the future, it can be continued by studying further the DRA structure and its effect on the performance of the massive MIMO antenna with various other structural components.