Abstract
In this paper, we present a game-theoretic approach for the purpose of deriving the problem of joint beamforming and power control in cognitive radio (CR) multiple-input multiple-output (MIMO) broadcast channels (CR MIMO-BCs), where the primary users (PUs) coexist with the secondary users (SUs) and they share the same spectrum. The cognitive base station (CBS), which is equipped with multiple antennas, is capable of transmitting data to the SU’s multiple-antenna receiver by employing the technology of beamforming. The proposed approach is an application of separable games, which are formally stated by the subgames of beamforming and power control. Furthermore, based on the model of noncooperative separate games, separable cost functions for the parameters of beamforming and power control are also proposed, showing that these cost functions are convex. Therefore, the convex theory of a noncooperative game can be employed to investigate the best response strategies as well as existence of Nash equilibrium solutions. Finally, we propose an iterative algorithm to achieve the optimal Nash equilibrium of the proposed joint beamforming subgame and power control subgame. Numerical results verify both the convergence and the tracking properties of the proposed algorithm for variant scenarios.
Similar content being viewed by others
1 Introduction
The radio spectrum available for wireless communication is extremely scarce due to the widely deployed wireless devices and services. On the other hand, recent studies and measurements have shown that most of the allocated bands are used inefficiently or underutilized [1–3]. In order to address the aforementioned challenges, a cognitive radio (CR) technology has recently been proposed for the purpose of dramatically improving spectrum utilization and supporting more new services [4]. In cognitive radio networks (CRNs), the licensed spectrum can be shared with secondary users (SUs), provided that they do not cause harmful interference to primary users (PUs). In order to support this spectrum reuse functionality, SUs are permitted to transmit once they detect a spectrum hole [5, 6]. Such schemes usually work when the spectrum is severely underutilized, or otherwise, SUs might not have sufficient opportunities to get channel access. Once PUs are found to be active, SUs must vacate the channels. Therefore, the secondary throughput would be significantly constrained, and the secondary system would suffer from a long latency.
As a spectral-efficient technology, multiple-input multiple-output (MIMO) is capable of providing extra spatial dimensions for signal transmission. MIMO technology can be employed by CRNs for the purpose of reducing interference at the PU and satisfying the demand of high data rate at the SU through carefully designing transmit/receive beamforming [7, 8]. As a result, SUs may access the licensed spectrum without causing harmful interference at the PUs, even if the PUs are also using the same spectrum at the same time. However, an additional spatial resource inherent in MIMO systems becomes a challenging task in the design of efficient spectrum-sharing, although this technology offers several advantages to enhance the system performances. Furthermore, CR spectrum-sharing imposes several new challenging issues on MIMO systems [9]. First, the idea of spectrum-sharing allows simultaneous transmissions of PUs and SUs, provided that the quality of service (QoS) of PUs is guaranteed. Secondly, the primary systems cannot deliberately provide their channel estimation to the secondary systems [10]. The aforementioned challenges may impose difficulty on pre-interference cancelation at the SU’s transmitter side.
CR MIMO broadcast channels (CR MIMO-BCs) have become a topic of increasing research interest for CRNs in recent years [11–13], with secondary systems coexisting with the primary systems. Unlike conventional MIMO-BCs, in CR MIMO-BCs, there exist interference between the PU link and the SU link as well as the multiple SUs’ interference. Furthermore, in order to protect the primary transmission, the total-power constraint and the individual-interference-power constraint for each primary receiver are considered. Since beamforming and power control techniques play an important role in interference suppression and power constraint in CR MIMO-BCs, a joint beamforming and power control scheme over CR MIMO-BCs was proposed to minimize the transmit power while satisfying signal-to-interference-plus-noise ratio (SINR) targets for the SUs and maintaining an acceptable interference level to the PUs [14]. The development of the scheme relies crucially on the BC multiple-access channel (BC-MAC) duality result [15, 16], which is only valid for the problem with a single-sum-power constraint. In [17], the problem of joint transmit beamforming and power control was considered in CR MIMO-BCs, with the cognitive multi-antenna base station (BS) being assumed to satisfy the QoS constraints of the served SUs while protecting one primary receiver from interference. It is also assumed that the number of single-antenna users is less than that deployed at the BS. Consequently, SUs may access the primary spectrum without causing harmful interference to the PUs.
For the case of non-zero-interference-power constraint in CR MIMO-BCs, both the SUs’ SNR constraints and the PUs’ interference power constraints usually result in quadratically constrained quadratic programming problems, which may not be directly solved by convex tools, especially when there is a rank constraint. Semidefinite programming (SDP) relaxation can be used to convert the aforementioned problem into a convex optimization problem by dropping the rank constraint, consequently generating a local optimum [18]. It is shown in [19] that under certain conditions, a new solution can be generated from the one obtained by SDP relaxation without ruining the constraints or changing the objection function. Actually, most of the resulting problems of joint beamforming and power control are inherently non-convex, and consequently, no global optimality of an efficient solution can be guaranteed theoretically [20]. Nonetheless, in [20], sufficient conditions were presented to constrain some design parameters, making the joint beamforming and power control problem become convex. Furthermore, in [21], a semi-distributed algorithm was proposed to obtain a local optimal solution to this problem. However, in general scenarios, the obtained local optimum may not be feasible for the original problem because its rank usually does not meet the solution’s requirement. As a result, approximation approaches may be used to generate a feasible solution [22–26].
In this paper, we model the problem of joint power control and beamforming in CR MIMO-BCs as a noncooperative game. Note that the noncooperative game theory for economists has been extensively investigated in terms of how rational players do not cooperate and interact in order to reach their goals. Lately, noncooperative game theory has also been widely applied to communications system. For example, in [27], joint Code Division Multiple Access (CDMA) codeword and power adaptation was formulated as a separable game in MIMO CR networks, with two corresponding subgames, i.e., the power control subgame and the codeword control subgame, being played. Furthermore, we also formulate separable games1 to solve the problem of joint power control and beamforming. Based on the proposed noncooperative separate game model, separable cost functions for beamforming and power control parameters are also derived, showing that these cost functions are convex. Furthermore, we use the convex theory of the noncooperative game to investigate the best response strategies as well as existence of the Nash equilibrium solutions. The best response strategies of users are then obtained by constrained minimization of the user cost function subject to constraints on user SINR and beamforming vector. The corresponding algorithm is derived using a game-theoretic approach in which separable cost functions with respect to beamforming and power are defined, such that joint beamforming and power adaptation is formulated as a separable game.
The rest of this paper is organized as follows: In Section 2, we describe the system model and problem statement. In Section 3, we present joint beamforming and power control as a noncooperative game. Section 4 provides numerical simulation results and discussions. Finally, conclusions are drawn in Section 5.
Notations: Scalar is denoted by a lowercase letter. Vector and matrix are denoted by a boldface lowercase letter and a boldface uppercase letter, respectively. I p denotes the p×p identity matrix. ∥·∥ represents the Euclidean norm of a vector. sgn[·] denotes sign function. For a matrix S, tr(S), rank(S), S H, and S T denote its trace, rank, Hermitian matrix, and transpose matrix, respectively. diag(s 1,s 2,⋯,s n ) denotes a diagonal matrix with diagonal elements given by s 1,s 2,⋯,s n . For a matrix S, S≥0 denotes the S is positively semidefined. {·} denotes the subset.
2 System model and problem statement
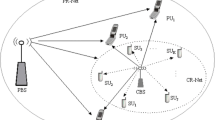
In this paper, we present an alternative approach to dealing with a variable number of active users and/or QoS requirements in a CDMA system. More specifically, we consider the system model of CR MIMO-BCs, as shown in Fig. 1, where the cognitive base station (CBS) and K SUs share the spectrum with N PUs, with the N t -antenna CBS sending independent information signals to K-different SUs. Without loss of generality, each SU is assumed to have N r (N r ≤N t ) antennas. Without loss of generality, both the primary base station (PBS) and PUs are assumed to be equipped with a single antenna. We assume that there is only one PU (N=1) and that it is enough to demonstrate the key aspects of spectrum-sharing while avoiding unnecessary complications [28, 29], while it is pertinent to investigate the general scenario where multiple PU and SU links coexist [30].
In CR MIMO-BCs, due to the coupled structure of the transmitted signals, the BC optimization problems are usually non-convex and thus cannot be solved directly. To tackle this difficulty, the non-convex BC problem is transformed into a convex MAC problem via a so-called BC-MAC duality relationship [31]. Under a single sum-power constraint or a set of a linear power constraint, the problem of BC can be solved as a minimax optimization problem in its dual MAC setting [32]. The block diagram of BC-MAC duality relationship for the transmission process is shown in Fig. 2.
The signal \({\mathbf {x}}\!\in \!{\mathbb {C}}^{M \!\times \!1}\) transmitted by the CBS is given by [33]
where s=[s 1,s 2,⋯s K ]T, with s k denoting the data stream for the kth SU (SUk) and satisfying E[|s k |2]=1, \({\mathbf {P}} = \text {diag}\{ \sqrt {{p_{1}}},\sqrt {{p_{2}}}, \cdots \sqrt {{p_{K}}} \}\), with p k denoting the transmitted power allocated to SUk, \({\mathbf {U}} = [{{\mathbf {u}}_{1}},{{\mathbf {u}}_{2}}, \cdots {{\mathbf {u}}_{K}}]\in {\mathbb {C}}^{N_{t} \times K}\) is the downlink beamformer matrix, with u k standing for the beamformer vector of the SUk with ∥u k ∥2=1. Furthermore, we assume that a perfect CSI of primary and secondary links is available at the CBS. The received signal \({{\mathbf {r}}_{k}}\in {\mathbb {C}}^{N_{r} \times 1}\) at the SUk is given by
where \({\mathbf {H_{k}}}\in {\mathbb {C}}^{N_{r} \times N_{t}}\) denotes the channel between the CBS and SUk. The vector \({\mathbf {n_{k}}}\in {\mathbb {C}}^{N_{r} \times 1}\) is the additive white Gaussian noise (AWGN), where n k ∼CN(0,σ 2 I). Parameters p p and s 0 denote the PBS transmission power and transmission data stream, respectively. Letting g k represent the channel power gain vector from PBS to the SUk, the right-hand side of (2) can be decomposed into three terms: the first term is the desired signal from CBS to the SUk, whereas the second and third terms denote the interference plus noise from the PBS and noise, respectively. Similarly, the receive signal at the PU from PBS to PU can be written as
where h p denotes the channel power gain vector from the CBS to the PU and n p is an AWGN item.
In (2), the covariance matrix Z k of the interference plus noise is given by
where \({{\mathbf {z}}_{k}} = {{\mathbf {H}}_{k}}\left ({\sum \limits _{l = 1,l \ne k}^{K} {{s_{l}}\sqrt {{p_{l}}} {{\mathbf {u}}_{l}}}} \right) + {s_{0}}\sqrt {{p_{p}}} {{\mathbf {g}}_{k}} + {{\mathbf {n}}_{k}}\). Since the combined interference and noise is not white anymore (its covariance is shown in (4)), the optimal maximum likelihood (ML) detector is equivalent to whitening the received signal, followed by applying the ML detector designed for white noise [33, 34]. We can thus whiten the received signal at the SUk by multiplying \({\mathbf {z}}_{k}^{- {1/2}}\) with r k :
where \({\tilde {\mathbf {H}}_{k}}\) and \({\tilde {\mathbf {z}}_{k}}\) are a transformed MIMO channel matrix and Gaussian white noise after the whitening transformation, respectively. Note that the noise-whitening filter should satisfy the condition of \(E\left [ {{{\tilde {\mathbf {z}}}_{k}}\tilde {\mathbf {z}}_{k}^{T}} \right ] = E\left [ {{\mathbf {Z}}_{_{k}}^{- {1/2}}{{\mathbf {z}}_{k}} \cdot {{\left ({{\mathbf {Z}}_{_{k}}^{- {1/2}}{{\mathbf {z}}_{k}}} \right)}^{T}}} \right ] = {{\mathbf {I}}_{{N_{r}}}}\). The singular value decomposition (SVD) [35] of \({\tilde {\mathbf {H}}_{k}}\) is defined as
where \({{\mathbf {\Lambda }}_{k}}\in {\mathbb {C}}^{N_{r} \times N_{t}}\) is a real-valued diagonal matrix and can be partitioned into
Furthermore, \({\rho _{k}} = \text {rank}\left ({{{\tilde {\mathbf {H}}}_{k}}} \right)\) denotes the rank of the SUk-transformed MIMO channel matrix, which is equivalent to the number of non-zero singular values and satisfies ρ k ≤ min(N t ,N r ). Substituting (7) into (5), we can obtain
Taking the partitions in (7) into account, the last (N r − ρ k ) zero components in the received signal \({\bar {\mathbf {r}}_{k}}\) can be ignored. Furthermore, the last (N t −ρ k ) components of the transformed beamforming vector are also set to zero for the purpose of avoiding wasting transmit power on those dimensions of zero singular values.
Thus, we focus only on those dimensions corresponding to strictly positive singular values of \({\tilde {\mathbf {H}}_{k}}\). To reduce dimensionality to the rank of \({\tilde {\mathbf {H}}_{k}}\), we take the first ρ k elements in \({\bar {\mathbf {r}}_{k}}\) and obtain
where \({\hat {\mathbf {u}}_{k}} = \left [\! \mathbf {I}_{\rho _{k}}\!\mathbf {0}_{\rho _{k} \!\times \! \left (N_{t} - \rho _{k} \right)} \right ]{\bar {\mathbf {u}}_{k}}\) and \({\hat {\mathbf {z}}_{k}} = \left [ {{\mathbf {I}}_{{\rho _{k}}}}{\mathbf {0}}_{{\rho _{k}} \times \left ({{N_{r}} - {\rho _{k}}} \right)} \right ]{\bar {\mathbf {z}}_{k}}\). We can invert the channel in (9) to obtain the equivalent expression [36]
The received signal \({\hat {\mathbf {r}}_{k,\text {inv}}}\) by matching the filtering is then given by
where the right-hand side of (11) comprises two terms: the first term is the desired signal and the second term denotes interference plus noise. The SINR at SUk can be derived as
where \({i_{k}} = \hat {\mathbf {u}}_{k}^{T}\hat {\mathbf {\Lambda }}_{k}^{- 2}{\hat {\mathbf {u}}_{k}}\) is the interference function that depends explicitly on the SUk beamformer \({\hat {\mathbf {u}}_{k}}\) as well as all the other users’ beamformer \({\hat {\mathbf {u}}_{l}}\) and power p l , ∀l≠k, but does not depend on SUk power.
In this setup, individual SUs may adjust their beamforming vector and powers in order to meet a set of specified target SINRs \(\{ \gamma _{1}^{*},\gamma _{2}^{*}, \cdots,\gamma _{K}^{*}\}\) with minimum transmitted power. The target SINRs must be admissible and satisfy [37, 38]
where N t is the CBS antenna numbers and denotes the signal space of dimension.
Game theory provides a powerful framework for analyzing the problem of competitive utility maximization in wireless communication systems and could indicate whether a stable point, i.e., NE point, exists. A noncooperative game is2 formally defined by using the set of players, the sets of strategies (or actions) that each player may take, and the individual player utility or cost functions.
In general, cost functions for a wireless system depend on the transmission power as well as QoS desired by a given user in the system. In CR MIMO-BCs, due to interference from other SUs and PU, the SU’s transmission power needs to pay off a higher price for the purpose of achieving the abovementioned goal. On the other hand, the SU’s transmission at optimal power will minimize the amount of interference. Therefore, the cost function of the SUk can be defined as
where λ is the pricing factor. Note that a higher λ implies that the SUs will pay off a higher price. Due to the condition of \({{\mathbf {u}}_{k}} \,=\, {{\mathbf {V}}_{k}}{\bar {\mathbf {u}}_{k}}\! =\! {{\mathbf {V}}_{k}}{\left [\! {{{\hat {\mathbf {u}}}_{k}}{{\mathbf {0}}_{\left (\! {{N_{t}}\! -\! {\rho _{k}}}\! \right) \times 1}}} \!\right ]^{T}} \,=\, \left [ {{{\hat {\mathbf {V}}}_{{N_{t}} \times {\rho _{k}}}}\!{{\mathbf {V}}_{{N_{t}} \times \left ({{N_{t}} - {\rho _{k}}} \right)}}} \right ]{\left [ {{{\hat {\mathbf {u}}}_{k}}{{\mathbf {0}}_{\left ({{N_{t}} - {\rho _{k}}} \right) \times 1}}} \right ]^{T}} = {\hat {\mathbf {V}}_{{N_{t}} \times {\rho _{k}}}}{\hat {\mathbf {u}}_{k}}\), the cost function of the SUk in (14) can be rewritten as
where \({{\mathbf {S}}_{k}} = \hat {\mathbf {\Lambda }}_{k}^{- 2} + \lambda \cdot {\hat {\mathbf {V}}^{T}}{{\mathbf {h}}_{p}}{\mathbf {h}}_{p}^{T}\hat {\mathbf {V}}\) is the correlation matrix of the interference plus noise.
3 Joint beamforming and power control as a noncooperative separable game
According to the separable game definition [39, ch. 11], the cost function in (15) is separable with respect to the parameters beamforming and power control, leading to a separable game with two separate subgames: beamforming subgame and power control subgame.
3.1 Noncooperative beamforming subgame
In the proposed noncooperative game, the SUs’ power are fixed and individual SUs are capable of adjusting their beamforming in their corresponding strategy spaces to minimize their corresponding cost function. The noncooperative beamforming subgame (NPBS) can be modeled as
where the components of NBPS are given as follows.
-
1.
Players SUk: k∈Ω={1,2,⋯,K}.
-
2.
Action spaces: \(\left \{ {{\overset {\frown }{\mathbf {u}}_{k}}} \right \}\) is the set of beamforming strategies for SUk.
-
3.
Cost functions: {J k (·)} is the cost function that maps the SUk beamforming spaces for fixed power control.
The cost function of NPBS is defined as
Here, our aim is to investigate the existence of a Nash equilibrium for NPBS as well as identify the best response strategies for SUs. Before establishing the uniqueness of the Nash equilibrium for NPBS, we state the following formal definitions [40, 41]:
Definition 1 (Nash equilibrium of NPBS): The beamforming matrix \(\overset {\frown }{\mathbf {U}} = [{\overset {\frown }{\mathbf {u}}_{1}},{\overset {\frown }{\mathbf {u}}_{2}}, \cdots {\overset {\frown }{\mathbf {u}}_{K}}]\) is a Nash equilibrium of NPBS if, for every SUk, we have
Definition 2 (Best response for NPBS): The best response strategy of SUk beamforming to the other SUs is the set
Definition 3 (Convex game): If the best response function of SUk is a standard function, then NE in this game will be unique. The corresponding game is convex for non-empty, closed, and bounded convex set \(\{ {\overset {\frown }{\mathbf {u}}_{k}}\}\), if the cost function of each SUk is in \({\overset {\frown }{\mathbf {u}}_{k}}\) for every fixed \({\overset {\frown }{\mathbf {u}}_{l}}\), where l≠k.
For a fixed SU’s power, the cost function in (17) is a quadratic form in the beamforming vector \({\overset {\frown }{\mathbf {u}}_{k}}\). Taking the second-order derivative of the cost function with respect to \({\overset {\frown }{\mathbf {u}}_{k}}\), we get
where S k is a positive definite matrix. Evidently, the cost function of NPBS is also convex. According to the results proved in Theorem 1 in [42], for concave games, we can extend in a straightforward way to prove the existence of a Nash equilibrium point for convex games [38]. As a consequence, we establish the existence of the equilibrium point for NPBS. In order to solve the best response of the NPBS Nash equilibrium, we defined the SUk Lagrangian function as
where α k is the Lagrange multipliers. Taking the first-order derivative with respect to the beamformer \({\overset {\frown }{\mathbf {u}}_{k}}\), it leads to the eigenvector equation
Let (22) equal to zero, the best response function of the NPBS Nash equilibrium is given by
where the best response strategy of NPBS is the eigenvector \({\overset {\frown }{\mathbf {\nu }}_{k}}\), corresponding to the minimum eigenvalue of S k . Thus, at the Nash equilibrium, all SUs beamforming will be the minimum eigenvectors of S k . In order to investigate whether the minimum eigenvector strategy is optimal for the SUk cost function or not, we use the Taylor series to expand the Lagrangian function around the point which satisfies the necessary Karush-Kuhn-Tucker (KKT) conditions [38, 43]. In this expansion, the term containing the first derivative is equal to zero, provided that the higher order terms are neglected. Therefore, we only prove that the second-order term of (21) in the Taylor expansion is positive and satisfies the KKT conditions. The second derivative of (21) is given by
which is positive and satisfies the KKT conditions [32, 34]. Hence, the Nash equilibrium point with respect to the constrained minimization of the SUk cost function is optimum.
3.2 Noncooperative power control subgame
In the proposed noncooperative game, the SUs’ beamforming vectors are assumed to be fixed, and individual SUs adjust their power in their corresponding strategy spaces for the purpose of minimizing their corresponding cost function. The noncooperative beamforming subgame (NPCS) can be modelled as
where the components of the NPCS are given in the list as follows.
-
1.
Players SUk: l∈Ω={1,2,⋯,K}.
-
2.
Action spaces: {p k } is the set of power control strategies for SUk.
-
3.
Cost functions: {J k (·)} is the cost function that maps the SUk power control spaces for fixed beamforming vectors.
The cost functions of NPCS is defined as
where \(\gamma _{k}^{*}\) is the SUk target SINR. In order to investigate the existence of a Nash equilibrium for NPCS and identify the best response strategies for SUs, we can define the SUk Lagrangian function as
where β k is a Lagrange multiplier. Taking the first-order derivative with respect to the multiplier β k , we obtain
which is a necessary condition for the constrained optimization problem (26), indicating that the SUk-transmitted power should match its target SINR by giving the interference function i k , i.e.,
where the best response function of NPCS is obtained from (29), and then \(\gamma _{k}^{*} \cdot {i_{k}}\) is the Nash equilibrium point. Similar to (24), we can use the Taylor series to expand the Lagrangian function around the Nash equilibrium point as [34]
In this case, the cost function of NPCS is a convex function, which is linear in p k . Thus, following [44], there exists a Nash equilibrium. This is also optimal corresponding to the best response strategy, which is capable of updating power to match the target SINR.
3.3 Iterative algorithm
In this section, our proposed algorithm employs incremental updates for beamforming vectors and transmitted powers, which are designed to reduce interference at downlink receivers subject to specified SINR and beamforming constraints. We firstly model the joint beamforming and power control subgame (JBPS) as
To find a Nash equilibrium for JBPS, we must consider the two subgames (NPBS and NPCS) to assure their corresponding best response strategies. However, direct application of the best response strategies is not guaranteed to converge to the optimal Nash equilibrium, although multiple Nash equilibrium points for the JBPS are possible to be achieved. Moreover, these best response strategies may cause large-angle deviation during updating of beamforming vectors and/or abrupt power control changes to meet the target SINRs. It is thus not desirable for a practical system, because it may increase error probability at the receiver or even lead to connection loss from the transmitter to the receiver. From a practical perspective, a more desirable approach can be employed to vary the SUs’ beamforming and power control in small increments.
In order to avoid the minimum eigenvector being far away in signal space from the current beamforming vector, we use an incremental update that adapts the user beamforming vector in the direction of the minimum eigenvector. Hence, the beamforming vectors update of SUk at step n of the algorithm can be given by
where β (called beamforming pricing factor) is a constant and \(m = {\mathop {\text {sgn}}} [\hat {\mathbf {u}}_{k}^{T}\left (n \right){{\boldsymbol {\nu }}_{k}}(n)]\).
From (29), the transmitted power corresponding to user k should match its target SINR. After the beamforming update in (32), the power value matching the desired target SINR is given by
In order to avoid abrupt variations, the power control updates of SUk at step n of the algorithm using a gradient-based approach and the corresponding power control algorithm in small increments are given by
where μ (0<μ<1) (called power pricing factor) is a constant. The joint beamforming and power control update algorithm is given in Table 1.
4 Numerical results and simulations
In this section, numerical simulation results are provided to validate the proposed theoretical analysis and examine the performance of our proposed algorithms for various scenarios simultaneously. In CR MIMO-BCs, the channels are subject to Rayleigh fading with zero mean and unity variance. Furthermore, 10,000 channel matrices are generated with Monte Carlo simulations. We consider the CBS with six antennas (N t =6) and the five SUs each equipped with four antennas (N r =4), and the noise covariance matrix is defined as W k =0.1I 4. In addition, the power control matrix and the target SINRs are initialized as P=0.1I 5 and γ ∗={2,1.9,1.8,1.7,1.5}, respectively, where the target SINRs for SUs are set to satisfy the admissibility condition in (13). Note that the following parameter values are used in all numerical simulations unless stated otherwise: μ=0.5, β=0.5, λ=0.1, and ε=10−6.
In Fig. 3, we examine the convergence speed of the proposed algorithm. It is well known the optimal beamforming signal can be obtained through the zero-forcing algorithm[45]. As observed from Fig. 3, after several iterations, the proposed algorithm converges to the optimal SINRs, and it can achieve better performance than zero-forcing algorithm. Evidently, the proposed algorithm has a fast converge speed.
Figures 4, 5, and 6 show the variations of SUs’ power, SINRs, and cost functions for variable target SINRs. These features are useful in CR MIMO-BCs, where different QoS requirements may lead to the target SINR variation. We assume that the system starts with P=0.1I 5 and γ ∗={2,1.9,1.8,1.7,1.5}, making a Nash equilibrium (NE) configuration be achieved at iteration 10. We then vary the first SU’s target SINR \(\gamma _{1}^{*} = 2\) to new value \(\gamma _{1}^{*} = 1\), leading the algorithm to reach a new NE configuration at iteration 35. Finally, we change SINR \(\gamma _{1}^{*} = 1\) back to its old value \(\gamma _{1}^{*} = 2\), and the system transitions back to the original set of target values between 30 iterations and 50 iterations. As a consequence, we can observe the system transitions from one optimal configuration to another one for variable target SINRs. The algorithm can also track variable target SINRs or a variable number of active users in the system and is therefore useful for dynamic wireless systems with varying QoS requirements. The beamforming matrices of the proposed algorithm are respectively obtained as follows:
Figures 7, 8, and 9 show the variations of SUs’ power, SINRs, and cost functions for a variable number of SUs. We start with five SUs, with different target SINRs γ ∗={2,1.9,1.8,1.7,1.5} being considered. The SUs’ beamforming matrix is initialized randomly, with the SUs’ power matrix being taken as P=0.1I 5. We then assume SU5 to be inactive. The remaining active SUs keep the same target SINR as γ ∗={2,1.9,1.8,1.7}, which satisfies the admissibility condition in (13). After that, we assume SU5 to be active in the system, so that the number of SUs becomes five again, and the same target SINR as before γ ∗={2,1.9,1.8,1.7,1.5} can be obtained. We note that the system remains in a optimal configuration until iteration 28 when user 5 is dropped from the system. This implies an increase of user SINRs above their corresponding targets due to decreasing multiuser interference. Moreover, we can observe that the proposed algorithm finally converges towards the unique NE configuration for a variable number of SUs. The proposed algorithm is illustrated with numerical examples obtained from simulations which illustrate convergence and tracking properties of the algorithm for different scenarios This change in system configuration triggers the adaptation stage of the algorithm, which yields beamforming matrix S 3.
As is the case with incremental algorithms, the convergence speed of the algorithm depends on the values of the corresponding increments specified by the algorithm constants β and μ. We performed extensive simulations of the proposed algorithm to study convergence to the optimal Nash equilibrium. Figures 10 and 11 illustrate the average number of ensemble iterations for the purpose of converging to the optimal NE with varying β and μ. We ran 1000 trials of the algorithm and recorded the number of ensemble iterations for convergence. It is observed that convergence to the optimal NE is mostly determined by the μ rather than β. Moreover, it can be seen that the optimal NE is reached in less than 20 ensemble iterations under constants of β=0.5 and μ=0.5 in all considered scenarios.
Figure 12 shows the variations of the total interference to PU versus the pricing factor λ. As expected, the total interference to PU is a monotonically decreasing function of λ. This is because SU will pay off a higher price to improve its QoS due to the interference from the other SUs and PU. Furthermore, we can also observe that the total interference to PU is minimized at λ=0.06 and the minimum interference of PU will remain unchanged while λ increases.
5 Conclusions
In this paper, the problem of joint beamforming and power control in CR MIMO-BCs has been formulated as a noncooperative separable game, which can be further divided into a beamforming subgame and power control subgame. We have investigated the best response strategies of NE solutions in terms of its corresponding subgames: in NPBS, players’ power control strategies are fixed and they are subject to KKT conditions to update their beamforming strategies. In NPCS, on the other hand, players’ beamforming strategies are fixed and they update only their power control strategies subject to target SINRs. It is shown that the best response function of NPBS can be formulated, with SU k beamforming vector corresponding to the minimum eigenvector of the matrix S k , whereas the best response function of NPCS is derived to enable the transmission with a power control that corresponds to the desired target SINR. Furthermore, we have proposed an iterative algorithm to achieve the optimal Nash equilibrium of JBPS. The proposed algorithm is capable of tracking the variation of target SINRs and/or number of SUs in the system and is therefore useful for dynamic wireless systems with varying QoS requirement. Finally, the proposed algorithm may achieve a faster convergence speed by setting different parameter β and μ values.
6 Endnotes
1 Separable games are a specific class of noncooperative games where the player’s cost is a separable function of their strategic choices [34, 39].
2 The game is noncooperative in the sense that a given player is interested only in minimization of its individual cost function, without paying attention to how its actions affect the other players.
References
SJ Kim, G Li, GB Giannakis, Multi-band cognitive radio spectrum sensing for quality-of-service traffic. IEEE Trans. Wireless Commun. 10(10), 3506–3515 (2011).
M Hasegawa, H Hirai, K Nagano, H Harada, K Aihara, Optimization for centralized and decentralized cognitive radio networks. Proc. IEEE. 102(4), 574–584 (2014).
S Akin, MC Gursoy, Performance analysis of cognitive radio systems with imperfect channel sensing and estimation. IEEE Trans. Commun. 63(5), 1554–1566 (2015).
Z Zhang, K Long, J Wang, Self-organization paradigms and optimization approaches for cognitive radio technologies: a survey. IEEE Wireless Commun. 20(2), 36–42 (2013).
S Stotas, A Nallanathan, On the throughput and spectrum sensing enhancement of opportunistic spectrum access cognitive radio networks. IEEE Trans. Wireless Commun. 1(1), 97–107 (2012).
L Sboui, Z Rezki, MS Alouini, A unified framework for the ergodic capacity of spectrum sharing cognitive radio systems. IEEE Trans. Wireless Commun. 12(2), 877–887 (2013).
A Liu, Y Liu, H Xiang, W Luo, Polite water-filling for weighted sum-rate maximization in MIMO B-MAC networks under multiple linear constraints. IEEE Trans.Signal Process. 60(2), 834–847 (2013).
F Gao, R Zhang, YC Liang, X Wang, Design of learning based MIMO cognitive radio systems. IEEE Trans. Veh. Technol. 59(4), 1707–1720 (2010).
DN Nguyen, M Krunz, Power minimization in MIMO cognitive networks using beamforming games. IEEE J. Sel. Area in Commun. 31(5), 916–925 (2013).
Y Xu, S Mao, Stackelberg game for cognitive radio networks with MIMO and distributed interference alignment. IEEE Trans. Veh. Technol. 63(2), 879–892 (2014).
CS Vaze, MK Varanasi, The degree-of-freedom regions of MIMO broadcast, interference, and cognitive radio channels with no CSIT. IEEE Trans. Inf. Theory. 58(8), 5354–5363 (2012).
DN Nguyen, M Krunz, Price-based joint beamforming and spectrum management in multi-antenna cognitive radio networks. IEEE J. Sel. Area in Commun. 30(11), 2295–2305 (2012).
S Singh, PD Teal, PA Dmochowski, AJ Coulson, Robust cognitive radio cooperative beamforming. IEEE Trans. Wireless Commun. 13(11), 6370–6381 (2014).
R Zhang, F Gao, YC Liang, Cognitive beamforming made practical: effective interference channel and learning-throughput tradeoff. IEEE Trans. Commun. 58(2), 706–718 (2010).
J Mao, G Xie, J Gao, Y Liu, Energy efficiency optimization for cognitive radio MIMO broadcast Channels. IEEE Commun. Letters. 17(2), 337–340 (2013).
C Xing, S Ma, Y Zhou, Matrix-monotonic optimization for MIMO systems. IEEE Trans. Signal Process. 63(2), 334–348 (2015).
M Beko, Efficient beamforming in cognitive radio multicast transmission. IEEE Trans. Wireless Commun. 11(11), 4108–4117 (2013).
S Burer, RD Monteiro, A nonlinear programming algorithm for solving semidefinite programs via low-rank factorization. Math. Program. 95(2), 329–357 (2003).
YJ Zhang, AMC So, Optimal spectrum sharing in MIMO cognitive radio networks via semidefinite programming. IEEE J. Sel. Area in Commun. 29(2), 362–373 (2011).
Y Huang, DP Palomar, S Zhang, Lorentz-positive maps and quadratic matrix inequalities with applications to robust MISO transmit beamforming. IEEE Trans. Signal Process. 61(5), 1121–1130 (2013).
E Song, Q Shi, M Sanjabi, R Sun, ZQ Luo, in Proc.IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP). Robust SINR constrained MISO downlink beamforming: when is semidefinite programming relaxation tight? (2011). 2012(1), 1–11.
H Du, T Ratnarajah, M Pesavento, CB Papadias, Joint transceiver beamforming in MIMO cognitive radio network via second-order cone programming. IEEE Trans. Signal Processing. 60(2), 781–792 (2012).
JH Noh, SJ Oh, Beamforming in a multi-user cognitive radio system with partial channel state information. IEEE Trans. Wireless Commun. 12(2), 616–625 (2013).
B Gopalakrishnan, ND Sidiropoulos, Cognitive transmit beamforming from binary CSIT. IEEE Trans. Signal Processing. 14(2), 895–906 (2015).
MM Zhao, Y Cai, Q Shi, B Champagne, M Zhao, Robust transceiver design for MISO interference channel with energy harvesting. IEEE Trans. Signal Process. 64(17), 4618–4633 (2016).
MM Zhao, Y Cai, Q Shi, M Hong, B Champagne, Joint transceiver designs for full-duplex K-Pair MIMO interference channel with SWIPT. IEEE Trans. Commun. 65(2), 890–905 (2017).
YJ Kim, HJ Lim, MG Song, GH Im, Power efficient transceiver designs for multi-cell coordination in MIMO cognitive radio networks. IEEE Trans. Commun. 61(10), 4127–4138 (2013).
L Zhang, YC Liang, Y Xin, Joint beamforming and power allocation for multiple access channels in cognitive radio networks. IEEE J. Sel. Areas in Commun. 26(1), 38–51 (2008).
Y He, S Dey, Sum rate maximization for cognitive MISO broadcast channels: beamforming design and large systems analysis. IEEE Trans. Wireless Commun. 13(5), 2383–2401 (2014).
K Huang, R Zhang, Cooperative feedback for multiantenna cognitive radio networks. IEEE Trans. Signal Process. 59(2), 747–758 (2011).
L Zhang, R Zhang, YC Liang, Y Xin, HV Poor, On Gaussian MIMO BC-MAC duality with multiple transmit covariance constraints. IEEE Trans. Infor. Theory. 58(4), 2064–2078 (2012).
G Dartmann, X Gong, W Afzal, G Ascheid, On the duality of the max-min beamforming problem with per-antenna and per-antenna-array power constraints. IEEE Trans. Veh. Technol. 58(4), 606–619 (2012).
S Abraham, DC Popescu, OA Dobre, Joint beamforming and power control in downlink multiuser MIMO system. IEEE Radio Wirel. Symp. (RWS). 15(3), 444–449 (2010).
C Lacatus, DC Popescu, Adaptive interference avoidance for dynamic wireless systems: a game-theoretic approach. IEEE J. Sel. Topics Signal Processing. 1(1), 189–202 (2007).
DC Popescu, C Rose, Interference aviodance and multiaccess vector channels. IEEE Trans. Commun. 55(8), 1466–1471 (2007).
DC Popescu, C Rose, Codeword optimization for uplink CDMA dispersive channel. IEEE Trans. Wireless Commun. 4(4), 1563–1574 (2005).
P Viswanath, V Anantharam, D Tse, Optimal sequences, power control and capacity of spread spectrum systems with multiuser linear receivers. IEEE Trans. Inf. Theory. 45(6), 1968–1983 (1999).
DC Popescu, DB Rawat, O Popescu, M Saquib, Game-theoretic approach to joint transmitter adaptation and power control in wireless systems. IEEE Trans. System, Man, and Cybernetics. 40(3), 675–682 (2010).
JCC McKinsey, Introduction to the theory of games (McGraw-Hill, New York, 1952).
HL Xiao, S Ouyang, Power control game in multi-source multi-relay cooperative communication systems with quality-of-service constraint. IEEE Trans. Intelligent Transportation Systems. 16(1), 41–50 (2015).
J Ni, H Xiao, Game Theoretic approach for joint transmit beamforming and power control in cognitive radio MIMO broadcast channels. EURASP J Wireless Commun. Netw. 2016(4), 1–6 (2016).
CW Sung, KW Shum, KK Leung, Stability of distributed power and signature sequence control for CDMA systems—a game-theoretic framework. IEEE Trans. Inf. Theory. 52(4), 1775–1780 (2006).
M Avriel, Nonlinear programming, analysis and methods, Englewood Cliffs (Prentice-Hall, NJ, 1976).
J Rosen, Existence and uniqueness of equilibrium point for concave N-person games Econometrica. 33(3), 550–534 (1965).
CK Wen, JC Chen, KK Wong, P Ting, Message passing algorithm for distributed downlink regularized zero-forcing beamforming with cooperative base stations. IEEE Trans. Wirel. Commun. 13(5), 2920–2930 (2014).
Acknowledgements
Thanks are due to Prof. Hailin Xiao for valuable discussion. The authors acknowledge the support from the opening project of Guangxi Key Laboratory of Wireless Wideband Communication and Signal Processing and the opening project of Key Laboratory of Cognitive Radio and Information Processing, Ministry of Education (CRKL150107). The authors also acknowledge the support from the open research fund of the National Mobile Communications Research Laboratory, Southeast University (No. 2015D05).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, S., Ni, J. & Peng, Q. Joint beamforming and power control algorithm for cognitive MIMO broadcast channels via game theory. J Wireless Com Network 2017, 137 (2017). https://doi.org/10.1186/s13638-017-0918-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-017-0918-z