Enhanced beamforming design and sum-rate maximization for two-way multi-relay networks

Abstract

In this paper, we investigate an enhanced relay beamforming design for two-way relay networks (TWRN). In order to reduce the computational complexity, we derive a sum of the inverse of the signal-to-noise ratio (SI-SNR) problem equivalent to the objective sum-rate (SR) problem. The SI-SNR problem can be reformulated as a simple optimization problem by using the Cholesky decomposition and Cauchy-Schwarz inequality, and solved by the interior-point method. The numerical results show that the proposed SI-SNR method can not only reduce the computational complexity but also have the same SR performance as that of the conventional works.

1 Introduction

Recently, the two-way relaying (TWR) has attracted significant interests in improving the spectral efficiency for wireless communication systems. Various cooperative two-way relaying schemes have been proposed, such as denoise-and-forward (DNF) [1, 2], compress-and-forward (CF) [3], decode-and-forward (DF) [4, 5], amplify-and-forward (AF) [1, 6, 7], and cooperative relaying protocols. Because of a less processing power requirement and efficiency, the AF scheme is the most widely used in the two-way relay channel (TWRC).

Relay precoder design methods have been investigated in [7–10]. In [7], the authors considered multi-user two-way relay networks (TWRN) with distributed single-antenna relays, where two approaches are considered, i.e., (1) null out all interference contributions at each user separately and (2) treat the interferences at each user as a whole and null out the power of the total interferences. In addition, a closed-form upper bound of the achievable sum-rate (SR) is derived and the same multiplexing gain is achieved when the number of relays is sufficiently large for the considered two approaches. For these two approaches, in order to null every interference (approach 1) and null the total interference (approach 2), the conditions N<2K ²+K and N≥2K(K−1)+1 should be satisfied, where N is the number of relay nodes and K is the number of the pairs of user nodes. In [8], the authors propose an optimization problem for the TWR system by using a signal-to-noise ratio (SNR) balancing result. In [9], the optimal structure of the source and relay precoding matrices for a two-way linear non-regenerative multiple-input multiple-output (MIMO) relay system is studied. In [10], the authors showed the global optimal solution can be obtained by the branch-and-bound algorithm. Nevertheless, the computational complexity is extremely high to find the orthogonal complement to solve the optimization problem in the above existing works. In order to reduce the computational complexity, [11–14] are investigated by using some effective ways. In [11], the authors derived the achievable SR upper bound of AF beamforming scheme and proposed the achievable SR maximizing relay beamforming scheme when the destination and the relay node have perfect knowledge of the channel state information (CSI) for forward and backward channels. A general power iterative algorithm is proposed which can solve the global optimization problem with low computational complexity when the object function form is a product of fractional quadratic functions. In [12], a determinant maximization problem of an AF based on the TWR by using QL-QR decomposition is investigated. In [13], the authors proposed a distributed TWR selection scheme which possesses low implementation complexity and the same diversity-multiplexing trade-off (DMT) performance as that of the conventional work. In [14], a channel norm (CN) scheduling scheme is proposed to reduce the complexity and computational cost at the relay.

To further reduce the computational complexity, we propose a novel and general distributed relay beamforming scheme for the TWR. Since the channel state information has to be exchanged between relays, the processing usually changes on a slow timescale and needs not create significant overhead. Therefore, following the distributed manner, the weight matrix is diagonal which guarantees that the relays transmit only their own received signal and there is no data exchange among the relays. Since the SR maximization problem is non-convex, we convert the objective problem into a sum of the inverse of the signal-to-noise ratio (SI-SNR) problem. By employing the Cholesky decomposition and Cauchy-Schwarz inequality, the SI-SNR problem can be approximately reformulated as a convex optimization problem which can be solved by using the interior-point method.

The rest of this paper is organized as follows. Section 2 describes a system model of the TWRC. In Section 3, we propose an SI-SNR problem and derive the semi-closed-form solution. The numerical results are presented to show the excellent performance of our proposed method for the TWRC in Section 4. Section 5 concludes this paper.

Notations: A ^T, A ⁻¹, A ^†, and tr{A} denote the transpose, the inverse, the pseudo-inverse and the trace of matrix A. d i a g(·) denotes a diagonal matrix and an N×N identity matrix is denoted by I _N . ∥·∥₂, E(·), and ⊙ stand for the Euclidean norm, the statistical expectation, and the Hadamard product. 〈a,b〉 is the inner product of a and b.

2 System model

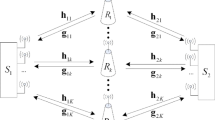
We consider a TWRC consisting of two source nodes S ₁ and S ₂ and N relay node R _N as shown in Fig. 1. Each node is equipped with a single antenna. We assume that the channels are reciprocal, i.e., the source-to-relay channel coefficients are the same as the relay-to-source channel coefficients. Assume f _i and g _i denote the channel coefficients from source 1 and source 2 to relay node i, respectively. Thus, for the total system, we have the channel vectors f=[f ₁,f ₂,...f _N ]^T and g=[g ₁,g ₂,…g _N ]^T. In the first time slot, for the source node S _t , for t∈{1,2}, the information signal x _t is transmitted to the relay nodes. In this paper, we assume that each transmit antenna satisfies the unity transmission power constraint, which is $\text {tr}\{x_{t}{x^{H}_{t}}\}=1$. The received signals at relay nodes can be expressed as

$$\begin{array}{@{}rcl@{}} \mathbf{k}_{R}=\sqrt{P_{1}}\mathbf{f}x_{1}+\sqrt{P_{2}}\mathbf{g}x_{2}+\mathbf{n}_{R}, \end{array} $$

(1)

Fig. 1

The two-way multi-relay network

where P _t denotes the transmit power, $\mathbf {k}_{R}\in {\mathbb {C}^{N\times 1}}$ indicates the received signal vector, and $\mathbf {n}_{R}\sim {\mathcal {CN}(0,\mathbf {I}_{N})}$ represents the additive white Gaussian noise (AWGN) vector with zero mean and the variance I _N at relay nodes.

In the second time slot, the relay node R _i linearly amplifies k _R with an N×N beamforming matrix W=d i a g(w), where w=[w ₁,w ₂,...,w _N ], and then broadcasts the amplified signal vector x _R to source nodes 1 and 2. Since the transmit power of souse node S _t is given as P _t , by assuming n _R with zero mean and the variance I _N and the transmitted signals x ₁ and x ₂ are independent, in order to normalize the relay transmit power, we propose the following power normalization vector:

$$\begin{array}{@{}rcl@{}} \rho=1/\sqrt{P_{1}+P_{2}+1}. \end{array} $$

(2)

The signal transmitted from relay node can be expressed as

$$\begin{array}{@{}rcl@{}} \mathbf{x}_{R}=\rho\textbf{W}\mathbf{k}_{R}. \end{array} $$

(3)

As shown in [7], to guarantee that the relays transmit only their own received signal and there is no data exchange among the relays, the weight matrix is diagonal which follows the distributed manner. From (3), the total transmit power used by the relay nodes can be expressed as

$$\begin{array}{@{}rcl@{}} P_{R}&=&\mathbf{E}\left\{\left\|\mathbf{x}_{R}\right\|^{2}_{2}\right\}=\text{tr}\left\{\rho^{2}\mathbf{W}\mathbf{k}_{R}\mathbf{k}^{H}_{R}\mathbf{W}^{H}\right\}\notag\\ &=&\text{tr}\left\{\mathbf{w}\mathbf{D}\mathbf{w}^{H}\right\}, \end{array} $$

(4)

where D=ρ ²{F F ^H+G G ^H+I _N } with F=d i a g(f) and G=d i a g(g). In TWRN, since the signal transmitted by the transceiver nodes reappear as self-interference, by employing the successive interference cancellation (SIC), the self-interference can be completely eliminated with perfect channel state information (CSI) [15]. Based on this principle and assuming the CSIs are perfectly known at each source node i, the self-interference components can be efficiently canceled. After the self-interference cancellation, the received signal vectors at S ₁ and S ₂ can be written as

$$\begin{array}{@{}rcl@{}} &&\mathbf{y}_{1}=\rho\sqrt{P_{2}}\mathbf{w}\mathbf{F}\mathbf{g}x_{2}+\rho\mathbf{w}\mathbf{F}\mathbf{n}_{R}+\mathbf{n}_{1}\notag\\ &&\mathbf{y}_{2}=\rho\sqrt{P_{1}}\mathbf{w}\mathbf{G}\mathbf{f}x_{1}+\rho\mathbf{w}\mathbf{G}\mathbf{n}_{R}+\mathbf{n}_{2}, \end{array} $$

(5)

where n _t is the noise vector at S _t with mean zero and variance 1. From (5), the SNR at sources 1 and 2 can be expressed as

$$\begin{array}{@{}rcl@{}} \text{SNR}_{1}=\frac{\rho^{2}P_{2}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}}{\rho^{2}\mathbf{w}\mathbf{D}_{1}\mathbf{w}^{H}+1}, \end{array} $$

(6)

and

$$\begin{array}{@{}rcl@{}} \text{SNR}_{2}=\frac{\rho^{2}P_{1}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}}{\rho^{2}\mathbf{w}\mathbf{D}_{2}\mathbf{w}^{H}+1}, \end{array} $$

(7)

where h=f⊙g, D ₁=F F ^H, and D ₂=G G ^H. In the next section, we will propose an enhanced beamforming design to efficiently obtain SR.

3 Enhanced beamforming design and sum-rate maximization

The SR of the two source nodes in the proposed system model can be written as:

$$\begin{array}{@{}rcl@{}} R_{\text{sum}}=R_{1}+R_{2}. \end{array} $$

(8)

Our goal is to find the relay amplification matrix W which maximizes the sum-rate R _sum subject to a power constraint at the relay. Under the definition of the mutual information, we have

$$\begin{array}{@{}rcl@{}} &&R_{t}=\frac{1}{2}\text{log}_{2}(1+\text{SNR}_{t}), \end{array} $$

(9)

where $\frac {1}{2}$ is due to the half-duplex relay. Synthesizing (8)–(9), the sum-rate can be expressed as

$$ \begin{aligned} R_{\text{sum}}=&\frac{1}{2}\text{log}_{2}\left(1+\frac{\rho^{2}P_{2}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}}{\rho^{2}\mathbf{w}\mathbf{D}_{1}\mathbf{w}^{H}+1}\right)\\ +&\frac{1}{2}\text{log}_{2}\left(1+\frac{\rho^{2}P_{1}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}}{\rho^{2}\mathbf{w}\mathbf{D}_{2}\mathbf{w}^{H}+1}\right). \end{aligned} $$

(10)

Therefore, the optimization problem of the sum-rate respect to the total relay power constraint can be formulated as:

$$\begin{array}{@{}rcl@{}} Q_{1}:~&\underset{\mathbf{w}}{\text{max}}&~~~~~~R_{\text{sum}} \end{array} $$

(11)

$$\begin{array}{@{}rcl@{}} &s.t.&~\mathbf{wDw}^{H}\leq{P_{R}}. \end{array} $$

(12)

Using log(a)+log(b)=log(a b), the sum-rate R _sum can be rewritten as

$$ \begin{aligned} R_{\text{sum}}=\frac{1}{2}\text{log}_{2}\left\{\left(1+\frac{\rho^{2}P_{2}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}}{\rho^{2}\mathbf{w}\mathbf{D}_{1}\mathbf{w}^{H}+1}\right)\right. \\ \times\left.\left(1+\frac{\rho^{2}P_{1}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}}{\rho^{2}\mathbf{w}\mathbf{D}_{2}\mathbf{w}^{H}+1}\right)\right\}. \end{aligned} $$

(13)

Since the optimal solution of {max (1+A)(1+B)} is equivalent to the problem $\left \{\text {min}~\left (\frac {1}{A}+\frac {1}{B}\right)\right \}$ [16] and $\frac {1}{2}\text {log}(x)$ is a monotonic function, consider the high transmit SNR case, (11) can be approximately converted into

$$ \begin{aligned} {}&\min\limits_{\mathbf{w}}~\frac{\rho^{2}\mathbf{w}\mathbf{D}_{1}\mathbf{w}^{H}+\rho^{2}/\alpha\mathbf{w}\mathbf{D}_{2}\mathbf{w}^{H}+1+1/\alpha}{\rho^{2}P_{2}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}}\\ {}\overset{(a)}{\approx}&\min\limits_{\mathbf{w}}~\frac{\rho^{2}\mathbf{w}\mathbf{D}_{1}\mathbf{w}^{H}+\rho^{2}/\alpha\mathbf{w}\mathbf{D}_{2}\mathbf{w}^{H}+1+1/\alpha}{\rho^{2}P_{2}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}+\rho^{2}}\\ {}\overset{(b)}{=}&\min\limits_{\mathbf{w}}~\underbrace{\frac{\mathbf{w}\mathbf{D}_{1}\mathbf{w}^{H}+1/\alpha\mathbf{w}\mathbf{D}_{2}\mathbf{w}^{H}}{P_{2}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}+1}}_{R_{A}}+\underbrace{\frac{\left(1+1/\alpha\right)/\rho^{2}}{P_{2}\mathbf{w}\mathbf{h}\mathbf{h}^{H}\mathbf{w}^{H}+1}}_{R_{B}}, \end{aligned} $$

(14)

where $\alpha =\frac {P_{1}}{P_{2}}$ and in (a), the addition “$\rho ^{2}=\frac {1}{P_{1}+P_{2}+1}$" in the denominator is extremely negligible compared to the other term in the denominator. On the other hand, the approximation (a) is completely necessary, which can help us to obtain the semi-closed-form expression of w. In order to efficiently obtain the optimal solution, (14) can be converted into parts R _A and R _B as shown in (b). Now, we have the equivalent optimization problem Q ₂ as

$$\begin{array}{@{}rcl@{}} Q_{2}:~&\underset{\mathbf{w}}{\text{min}}&~~R_{A}+R_{B} \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} &s.t.&~\mathbf{wDw}^{H}\leq{P_{R}}. \end{array} $$

(16)

Proposition 1.

The optimization problem Q ₂ is equivalent to Q ₃ which is given as

$$\begin{array}{@{}rcl@{}} Q_{3}:~&\underset{\mathbf{w}}{\text{min}}&~~\widetilde{R}_{A}+R^{*}_{B} \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} &s.t.&~\mathbf{wDw}^{H}\leq{P_{R}}, \end{array} $$

(18)

where $\widetilde {R}_{A}=\text {tr}\left \{\Delta ^{H}\left (P_{2}\mathbf {hh}^{H}+\frac {1}{\varsigma }\mathbf {I}_{N}\right)^{-1}\Delta \right \}$ with $\mathbf {D}_{1}+\frac {1}{\alpha }\mathbf {D}_{2}=\Delta \Delta ^{H}$ and $R_{B}^{*}$ serve as the upper bounds of R _A and R _B , respectively.

Proof

Similar to [17], by introducing the auxiliary optimization variables τ _A and τ _B , the optimization problem (15) can be recast in the epigraph form [18] as {min (τ _A +τ _B )},s.t. R _A ≤τ _A ,R _B ≤τ _B . For the term R _A in the second equality of (14), since D ₁ and $\frac {1}{\alpha }\mathbf {D}_{2}$ are hermitian and positive definite, by applying Cholesky decomposition [19], we have

$$\begin{array}{@{}rcl@{}} \mathbf{D}_{1}+\frac{1}{\alpha}\mathbf{D}_{2}=\Delta\Delta^{H}, \end{array} $$

(19)

where Δ denotes a lower triangular matrix. We can rewrite R _A as

$$\begin{array}{@{}rcl@{}} R_{A}&=&\frac{\mathbf{w}\left(\mathbf{D}_{1}+\frac{1}{\alpha}\mathbf{D}_{2}\right)\mathbf{w}^{H}}{\mathbf{w}\left(P_{2}\mathbf{h}\mathbf{h}^{H}+\frac{1}{\varsigma}\mathbf{I}_{N}\right)\mathbf{w}^{H}}\notag\\ &\overset{(a)}{\leq}&\text{tr}\left\{\Delta^{H}\left(P_{2}\mathbf{hh}^{H}+\frac{1}{\varsigma}\mathbf{I}_{N}\right)^{-1}\Delta\right\}=\widetilde{R}_{A}, \end{array} $$

(20)

where ς=∥w∥² and (a) is due to the Cauchy-Schwarz inequality ([20], Appendix A), i.e., |〈u,v〉|²≤〈u,u〉·〈v,v〉.

Interestingly, $\widetilde {R}_{A}$ has nothing to relate to the minimum solution of R _sum which serves as the upper bound of R _A . On the other hand, consider that the SNR at each relay is identically distributed, the term of R _B can be relaxed as

$$\begin{array}{@{}rcl@{}} R_{B}=\sum_{i=1}^{N}\frac{\varsigma}{P_{2}{h^{2}_{i}}{w^{2}_{i}}+1}, \end{array} $$

(21)

where ς=(1+1/α)ρ ² the ith diagonal element of h h ^H is defined as ${h^{2}_{i}}$. From (21), the first-order and the second-order derivatives of R _B with respect to the relay beamforming factor w _i can be respectively derived as

$$\begin{array}{@{}rcl@{}} \frac{\partial R_{B}}{\partial w_{i}}=-\sum_{i=1}^{N}\frac{2\varsigma P_{2}{h^{2}_{i}}w_{i}}{\left(P_{2}{h^{2}_{i}}{w^{2}_{i}}+1\right)^{2}}, \end{array} $$

(22)

and

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}R_{B}}{\partial {w^{2}_{i}}}=\sum_{i=1}^{N}\left(\frac{8\varsigma {P^{2}_{2}}{h^{4}_{i}}{w^{2}_{i}}}{\left(P_{2}{h^{2}_{i}}{w^{2}_{i}}+1\right)^{3}}-\frac{2\varsigma P_{2}{h^{2}_{i}}}{\left(P_{2}{h^{2}_{i}}{w^{2}_{i}}+1\right)^{2}}\right). \end{array} $$

(23)

From (23), it is easy to see that as long as $-\sqrt {\frac {1}{3P_{2}{h^{2}_{i}}}}<w_{i}<\sqrt {\frac {1}{3P_{2}{h^{2}_{i}}}}$, for w _i ≠0 (this case is out of the scope), it follows $\frac {\partial ^{2}R_{B}}{\partial {w^{2}_{i}}}<0$; otherwise, $\frac {\partial ^{2}R_{B}}{\partial {w^{2}_{i}}}>0$. Since $\frac {\partial R_{B}}{\partial w_{i}}$ is a decreasing function for $-\sqrt {\frac {1}{3P_{2}{h^{2}_{i}}}}<w_{i}<\sqrt {\frac {1}{3P_{2}{h^{2}_{i}}}}$, meanwhile $\frac {\partial R_{B}}{\partial w_{i}}$ is a increasing function for $w_{i}<-\sqrt {\frac {1}{3P_{2}{h^{2}_{i}}}}$ and $\frac {\partial R_{B}}{\partial w_{i}}<0$ for $w_{i}>\sqrt {\frac {1}{3P_{2}{h^{2}_{i}}}}$, there exists maximum $R^{*}_{B}$ associated with min|w _i |, which can be efficiently solved by the interior-point method [18]. By replacing $\widetilde {R}_{A}=\tau _{A}$ and $R^{*}_{B}=\tau _{B}$, we have the problem Q ₃. This completes the proof. □

According to Proposition 1, the optimization problem Q ₃ can be finally expressed as

$$\begin{array}{@{}rcl@{}} Q_{4}:~&\underset{\mathbf{w}}{\text{min}}&~~~~~R^{*}_{B} \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} &s.t.&\mathbf{wDw}^{H}\leq{P_{R}}. \end{array} $$

(25)

The Lagrangian function associated with problems (24) and (25) is given by

$$\begin{array}{@{}rcl@{}} L_{\mathbf{v}}&=&\text{tr}(R_{B})+\mu\text{tr}\left(\mathbf{wDw}^{H}-P_{R}\right), \end{array} $$

(26)

where μ≥0 is the Lagrange multiplier. Making the derivative of L _v with respect to w ^H be zero, we have

$$\begin{array}{@{}rcl@{}} \frac{\partial{L_{\mathbf{V}}}}{\partial{\mathbf{w}^{H}}}=-\eta\left(P_{2}\mathbf{w}\mathbf{hh}^{H}\mathbf{w}^{H}+1\right)^{-2}\mathbf{w}\mathbf{hh}^{H}+\mu{\mathbf{wD}}, \end{array} $$

(27)

where η=2ς P ₂. When μ≥0, since h ^H is nonsingular, we can obtain

$$\begin{array}{@{}rcl@{}} \eta\left(P_{2}\mathbf{w}\mathbf{hh}^{H}\mathbf{w}^{H}+1\right)^{-2}\mathbf{wh}=\mu\mathbf{wD}\left(\mathbf{h}^{H}\right)^{-1}. \end{array} $$

(28)

Multiplying both sides by $\mathbf {w}^{\dag }\in {\mathbb {C}^{N\times {1}}}$ and (h)⁻¹, we have

$$\begin{array}{@{}rcl@{}} \eta\mathbf{h}^{-1}\mathbf{w}^{\dag}\left(P_{2}\mathbf{w}\mathbf{hh}^{H}\mathbf{w}^{H}+1\right)^{-2}\mathbf{wh}=\mu\mathbf{h}^{-1}\mathbf{D}\left(\mathbf{h}^{H}\right)^{-1}. \end{array} $$

(29)

Using the fact that (I _N +A A ^H)⁻¹ A=A(I _M +A ^H A)⁻¹ (which follows from the matrix inversion lemma) for any N×M matrix A, we can rewrite (29) as

$$\begin{array}{@{}rcl@{}} \eta\left(P_{2}\mathbf{h}^{H}\mathbf{w}^{H}\mathbf{w}\mathbf{h}+\mathbf{I}_{N}\right)^{-2}=\mu\mathbf{h}^{-1}\mathbf{D}\left(\mathbf{h}^{H}\right)^{-1}. \end{array} $$

(30)

Solving (30) for w, we have

$$\begin{array}{@{}rcl@{}} \mathbf{w}=\sqrt{\frac{1}{P_{2}}}\left(\sqrt{\frac{\eta}{\mu}}\left(\mathbf{h}^{H}\right)^{-\frac{1}{2}}\mathbf{D}^{-1}\mathbf{h}^{-\frac{1}{2}}-\left(\mathbf{hh}^{H}\right)^{-1}\right)^{\frac{1}{2}}. \end{array} $$

(31)

Synthesizing Proposition 1 and (31), when

ς=∥w∥² holds, the solutions of R _A and R _B are always optimum. Finally, we have the solution as

$$\begin{array}{@{}rcl@{}} L^{*}_{\mathbf{v}}&\triangleq&\text{tr}\left(\widetilde{R}_{A}+R^{*}_{B}\right)+\mu\text{tr}\left(\mathbf{wD}\mathbf{w}^{H}-P_{R}\right). \end{array} $$

(32)

Now, we summarize the proposed beamforming method in Algorithm 1.

Comparing with the conventional algorithm in [10], the proposed beamforming Algorithm 1 significantly reduces the computational complexity. This is because, to obtain the maximum solution of SR in [10], the iterative branch-and-bound algorithm is used which is problematic in practical systems. In contrast, in our proposed beamforming Algorithm 1, the near (at least local) optimal solution of w can be obtained without iterations. In addition, in the proposed beamforming method, we efficiently convert the objective SR problem into a convex and low-computation-cost one, i.e., $\text {max}~R_{\text {sum}}\longrightarrow \text {min}~R^{*}_{B}$.

4 Numerical results

In this section, we measure the performance of the proposed Algorithm 1 in terms of sum-rate compared with the branch-and-bound algorithm in [10]. In all simulations, the channel estimates f and g are assumed to be reciprocal and identically distributed complex Gaussian random variables. We further assume that the noise variances of n _R ,n _t for t=1,2, are equally given as σ ²=1. In addition, the upper bound solution of SR is obtained by using the exhaustive search algorithm. Comparisons are made with the branch-and-bound algorithm [10] in two different system setups: (1) N=2 and (2) N=3.

In Fig. 2, we compare the average SR performance for the proposed method with the optimal and one-iteration solutions of branch-and-bound method [10] versus transmit SNR, i.e., P ₁=P ₂, with R _N =2 and R _N =3 relay nodes. The optimal solution by using the exhaustive search method serves as the upper bound. It is found that the proposed method is closed to the optimum of [10] and has a remarkable improvement than the one iteration solution. This is because the Cauchy-Schwarz inequality is employed to obtain $\widetilde {R}_{A}$ in (20) which leads to the extreme loss of the performance. In addition, the solution of our proposed method is closed to the one in [10] with increasing transmit power. This is because the approximation of (a) in (14) is negligible at high SNR.

Fig. 2

Average SR performance versus transmit SNR, P ₁=P ₂

Figure 3 exhibits the average SR performance for the proposed method with the optimal and one-iteration solutions of branch-and-bound method [10] versus P ₂ with fixed P ₁=5. It is clear from Fig. 3 that the solution of our proposed method shows better performance than that of the one iteration [10], and the advantage is increased with greater number of relay N. In addition, it is easy to see that the performances of our proposed scheme and the optimal one in [10] are close at high SNR, which supports the practical utility of our design. In Fig. 4, we compare the average SR performance for our proposed scheme by using Algorithm 1 versus the number of relay node N with the optimal one, where the cases P ₁=P ₂=5 and P ₁=P ₂=10 are considered. Remarkably, the performance gap between the proposed one and the optimal one is smaller for the higher SNR case.

Fig. 3

Average SR performance versus P ₂ with fixed P ₁=5

Fig. 4

Average SR performance versus the number of the relay nodes N with fixed P ₁=P ₂=5 and P ₁=P ₂=10

5 Conclusions

In this paper, we considered the TWRN with the enhanced relay beamforming design and proposed a low computational complexity method to solve the SR maximization problem. The objective problem was efficiently converted into a SI-SNR problem which is a simple and low-computation-cost one. Finally, the semi-closed-form solution of SI-SNR problem is derived. Numerical results showed that the performance of the proposed SI-SNR is improved compared to the existing one.