Dynamic C-RAN resource sharing scheme based on a hierarchical game approach

Abstract

Over the past decade, wireless applications have experienced tremendous growth, and this growth is likely to multiply in the near future. To cope with expected drastic data traffic growth, a new cloud computing-based radio access network (C-RAN) has been proposed for next-generation cellular networks. It is considered as a cost-efficient way of meeting high resource demand of future wireless access networks. In this paper, we propose a novel resource sharing scheme for future C-RAN systems. Based on the Indian buffet game, we formulate the C-RAN resource allocation problem as a two-level game model and find an effective solution according to the coopetition approach. Our proposed scheme constantly monitors the current C-RAN system conditions and adaptively responds in a distributed manner. The experimental results validate the effectiveness and efficiency of our proposed scheme under dynamic C-RAN situations.

1 Introduction

In recent years, the radio access network (RAN) is commonly used to support the exponential growth of mobile communications. Conceptually, RAN resides among network devices such as a mobile phone, a computer, or any remotely controlled machine and provides connections with core networks. However, traditional RAN architecture has been faced with a number of challenges. First, a highly loaded base station (BS) cannot share processing power with other idle or less loaded BSs; it results in a poor resource utilization. Second, a BS equipment serves only radio frequency channels in each physical cell, where BS’s resources cannot be shared with other BSs in different cells. Finally, BSs built on proprietary hardware cannot have a flexibility to upgrade radio networks [1, 2].

To overcome these problems, cloud computing-based radio access network (C-RAN) is widely considered as a promising paradigm, which can bridge the gap between the wireless communication demands of end users and the capacity of radio access networks. To meet users’ high resource demands, the C-RAN consolidates BSs to a central cloud and takes a benefit from the cloud computing elasticity, which allows dynamic provisioning of cloud BS resources [1, 3]. In C-RAN, the baseband processing unit (BPU) of traditional BSs is pooled and moved into a centralized location. By virtualization, the computing resources in the BPU pool can be dynamically shared among all the cells in the network while allowing a significant improvement in computing resource utilization and power efficiency. Currently, there have been a number of researches on the computing resource allocation for the virtualized BPUs. However, they are not realizable in a practical system because of the computational complexity [4].

Game theory is the formal study of conflict and cooperation and can be used to model a multiplayer decision-making process and to analyze the manner in which players interact with each other during this process. Therefore, the concepts of game theory provide a language in which to formulate, structure, analyze, and understand strategic scenarios. This concept drew great attentions in both areas of economics and computer science [5]. In 2013, C. Jiang introduced the fundamental notion of an Indian buffet game to study how game players make multiple concurrent selections under uncertain system states [6]. Specifically, the Indian buffet game model can reveal how players learn the uncertainty through social learning and make optimal decisions to maximize their own expected utilities by considering negative network externality [7]. This game model is well suited for the C-RAN resource sharing problem.

Motivated by the above discussion, we design a new C-RAN resource sharing scheme based on the Indian game model. The key feature of our scheme is to develop a decentralized mechanism according to the two-level coopetition approach. The term “coopetition” is a neologism coined to describe cooperative competition. Therefore, coopetition is defined as the phenomenon that differs from competition or cooperation and stresses two faces, i.e., cooperation and competition, of one relationship in the same situation [8]. In this study, our proposed game model consists of two levels: the upper- and lower-level Indian buffet games. At the upper-level game, cloud resources are shared in a cooperative manner. At the lower-level game, allocated resources are distributed in a non-cooperative manner. Based on the hierarchical interconnection of the two game models, control decisions can cause cascade interactions to reach a mutually satisfactory solution.

Usually, different C-RAN agents may pursue different interests and act individually to maximize their own profits. This self-organizing feature can add autonomics into C-RAN systems and help to ease the heavy burden of complex centralized control algorithms. Based on the recursive best-response algorithm, we draw on the concept of a learning perspective and investigate some of the reasons and probable lines for justifying each system agent’s behavior. The dynamics of the interactive feedback learning mechanism can allow control decisions to be dynamically adjustable. In addition, by employing the coopetition approach, control decisions are mutually dependent on each other to resolve conflicting performance criteria.

1.1 Related work

Over the years, a lot of state-of-the-art research work on the C-RAN resource sharing problem has been conducted [4, 9, 10]. The baseband processing units virtualization (BPUV) scheme [4] was proposed for the baseband processing unit virtualization. It was formulated as a bin packing problem, where each baseband processing unit was treated as a bin with finite computing resources, expressed in million operations per time-slot (MOPTS). In addition, the dynamics of the cell traffic load was treated as an item that needed to be packed into the bins with the size equal to the computing resources in MOPTS, required to support the traffic load. To solve the optimization problem and simultaneously improve the standard solver for the bin packing problem, the BPUV scheme was designed based on a heuristic simulated annealing approach [4].

The joint cloud computing and network (JCCN) scheme [9] was proposed to jointly study dynamic cloud and wireless network operations so as to improve end-to-end performance in the mobile cloud computing environment. This scheme considered not only the spectrum efficiency in wireless networks but also the pricing information in the cloud, based on which power allocation and interference management in wireless networks were performed. The JCCN scheme formulated the problems of cloud media service price decision, resource allocation, and the interference management in the mobile cloud computing environment as a three-level Stackelberg game [9].

The cloud provider’s resource sharing (CPRS) scheme [10] was developed to study the cooperative behavior of multiple cloud providers. In the CPRS scheme, a hierarchical cooperative game model was designed; it was composed of two interrelated cooperative games to analyze the decisions of cloud providers to support internal users and to offer service to public cloud users. In the lower-level, the CPRS scheme implemented a stochastic linear programming game model to study the resource and revenue sharing for a given coalition of cloud providers. In the upper-level, the CPRS scheme formulated the coalitional game for which the cloud providers can form the groups of cooperation to share resource and revenue. Finally, the analytical model based on a Markov chain was used to obtain stable coalitional structure [10]. All the earlier work has attracted a lot of attention and introduced unique challenges to efficiently solve the resource sharing problem in C-RAN systems. Compared to these schemes [4, 9] and [10], our proposed scheme attains better system performance.

The remainder of this paper is structured as follows. In Section 2, we outline the C-RAN architecture in detail. Section 3 describes the Indian buffet game model for C-RAN systems. And then, the proposed algorithm is explained step by step in Section 4. In Section 5, we show the simulation results. Through simulation, we show the ability of the proposed scheme to achieve high accuracy and promptness in dynamic C-RAN environments. Finally, we draw conclusions in Section 6.

2 Cloud radio access network architecture

The C-RAN is a novel mobile network architecture, which has a potential to optimize cost and energy consumption in the field of mobile networks. In C-RAN systems, there are multiple cloud providers (CPs), which can generate more revenue from the sharing of available resources. CPs have their system resources, such as a CPU core, memory, storage, and network bandwidth. To ensure the optimal usage of cloud resources, baseband processing is centralized in a virtualized baseband units pool (VBP). The VBP can be shared by different CPs and multiple BSs. Therefore, the VBP is in a unique position as a cloud brokering between the BSs and the CPs for cloud services while increasing resource efficiency and system throughput [11].

In the RAN architecture, a small base station (SBS) covers a small area and communicates with the mobile users (MUs) through wireless links. SBSs provide the managed connectivity and offer flexibility in real-time demands. To improve C-RAN system efficiency, CPs can offer their available resources to SBSs through the VBP, and SBSs can provide services to MUs based on their obtained resources. Without loss of generality, each SBS is assumed to acts as a virtual machine, and MUs’ applications are executed through the virtualization technology. The general architecture of a hierarchical C-RAN system is shown in Fig. 1.

Fig. 1

Hierarchical C-RAN system structure

In this study, we consider a C-RAN architecture with one VBP, 10 SBSs, and 100 MUs, and system resources are the computing capacities of CPU, memory, storage, and bandwidth. These resources can be used by the MUs through the VBP to gain more revenue. For the rest of this paper, we refer the organization that CPs cooperate to form a logical pool of computing resources to support MUs’ applications. Each MU application service has its own application type and requires different resource requirements.

3 Indian buffet game model for C-RAN systems

Let us consider an Indian buffet restaurant which provides m dishes denoted by d ₁, d ₂,…, d _m . Each dish can be shared among multiple guests. Each guest can select sequentially multiple dishes to get different meals. The utility of each dish can be interpreted as the deliciousness and quantity. All guests are rational in the sense that they will select dishes which can maximize their own satisfactions. In such a case, the multiple dish-selection problem can be formulated to be a non-cooperative game, called the Indian buffet game. In the traditional Indian buffet game, the main goal is to study how guests in a buffet restaurant learn the uncertain dishes’ states and make multiple concurrent decisions by not only considering the current utility but also taking into account the influence of subsequent players’ decisions [5, 7].

During the C-RAN system operations, system agents should make decisions individually. In this situation, a main issue for each agent is how to perform well by considering the mutual interaction relationship and dynamically adjust their decisions to maximize their own profits. In this study, we develop a new C-RAN system resource sharing scheme based on the Indian buffet game model. In our proposed scheme, the dynamic operation of VBP, SBSs, and MUs is formulated as a two-level Indian buffet game. At the first stage, the VBP and SBSs play the upper-level Indian buffet game; the VBP distribute the available resources to each SBS by using a cooperative manner. At the second stage, multiple MUs decide to purchase the resource from their corresponding SBS by employing a non-cooperative manner. Based on this hierarchical coopetition approach, we assume that all game players (VBP, SBSs, and MUs) are rational and independent of gaining the profit as much as possible. Therefore, for the implementation practicality, our proposed scheme is designed in an entirely distributed and self-organizing interactive fashion.

Mathematically, our upper-level Indian buffet game (${\mathbb{G}}^U$) can be defined as ${\mathbb{G}}^U=\left\{\mathrm{\mathbb{N}},\ \mathbb{D},\ {\left\{{\boldsymbol{S}}_i\right\}}_{i\in \mathrm{\mathbb{N}}},\ {\left\{{U}_i\right\}}_{i\in \mathrm{\mathbb{N}}},\ T\right\}$ at each time period t of gameplay.

• ℕ is the finite set of players $\mathrm{\mathbb{N}}=\left\{\mathbf{\mathcal{C}},\mathbf{\mathcal{B}}\right\}$ where $\mathbf{\mathcal{C}}$ = {VBP} represents one VBP and ℬ = {b ₁, …, b _n } is a set of multiple SBSs, which are assumed as guests in the upper-level Indian restaurant.

• $\mathbb{D}$ is the finite set of resources $\mathbb{D}=\Big\{{d}_1$, d ₂,…, d _l } in the VBP. Elements in $\mathbb{D}$ metaphorically represent different dishes on the buffet table in the upper-level Indian restaurant.

• S _i is the set of strategies with the player i. If the player i is the VBP, i.e., $i\in \mathbf{\mathcal{C}}$, a strategy set can be defined as S _i  = {${\delta}_i^1$, ${\delta}_i^2$,…, ${\delta}_i^l$} where ${\delta}_i^k$ is the distribution status of kth resource, i.e., 1 ≤ k ≤ l. If the player i is a SBS, i.e., i ∈ ℬ, the player i can request multiple resources. Therefore, the strategy set can be defined as a combination of requested resources S _i  = {∅, {${d}_i^1\left({\mathrm{\mathcal{I}}}_i^1\right)$}, {${d}_i^1\left({\mathrm{\mathcal{I}}}_i^1\right)$, ${d}_i^2$(${\mathrm{\mathcal{I}}}_i^2$)},…, {${d}_i^1\left({\mathrm{\mathcal{I}}}_i^1\right)$, ${d}_i^2\left({\mathrm{\mathcal{I}}}_i^2\right)$,…, ${d}_i^l\left({\mathrm{\mathcal{I}}}_i^l\right)$}} where ${\mathrm{\mathcal{I}}}_i^k$ is the player i’s requested amount for the kth resource; each player’s strategy set is finite with 2^l elements.

• The U _i is the payoff received by the player i. If the player i is the VBP, i.e., $i\in \mathbf{\mathcal{C}}$, it is the total profit obtained from the resource distribution for SBSs. If the player i is a SBS, i.e., i ∈ ℬ, the payoff is determined as the outcomes of the distributed resources minus the cost of corresponding resources.

• The T is a time period. The ${\mathbb{G}}^U$ is repeated t ∈ T < ∞ time periods with imperfect information.

Based on the distributed resources, SBSs are responsible to support MUs’ services while ensuring the required quality of service (QoS). Usually, SBSs deploy sparsely with each other to avoid mutual interference and are operated in a time-slotted manner. To formulate interactions between SBSs and MUs, our lower-level Indian buffet game (${\mathbb{G}}^L$) can be defined as ${\mathbb{G}}^L=\left\{\mathrm{\mathbb{P}},{\left\{{\mathbf{\mathcal{L}}}_i\right\}}_{i\in \mathrm{\mathbb{P}}},\ {\left\{{\mathbf{\mathcal{T}}}_i\right\}}_{i\in \mathrm{\mathbb{P}}},\ {\left\{{U}_i\right\}}_{i\in \mathrm{\mathbb{P}}},\ T\right\}$ at each time period t of gameplay.

• ℙ is the finite set of players $\mathrm{\mathbb{P}}=\left\{\mathbf{\mathcal{B}},\mathbf{\mathcal{X}}\right\}$ where ℬ = {b ₁, …, b _n } is a set of multiple SBSs and $\mathbf{\mathcal{X}}$ = {x ₁, …, x _m } is a set of multiple MUs, which are assumed guests in the lower-level Indian restaurant.

• ${\mathbf{\mathcal{L}}}_i=\Big\{{\mathrm{\mathcal{R}}}_i^1$, ${\mathrm{\mathcal{R}}}_i^2$,…, ${\mathrm{\mathcal{R}}}_i^l\Big\}$ is the finite set of the player i’s resources, i.e., i ∈ ℬ. Elements in ℒ _i metaphorically represent different dishes on the buffet table in the ith lower-level Indian restaurant; there are total n lower-level Indian restaurants.

• ${\mathbf{\mathcal{T}}}_i$ is the set of strategies with the player i. If the player i is a SBS, i.e., i ∈ ℬ, the strategy set can be defined as ${\mathbf{\mathcal{T}}}_i$ = {${\lambda}_i^1$, ${\lambda}_i^2$,…, ${\lambda}_i^l$} where ${\lambda}_i^k$ is the price of the kth resource in the ith SBS. If the player i is a MU, i.e., $i\in \mathbf{\mathcal{X}}$, the player i can request multiple resources. Therefore, the strategy set can be defined as a combination of requested resources ${\mathbf{\mathcal{T}}}_i$ = {∅, {${\mathrm{\mathcal{R}}}_i^1\left({\xi}_i^1\right)$}, {${\mathrm{\mathcal{R}}}_i^1\left({\xi}_i^1\right)$,${\mathrm{\mathcal{R}}}_i^2$(${\xi}_i^2$)},…, {${\mathrm{\mathcal{R}}}_i^1\left({\xi}_i^1\right)$, ${\mathrm{\mathcal{R}}}_i^2\left({\xi}_i^2\right)$,…, ${\mathrm{\mathcal{R}}}_i^l\left({\xi}_i^l\right)$}} where ${\xi}_i^k$ is the MU i’s request amount for the kth resource.

• The U _i is the payoff received by the player i. If the player i is a SBS, i.e., i ∈ ℬ, it is the total profit obtained from the resource allocation for MUs. If the player i is a MU, i.e., $i\in \mathbf{\mathcal{X}}$, the payoff is determined as the outcomes of the allocated resources minus the cost of corresponding resources.

• The T is a time period. The ${\mathbb{G}}^L$ is repeated t ∈ T < ∞ time periods with imperfect information.

4 Proposed resource sharing algorithm in C-RAN systems

In this section, we present our resource sharing algorithm, which employs a hierarchical two-level approach. And then, the proposed scheme is described strategically in a nine-step procedure through the coopetition concept.

4.1 C-RAN resource sharing in the upper Indian buffet game

In this sub-section, we consider the upper-level Indian buffet game. In C-RAN systems, there are multiple resource types, and multiple SBSs request different resources to the VBP. In this study, we mainly consider four resource types: CPU, memory, storage, and network bandwidth. Let $\mathbb{D}$ denote a set of resources in the VBP; $\mathbb{D}=\Big\{{d}_1$ = CPU; d ₂ = memory; d ₃ = storage; d ₄ = bandwidth } where each d represents the available amount of corresponding resource. Virtualization technology is used to collect these resources from CPs, and they are dynamically shared among SBSs. In our upper-level Indian buffet game, there are one VBP and n SBSs. The VBP is responsible for the cloud resource control and distributes resources over multiple SBSs. Each SBS is deployed for each microcell and covers relatively a small area. In general, SBSs are situated around high traffic density hot spots to support QoS-ensured applications. To get an effective solution for the upper-level Indian game, we focused on the basic concept of the shapley value (SV). It is a well-known solution idea for ensuring an equitable division, i.e., the fairest allocation, of collectively gained profits among the several collaborative players [5].

When the requested amount of kth resource (${\partial}_i^k$, 1 ≤ k ≤ 4) of the ith SBS (SBS _i ) is less than the distributed resource (${\mathcal{A}}_i^k$), i.e., ${\partial}_i^k<{\mathcal{A}}_i^k$; the SBS _i can waste this excess resource, and the property loss is estimated based on the resource unit price ($U\_{\mathcal{P}}_i^k$). $U\_{\mathcal{P}}_i^k$ value is adaptively adjusted in the lower-level Indian buffet game; it is discussed in Section 4.3. In this case, the value function (v(SBS _i )) of the SBS _i becomes $v\left({\mathrm{SBS}}_i\right)=-U\_{\mathcal{P}}_i^k\times \left({\mathcal{A}}_i^k-{\partial}_i^k\right)$. Conversely, if ${\partial}_i^k>{\mathcal{A}}_i^k$, the deficient resource amount $\left({\partial}_i^k-{\mathcal{A}}_i^k\right)$ is needed in the SBS _i . Therefore, the value function becomes $v\left({\mathrm{SBS}}_i\right)=U\_{\mathcal{P}}_i^k\times \left({\partial}_i^k-{\mathcal{A}}_i^k\right)$. We assume that ℕ = {$\mathbf{\mathcal{C}}$ = {VBP}∪ ℬ = {b ₁, …, b _n }} is a set of upper game players and v(·) is a real valued function defined on all subsets of ℬ satisfying v(∅) = 0. Therefore, in our game model, a nonempty subset (c) of ℬ is called a coalition. A set of games with a finite number of players is denoted by Γ. Given a game (ℬ, v(·)) ∈ Γ, let ℂ^k be a coalition structure of ℬ for the kth resource. In particular, ${\mathrm{\mathbb{C}}}^k=\left\{{\boldsymbol{c}}_1^k, \dots,\ {\boldsymbol{c}}_j^k\right\}$ is a partition of ℬ, that is, ${\boldsymbol{c}}_f^k\kern0.5em {\displaystyle {\displaystyle \cap \kern0.5em {\boldsymbol{c}}_h^k=\varnothing }}$ for f ≠ h and ${\displaystyle {\cup}_{t=1}^j{\boldsymbol{c}}_t^k=\mathbf{\mathcal{B}}}$.

Let θ be an order on ℬ, that is, θ is a bijection on ℬ. A set of all the orders on ℬ is denoted by Θ(ℬ) [12, 13]. A set of game players preceding the player i for the kth resource at order θ is ${\mathfrak{A}}_i^{\theta }(k)=\left\{j\in \mathbf{\mathcal{B}}\ :\ \theta (j)<\theta (i)\right\}$. Therefore, $v\left({\mathfrak{A}}_i^{\theta }(k)\right)$ can be expressed as

$$ v\left({\mathfrak{A}}_i^{\theta }(k)\right)=U\_{\mathcal{P}}_i^k\times {\left[{\displaystyle \sum_{q\in {\mathfrak{A}}_q^{\theta }(k)}}{\partial}_q^k-{\displaystyle \sum_{q\in {\mathfrak{A}}_q^{\theta }(k)}}{\mathcal{A}}_q^k\right]}^{+}-U\_{\mathcal{P}}_i^k\times {\left[{\displaystyle \sum_{q\in {\mathfrak{A}}_q^{\theta }(k)}}{\mathcal{A}}_q^k-{\displaystyle \sum_{q\in {\mathfrak{A}}_q^{\theta }(k)}}{\partial}_q^k\right]}^{+} $$

(1)

$$ \mathrm{s}.\mathrm{t}.,{\left[x\right]}^{+}= \max \left(x,\ 0\right) $$

A marginal contribution of the player i at order θ in (ℬ, v(·), k) is defined by ${\mathcal{S}}_i^{\theta}\left(\mathbf{\mathcal{B}},\ v,k\right)=v\left({\mathfrak{A}}_i^{\theta }(k){\displaystyle \cup}\left\{i\right\}\right)-v\left({\mathfrak{A}}_i^{\theta }(k)\right)$. Then the SV of (ℬ, v(·), k) is defined as follows [12]:

$$ S{V}_i\left(\mathbf{\mathcal{B}},\ v,k\right)=\frac{1}{\left|\Theta \left(\mathbf{\mathcal{B}}\right)\right|}\times {\displaystyle \sum_{\theta \in \Theta \left(\mathbf{\mathcal{B}}\right)}}\left({\mathcal{S}}_i^{\theta}\left(\mathbf{\mathcal{B}},\ v,k\right)\right),\kern1.25em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{all}\ i\in \mathbf{\mathcal{B}} $$

(2)

where | · | represents the cardinality of the set. Therefore, the SV is an average of marginal contribution vectors where each order θ ∈ Θ(ℬ) occurs in an equal probability, that is, 1/|Θ(ℬ)|. Under the cooperative game situation, SV provides a unique solution with the desirable properties: (i) efficiency, (ii) symmetry, (iii) additivity, and (iv) dummy [5, 12].

Although the SV is quite an interesting concept, and provides an optimal and fair solution for many applications, its main drawback is its computational complexity: the number of computations will increase prohibitively when the number of game players increases. Therefore, applications that utilize the SV remain scarce [12, 13]. In this study, if all possible orderings of SBSs (Θ(ℬ)) have to be taken into account in calculating Eqs. (1) and (2), the computational complexity of calculating the SV can be very high and too heavy to be implemented in real C-RAN operations. To resolve this problem, we adopt the new concept of an asymptotic shapley value (A_SV) approach, which is an approximation method for the SV under a large number of players [12, 13]. For the kth resource, let the A_SV of player i be ${\phi}_i^k$; it is given as follows:

$$ {\phi}_i^k=\left\{\begin{array}{c}\hfill \left(U\_{\mathcal{P}}_i^k\times {\displaystyle \underset{\mathsf{0}}{\overset{\mathsf{1}}{\int }}}\kern0.5em \mathrm{e}\mathrm{r}\mathrm{f}\left(\frac{\sqrt{{\mathcal{P}}_u^k}\times \tau }{\sqrt{2}\times \eta}\right)dp\right)\times \left({\partial}_i^k-{\mathcal{A}}_i^k\right), \kern2.25em if\kern0.75em \frac{\mu_s^k\times {N}_s^k}{\mu_B^k\times {N}_B^k}=1\hfill \\ {}\hfill \hfill \\ {}\hfill \kern3.25em U\_{\mathcal{P}}_i^k\times \left({\partial}_i^k-{\mathcal{A}}_i^k\right)\kern9.5em ,\kern2em if\kern0.75em \frac{\mu_s^k\times {N}_s^k}{\mu_B^k\times {N}_B^k}\ne 1\hfill \end{array}\kern0.75em \right. $$

(3)

$$ \mathrm{s}.\mathrm{t}.,\ \mathrm{e}\mathrm{r}\mathrm{f}(x)=\frac{1}{\sqrt{\left|\Theta \left(\mathbf{\mathcal{B}}\right)\right|}}{\displaystyle \underset{-x}{\overset{x}{\int }}}\kern0.5em {e}^{-{y}^2} dy,\eta =\sqrt{\frac{\mu_B^k\times {\left({\sigma}_S^k\right)}^2+{\mu}_s^k\times {\left({\sigma}_B^k\right)}^2}{\mu_B^k+{\mu}_s^k}},\ \tau =\frac{\mu_s^k\times {N}_s^k-{\mu}_B^k\times {N}_B^k}{\sqrt{\mathbf{\mathcal{B}}}} $$

where ${N}_s^k$ and ${N}_B^k$ are the number of players with the condition of ${\partial}^k-{\mathcal{A}}^k$ < 0 and the condition of ${\partial}^k-{\mathcal{A}}^k$ ≥ 0, respectively. ${\mu}_s^k$ and ${\mu}_B^k$ (or ${\left({\sigma}_S^k\right)}^2$ and ${\left({\sigma}_B^k\right)}^2$) are the mean (or variance) of total wasted and needed kth resource, respectively. The method for obtaining the proof of the derivation of A_SV value can be found in [13].

Under dynamic C-RAN environments, fixed resource distribution methods cannot effectively adapt to changing system conditions. In this study, we treat the resource distribution for multiple SBSs as an online decision problem. At the time period t, the total amount of available kth resource ($\mathcal{A}\_{\mathrm{\mathcal{R}}}_t^k$) is dynamically re-distributed over SBSs according to ϕ ^k values. In order to apply the time-driven implementation of resource re-distribution, we partition the time axis into equal intervals of length unit_time. At the end of each time period, the re-distributed kth resource amount for the SBS _i (${\Pi}_i^k$(t)) is obtained periodically as follows.

$$ {\Pi}_i^k(t)=\mathcal{A}\_{\mathrm{\mathcal{R}}}_t^k \times \kern0.5em \frac{\phi_i^k+\left|\underset{j\in \mathbf{\mathcal{B}}}{ \min}\left\{{\phi}_j^k\right\}\right|}{{\displaystyle {\sum}_{b\in \mathbf{\mathcal{B}}}}\left({\phi}_b^k+\left|\underset{j\in \mathbf{\mathcal{B}}}{ \min}\left\{{\phi}_j^k\right\}\right|\right)},\kern1.5em \mathrm{s}.\mathrm{t}.,\kern0.75em t\in T $$

(4)

4.2 C-RAN resource sharing in a lower-level Indian buffet game

In the lower-level Indian game model, multiple MUs request different resources to their corresponding SBS. Let ${\mathrm{MU}}_i^j$ be the MU j in the area of SBS _i and ℒ _i denote a set of resources in the ith SBS; ℒ _i  = {${\mathrm{\mathcal{R}}}_i^1$ = CPU, ${\mathrm{\mathcal{R}}}_i^2$ = memory, ${\mathrm{\mathcal{R}}}_i^3$ = storage, ${\mathrm{\mathcal{R}}}_i^4$ = bandwidth}. Each ${\mathrm{\mathcal{R}}}_i^k$ represents the available amount of kth resource in the SBS _i ; these resources are obtained from the VBP through the upper-level Indian game. Individual MU attempts to actually purchase multiple resources based on their unit prices $U\_{\mathcal{P}}_i^k$, where 1 ≤ k ≤ 4 and i ∈ ℬ.

Our lower-level Indian game deals with the resource allocation problem while maximizing resource efficiencies. Based on the reciprocal relationship between SBSs and MUs, we adaptively allocate SBSs’ resources to each MU. From the viewpoint of MUs, their payoffs correspond to the received benefit minus the incurred cost [14]. Based on its expected payoff, each MU attempts to find the best actions. The MU j’s utility function of kth resource (${U}_j^k$) in the ith SBS is defined as follows.

$$ {U}_j^k\left({\xi}_j^k(i)\right)={b}_j\left({\xi}_j^k(i)\right)-c\left(U\_{\mathcal{P}}_i^k,{\xi}_j^k(i)\right) $$

(5)

s.t., ${b}_j\left({\xi}_j^k(i)\right)={\omega}_j^k\times \log \left({\xi}_j^k(i)\right)$ and mp ^k ≤ $U\_{\mathcal{P}}_i^k$ ≤ Mp ^k

where ${\xi}_j^k(i)$ is the MU j’s requested amount of kth resource in the SBS _i and ${b}_j\left({\xi}_j^k(i)\right)$ is the received benefit for the MU j. ${\omega}_j^k$ represents a payment that the MU j would spend for the kth resource based on its perceived worth. The $U\_{\mathcal{P}}_i^k$ is the unit price for the kth resource unit in the SBS _i and $c\left(U\_{\mathcal{P}}_i^k(i),{\xi}_j^k(i)\right)$ is the cost function of SBS _i . Each SBS decides the $U\_{\mathcal{P}}_i^k$ between the pre-defined minimum (mp ^k) and the maximum (Mp ^k) price boundaries. In general, a received benefit typically follows a model of diminishing returns to scale; MU’s marginal benefit diminishes with increasing bandwidth [14]. Based on this consideration, our received benefit can be represented in a general form of log function. In a distributed self-regarding fashion, each individual MU is independently interested in the sole goal of maximizing his/her utility function as

$$ \underset{\xi_j^k(i)\ge 0}{\mathbf{max}\ }{U}_j^k\left({\xi}_j^k(i)\right) = \underset{\xi_j^k(i)\ge 0}{\mathbf{max}}\ \left\{\left({b}_j\left({\xi}_j^k(i)\right)-c\Big(U\_{\mathcal{P}}_i^k(i),{\xi}_j^k(i)\right)\right\} $$

(6)

From the viewpoint of SBSs, the most important criterion is a total revenue; it is defined as the sum of payments from MUs [15]. Based on the $U\_{\mathcal{P}}_i^k$ and the total allocated resource amounts for MU’s, the total revenue of all SBSs (Ψ) is given by

$$ \boldsymbol{\varPsi} ={\displaystyle \sum_{i=1}^n}{\varPsi}_i={\displaystyle \sum_{i=1}^n}{\displaystyle \sum_{k=1}^l}\left(U\_{\mathcal{P}}_i^k\times {T}_i^k\right) = {\displaystyle \sum_{i=1}^n}{\displaystyle \sum_{k=1}^l}{\displaystyle \sum_{j=1}^m}\left(U\_{\mathcal{P}}_i^k\times {\xi}_j^k(i)\times {\mathfrak{l}}_j^k(i)\right) $$

(7)

s.t., ${\mathfrak{l}}_j^k(i)$ = $\left\{\begin{array}{l}1,\kern0.75em i\mathrm{f}\ \mathrm{the}\ \mathrm{requested}\ {\xi}_j^k(i)\ \mathrm{is}\ \mathrm{actually}\ \mathrm{allocated}\\ {}\begin{array}{c}\hfill \kern0.5em \hfill \\ {}\hfill \kern0.5em 0,\kern0.75em \mathrm{otherwise}\kern15.75em \hfill \end{array}\end{array}\right.$where n, l, and m are the total number of SBSs, resources, and MUs, respectively. Each SBS adaptively controls its own $U\_{\mathcal{P}}^k$ to maximize the revenue in a distributed manner. Our traffic model is assumed based on the elastic demand paradigm; according to the current $U\_{\mathcal{P}}^k$, MUs can adapt their resource requests. It is relevant in real-world situations where MUs’ requests may be influenced by the price [16, 17]. In response to ${\omega}_j^k$, the MU j can derive the ${\xi}_j^k(i)\kern0.5em \left( = {\omega}_j^k/U\_{\mathcal{P}}_i^k\right)$. In the SBS _i , the total requested resource amount from corresponding MUs is defined as

$$ {\displaystyle \sum_{k=1}^l}{\displaystyle \sum_{j=1}^m}{\xi}_j^k(i)\kern0.5em =\kern1em {\displaystyle \sum_{k=1}^l}\left(\frac{{\displaystyle {\sum}_{j=1}^m}{\omega}_j^k\ }{U\_{\mathcal{P}}_i^k}\right) $$

(8)

When the price is low, more MUs are attracted to participate in C-RAN services because of the good satisfactory payoff. However, if the price is high, MUs’ requests are reduced because of the unsatisfactory payoff. Therefore, to deal with the congestion problem, a higher price is suitable to match the resource capacity constraint while reducing the potential demands. In order to achieve the demand-supply balance, the current price should increase or decrease by $\varDelta U\_{\mathcal{P}}^k$.

In our proposed scheme, SBSs individually take account of previous price strategies to update their beliefs about what is the best-response price strategy in the future. If a strategy change can bring a higher payoff, SBSs have a tendency to move in the direction of that successful change, and vice versa. Therefore, SBSs dynamically tune their current strategies based on the payoff history. For the kth resource, the SBS _i ’s price strategy at the time period t + 1 (${\lambda}_i^k$(t + 1)) is defined as

$$ \left\{\begin{array}{c}\hfill {\lambda}_i^k\left(t+1\right)=\varLambda \left[{\lambda}_i^k(t)+\left|\Delta U\_{\mathcal{P}}_i^k(t)\right|\right],\kern0.5em If\kern0.5em \varOmega >0\hfill \\ {}\hfill \hfill \\ {}\hfill {\lambda}_i^k\left(t+1\right)=\varLambda \left[{\lambda}_i^k(t)-\left|\Delta U\_{\mathcal{P}}_i^k(t)\right|\right],\kern0.5em If\kern0.5em \varOmega \le 0\hfill \end{array}\right. $$

(9)

s.t., $\Delta U\_{\mathcal{P}}_i^k(t)=\frac{\left({\varPsi}_i^k(t)-{\varPsi}_i^k\left(t-1\right)\right)}{\varPsi_i^{t-1}\left(t-1\right)}$, $\Omega =\frac{\left({\lambda}_i^k(t)-{\lambda}_i^k\left(t-1\right)\right)}{\Delta U\_{\mathcal{P}}_i^k(t)}$, and $\boldsymbol{\varLambda} \left[\mathcal{K}\right]=\left\{\begin{array}{c}\hfill \boldsymbol{\varLambda} \left[\mathcal{K}\right]=m{p}^k,\ if\kern0.5em K<m{p}^k\kern2.5em \hfill \\ {}\hfill \boldsymbol{\varLambda} \left[\mathcal{K}\right]=K,\ if\kern0.5em m{p}^k\le K\le M{p}^k\hfill \\ {}\hfill \kern1em \boldsymbol{\varLambda} \left[\mathcal{K}\right]=M{p}^k,\ if\kern0.5em K>M{p}^{k\kern0.5em }\kern2.25em \hfill \end{array}\right.$

where ${\varPsi}_i^k(t)$ and ${\lambda}_i^k(t)$ are the SBS _i ’s revenue and price strategy for the kth resource at the time period t, respectively. $\left|\Delta U\_{\mathcal{P}}_i^k(t)\right|$ represents the absolute value of $\Delta U\_{\mathcal{P}}_i^k(t)$. According to Eq (7), the strategy profile of all SBSs can be denoted by a n × l matrix as follows:

$$ {\mathbf{\mathcal{T}}}_i(t) = \left\{{\lambda}_i^1(t),\ {\lambda}_i^2(t),\dots .\ {\lambda}_i^l(t)\right\}=\left[\begin{array}{c}\hfill {\lambda}_1^1(t),\hfill \\ {}\hfill {\lambda}_2^1(t),\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {\lambda}_n^1(t),\hfill \end{array}\begin{array}{c}\hfill\ {\lambda}_1^2(t),\hfill \\ {}\hfill\ {\lambda}_2^2(t),\ \hfill \\ {}\hfill \vdots \hfill \\ {}\hfill\ {\lambda}_n^2(t),\hfill \end{array}\begin{array}{c}\hfill\ \cdots \hfill \\ {}\hfill\ \cdots \hfill \\ {}\hfill \ddots \hfill \\ {}\hfill\ \cdots \hfill \end{array}\begin{array}{c}\hfill, {\lambda}_1^l(t)\hfill \\ {}\hfill, {\lambda}_2^l(t)\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill, {\lambda}_n^l(t)\hfill \end{array}\right],\kern0.5em \mathrm{s}.\mathrm{t}.,\kern0.5em i\in \mathbf{\mathcal{B}} $$

(10)

4.3 The main steps of the proposed algorithm

For the advanced wireless processing and reduced cost, C-RAN architecture is an attractive and innovative idea in both academic and industry fields. It can effectively support growing users’ needs. In this study, we present a novel C-RAN resource sharing scheme based on the two-level Indian buffet game model. In the upper-level Indian buffet game, available resources of CPs are distributed to SBSs based on the concept of A_SV. In the lower-level Indian buffet game, Individual SBS allocate the distributed resources to MUs according to the non-cooperative manner. Based on our coopetition paradigm, the VBU, SBSs, and MUs repeatedly interact with each other to effectively share the C-RAN resources. Therefore, in the proposed scheme, strategy decisions are coupled with one another; the result of the each player’s decisions is the input back to the other player’s decision process. The dynamics of the hierarchical feedback mechanism can cause cascade interactions of game players, and they can make their decisions to quickly find the most profitable solution while improving resource utilization and MUs’ satisfactions. In a constantly changing C-RAN system environment, it is a practical and suitable approach. The main steps of our resource sharing scheme are given next.

• Step 1: At the initial time, all SBSs have same price strategies ($\mathbf{\mathcal{T}}$). At the beginning of the game, this starting guess is a reasonable assumption.

• Step 2: At each game period, the VBP collects available resources from CPs using the virtualization technology and distributes these resources to each SBS according to Eqs. (1)–(4).

• Step 3: Individual MU in each cell attempts to actually purchase multiple resources from corresponding SBS. Based on this information, each SBS dynamically decides the price strategy ($\mathbf{\mathcal{T}}$) using Eqs. (6) and (7).

• Step 4: At each game period, the VBP re-distributes periodically the CP resources based on the currently calculating ϕ values; it is the upper-level Indian game.

• Step 5: Based on the current price ($\mathbf{\mathcal{T}}$), each MU dynamically decides the amount of purchasing resources according to Eq. (6).

• Step 6: Strategy decisions for each game player are made in an entirely distributed manner.

• Step 7: Under widely diverse C-RAN environments, the VBP, SBSs, and MUs are self-monitoring constantly based on the iterative feedback mechanism.

• Step 8: If the change of prices in all SBSs is within a pre-defined bound (ε), this change is negligible; proceed to step 9. Otherwise, proceed to step 2 for the next iteration.

• Step 9: Game is temporarily over. Ultimately, the proposed scheme reaches an effective resource sharing solution. When the C-RAN system status is changed, it can re-trigger another game-based resource sharing procedure.

5 Performance evaluation

In this section, the effectiveness of our proposed scheme is validated through simulation. Using a simulation model, the performance of our proposed scheme is compared with three existing C-RAN resource sharing schemes—the BPUV scheme [4], JCCN scheme [9], and CPRS scheme [10]. All schemes are implemented with a polynomial time computational complexity.

5.1 Simulation model, parameters, and scenario

In this study, we used the simulation tool MATLAB to develop our simulation model. MATLAB is one of the most widely used tools in a number of scientific simulation fields, such as digital processing, telecommunications, and mathematical analysis. In particular, MATLAB’s high-level syntax and dynamic types are ideal for model prototyping. The assumptions implemented in our simulation model are as follows.

• The simulated model was assumed as a C-RAN system with one VBP, 10 SBSs, and 100 MUs.

• The process for new application service requests was Poisson with rate σ (applications/MU/s), and the range of offered load was varied from 0 to 3.0.

• The total capacity of resources were CPU (d ₁ = 3.6 GHz), memory (d ₂ = 240 Mbyte), storage (d ₃ = 480 Gbyte), and bandwidth (d ₁ = 30 Mbps).

• System performance measures obtained on the basis of 50 simulation runs were plotted as a function of the offered load.

• Each application service had its own application type and requires different resource requirements. They were generated with equal probability.

• The durations of services were exponentially distributed.

• SBSs had the pre-defined minimum and maximum resource unit prices.

• For simplicity, we assumed the absence of noise or physical obstacles in our experiments.

In order to emulate a real C-RAN system environment and for a fair comparison, application types, characteristics, and system parameters are carefully selected for a realistic simulation scenario. Table 1 shows the application types and system parameters used in our simulation.

Table 1 Application and system parameters used in the simulation experiment

5.2 Simulation results

As mentioned earlier, the BPUV scheme [4], JCCN scheme [9], and CPRS scheme [10] have been recently published and introduced unique challenges to efficiently solve the resource sharing problem in C-RAN systems. However, they are successful only in certain circumstances. Compared to these schemes, we can confirm the superiority of our proposed hierarchical game approach.

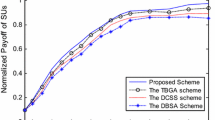
Figure 2 shows the normalized payoff of each scheme. It is measured as a normalized utility sum of all game players. To maximize the C-RAN system performance, payoff is an important performance metric. Under various application service requests, the VBU, SBSs, and MUs repeatedly interact with each other to effectively share the C-RAN resources. Therefore, our hierarchical game-based approach effectively controls resources and could lead to a higher payoff than other existing methods.

Fig. 2

Normalized payoff

Figure 3 presents the resource efficiency in the C-RAN system. In general, resource efficiency is the rate of actively used resource amount over the total resource amount. A key observation from the results shown in Fig. 3 is that all the schemes have similar trends. This trend implies that under higher service requests, a better resource efficiency is obtained. This is intuitively correct. According to the coopetition approach, the proposed scheme is flexible to sense the dynamic changing system environment while improving the resource efficiency. From the simulation results, we can see that our proposed scheme effectively shares C-RAN resources while maintaining a higher resource efficiency than other existing schemes.

Fig. 3

C-RAN resource efficiency

The curves in Fig. 4 show the performance analysis in terms of throughput loss ratio. In this study, throughput loss ratio is defined as the percentage of possible system outcome that is lost through ineffective resource operations. The purpose is to enhance the C-RAN throughput system through suitable consequences of coopetition interactions. Based on the feedback interaction process, our scheme constantly monitors the current C-RAN system conditions and efficiently solves the resource sharing problems. When designing an effective resource sharing mechanism for the C-RAN system, it is a highly desirable property. From the simulation results, the main observation is that we can maintain a lower throughput loss ratio than other existing schemes.

Fig. 4

Throughput loss ratio

Figure 5 presents the performance comparison in terms of QoS satisfaction probability. From the viewpoint of MUs, this is a very important factor. In this study, it is estimated as the percentage of the successfully serviced applications. To improve the MUs’ satisfaction level, our game-based approach iteratively interacts with the current system conditions and adjusts the allocated resource in a step-by-step manner. The simulation results show that the proposed scheme achieves a higher QoS satisfaction probability than other existing schemes.

Fig. 5

QoS satisfaction probability

5.3 Analysis and discussion

In summary, the simulation analysis obtained from Figs. 2, 3, 4, and 5 shows the performance trends of all the schemes. They are very similar. This is because the main design goals of all the schemes are the same. However, based on the two-level Indian buffet game approach, the proposed scheme adaptively responds to the current C-RAN system conditions in a distributed manner. Therefore, we can say that the proposed scheme is much more flexible, adaptable, and able to sense the current C-RAN environment. Therefore, as expected, we achieve a better C-RAN system performance than the BPUV scheme [4], JCCN scheme [9], and CPRS scheme [10].

In general, many existing schemes are one-sided protocols and strongly specialized for specific control issues. The existing schemes in [4, 9, 10] cannot adaptively estimate the current C-RAN system conditions and resolved the C-RAN resource sharing problem by using fixed system parameters. However, the proposed scheme is quite adaptive to a dynamic C-RAN system according to the two-level game-based online approach. Therefore, we can provide the flexibility and adaptability for the current system conditions. To estimate the flexibility and adaptability, we define a weighted flexibility and adaptability ($\mathbb{W}$) as a performance metric for overall performance and study the performance of different schemes based on this metric. Let N_P be the normalized payoff, R_E be the resource efficiency, and S_P be the QoS satisfaction probability. Let ς _{N_P} , ς _{R_E} , and ς _{S_P} be the relative weights for the three performance measures. Here, we define the $\mathbb{W}$ based on the weights ς _{N_P}  = 0.4, ς _{R_E}  = 0.3, and ς _{S_P}  = 0.3 as

$$ \mathbb{W}=\left({\varsigma}_{N\_P}\times N\_P\right)+\left({\varsigma}_{R\_E}\times R\_E\right)+\left({\varsigma}_{S\_P}\times S\_\right) $$

(11)

Figure 6 shows the weighted flexibility and adaptability ($\mathbb{W}$). Based on the Indian buffet game model, the proposed scheme can manage the C-RAN resource fairly well while achieving a higher performance. This result clearly shows that the proposed scheme is quite flexible and adaptable for real C-RAN system operations.

Fig. 6

Weighted flexibility and adaptability ($\mathbb{W}$)

6 Conclusions

Efficient and fine-grained resource sharing becomes an increasingly important and attractive control issue for new-generation C-RAN systems. In this work, we propose a novel multi-resource sharing scheme, which is framed as a two-level Indian buffet game model: the upper-level Indian game is played among VBP-SBSs, and the lower-level Indian game is played among SBSs-MUs. Based on the hierarchical interaction mechanism, the VBP, SBSs, and MUs are intertwined and make decisions during the step-by-step interactive feedback process. The novelty of our work lies in the fact that we develop a new resource sharing paradigm and apply this paradigm to control the C-RAN environment while comparing its performance to other existing schemes. From the simulation results, we can claim that our proposed approach effectively works to improve the system efficiency and utilization of resource usage in dynamically changeable C-RAN environments.

In this study, only a specific implementation case of the Indian buffet game is addressed as a restricted version. However, there are insights that can be applied to open questions in the field of various resource sharing research areas. Therefore, our work opens a door to some interesting extensions. For the future work, revenue sharing algorithms with cooperative game models can be implemented. Another issue for further study is how the quality of experience (QoE) could be resolved with the original QoS in C-RAN systems.