1 Introduction

The paradigm of cooperative communication has been shown to provide significant advantages in cellular networks (and many other applications) for more than a decade [1]. With the deployment of LTE networks across the world in recent years [2] and the shifting of focus in the research community to 5G cellular technology [3], the ideas surrounding cooperative communication are evolving. Of particular interest in the discussion of 5G is relay-aided communication. The heterogeneous structure of 5G networks will consist of layers of macrocells, small cells, relays, and device-to-device (D2D) networks [4]. In areas lacking a wired backhaul infrastructure, relays are, and will continue to be, deployed to act as picocell base stations to local user equipments (UEs) and to mimic (for the most part) a UE in the view of the macrocell base station. Within the D2D networking paradigm, relays will form a key component in the control infrastructure of a 5G network, linking D2D networks to the macrocell base station [4]. This idea can be further extended to connect D2D clusters to the macrocell by using one of the constituent UEs in the cluster as a relay [5, 6].

Fixed-gain amplify-and-forward (FGAF) relay systems have attracted a lot of attention recently due to their low complexity in practical implementation. To date, numerous efforts have been devoted to the performance analysis of dual-hop FGAF relay systems (see [7] and the references therein), including error rate, capacity, and outage calculations. With regard to the latter, closed-form outage probability expressions for dual-hop FGAF were derived in [8] for Rayleigh fading channels, in [7, 9, 10] for Nakagami-m channels, and in [11] for Rician channels. In [12], a moment generation function (MGF) approach was used to analyze the performance of dual-hop FGAF systems operating in arbitrary, or generalized, fading conditions. Heterogeneous fading conditions were also considered in [13] in the context of systems employing maximum ratio combining and transmit antenna selection at the relay. Many of these reported results were recently generalized and incorporated into a multi-hop framework in [14].

Relay selection, the process by which one relay is chosen among all the available relays to forward the data from the source to the destination [15], has been shown to be a simple and effective scheme that offers the same diversity order as cooperative schemes that use all available relays [16]. Recently, this concept has been considered within the 5G framework [17]. Three main selection schemes have been considered in the literature: (1) first-hop selection (FHS), in which the selected relay maximizes the signal-to-noise ratio (SNR) at the first hop; 2) second-hop selection (SHS), in which the second-hop SNR is maximized; and (3) dual-hop selection (DHS), where the the end-to-end SNR is the objective to be optimized1. Several published works have analyzed the outage probability for dual-hop AF relay selection systems [18–21]. However, the outage probability analysis carried out to date for such systems presents three main limitations:

  1. 1.

    Much of the published literature considers FHS or DHS, neglecting the case of SHS despite the fact that the latter is an important practical model.

  2. 2.

    Source-relay (S-R) and relay-destination (R-D) channels have largely been assumed to follow Rayleigh, Nakagami-m, or Rician distributions in relay selection systems, with some important fading distributions having been largely ignored (e.g., Weibull and Hoyt).

  3. 3.

    Heterogeneous fading conditions have generally not been studied for relay selection channels, although such scenarios may arise in a plethora of applications, such as a cellular base station transmitting to a relay located in an enterprise zone, which then conveys the signal to users inside an office block.

In this paper, we aim to overcome the aforementioned limitations by presenting a framework for analyzing the outage probability of FGAF systems employing relay selection in heterogeneous channel conditions. The proposed framework applies generally for arbitrary configurations of S-R/R-D channels, e.g., Nakagami-m/Rician, Hoyt/Weibull, etc. In order to facilitate exposition, we focus on Nakagami-m fading in this work and derive the outage probability for systems operating in heterogeneous channels for FHS, SHS, and DHS selection strategies. We also provide complete diversity results for each selection mechanism and qualitatively discuss the application of the framework to other fading configurations.

The rest of the paper is organized as follows. The dual-hop FGAF system model is presented in the “System model” section. The analytical framework is detailed in the “Analytical outage probability framework” section, which is then applied in the “Analysis for Nakagami-m ” section to study heterogeneous Nakagami-m scenarios. The analysis is corroborated with numerical results in the “Simulation results and discussion” section. Extending the framework to other more general fading configurations is discussed and concluding remarks are given in the “Conclusions” section.

2 System model

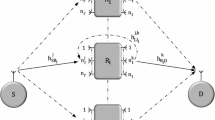
Consider a dual-hop transmission system where N≥1 relays are available to forward information from a source node to a destination node using an FGAF protocol (see Fig. 1). There is no direct S-D link. Suppose the nth relay is selected among the N available relays. A complex symbol with unit average power is transmitted from the source to the selected relay over a flat fading channel h 1,n . The received signal at this relay is then amplified with a fixed gain G, then transmitted from the relay to the destination over a flat fading channel h 2,n . We assume that h 1,n and h 2,n are independent but not necessarily identically distributed random variables.

Fig. 1
figure 1

Relay selection. Illustration of the dual-hop FGAF relay selection system model. Solid lines indicate the selected path

Full size image

Define \(\bar {\gamma }\) as a reference average received SNR parameter. Clearly, the average received SNR values corresponding to different hops will be different in practice. This is accounted for in the model by denoting the variances of the zero mean additive white Gaussian noise at the nth relay and the destination as \(\sigma ^{2}_{1,n}\) and \({\sigma ^{2}_{2}}\), respectively, and defining parameters ρ 1,n and ρ 2 such that \(\bar \gamma = \rho _{1,n}/\sigma ^{2}_{1,n}\) for n=1,…,N and \(\bar \gamma = \rho _{2}/{\sigma ^{2}_{2}}\). Thus, the SNR at the nth relay of the first hop is given by \(X_{n}=\frac {|h_{1,n}|^{2}}{\rho _{1,n}}\bar {\gamma }\), and the SNR corresponding to the local channel at the destination (i.e., not the end-to-end SNR) is \(Y_{n}=\frac {|h_{2,n}|^{2}}{\rho _{2}}\bar {\gamma }\).

For the relay selection process, a single relay is chosen among the N available relays according to the FHS, SHS, or DHS selection criteria. For FHS, the selection is made at the source to maximize the received SNR at the relay. The chosen relay can be notified of its selection through, for example, a dedicated control channel. Exact details of how control signaling might be performed are beyond the scope of this paper. Consequently, under the FHS approach, the kth relay is selected such that k= arg max{X n }. Analogously, for SHS, we have k= arg max{Y n }. Finally, for DHS, global channel knowledge is used to select the relay that maximizes the end-to-end SNR, which we denote by γ n for the nth path. Thus, in this case, we can write k= arg max{γ n }.

3 Analytical outage probability framework

Suppose the kth relay is selected to convey the source message to the destination. Irrespective of the selection criteria, we can write the end-to-end SNR as

$$ \gamma_{k}=\frac{X_{k}Y_{k}}{Y_{k}+C_{k}} $$
((1))

where \(C_{k} =\bar {\gamma }/(G^{2}\rho _{1k})\). For DHS, the SNR outage probability2 can be written as

$$ P_{\mathrm{o}}(z) = \prod_{n=1}^{N} P(\gamma_{n}\leq z) $$
((2))

where z is the outage threshold. For both FHS and SHS, we let ℘ h,k denote the probability that the kth relay is selected according to criteria h∈{FHS, SHS}. Applying the law of total probability, we can write

$$ P_{\mathrm{o}}(z) = \sum_{k=1}^{N} \wp_{h,k}P(\gamma_{k} < z). $$
((3))

Note that we have slightly abused notation here since P(γ k <z) is conditioned on the selection mechanism (FHS or SHS) and the index of the selected relay k. Nevertheless, the important point is that γ k is a function of two independent variates, X k and Y k . This enables us to write a general formula for the cumulative distribution function (c.d.f.) of γ k , which we encompass in the following lemma (the proof is given in the Appendix).

Lemma 1.

Let γ k be defined as in (1). Then, the c.d.f. of γ k can be written as

$$ P(\gamma_{k} < z) = 1-\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}\lambda_{k}(s,z)\,\mathrm{d} s $$
((4))

where c is a real constant3, and

$$ \lambda_{k}(s,z) = \frac{(C_{k} z)^{-s}}{s} \int_{0}^{\infty} x^{s}f_{X_{k}}(x+z) \,\mathrm{d} x \int_{0}^{\infty} y^{s} f_{Y_{k}}(y)\,\mathrm{d} y. $$
((5))

Although the lemma seems somewhat inaccessible due to the integrals, we note that it provides an exact expression as a functional of the first- and second-hop fading density functions, regardless of the underlying distributions. The only stipulation is that the channels corresponding to the two hops are statistically independent, a condition that is often, if not always, satisfied in practice. We will revisit that and apply this lemma to a great effect in the next section.

Turning our attention to FHS and SHS, it remains to calculate ℘ h,k . For FHS, this quantity is given by

$$\begin{array}{*{20}l} \wp_{\text{FHS},k} &= P\left(\max\{X_{1}, \ldots, X_{k-1}, X_{k+1}, \ldots, X_{N}\}\leq X_{k}\right) \\ &= \int_{0}^{\infty} f_{X_{k}}(x)\prod_{n\neq k} P(X_{n} \leq x) \,\mathrm{d} x \end{array} $$
((6))

where it is assumed that {X n } are statistically independent. The expression for ℘ SHS,k is the same, but with Y replacing X.

Applying Lemma 1, we can now write the outage probability for DHS as

$$ P_{\mathrm{o}}(z) = \prod_{k=1}^{N}\left(1-\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}\lambda_{k}(s,z)\,\mathrm{d} s\right) $$
((7))

and the outage probability for FHS and SHS as

$$ P_{\mathrm{o}}(z) = 1- \sum_{k=1}^{N}\wp_{h,k}\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}\lambda_{k}(s,z)\,\mathrm{d} s $$
((8))

Consequently, to apply this framework, we must be able to calculate the functional λ k (s,z) as well as the contour integral

$$ \iota_{k}(z) = \frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}\lambda_{k}(s,z)\,\mathrm{d} s. $$
((9))

Since λ k (s,z) is determined by the channel distributions, it can often be calculated easily. For the contour integral, we will exploit the pole structure of λ k (s,z) and apply the residue theorem from complex analysis to solve the integral, thus yielding series expressions of the outage probabilities in general. These technical details will be the focus of the next section.

4 Analysis for Nakagami-m

For the purpose of presenting how the analytical framework can be applied, we assume the channels for the two hops adhere to the same class of distribution, but may have different parameters. The same approach can be used to study arbitrary combinations of fading distributions for the different channels.

Suppose all channels adhere to a Nakagami-m small-scale fading model. In this case, the probability density function (p.d.f.) of X n is given by

$$ f_{X_{n}}(x) = \frac{\rho_{1,n}^{m_{1,n}}x^{m_{1,n}-1}e^{-\frac{\rho_{1,n}}{\theta_{1,n} \bar\gamma}x}}{\theta_{1,n}^{m_{1,n}} \bar\gamma^{m_{1,n}} \Gamma({m_{1,n}})}, \quad x\geq 0 $$
((10))

and the p.d.f. of Y n is defined similarly. The corresponding c.d.f. of X n is given by

$$ P(X_{n} \leq x) =\frac{\gamma(m_{1,n}, {\rho_{1,n}x}/({\theta_{1,n}\bar{\gamma}}))}{\Gamma(m_{1,n})},\quad x\geq 0 $$
((11))

where \(\gamma (a,x) = {\int _{0}^{x}}{t^{a-1}e^{-t} \,\mathrm {d} t}\) is the lower incomplete gamma function [22]. The parameter m 1,n >1/2 is the shape parameter of the distribution (denoted by m 2,n for the p.d.f. of Y n ) while \(\theta _{1,n} = \mathbb E[|h_{1,n}|^{2}]\) is effectively the scale parameter (correspondingly, θ 2,n for Y n ).

4.1 FHS

To calculate P o(z) for the FHS scheme, let us first consider the probability that the kth relay is selected. Using the absolutely convergent series expansion

$$ \gamma(a,x)=\Gamma(a)x^{a} e^{-x}\sum_{k=0}^{\infty}\frac{x^{k}}{\Gamma(a+k+1)} $$
((12))

along with (6) enables us to write

$$ \begin{aligned} \wp_{\text{FHS},k} &= \frac{1}{\Gamma(m_{1,k})}\prod_{n=1}^{N}\left(\frac{\rho_{1,n}}{\theta_{1,n}\beta_{1}}\right)^{m_{1,n}} \\ &\quad\times\sum_{\mathcal L_{k}} \Gamma(\tilde{m}_{1,k})\prod_{n=1 \atop n\neq k}^{N}{\left(\frac{\rho_{1,n}}{\theta_{1,n}\beta_{1}}\right)^{l_{n}}}\frac{1}{\Gamma(m_{1,n}+l_{n}+1)} \end{aligned} $$
((13))

where the summation is (N−1)-fold, with the indices being the set \(\mathcal L_{k} = \{l_{1},\ldots, l_{k-1}, l_{k+1}, \ldots, l_{N}\}\), with l n =0,1,2,… for all n. In addition, \(\beta _{1}=\sum _{n=1}^{N}{\rho _{1,n}}/{\theta _{1,n}}\) and \(\tilde {m}_{1,k}=\sum _{n=1}^{N} m_{1,n}+\sum _{n=1,\,n\neq k}^{N}l_{n}\).

Now consider the calculation of λ k (s,z) in Lemma 1. The second integral in (5) is a gamma function. The calculation of the first integral follows from an application of the theory of order statistics (cf. [12, eq. (17)]) to obtain an expression for \(f_{X_{k}}\). Using the series expansion for the lower incomplete gamma function mentioned above, the result can be written as

$$ {\fontsize{9.3}{6}\begin{aligned} \lambda_{k}(s,z) &= \frac{e^{-\frac{z\beta_{1}}{\bar{\gamma}}}}{\Gamma(m_{2,k})}\prod_{n=1}^{N} \left(\frac{\rho_{1,n}z}{\theta_{1,n}\bar{\gamma}}\right)^{m_{1,n}}\sum_{n=1}^{N}\frac{1}{\Gamma(m_{1,n})}\\ &\quad\times\sum_{\mathcal{L}_{n}}\prod_{q=1\atop q\neq n}^{N}\left(\frac{\rho_{1,q}z} {\theta_{1,q}\bar{\gamma}}\right)^{l_{q}} \frac{1}{\Gamma(m_{1,q}+l_{q}+1)} \\ &\quad\times {A_{k}^{s}}\Gamma(s)\Gamma(s+m_{2,k})U(s+1, \tilde{m}_{1,n}+s+1, {z\beta_{1}}/{\bar{\gamma}}) \end{aligned}} $$
((14))

where A k =G 2 ρ 1,k θ 2,k /ρ 2 and

$$ U(a,b,x)=\Gamma(a)^{-1}\int_{0}^{\infty} t^{a-1}(1+t)^{b-a-1}e^{-xt}\,\mathrm{d} t $$
((15))

is the confluent hypergeometric function (Tricomi’s solution) [23].

We are now in a position to calculate the integral ι k (z) and thus the outage probability, which is made much easier than it may first appear through the use of the residue theorem [24]. More specifically, we note that for a fixed third argument, U(·,·,·) is entire in its first two arguments [23]. Furthermore, for some complex number a, Γ(x+a) has simple poles at x=−a−j for j=0,1,…. It follows from the Mellin inversion theorem [25] that the path of integration that defines ι k (z) is a line extending from −i ∞ to i ∞ just to the right of the imaginary axis, i.e., c>0 in (9). By noting that we can construct a path in the left half s-plane such that as |s|→∞ then \(|\int \lambda _{k}(s,z)\,\mathrm {d} s|\rightarrow 0\) along this path4, we can close the path of integration over which ι k (z) is defined with a semi-circular arc traversing this half plane counter-clockwise from i ∞ to −i ∞, thereby encircling the poles of λ k (s,z). Finally, we can employ the residue theorem to obtain a series expression for ι k (z). For the case where m 2,k is not an integer5, we end up with the expression

$$ {\fontsize{9}{6}\begin{aligned} \iota_{k}(z) &= \frac{e^{-\frac{z\beta_{1}}{\bar{\gamma}}}}{\Gamma(m_{2,k})}\prod_{n=1}^{N} \left(\frac{\rho_{1,n}z}{\theta_{1,n}\bar{\gamma}}\right)^{m_{1,n}}\sum_{n=1}^{N}\frac{1}{\Gamma(m_{1,n})}\\ &\quad\times\sum_{\mathcal{L}_{n}}\prod_{q=1\atop q\neq n}^{N}\left(\frac{\rho_{1,q}z}{\theta_{1,q}\bar{\gamma}}\right)^{l_{q}} \frac{1}{\Gamma(m_{1,q}+l_{q}+1)} \sum_{j=0}^{\infty}\frac{(-A_{k})^{-j}}{j!} \\ &\quad\times\left(\Gamma(m_{2,k}-j)U\!\left(1-j, \tilde{m}_{1,n}+1-j, \frac{z\beta_{1}}{\bar{\gamma}}\right)\right.\\ &\quad+ A_{k}^{-m_{2,k}}\Gamma(-j-m_{2,k})U\left(1-j-m_{2,k}, \tilde{m}_{1,n}+1-j\right.\\ &\left.\left.\quad-m_{2,k}, \frac{z\beta_{1}}{\bar{\gamma}}\right)\right). \end{aligned}} $$
((16))

Applying (16) to (8) gives the outage probability for FHS in Nakagami-m channels.

Although the outage probability is expressed as an infinite series, we will verify later that truncating the series to only a few terms provides an excellent approximation. Moreover, the hypergeometric function U(·,·,x) is well behaved for small arguments6, and thus, it is possible to construct an asymptotic series of Poincaré type for \(\bar {\gamma } \rightarrow \infty \). Discussion of such an activity is rather involved and would detract from the focus of this paper; hence, we defer it to a future contribution.

We also note that the outage expression given above applies to the general case where each of the N available channels at a given hop is subject to non-identical Nakagami-m fading with different scale and shape parameters, i.e., m 1,n ≠m 1,q for n≠q and so on. The result is therefore more general than that given in [19], where the outage probabilities are obtained for the case where m 1,n =m 1 and m 2,n =m 2 for all n.

To conclude this subsection, we provide a brief note on the case where m 2,k is an integer. Under this condition, λ k (s,z) has second-order poles at s=−m 2,k ,−m 2,k −1,…. The residue theorem can still be applied, but the calculations become cumbersome, and careful bookkeeping must be enforced in order to ensure the resulting series expansion is accurate. This is particularly true when \(\tilde {m}_{1,n}\) has certain properties (such as being an integer), as this will cause the structure of the expansion to vary. For our practical purposes, however, it is much more intuitive and efficient to evaluate the outage probability using non-integer values of m 2,k to approximate integers. We will show through simulations that this simple approximation works very well in practice.

4.2 SHS

The outage probability for SHS can be obtained by following a similar approach as was outlined above for FHS. Without presenting the details of the calculations, we directly present the outage probability expression to be

$$ {\fontsize{8.7}{6}\begin{aligned} P_{\mathrm{o}}(z)&=1-\prod_{n=1}^{N}\left(\frac{\rho_{2}}{\theta_{2,n}\beta_{2}}\right)^{m_{2,n}}\sum_{n=1}^{N}\frac{1}{\Gamma(m_{2,n})}\\ &\quad\times\sum_{\mathcal{L}_{n}}\prod_{q=1\atop q\neq n}^{N}\left(\frac{\rho_{2}}{\theta_{2,q}\beta_{2}}\right)^{l_{q}}\frac{1}{\Gamma(m_{2,q}+l_{q}+1)}\\ &\quad\times\sum_{k=1}^{N}\frac{\wp_{\text{SHS},k}}{\Gamma(m_{1,k})}\left(\frac{\rho_{1,k}z}{\theta_{1,k}\bar{\gamma}}\right)^{m_{1,k}}e^{-\frac{z\rho_{1,k}}{\theta_{1,k}\bar{\gamma}}}\\ &\quad\times \sum_{j=0}^{\infty}\frac{(-1)^{j}}{j!}\left(\frac{G^{2}\rho_{1,k}}{\beta_{2}}\right)^{-j} \left({\vphantom{\left(\frac{G^{2}\rho_{1,k}}{\beta_{2}}\right)}}\Gamma(\tilde{m}_{2,n}-j)U\left({\vphantom{\left(\frac{G^{2}\rho_{1,k}}{\beta_{2}}\right)}}1-j, m_{1,k}\right.\right.\\ &\quad\left.+1-j, \frac{\rho_{1k}z}{\theta_{1,k}\bar{\gamma}}\right) +\left(\frac{G^{2}\rho_{1,k}}{\beta_{2}}\right)^{-\tilde{m}_{2,n}} \Gamma(-j-\tilde{m}_{2,n})\\ &\quad\times\left.U\left(1-j-\tilde{m}_{2,n}, 1 + m_{1,k}-j-\tilde{m}_{2,n}, \frac{\rho_{1,k}z}{\theta_{1,k}\bar{\gamma}}\right)\right) \end{aligned}} $$
((17))

where β 2 and \(\tilde {m}_{2,k}\) are defined in a similar manner to β 1 and \(\tilde {m}_{1,k}\).

4.3 Single relay

Letting N=1 corresponds to the case where there is a single relay, and thus, selection does not take place, i.e., the system model is the canonical dual-hop FGAF topology with no direct link. The outage probability can be calculated from Lemma 1 where, clearly, k=1 and \(f_{X_{k}}\) and \(f_{Y_{k}}\) take the form given in (10). The resulting expression for the outage probability is

$$ {\begin{aligned} P_{\mathrm{o}}(z) &= 1-\frac{\left(\frac{\rho_{1}z}{\theta_{1}\bar{\gamma}}\right)^{m_{1}} e^{-\frac{z\rho_{1}} {\theta_{1}\bar{\gamma}}}}{\Gamma(m_{1})\Gamma(m_{2})} \sum_{j=0}^{\infty}\frac{1}{j!} \left(-\frac{\rho_{2}}{G^{2}\theta_{2}\rho_{1}}\right)^{j}\\ &\quad\times\left(\Gamma(m_{2}-j)U\!\left(1-j,m_{1}+1-j, \frac{z\rho_{1}}{\theta_{1}\bar{\gamma}}\right)\right.\\ &\quad+\left(\frac{\rho_{2}}{G^{2}\theta_{2}\rho_{1}}\right)^{m_{2}}\Gamma(-j-m_{2}) U\!\left(1-j-m_{2}, m_{1}\right.\\ &\left.\left.-m_{2}+1-j, \frac{z\rho_{1}}{\theta_{1}\bar{\gamma}}\right)\right) \end{aligned}} $$
((18))

where θ q and m q are the scale and shape parameters for the Nakagami-m channel at the qth hop, and \(\rho _{q}={\sigma ^{2}_{q}}\bar {\gamma }\) where \({\sigma ^{2}_{1}}\) and \({\sigma ^{2}_{2}}\) are the noise variances at the relay and the destination, respectively.

Although an outage expression for dual-hop FGAF systems with a single relay operating in Nakagami-m fading channels was provided in [7, eq. (20)], the result presented here is simpler and easier to evaluate numerically. To the best of our knowledge, (18) has not been reported in the literature.

4.4 DHS

The outage probability for DHS is obtained by substituting the expression for P o(z) given by (18) for the quantity in the brackets of (7), i.e., \(1-\frac {1}{2\pi i}\int _{c-i\infty }^{c+i\infty }\lambda _{k}(s,z) = P_{\mathrm {o}}(z)\). In doing so, all parameters should be replaced by those corresponding to the kth path for k=1,…,N. We omit the explicit expression for brevity.

4.5 Diversity analysis

As mentioned above, one may obtain asymptotic expansions for the outage probabilities corresponding to the abovementioned scenarios. Although a full asymptotic theory is rather involved and beyond the scope of this paper, it is relatively straightforward to obtain the diversity order for FHS, SHS, and DHS. This can be done in a rather cumbersome manner by invoking the series expansion representation of U(·,·,x) (cf. [23]) and retaining the leading order in \(\bar \gamma \). It is, however, much more straightforward to use the theorem recently reported in [14]. For the two-hop relay selection schemes treated here, this theorem states that the outage probability of the system decays asymptotically like \(O\left (\left (\ln \bar \gamma \right)^{\kappa -1} \bar \gamma ^{\Re (s_{0})}\right)\) where s 0 is the pole (of order κ) of the function

$$ G(s) = \mathbb E\left[{Z_{1}^{s}}\right]E\left[{Z_{2}^{s}}\right] $$
((19))

that lies furthest to the right in the s-plane, with Z 1 and Z 2 respectively denoting the local first- and second-hop SNRs after selection. A consequence of this theorem is that the diversity order, defined in the usual way as

$$ d = {\lim}_{\bar\gamma \rightarrow \infty} \frac{\ln P_{\mathrm{o}}(z)}{-\ln \bar\gamma}, $$
((20))

is simply given by (see [14] for details)

$$ d = -s_{0}. $$
((21))

First, consider the FHS scheme, and suppose all shape parameters in the first hop are distinct7. For this case, let

$$ n^{\star} = \arg\max_{n}\{X_{n}\} $$
((22))

such that \(Z_{1} = X_{n^{\star }}\phantom {\dot {i}\!}\) and \(Z_{2} = Y_{n^{\star }}\phantom {\dot {i}\!}\). The p.d.f. of Z 1 is

$$\begin{array}{*{20}l} f_{Z_{1}}(z) &= \frac{\partial}{\partial z}\left\{P(X_{1} \leq z) \cdots P(X_{N} \leq z)\right\} \\ &= \sum_{n=1}^{N} f_{X_{n}}(z) \prod_{k\neq n} P(X_{k} \leq z) \end{array} $$
((23))

where \(f_{X_{n}}(z)\) and P(X k ≤z) are given in (10) and (11), respectively. Using (12), it is straightforward to show that

$$ \begin{aligned} \mathbb E[Z_{1}] =&\, \int_{0}^{\infty} z^{s} f_{Z_{1}}(z) \,\mathrm{d} z = a_{0} \Gamma(\zeta + s)\\ &+ a_{1} \Gamma(\zeta + 1 + s) + \ldots \end{aligned} $$
((24))

where \(\zeta = \sum _{n=1}^{N} m_{1,n}\). Consequently, the pole that lies furthest to the right in the s-plane is s=−ζ. Moreover, it is easy to see that

$$ \mathbb E[Z_{2}] \propto \Gamma(m_{2,n^{\star}}+s) $$
((25))

which has a dominant pole at \(s = -m_{2,n^{\star }}\phantom {\dot {i}\!}\). In systems employing selection diversity, it is well known that outage is dominated by the worst case channel. Since all second-hop channels are independent, this pertains to the case where the selection process results in the second channel having the minimum shape parameter. It follows from this fact and the calculations above that the diversity order for FHS is

$$ d = \min\left\{\sum_{n=1}^{N} m_{1,n},m_{2,1},\ldots,m_{2,N}\right\}. $$
((26))

Using a similar approach, it can be shown that the diversity order for SHS is

$$ d = \min\left\{\sum_{n=1}^{N} m_{2,n},m_{1,1},\ldots,m_{1,N}\right\}. $$
((27))

To calculate the diversity order for DHS, it is easiest to substitute (2) into (20), which leads to

$$ d = \sum_{n=1}^{N} \min\{m_{1,n},m_{2,n}\}. $$
((28))

These results are summarized in Table 1. One can confirm that these diversity orders specialize to the previous published results when the scale parameters and shape parameters are the same for all N channels for a given hop (see [19, Th. 3]).

Table 1 Diversity orders for FHS, SHS, and DHS in Nakagami-m fading
Full size table

5 Simulation results and discussion

In this section, we present numerical results in an effort to validate the analysis presented above. For all of the results presented below, we consider the case where there are two relays available, i.e., N=2, and the ρ and θ parameters are all set to 1 if not otherwise stated.

Various channel configurations were considered; Table 2 provides an overview, and the corresponding diversity orders are given in Table 3. For configurations Nak-1 and Nak-2, we considered the case where there is only a single relay, and the channels in both hops are non-identically or identically distributed, respectively. For configurations Nak-3, Nak-4, and Nak-5, we considered systems with relay selection, where Nak-3 and Nak-4 represent the cases where the N channels are identically distributed at the second hop and the first hop, respectively, and Nak-5 describes the case where all channels at all relays in both hops are identically distributed. Nak-6 considered the generalized case where the fading parameters are arbitrarily chosen such that channels corresponding to each relay for each hop are non-identically distributed, and the θ and ρ parameters for this case are also arbitrarily chosen to be θ 1,1=0.6, θ 1,2=0.8, θ 2,1=0.9, θ 2,2=1.1, ρ 1,1=1, ρ 1,2=0.9, and ρ 2=0.8. Note that for the Nak-2 configuration, we have deliberately chosen the parameters such that m 2 is an integer. The effect of second-order poles in this case was discussed in the “Analysis for Nakagami-m ” section. Here, instead of considering the residues at the second-order poles, we simply use a non-integer value of m 2 to obtain approximate numerical results. It will be shown that such an approximation yields reasonably accurate results compared with numerical simulations.

Table 2 Shape parameter definitions for different dual-hop Nakagami-m fading configurations. Values that span two columns indicate a single-relay system
Full size table
Table 3 Diversity orders corresponding to configurations outlined in Table 2
Full size table

Figures 2, 3, and 4 depict the results for channels Nak-1 to Nak-5 with FHS, SHS, and DHS, respectively. It is shown that the analytical results agree well with the simulations for all SNR values, even though the series expressions were truncated to ten terms. In addition, the diversity orders given in Table 3 can be verified from the figures. In particular, it is observed in Fig. 4 that the outage probability corresponding to Nak-5 outperforms that for Nak-2 at SNR values greater than 10 dB due to the higher diversity gain associated with Nak-5. An additional interesting feature that is brought out in these results is the importance of properly choosing the selection scheme according to the prevailing statistical channel conditions. Observing Figs. 2 and 3, we see that the Nak-4 relay selection system performs worse than the single-relay Nak-1 system for SNR values greater than 10 dB when FHS is employed (see Fig. 2). This is due to the comparatively low diversity order resulting from the selection process (see Table 3). However, if SHS is employed in the Nak-4 system, the diversity advantage offered by the selection scheme is realized, as shown in Fig. 3.

Fig. 2
figure 2

FHS outage probability. Outage probability of dual-hop FGAF systems with FHS

Full size image
Fig. 3
figure 3

SHS outage probability. Outage probability of dual-hop FGAF systems with SHS

Full size image
Fig. 4
figure 4

DHS outage probability. Outage probability of dual-hop FGAF systems with DHS

Full size image

Figure 5 illustrates the outage probability for the Nak-6 configuration. Again, the numerical results are shown to agree with the simulation results for all selection schemes. In addition, it is observed that for this particular configuration, FHS significantly outperforms SHS owing to the fact that the diversity order offered by the former is 2.4, whereas it is 0.9 in the latter case. The disparity in the diversity orders due to the use of different selection strategies provides significant insights into practical design for relay selection systems.

Fig. 5
figure 5

Outage probability for non-identically distributed channels. Outage probability of Nak-6 dual-hop FGAF systems for FHS, SHS, and DHS

Full size image

In Fig. 6, we present the numerical results obtained by setting the shape parameters to 1 (i.e., Rayleigh fading) at the second hop or at both hops, thus depicting Nakagami-Rayleigh or Rayleigh-Rayleigh fading scenarios. The results in Fig. 6 were obtained by using m 1,1=1.3 and m 1,2=2.5 at the first hop for the Nakagami-Rayleigh configuration. It is observed that for all three selection methods, the Nakagami-Rayleigh configuration provides better performance than the Rayleigh-Rayleigh mode, which satisfies intuition since Rayleigh channels exhibit more severe fading than Nakagami-m channels. It is also interesting to observe that SHS yields an outage gain compared to FHS in the Nakagami-Rayleigh channel, indicating the advantage of performing selection at the hop that experiences more severe fading.

Fig. 6
figure 6

Outage probability for heterogeneous channels. Outage probability of dual-hop FGAF systems using three selection schemes for different channel configurations

Full size image

6 Conclusions

The framework presented herein can be applied to analyze many practical system configurations. The key components that are required are derived from Lemma 1, whence we see that density functions of the effective channel gains X k and Y k are required along with integrals that are closely linked to their Mellin transforms. Certainly, having this information available makes the calculation of ℘ h,k possible in re (6) as a series expansion if not in a simple closed form.

Taking a step back, it is clear that the example discussed in the previous section was made possible by the pole structure of λ k (s,z), which in turn arose from the Mellin transform properties of the densities f X and f Y . These p.d.f.s are simply gamma kernels, and thus, it stands to reason that very similar techniques can be brought to bear to analyze systems involving other related distributions. To illustrate this point further, let us consider the case where each hop experiences Weibull fading. In this case, the first integral in (5) will have the form

$$ \theta^{s} \Gamma(s/m + 1) $$
((29))

for some shape and scale parameters m and θ, the poles of which lie at s=−m(1+j) for j=0,1,…. Thus, we can see that problems involving Weibull distributions will also experience a rich pole structure, and the full power of the residue theorem will be applicable.

Other fading distributions are also worth considering within this framework. Rician and Hoyt densities involve Bessel functions, which lead to hypergeometric functions (1 F 1 in the case of Rician and 2 F 1 in the case of Hoyt) through the evaluation of the integral \(\int x^{s} f_{X}(x) \,\mathrm {d} x\) in (5). But these functions are either entire or meromorphic in the arguments and thus can be dealt with by calculating the residues just as was done for Nakagami-m fading. Although the method is straightforward, the exact results are often challenging to interpret in written form given only a few pages in which to do so, and thus, we have omitted them from this discussion.

It should be clear by now that the fading distributions corresponding to each hop in the network need not belong to the same class, e.g., Rician, Weibull, etc. Indeed, the power of the framework is that it is relatively agnostic to the functions f X and f Y , as long as the related integrals given in (5) exist and the result facilitates contour integration vis-à-vis (4).

As a final note, we have liberally made use of infinite series representations of special functions through this analysis. For the examples discussed in the previous section, these series were convergent and thus well behaved under the operation of integration. However, if one is concerned mostly with asymptotics (e.g., high SNR), this condition need not be satisfied. In fact, very accurate approximations to the outage probability of some relatively complex systems can be attained from truncated asymptotic series. Again, we leave the details to another forum due to space restrictions.

7 Endnotes

1 The term partial selection is also used in the literature to describe relay selection based on channel knowledge pertaining to a single hop.

2 As is customary, we consider SNR outage since there is a one-to-one relationship between this performance metric, mutual information outage, and many symbol-error-rate outage expressions encountered in practice when flat fading is assumed.

3 This constant arises from the use of the Mellin inversion theorem [25] and basically separates the poles of the integrand in a particular and well-defined way for a given function λ k . The interval in which c lies is explored for specific examples in the next section.

4 This follows from Stirling’s formula [22] and an application of Jordan’s lemma [26].

5 We will return to the case where m 2,k is an integer later.

6 Technically, there is a singularity at x=0, but for the purposes of our system analysis, this condition will never hold.

7 When the shape parameters are not distinct, the same approach that is outlined in this section can be taken, but the algebra and differentiation become cumbersome.

8 Appendix

The following is a proof of Lemma 1. First, recall that the Mellin transform of a function f is defined as \(\mathbb M[f;s]=\int _{0}^{\infty }{x^{s-1}f(x) \,\mathrm {d} x}\) when the integral converges. Moreover, the inverse transform is given by

$$ f(x) = \frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}x^{-s}\mathbb M[f;s] \,\mathrm{d} s $$
((30))

for \(c\in \mathbb R\) in the strip of analyticity of \(\mathbb M[f;s]\). It can be shown using integration by parts that if f X (x) is the p.d.f. of X, defined for x≥0, and \(\mathcal {F}_{X}(x)=\int _{x}^{\infty }f_{X}(t)\,\mathrm {d} t\) is the complementary c.d.f (c.c.d.f.) of X, then

$$ \mathbb M[\mathcal{F}_{X};s]=s^{-1}\mathbb M[f_{X}; s+1] $$
((31))

for probability distributions with exponentially decaying tails. Finally, we recall that given two independent random variables X and Y and their product Z=X Y, the Mellin transform of the density f Z is the product of the transforms of the densities f X and f Y , i.e., \(\mathbb M[f_{Z};s] = \mathbb M[f_{X};s] \mathbb M[f_{Y};s]\).

Now, omitting the subscript k, we can write P(γ<z) as

$$ \begin{aligned} 1 &- P(XY \geq z(Y+C)) \\ &=1- P(X > z)P((X-z)Y \geq Cz | X > z). \end{aligned} $$
((32))

Define the variate W=X−z conditioned on X>z, and let U=W Y. We seek the c.c.d.f. of U. The density of W is given by \(f_{W}(w) = f_{X}(w+z)/\mathcal F_{X}(z)\). But from the properties of Mellin transforms detailed above, we can write

$$ \mathbb M[f_{U};s] = \int_{0}^{\infty}{w^{s-1}\frac{f_{X}(w+z)}{\mathcal F_{X}(z)}\,\mathrm{d} w} \int_{0}^{\infty}{y^{s-1}f_{Y}(y)\,\mathrm{d} y}. $$
((33))

The result stated in the lemma follows by using (31) along with the inversion formula (30) and substituting into (32).