1 Introduction

Compared with the traditional radars, a 60-GHz millimeter-wave (mm-Wave) radar is promising to more adverse environmental conditions, e.g., fog, rain, and snow, which may recognize the target more accurately [1,2]. The earlier research of 60-GHz systems is mainly focused on some military applications, e.g., the frequency-modulated continuous wave (FM-CW) radars and crash-avoidance radars [3]. With the potential of providing high data rate of Gbps, 60-GHz mm-Wave communications have also drawn the world-wide attentions, which have also been considered as not only a promising candidate for the emerging fifth-generation (5G) communications but also an innovative idea for radar and sonar systems [3]. A major advantage of 60-GHz communications over other techniques is the enormous vacant bandwidth available at this mm-Wave band. For instance, the USA has assigned 57- to 64- [4] GHz for 60-GHz communications. Further adopting a large effective isotropic radiated power (EIRP), the achieved transmission rate may easily surpass IEEE 802.11n or UWB [5]. In the current wireless personal area networks standard, e.g., IEEE 802.11ad and 802.15.3c, the single-carrier modulations have also been recommended as a physical layer (PHY) solution due to its flexibility and implementation simplicity.

As a double-edge sword, both the 60-GHz radars and commercial communications, however, also encounters some challenges from practical hardware impairments. Due to its high operating frequencies and high emission power, 60-GHz millimeter communications may suffer seriously from nonlinear power amplifier (PA) [5,6], which will significantly degrade its transmission performance. It is well known that the coding approach may reduce the bit error ratio (BER) even in the presence of nonlinear distortions, which can be suggested as a feasible approach to combat the performance degradation aroused by nonlinear PA.

Since the 60-GHz communications are mainly oriented toward high-speed transmissions, the date rate is very huge and the frame length is therefore extremely long. This may, in practice, facilitate the designing of coding schemes, by concentrating on improving the transmission performance. For example, in the IEEE 802.11ad standard draft, low-density parity-check (LDPC) with a length of 672 bits can be specified in the encoding method [6]. Unfortunately, with the nonlinear PA, it is shown that even such a long LDPC code has been applied, the BER performance seems still to be less attractive to practical use (especially for the high-order modulations).

In this paper, we suggest a promising coding scheme to further promote the BER performance of 60-GHz communication with nonlinear PA. Firstly, an original construction scheme for polar code is applied to a 60-GHz system, which however has been constrained only to the 2 × 2 matrix: F = \( \left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 1\hfill & \hfill 1\hfill \end{array}\right] \). Secondly, after mathematically analyzing the polarization feature of any l × l matrix, two algorithms are proposed to calculate the Bhattacharyya parameters and likelihood ratios, respectively, the former of which are the most vital components for constructing a generalized polar code scheme after an l × l matrix with polarization feature is specified, while the latter of which are the necessary preparation for a mature decoding method. Therefore, generalized polar code schemes can be created after given a specified l × l matrix with polarization feature. In order to testify the validity of two algorithms, as well as to testify the effectiveness of polar code schemes when combatting with nonlinear distortion in a 60-GHz system, a new polar code scheme based on an example 3 × 3 matrix is proposed. Experimental simulations verify firstly the two algorithms for constructing generalized polar code schemes and decoding schemes, secondly the effectiveness of our new polar code scheme, which will significantly promote the transmission performance of 60-GHz communications, especially in the presence of nonlinear distortions aroused by the radio frequency PA. It is also demonstrated that, compared with the popular LDPC code, the two polar code schemes can acquire more competitive BER performance, which hence provides a greater promise to practical use.

The rest of this investigation is listed as follows. Section 2 described the system model and successive cancellation (SC) modulation schemes on 60-GHz millimeter-wave communications. Then, in Section 3, the basic idea of polar code is introduced, based on which, polarization feature is provided and testified through mathematical means. Then come recursive Z algorithm and recursive likelihood ratio algorithm in order to deal with two difficulties in designing constructing and decoding schemes, for any generalized polar code specified by matrix with a polarization feature. In addition, a generalized polar coding scheme is given, which not only testifies the effectiveness of recursive Z algorithm and recursive likelihood ratio algorithm, but can be considered as a newly proposed polar code scheme designed for 60-GHz millimeter-wave communications. Experimental simulations and performance evaluations are provided in Section 4. The whole investigation is finally concluded in Section 5.

2 System model

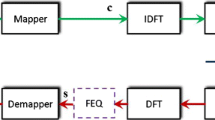
A typical schematic structure of 60-GHz millimeter-wave communication system is given by Figure 1. The source sink generates random binary bits, which are then fed into a coding module where the polar coding and LDPC will be used. Then, the coded signal will pass through a modulation module which will map them into baseband complex signals based on the prescribed modulating method (typically, high-order modulation will be used, e.g., QPSK and 16-QAM). Next, the emission signals will be distorted by a nonlinear PA, and finally, go through the channel by adding complex Gaussian noise in the receiver. In the receiver, the contaminated signals will be demodulated into binary bits and get decoded.

Figure 1
figure 1

System model.

Full size image

2.1 Nonlinearity of PA

After the modulation, signals passed through a nonlinear PA operating in high-frequency bands, the nonlinear distortions will occur inevitably. The bad influences of nonlinearity may lead to the distortions of both amplitudes and phases in output signals [7], which may be usually characterized by the amplitude-amplitude (AM-AM) model and amplitude-phase (AM-PM) model signal’s amplitude, respectively. These two mathematical models are specified as below, i.e.:

$$ G(A)=g\frac{A}{{\left(1+{\left(\frac{gA}{A_{sat}}\right)}^{2s}\right)}^{\frac{1}{2s}}} $$
(1)
$$ \varphi (A)=\frac{a{A}^{q1}}{\left(1+{\left(\frac{A}{b}\right)}^{q2}\right)} $$
(2)

According to the IEEE 802.11ad standard, A and G(A) represent the amplitude of input and output, respectively, the latter of which has a saturation that Asat = 0.58, while g, the linear gain, takes its value at 4.65. Parameter s = 0.81 denotes smoothness of the inflection point of distortion. In the latter expression, φ(A) denotes the distortion of PM, and parameters a, b, q1, and q2 take value at 2560, 0.114, 2.4, 2.3, respectively [6].

Figure 2 shows the typical mapping curve of AM-AM and AM-PM regulated by the IEEE 802.11ad, from which we may note that the distortions will become more obvious with the increasing of input amplitudes.

Figure 2
figure 2

Plot of distortions of nonlinear PA.

Full size image

2.2 Modulation schemes

In this paper, binary phase shift keying (BPSK), quadrature phase shift keying (QPSK), 16 quadrature amplitude modulation (16QAM), and orthogonal frequency-division multiplexing (OFDM) will be considered for modulation methods. According to Figure 2, the distortions of PSK signals after passing through a nonlinear power amplifier (NLPA) can be neutralized by tilting the coordinate axis back, a fixed angel that equals to the distortion of phase, since the PSK signals have the identical amplitudes. QAM signals can be also calibrated through a method that proportional reduces the signal’s amplitude into a linear area, which can still maintain a relatively distinguished constellation map for demodulating. Unfortunately, OFDM signals, which are extremely sensitive to nonlinear distortions due to its high peak-to-average power ratio (PAPR), may have the worst effect of NLPA distortion since the IFFT process builds an irregular set of OFDM signals.

3 Polar code for 60-GHz communication

A polar code is a kind of G N -coset code inspired by a phenomenon called channel polarization, which can be achieved by recursively combining with N channel \( W:\mathcal{X}\to \mathcal{Y} \) and then splitting the combined channels into N channels through information theory. With this method, the theoretical BER of some channels approach nearly to 0, while the rest of them are close to 1. And the channel capacities among those channels go through opposite directions. Those channels whose theoretical BER are approaching to 0, in other words, whose channel capacities are approaching to 1, are defined as good channels and will be selected to transmit data since the lower the theoretical BER means a better distribution of channel capacity.

We firstly utilize \( {\mathbf{a}}_i^j \) to denote a vector (a i ,a i+1,…,a j ), where i and j are natural numbers with normally i ≤ j. Otherwise, \( {\mathbf{a}}_i^j \) is regarded as void while i > j.

Define a binary-input discrete memoryless channel (B-DMC) \( W:\mathcal{X}\to \mathcal{Y} \), with a fixed input set {0,1}, and an arbitrary output set, is defined as symmetric only when a permutation \( \varPi :\mathcal{Y}\to \mathcal{Y} \) exists, that is, there exists a π makes sense for W(y|0) = W(Π(y)|1) for all \( y\in \mathcal{Y} \).

When a fixed \( W:\mathcal{X}\to \mathcal{Y} \) is given, I(W) is defined as the mutual information between the input and output of \( W:\mathcal{X}\to \mathcal{Y} \) . I(W) has a spectrum of [0,1], and only when inputs have uniform distribution, I(W) can be considered as the capacity of channel with an expression below:

$$ I(W)={\displaystyle \sum_{y\in \mathbf{\mathcal{Y}}}}{\displaystyle \sum_{x\in \mathbf{\mathcal{X}}}}\frac{1}{2}W\left(y\Big|x\right) \log \frac{W\left(y\Big|x\right)}{\frac{1}{2}W\left(y\Big|0\right)+\frac{1}{2}W\left(y\Big|1\right)} $$
(3)

Also, Z(W) is defined to quantize the theoretical BER as the Bhattacharyya parameter of \( W:\mathcal{X}\to \mathcal{Y} \) and has an expression as:

$$ Z(W)={\displaystyle \sum_{y\in \mathbf{\mathcal{Y}}}}\sqrt{W\left(y\Big|0\right)W\left(y\Big|1\right)} $$
(4)

And the lower the Bhattacharyya parameter of one channel, the higher the channel capacity it obtains [8].

We regard 1ε = 1 only when a group of variables (x,y) that correspond with a set where \( \varepsilon = \left\{x\in X,y\in \mathcal{Y}:W\left(y\Big|x\right)\ \le\ W\left(y\Big|x + 1\right)\right\} \), otherwise, 1ε = 0. Therefore,

$$ \begin{array}{c}Z(W)\\ {}={\displaystyle \sum_{y\in \mathbf{\mathcal{Y}}}}\sqrt{W\left(y\Big|0\right)W\left(y\Big|1\right)}\\ {}\ge {\displaystyle \sum_{y\in \mathbf{\mathcal{Y}}}}\left[\frac{1}{2}W\left(y\Big|0\right)+\frac{1}{2}W\left(y\Big|1\right)\right]\cdotp {1}_{\varepsilon}\\ {}=\frac{1}{2}{\displaystyle \sum_{x\in \mathbf{\mathcal{X}},y\in \mathbf{\mathcal{Y}}}}W\left(y\Big|x\right)\cdotp {1}_{\varepsilon}\\ {}={P}_e\left(W\ \right)\end{array} $$
(5)

where P e (W) is the theoretical BER through maximum likelihood ratio decoding method. So Z(W) is an upper bound of theoretical BER and can be reduced to improve the transmission performance.

3.1 Channel combining

For any arbitrary positive integer l and an l × l invertible matrix F with entries in {0,1}, consider a process that a random l-vector \( {\mathbf{U}}_1^l \) with a uniform distribution over {0,1}l firstly multiply the matrix F over GF(2) and then passes through the channel \( W:\mathcal{X}\to \mathcal{Y} \) to generate a random vector of output. Let \( {\mathbf{Y}}_1^l \) denote the output. Therefore, the channel transmission probabilities between \( {\mathbf{U}}_1^l \) and \( {\mathbf{Y}}_1^l \) can be expressed as below:

$$ {W}_l\left({\mathbf{y}}_1^l\Big|{\mathbf{u}}_1^l\right)={\displaystyle \prod_{k=1}^l}W\left({y}_k\Big|{\left({\mathbf{u}}_1^l\cdotp \mathbf{F}\right)}_k\right) $$
(6)

where \( {\mathbf{u}}_1^l \) and \( {y}_1^l \) denote a sample of \( {\mathbf{U}}_1^l \) and \( {\mathbf{Y}}_1^l \), respectively.

The process described above is called channel combining and can be illustrated in Figure 3.

Figure 3
figure 3

One step of channel combination.

Full size image

Figure 4 illustrates an n-step (N = l n) of channel combination, where input (U1,U2,…,U N ) denotes a random vector of variables while output (Y1,Y2,…,Y N ) denotes another vector of variables. \( {\mathbf{R}}_N^l \) is a kind of permutation matrix that reassigns a series of random variables (V1,V2,…,V N ) generated by (U1,U2,…,U N ) passing through matrix F.

Figure 4
figure 4

n -step of channel combination.

Full size image

By operating such process, a combining channel \( {W}_N:{\mathbf{U}}_1^N\to {\mathbf{Y}}_1^N \) can be created, with the transmission probabilities expressed below:

$$ {W}_N\left({\mathbf{y}}_1^N\Big|{\mathbf{u}}_1^N\right)={\displaystyle \prod_{k=1}^l}{W}_{N/l}\left({\mathbf{y}}_{kN/l+1}^{\left(k+1\right)N/l}\Big|{\mathbf{v}}_{1,k}^N\right) $$
(7)

where \( {\mathbf{v}}_{1,k}^N \) is a newly generated vector created by permutation matrix \( {\mathbf{R}}_N^l \), a reassignment method that alters the order of the random vector \( {\mathbf{V}}_1^N \) into \( {\mathbf{V}}_{1,k}^N=\left({V}_k,{V}_{l+k},\dots, {V}_{ml+k}\right),\ k=1,2,\dots, l,\kern0.5em \left(\mathrm{m}+1\right)l\le N<\left(\mathrm{m}+2\right)l \). Also, \( {\mathbf{u}}_1^N,\ {\mathbf{y}}_1^N \) and \( {\mathbf{v}}_1^N \) denote a sample of \( {\mathbf{U}}_1^l,{\mathbf{Y}}_1^l\ \mathrm{and}\ {\mathbf{V}}_1^N \), respectively.

According to the combination recursive process described before, prior to reach the final N-number of W, the input data \( {\mathbf{u}}_1^N \) can be equivalently transform into \( {\mathbf{x}}_1^N \) through a linear transformation, that is:

$$ {\mathbf{x}}_1^N = {\mathbf{u}}_1^N\cdotp {\mathbf{G}}_N $$
(8)

where G N is called generator matrix. According to the combination process in Figure 4, G N can be calculated recursively as below:

$$ \begin{array}{c}{\mathbf{G}}_N=\left({\mathbf{I}}_{N/l}\otimes \mathbf{F}\right)\cdotp {\mathbf{R}}_N^l\cdotp \left({\mathbf{I}}_l\otimes {\mathbf{G}}_{N/l}\right)\\ {}={\mathbf{R}}_N^l\cdotp \left(\mathbf{F}\otimes {\mathbf{I}}_{N/l}\right)\cdotp \left({\mathbf{I}}_l\otimes {\mathbf{G}}_{N/l}\right)\\ {}={\mathbf{R}}_N^l\cdotp \left(\mathbf{F}\otimes {\mathbf{G}}_{N/l}\right)\\ {}={\mathbf{R}}_N^l\left(\mathbf{F}\otimes \left({\mathbf{R}}_{N/l}^l\left(\mathbf{F}\otimes {\mathbf{G}}_{N/{l}^2}\right)\right)\right)\ \\ {}={\mathbf{R}}_N^l\left({\mathbf{I}}_2\otimes {\mathbf{R}}_{N/l}^l\right)\left({\mathbf{F}}^{\otimes 2}\otimes {\mathbf{G}}_{N/{l}^2}\right)\ \\ {}={\mathbf{R}}_N^l\left({\mathbf{I}}_l\otimes {\mathbf{R}}_{N/l}^l\right)\left({\mathbf{I}}_{l^2}\otimes {\mathbf{R}}_{N/{l}^2}^l\right)\cdots \left({\mathbf{I}}_{N/l}\otimes {\mathbf{R}}_l^l\right)\otimes {\mathbf{F}}^{\otimes n}\end{array} $$
(9)

where I k is defined as k × k unit matrix and ⊗ denotes the Kronecker multiplication and G 1 represents 1 × 1 unit matrix.

3.2 Channel splitting

We start this part by analyzing the information theory formula below:

$$ \begin{array}{c}I\left({\mathbf{U}}_1^N;{\mathbf{Y}}_1^N\right)={\displaystyle \sum_{i=1}^N}I\left({U}_i;{\mathbf{Y}}_1^N\Big|{\mathbf{U}}_1^{i-1}\right)\\ {}={\displaystyle \sum_{i=1}^N}\left[I\left({U}_i;{\mathbf{Y}}_1^N,{\mathbf{U}}_1^{i-1}\right)-I\left({U}_i;{\mathbf{U}}_1^{i-1}\right)\right]\\ {}={\displaystyle \sum_{i=1}^N}I\left({U}_i;{\mathbf{Y}}_1^N,{\mathbf{U}}_1^{i-1}\right)\end{array} $$
(10)

where \( I\left({U}_i;{U}_1^{\left(i-1\right)}\right)=0 \) because of the independent source \( {\mathbf{U}}_1^N \).

Define \( {W}_N^i:{U}_i\to {Y}_1^N\times {U}_1^{\left(i-1\right)},1\le i\le N \) as a channel by splitting the combining channel \( {W}_N:{\mathbf{U}}_1^N\to {\mathbf{Y}}_1^N \) based on Equation 10 and calculate transmission probabilities:

$$ \begin{array}{c}{W}_N^i\left({\mathbf{y}}_1^N,{\mathbf{u}}_1^{i-1}\Big|{u}_i\right)=\frac{ \Pr \left({\mathbf{y}}_1^N,{\mathbf{u}}_1^i\right)}{ \Pr \left({u}_i\right)}\cdotp {\displaystyle \sum_{{\mathbf{u}}_{i+1}^N}} \Pr \left({\mathbf{u}}_{i+1}^N\right)\\ {}={\displaystyle \sum_{{\mathbf{u}}_{i+1}^N}}\frac{ \Pr \left({\mathbf{y}}_1^N,{\mathbf{u}}_1^N\right)}{ \Pr \left({u}_i\right)}\\ {}={\displaystyle \sum_{{\mathbf{u}}_{i+1}^N}}\frac{ \Pr \left({\mathbf{y}}_1^N\Big|{\mathbf{u}}_1^N\right)}{ \Pr \left({u}_i\right)} \Pr \left({\mathbf{u}}_1^N\right)\end{array} $$
(11)

Therefore, by combining the transition probabilities of \( {W}_N^i \) and \( {W}_{N/l}^i \), the recursive formula is:

$$ {W}_N^{l\left(i-1\right)+j}\left({\mathbf{y}}_1^N,{\mathbf{u}}_1^{l\left(i-1\right)+j-1}\Big|{u}_{l\left(i-1\right)+j}\right)=\frac{1}{2^{l-1}}{\displaystyle \sum_{u_{l\left(i-1\right)+j+1}}^{u_{li}}}{\displaystyle \prod_{k=1}^l}{W}_{N/l}^i\left({\mathbf{y}}_{kN/l+1}^{\left(1+k\right)N/l},{\mathbf{v}}_{1,k}^{l\left(i-1\right)}\right|{\left({\mathbf{u}}_{l\left(i-1\right)+1}^{li}\cdotp \mathbf{F}\right)}_k $$
(12)

In Formula 12 \( {\mathbf{v}}_{\left(i-1\right)l+1}^{il}={\mathbf{u}}_{\left(i-1\right)l+1}^{il}\cdotp \mathbf{F} \), 1 ≤ i ≤ N/l, and 1 ≤ j ≤ l.

Example 1: Arikan’s scheme given that:

$$ \mathbf{F}=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 1\hfill & \hfill 1\hfill \end{array}\right] $$

We can calculate a generator matrix G N . with a specified N = 2n. In order to select split channels for transmissions, Arikan has provided a set of formulas [8] to calculate the Bhattacharyya parameter of each split channel, that is:

$$ \left\{\begin{array}{l}Z\left({W}_N^{2i-1}\right)=-Z{\left({W}_{N/2}^i\right)}^2+2Z\left({W}_{N/2}^i\right)\\ {}Z\left({W}_N^{2i}\right)=Z{\left({W}_{N/2}^i\right)}^2\end{array}\right. $$
(13)

As well, when utilizing successive cancellation (SC) decode method, it may come up with a set of formulas to calculate likelihood ratio,

$$ \left\{\begin{array}{l}{L}_N^{2i-1}\left({\mathbf{y}}_1^N,{\widehat{\mathbf{u}}}_1^{2i-2}\right)=\frac{L_{N/2}^i\left({\mathbf{y}}_1^{N/2},{\widehat{\mathbf{u}}}_{1,1}^{2i-2}\oplus {\widehat{\mathbf{u}}}_{1,2}^{2i-2}\right){L}_{N/2}^i\left({\mathbf{y}}_{N/2+1}^N,{\widehat{\mathbf{u}}}_{1,2}^{2i-2}\right)+1}{L_{N/2}^i\left({\mathbf{y}}_1^{N/2},{\widehat{\mathbf{u}}}_{1,1}^{2i-2}\oplus {\widehat{\mathbf{u}}}_{1,2}^{2i-2}\right)+{L}_{N/2}^i\left({\mathbf{y}}_{N/2+1}^N,{\widehat{\mathbf{u}}}_{1,2}^{2i-2}\right)}\\ {}{L}_N^{2i}\left({\mathbf{y}}_1^N,{\widehat{\mathbf{u}}}_1^{2i-1}\right)={\left[{L}_{N/2}^i\left({\mathbf{y}}_1^{N/2},{\widehat{\mathbf{u}}}_{1,1}^{2i-2}\oplus {\widehat{\mathbf{u}}}_{1,2}^{2i-2}\right)\right]}^{1-2{\widehat{u}}_{2i-1}}\cdotp {L}_{N/2}^i\left({\mathbf{y}}_{N/2+1}^N,{\widehat{\mathbf{u}}}_{1,2}^{2i-2}\right)\end{array}\right. $$
(14)

These formulas are only available for the 2 × 2 matrix \( \mathbf{F}=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 1\hfill & \hfill 1\hfill \end{array}\right] \), however, but not for other specified matrix, which limits the wide application of polar code. In order to tackle this problem, we first should to identify what kind of matrix has the feature to generate polar code, and this feature referred as to polarization feature.

3.3 Polarization feature

Define \( {W}^k:\left\{0,\ 1\right\}\ \to {\mathcal{Y}}^k \) as a channel with an input x, outputs \( {\mathbf{y}}_1^k \) and transmission probabilities:

$$ {W}^k\left({\mathbf{y}}_1^k\Big|x\right)={\displaystyle \prod_{j=1}^k}W\left({y}_j\Big|x\right) $$
(15)

\( {W}^k:\left\{0,\ 1\right\}\ \to {\mathcal{Y}}^k \) implies a channel extension of \( W:\mathcal{X}\to \mathcal{Y} \), which has a Bhattacharyya parameter:

$$ \begin{array}{c}Z\left({W}^k\right)={\displaystyle \sum_{{\mathbf{y}}_1^k}}\sqrt{W^k\left({\mathbf{y}}_1^k\Big|0\right){W}^k\left({\mathbf{y}}_1^k\Big|1\right)}\\ {}={\displaystyle \sum_{{\mathbf{y}}_1^k}}\sqrt{{\displaystyle \prod_{j=1}^k}W\left({y}_j\Big|0\right)W\left({y}_j\Big|1\right)}\\ {}={\displaystyle \prod_{j=1}^k{\displaystyle \sum_{y_j}\sqrt{W\left({y}_j\Big|0\right)W\left({y}_j\Big|1\right)}}}\\ {}=Z{(W)}^k\end{array} $$
(16)

Note that Z(W)∈[0,1], so limk→∞Z(W)k = 0, which implies that by extending channel \( W:\mathcal{X}\to \mathcal{Y} \), we, to some extent, can improve the transmission performance.

Therefore, a paraphrase is given for channel polarization, F is a polarizing matrix when there exists at least an i∈{1,2,…,l}, makes sense that:

$$ Z\left({W}_l^i\right)\propto Z{(W)}^k $$
(17)

Some attributes of a polarizing matrix F maybe of interest. When the last row of F has k > 1 unit elements, whose subscripts compose a set J = {j 1,j 2,…,j k }, then the transmission probability of \( {W}_l^l \) can be calculated by:

$$ \begin{array}{c}{W}_l^l\left({\mathbf{y}}_1^l,{\mathbf{u}}_1^{l-1}\Big|{u}_l\right)\\ {}=\frac{1}{2^{l-1}}{W}_l\left({\mathbf{y}}_1^l\Big|{\mathbf{u}}_1^l\right)\\ {}=\frac{1}{2^{l-1}}{\displaystyle \prod_{j=1}^l}W\left({y}_j\Big|{\left({\mathbf{u}}_1^l\cdotp \mathbf{F}\right)}_j\right)\end{array} $$
(18)

Accordingly, the Bhattacharyya parameter is given as below:

$$ \begin{array}{c}\mathrm{Z}\left({W}_l^l\right)\\ {}={\displaystyle \sum_{{\mathbf{y}}_1^l,{\mathbf{u}}_1^{l-1}}}\sqrt{W_l^l\left({\mathbf{y}}_1^l,{\mathbf{u}}_1^{l-1}\Big|0\right){W}_l^l\left({\mathbf{y}}_1^l,{\mathbf{u}}_1^{l-1}\Big|1\right)}\\ {}=\frac{1}{2^{l-1}}{\displaystyle \sum_{{\mathbf{y}}_1^l,{\mathbf{u}}_1^{l-1}}}{\displaystyle \prod_{j\notin \mathcal{J}}}W\left({y}_j\Big|{\left({\mathbf{u}}_1^l\cdotp \mathbf{F}\right)}_j\right)\cdotp \sqrt{{\displaystyle \prod_{j\in \mathcal{J}}}W\left({y}_j\Big|{\left({\mathbf{u}}_1^{l-1}\cdotp {\mathbf{F}}_{l-1}\right)}_j\oplus 0\right)\cdotp W\left({y}_j\Big|{\left({\mathbf{u}}_1^{l-1}\cdotp {\mathbf{F}}_{l-1}\right)}_j\oplus 1\right)}\\ {}=\frac{1}{2^{l-1}}{\displaystyle \sum_{y_j,{\mathbf{u}}_1^{l-1}}}{\displaystyle \prod_{j\notin \mathcal{J}}}W\left({y}_j\Big|{\left({\mathbf{u}}_1^l\mathbf{F}\right)}_j\right)\cdotp Z{(W)}^k\end{array} $$
(19)

which satisfies Equation 17, and F l-1 denotes a sub-matrix of F by removing its last row.

Consider more general circumstances in which any split channel \( {W}_l^{l-i} \) with transmission probability:

$$ \begin{array}{c}{W}_l^{l-i}\left({\mathbf{y}}_1^l,{\mathbf{u}}_1^{l-i-1}\Big|{u}_{l-i}\right)\\ {}=\frac{1}{2^{l-1}}{\displaystyle \sum_{{\mathbf{u}}_{l-i+1}^l}}{W}_l\left({\mathbf{y}}_1^l\Big|{\mathbf{u}}_1^l\right)\\ {}=\frac{1}{2^{l-1}}{\displaystyle \sum_{{\mathbf{u}}_{l-i+1}^l}} \Pr \left({\mathbf{y}}_1^{l-1}\Big|{\mathbf{u}}_1^l\right)\cdotp \Pr \left({y}_l\Big|{\mathbf{y}}_1^{l-1},{\mathbf{u}}_1^l\right)\end{array} $$
(20)

When the last row of F has only one unit element, due to the permutation feature, we assume the unit element is the last element in this row; then, the channel transmission probability can be rewritten into:

$$ \begin{array}{c}{W}_l^{l-i}\left({\mathbf{y}}_1^l,{\mathbf{u}}_1^{l-i-1}\Big|{u}_{l-i}\right)\\ {}=\frac{1}{2^{l-1}}{\displaystyle \sum_{{\mathbf{u}}_{l-i+1}^l}} \Pr \left({\mathbf{y}}_1^{l-1}\Big|{\mathbf{u}}_1^{l-1}\right)\cdotp \Pr \left({y}_l\Big|{\mathbf{y}}_1^{l-1},{\mathbf{u}}_1^l\right)\\ {}=\frac{1}{2^{l-1}}\left[W\left({y}_l\Big|0\right)+W\left({y}_l\Big|1\right)\right]\cdotp {\displaystyle \sum_{{\mathbf{u}}_{l-i+1}^{l-1}}}{W}_{l-1}\left({\mathbf{y}}_1^{l-1}\Big|{\mathbf{u}}_1^{l-1}\right)\end{array} $$
(21)

Therefore, the output Y l is independent of inputs to the channel \( {W}_l^{l-i} \), indicating that the split channels \( {W}_l^1,{W}_l^2,\dots, {W}_l^{l-1} \) are defined on matrix F l − 1, which are obtained by removing the last row and last column of F.

Based in a recursive analysis on F l − i, we may finally conclude that a matrix F does not have polarization feature when F is an upper triangular matrix.

3.4 Two difficulties of a polar code

Two technical difficulties remain in how to design constructing and decoding schemes for a generalized polar code that based on any specified matrix. That is, firstly, we need Bhattacharyya parameters of each split channels to select channels for data transmission. Secondly, a group of recursive formulas is demanded as a necessity of preparation to implement decoding scheme, the successive cancellation decode (SC). There come two algorithms we proposed, to cope with the two realistic challenges we mentioned.

3.5 Recursive Z algorithm

For a more general case, we firstly propose an algorithm calculating Bhattacharyya parameters by defining \( {\mathbf{c}}_0=\left({\mathbf{u}}_1^{i-1},0,{\mathbf{t}}_{i+1}^l\right)\cdot \mathbf{F} \) and \( {\mathbf{c}}_1=\left({\mathbf{u}}_1^{i-1},1,{\mathbf{w}}_{i+1}^l\right)\cdot \mathbf{F} \). S 0 is a set of indices that where both c 0 and c 1 are equal to 0, while S 1 is a set of indices that indicate the elements of both c 0 and c 1 are equal to 1. Therefore, the Bhattacharyya parameter of each split channel \( {W}_l^l \) can be calculated below:

$$ \begin{array}{c}Z\left({W}_l^i\right)\\ {}=\frac{1}{2^{l-1}}{\displaystyle \sum_{{\mathbf{y}}_1^l,{\mathbf{u}}_1^{i-1}}}\sqrt{{\displaystyle \sum_{{\mathbf{t}}_{i+1}^l,{\mathbf{w}}_{i+1}^l}}{W}_l\left({\mathbf{y}}_1^l\Big|{\mathbf{u}}_1^{i-1},0,{\mathbf{t}}_{i+1}^l\right){W}_l\left({\mathbf{y}}_1^l\Big|{\mathbf{u}}_1^{i-1},1,{\mathbf{w}}_{i+1}^l\right)}\\ {}=\frac{1}{2^{l-1}}{\displaystyle \sum_{{\mathbf{y}}_1^l,{\mathbf{u}}_1^{i-1}}}\sqrt{{\displaystyle \sum_{{\mathbf{t}}_{i+1}^l,{\mathbf{w}}_{i+1}^l}}{\displaystyle \prod_{j=1}^l}W\left({y}_j\Big|{\left({\mathbf{c}}_0\right)}_j\right)W\left({y}_j\Big|{\left({\mathbf{c}}_1\right)}_j\right)}\\ {}=\frac{1}{2^{l-1}}{\displaystyle \sum_{{\mathbf{y}}_1^l,{\mathbf{u}}_1^{i-1}}}\ \sqrt{{\displaystyle \sum_{{\mathbf{t}}_{i+1}^l,{\mathbf{w}}_{i+1}^l}}{\displaystyle \prod_{j\in {\mathcal{S}}_0}}W{\left({y}_j\Big|0\right)}^2{\displaystyle \prod_{j\in {\mathcal{S}}_1}}W{\left({y}_j\Big|1\right)}^2{\displaystyle \prod_{j\notin {\mathcal{S}}_0{\displaystyle \cup }{\mathcal{S}}_1}}W\left({y}_j\Big|0\right)W\left({y}_j\Big|1\right)}\end{array} $$
(22)

where (c 0) j and (c 1) j denote the jth element of c 0 and c 1. Thus, by traversing \( {\mathbf{y}}_1^l,{\mathbf{u}}_1^{i-1},{\mathbf{t}}_{i+1}^l,{\mathbf{w}}_{i+1}^l \), respectively, we can obtain \( Z\left({W}_l^i\right) \); therefore, calculate \( Z\left({W}_N^i\right) \), recursively.

Example 2: given a matrix

$$ \mathbf{F}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right] $$

with a BEC channel, according to the recursive Z algorithm above, the recursive Bhattacharyya parameters can be calculated below:

$$ \left\{\begin{array}{l}Z\left({W}_N^{3i-2}\right)=-Z{\left({W}_{N/3}^i\right)}^3+Z{\left({W}_{N/3}^i\right)}^2+Z\left({W}_{N/3}^i\right)\\ {}Z\left({W}_N^{3i-1}\right)=-Z{\left({W}_{N/3}^i\right)}^2+2Z\left({W}_{N/3}^i\right)\\ {}Z\left({W}_N^{3i}\right)=Z{\left({W}_{N/3}^i\right)}^3\end{array}\right. $$
(23)

Figure 5 shows a three-step process of channel polarization, each knot denotes a split channel and has a vector, in which the left parameter represents e number of split channels, while the right one represents the Bhattacharyya parameter. Knots on the right side are the split channels through this three-step polarization, of which the green ones are those good channels selected to transmit data since the lower the Bhattacharyya parameter, the higher the channel capacity they have gained.

Figure 5
figure 5

Process of channel polarization.

Full size image

Therefore, by generating a 3 × 3 based polar code scheme, we testified the recursive Z algorithm is effective on constructing generalized polar coding scheme, which means as long as we can find a matrix that has a polarization feature, we can realize a new polar coding scheme based on that matrix. It has been testified that in order to gain a higher error exponent than 0.5, the length of a polarization matrix has to be more than 16 [9,10].

3.6 Recursive likelihood ratio algorithm

We define likelihood ratio in SC decode method as below,

$$ {L}_N^i\left({\mathbf{y}}_1^N,{\widehat{\mathbf{u}}}_1^{i-1}\right)=\frac{W_N^i\left({\mathbf{y}}_1^N,{\widehat{\mathbf{u}}}_1^{i-1}\Big|\widehat{u_i}=0\right)}{W_N^i\left({\mathbf{y}}_1^N,{\widehat{\mathbf{u}}}_1^{i-1}\Big|\widehat{u_i}=1\right)} $$
(24)

where \( {\widehat{\mathrm{u}}}_1^{i-1} \) denotes the received data whose values have been decided successively, while û i denotes a statistical decision of u i , whose value has not been decided yet.

Obviously, through Expression 13, we can literally calculate \( {L}_N^i\left({\mathbf{y}}_1^N,{\widehat{\mathrm{u}}}_1^{i-1}\right) \), but amounts of complexity accompanies. Instead, a more efficient FFT-like method is proposed to calculate \( {L}_N^i\left({\mathbf{y}}_1^N,{\widehat{\mathrm{u}}}_1^{i-1}\right) \) based on the recursive feature of polar code.

The likelihood ratio can be rewritten as below:

$$ \begin{array}{c}{L}_l^i\left({\mathbf{y}}_1^l,{\widehat{\mathbf{u}}}_1^{i-1}\right)=\frac{W_l^i\left({\mathbf{y}}_1^l,{\widehat{\mathbf{u}}}_1^{i-1}\Big|\widehat{u_i}=0\right)}{W_l^i\left({\mathbf{y}}_1^l,{\widehat{\mathbf{u}}}_1^{i-1}\Big|\widehat{u_i}=1\right)}\\ {}=\frac{{\displaystyle {\sum}_{{\mathbf{t}}_{i+1}^l}}{W}_l\left({\mathbf{y}}_1^l\Big|{\mathbf{u}}_1^{i-1},0,{\mathbf{v}}_{i+1}^l\right)}{{\displaystyle {\sum}_{{\mathbf{w}}_{i+1}^l}}{W}_l\left({\mathbf{y}}_1^l\Big|{\mathbf{u}}_1^{i-1},1,{\mathbf{w}}_{i+1}^l\right)}\\ {}=\frac{{\displaystyle {\sum}_{{\mathbf{t}}_{i+1}^l}}{\displaystyle {\prod}_{j=1}^l}W\left({y}_j\Big|{\left({\mathbf{c}}_0\right)}_j\right)}{{\displaystyle {\sum}_{{\mathbf{w}}_{i+1}^l}}{\displaystyle {\prod}_{j=1}^l}W\left({y}_j\Big|{\left({\mathbf{c}}_1\right)}_j\right)}\end{array} $$
(25)

Note S 0 as a set of indices where c 0 equal to 0, while S 1 denotes a set of indices where c 1 equals to 0. Consider that:

$$ {\displaystyle \sum_{{\mathbf{t}}_{i+1}^l}}{\displaystyle \prod_{j=1}^l}W\left({y}_j\Big|1\right)={\displaystyle \sum_{{\mathbf{w}}_{i+1}^l}}{\displaystyle \prod_{j=1}^l}W\left({y}_j\Big|1\right) $$
(26)

The numerator and denominator of the right side of Expression 25 can be expressed, respectively:

$$ \left\{\begin{array}{l}\frac{{\displaystyle {\prod}_{j=1}^l}W\left({y}_j\Big|{\left({\mathbf{c}}_0\right)}_j\right)}{{\displaystyle {\prod}_{j=1}^l}W\left({y}_j\Big|1\right)}={\displaystyle \prod_{j\in {\mathrm{S}}_0}}{L}_1^1\left({y}_j\right)\\ {}\frac{{\displaystyle {\prod}_{j=1}^l}W\left({y}_j\Big|{\left({\mathbf{c}}_1\right)}_j\right)}{{\displaystyle {\prod}_{j=1}^l}W\left({y}_j\Big|1\right)}={\displaystyle \prod_{j\in {\mathrm{S}}_1}}{L}_1^1\left({y}_j\right)\end{array}\right. $$
(27)

Thus:

$$ {L}_l^i\left({\mathbf{y}}_1^l,{\widehat{\mathbf{u}}}_1^{i-1}\right)=\frac{{\displaystyle {\sum}_{{\mathbf{t}}_{i+1}^l}}{\displaystyle {\prod}_{j\in {\mathrm{S}}_0}}{L}_1^1\left({y}_j\right)}{{\displaystyle {\sum}_{{\mathbf{w}}_{i+1}^l}}{\displaystyle {\prod}_{j\in {\mathrm{S}}_1}}{L}_1^1\left({y}_j\right)} $$
(28)

By traversing \( {\widehat{\mathrm{u}}}_1^{i-1},{\mathbf{t}}_{i+1}^l,{\mathbf{w}}_{i+1}^l \), respectively, we can calculate \( {L}_l^i\left({\mathbf{y}}_1^l,{\widehat{\mathrm{u}}}_1^{i-1}\right) \) depending on various \( {\widehat{\mathrm{u}}}_1^{i-1} \), and recursively calculate \( {L}_N^i\left({\mathbf{y}}_1^N,{\widehat{\mathrm{u}}}_1^{i-1}\right) \).

Example 3: Consider the matrix given before with a BEC channel:

$$ \mathbf{F}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right] $$

The recursive form of likelihood ratio based on recursive likelihood ratio algorithm can be calculated below:

$$ \left\{\begin{array}{l}{L}_N^{3i-2}\left({\mathbf{y}}_1^N,{\widehat{\mathbf{u}}}_1^{3i-3}\right)=\frac{\alpha \beta \gamma +\alpha \gamma +\beta +1}{\beta \gamma +\alpha \beta +\alpha +\gamma}\\ {}\ {L}_N^{3i-1}\left({\mathbf{y}}_1^N,{\widehat{\mathbf{u}}}_1^{3i-2}\right)=={\left(\frac{\alpha \beta \gamma +1}{\beta +\alpha \gamma}\right)}^{\left(1-{\widehat{u}}_{3i-2}\right)}\cdotp {\left(\frac{\beta \gamma +\alpha }{\alpha \beta +\gamma}\right)}^{{\widehat{u}}_{3i-2}}\\ {}{L}_N^{3i}\left({\mathbf{y}}_1^N,{\widehat{\mathbf{u}}}_1^{3i-1}\right)={\alpha}^{\left(1-2{\widehat{u}}_{3i-2}\right)\left(1-2{\widehat{u}}_{3i-1}\right)}\beta {\gamma}^{\left(1-2{\widehat{u}}_{3i-1}\right)}\end{array}\right. $$
(29)

where:

$$ \left\{\begin{array}{l}\alpha ={L}_{N/3}^i\left({\mathbf{y}}_1^{N/3},{\widehat{\mathbf{u}}}_{1,1}^{3i-3}\oplus {\widehat{\mathbf{u}}}_{1,2}^{3i-3}\oplus {\widehat{\mathbf{u}}}_{1,3}^{3i-3}\right)\\ {}\beta ={L}_{N/3}^i\left({\mathbf{y}}_{N/3+1}^{2N/3},{\widehat{\mathbf{u}}}_{1,3}^{3i-3}\right)\\ {}\gamma ={L}_{N/3}^i\left({\mathbf{y}}_{2N/3+1}^N,{\widehat{\mathbf{u}}}_{1,2}^{3i-3}\oplus {\widehat{\mathbf{u}}}_{1,3}^{3i-3}\right)\end{array}\right. $$

According to Equation 29, a FFT-like SC decode method can be created; that is, calculating each \( {L}_N^i\left({\mathbf{y}}_1^N,{\widehat{\mathrm{u}}}_1^{i-1}\right) \) demands only its three ex-step parameters, which recursively, creates a method that has only a complexity of O(Nlog3N).

4 Experimental simulations

In the experimental simulations, we mainly focus on the line-of-sight (LOS) scenarios, in which the first LOS path may have an extremely strong energy [11]. This is justified by wide adoptions of beam-forming techniques [12,13]. In this case, the single-path complex Gaussian channel can be used for the simplicity of analysis [14,15]. The sampling rate is relatively high at 60GHz band, which may be further reduced by some recent signal processing techniques, such as sampling conversion [16] or compressive sensing. The code rate is fixed at 1/2, the erasure probability (∈) is 0.1. We give the rest of channels with 0 bits. In the experiments, the classical polar code composed by Arikan (i.e., l = 2), which is denoted by polarcode 2, is also used for comparative analysis. Meanwhile, the popular LDPC scheme, based on a 336/672 check matrix, proposed and approved by the IEEE 802.11ad standard [6] has also been adopted.

Firstly, a channel polarization histogram based on: F = \( \left[\begin{array}{lll}1\hfill & 0\hfill & 0\hfill \\ {}1\hfill & 0\hfill & 1\hfill \\ {}1\hfill & 1\hfill & 1\hfill \end{array}\right] \) is shown in Figure 6. We may notice that the ratio of Bhattacharyya parameters approaching to 0 is 90%, while the ratio of those channels whose capacities are approaching to 1 is less than 10%. According to the channel polarization theory proposed by Arikan [7], we can conclude that the generalized matrix has the polarization feature and the recursive Z algorithm can be used to effectively calculate Bhattacharyya parameters.

Figure 6
figure 6

Channel polarization histogram.

Full size image

In the simulations, BPSK, QPSK, and 16QAM are then employed. In order to build simulations in an environment of NLPA, the operational voltage on the PA inputs was defined within a range of (0.3, 1), which, according to Figure 2, can generate nonlinear distortion of outputs. The BER performances of these modulated signals have been plotted by Figures 7, 8 and 9, respectively. It is obviously noted that the BER performance of both the polar code, and LDPC will be significantly reduced, compared with the noncoding situation. There, the coding scheme can be viewed as an effective approach to combat the realistic nonlinearity in 60-GHz millimeter-wave communications. Second, it is seen that, in the considered BPSK, QPSK, and 16QAM signals, the polar code may usually surpass the popular LDPC in high SNR regions. Taking the QPSK signals of SNR = 2 dB, for example, the BER may even approach 8 × 10−3. In comparison, the BER value of LDPC is only 4 × 10−2. Roughly, a detection gain of 0.6 dB can be acquired by the polar code. Third, it is shown that the 16QAM is more vulnerable to 60-GHz nonlinear PAs (NLPAs), compared with other lower-order modulation schemes. Finally, we may note that, in the case of 16QAM signals with NLPA, the designed polar code seems to be comparative with the class polar code of l = 2, which (with l = 3), however, may be of more flexibility and efficiency in frame designing and multi-complexity.

Figure 7
figure 7

BER performance of BPSK modulated signals.

Full size image
Figure 8
figure 8

BER performance of QPSK modulated signals.

Full size image
Figure 9
figure 9

BER performance of 16QAM modulated signals.

Full size image

5 Conclusion

The transmission performance of 60-GHz mm-Wave communications is significantly vulnerable to hardware impairments, especially the evitable nonlinearity of PA. To deal with such drawbacks, polar code is proposed for 60-GHz systems in this investigation. In order to generalize the originally posed classical scheme that only is applied to a 2 × 2 matrix, a promising recursive Z algorithm and recursive likelihood ratio algorithm are proposed for selecting split channels and SC decoding scheme, which can be then conveniently applied in construction of polar code of any fixed matrix with polarization features. The provided experimental simulations have verified the proposed algorithms as well as polar coding schemes, which may obtain more promising BER performance in the presence of either linear PA or nonlinear PA than LDPC scheme and which have a lesser decoding complexity than LDPCs. By significantly reducing the BER, polar code schemes may be considered as a potential candidate for the emerging 5G mm-Wave communications of extremely high data rates.