1 Introduction

Source localization is one of the major topics in the fields of radar, sonar, wireless communication and speech recognition location [1,2,3,4]. In the past decades, researchers have developed various high-resolution algorithms, among which the most widely used are the multiple signal classification (MUSIC) [5] and estimation of signal parameters via rotational invariance techniques (ESPRIT) [6] algorithms. According to the definition of the Fresnel region [7], the types of sources can be divided into far-field (FF) and near-field (NF) sources. In the FF case, the data received by the sensors collect the DOA information, while in the NF case, the data received by the sensors contain range and DOA information. In the presence of these two sources separately, many methods have achieved good estimation results [8,9,10,11,12,13]. In many situations, where FF sources and NF sources coexist, such as microphone array positioning [14, 15] and the sixth-generation (6G) mobile communication system [16,17,18], the above algorithms may not work.

In order to solve mixed-field source localization problem, some corresponding algorithms have also been developed recently. In [19], an algorithm based on second-order cumulants has been proposed, which used an oblique projection matrix to distinguish FF sources from NF sources. Zuo et al. [20] have proposed an algorithm without eigenvalue decomposition, and they used an alternate iterative scheme to promote the estimation accuracy of the oblique projection operator. In [21], a two-stage MUSIC algorithm has been developed to localize the mixed field by constructing two fourth-order cumulant matrices. For non-circular signals, a rank reduction (RARE) algorithm has been proposed in [22], which used three MUSIC-like estimators to locate the mixed-field sources. The above algorithms were proposed on the basis of uniform linear array (ULA), and most did not apply to sparse linear array (SLA) [23].

Since the SLA was developed, it has attracted extensive attention from researchers. By utilizing the coarray of physical array, the SLA can expand the array aperture, which dramatically improves the estimation accuracy and resolution of DOA estimation. However, the sparse array formation and algorithm based on the FF case cannot be directly used for mixed-field localization. Many researchers have developed symmetric arrays and algorithms suitable for mixed-field localization in SLA case. Wang et al. [24] have proposed a symmetric nested array (SNA) via symmetric the traditional nested array, and they used mixed-order statistics to estimate DOA and range. The algorithm had medium computational complexity and improved resolution and accuracy. Zheng et al. [25] have designed a symmetrical double-nested array (SDNA), which further improved the virtual array aperture compared to the traditional SNA. They combined oblique projection technology with spatial smoothing MUSIC (SS-MUSIC). Specifically, the NF component was extracted by the oblique projection matrix, and the DOA of the NF source was estimated by SS-MUSIC. Shen et al. [26] have developed an improved symmetric nested array (ISNA) and utilized a sparse reconstruction technique for DOA estimation. Compared with the previous symmetric nested arrays and algorithms, the array and algorithm proposed in [26] had more advantages in estimation accuracy and array aperture.

The algorithms mentioned above can be roughly divided into two categories. The first one is based on SS-MUSIC, such as [22, 24, 25]. This kind of algorithm can only use consecutive lags and waste some unique lags, which loses array aperture and reduces estimation accuracy. The other is based on sparse reconstruction techniques, such as the Least Absolute Shrinkage and Selection Operator (LASSO) algorithm mentioned in [26]. The LASSO algorithm can make full use of all unique lags, but this algorithm is an on-grid sparsity-based algorithm, and the performance of the algorithm is affected by the grid. To solve basis mismatch issue brought by the gridless methods, an algorithm based on atomic norm minimization was proposed and has achieved remarkable results in DOA estimation of FF sources [27,28,29]. Wu et al. [30] have introduced this method into mixed-field location and proposed the mixed sparse approach (MSA), but it was reconstructed on physical array, which would introduce a large fitting error.

In this paper, we propose a sparse matrix interpolation reconstruction algorithm on the basis of atomic norm minimization. Compared to second-order statistics, the mixed-field localization algorithm based on fourth-order cumulant can produce more virtual arrays; the fourth-order cumulant algorithm has low computational complexity compared to higher-order cumulant such as sixth-order cumulant. The proposed algorithm is able to exploit the full range of unique lags and avoids the base mismatch problem. In addition, different from Wu’s method, we perform interpolation reconstruction on the fourth-order cumulator matrix, which can reduce the fitting error. Firstly, construct an interpolation matrix, where the positions of the holes are filled with zero elements, in place of the Toeplitz matrix produced by the fourth-order cumulant, and the interpolated matrix can be regarded as produced by ULA. Then, the interpolated matrix is reconstructed adopting the method of atomic norm minimization, which is gridless. The reconstructed matrix contains all unique lags; therefore, a more accurate DOA estimation can be realized. Our key contributions are summarized as follows:

  1. (1)

    Similar to the covariance matrix under second-order statistics, we derive expressions for the covariance-like Toeplitz matrix and sparse Toeplitz matrix under fourth-order cumulants, corresponding to unique lags and unique lags with holes, respectively. By using the matrix filling theory, we complete the information of the hole and maximize the use of the array accepted data.

  2. (2)

    The Toeplitz matrix is reconstructed by atomic norm minimization. This method is gridless, and compared with LASSO algorithm, it avoids the base mismatch problem and improves the accuracy. Because the idea of matrix interpolation is adopted, the DOF of the algorithm is also higher than that of the LASSO algorithm.

  3. (3)

    Compared with Wu’s algorithm, the proposed algorithm interpolates on the virtual array, and the reconstructed Toeplitz matrix is closer to the ideal case, and the algorithm has better performance.

  4. (4)

    Through various experimental simulations, the superiority of the proposed algorithm is verified.

The rest of this paper is organized as follows. In Sect. 2, the signal model is introduced. In Sect. 3, we present the proposed sparse matrix reconstruction algorithm on the basis of atomic norm minimization. Section 4 provides the performance analysis, and Sect. 5 draws the conclusions.

Notations Uppercase(lowercase) characters are used to donate matrices (vectors). \({\left( \cdot \right) ^*}\), \({\left( \cdot \right) ^T}\) and \({\left( \cdot \right) ^H}\) donate the complex conjugate, transpose and conjugate transpose. \(\textrm{vec}\left( \cdot \right)\) donates the vectorization operator, \(E\left( \cdot \right)\) is the expectation operator, and \(\mathrm diag\left( \cdot \right)\) is the diagonalization operator. \(\left\langle \varvec{c} \right\rangle {}_i\) stands for the ith element of \(\varvec{c}\). \({\left\| \cdot \right\| _2}\) donates the \(l_2\) norms. Hollow letters, such as \(\mathbb {N}\), represent the set of integers. \(\circ\), \(\otimes\) and \(\odot\) donate the Hadamard product, Kronecker product and Khatri–Rao product.

2 Signal model

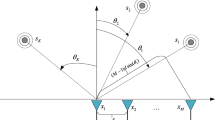
Assume that mixed FF and NF narrowband sources impinge onto a symmetry array with \(2M+1\) sensors. The inter-element spacing is \(d \le \lambda /4\), where \(\lambda\) is the signal wavelength, and the array sensors are indexed as \({\Omega _{\mathbb {M}}}\mathrm{{ = }}\left\{ { \Omega _{- M}, \Omega _{-(M-1)}, \cdots \Omega _{- 1},\Omega _{0},\Omega _1, \cdots ,\Omega _{M-1},\Omega _M} \right\}\). Array aperture D is the spacing between the first sensor and the last sensor, and let \(N=D/(2d)\), visibly \(N=\Omega _M\). For ULA, N is equal to M, and for SLA, \(N>M\).

The signals received by the mth sensor are written as

$$\begin{aligned} {x_m}\left( t \right) = \sum \limits _{k = 1}^K {{s_k}\left( t \right) {e^{j{\tau _{mk}}}} + {n_m}\left( t \right) }, \end{aligned}$$
(1)

where \({s_k}\left( t \right)\) donates the kth received signal, \({n_m}\left( t \right)\) donates the additive Gaussian white noise of the mth sensor, and \({\tau _{mk}}\) is the phase shift associated with the propagation time delay of the kth source between the mth sensor and the sensor reference point. In the case of NF source, the expression for \({\tau _{mk}}\) is as

$$\begin{aligned} {\tau _{mk}} = \Omega _m{\omega _k} + {\Omega _m^2}{\phi _k}, \end{aligned}$$
(2)

where

$$\begin{aligned} {\omega _k} = - 2\pi \frac{d}{\lambda }\sin {\theta _k}, \end{aligned}$$
(3)
$$\begin{aligned} {\phi _k} = \pi \frac{{{d^2}}}{{\lambda {r_k}}}{\cos ^2}{\theta _k}, \end{aligned}$$
(4)

where \({\theta _k}\) donates the DOA of the kth source and \(r_k\) donates the range of the kth NF source, respectively. The NF sources locate in the Fresnel region, i.e., \({r_k} \in \left[ {0.62{{\left( {{D^3}/\lambda } \right) }^{1/2}},2{D^2}/\lambda } \right]\). Otherwise, if the kth source locates in the FF region, which means \(r_k\) is greater than \(2{\mathrm{{D}}^2}/\lambda\), \({\tau _{mk}}\) can be expressed as

$$\begin{aligned} {\tau _{mk}} = \Omega _m{\omega _k}. \end{aligned}$$
(5)

Assuming that there are K sources in total, the first \(K_1\) are FF sources, and the remaining \(K-K_1\) are NF sources. The matrix form of (1) can be expressed as

$$\begin{aligned} \varvec{x}\left( t \right) = \varvec{A_{F}}\varvec{s_{F}}\left( t \right) + \varvec{A_{N}}\varvec{s_{N}} + \varvec{n}\left( t \right) , \end{aligned}$$
(6)

where \(\varvec{x}\left( t \right) \in {\mathbb {R}^{\left( {2M + 1} \right) \times 1}}\) is the sensor received signal, \(\varvec{n}\left( t \right) \in {\mathbb {R}^{\left( {2M + 1} \right) \times 1}}\) is noise matrix, and

$$\begin{aligned} \varvec{x}\left( t \right)= & {} [{x_{\Omega _{ - M}}}\left( t \right) , \ldots ,{x_{\Omega _0}}\left( t \right) , \ldots ,{x_{\Omega _M}}\left( t \right) ]^T, \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \varvec{n}\left( t \right) = [{n_{\Omega _{ - M}}}\left( t \right) , \ldots ,{n_{\Omega _0}}\left( t \right) , \ldots ,{n_{\Omega _M}}\left( t \right) ]^T, \end{aligned}$$
(8)
$$\begin{aligned} \varvec{A_F}= & {} [\varvec{a}\left( {{\theta _1}} \right) , \ldots ,\varvec{a}\left( {{\theta _{{K_1}}}} \right) ], \end{aligned}$$
(9)
$$\begin{aligned} \varvec{A_N}= & {} [\varvec{a}\left( {{\theta _{{K_1} + 1}},{r_{{K_1} + 1}}} \right) , \ldots ,\varvec{a}\left( {{\theta _K},{r_K}} \right) ], \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \varvec{s_F}\left( t \right) = [{s_1}\left( t \right) , \ldots ,{s_{{K_1}}}\left( t \right) ]^T, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \varvec{s_N}\left( t \right) = {[{s_{{K_1} + 1}}\left( t \right) , \ldots ,{s_K}\left( t \right) ]^T}, \end{aligned}$$
(12)

where

$$\begin{aligned} \varvec{a}\left( {{\theta _k},{r_k}} \right) = {[{e^{j\left( { \Omega _{-M}{\omega _k} + {\Omega _{-M}^2}{\phi _k}} \right) }}, \ldots ,1, \ldots ,{e^{j\left( {\Omega _M{\omega _k} + {\Omega _M^2}{\phi _k}} \right) }}]^T} \end{aligned}$$
(13)

donates the steering vector (Fig. 1).

Fig. 1
figure 1

Linear array configuration

Full size image

For the full paper, follow the following assumptions:

  1. (1)

    The source signals are non-Gaussian processes with nonzero kurtosis and are independent of each other.

  2. (2)

    The noise signals of the sensors are additive white Gaussian noise with zero mean, which is independent of the source signals.

  3. (3)

    The inter-sensors spacing is no greater than one quarter wavelength, which can suppress ambiguity in the DOA estimation.

3 Proposed algorithm

In this section, we propose an interpolation algorithm based on atomic norm minimization for the mixed NF and FF sources localization problem. The proposed algorithm can be divided into two operations: A. DOA estimation and B. source classification and range estimation.

3.1 DOA estimation of mixed-field sources

On the basis of the prior assumptions, a Hermitian matrix with the elimination range parameter and only DOA information is constructed by using the fourth-order cumulant. Detailedly, the fourth-order cumulant is defined as

$$\begin{aligned} {\text{cum}}\left\{ {x_{m} (t),x_{n}^{*} (t),x_{p}^{*} (t),x_{q} (t)} \right\} & = & {\text{cum}}\left\{ {\sum\limits_{{k = 1}}^{K} {s_{k} } (t)e^{{j(\Omega _{m} \omega _{k} + \Omega _{m}^{2} \phi _{k} )}} ,(\sum\limits_{{k = 1}}^{K} {s_{k} } (t)e^{{j(\Omega _{n} \omega _{k} + \Omega _{n}^{2} \phi _{k} )}} )^{*} ,\left(\sum\limits_{{k = 1}}^{K} {s_{k} } (t)e^{{j(\Omega _{p} \omega _{k} + \Omega _{p}^{2} \phi _{k} )}} \right)^{*} ,\sum\limits_{{k = 1}}^{K} {s_{k} } (t)e^{{j(\Omega _{q} \omega _{k} + \Omega _{q}^{2} \phi _{k} )}} } \right\} \\ = \sum\limits_{{k = 1}}^{K} {e^{{j\{ [(\Omega _{m} - \Omega _{n} ) - (\Omega _{p} - \Omega _{q} )]\omega _{k} + [(\Omega _{m}^{2} - \Omega _{n}^{2} ) - (\Omega _{p}^{2} - \Omega _{q}^{2} )]\phi _{k} \} }} } \quad \times {\text{cum}}\left\{ {s_{k} (t),s_{k}^{*} (t),s_{k}^{*} (t),s_{k} (t)} \right\} \\ = \sum\limits_{{k = 1}}^{K} {c_{{4,s_{k} }} } e^{{j\{ [(\Omega _{m} - \Omega _{n} ) - (\Omega _{p} - \Omega _{q} )]\omega _{k} + [(\Omega _{m}^{2} - \Omega _{n}^{2} ) - (\Omega _{p}^{2} - \Omega _{q}^{2} )]\phi _{k} \} }} \\ \end{aligned}$$
(14)

where \(c_{4,s_k}\)=\(\textrm{cum}\left\{ s_k(t),s^*_k(t),s^*_k(t),s_k(t)\right\}\) is the fourth-order cumulant of the \(s_k\).

Assume \(n=-m\), \(q=-p\), then (14) can be re-expressed as

$$cum\left\{ {x_{m} (t),x_{{ - m}}^{*} (t),x_{p}^{*} (t),x_{{ - p}} (t)} \right\} = \sum\limits_{{k = 1}}^{K} {c_{{4,s_{k} }} } e^{{j2(\Omega _{m} - \Omega _{p} )\omega _{k} }}$$
(15)

(15) is just represented by the DOAs of the sources. Let \({\bar{m}} = m + \Omega _M + 1\) and \({\bar{p}} = p + \Omega _M + 1\), we obtain a cumulant matrix \(\varvec{C}_1\) and the\(\left( {{\bar{m}},{\bar{p}}} \right)\)th of \(\varvec{C}_1\) is expressed as

$$\begin{aligned} \varvec{C}_{1} \left( {\bar{m},\bar{p}} \right) & & = & cum\left\{ {x_{{\bar{m} - \Omega _{M} - 1}} \left( t \right),x_{{ - \bar{m} + \Omega _{M} + 1}}^{*} \left( t \right),x_{{\bar{p} - \Omega _{M} - 1}}^{*} \left( t \right),x_{{ - \bar{p} + \Omega _{M} + 1}} \left( t \right)} \right\}\quad \quad \quad \quad \\ = \sum\limits_{{k = 1}}^{K} {c_{{4,s_{k} }} e^{{j2\left( {\bar{m} - \Omega _{M} - 1} \right)\omega _{k} }} \times \left( {e^{{j2\left( {\bar{p} - \Omega _{M} - 1} \right)\omega _{k} }} } \right)^{*} } \\ \end{aligned}$$
(16)

In matrix form, \(\varvec{C}_1\) can be expressed as

$$\begin{aligned} \varvec{{C_1} = B{C_{4s}}{B^H}} \end{aligned}$$
(17)

where \(\varvec{C_{4s}} = \textrm{diag}\left[ {{c_{4,{s_1}}},...,{c_{4,{s_K}}}} \right]\), \(\varvec{B} = \left[ {\varvec{b}\left( {{\theta _1}} \right) , \ldots ,\varvec{b}\left( {{\theta _K}} \right) } \right] \in {\mathbb {R}^{\left( {2\Omega _M + 1} \right) \times K}}\) can be regarded as a special steering matrix without range parameter \(r_k\) with

$$\begin{aligned} \varvec{b}\left( {{\theta _k}} \right) = \left[ {{e^{ - j2\Omega _M{\omega _k}}}, \ldots ,1, \ldots ,{e^{j2\Omega _M{\omega _k}}}} \right] ^T. \end{aligned}$$
(18)

Then, by vectorizing matrix \(\varvec{C}_1\), vector \(\varvec{c}_L\) is obtained

$$\begin{aligned} \varvec{c_L} = \textrm{vec} \left( {\varvec{C_1}} \right) = \left( {\varvec{B^*} \odot \varvec{B}} \right) \varvec{C}^{'}_{4s} \end{aligned}$$
(19)

where \(\varvec{C}_{4s}^{'} = {\left[ {{c_{4,{s_1}}}, \ldots ,{c_{4,{s_K}}}} \right] ^T}\). \(\varvec{c}_L\) behaves like the received data of a new line array without noise and the matrix \({{\varvec{B}^*} \odot \varvec{B}}\) is a new array steering matrix whose sensor positions are determined by set:

$$\begin{aligned} {\mathbb {N}} = \left\{ {{{\Omega _p} - {\Omega _q}\left| {-M \le p,q \le M} \right. } }\right\} . \end{aligned}$$
(20)

Removing duplicates in \(\varvec{c}_L\) and rearranging them, then we obtain a new vector \(\varvec{c}_G\):

$$\begin{aligned} \varvec{c_G} = \varvec{G}\varvec{c_L} = \varvec{A_G}\varvec{C}_{4s}^{'} \end{aligned}$$
(21)

where \(\varvec{A_G} \in {\mathbb {R}^{\left| {\mathbb {N}} \right| \times K}}\) is a coarray manifold matrix, and \(| \mathbb {N} |\) represents the cardinality of the set \(\mathbb {N}\). \(\varvec{G}\) is a selection matrix defined as

$$\begin{aligned} \begin{aligned} {\left\langle \varvec{G} \right\rangle _{i,p + \left( {q - 1} \right) (2M + 1)}} = \ {\left\{ \begin{array}{ll} \frac{1}{{\mathbb {M}\left( {{n_i}} \right) }},&{}\left( {{{\Omega _p},{\Omega _q}}} \right) \in \mathbb {M}\left( {{n_i}} \right) \\ {0,}&{}\textrm{otherwise} \end{array}\right. }\\ {{-M \le p,q \le M}} \end{aligned} \end{aligned}$$
(22)

where the set \({\mathbb {M}}\left( {{\Omega _i}} \right)\) contains each pair \(\left( {{\Omega _p} - {\Omega _q}} \right)\) that contributes to the coarray index \(\Omega _i\), which is

$$\begin{aligned} {\mathbb {M}}\left( {{\Omega _i}} \right) = {\left\{ {\left( {{\Omega _p},{\Omega _q}} \right) \in {\Omega _\mathbb {M} ^2}\left| {{\Omega _p} - {\Omega _q} = {\Omega _i}} \right. } \right\} ,{\Omega _i} \in {\mathbb {N}}}. \end{aligned}$$
(23)

For example, for a linear array configuration with \(\Omega _\mathbb {M} = \left\{ { - 2,0,2} \right\}\), we have \({\mathbb {N}} = \left\{ { - 4, - 2,0,2,4} \right\}\) and \(\varvec{G}\) is given as

$$\begin{aligned} \varvec{G} = \begin{bmatrix} 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}{\frac{1}{2}}&{}0&{}0&{}0&{}{\frac{1}{2}}&{}0\\ {\frac{1}{3}}&{}0&{}0&{}0&{}{\frac{1}{3}}&{}0&{}0&{}0&{}{\frac{1}{3}}\\ 0&{}{\frac{1}{2}}&{}0&{}0&{}0&{}{\frac{1}{2}}&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0 \end{bmatrix}. \end{aligned}$$
(24)

From the vector \(\varvec{c}_G\), a new Toeplitz matrix can be constructed:

$$\begin{aligned} \varvec{C_G} = \begin{bmatrix} {{{\left\langle {\varvec{c_G}} \right\rangle }_0}}&{}{{{\left\langle {\varvec{c_G}} \right\rangle }_{ - 1}}}&{} \cdots &{}{{{\left\langle {\varvec{c_G}} \right\rangle }_{ - {L_{\mathbb {N}}} + 1}}}\\ {{{\left\langle {\varvec{c_G}} \right\rangle }_1}}&{}{{{\left\langle {\varvec{c_G}} \right\rangle }_0}}&{} \cdots &{}{{{\left\langle {\varvec{c_G}} \right\rangle }_{ - {L_{\mathbb {N}}} + 2}}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{{\left\langle {\varvec{c_G}} \right\rangle }_{{L_{\mathbb {N}}} - 1}}}&{}{{{\left\langle {\varvec{c_G}} \right\rangle }_{{L_{\mathbb {N}}} - 2}}}&{} \cdots &{}{{{\left\langle {\varvec{c_G}} \right\rangle }_0}} \end{bmatrix} \end{aligned}$$
(25)

where \({L_{\mathbb {N}}} = \left( {\left| {\mathbb {N}} \right| + 1} \right) /2\).

In [31], a Toeplitz matrix is proposed to replace the covariance matrix in the spatial smoothing algorithm. Similar to the covariance matrix in [31], (17) can be regarded as a special covariance matrix without noise; therefore, (25) is also a substitute matrix for the smoothed covariance matrix, and the DOA information can be obtained by processing (25) with the subspace algorithm. For a detailed proving process, please refer to [31].

Notably, when the coarray is continuous, \(\varvec{C}_G\) can be directly used to obtain the DOA information. When the coarray is discontinuous, the conventional algorithms need to select a continuous part, which will lose the array aperture. Next, a sparse matrix is constructed with holes to utilize all the unique lags.

Define the interpolated signal vector \(\varvec{c}_I\) and initialize it as

$$\begin{aligned} {\left\langle {\varvec{c_I}} \right\rangle _i} = \left\{ \begin{array}{l} {\left\langle {\varvec{c_G}} \right\rangle _i},\quad i \in \mathbb {N}\\ 0,\quad \quad \quad i \in \mathbb {V}/\mathbb {N} \end{array}. \right. \end{aligned}$$
(26)

The measurements of the unique lags in vector \(\varvec{c}_I\) correspond to vector \(\varvec{c}_G\), and the interpolation sensors are initialized to zeros. \(i \in \mathbb {V}/\mathbb {N}\) means i is in \(\mathbb {V}\) but not in \(\mathbb {N}\). After interpolation, the vector \(\varvec{c}_I\) can be regarded as the signal accepted by the ULA with the sensor positions as the integer set \(\mathbb {V}\):

$$\begin{aligned} {\mathbb {V}} = \left\{ {i\left| {\min \left( {\mathbb {N}} \right) \le i \le \max \left( {\mathbb {N}} \right) } \right. } \right\} . \end{aligned}$$
(27)

From the interpolate vector \(\varvec{c}_I\) , construct an interpolated Toeplitz matrix:

$$\begin{aligned} \varvec{C_I} = \begin{bmatrix} {{{\left\langle {\varvec{c_I}} \right\rangle }_0}}&{}{{{\left\langle {\varvec{c_I}} \right\rangle }_{ - 1}}}&{} \cdots &{}{{{\left\langle {\varvec{c_I}} \right\rangle }_{ - {L_{\mathbb {V}}} + 1}}}\\ {{{\left\langle {\varvec{c_I}} \right\rangle }_1}}&{}{{{\left\langle {\varvec{c_I}} \right\rangle }_0}}&{} \cdots &{}{{{\left\langle {\varvec{c_I}} \right\rangle }_{ - {L_{\mathbb {V}}} + 2}}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{{\left\langle {\varvec{c_I}} \right\rangle }_{{L_{\mathbb {V}}} - 1}}}&{}{{{\left\langle {\varvec{c_I}} \right\rangle }_{{L_{\mathbb {V}}} - 2}}}&{} \cdots &{}{{{\left\langle {\varvec{c_I}} \right\rangle }_0}} \end{bmatrix} \end{aligned}$$
(28)

where \({L_{\mathbb {V}}} = \left( {\left| {\mathbb {V}} \right| + 1} \right) /2\), and obviously, \(N=(L_\mathbb {V}-1)/2\). \(\varvec{C}_I\) contains all values in \(\varvec{C}_G\) and zeros resulting from interpolation.

The concept of atomic norm is proposed in [11], which summarizes several commonly used norm for sparse representation and recovery, e.g., the \({\ell _1}\) norm and the nuclear norm. Use the atomic norm minimization method to reconstruct the interpolation matrix \(\varvec{C}_I\), first rewrite the matrix \(\varvec{C}_I\) as

$$\begin{aligned} \varvec{C} = \bar{\varvec{B}}{\varvec{C}_{4s}}{\bar{\varvec{B}}^H} = \sum \limits _{k = 1}^K {{c_{4,{s_k}}}\left( {\bar{\varvec{b}}\left( {{\theta _k}} \right) {\bar{\varvec{b}}^H}\left( {{\theta _k}} \right) } \right) } \end{aligned}$$
(29)

where \(\bar{\varvec{B}}= \left[ {\bar{\varvec{b}}\left( {{\theta _1}} \right) , \ldots ,\bar{\varvec{b}}\left( {{\theta _K}} \right) } \right] \in {\mathbb {R}^{\left( {2N + 1} \right) \times K}}\), and \(\bar{\varvec{b}}\left( {{\theta _k}} \right) = \left[ {{e^{ - j2N{\omega _k}}}, \ldots ,1, \ldots ,{e^{j2N{\omega _k}}}} \right] ^T\).

Then, define an atom set

$$\begin{aligned} \varvec{A} = \left\{ {\bar{\varvec{B}}\left( {{\alpha _k}} \right) =\bar{\varvec{b}}\left( {{\alpha _k}} \right) {\bar{\varvec{b}}^H}\left( {{\alpha _k}} \right) ,{\alpha _k} \in ({ - 90^\circ ,90^\circ } ]} \right\} . \end{aligned}$$
(30)
figure a

Evidently, \(\varvec{C}\) is a linear combination of K atoms in atomic set A, and similarly, \(\varvec{C}_G\) and \(\varvec{C}_I\) are also linear combinations of atomic set A. The atomic \({\ell _0}\) norm represents the minimum number of atoms that can synthesize \(\varvec{C}\) and is defined as:

$$\begin{aligned} {\left\| \varvec{C} \right\| _{A,0}} = \inf \left\{ {{{\mathcal {K}}}\mathrm{{}}:\varvec{C} = \sum \limits _{k = 1}^{{{\mathcal {K}}}\mathrm{{}}} {{c_{4,{s_k}}}\bar{\varvec{B}}\left( {{\alpha _k}} \right) } ,{c_{4,{s_k}}} > 0} \right\} \end{aligned}$$
(31)

where \(\mathrm inf\) donates the infimum. While minimizing (31) is an NP-hard problem, the atomic norm convex relaxation is introduced as

$$\begin{aligned} \begin{aligned} {\Vert \varvec{C} \Vert _A}&= \inf \left\{ {h> 0:\varvec{C} \in h \ \textrm{conv}\left( A \right) } \right\} \\&= \inf \left\{ {\sum \limits _k {{c_{4,{s_k}}}} \bigg | \varvec{C} = \sum \limits _k {{c_{4,{s_k}}}\bar{\varvec{B}}\left( {{\alpha _k}} \right) ,{c_{4,{s_k}}} > 0} } \right\} \end{aligned} \end{aligned}$$
(32)

where \(\mathrm conv(A)\) is the convex hull. The atomic norm of virtual matrix \(\varvec{C}_I\) can be displayed in an equivalent semi-definite programming (SDP) form as

$$\begin{aligned} \begin{array}{l} {\left\| \varvec{C} \right\| _A} = \mathop {\inf }\limits _{\varvec{u},\varvec{W},\varvec{C}} \Big \{ \frac{1}{{2{L_{\mathbb {V}}}}}\textrm{tr}\left( {\varvec{T}\left( u \right) } \right) + \frac{1}{{2{L_{\mathbb {V}}}}}\textrm{tr}\left( \varvec{W} \right) \\ \quad \quad \quad \quad \quad \quad \quad \quad \left| {\left[ {\begin{array}{*{20}{c}} {\varvec{T}\left( u \right) }&{}\varvec{C}\\ {{\varvec{C}^H}}&{}\varvec{W} \end{array}} \right] } \right. > 0\Big \} \end{array} \end{aligned}$$
(33)

where \(\mathrm tr( \cdot )\) donates the trace operator and \(\varvec{T}(u)\) is a Hermitian Toeplitz matrix with vector \(\varvec{u}\) as its first column. Taking into account the relationship between \(\varvec{R}_I\) and \(\varvec{R}\), (33) can be rewritten as a convex optimization problem, and its expression is as follows

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{\varvec{W},\varvec{u},\varvec{C}} \quad \textrm{tr}\left[ {\varvec{W} + \varvec{T}(u)} \right] \\ s.t. \quad \left[ {\begin{array}{*{20}{c}} {\varvec{T}\left( u \right) }&{}\varvec{C}\\ {{\varvec{C}^H}}&{}\varvec{W} \end{array}} \right] > 0,\\ \left\| {\varvec{C} \circ \varvec{F} - {\varvec{C}_I}} \right\| _2^2 \le \varepsilon , \end{array} \end{aligned}$$
(34)

where \(\varvec{F}\) is a selection matrix consisting of 0s and 1s to distinguish zero and nonzero values in matrix \(\varvec{C}_I\), specifically, the 1s in matrix \(\varvec{F}\) correspond to the nonzero values in matrix \(\varvec{C}_I\), and the 0s correspond to the zero values. \(\varepsilon\) is a threshold for fitting error.

The optimization problem (34) can be solved by some classical and efficient software tools, such as CVX [32] or SeDuMi [33]. The matrix \(\varvec{C}_I\) will be reconstructed as the Hermitian Toeplitz matrix \(\varvec{T}(u)\). It should be pointed out that, after interpolation and restoration, the \(\varvec{T}(u)\) is a \(L_\mathbb {V} \times L_\mathbb {V}\) matrix, so the maximum number of detectable sources can be greater than the number of physical sensors. Algorithm 1 summarizes the proposed DOA algorithm for sparse matrix interpolation.

3.2 Range estimation of the NF sources

In order to obtain the range estimations of NF sources, the covariance matrix \(\varvec{R}_{xx} = E\left\{ {\varvec{x}\left( t \right) {\varvec{x}^H}\left( t \right) } \right\}\) needs to be calculated first. Perform eigen-decomposition on \(\varvec{R}_{xx} = E\left\{ {\varvec{x}\left( t \right) {\varvec{x}^H}\left( t \right) } \right\}\) yields:

$$\begin{aligned} {\varvec{R}_{xx}} = {\varvec{U}_s}{\Lambda _s}{\varvec{U}_s} + {\varvec{U}_n}{\Lambda _n}{\varvec{U}_n}, \end{aligned}$$
(35)

where \(\Lambda _s\) contains the K largest eigenvalues of \(\varvec{R}_{xx}\) and \(\varvec{U}_s\) is the corresponding eigenvalues, \(\Lambda _n\) contains the \(2M+1-K\) smallest eigenvalues of \(\varvec{R}_{xx}\) and \(\varvec{U}_n\) denotes the corresponding eigenvectors. With the DOA estimates \(\left\{ {{{\hat{\theta }}_k},k = 1,2, \ldots ,K} \right\}\), taking the \({\hat{\theta }_k}\) into \(\varvec{a}\left( {{\theta _k},{r}} \right)\), the range of the kth source is estimated as

$$\begin{aligned} {r_k} = \mathop {\min }\limits _r \left( {{\varvec{a}\left( {{\theta _k},r} \right) }{\varvec{U}_n}\varvec{U}_n^H{{\varvec{a}^H}\left( {{\theta _k},r} \right) }} \right) . \end{aligned}$$
(36)

When \({r_k} = \infty\), the FF sources can be distinguished; when \(r_k\) is in the Fresnel region, the range of NF sources can be obtained. \({\hat{\theta }_k}\) and \(r_k\) will be matched automatically, and no redundant operations are required.

3.3 Discussion

Multiple FF and NF sources with the same DOAs According to (36), when the FF sources and the NF sources have the same DOAs, the proposed algorithm automatically classifies the DOAs to the NF sources. Therefore, an additional operation is required to distinguish NF sources DOAs, which is given by

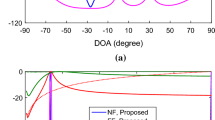
$$\begin{aligned} {\theta _{FF}} = \mathop {\min }\limits _\theta \left( {{\varvec{a}\left( {\theta ,\infty } \right) }{\varvec{U}_n}\varvec{U}_n^H{{\varvec{a}^H}\left( {\theta ,\infty } \right) }} \right) . \end{aligned}$$
(37)

To make it clearer, assume there are four signal sources, \(\left( { - 30^\circ ,\infty } \right) \left( { - 10^\circ ,\infty } \right) \left( { - 10^\circ ,8\lambda } \right) \left( {30^\circ ,14\lambda } \right)\), and linear array is \({\Omega _M} = \left\{ { - 9, - 3, - 2,0,2,3,9} \right\}\). After Algorithm 1, three estimated \(\theta _k\) are obtained, \(\theta _k=-30^\circ , -10^\circ , {30^\circ }\). Substitute the estimated \(\theta _k\) into (36) in turn, and the result is shown in Fig. 2a, from which we can only distinguish the information of two NF sources and one FF source. Then according to (37), we get the result shown in Fig.2b, from which we can distinguish the DOAs of the FF sources.

Note that there is a weak spectral peak at the position of \(\theta _k=30^\circ\), which is because the steering vector \(\varvec{a}( {\theta _k ,r_k})\) of the NF source has a certain orthogonality with the noise subspace \(U_n\). When \(r_k\) is larger, this spectral peak is higher, and when \(r_k=\infty\), the steering vector \(\varvec{a}( {\theta _k ,r_k})\) becomes \(\varvec{a}( {\theta _k ,\infty })\) and this spectral peak correspondingly becomes the FF spectral peak.

Fig. 2
figure 2

Mixed-field sources location with same DOAs. (SNR=20dB and T=2000)

Full size image

4 Simulation results

In this section, the performance of the proposed algorithm is evaluated through different simulations. Specifically, we compare the proposed algorithm with oblique projection MUSIC (OPMUSIC) algorithm [19], mixed-order MUSIC algorithm [24], MSA algorithm [30] and LASSO algorithm [26]. In all simulations, the inter-sensor spacing is \(d = \lambda /4\), the signal model is \({e^{j{\varphi _t}}}\) where the phase is uniformly distributed in \(\left[ {0,2\pi } \right]\), and the parameter \(\varepsilon\) in (17) is set to \({10^{ - 8}}\). For the parameter h and \(\beta\) in the LASSO and MSA algorithm, the optimal value of 0.6 and 0.5 are adopted, separately.

In the first three simulations, the performances of the proposed algorithm under symmetry ULA, symmetry SLA and underdetermined conditions are simulated, respectively. In the last simulation, the performance of the proposed algorithm in classical symmetric arrays is verified. Algorithm performance is evaluated by root-mean-square error (RMSE), with an average of \(\gamma =500\) Monte Carlo trials:

$$\begin{aligned} \textrm{RMSE} = \sqrt{\frac{1}{{K'\gamma }}\sum \limits _{i = 1}^{\gamma } {\sum \limits _{k = 1}^{K'} {{{\left( {a_k^{i} - {a_k}} \right) }^2}} } } \end{aligned}$$
(38)

where \(a_k\) represents the real \({\theta _k}\) or \(r_k\), and correspondingly, \({\hat{a}}_k^i\) is the estimated \({\theta _k}\) or \(r_k\) for the ith trail. \(K'\) is the number of sources, and if the RMSE of the FF sources is required, then \(K'\) is equal to \({K_1}\); if the RMSE of the NF sources is required, \(K'\) is \(K-{K_1}\).

Fig. 3
figure 3

Performance comparison in ULA case with \({\Omega _\mathbb {M}} = \left[ { -4, -3, -2, - 1,0,1,2,3,4} \right]\) and \(T=2000\)

Full size image
Fig. 4
figure 4

Performance comparison in SLA case with \({\Omega _\mathbb {M}} = \left[ { -9, -6, -3, -2,0,2,3,6,9} \right]\) and \(T=2000\)

Full size image

4.1 The ULA case

In the first simulation, assume that one narrowband FF source \(\left( { - 10^\circ \infty } \right)\) and one narrowband NF source \(\left( {10^\circ ,3\lambda } \right)\) impinge onto a symmetrical ULA with nine sensors. Figure 3 shows the performance of different algorithms in symmetry ULA with the SNR varying from \(-\) 5 to 30dB, and the snapshots are set to \(T=2000\). The simulation results show that in the case of ULA, the performance of the proposed algorithm is comparable to that of LASSO and mixed-order, and better than that of MSA. Because there are no holes in the matrix \(\varvec{C}_1\) generated by the ULA, the proposed algorithm has no obvious advantage over other excellent algorithms. But this simulation verifies that the proposed algorithm is also applicable to ULA. MSA algorithm has poor performance because of its large fitting error.

From Fig. 3a, it can be seen that the OPMUSIC algorithm is very different from other algorithms, because the OPMUSIC algorithm is based on the second-order cumulant and the rest of the algorithms use the fourth-order cumulant. This also verifies the discussion in Sect. 2 about the Cramér–Rao bound from one aspect. The estimation of the fourth-order statistics itself has errors; therefore, the proposed algorithm performance is not superior to the conventional algorithm based on the second-order statistics. From Fig. 3b, the OPMUSIC algorithm has the same performance as other algorithms, which is because the algorithm needs to use the anti-diagonal elements of the covariance matrix to remove the range parameter influence when performing NF source DOA estimation. From Fig. 3c, the estimation of range is mainly affected by the array aperture and DOA estimation accuracy. Since the same array aperture is used and the DOA estimation accuracy is the same, the proposed algorithm has the same range estimation accuracy as the other algorithms.

4.2 The SLA case

In the second simulation, instead of symmetry ULA, we use symmetry SLA of nine sensors with \({\Omega _\mathbb {M}} = \left[ { - 9 - 6, - 3, - 2,0,2,3,6,9} \right]\), and the Fresnel region is \(\left[ {6\lambda ,40\lambda } \right]\). The simulation results are shown in Fig. 4. It can be seen that for DOA estimation of FF sources, the proposed algorithm outperforms other algorithms except OPMUSIC algorithm which uses second-order cumulants. For the DOA estimation of NF sources, the proposed algorithm is the best among the five algorithms.

Compared with LASSO and other classical compressed sensing algorithms, MSA and the proposed algorithm adopt atomic norm minimization method, which has two advantages:

  1. (1)

    DOA estimation can be performed in a gridless manner;

  2. (2)

    More unique lags can be exploited.

Therefore, the performance of the algorithm is further improved. The OPMUSIC algorithm is on the basis of second-order statistics and needs to use the anti-diagonal elements of the covariance matrix for DOA estimation of the NF sources; therefore, it is not suitable for symmetry SLA. The MSA algorithm needs to complete more interpolation sensors, so its performance is inferior to that of the proposed algorithm in the case of high SNR. From Fig. 4c, in the case of the same array aperture, the DOA estimation accuracy of the proposed algorithm is higher, so is its range estimation accuracy.

Fig. 5
figure 5

Performance of underdetermined estimation (\({\Omega _\mathbb {M}} = \left[ { -9, -6, -3, -2,0,2,3,6,9} \right]\), \(T=20000\) and SNR=20dB)

Full size image

4.3 Underdetermined estimation

The most significant advantage of the sparse array is that it can perform underdetermined estimation. Still, the traditional algorithm needs to use consecutive lags, which will lose the array aperture and reduce the estimation accuracy. In the third simulation, we show the performance of the proposed algorithm in underdetermined estimation. Specifically, it is assumed that ten narrowband sources, five FF sources from \(( - 50^\circ ,\infty )( - 40^\circ ,\infty )( - 30^\circ ,\infty )( - 20^\circ ,\infty )( - 10^\circ ,\infty )\) and five NF sources from \(( 10^\circ ,12\lambda )( 20^\circ ,14\lambda )( 30^\circ ,16\lambda )( 40^\circ ,18\lambda )( 50^\circ ,20\lambda )\), impinge on symmetry SLA with nine sensors, where the array location is \({\Omega _\mathbb {M}} = \left[ { - 9 - 6, - 3, - 2,0,2,3,6,9} \right]\), and the Fresnel region is \(\left[ {6\lambda ,40\lambda } \right]\). Figure 5 shows the MUSIC spectrum of the proposed algorithm. Figure 6 shows the performance comparison of different algorithms.

Under this simulation condition, the consecutive lags applied by mixed-order algorithm are \([ -9, - 8, \ldots 0, \ldots 8,9]\) and the number of unique lags used by the LASSO algorithm is 27. After interpolation and completion, the number of unique lags used by the MSA and proposed algorithms is 37. From Fig. 6, the performance of the proposed algorithm is significantly better than other algorithms.

Fig. 6
figure 6

Underdetermined estimation performance (\({\Omega _\mathbb {M}} = \left[ { -9, -6, -3, -2,0,2,3,6,9} \right]\), \(T=20000\) and \(K=10\))

Full size image

4.4 Applied to classical symmetric linear arrays

From (34), it can be concluded that the number and distribution of zeros in matrix \(\varvec{C}_I\) affect the reconstruction accuracy. To verify the applicability of the proposed algorithm, in the fourth simulation, we apply the proposed algorithm to several mainstream symmetric array configurations and compare it with the MSA algorithm, and the simulation results are shown in Fig. 7. Four symmetric array configurations are considered: symmetric nested array I (SNA I) [24], symmetric double-nested array (SDNA) [25], symmetric nested array II (SNA II) [34] and improved symmetric nested array (ISNA) [26]. Each configuration uses nine physical sensors, the Fresnel region is \(\left[ {5\lambda ,30\lambda } \right]\), and the number of sources is six, \(( - 30^\circ ,\infty )( - 20^\circ ,\infty )( - 10^\circ ,\infty )( 10^\circ ,10\lambda )( 20^\circ ,17\lambda )( 30^\circ , 25\lambda )\).

Fig. 7
figure 7

Applied to classical symmetric linear arrays (\(T=20000\), nine sensors and \(K=6\))

Full size image

As can be seen from Fig. 7, among the above four classical symmetric formations, the proposed algorithm performs better than MSA in the case of high SNR. The proposed algorithm is based on high-order cumulant matrix for interpolation reconstruction. Compared with MSA for interpolation reconstruction on physical array, fewer 0 values need to be recovered and the fitting error is smaller. Therefore, the reconstructed matrix is closer to the true value.

4.5 FF and the NF sources share the same DOAs

In the last simulation, we simulate the performance of the proposed algorithm when some FF and NF sources share the same DOAs. Four mixed-field sources, \(( 10^\circ ,\infty )( 30^\circ ,\infty )( 10^\circ ,12\lambda )( 30^\circ ,14\lambda )\) , impinge on symmetry SLA with nine sensors, where the array location is \({\Omega _\mathbb {M}} = \left[ { - 9 - 6, - 3, - 2,0,2,3,6,9} \right]\). The simulation results are shown in Fig. 8. It can be seen that the LASSO and MIX algorithms are unable to discriminate when mixed-field sources have the same angle; the MSA algorithm discriminates by distance, which has less impact on the DOA estimation; and the proposed algorithm achieves discrimination by an additional step, which increases the estimation accuracy of FF sources.

Fig. 8
figure 8

FF and the NF sources share the same DOAs ( \(T=20000\), \(( 10^\circ ,\infty )( 30^\circ ,\infty )( 10^\circ ,12\lambda )( 30^\circ ,14\lambda )\))

Full size image

5 Conclusions

In this paper, we propose a high-performance algorithm for the mixed-field localization problem. By interpolating the higher-order cumulant matrix, we get a Toeplitz matrix of higher dimensionality. The interpolation matrix is then restored using atomic norm minimization. Through the above operations, in the symmetry SLA, the proposed algorithm can use more unique lags, so the performance of the algorithm is better. The superiority of the proposed algorithm is verified by theoretical analysis and simulation results.

It should be pointed out that the proposed algorithm is applicable not only to linear array, but also to sparse planar array mixed-field sources location problem. Therefore, the performance of the proposed algorithm in two-dimensional (2D) localization is very worthy of future investigation. In addition, the resolution of gridless algorithms is low [35], so how to improve the resolution of the proposed algorithm is also an important research direction in the future.