1 Introduction

Multi-target tracking using multi-static tracking systems has a long history [1,2,3,4,5]. Classical multi-target tracking methods, such as the joint probabilistic data association filter [6], the multiple hypothesis tracking algorithm [7, 8] and the track-before-detect paradigm [9,10,11], have been widely studied. Recently, the multi-static Doppler radar system has attracted a lot of attention in the field of passive surveillance [12, 13]. The transmitters are typically the commercial frequency modulation (FM) radio transmitters, digital audio/video broadcasters (DAB/DVB), or global system for mobile communications (GSM) base stations [14]. The radar receivers can typically measure the multi-static range, direction-of-arrival (DOA) and Doppler shift. The Doppler-shift measurement is widely considered in the multi-static radar systems and the main reasons are twofold. On the one hand, the Doppler measuring sensors are low cost and do not require a hardware array. On the other hand, Doppler-shift measurements are typically accurate. Although the Doppler measurement has been used in localization and tracking for a long history, existing studies mainly analyze the observability of the target [15, 16] and consider the optimal positioning of multi-static systems [17, 18]. The problem of sensor management for multi-target tracking in multi-static Doppler radar system has not been fully studied, and this paper presents a novel receiver selection solution.

Mahler’s finite set statistics (FISST) [19, 20] is an elegant Bayesian formulation based on the random finite set (RFS) theory, providing a unified approach to addressing the stochastic nature of the multi-target sensor management problem. Based on the FISST, the probability hypothesis density (PHD) filter [21], the cardinalized PHD (CPHD) filter [22], and the multi-Bernoulli filter [23] have been developed and attracted a lot of attention. The PHD, CPHD, and multi-Bernoulli filters are approximations of the complicated Bayes multi-target filter. The PHD and CPHD filters propagate moments and cardinality distributions, while the multi-Bernoulli filter propagates the parameters of a multi-Bernoulli distribution. These filters assume that the targets are indistinguishable and hence cannot output target trajectories. By using the labeled RFS formulation [24, 25], the generalized labeled multi-Bernoulli (GLMB) filter [26] and the labeled multi-Bernoulli (LMB) filter [27] have be proposed to address target trajectories. Multi-target densities within the iteration of the GLMB filter are weighted sums of multi-target exponentials. The LMB filter can be regarded as an efficient approximation of the GLMB filter and an improved approximation of the multi-Bernoulli filter. With the advantages of the GLMB filter and the multi-Bernoulli filter, the LMB filter not only has straightforward particle implementations and state estimation, but also outputs target tracks and gives better performance.

To provide a balance in the tracking accuracy and communication constraints of the multi-sensor system, intelligent sensor management is required to report high quality target-related measurements. Due to energy and bandwidth constraints, a subset of sensors is selected from all sensors to collect high quality measurements. Multi-target sensor management is essentially an optimal nonlinear stochastic control problem, aiming at making the right management decision at the right time. Within the RFS framework, sensor management is generally formulated as a partially observed Markov decision process (POMDP). The elements of a POMDP include a set of admissible sensor management commands, the current (uncertain) information state, and the objective function function associated with each command. Several objective functions have been proposed within the POMDP, which are mainly driven by information theoretic measures and specific tasks. A measure of information gain is the divergence between the predicted and updated multi-target densities. Although the Kullback–Leibler divergence [28] and Rényi [29] divergence have been widely used, they cannot be computed analytically. In [30, 31], the authors derived closed form Cauchy–Schwarz divergences for Poisson and GLMB models. The Cauchy–Schwarz divergence has been applied in observer trajectory optimization [31], drone path-planning [32], and multi-sensor control [33]. The objective functions driven by tasks include, but not be limited to, the posterior expected number of targets [34,35,36], the cardinality variance [37], and the statistical mean of the optimal sub-pattern assignment (OSPA) error [38]. Our recent work [39] considers the legacy tracks and the measurement-updated tracks separately, to make full use of the information involved in the updated multi-target density.

In this paper, we consider the receiver selection problem for multi-target tracking using the multi-static Doppler radar system. Multiple targets move in the surveillance area and the number of targets and their states vary over time. With the movement of the multi-target, receivers in the multi-static Doppler radar system are adaptively selected. However, since transmit and receive antennas are placed at different locations, measurements collected by multi-static systems are typically subjected to noise corruption, missed detections, and false alarms. Worse, a single Doppler measurement cannot provide complete information on the target state, known as single-sensor unobservability. Accurate estimation of the number of targets and their tracks from Doppler measurements is difficult, and the difficulty is further compounded by receiver selection. We model the multi-target state as a LMB RFS and use the LMB filter for tracking. For receiver selection, the cardinality variance derived from the LMB distribution is used as a selection criterion under the POMDP framework. The reasons for using the cardinality variance are twofold. First, the cardinality variance has a closed-form expression and its calculation is very simple. Second, the cardinality variance is a measure of the accuracy of the number of targets, which is closely related to the tracking accuracy. To increase the diversity of the selected sensors and overcome the low observability of the Doppler measurement, the receivers selected at the previous time steps are taken into account for receiver selection at the current time step. We set up a window for the receivers selected from previous time steps to the current time step and confirm that the sensors in the window are different. Simulation experiments study the tracking performance of the proposed method using different window lengths and validate the effectiveness of the proposed method.

The paper is organized as follows. In Sect. 2, the necessary background on the multi-static Doppler radar system, the labeled RFS, and the LMB recursion is briefly introduced. Then, motivations and details of the window-added receiver selection are given in Sect. 3. In Sect. 4, results and discussion are given. Finally, Sect. 5 concludes the paper.

2 Background

2.1 Multi-static Doppler radar system

We assume a multi-static Doppler radar system composed of one transmitter and several receivers, as illustrated in Fig. 1. The multi-static Doppler radar system is assumed to be cooperative so that all information of the transmitter and receivers are available.

Fig. 1
figure 1

Multi-static Doppler-only surveillance system in the \(x-y\) plane

Full size image

In the multi-static Doppler system, a transmitter located at \(t=[t_{x},t_{y}]^{\rm T}\) illuminates the target \(x_{k}\) with position \(p_{k}=[p_{x,k},p_{x,k}]^{\rm T}\) and velocity \({\dot{p}}_{k}=[{\dot{p}}_{x,k},{\dot{p}}_{x,k}]^{\rm T}\). If the signal is scattered by the target, receiver j with position \(r^{(j)}=[r_{x}^{(j)},r_{y}^{(j)}]^{\rm T}\) will receive it and report a Doppler measurement as

$$\begin{aligned} z_{k}^{(j)}=-{\dot{p}}_{k}^{\mathrm {T}}\left[ \frac{p_{k}-r^{(j)}}{\left\| p_{k}-r^{(j)}\right\| }+\frac{p_{k}-t}{\left\| p_{k}-t\right\| }\right] \frac{f_{c}}{c}+\varepsilon _{k}^{(j)} \end{aligned}$$
(1)

where c is the speed of light, \(f_{c}\) is the carrier frequency, and \(\varepsilon _{k}^{(j)}\) is the zero mean white Gaussian measurement noise with standard deviation \(\sigma _{\varepsilon }\). The Doppler shift can be positive or negative. The interval of the Doppler measurements is given as an interval \([-f_{0},+f_{o}]\), where \(f_{o}\) is the maximal possible value of the Doppler measurement. The distribution of false detections (clutter) is time invariant and independent of the target state. It is assumed that the false detections are distributed uniformly over the measurement space, and the number of false detections is Poisson distributed with the constant mean value \(\uplambda ^{(j)}\) for receiver j.

2.2 Bayes multi-target filter

The Bayes multi-target filter [19, 20] is an extension of the Bayes single-target filter using the RFS to describe the multi-target state. An RFS is a finite-set-valued random variable that the points are random and unordered and that the number of points is random. Assuming that the target states take values from a state space \({\mathbb {X}}\), the multi-target state space is the space of all finite subsets of \({\mathbb {X}}\) and denoted as \({\mathcal {F}}(\mathbb {X\text {)}}\). To distinguish between different targets, a mark \(\ell \in {\mathbb {L}}\) is augmented to the state of each target in the labeled RFS model. In this way, the multi-target state is considered as a finite set on \({\mathbb {X}}\times {\mathbb {L}}\). For convention, single target states are denoted by small letters (e.g., x, \({\varvec{x}}\)) and multi-target states are denoted by capital letters (e.g., X, \({\varvec{X}}\)). To distinguish labeled states and their distributions from the unlabeled, the labeled ones are denoted by bold face letters (e.g., \({\varvec{x}}\), \({\varvec{X}}\), \(\varvec{\pi }\)).

At time k, it is assumed that there are \(N_k\) target states \({\varvec{x}}_{k,1},\ldots ,{\varvec{x}}_{k,N_k}\) taking values in the labeled state space \({\mathbb {X}}\times {\mathbb {L}}\), and \(M_k\) measurements \(z_{k,1},\ldots ,z_{k,M_k}\) taking values in an observation space \({\mathbb {Z}}\). The set of targets is denoted as the multi-target state \({\varvec{X}}_{k}=\{{\varvec{x}}_{k,1},\ldots ,{\varvec{x}}_{k,N_k}\}\in {\mathcal {F}}(\mathbb {X\times {\mathbb {L}}\text {)}}\). The set of observations is treated as the multi-target observation \(Z_{k}=\{z{}_{k,1},\ldots ,z_{k,M(k)}\}\in {\mathcal {F}}(\mathbb {Z\text {)}}\). Let \(\varvec{\mathbf {\pi }}_{k}({\varvec{X}}_{k}|Z_{1:k})\) denote the multi-target filtering density at time k and \(\varvec{\mathbf {\pi }}_{k|k-1}({\varvec{X}}_{k}|Z_{1:k-1})\) denote the multi-target prediction density to time k. The multi-target Bayes filter propagates \(\varvec{\mathbf {\pi }}_{k}\) in time according to the following update and prediction

$$\begin{aligned} \varvec{\mathbf {\pi }}_{k}({\varvec{X}}_{k}|Z_{1:k})&=\frac{g_{k}(Z_{k}|{\varvec{X}}_{k})\varvec{\mathbf {\pi }}_{k|k-1}({\varvec{X}}_{k}|Z_{1:k-1})}{\int g_{k}(Z_{k}|{\varvec{X}})\varvec{\mathbf {\pi }}_{k|k-1}({\varvec{X}}|Z_{1:k-1})\delta {\varvec{X}}}, \end{aligned}$$
(2)
$$\begin{aligned} \varvec{\mathbf {\pi }}_{k|k-1}({\varvec{X}}_{k}|Z_{1:k-1})&=\int {\varvec{f}}_{k|k-1}({\varvec{X}}_{k}|{\varvec{X}})\varvec{\mathbf {\pi }}_{k-1}({\varvec{X}}|Z_{1:k-1})\delta {\varvec{X}}, \end{aligned}$$
(3)

where \({\varvec{f}}_{k|k-1}(\cdot |\mathbf {\cdot })\) is the multi-target transition density, \(g_{k}(\cdot |\mathbf {\cdot })\) is the multi-target likelihood, and \(Z_{1:k}=(Z_{1},\ldots ,Z_{k})\) contains all the measurements accumulated up to time k. The integrals in Eqs. (2)–(3) are set integrals but not ordinary integrals. The set integral for a function \(f:{\mathcal {F}}({\mathbb {X}}\mathbb {\times L})\rightarrow {\mathbb {R}}\) is given by

$$\begin{aligned} \int {\varvec{f}}({\varvec{X}})\delta {\varvec{X}}=\sum _{i=0}^{\infty }\frac{1}{i!}\sum _{(\ell _{1},\ldots ,\ell _{i})\in {\mathbb {L}}^{i}}\int {\varvec{f}}(\{(x_{1},\ell _{1}),\ldots ,(x_{i},\ell _{i})\})d(x_{1},\ldots ,x_{i}). \end{aligned}$$
(4)

2.3 Labeled multi-Bernoulli filter

The multi-Bernoulli filter was proposed in [23] as an approximation of the Bayes multi-target filter by approximating the posterior as a multi-Bernoulli RFS. Compared to the multi-Bernoulli filter, the LMB filter does not exhibit a cardinality bias and can output target tracks. The LMB distribution is described by \(\varvec{\pi }=\{(r^{(\ell )},p^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {L}}}\) in which \(r^{(\ell )}\) indicates the existence probability of a target with label \(\ell \in {\mathbb {L}}\), and \(p^{(\ell )}(x)\) is the the spatial distribution of the target’s state \(x\in {\mathbb {X}}\) when it exists [27]. The LMB RFS density is given by

$$\begin{aligned} \varvec{\pi }({\varvec{X}})=\Delta ({\varvec{X}})w({\mathcal {L}}({\varvec{X}}))[p]^{{\varvec{X}}}, \end{aligned}$$
(5)

where \({\mathcal {L}}({\varvec{X}})\) denotes the set of all possible labels obtained from \({\varvec{X}}\), and

$$\begin{aligned} w(L)&=\prod _{i\in {\mathbb {L}}}(1-r^{(i)})\prod _{i\in {\mathbb {L}}}\frac{1_{{\mathbb {L}}}r^{(\ell )}}{(1-r^{(\ell )})}, \end{aligned}$$
(6)
$$\begin{aligned}[p]^{{\varvec{X}}}&=\prod _{(x,\ell )\in {\varvec{X}}}p{}^{(\ell )}(x). \end{aligned}$$
(7)

If the prior distribution is an LMB distribution denoted as \(\{(r^{(\ell )},p^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {L}}}\), the predicted LMB distribution under the Bayes filtering framework evolves the survival LMB components and the birth LMB components, as follows:

$$\begin{aligned} \varvec{\pi }_{+}=\{(r_{+,S}^{(\ell )},p_{+,S}^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {L}}}\cup \{(r_{B}^{(\ell )},p_{B}^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {B}}}, \end{aligned}$$
(8)

where

$$\begin{aligned} r_{+,S}^{(\ell )}&=\eta _{S}(\ell )r^{(\ell )}, \end{aligned}$$
(9)
$$\begin{aligned} p_{+,s}^{(\ell )}(\cdot )&=\frac{\left\langle p_{S}(\cdot ,\ell )f(x|\cdot ,\ell ),p(\cdot ,\ell )\right\rangle }{\eta _{S}(\ell )}, \end{aligned}$$
(10)

\(f(x|x',\ell )\) is the transition density for track \(\ell\), \(p_{S}(\cdot ,\ell )\) is the state dependent survival probability, \(\eta _{S}(\ell )=\left\langle p_{S}(\cdot ,\ell ),p(\cdot ,\ell )\right\rangle\) is the survival probability of track \(\ell\), and the standard inner product \(\left\langle f,g\right\rangle \triangleq \int f(x)g(x)dx\).

Let the predicted LMB distribution denote as \(\varvec{\pi }_{+}=\{(r_{+}^{(\ell )},p_{+}^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {L}}_{+}}\), the posterior multi-target density is approximated as follows [27]:

$$\begin{aligned} \varvec{\pi }(\cdot |Z)=\{(r^{(\ell )},p^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {L}}_{+}}, \end{aligned}$$
(11)

where

$$\begin{aligned} r^{(\ell )}&=\sum _{(I_{+},\theta )\in {\mathcal {F}}({\mathbb {L}}_{+})\times \Theta _{I_{+}}}w^{(I_{+},\theta )}(Z)1_{I_{+}}(\ell ), \end{aligned}$$
(12)
$$\begin{aligned} p^{(\ell )}(x)&=\frac{1}{r^{(\ell )}}\sum _{(I_{+},\theta )\in {\mathcal {F}}({\mathbb {L}}_{+})\times \Theta _{I_{+}}}w^{(I_{+},\theta )}(Z)\times 1_{I_{+}}(\ell )p^{(\theta )}(x,\ell ), \end{aligned}$$
(13)
$$\begin{aligned} w^{(I_{+},\theta )}(Z)&\propto w_{+}(I_{+})[\eta _{Z}^{(\theta )}(\ell )]^{I_{+}}, \end{aligned}$$
(14)
$$\begin{aligned} p^{(\theta )}(x,\ell |Z)&=\frac{p_{+}(x,\ell )\psi _{Z}(x,\ell ;\theta )}{\eta _{Z}^{(\theta )}(\ell )}, \end{aligned}$$
(15)
$$\begin{aligned} \eta _{Z}^{(\theta )}(\ell )&=\left\langle p_{+}(\cdot ,\ell ),\psi _{Z}(\cdot ,\ell ;\theta )\right\rangle , \end{aligned}$$
(16)
$$\begin{aligned} \psi _{Z}(x,\ell ;\theta )&={\left\{ \begin{array}{ll} \frac{p_{D}(x,\ell )g(z_{\theta (\ell )}|x;\ell )}{\kappa (z_{\theta (\ell )})}, &{} \text {if }\theta (\ell )>0,\\ 1-p_{D}(x,\ell ), &{} \text {if }\theta (\ell )=0, \end{array}\right. } \end{aligned}$$
(17)

and \(g(z|x;\ell )\) is the single target likelihood, \(\kappa (\cdot )\) is the clutter intensity, \(\Theta _{I_{+}}\) is the space of mappings \(\theta :I_{+}\rightarrow \{0,1,\ldots ,|Z|\}\), and the inclusion function \(1_{S}(X)=1, \mathrm {if}~X\subseteq S\), otherwise, \(1_{S}(X)=0\).

There are two implementations of the LMB recursion: one is using the sequential Monte Carlo (SMC) method and the other is using Gaussian mixtures (GM). The GM implementation is popular because it provides a closed form analytic solution to the recursions under linear Gaussian target dynamics and measurement models. Alternatively, SMC implementation has the natural ability of handling nonlinear target dynamics and measurement models. In this paper, the SMC implementation is adopted to handle the nonlinear dynamic and measurement models.

3 Methods

On the basis of the signal model proposed in Sect. 2, this section proposes a novel receiver selection method for multi-target tracking in the multi-static Doppler radar system. The receiver selection problem is formulated as a POMDP model [40], in which the multi-target dynamics is a Markov process, but there is no direct access to current states. The POMDP model consists of the following main components:

  • \({\varvec{X}}_{k}\): the labeled multi-target state at current time k;

  • \({\varvec{f}}_{k|k-1}({\varvec{X}}_{k}|{\varvec{X}}_{k-1})\): the multi-target state transition function;

  • \(g_{k}(Z_{k}|{\varvec{X}}_{k})\): the multi-target likelihood;

  • \({\mathbb {I}}\): a finite set of receivers for selection;

  • \(\vartheta ({\varvec{X}}_{k-1},I_{k},{\varvec{X}}_{k})\): the objective function associated with the command \(I_{k}\subseteq {\mathbb {I}}\).

At each time step, the optimal receiver \(I_{k}^{*}\) is selected by optimizing the statistical mean of the objective function:

$$\begin{aligned} I_{k}^{*}=\underset{I_{k}\subseteq {\mathbb {I}}}{\text{arg ~max}}/{\text {min}}\left\{ E_{Z_{k}^{(I_{k})}}\left[ \vartheta ({\varvec{X}}_{k-1},I_{k},{\varvec{X}}_{k})\right] \right\} . \end{aligned}$$
(18)

Several objective functions have been proposed for sensor management but there are few studies on receiver selection in the multi-static Doppler radar system [41, 42].

Different from other sensor management solutions, receiver selection in the multi-static Doppler radar system is more complicated. If the same receiver is selected for multiple consecutive time steps, the tracking performance of the system is poor and even fails. This is because the observability of the Doppler measurement is low that it is difficult for a single receiver to provide sufficient target information [41, 43, 44]. To overcome this problem, we develop a novel window-added approach that adaptively select an appropriate receiver with the moving of targets. The window technique is used to overcome the single-sensor unobservability problem and obtain the multi-sensor diversity gain.

3.1 Objective function

For the POMDP model, we use a task-driven objective function termed as the cardinality variance [37], because it has the analytical expression and shows good performances in many sensor management applications. Let the LMB posterior parameterized by \(\varvec{\pi }(\cdot |Z)=\{(r^{(\ell )},p^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {L}}_{+}}\), the cardinality variance associated with the selection command \(I_{k}\subseteq {\mathbb {I}}\) is given by

$$\begin{aligned} \sigma _{|{\varvec{X}}|}^{2}=\sum _{\ell \in {\mathbb {L}}_{+}}r^{(\ell )}(I{}_{k})[1-r^{(\ell )}(I_{k})]. \end{aligned}$$
(19)

Therefore, the objective function used in this paper is denoted as

$$\begin{aligned} \vartheta ({\varvec{X}}_{k-1},I_{k},{\varvec{X}}_{k})=\sigma _{|{\varvec{X}}|}^{2}=\sum _{\ell \in {\mathbb {L}}_{+}}r^{(\ell )}(I{}_{k})[1-r^{(\ell )}(I_{k})]. \end{aligned}$$
(20)

At each time step, the optimal receiver \(I_{k}^{*}\) is selected by minimizing the statistical mean of the objective function

$$\begin{aligned} I_{k}^{*}=\underset{I_{k}\subseteq {\mathbb {I}}}{\text {arg\,min}}\left\{ E_{Z_{k}^{(I_{k})}}\left[ \vartheta ({\varvec{X}}_{k-1},I_{k},{\varvec{X}}_{k})\right] \right\} . \end{aligned}$$
(21)

where \(Z_{k}^{(I_{k})}\) denotes the set of measurements collected by the receiver \(I_{k}\). To obtain the LMB posterior \(\varvec{\pi }(\cdot |Z)=\{(r^{(\ell )},p^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {L}}_{+}}\) and compute the objective function, it is necessary to estimate all possible measurement sets and use them to update the predicted LMB distribution. This is computationally expensive. In order to reduce the computation, a simple method named the predicted ideal measurement set (PIMS) [34] is used here to estimate the possible measurements. First, the number \({\hat{n}}\) of target is estimated using the predicted LMB RFS density. Then, \({\hat{n}}\) labels corresponding to highest probabilities of existence are obtained from the predicted LMB RFS density. For each of these labels, the target state \({\hat{x}}^{(\ell )}\) is estimated. Under the ideal assumption of no measurement noise, no clutter, and perfect detection, a predicted ideal measurement is generated for each target \({\hat{x}}^{(\ell )}\). The pseudo-updated of the LMB RFS density is implemented using the PIMS, and then the objective function (20) is computed.

3.2 Window-added receiver selection

In this paper, we propose to use a dynamic sliding window within the receiver selection procedure. The window keeps the indices of receivers selected from previous time steps to the current time step. The dynamic window moves automatically with time. We confirm that the indices of receivers in the window are different when the receiver selected at the current time is added, to improve the diversity of the selected receivers. Mathematically, the receiver selection is developed as follows:

$$\begin{aligned} I_{k}^{*}=\underset{I_{k}\subseteq {\mathbb {I}}}{\text {arg min}}\{\vartheta ({\varvec{X}}_{k-1},I_{k},W_{k},{\varvec{X}}_{k})\}. \end{aligned}$$
(22)

where \(W_{k}=[I_{k-L+1},\ldots ,I_{k}]\) indicates the dynamic sliding window, and L is the fixed length of the window. Note that the expectation term in Eq. (21) does not appear, as the PIMS approach is used instead of all possible sets of measurements.

If the index of the receiver selected at the current time step k is the same with an existing index in the window. Then, this receiver is removed from the set \({\mathbb {I}}\) of receivers for selection and the receiver selection formulated as Eq. (22) will be repeated until the indices of receivers within the window are unique. An example of the sliding window is illustrated in Fig. 2.

Fig. 2
figure 2

An example of the sliding window

Full size image

The step-by-step pseudocode for a single run \(k=L,L+1,\ldots\) is given in Algorithm 1. It is assumed that the following parameters are always available to the tracking system:

  • parameters of the multi-static system: transmitter position \(t=[t_{x},t_{y}]^{T}\), carrier frequency \(f_{c}\), receiver position \(r^{(j)}=[r_{x}^{(j)},r_{y}^{(j)}]^{T}\), detection probability \(p_{D}^{(j)}(\cdot )\), and clutter intensity \(\kappa (\cdot )\);

  • LMB birth distribution: \(\{(r_{B}^{(\ell )},p_{B}^{(\ell )}(\cdot ))\}_{\ell \in {\mathbb {B}}}\)

  • survival probability function: \(p_{S}(x,\ell )\);

  • single-target transition density \(f(x|\cdot ,\ell )\) and likelihood \(g(z|x,\ell )\).

figure a

Note that a suitable window length is important for the proposed window-added receiver selection method. A suitable window length helps to collect more effective information about the targets being tracked and improve the tracking performance. If the window length is short, the diversity of the selected receivers is less improved. When the window length \(L=1\), the proposed method degenerates into the ordinary cardinality variance based sensor selection method. In this case, it is likely that the same receiver is selected for multiple consecutive time steps and the tracking performance is poor. If the window length is overlong, the influence of high-quality receivers can be reduced and the tracking performance is less satisfactory. Therefore, the window length needs to be carefully chosen.

4 Results and discussion

We present numerical results using a multi-static Doppler radar system borrowed from [42] where one transmitter and ten receivers placed in the x-y plane as shown in Fig. 3. The transmitter is placed at the origin of the x-y plane with transmitting frequency \(f_{c}=900\) MHz. The sampling interval is fixed as \(T_s=10\) s. The standard deviation of measurement noise is \(\sigma _{\varepsilon }^{(j)}=\sigma _{\varepsilon }=1\) Hz which is the same for all receivers \(j=1,2,...,10\). The received measurements are distributed over \([-200\ \text {Hz},200\ \text {Hz}]\). The Poisson parameter of the false detections (clutter) is \(\uplambda ^{(j)}=2\) for receiver j. If the target is detected by receiver j, the receiver will report a Doppler measurement. For receiver j, the probability of detection is modeled as \(p_{D}^{(j)}(x_{k})=1-\phi (\left\| p_{k}-r^{(j)}\right\| ;\alpha ,\beta )\), where \(d_{k,j}=\left\| p_{k}-r^{(j)}\right\|\) is the distance between the target and the receiver, and \(\phi (d;\alpha ,\beta )=\int _{-\infty }^{d}{\mathcal {N}}(v;\alpha ,\beta )dv\) is the Gaussian cumulative distribution function with \(\alpha =12\) km and \(\beta =(3\ \text {km})^{2}\).

Fig. 3
figure 3

The locations of receivers (blue squares) and the transmitter (red star)

Full size image

We use two different scenarios to validate the performance of the proposed approach. In both scenarios, receivers are selected adaptively with the moving of the target. The average tracking performances are obtained over 100 Monte Carlo (MC) runs. As for the quantification of the tracking error, the OSPA [45] and \(\mathrm {OSPA}^{(2)}\) [46, 47] error distances are used. The OSPA metric [45] estimates errors in both localization and cardinality by measuring the distance between two sets of states and is widely used in evaluating tracking performances in the RFS based tracking field. However, the OSPA metric does not take into account track labeling errors. Recently, the \(\mathrm {OSPA}^{(2)}\) metric [46, 47] has been developed as an adaptation of the OSPA metric to accommodate sets of tracks, carrying the interpretation of a per-track per-time error. Note that a window is used in computing \(\mathrm {OSPA}^{(2)}\) and this window is unrelated to the one used in this paper. The length of the window used in computing \(\mathrm {OSPA}^{(2)}\) is denoted as w.

4.1 Single target simulation

This scenario considers tracking of a single target with nearly constant velocity (NCV) motion. The unlabeled state includes the target position and the target velocity, denoted as \(x_{k}=[p_{x,k},{\dot{p}}_{x,k},p_{y,k},{\dot{p}}_{y,k}]^{\rm T}\). With the NCV model, the transition density of the target state is \(f_{k|k-1}(x_{k}|x_{k-1},\ell )={\mathcal {N}}(x_{k};F_{k-1}x_{k-1},Q_{k-1})\), where

$$\begin{aligned} F_{k-1}=\left[ \begin{array}{cccc} 1 &{}\quad T &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad T\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{array}\right] ,Q_{k-1}=\sigma _{w}^{2}\left[ \begin{array}{cccc} \frac{T^{4}}{4} &{}\quad \frac{T^{3}}{2} &{}\quad 0 &{}\quad 0\\ \frac{T^{3}}{2} &{}\quad T^{2} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \frac{T^{4}}{4} &{}\quad \frac{T^{3}}{2}\\ 0 &{}\quad 0 &{}\quad \frac{T^{3}}{2} &{}\quad T^{2} \end{array}\right] , \end{aligned}$$
(23)

where \(\sigma _{w}=0.01\ \text{m/s}^{2}\) is the standard deviation of the acceleration noise long the x or y axis. The target exists for discrete-time indices \(k=1,2,\ldots ,30\) and its trajectory is shown in Fig. 4. For the LMB recursion, the birth LMB distribution is parameterized by \(\{(r_{B},p_{B})\}\), where \(r_{B}=0.02\) and \(p_{B}={\mathcal {N}}(x;m_{B},P_{B})\) with \(m_{B}=[2000\ \text {m},0\ \text {m/s},-1000\ \text {m},0\ \text {m/s}]^{\rm T}\) and \(P_{B}=\text {diag}([50\ \text {m},50\ \text {m/s},50\ \text {m},50\ \text {m/s}]^{\rm T})^{2}\).

Fig. 4
figure 4

Single target trajectory and start/stop position is shown with with \(\circ /\vartriangle\)

Full size image

The performance of the proposed method is validated using windows with different lengths, i.e., \(L=1\), \(L=2\), \(L=3\), \(L=4\), \(L=5\), and \(L=6\). Note that, using a window with length \(L=1\) indicates that the indices of receivers selected at the previous time steps are not considered for receiver selection at the current time step. In this case, the proposed method degenerates into the ordinary cardinality variance based sensor selection method. The random selection is also used as a comparative method, in which each receiver has an equal probability to be selected.

The average OSPA distance (with parameters \(p=1\) and \(c=10000\) m) and \(\mathrm {OSPA}^{(2)}\) distance (with the same c, p, and window length \(w=10\)) are given in Fig. 5a, b, respectively. In accordance with our intuition, it can be observed that both the OSPA and \(\mathrm {OSPA}^{(2)}\) distance errors of the proposed method decrease as the window length L increases from 1 to 4. When the window length L increases to 5 and 6, the tracking performance is decreased compared with that of \(L=3\) and \(L=4\). This indicates that a suitable window length is important and needs to be chosen carefully. For this scenario, it can be observed from the results that a suitable window length is \(L=3\) or \(L=4\).

Fig. 5
figure 5

Average OSPA and \(\mathrm {OSPA}^{(2)}\) errors in single target simulation

Full size image

4.2 Multi-target simulation

In this scenario, a nearly constant turn (NCT) model is considered. The target state is denoted as \(x_{k}=[{\widetilde{x}}_{k}^{\rm T},\omega _{k}]^{\rm T}\) comprising the target position and velocity as \({\widetilde{x}}_{k}=[p_{x,k},{\dot{p}}_{x,k},p_{y,k},{\dot{p}}_{y,k}]^{\rm T}\) as well as the turn rate \(\omega _{k}\). The NCT transition is modeled as follows:

$$\begin{aligned} x_{k}=f(x_{k-1})+Gw_{k-1}, \end{aligned}$$
(24)

where

$$\begin{aligned} f(x_{k-1})&=F(\omega _{k-1})x_{k-1}, \end{aligned}$$
(25)
$$\begin{aligned} F(\omega _{k-1})&=\left[ \begin{array}{ccccc} 1 &{}\quad \frac{\sin \omega _{k-1}T}{\omega _{k-1}} &{}\quad 0 &{}\quad -\frac{1-\cos \omega _{k-1}T}{\omega _{k-1}} &{}\quad 0\\ 0 &{}\quad \cos \omega _{k-1}T &{}\quad 0 &{}\quad -\sin \omega _{k-1}T &{}\quad 0\\ 0 &{}\quad \frac{1-\cos \omega _{k-1}T}{\omega _{k-1}} &{}\quad 1 &{}\quad \frac{\sin \omega _{k-1}T}{\omega _{k-1}} &{}\quad 0\\ 0 &{}\quad \sin \omega _{k-1}T &{}\quad 0 &{}\quad \cos \omega _{k-1}T &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{array}\right] , \end{aligned}$$
(26)
$$\begin{aligned} G&=\left[ \begin{array}{ccc} \frac{T^{2}}{2} &{}\quad 0 &{}\quad 0\\ T &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \frac{T^{2}}{2} &{}\quad 0\\ 0 &{}\quad T &{}\quad 0\\ 0 &{}\quad 0 &{}\quad T \end{array}\right] , \end{aligned}$$
(27)
$$\begin{aligned} w_{k-1}&:=[w_{x,k-1},w_{y,k-1},w_{\omega ,k-1}]^{\rm T}, \end{aligned}$$
(28)

and \(w_{k-1}\sim {\mathcal {N}}(w_{k-1};0,Q_{k-1})\) is a Gaussian process noise with covariance \(Q_{k-1}=\text{diag}(\sigma _{x}^{2},\sigma _{y}^{2},\sigma _{\omega }^{2})\), where \(\sigma _{x}=\sigma _{y}=1.0\times 10^{-4}\text{m/s}^{2}\) and \(\sigma _{\omega }=1.0\times 10^{-9}\text{rad/s}^{2}\) are standard deviations of x and y components of acceleration process noise and angular acceleration process noise, respectively.

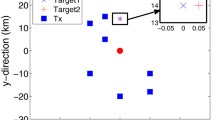
Three targets moving with the NCT motion appear in the surveillance area and their trajectories are shown in Fig. 6, in which target 1 is born at \(k=1\), target 2 is born at \(k=10\), target 3 is born at \(k=20\), and the angular velocities of these targets are \(\omega _{k-1}=1/4\times \pi /180\). Note that the angular velocity, the target position and the target velocity are unknown to the LMB filter. During the tracking process, the LMB filter will estimate these parameters. The birth LMB distribution is parameterized as \(f_{B}(x)=\{w_{B},p_{B}^{(i)}\}_{i=1}^{3}\), where the common existence probabilities \(w_{B}=0.02\), and \(p_{B}^{(i)}(x)={\mathcal {N}}(x;m_{B}^{(i)},P_{B})\) with

$$\begin{aligned} m_{B}^{{(1)}} & = [\begin{array}{*{20}l} {1000\;{\text{m,}}} \hfill & {0\;{\text{m/s,}}} \hfill & {2000\;{\text{m,}}} \hfill & {0\;{\text{m/s,}}} \hfill & {0\;{\text{rad/s}}} \hfill \\ \end{array} ]^{{\text{T}}} , \\ m_{B}^{{(2)}} & = [\begin{array}{*{20}l} {1000\;{\text{m,}}} \hfill & {0\;{\text{m/s,}}} \hfill & {3000\;{\text{m,}}} \hfill & {0\;{\text{m/s,}}} \hfill & {0\;{\text{rad/s}}} \hfill \\ \end{array} ]^{{\text{T}}} , \\ m_{B}^{{(3)}} & = [\begin{array}{*{20}l} {1000\;{\text{m,}}} \hfill & {0\;{\text{m/s,}}} \hfill & {4000\;{\text{m,}}} \hfill & {0\;{\text{m/s,}}} \hfill & {0\;{\text{rad/s}}} \hfill \\ \end{array} ]^{{\text{T}}} , \\ P_{B} & = \left( {{\text{diag}}[\begin{array}{*{20}l} {10\;{\text{m,}}} \hfill & {10\;{\text{m/s,}}} \hfill & {10\;{\text{m,}}} \hfill & {10\;{\text{m/s,}}} \hfill & {\left( {\pi /90} \right)\;{\text{rad/s}}} \hfill \\ \end{array} ]} \right)^{{\text{2}}} . \\ \end{aligned}$$
Fig. 6
figure 6

Multi-target trajectories and start/stop positions are shown with with \(\circ /\vartriangle\)

Full size image

The average OSPA distance (with parameters \(p=1\) and \(c=1000\) m) and \(\mathrm {OSPA}^{(2)}\) distance (with the same c, p, and window length \(\varpi =10\)) are shown in Fig. 7a, b, respectively. The tracking accuracy is improved as the window length L increases from 1 to 5. For the window length \(L=6\), the tracking performance is decreased compared with that of \(L=3\), \(L=4\) and \(L=5\). Therefore, the window length \(L=6\) is overlong for this scenario. When the window length \(L=1\), the performance of the proposed method is even worse than the random selection method. This is because the proposed method with the window length \(L=1\) tends to select the same receiver for several consecutive time steps. Since the observability of the target state from the Doppler measurement is low, less information about the target can be obtained if the same receiver is selected at several consecutive time steps. Thus, the “observability” of the targets is a crucial factor in determining the performance of sensor management.

Fig. 7
figure 7

Average OSPA and \(\mathrm {OSPA}^{(2)}\) errors in multi-target simulation

Full size image

5 Conclusion

We have proposed a novel receiver selection solution for multi-target tracking using the multi-static Doppler radar system. To increase the diversity of the selected sensors and overcome the low observability of the Doppler measurement, the receivers selected at previous time steps are taken into account. We set up a window for receivers selected from previous time steps to the current time step and confirm that the receivers in the window are different. Numerical results for two different tracking scenarios are presented. The results verify the validity of the window-added strategy. A larger window indicates that the collected Doppler measurements provide more information about the target state. When the window length \(L=1\), the proposed method degenerates into ordinary cardinality variance based sensor selection and performs worse than the random selection method. Our future work will consider receiver selection and tracking while estimating unknown clutter statistics. What’s more, developing a mathematical criterion to find the suitable window length is also a future work direction.