1 Introduction

The video compression technique is utilized in digital image processing to reduce the redundancy of video information and increase the storage capacity and transmission rate efficiently. In recent years, video compression has been widely used in video codec devices, such as video conference equipment, video communication devices, and digital TVs. Groups such as the International Organization for Standardization (ISO) [1], International Telecommunication Union Telecommunication Standardization Sector (ITU-T) [2, 3], and Microsoft Corporation [4, 5] have developed various transform dimensions and coefficients for corresponding standards. The next-generation video coding standard, which is referred to as high-efficiency video coding (HEVC), is expected to provide approximately 50% reduction in the bit rate (at similar visual quality) over the current standard (H.264/AVC). HEVC is intended for larger resolutions and higher frame rates than the H.264/AVC standard [6–10]. In HEVC, the largest coding unit can be up to 64×64 in size, and transform sizes of 4×4,8×8,16×16, and 32×32 are supported [11]. Multiple transform sizes improve the compression performance; however, they also increase the implementation complexity [12–14].

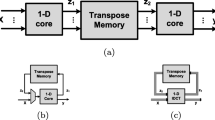
Recently, many researchers have implemented integer transforms, especially for HEVC [15–24]. The row-column decomposition structure is widely used to design a two-dimensional (2-D) transform core. In general, the 2-D transform core is directly implemented using two one-dimensional (1-D) cores and a transposed memory. This method can achieve a high-throughput rate; however, it results in the wastage of a considerable amount of circuit area. Many architectures use this structure to implement the inverse transform [15, 16]. According to the area consideration, the multiplexer structure is introduced. The multiplexer controls the 1-D inverse discrete cosine transform (IDCT) core, which calculates the first-dimensional (1st-D) and second-dimensional (2nd-D) operations. The 1-D IDCT core uses matrix decomposition to save the circuit area. Thus, the circuit area can be reduced. However, the throughput rate decreases compared with the original speed [17]. In [18], a single 1-D core was proposed for executing 1st-D and 2nd-D computation simultaneously, which can allow the throughput rate to be maintained the same as the clock rate. To improve the throughput rate, Chen and Ko [19] presented a 32-point IDCT for HEVC. The IDCT utilizes 32 parallel computation paths to reach an ultrahigh-throughput rate of 6.4 giga-pixel per second (GP/s). However, the parallel computation architecture considerably increases the circuit area overhead [19]. The horizontal and vertical line buffer for reference sample is presented in [20], which only costs 0.8K bit and is implemented by register files with SRAM-free. Based on this buffer, the 32-pixel transform unit can achieve a frequency of 400 MHz for a 65-nm process. The resource-sharing pipelined architecture [21] is synthesized by using NanGate OpenPDK 45 nm library achieving a 222-MHz clock rate and supporting real-time decoding of 4096×3072 video sequences with 70 fps.

This paper proposes an inverse transform core for HEVC applications supporting multiple transform sizes. The IDCT core utilizes a single 1-D core and transposed memory to achieve a low-area design. The 1-D IDCT core adapts the symmetric property of the transform coefficient matrix, and the 32-point transform can be decomposed into 16-, 8-, and 4-point matrix products. Moreover, the proposed core uses a shift-and-add unit (SAU) to share the hardware resource among multiple transform dimension matrix products and also uses the proposed data control flow to share the computation resource. Thus, the proposed IDCT core can execute 1st-D and 2nd-D computation simultaneously. The proposed circuit can maintain the throughput rate to be the same as the operating frequency. The proposed 2-D IDCT core, which is implemented into 90-nm complementary metal-oxide-semiconductor (CMOS) technology, has a throughput rate of 250 MP/s so that it can meet the full high definition (HD) 1080p requirement with only 110 K gate counts. The main contribution of this work is listed as follows:

  • The multiple transform sizes including 32-, 16-, 8-, and 4-point transformations are supported HEVC applications.

  • Using a single 1-D core and transposed memory to achieve a low-area design.

  • Using the proposed data control flow to share the computation resource, and the IDCT core can execute 1st-D and 2nd-D computation simultaneously achieving a high-throughput rate.

Consequently, the proposed IDCT achieves high-throughput and low-area design supporting multiple transform sizes for HEVC applications.

This paper is organized as follows. Section 2.1 presents the mathematical derivation of the 32-point IDCT. Section 2.2 describes the proposed architecture, which uses resource and timing sharing. This section also describes the hardware architecture based on SAU computation for multiple transform dimensions and the proposed data control flow. Section 3 includes the comparisons and discussion, and the conclusions are presented in Section 4.

2 Method

2.1 Algorithm of the 32-point IDCT

The transform computation in HEVC uses a set of IDCT transform matrices. In general, a 2-D inverse transform can be obtained by performing two 1-D IDCTs through the row-column decompensation method.

$$\begin{array}{*{20}l} \mathbf{y}&=\mathbf{CZC^{T}} \end{array} $$
(1)
$$\begin{array}{*{20}l} \mathbf{y^{T}}&=\mathbf{C^{T}\left(CZ\right)^{T}} = \mathbf{C^{T}x^{T}} \end{array} $$
(2)

The 32-point 1-D IDCT can be expressed as follows:

$$\begin{array}{*{20}l} \mathbf{x}&={\mathbf{C}\mathbf{Z}} \end{array} $$
(3)
$$\begin{array}{*{20}l} \mathbf{x}&=\left[\begin{array}{cccc} x_{0} & x_{1} & \ldots & x_{31} \end{array} \right]^{T} \end{array} $$
(4)
$$\begin{array}{*{20}l} \mathbf{Z}&=\left[\begin{array}{cccc} Z_{0} & Z_{1} & \ldots & Z_{31} \end{array} \right]^{T} \end{array} $$
(5)

where C indicates the 32×32 coefficient matrix.

According to the symmetric property, Eq. (3) can be decomposed into two separate equations:

$$\begin{array}{*{20}l} \mathbf{x_{16u}}&= \mathbf{C_{16e}}\mathbf{Z_{16e}}+\mathbf{C_{16o}}\mathbf{Z_{16o}}=\mathbf{A}+\mathbf{B} \end{array} $$
(6)
$$\begin{array}{*{20}l} \mathbf{x_{16d}}&= \mathbf{C_{16e}}\mathbf{Z_{16e}}-\mathbf{C_{16o}}\mathbf{Z_{16o}}=\mathbf{A}-\mathbf{B} \end{array} $$
(7)

where

$$\begin{array}{*{20}l} \mathbf{x_{16u}}&=\left[\begin{array}{cccc} x_{0} & x_{1} & \ldots & x_{15} \end{array} \right]^{T} \end{array} $$
(8)
$$\begin{array}{*{20}l} \mathbf{x_{16d}}&=\left[\begin{array}{cccc} x_{16} & x_{17} & \ldots & x_{31} \end{array} \right]^{T} \end{array} $$
(9)
$$\begin{array}{*{20}l} \mathbf{Z_{16e}}&=\left[\begin{array}{cccc} Z_{0} & Z_{2} & \ldots & Z_{30} \end{array} \right]^{T} \end{array} $$
(10)
$$\begin{array}{*{20}l} \mathbf{Z_{16o}}&=\left[\begin{array}{cccc} Z_{1} & Z_{3} & \ldots & Z_{31} \end{array} \right]^{T} \end{array} $$
(11)

C16e and C16o are the 16-point even and odd coefficient matrices, respectively, for the 32-point transform. The coefficient of C16e is presented in Eq. (12). The 16-point even-part computation can be further divided into 8-point even and odd computations.

$$ \begin{aligned} \mathbf{C_{16e}} = \left[\begin{array}{cccccccccccccccc} 64& 64 & 64 & 64 &64 &64 &64 &64 &64 &64 &64 &64 &64 &64 &64 &64 \\ 90& 87 & 80 & 70 &57 &43 &25 &9 &-9 &-25&-43&-57&-70&-80&-87& 90 \\ 89& 75 & 50 & 18 &-18 &-50&-75&-89&-89&-75&-50&-18& 18& 50& 75& 89 \\ 87& 57 & 9 &-43 &-80 &-90&-70&-25&25 &70 &90 &80 &43 &-9 &-57& -87 \\ 83& 36 & -36&-83 &-83 &-36& 36&83 &83 &36 &-36&-83&-83&-36& 36& 83 \\ 80& 9 & -70&-87 &-25 &57 &90 &43 &-43&-90&-57& 25& 87& 70&-9 &-80 \\ 75& -18& -89&-50 &50 &89 &18 &-75&-75&18 &89 &50 &-50&-89&-18& 75 \\ 70& -43& -87& 9 &90 &25 &-80&-57& 57&80 &-25&-90&-9 &87 &43 &-70 \\ 64& -64& -64& 64 &64 &-64&-64& 64& 64&-64&-64& 64& 64&-64&-64& 64 \\ 57& -80& -25& 90 &-9 &-87& 43& 70&-70&-43& 87& 9 &-90& 25& 80& -57 \\ 50& -89& 18& 75 &-75 &-18& 89&-50&-50&89 &-18&-75& 75& 18&-89& 50 \\ 43& -90& 57& 25 &-87 & 70& 9 &-80& 80&-9 &-70& 87&-25&-57& 90& -43 \\ 36& -83& 83& -36& -36& 83&-83& 36& 36&-83& 83&-36&-36& 83&-83& 36 \\ 25& -70& 90& -80& 43 &9 &-57& 87&-87& 57&-9 &-43& 80&-90& 70& -25 \\ 18& -50& 75& -89& 89 &-75& 50&-18&-18& 50&-75& 89&-89& 75&-50& 18 \\ 9 & -25 & 43& -57& 70 &-80& 87&-90& 90&-87& 80&-70& 57&-43& 25& -9 \end{array} \right] \end{aligned} $$
(12)
$$\begin{array}{*{20}l} \mathbf{x_{16u}}&= \left[\begin{array}{c} \mathbf{x_{8u}} \\ \mathbf{x_{8d}}\end{array} \right] \end{array} $$
(13)
$$\begin{array}{*{20}l} \mathbf{x_{8u}}&= \mathbf{C_{8e}}\mathbf{Z_{8e}}+\mathbf{C_{8o}}\mathbf{Z_{8o}}=\mathbf{a}+\mathbf{b} \end{array} $$
(14)
$$\begin{array}{*{20}l} \mathbf{x_{8d}}&= \mathbf{C_{8e}}\mathbf{Z_{8e}}-\mathbf{C_{8o}}\mathbf{Z_{8o}}=\mathbf{a}-\mathbf{b} \end{array} $$
(15)

and

$$\begin{array}{*{20}l} \mathbf{x_{8u}}&=\left[\begin{array}{cccc} x_{0} & x_{1} & \ldots & x_{7} \end{array} \right]^{T} \end{array} $$
(16)
$$\begin{array}{*{20}l} \mathbf{x_{8d}}&=\left[\begin{array}{cccc} x_{8} & x_{9} & \ldots & x_{15} \end{array} \right]^{T} \end{array} $$
(17)
$$\begin{array}{*{20}l} \mathbf{Z_{8e}}&=\left[\begin{array}{cccc} Z_{0} & Z_{4} & \ldots & Z_{28} \end{array} \right]^{T} \end{array} $$
(18)
$$\begin{array}{*{20}l} \mathbf{Z_{8o}}&=\left[\begin{array}{cccc} Z_{2} & Z_{6} & \ldots & Z_{30} \end{array} \right]^{T} \end{array} $$
(19)

Moreover, the 8-point even-part computation can be divided into the following equations:

$$\begin{array}{*{20}l} \mathbf{x_{8u}}&=\left[\begin{array}{c} \mathbf{x_{4u}} \\ \mathbf{x_{4d}} \end{array} \right] \end{array} $$
(20)
$$\begin{array}{*{20}l} \mathbf{x_{4u}}&= \mathbf{C_{4e}}\mathbf{Z_{4e}}+\mathbf{C_{4o}}\mathbf{Z_{4o}}=\alpha+\beta \end{array} $$
(21)
$$\begin{array}{*{20}l} \mathbf{x_{4d}}&= \mathbf{C_{4e}}\mathbf{Z_{4e}}-\mathbf{C_{4o}}\mathbf{Z_{4o}}=\alpha-\beta \end{array} $$
(22)

and

$$\begin{array}{*{20}l} \mathbf{x_{4u}}&=\left[\begin{array}{cccc} x_{0} & x_{1} & x_{2} & x_{3} \end{array} \right]^{T} \end{array} $$
(23)
$$\begin{array}{*{20}l} \mathbf{x_{4d}}&=\left[\begin{array}{cccc} x_{4} & x_{5} & x_{6} & x_{7} \end{array} \right]^{T} \end{array} $$
(24)
$$\begin{array}{*{20}l} \mathbf{Z_{4e}}&=\left[\begin{array}{cccc} Z_{0} & Z_{8} & Z_{16} & Z_{24} \end{array} \right]^{T} \end{array} $$
(25)
$$\begin{array}{*{20}l} \mathbf{Z_{4o}}&=\left[\begin{array}{cccc} Z_{4} & Z_{12} & Z_{20} & Z_{28} \end{array} \right]^{T} \end{array} $$
(26)

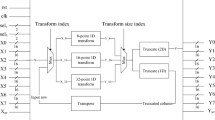
Thus, the entire 32-point IDCT computation can be decomposed into 16-, 8-, and 4-point operations, as displayed in Fig. 1. The 16-point IDCT computation can be decomposed into 8- and 4-point operations (the 4-point even, 4-point odd, BF4, 8-point odd, and BF8 modules); 8-point IDCT can be calculated by using 4-point even, 4-point odd, and BF4 modules. The 4-point IDCT is implemented as a 4-point even module.

Fig. 1
figure 1

Decomposition of the 32-point inverse discrete cosine transform (IDCT) computation

Full size image

2.2 Proposed architecture

Compared to the multiple computation path IDCT [19], the proposed 2-D IDCT core is composed of one 1-D transform core and one transposed memory (TMEM) to achieve a small-area design. The 1-D IDCT core utilizes the proposed data shared in the time scheme such that the throughput rate can be maintained the same as the operation frequency. The 1-D core supports full HD 1080p, which requires 1080×1920×60=124,416,000 pel/s ≃125 MP/s. The entire architecture is illustrated in Fig. 2.

Fig. 2
figure 2

Architecture of the proposed two-dimensional (2-D) IDCT

Full size image

2.2.1 1-D IDCT core

The 1-D 32-point IDCT core comprises a 4-point even-part process element (PEE4), a 4-point odd-part process element (PEO4), an 8-point odd-part process element (PEO8), a 16-point odd-part process element (PEO16), and three butterfly (BF) modules. The process elements (PEs) are designed using add-and-shift to share the hardware resources. The matrix product of the PEO4 computation can be expressed as follows:

$$ \left[\begin{array}{c} \beta_{0}\\ \beta_{1}\\ \beta_{2}\\ \beta_{3} \end{array} \right] = \left[\begin{array}{cccc} 89 & 75 & 50 & 18 \\ 75 & -18 & -89 & -50 \\ 50 & -89 & 18 & 75 \\ 18 & -50 & 75 & -89 \end{array} \right] \left[\begin{array}{c} Z_{0}\\ Z_{1}\\ Z_{2}\\ Z_{3} \end{array} \right] $$
(27)

Four coefficients {89,75,50,18} with different signs are used to multiply the inputs \(\left [\begin {array}{cccc} Z_{0} & Z_{1} & Z_{2} & Z_{3} \end {array} \right ]^{T}\). Thus, the matrix product operation can be simplified using the multiple constant multiplication technique.

$$\begin{array}{*{20}l} 89\cdot Z&=64\cdot Z + 25\cdot Z \end{array} $$
(28)
$$\begin{array}{*{20}l} 75\cdot Z&=(4+1)\cdot25\cdot Z \end{array} $$
(29)
$$\begin{array}{*{20}l} 50\cdot Z&=2\cdot25Z \end{array} $$
(30)
$$\begin{array}{*{20}l} 18\cdot Z&=2\cdot(9\cdot Z) \end{array} $$
(31)

The sharing architecture called four operands SAU (SAU4) is displayed on the left side of Fig. 3. SAU4 uses the shift-and-add function instead of the multiplier function to reduce the area cost. Furthermore, it shares the same hardware resource among the constant multiplications. Then, the sign-and-interconnection circuit maintains the matrix product. Finally, four accumulators (ACCs) sum the product results for every four clock cycles. Thus, every four clock cycles, the outputs β0,β1,β2, and β3 complete the computation in Eq. (27).

Fig. 3
figure 3

Architecture of the PEO4 module

Full size image

2.2.2 Architecture of the 8-, 16-, and 32-point IDCTs

The architecture of the 8-point IDCT, which is called PEE8, is displayed in Fig. 4. PEE8 consists of the PEE4, PEO4, and BF4 modules, which execute the computations in Eqs. (20)–(22). The PEO4 module executes the matrix product C4oZ4o, as illustrated in Fig. 3. The even-part computation (C4eZ4e) is also implemented in SAU3, sign-and-interconnection circuits, ACCs, and registers (D). The four ACCs and four registers are used to sum the product results for every four clock cycles and send them in the following four clock cycles. The BF4 module adds and subtracts C4oZ4o and C4eZ4e to output x4u and x4d.

Fig. 4
figure 4

Architecture of the 8-point IDCT as PEE8

Full size image

Moreover, the 16-point IDCT consists of the PEO8, PEE8, and BF8 modules. The PEO8 module calculates the odd part of the 16-point transformation (C8oZ8o), as indicated in Eqs. (14) and (15). The lower half of Fig. 5 illustrates the architecture of the PEO8 module. The SAU8 module shares the hardware resources by using the shift-and-add architecture, and the BF8 module controls the addition and subtraction output.

Fig. 5
figure 5

Architecture of the 16-point IDCT as PEE16

Full size image

The BF16 module calculates the final results before transpose and output. Thus, C16oZ16o and C16eZ16e in Eqs. (6) and (7) can be calculated using PEO16 and PEE16, respectively. The architecture of PEO16 is displayed in Fig. 6. The mixed SAU16 (SAU16M) module, which uses the shift-and-add architecture, executes the 16-point matrix product C16oZ16o as well as the 16-point C16eZ16e, 8-point C8eZ8e, and 4-point C4eZ4e by supporting variable transform sizes (32-, 16-, 8-, and 4-point matrix products). Thus, x16o,x16u,x8u, and x4u can be obtained from PEO16 according to the adaptive transform size.

Fig. 6
figure 6

Architecture of the PEO16 module

Full size image

2.2.3 Data flow of the proposed IDCT

The proposed IDCT core has a 1-D core and TMEM. The 1st-D and 2nd-D computations can be executed in the same 1-D core through the proposed data control scheme to save hardware cost. Thus, the proposed IDCT core can achieve a high throughput and low area.

According to the reorder registers and MUX, the 1st-D/2nd-D data is input into the 16-point odd-/even-part PE during the first 16 cycles of the 32-cycle period. The 1st-D/2nd-D data is then input into the 16-point even-/odd-part PE during the following 16 cycles of the 32-cycle period. Thus, the 1st-D and 2nd-D computations can share the same hardware resources during the 32-cycle period. For the 32-point transform, the PEE4 module executes in the first four clock cycles, the PEO4 module executes in the following four cycles, and the PEE4 module outputs the results to BF4. When the PEO4 module outputs the results to BF4, the BF4 module begins calculating the addition and subtraction as per Eqs. (21) and (22). In the following eight cycles, the PEO8 module calculates the matrix product C8oZ8o and the BF4 module simultaneously outputs the results. In cycles 1624, the PEO8 module outputs the computation results to BF8 and BF8 executes addition and subtraction. The BF8 module then outputs the addition results in cycles 1624 and the subtraction results in cycles 2432. The PEO16 module executes the matrix product C16oZ16o when BF8 outputs the addition and subtraction results to BF16. In the 48th cycle, BF16 outputs the first 32-point 1-D transform data and inputs the following 32-point transform data. After 1008 cycles, the 2nd-D data is output from the TMEM and fed into the PEE4 module. In these 16 cycles, the PEE4, PEO4, BF4, PEO8, and BF8 modules execute the 2nd-D data due to the ideal time of these circuit resources. In the following 16 cycles, the PEE4, PEO4, BF4, PEO8, and BF8 modules execute the 1st-D data and the PEO16 and BF16 modules execute the 2nd-D data. The 2-D transform data is starting output at the 1040 cycle; thus, the latency of the proposed core is 1040 clock cycles. The core takes 2064 cycles to complete the 32×32 IDCT transformation. According the proposed data flow (Fig. 7), the proposed circuit can maintain the throughput rate to be the same as the operation frequency.

Fig. 7
figure 7

Data flow of the proposed IDCT circuit

Full size image

3 Results and discussion

To indicate the performance of the proposed circuit, the very-large-scale integration implementation is described in the following subsection. The proposed circuit is also compared with other circuit designs in the literature.

3.1 Chip implementation

The proposed 32-point 2-D IDCT core is implemented in a 1-V Taiwan semiconductor manufacturing (TSMC) 90-nm 1P9M CMOS process. It uses the Synopsys Design Compiler to synthesize the register transfer language code and the Cadence Encounter Digital Implementation for placement and routing (P&R). The proposed IDCT core is operated at 250 MHz with a power consumption of 49 mW to meet the full HD 1080p specifications. The total gate count of the proposed core is 110 K. The gate counts of 1-D IDCT core and TMEM are 80 K and 30 K, respectively. The characteristics of the IDCT are presented in Table 1. The input data is 18-bit and the output data is 14-bit. There are 22 input pins, 14 output pins, and 13 power pins. The layout of the proposed 2-D IDCT core is displayed in Fig. 8, including the 1-D IDCT and TMEM.

Fig. 8
figure 8

Chip layout of the proposed 2-D IDCT core

Full size image
Table 1 Chip characteristics of the proposed 2-D IDCT core
Full size table

3.2 Comparison with existing studies

Table 2 presents a comparison of the proposed 2-D inverse transform core with existing methods. In [8] and [16], dual 1-D cores with a transpose memory have been used in the implementation of the 2-D inverse transform. A low-energy HEVC inverse transform core was presented in [8]. The design has 142-K three-input NAND gates without a transpose memory. Park et al. employed high-throughput structures for a 32×32 transform and incurred a high area overhead because the memory modules used the register structure [16]. The design only supports the 32- and 16-point inverse transforms, which are insufficient for HEVC applications. The high-performance core associated with 90-nm technology can support 3840×2160@30fps; however, the structure of the multiplexer reduces the operating frequency by half [17]. An ultra-low-cost IDCT employing a single 1-D core with a transposed memory was presented in [18] for the execution of 2-D transforms. This approach considerably reduced the circuit area. However, the design only supports the 32-point HEVC inverse transform, which is insufficient for HEVC application. An ultrahigh-throughput design was presented in [19]. The 16 parallel computation streams achieved a throughput rate of 6.4 GP/s for supporting multiple trans- form dimensions when implemented into 40-nm CMOS technology. However, a very large area cost is incurred by the design in [19]. The low-area cost design for multiple transform size HEVC applications using shifts and additions is presented in [22], in which 112 K gate counts are required for a 2-D IDCT transform. The 2-D DCT/IDCT [24] computes 2-D 4-/8-/16-/32-point DCT/IDCT and consumes 120 K gates supporting the 4K HEVC video sequences. As presented in Table 2, the proposed design achieves the smallest area cost when supporting multiple transform dimensions.

Table 2 Comparison of inverse 2-D transform cores
Full size table

4 Conclusions

This paper proposes a low-area 2-D IDCT core that supports multiple transform sizes for HEVC application. Compared with previously proposed designs, the proposed core has the smallest circuit area when supporting multiple dimension transforms. Moreover, the throughput rate can be maintained the same as the operation frequency (250 MHz). Consequently, the proposed 2-D IDCT core is suitable for HEVC video and next-generation video transform applications.