1 Introduction

Discrete wavelet transform (DWT) [1–5] is a linear signal processing technique that transforms a time domain signal to “wavelet” domain [6]. DWT is usually implemented using the finite impulse response (FIR) filter bank structures [7]. Figure 1 shows a convolution-based five-tap FIR filter with five multipliers, known as multiplier-accumulator (MAC) structure. In Fig. 1, the multipliers are involved in multiplying an input x[n] with filter coefficients, b i . The direct implementation of the N-tap filter requires N multipliers, which are an expensive resource in field-programmable gate array (FPGA). With regard to this fact, it is known and clear that convolution-based method requires massive computations, takes more physical space, and consumes more power [8]; hence, lifting-based (LS) [9] has been developed and implemented to improve these limitation.

Fig. 1
figure 1

Five-tap finite impulse response filter

Full size image

In this work, we preferred the conventional convolution-based DWT implementation over the LS for the following reasons. In LS, as the critical path delay (CPD) increases, the energy per operation increases and the operating frequency decreases [10]. In [11, 12], the authors found out that as the length of the filter (N) increases, the CPD is increased, respectively. Hence, the sequence of multiplication and addition will be longer than the convolution-based scheme. Therefore, LS is observed to have poor scalability and is inappropriate for large filter lengths [13, 14]. In addition, LS requires temporary registers to store the intermediate results, which takes up more storage area and as well consumes more power [15, 16]. For these reasons, we decided to implement the DWT using the convolution-based approach, but with multiplierless architecture.

Multiplierless approaches eliminate the use of multipliers by replacing individual coefficient multipliers with a single multiplier block, known as a multiple constant multiplication (MCM). Because filter coefficients are fixed and determined in advanced, the multiplication of filter coefficients by an input leads to area, delay, and power-efficient architectures [17].

The existing multiplierless algorithms can be divided into two general classes: they either reduce the number of multipliers or totally replace them with a simplified circuit logic. The most popular reduction algorithms are graph-based eliminations (GE) [18] and common subexpression elimination (CSE) techniques [19–21]. The drawback of CSE algorithms is that its performance depends on the representations of the coefficients and also limited by the constant bit widths [20], whereas the GE require more computational resources due to a larger search space [22].

On the other hand, several multiplierless architectures that eliminate all multipliers have been proposed. Distributed arithmetic (DA) efficiently performs the inner product function in a bit-serial manner via a look-up table (LUT) scheme, followed by shift accumulation operations [23–25]. Based on our previous experience, we identified that the ROM size in DA-based structures increases with the increase in the word length [26]. Residue number system (RNS) is a highly parallel non-weighted arithmetic system that is based on the residue of division operation of integers using the look-up table (LUT) scheme [27–29]. The key advantage of RNS is gained by reducing an arithmetic operation to a set of concurrent, but simple, operations. Another advantage of RNS is its large dynamic range, which is divided into independent smaller ranges, where addition and multiplication operations are performed in parallel without a carry propagation among them. Several applications, such as digital filters, benefit from the RNS implementation, e.g., [30–32]. To the best of our knowledge, the aforementioned approaches consider only one-level DWT implementation.

1.1 Contribution of this paper

This article focuses exclusively on the implementation of two-level multiplier-free DWT. We propose a new design of two-level RNS-based DWT that efficiently uses the memory elements in the first-level DWT and do not employ any memory element in the next levels. In addition, this design eliminates the use of multiple residue-to-binary converters (RBCs) between consecutive levels. Generally, the number of level is bounded by the output word length and we determine it mathematically (Eqs. 15 and 16). Finally, the proposed RNS-based approach could achieve high PSNR values with simple hardware structure and consume less power.

The remainder of this paper is organized as follows: In Section 2, the theoretical background on RNS is given. Section 3 illustrates the implementation of discrete wavelet transform. The implementation of the proposed two-level RNS is also presented. We further show an analytical comparison between these approaches. Section 4 presents the performance results. Finally, conclusions are drawn in Section 5.

2 Preliminaries

2.1 Discrete wavelet transform

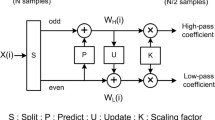
The wavelet decomposition mainly depends on the orthonormal filter banks. Figure 2 shows a two-channel wavelet structure for decomposition, where x[ n] is the input signal, g[ n] is the high-pass filter, h[ n] is the low-pass filter, and ↓2 is the down-sampling by a factor of two. By this way, each filter creates a series of coefficients that represent and compact the original signal information.

Fig. 2
figure 2

Multi-resolution wavelet decomposition. The block diagram of the two-channel two-level discrete wavelet transform decomposition (J=2) that decomposes a discrete signal into two parts. Note that ↓2 is keeping one sample out of two; a i and d i are the approximation and details at level i, respectively

Full size image

Mathematically, a signal y[ n] consists of high and low-frequency components, as shown in Eq. (1). It shows that the obtained signal can be represented by using half the coefficients, because they are decimated by 2.

$$ y[\!n] = y_{\text{high}} [\!n-1] + y_{\text{low}} [\!n-1] $$
(1)

The decimated low-pass filtered output is recursively passed through identical filter banks in order to add the dimension of varying resolution at every stage. Equations (2) and (3) mathematically express the filtering process of a signal through a digital high-pass filter g[ k] and low-pass filter h[ k]. This operation corresponds to a convolution with an impulse response of k-tap filters.

$$ y_{\text{high}} [\!n]= \sum\limits_{k} g[\!k].x[\!2n-k] $$
(2)
$$ y_{\text{low}} [\!n]= \sum\limits_{k} h[\!k].x[\!2n-k] $$
(3)

where n becomes 2n, representing the down-sampling process. The output ylow[ n] provides an approximation signal, while yhigh[ n] provides the detailed signal. There have been several wavelet filters proposed in literature, but in this paper, we have restricted ourselves to Daubechies wavelet filters only [33]. Because the down-sampling process follows each filter (as shown in Fig. 2), Eq. (3) can be rewritten without the decimation factor as:

$$ y[\!n] = \sum\limits_{k=0}^{N-1} h[\!k].x[\!n-k] $$
(4)

where N is the number filter tap. For the sake of simplicity of representing Eq. (4), x[ n−k] is replaced by x[ k].

2.2 Residue number system (RNS)

RNS [27, 28] is a non-weighted number system that performs parallel carry-free addition and multiplication arithmetic. In DSP applications, which require intensive computations, the carry-free propagation allows for concurrent computation in each residue channel.

Another aspect of using RNS is that an integer, within a large dynamic range, can be uniquely represented by set of residues, P, that are of much smaller values, corresponding to the size of the moduli set.

The RNS moduli set, P=m1,m2,…,m q , consists of q channels. Each m i represents a positive relatively prime integer, that is GCD (m i ,m j )=1, for i≠j.1 Any number, \( X \in \mathbb {Z}_{M} = {0,1, \dots M-1} \), is uniquely represented in RNS by its residues \( | X |_{m_{i}} \), which is the remainder of division X by m i and M is defined in Eq. (5),

$$ M = \Pi_{i=1}^{q} m_{i} = m_{1}*m_{2}*\dots *m_{q} $$
(5)

M determines the range of unsigned numbers in [0,M−1]. In particular, M should be greater than the largest expected output.

In the RNS representation, addition and multiplication are performed entirely in parallel on each modulo,

$$ Z = X \circ Y \overset{RNS}{\longrightarrow} Z_{m_{i}}= | X_{m_{i}} \circ Y_{m_{i}} |_{m_{i}} $$
(6)

where ∘ represents the addition, subtraction, or multiplication operation; and m i ∈P.

Mapping from the RNS system to integers, \(\mathbb {Z} \), is performed by Chinese reminder theorem (CRT) [34–36]. The CRT states that binary/decimal representation of a number can be obtained from its RNS through Eq. (7), provided all elements of the moduli set are pairwise relatively prime.

$$ |X|_{M} = (x_{1}, x_{2},... x_{q}) = | \sum\limits_{i=1}^{q} \hat{M_{i}} | \alpha_{i} x_{i}|_{m_{i}} |_{M} $$
(7)

where \( \hat {M_{i}} = M/{m_{i}} \) and \( \alpha _{i} = |\hat {M_{i}}^{-1}|_{m_{i}} \) is the multiplicative inverse of \( \hat {M_{i}} \) with respect to m i .

The implementation of RNS-based DWT is obtained by substituting Eq. (6) into (4)

$$ y\left[n\right]_{m_{i}}= y_{m_{i}} = |\left(\sum\limits_{k=0}^{N-1} |h\left[k\right]_{m_{i}}. x\left[n-k\right]_{m_{i}}|_{m_{i}}\right)|_{m_{i}} $$
(8)

for each m i ∈P. This implies that a q-channel DWT is implemented by q FIR filters that are working in parallel.

For designing an efficient RNS-based DWT, the choice of the moduli set and hardware design of residue-to-binary conversion are two critical issues that should be considered. Most widely studied moduli sets are given as a power of two due to the attractive arithmetic properties of these modulo sets. For example, {2n−1,2n,2n+1−1} [37] {2n−1,2n,2n+1} [38] and {2n,22n−1,22n+1} [39] have been investigated. A four-moduli set has been suggested to increase the dynamic range, e.g., {2n−1,2n,2n+1,2n+1−1} [40] and {2n−1,2n,2n+1,22n+1} [41].

In this work, the moduli set P n ={2n−1,2n,2n+1−1} is used for three reasons. First reason being that the modular adder is simple and identical for both m1=2n−1 and m3=2n+1−1. Secondly, for small n=7, the dynamic range of P7 is large and M is equal to 4145280, which would efficiently express real numbers in the range [−2.5,2.5] using 16-bit fixed-point representation, provided scaling and rounding are done properly. We assume that this interval is sufficient to map the input values, which does not exceeds ± 2. Thirdly, the reverse converter unit is simple and regular [36] because it does not employ any memory.

3 DWT implementation methodology

As mentioned in the previous sections, the wavelet transform of a signal can be performed by FIR filters, where the convolution operations are achieved by multiplying an input signal by the wavelet coefficients. In contrast, RNS-based approach has replaced the multiplication units with a suitable memory to perform the multiplication operations.

3.1 DWT implementation using RNS

Figure 3 shows the steps that are involved in RNS-based DWT approach. These steps are divided into offline and online steps. The offline steps are performed by converting the filter coefficients to RNS numbers and storing the result in a LUT. The online steps are used in converting each input values into RNS-system, before performing the filtering operations. Finally, the produced result is converted back to real-number system. We explained these process in Section 3.1.1.

Fig. 3
figure 3

The RNS-based DWT offline and online steps to perform the filtering operations. The offline steps are performed one time, while the online are performed for each input. q is the number of channels

Full size image

In general, the implementation of RNS-based DWT has essentially three components— i.e., the modulo adders (MA), forward and reverse converter. The forward converter, also known as binary-to-residue converter (BRC), is used to convert a binary input number to residue numbers. In contrast, the reverse converter, also known as residue-to-binary converter (RBC), is used to obtain the result in a binary format from the residue numbers. These components are shown in Fig. 4. We will refer to the RNS-system, which does not include RBC, as a forward-converter and modular-adders (FCMA), shown inside the dashed-line box in Fig. 4.

Fig. 4
figure 4

The block diagram of DB2 RNS-based architecture. BRC stands for binary-to-residue converter, RBC stands for residue-to-binary converter and MA represents for modulo adder

Full size image

3.1.1 Binary-to-residue converter (BRC)

The BRC is used to convert the result of multiplying an input number by a wavelet coefficient to q residue numbers by using LUT, shift, and modulo adders, where q is the number of channels. This procedure ensures that the multiplication operation is performed by using only memory.

3.1.1.1 RNS-system number conversion

The received input and wavelet coefficients span the real number and might take small values. One of the main limitation of using RNS-number representation is that it only operates with positive integer numbers from [0,M−1]. The DWT coefficients are generally close to zero and between − 1 and 1. Therefore, it is important to cope with both negative numbers and small numbers. To handle negative numbers, we mapped the real number to RNS range. Assuming the input samples are in [− 2.5,2.5], we mapped any value in this range to a unique value in [0,(M−1)]. Any sample, which does not fit this interval, will produce incorrect values. Hence, the interval should be large enough to map all the numbers.

In principle, the received sample X[i] is shifted y positions to the left (multiplying by 2y, step 4 in Fig. 3). This step ensures that X[i] is a y-bit fixed point integer. In a similar manner, the wavelet coefficients are scaled by shifting it z positions to the left (step 1 in Fig. 3). In our design, we set the filter scaling factor z to 11 and as a result, the coefficients of DB2 (Eq. 9) are multiplied by 211 and rewritten as shown in Eq. 9.

$$ {\begin{aligned} y_{\text{low}}[\!n] &= -266 ~x[\!n] + 459 ~x[\!n-1]\\ & \quad + 1713 ~x[\!n-2]+ 989~ x[\!n-3] \end{aligned}} $$
(9)
3.1.1.2 Modulo m i multiplier

The multiplication of the received sample by the filter coefficients, which are constants, can be performed via indexing the LUT. It is critical to identify the size of LUT because as the word length, w, of the received sample is increased, the memory size becomes 2w. Additionally, the design require q LUTs to perform the modulo multiplication.

We suggested several techniques to overcome these inadequate requirements. Instead of preserving a dedicated memory for each modulo m i , one memory that contains all module results is used. In this scheme, each word at location j contains q modules of h k ∗j∗211. Figure 5 shows the internal BRC block design of the three-channel moduli set P7={127,128,255} with its memory-map at the right top corner. This shows that, for a location j, the least significant 8-bit contains \(\phantom {\dot {i}\!} | h_{k} * x |_{m_{3}} \), the next 7-bit contains \(\phantom {\dot {i}\!} | h_{k} * x |_{m_{2}} \) and the most significant 7−bit contains \(\phantom {\dot {i}\!} | h_{k} * x |_{m_{1}} \), which can be generalized as shown in Eq. (10) (steps 2 and 3 from Fig. 3). The advantage of this method is that no extra hardware is required to separate each module value. Table 1 shows the memory contents of h1 in RNS system using 4×22 LUT.

$$ {\begin{aligned} \text{ROM}(j) &= |~h_{k}*j*2^{11} |_{m_{1}} ~*~ 2^{2n+1}\\ & \quad + | h_{k}*j*2^{11} |_{m_{2}} ~*~ 2^{n+1 }\\ & \quad + | h_{k} ~*~ j*2^{11} |_{m_{3}}, \quad j=\left[0,2^{w}\right] \end{aligned}} $$
(10)
Fig. 5
figure 5

The block diagram of the binary-to-residue converter for the three-channel RNS-based DWT, P7={127,128,255} (a) with two, (b) with four identical memories. The green blocks are not required because the shift result is always zero for m2. The memory content at location j is as shown in the upper corner

Full size image
Table 1 The memory content of h0 = −0.1294 or 757(− 266) multiplied by 211 in P7={127,128,255} when word length is 4
Full size table

It is obvious that if the input word length is 16 bits, then the LUT size becomes huge because 216 locations will be needed. One way to reduce the size of memory is to divide it into smaller size, each consisting of 2×22 bits or 4×22 bits. Figure 5 shows the block diagram of the binary-to-residue converter with two and four memories, respectively. However, the output of each memory should be combined, so that the final result is correct. It is worth noting that this division comes with a cost in terms of additional adders and registers are used (discussed in Section 3.4).

According to the previous improvements, the RNS-based system works as follows (step 5 from Fig. 3). Suppose that four memories are used, each of 16 locations. The input X16−bit=(x1,x2,x3,x4) will be divided into four segments. Each 4-bit segment will be fed into one memory, so that the 22-bit can be found, which will then be divided into three outputs, corresponding to \(\phantom {\dot {i}\!} |h_{k}*x_{l}*2^{11}|_{m_{i}} \). We want to emphasize that this result is the multiplication of each 4-bit with a filter coefficient with respect to m i .

To obtain the final multiplication’s result, each m i output will be shifted by l positions, where l is the index of the lowest input bit (4, 8, or 12). The modular multiplication and shift for 2n−1 and 2n+1−1 can be achieved by a left circular shift (left rotate) for l positions, whereas the modular multiplication and shift for 2n can be achieved by a left shift for l positions [37]. Finally, the modulo adder adds the corresponding output.

3.1.2 Modulo adder (MA)

The modulo adders are required for adding the results from a modular multiplier as well as for the reverse converter. In this work, two types of MAs are necessary—i.e., the first one is based on 2n and the other is based on 2n−1. Modulo 2n adder is just the lowest n bits of adding two integer numbers, where the carry is ignored. Modulo 2n−1 adder differs from modulo 2n adder in that the carry should be considered to limit the result to not be greater than 2n−1, as in Eq. (11).

$$ |x+y|_{2^{n}-1} =\left\{ \begin{array}{ll} x + y & \text{if} ~x+ y \leqslant 2^{n}-1,\\ x + y + 1 & \text{otherwise } \end{array} \right. $$
(11)

To improve the design and enhance the speed, a parallel-prefix carry computational structure is used [42–44], which allows the implementation of highly efficient combinational and pipelined circuits for modular arithmetic.

3.1.3 The reverse converter

The Chinese remainder theorem (CRT) [34] provides the theoretical basis for converting a residue number into a natural integer. The direct implementation of the CRT is inefficient because it requires a divider unit and several multipliers to determine the final output. However, the moduli set P n ={2n−1,2n,2n+1−1} can be efficiently implemented by four modulo adders and two multiplexers (step 6 from Fig. 3) [36]. Figure 6 shows the block diagram of the RBC of P7, which is adapted from [36]. The output of the RBC is unsigned (3∗n+1)-bit integer number. The actual signed number can be found by shifting the result y+z positions to the left, which is equivalent to dividing by 2y+z. y and z are the scaled values of the input and wavelet coefficients, respectively. Generally, the word length of one-level DWT is bounded by Eq. 12 and should not exceed 3∗n−2 bits. Subtracting 3 is required because 2.5 is added to the input samples in order to have a 3-bit unsigned integer.

$$ 3*n+1 \geq y+z+3 $$
(12)
Fig. 6
figure 6

The block diagram of the pipelined residue-to-binary converter for the three-channel RNS-based DWT, P7={127,128,255}. Four identical 2n+1−1 MAs, three subtractors and two multiplexers are generally required for RBC. Two shift registers are used for extending the 7-bit input by one bit. In the real implementation this operation does not add any cost because this operation is just equivalent to appending 0 at the first location of the input signal

Full size image

3.2 Example

In this subsection, an example with input x[1] = − 0.4 is given to illustrate how the RNS-based works. Each input is added to 2.5 and then multiplied by 28. Therefore, if x[1] = − 0.4, the result is 538. Then, this value is multiplied by the scaled h0=− 266 in P7. The sample input can be rewritten as (0000 0010 0001 1010)2 or x1=0, x2=2, x3=1 and x4=10. These values are used to index the memory and the value of multiplying x i by h0 can be found in Table 1—i.e., 0, 3402985, 3798772 and 236689, respectively. From the table, the corresponding module of x1 is \((0, 0, 0)_{P_{7}}\), x2 is \((103, 108, 233)_{P_{7}}\), x3 is \((115, 118, 244)_{P_{7}}\) and the corresponding module of x4 is \( (7,28,145)_{P_{7}} \). After that, the value of h0∗x2 is shifted eight-position corresponding to m i and the value of h0∗x3 is shifted four-position corresponding to m i . For the case of x3, the mid value is shifted 8 bit to the left, whereas the other values is circular shifted by 8 bit to the left and the result becomes \( (79, 0, 233)_{P_{7}}\). It is worth noting that the mid value is always 0 because the word width is 7 and is less than the shift value, 8. For the case of x2, the mid value is shifted 4 bit to the left, whereas the other values is circular shifted for four positions and the result becomes \( (62, 96, 79)_{P_{7}}\). The sum of the partial results, performed via tree of two-input MAs, is \( (148,124,457)_{P_{7}} \) or \( (21,124,202)_{P_{7}} \), which is equivalent to (mod(− 143108,127),mod(− 143108,128), mod(− 143108,255)), respectively. Finally, the output of this memory-based multiplication is aggregated with next filter-taps using MAs.

3.3 Two-level DWT implementation

The two-level discrete wavelet transform comprises of two cascaded one-level DWTs (in series), where the output of the first level is fed into the second level (as shown in Fig. 2). Figure 7a shows the design of two-level RNS-based DWT, which involves two identical FCMA and two RBC blocks. The FCMA block is the RNS-based filtering (multiplication) block. It is obvious that converting between the number systems back and forth introduces some latency. Latency is defined as the number of clock cycles required to generate the first output sample once the input signal is applied. The latency, τ, of the two-level design is given by

$$ \tau = 2* (\tau_{FCMA} + \tau_{RBC}) $$
(13)
Fig. 7
figure 7

The block diagram of two-level RNS-based DWT design (a), the full design with two RBCs, and (b) the proposed design, which eliminates the middle RBC to improve the latency. FCMA represents FIR filtering process in RNS

Full size image

where τ FCMA is the RNS-based filter latency and τ RBC is the RNS-to-binary converting delay, respectively.

In this work, we suggest to eliminate the first RBC and feed the output of the first FCMA block into the second block, as shown in Fig. 7b. The advantage of this elimination is that the final output will be solely computed by one RBC component and one shift register. As a result, the latency becomes:

$$ \tau = 2 * \tau_{\text{FCMA}} + \tau_{\text{RBC}} $$
(14)

The only restriction is that the range of the used moduli-set should be greater than the maximum expected value, th o , which can be computed as follows:

$${} {th}_{o} = \left(\sum\limits_{k} h_{k}\right)^{2} * \max(x\left[n\right]) * (2^{z})^{2} * 2^{y} \leqslant M -1\quad $$
(15)

where h k is the kth DWT coefficient; x[n] is the input; y and z are the input and filter scaling factors, respectively; and M is the maximum range from Eq. (5). As a consequence, the word length of two-level DWT is bounded by Eq. 16 and should not exceed 3∗n−2 bits.

$$ 3*n+1 \geq y + (2*z) + 3 $$
(16)

where (3∗n+1) is the moduli-set word length. Eventually, Eq. 16 can be generalized to any DWT level, (l), by using the following inequality:

$$ 3*n-2 \geq y + (l*z) $$
(17)

3.3.1 The design of the second FCMA

The FCMA of the proposed stage can be implemented by two different techniques. The first one is based on memory that stores the multiplication result of multiplying an integer by the filter coefficient (Fig. 8a) and the second one is based on shift-add operations of the input by 2r, where r is the position of each “1” of the filter coefficient (Fig. 8b). For example, from Table 1, h0 is equal to 757 or (01011110101)2, which is required to (circular) shift the input by 0,2,4,5,6,7,9 and adding them to find the final multiplication result. The key feature of this technique is that each multiplication operation is a left (circular) shift, which can be implemented by rewiring the order of the input bits. Indeed, the implementation is simple, and does not require any special circuits except several MAs to sum up the result. In the following sections, we refer to the optimized FCMA as memory-based, if it employs memory elements or shift-based, if it does not employ any memory.

Fig. 8
figure 8

The proposed FCMA block diagram of the second stage module, which directly performs a residue number multiplication by the filter coefficient at channel q. The Mi0,Mi1 and Mi2 blocks are identical memories of 4×n and contain values of m i ∗2z∗h k ∗j, where h k is the kth filter tap and j∈[0,16]. (a) Using memories. (b) Using shift operators and MAs

Full size image

3.4 Hardware complexity

3.4.1 Memory usage

RNS techniques employs memory elements as a key resource to avoid multiplying two input variables. As the number of level increases, the number of memory elements changes. Assuming that the length of the received word is w−bit and there are N filter-tap, we define the size of a memory element by a×b, where a and b are the word size of input and output, respectively. The value of a determines the size of the memory, 2a. The total number of memory elements that is occupied by an RNS-based filter is N∗⌈w/a⌉ of (a×b). This Eq. shows that the number of memory elements increases linearly with the number of filter taps (as shown in Fig. 8a), while the memory size remains constant (a×b), but increased as a and b increase. The only overhead with large a is that the number of MA, which are required to sum up the final result, is increased. Table 2 shows a comparison of the memory usage when w=16.

Table 2 Occupied memories that are used by RNS-based DB2 DWT approaches. The input word length, w, is 16 bits and b=3∗n+1
Full size table

If the FCMA at the second stage is implemented by means of memory (memory-based FCMA), then the number of required memory can be calculated as follows:

$$ q * N * \left(\left\lceil \frac{n}{a} \right\rceil \right) $$
(18)

For instance, a three-channel of P10 FCMA has 6 memories of (4×10) and 3 memories of (4×11). Therefore, the FCMA at the second stage requires 36 memory elements and in total 52 are required for the whole design.

The design of FCMA at the second stage can be improved by eliminating all the memory at FCMA, as shown in Fig. 8b. In this case, the proposed shift-based FCMA performs the multiplying operations via shift operations and MA units. The shift operation is always performed via rewiring the bits [37], which has no cost in terms of delay and hardware.

3.4.2 Adder counts

In addition to the memory complexity, we could derive an expression for the overall adder counts. In the following analysis, we can neglect the difference between (2n−1) and (2n+1−1) MAs because it will not affect the total number of MAs.

For a word length w and N-tap filter, the q-channel FCMA implementation requires N BRC blocks and (q∗(N−1)) two-input MA blocks to compute the final result (Fig. 4). Each BRC requires at most (q∗(w/a−1)) two-input MA blocks (Fig. 5). Likewise, the RBC has four MA blocks, three subtractors, and two multiplexers. Thus, the total number of MA blocks at one-level RNS-based is given by:

$$ \begin{aligned} \text{MA}_{t} &= q*N * (w/a - 1) + q * (N - 1) + 4 \\ &= q*N*w/a -qN +qN - q + 4\\ &= q*(N*w/a -1) + 4 \end{aligned} $$
(19)

For instance, three-channel DB2 implementation requires 9 MA blocks to sum up the final result, and in total P7 RNS-based implementation has a total of 49 MA blocks when w = 16 and a = 4 bits.

If the FCMA of the second stage is implemented by means of memory, then each unit requires \( (q*((\lceil \frac {n}{a} \rceil) - 1)) \) MAs to sum the output of each tap (Fig. 8a). In addition, (q∗(N−1)) MAs are required to sum all the output of all taps. This means, \( (N * q*((\lceil \frac {n}{a} \rceil) - 1) + q * (N-1)) \) MAs are used for the memory based proposed approach.

In contrast, if the FCMA of the second stage is implemented by rewiring the input of the first stage, then each tap requires at most q∗(n−1) MAs, where n is the channel width. However, not all of these MAs are required, because the shift operations are applied to the binary ones of the filter coefficients. For example, from Table 1, h0 equal to (757)10 or (01011110101)2. This means that the proposed approach requires \( q (\bar {n} - 1)= 3*6 = 18\) modulo adders, where \( \bar {n} \) is the average of binary ones in h j ∗2z. Table 3 summarizes the number of memories and MAs of each implementation, respectively.

Table 3 Memory usage and adders for RNS-based approaches for N-tap DWT
Full size table

It is clear that as (w/a) increases, the number of MA increases because (w/a−1) MA are required to construct MA tree. Hence, the critical path delay (PSD) involves one multiplier followed by log2(w/a−1) levels MA tree. As a consequence, there is a trade-off between the number of memory and its size on the overall performance of the system.

4 Simulation results, performance analysis, and validation

In the previous section, we have demonstrated the design of the DWT by using a residue number system. The two-level DWT RNS-based has been designed, implemented and tested with series of simulations to verify the DWT functionality. Experiments were carried out on the Xilinx ZC706 evaluation board [45]. The performance of the proposed approach was compared with the distributed arithmetic (DA) [3], which is a multiplierless DWT. We also considered the direct DWT implementation using an IP FIR Compiler 6.3 (FIR6.3) block, which provides a common interface to generate highly parameterizable, area-efficient, high-performance FIR filters [46].

In the following experiments, the moduli sets of P7={127,128,255},P10={1023,1024,2047}, and P13={8191,8192,16383} were used. The dynamic range of these sets are M=4161536,2144338944, and 1099310309376, respectively. In fact, the moduli sets of P10 and P13 are selected because their dynamic range are greater than th o . For instance, Eq. 15 shows that th o =1279020283 for P10 with y=6,z=11, and \( \sum (h_{i}) = 1.5436 \). In all RNS-based implementations, the input word length was set to 16 bits.

4.1 Resource utilization and system performance

Table 4 summarizes the resource use by RNS-based components— i.e., FCMA and reverse-binary converter (RBC) when using 2×b memory, where ‘b’ is the output word length of P n and equal to (3∗n+1). The two-level, three-channel RNS contains two FCMA units and 3 different MAs (Fig. 5b). The RBC unit consumes fewer resources and less power with the operating frequency in all models being approximately equal and as high as 350 MHz or more. The optimized shift-based FCMA consume less power but the number of occupied slices is doubled compared to the memory-based implementation. Finally, it is clear that the BRAM consumes most power in all memory-based models (approximately 16 mW).

Table 4 FPGA resource utilization and system performance for the RNS components— i.e., FCMA and reverse converter
Full size table

4.2 Two-level DWT evaluation

Table 5 lists the resource consumption and the system performance for the two-level DWT implementations when two memory elements are used in each filter-tap. The FIR-based model shows better performance compared to all multiplierless architectures but it requires several multiplier units, known as DSP48E in modern FPGA [45].

Table 5 FPGA resource utilization and system performance of two-level DB2 DWT implementation with ZC706
Full size table

It is also observed that the maximum frequency of all RNS-based schemes is higher than DA-based DWT. Because the only change among P7, P10, and P13 implementations is the moduli-set width, the maximum operating frequencies slightly changes among these designs. Furthermore, the two-level DB2 filter bank was designed with maximum operating frequencies between 260 and 360 MHz for full and optimized shift-based FCMA, respectively. However, P7 RNS-based is the only model that has less resources compared to DA-based because of its small word length.

Furthermore, Table 5 shows that the RNS schemes consume less power compared to DA-based DWT. The exception is that the Full model of P13, which occurred due to the hardware usage and the memory-size—i.e., 8×40. The large size of the memory can further be split into smaller memory (as shown in Fig. 5). Table 6 presents the impact of using four-memory in each filter-tap on the power. It is obvious that the power consumption is increased as the number of memory and its size increase. The proposed shift-based RNS model compared to these models showed a better performance regards to power and maximum operating frequency. In spite of the deficiency in terms occupied slices, the proposed model has less number of memories and multipliers compared to DA- and FIR-based schemes.

Table 6 The effect of using four memories in each filter-tap with ZC706
Full size table

4.3 Functionality verification

In this experiment, a sinusoidal signal is applied on each approach to verify the functionality of each design. Figure 9 shows a comparison among all RNS-based implementations with FIR- and DA-based implementations. It indicates that the proposed approaches are ahead of other implementations. To be more accurate, the two-level DB2 DWT implementations were simulated by DSP Logic Analyzer and the result is shown in Fig. 10. It depicts that the signals resulting from Full RNS- and FIR-based lag behind the proposed architecture by 80 ns or 8 clock cycles, whereas the signal resulting from DA-based lags by 4 clock cycles.

Fig. 9
figure 9

Comparison among all two-level DWT approaches when a sinusoidal signal is applied

Full size image
Fig. 10
figure 10

The output of two-level DWT using DSP Logic Analyzer when a sin wave is applied. Each clock cycle is 10 ns

Full size image

Eventually, we have verified the simulated result on ZC706 development kit and the simulation and hardware co-simulation results of the two-level DB2 implementations are highly correlated, as shown in Fig. 11.

Fig. 11
figure 11

The output of the two-level DWT when a pattern-based signal [4] is applied. It is used to extract the main features of the received signal

Full size image

4.4 Precision analysis

Generally, convolution-based DWT involves floating-point operations, which introduces rounding errors. Because the filter-banks coefficients, designing by means of floating-point, require large hardware resources to retain the precision, we replaced the floating-point method with RNS numbering system. We simply multiplied the input by 2y and the filter coefficients by 2z. At the end, we converted the result back to floating-point number. PSNR is the most commonly used method to measure the quality of the result. In fact, it measures the peak error and high PSNR means better quality and that less error is introduced to the result.

We carried out the precision analysis for the first and second levels. The Daubechies wavelet with four coefficients were used and the result of each level was compared with the actual double-precision values via MATLAB. Table 7 shows the behavior of the proposed approaches in terms of input and wavelet coefficients precision. The output precision is set to Q5,16 for all implementations. It is worth noting that employing the memory-based FCMA or shift-based FCMA at the second level has no effect on the output because both schemes compute identical results.

Table 7 The PSNR values of one- and two-level of different DWT implementations
Full size table

The optimized two-level with P10 has a maximum input scaling factor of 6 (due to Eq. 16). As a consequence, we cannot adapt their scaling factors. In contrast, the optimized two-level of P13 has higher input and filter coefficients scaling factors due to its large word length, which enables it to have large accuracy values.

Table 7 presents that the maximum achieved PSNR of P7 set is 56.5 dB and 41.87 for the first and second level, respectively. We could not achieve better accuracy with the specified scaling factors because y+z+3=21≤(3∗7)+1=22 (see Eq. 16). If an application requires higher accuracy values, then different moduli set with large n should be selected. Figure 12 compares the effect of changing the scaling factors of two different moduli sets, P10 and P13 for one-level DB2 RNS-based approach. The input scaling factor was varied between 8-bit and 13-bit, and filter scaling factor was varied between 11 and 18. As expected, lower scaler factors produces PSNR equal to 60 dB. While the maximum PSNR equal to 90.37 is obtained with y=13 and z=18 for P13, the maximum PSNR of P10 is obtained when y=12 and z=16 (Eq. (12)). It is worth mentioning that as the filter scaling factor increases, no hardware cost is added to the design, because all the changes correspondingly occurred in the memory contents. Figure 13 shows the effect of the scaling factors for two-level DB2 RNS-based approach. The proposed 2-stage RNS-based P13 with z=13, has maximum PSNR of 54.5 dB, which is roughly equal to the full model with z=11.

Fig. 12
figure 12

The impact of input, y, and wavelet filter coefficients, z, scaling factors of one-level RNS-based implementation on PSNR, with respect to (a) P10 and (b) P13 moduli sets

Full size image
Fig. 13
figure 13

The impact of input, y, and wavelet filter coefficients, z, scaling factors of two-level RNS-based implementation with respect to P10 and P13 moduli sets on PSNR

Full size image

5 Conclusions

In this article, we have addressed the development of a multiplierless scheme for two-level RNS-based DWT, which can be adapted to any moduli set, with any number of channel. This approach intensively use memory to speed up the entire processing time. In order to achieve low latency, we incorporated two novel ideas into the two-level proposed design, as follows: (1) eliminating the intermediate RBC unit; (2) replacing the internal memory of the second level by simple circular shift operations. A key feature of this approach is that the user can change the scaling factors, y and z, either to achieve high PSNR values or lowering the PSNR value in order to design multi-level DWT with low latency.

The trade-off between system performances and resource consumption was addressed. Experiment results showed that the RNS-based approach would be more appropriate for multi-level DWT because the number of memory element is always constant as the number of level is increased. In addition, it is observed that the proposed RNS-based DWT implementation has lower latency than FIR and P n RNS-based implementations. Finally, an acceptable precision can be achieved by adapting the scaling factors. Table 8 indicates the advantage and disadvantages of each moduli-set.

Table 8 A comparison between RNS-based implementations using moduli-set P n
Full size table

Given the implementation examples for experimental verifications and analysis, the approach was validated on a ZYNQ ZC706 development kit. The co-simulation results have also been verified and compared with the simulation environment. The complexity and optimization of multi-level DWT with respect to hardware structure provides a foundation for employing an appropriate algorithm for high-performance applications, such as in cognitive communication, where DWT analysis is combined with machine learning algorithms.

6 Appendix 1

6.1 Acronyms

BRAM Block RAM

BRC Binary-to-residue converter

CC Clock cycle

CLB Configurable logic block

CPD Critical path delay

CRT Chinese reminder theorem

CSE Common subexpression elimination

DA Distributed arithmetic

DSP Digital signal processing

DWT Discrete wavelet transform

GCD Greatest common divisor

GE Graph-based eliminations

FCMA Forward-converter and modular adders

FIR Finite impulse response

FPGA Field-programmable gate array

LS Lifting-based schemeLUT Look-up table

MA Modular adder

MAC Multiplier-accumulator

MCM Multiple constant multiplications

PSNR Peak signal-to-noise ratio

RBC Reverse-binary converter

RNS Residue number system

7 Appendix 2

7.1 Mathematical symbols

a×b The memory word size

l Number of DWT levels

M The maximum range of P n

N Number of filter tap

h k The low-pass kth filter coefficient

m The number of magnitude bits

m i The ith moduli of P n

n The moduli set base (e.g. P7)

q Number of RNS channel

τ Latency

w Word length

y The input scaling factor

z The filter scaling factor