1 Introduction

1.1 Motivation and related works

High-resolution radar can achieve a high range resolution by transmitting a wideband signal and using modern pulse compression techniques [1]. In most cases, the range extent of the target to be detected is much larger than the range resolution of radar. As a consequence of this situation, the target “appears” in multiple different range cells of radar echoes, so it is also called a range distributed target [2]. The echoes of the range distributed targets can capture abundant target structure information such as target size and scattering distribution; hence, they have widely been used for target recognition, classification, and accurate tracking [3, 4]. With the extensive applications of high-resolution radars, the problem of detecting range distributed targets arises naturally and has received considerable attention [5–7]. Nevertheless, it is known that for high-resolution radars, sea clutter character becomes very complex and sea clutter is often highly non-Gaussian, even spiky [8]. In signal processing research area, it is always a challenging problem to design an effective detector for range distributed targets embedded within sea clutter.

During the past decades, many works have been directed so far towards the methods to improve the detection capability of range distributed targets in sea clutter. Adaptive detection methods based on the compound-Gaussian model of sea clutter are widely used in the range distributed target detection in sea clutter [9–24]. The typical examples are the generalized likelihood ratio test (GLRT) based detectors [9–11], the detectors with Rao and Wald tests [12–14], the spatial scattering density GLRT (SDD-GLRT) detector [15], the two-step GLRT which can be used in the partically homogeneous environment [16], the deterministic scatterer model GLRT based on order statistics detector (OS-DSM-GLRT), the adaptive beamformer orthogonal rejection test (ABORT) [17], and adaptive normalized matched filter (ANMF) [19, 20]. In [21] shows an adaptive scheme to detect extended and multiple point-like targets embedded in correlated Gaussian noise, the detectors designed in this paper guarantee satisfactory performance, and some of detectors have less time-consuming character. In [22], some a priori knowledge about the operating environment is exploited and used in the detector design stage, and the results show that the use of a priori information can lead to a detection performance quite close to the optimum receiver. In [23, 24], a unifying framework for adaptive radar detection is established. This framework is used to deal with the problem of adaptive multichannel signal detection in homogeneous Gaussian disturbance with unknown covariance matrix and structured deterministic interference. A modified version of generalized multivariate analysis of variance (I-GMANOVA) is studied in [23, 24]. Those detectors consist of an adaptive whitening filter to suppress clutter followed by a matched receiver. Due to the complex dynamic nature of sea clutter, the adaptive whitening filter can not be effectively implemented; thus, the detection performance of these detectors shows some deterioration. In addition, some of them are very time-consuming.

The alternative methods are based on the binary integration detection strategy (sometimes called an M out of L detector, M/L detector) [25–28]. Those detectors are usually comprised of an initial binary detector followed by a binary accumulator to extract targets with sufficient range extent. The first-stage detection of those detectors is essentially a simplification of the likelihood ratio test (LRT). The different statistical models of clutter are needed to formulate the LRT in different sea clutter backgrounds. Their performance may become extremely bad when the second threshold is improperly chosen. However, these detectors are easy to be realized in engineering.

Recently, by analyzing the real high-resolution sea clutter datasets, many unconventional methods exploiting the features of clutter have been developed [29–34]. Several researchers have demonstrated that the sea clutter time series exhibit fractal and multiracial behaviors. Starting from this result, the fractal-based detectors are developed, for example, multifractal analysis based on Hurst exponent [29], multifractal analysis based on blind box-counting [30], high-order fractal feature [31], and joint fractal with the combination of Hurst exponent and intercept [32]. It has been shown that these fractal-based detectors can achieve very high detection accuracy within a long observation time, but during the several-second observation time, their detection performance suffers from some degradation [32].

In fact, sea clutter data is highly nonstationary, but this fact is not taken into consideration in designing all aforementioned detectors. Thus, those detectors can not work well in nonstationary sea clutter. In order to break the limitation of sea clutter nonstationary property, another popular feature-based detection method using the consistency factor of speckle is proposed in [34]. That detector can eliminate the influence of nonstationary part of sea clutter and achieve better detection performance. However, that detector becomes very time-consuming when the ratio between the range extent of the target to be detected and the range resolution cell of radar is large.

To this end, we propose a novel and functional feature-based detector for the detection of the range distributed target in sea clutter. As verified by the analyzed results of the intelligent pixel-processing (IPIX) radar data sets in [34, 35], the nonstationary property of the high-resolution sea clutter is mainly reflected in the texture and that of the speckle is not very severe. Generally, the speckle and texture components can be regarded to be statistically independent. Thus, the overall autocorrelation function of sea clutter is the product of autocorrelation functions of these two components. In practice, it is dominated by the speckle component. The correlation time of the speckle component is around milliseconds [36]. Conversely, the target may exhibit strong correlation characteristic and usually has long correlation time. Inspired by this and the works presented in [34], we design a correlation feature-based detector for detecting the range distributed targets embedded within sea clutter.

1.2 Summary of the contributions and paper organization

The main contributions of our present study are summarized as follows:

  • We design a correlation feature-based detector for detecting the range distributed targets embedded within sea clutter. This detector is an extension of the binary integration detector, while overcoming its shortcomings of the statistical model dependency and maintaining its high efficiency.

  • We use the complex signals of clutter and target returns to extract the correlation feature and set the rule of the binary detector based on this feature at the first-stage detection of the proposed detector. Thus, the negative effect of the nonstationary texture on the detector can be effectively eliminated.

  • In order to improve the robustness of the detector, the modified entropy is applied to adaptively estimate the numbers of strong scatterers of target, and the optimal selection of the second threshold M can then be determined according to this estimation.

  • We make comparision of our detector with the fractal-based detector [29] and the feature-based detector [34]; the proposed detector can attain better detection performance but require lower computational complexity.

The rest of this paper is organized as follows. Section 2 shows the the aim, design, and setting of the study; Section 2.1 contains the formulation for the problem and describes the signal model; and Section 2.2 analyzes the correlation characteristic of the radar-received signals and defines the decreasing rate of the correlation time as a correlation feature. Then, the statistics results of this correlation feature for the sea clutter and targets are presented in Section 2.3, according to the disparity of the correlation features of clutter and targets, a new correlation feature-based detection scheme is proposed. In Section 3, the proposed algorithm is verified by the experimental results with measured radar data. Finally, we conclude our paper in Section 4.

Notation: The symbols which are used in our paper are as follows: N represents the number of pulses; z r represents the received signal vector of the rth range cell; s r represents the target echo vector of the rth range cell; c r represents the clutter vector of the rth range cell; τ r (n) and g r (n) represent the texture and the speckle component, respectively; P r represents the number of target scatterers in the rth range cell; ar,p and fr,p represent the complex amplitude and the Doppler offset of the pth scatterer in the rth range cell, respectively; and T represents the pulse reptition interval of the radar. m represents the delay variable; Rτ,r(m) and Rg,r(m) represent the normalized autocorrelation function for the clutter texture and the speckle components, respectively; SCR r represents the signal-clutter-ratio (SCR) for the rth range cell; f r represents the approximation of the Doppler offsets of rth range cell; m r represents the correlation time for the rth range cell; γ r represents the decreasing rate of the correlation time; R r (m r ) represents the autocorrelation coefficient at m r ; η1 represents the detection threshold of the binary detector; \(d_{r}^{(n)}\) represents the detector output through the nth detection threshold; and M represents the second detection threshold. h e represents the number of range cells occupied by the strong scatterers of the range distributed target; e i and g i represent the normalized sub-sequences of \(\left \{ {{\gamma _{(1)}}, \cdots,{\gamma _{(h)}}} \right \}\) and \(\left \{ {{\gamma _{(h + 1)}}, \cdots,{\gamma _{(L)}}} \right \}\), respectively; h represents the hypotheses number; H(h) represents the nomalized estimation for h; P fa represents the overall false alarm probability of the binary integration detector; Pfa1 represents the false alarm probability of the binary detector; and \(C_{L}^{m}\) represents the number of combination of L items taken m at a time.

2 Methods

2.1 Problem statement and signal model

It is assumed that data are collected from a coherent train composed of N pulses. For the sake of simplicity, we assume that the range distributed target is completely contained within L consecutive range cells and the range migration is neglected during a coherent processing interval equal to a time duration of the N pulses. Herein, the power spectrum of detected white noise is about 20 dB below that of sea clutter, and there is no jamming presence; therefore, the clutter dominant environment is considered, and the noise is ignored. For the rth range cell, \({{\mathbf {z}}_{r}} = {\left [ {{z_{r}}(1), \ldots,{z_{r}}(N)} \right ]^{T}}\) denotes the received signal vector, \({{\mathbf {s}}_{r}} = {\left [ {{s_{r}}(1), \ldots,{s_{r}}(N)} \right ]^{T}}\) denotes the target echo vector, and \({{\mathbf {c}}_{r}} = {\left [ {{c_{r}}(1), \ldots,{c_{r}}(N)} \right ]^{T}}\) is the clutter vector. Generally, s r and c r are statistically independent of each other. Accordingly, the problem of detecting the presence of a range distributed target in the sea clutter can then be formulated in terms of the following binary hypotheses test:

$$ \left\{ \begin{array}{l} {H_{0}}:{{\mathbf{z}}_{r}} = {{\mathbf{c}}_{r}},r = 1, \ldots,L\\ {H_{1}}:{{\mathbf{z}}_{r}} = {{\mathbf{s}}_{r}} + {{\mathbf{c}}_{r}},r = 1, \ldots,L \end{array}.\right. $$
(1)

If H0 hypothesis is accepted, only the sea clutter exist; otherwise, if H1 hypothesis is accepted, this means the presence of a range distributed target in the sea clutter.

In many realistic high-resolution radar applications, it is generally accepted that the compound-Gaussian model, which arises from the product of two independent random variables, is used to describe the sea clutter. According to this model, the discrete-range-time expression of the received complex sea clutter samples can be given by

$$ {c_{r}}(n) = \sqrt {{\tau_{r}}(n)} {g_{r}}(n), n = 1, \ldots,N, $$
(2)

where g r (n), commonly named the speckle component, is a zero-mean complex Gaussian random process that accounts for the local sea backscatter and τ r (n), the so-called texture, is a real positive random process that represents the power variations of the local backscatter.

The target returns in each range cell can be modelled as the sum of the contribution of scatterers. Generally, within a coherent processing interval, each scatterer of the target on the sea surface, such as a boat or ship, can be regarded to have a constant radar cross section and a constant radial velocity. Therefore, the sample s r (n) of the target returns can be expressed as a simple form as follows [18]:

$$ {s_{r}}(n) = \sum\limits_{p = 1}^{{P_{r}}} {{a_{r,p}}{e^{- j2\pi (n - 1){f_{r,p}}T}}}, n = 1, \ldots,N, $$
(3)

where P r is the number of target scatterers in the rth range cell. ar,p and fr,p are the complex amplitude and Doppler offset of the pth scatterer in the rth range cell, respectively. T is the pulse repetition interval of the radar. The implied vector form of s r are shown as follows:

$$ {{\mathbf{s}}_{r}} = \left[\sum\limits_{p = 1}^{P_{r}}{a_{r,p}}, \ldots,\sum\limits_{p = 1}^{{P_{r}}} {{a_{r,p}}{e^{- j2\pi (N - 1){f_{r,p}}T}}}\right]^{T}. $$
(4)

2.2 Temporal correlation characteristic of the received signal

The temporal correlation of the received signal is referred to the correlation of multiple successive pulse returns within the same range cell and is usually described by the normalized autocorrelation function. The normalized autocorrelation function of the received signal vector z r is defined as

$$ {R_{r}}(m) = \frac{{\sum\limits_{n = 1}^{N - m} {{z_{r}}^{*}(n + m){z_{r}}(n)} }}{{\sum\limits_{n = 1}^{N} {{{\left| {{z_{r}}(n)} \right|}^{2}}} }}, $$
(5)

where superscript \({\left (\bullet \right)^{\mathrm {*}}}\) denotes the conjugate operation. m is the delay variable.

The normalized autocorrelation function under H0 hypothesis can be expressed as

$$ {R_{r}}(m\left| {{H_{0}}} \right.) =R_{c,r}= \frac{{\sum\limits_{n = 1}^{N - m} {{c_{r}}^{*}(n + m){c_{r}}(n)} }}{{\sum\limits_{n = 1}^{N} {{{\left| {{c_{r}}(n)} \right|}^{2}}} }}. $$
(6)

According to the sea clutter model given in Eq. (2), we have

$$ {R_{c,r}}(m) = {R_{\tau,r}}(m){R_{g,r}}(m), $$
(7)

where Rτ,r(m) and Rg,r(m) are the normalized autocorrelation functions for the clutter texture and speckle components, respectively. Equation (7) clearly shows that the overall normalized autocorrelation function of sea clutter is influenced by the correlation characteristics of the texture and speckle components. Due to their different physical origins, the clutter texture and speckle components exhibit very different correlation characteristics [36, 37]. The speckle component is associated with the detailed scatterers of the clutter in any range cell. It rapidly varies and has short correlation time that is around milliseconds. On the other hand, the texture component results from a bunching of scatterers associated with the long sea waves and swells. It has a longer correlation time that stretches to seconds. As has already been pointed out by Farina in [36] and by Greco in [37], for the sea clutter in a short time, its temporal correlation characteristic is dominated by the speckle component. Accordingly, the coherent signals z r ,r=1,…,L under H0 hypothesis have fairly short temporal decorrelation time equal to that of the speckle component of sea clutter.

Under H1 hypothesis, the normalized autocorrelation function of the received signal can be expressed as

$$\begin{array}{*{20}l} \begin{aligned} {R_{r}}(m\left| {{H_{1}}} \right.) &= \cfrac{{\sum\limits_{n = 1}^{N - m} {s_{r}^{*}(n + m){s_{r}}(n)} }}{{\sum\limits_{n = 1}^{N} {{{\left| {{s_{r}}(n)} \right|}^{2}}} {\mathrm{+ }}\sum\limits_{n = 1}^{N} {{{\left| {{c_{r}}(n)} \right|}^{2}}} }}\\ & \quad +\cfrac{{\sum\limits_{n = 1}^{N - m} {c_{r}^{*}(n + m){c_{r}}(n)} }}{{\sum\limits_{n = 1}^{N} {{{\left| {{s_{r}}(n)} \right|}^{2}}} {\mathrm{+ }}\sum\limits_{n = 1}^{N} {{{\left| {{c_{r}}(n)} \right|}^{2}}} }} \end{aligned}. \end{array} $$
(8)

The SCR for the rth range cell is denoted as \(SC{R_{r}} = {{\sum \limits _{n = 1}^{N} {{\left | {{s_{r}}(n)} \right |}^{2}}} / {\sum \limits _{n = 1}^{N} {{{\left | {{c_{r}}(n)} \right |}^{2}}}}}\). Then, Eq. (7) can be re-expressed as

$$ {{R_{r}}(m\left| {{H_{1}}} \right.)} =\!{ \cfrac{{SCR_{r} \cdot {R_{s,r}}(m)}}{{(1 + SCR_{r})}}} + \!{\cfrac{{{R_{c,r}}(m)}}{{(1 + SCR_{r})}}}, $$
(9)

where \({R_{s,r}}(m) = {{\sum \limits _{n = 1}^{N - m} {s_{r}^{*}(n + m){s_{r}}(n)}} / {\sum \limits _{n = 1}^{N} {{{\left | {{s_{r}}(n)} \right |}^{2}}} }}\) is the complex autocorrelation function of the target returns. The targets used in the experiment have good rigid construction (targets are ships), and we detect those targets at considerable distances; therefore, it is an acceptable assumption that all scatterers of the target keep comparable radial velocity at each time instant. Thus, their Doppler offsets are approximately equal and denoted as f r . According to Eq. (3), the autocorrelation function of the target returns can then be approximated as

$$\begin{array}{*{20}l} \begin{aligned} {R_{s,r}}(m) & \approx \frac{{\left[ {\sum\limits_{n = 1}^{N - m} {{{\left({\sum\limits_{p = 1}^{{P_{r}}} {{a_{r,p}}}} \right)}^{*}}\left({\sum\limits_{p = 1}^{{P_{r}}} {{a_{r,p}}}} \right)}} \right]{e^{j2\pi m{f_{r}}T}}}}{{N{{\left({\sum\limits_{p = 1}^{{P_{r}}} {{a_{r,p}}}} \right)}^{*}}\left({\sum\limits_{p = 1}^{{P_{r}}} {{a_{r,p}}}} \right)}} \\ &\,=\,\cfrac{{(N - m){e^{j2\pi m{f_{r}}T}}}}{N}. \end{aligned} \end{array} $$
(10)

Equations (9) and (10) clearly show that when the target exists and SCR is not low, the temporal autocorrelation function of the received signal no longer decreases more rapidly. Thus, the coherent signals z r ,r=1,…,L under H1 hypothesis have longer temporal decorrelation time.

We give an example to illustrate the disparity of the temporal autocorrelation functions of the sea clutter and target by analyzing the recorded datasets. The datasets are collected by the Ka-band coherent radar at the staring mode with the pulse repetition frequency of 1000 Hz; this radar system transmits a train of chirp pulses. The signal bandwidth is 100 MHz, and the grazing angle is 10° during the time when the sea clutter data are collected. The specification of the high-resolution sea clutter is shown in Table 1.

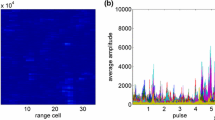
Table 1 The specification of the high-resolution sea clutter
Full size table

Figure 1 shows the amplitude-range-pulse maps of the recorded data samples for the clutter and two range distributed targets. The clutter dataset consists of 900 range cells, and the number of time samples in each range cell is 63500 (equal to a recorded duration of 63.5 s). For two target datasets, the number of time samples in each range cell is 512 (equal to a recorded duration of 0.512 s). The number of range cells is 160 for target 1 and 250 for target 2. Figure 1a clearly shows the periodic variation of the clutter amplitude with range and time due to the sea wave pattern. This heterogeneity of sea clutter may result in a rapid decline of the detection performance for the homogenous sea clutter hypothesis- based detector. In Fig. 1b and c, the data are collected in the high SCR case. The target 1 mainly locates in the 35th to 155th range cells, and the target 2 mainly locates in the 61st to 210th range cells. It is apparent that the amplitudes of the received target returns are also spatially heterogeneous. The powers of both two range distributed targets are concentrated in several range cells. Moreover, in those range cells, the amplitudes of the target returns are expected to appear as a long horizontal time-coherent line.

Fig. 1
figure 1

Amplitude-range-pulse maps of the recorded data samples: a Sea clutter. b target 1. c target 2

Full size image

For each range cell, all pulse samples are divided into 496 nonoverlapping groups for the clutter and 4 nonoverlapping groups for the range distributed targets; thus, each group contains 128 successive pulse samples. According to Eq. (5), the temporal autocorrelation function of each group is estimated. Figure 2 exhibits the examples of the estimated correlation function. As expected, there are very evident differences of the temporal autocorrelation functions between the clutter and targets. In all range cells, the temporal autocorrelation function of the clutter rapidly decreases at first, and then, it slowly decays. Conversely, in the strong scattering range cells, the decline of the temporal autocorrelation function of targets is slow. Especially, in Fig. 2b, the decline of target 1 can be approximated as a linear function of the lag number m, which agrees well with Eq. (10).

Fig. 2
figure 2

Autocorrelation function of the recorded data samples: a Sea clutter. b target 1. c target 2

Full size image

The correlation time is usually defined as the interval in which the correlation coefficient decays from the maximum 1 to 1/e=0.368. However, the correlation coefficients for most range cells are impossible to just be 1/e=0.368 due to the pulse sampling. Herein, the correlation time is extended to refer as the smallest lag number of which corresponding correlation coefficient is less than 1/e=0.368. It is denoted as m r . Figure 3 shows the statistical results of the correlation times for the sea clutter and targets. It can be seen from the results that the differences of the correlation times between the sea clutter and targets are distinguishable just by inspection. The correlation time of the sea clutter is smaller than that of the targets statistically. However, there are only a few discrete samples of the correlation time for sea clutter. In this case, it is very difficult to guarantee the constant false alarm rate (CFAR) property of the detector. To overcome this major obstacle, the decreasing rate of the correlation time is used. It is defined as

$$ {\gamma_{r}} = \cfrac{{{m_{r}}}}{{1 - {R_{r}}({m_{r}})}}, $$
(11)
Fig. 3
figure 3

Statistical results of the correlation time for the sea clutter and targets

Full size image

where R r (m r ) is the autocorrelation coefficient at the correlation time m r for the rth range cell. The relationship between autocorrelation function and power spectrum of the sea clutter is proved to hold as a Fourier transform pair. The correlation time can also be defined by the 3-dB bandwidth of power spectrum f3dB related to the time delay of the correlation function, and the correlation time is anticorrelated with f3dB [33]. Thus, the wider the f3dB is, the shorter the correlation time of sea clutter is, and the less decreasing rate can be obtain.

Figure 4 shows the statistical results of the decreasing rate of the correlation time for the sea clutter and targets. As analysed earlier, the targets have long correlation time, but the correlation time of sea clutter is short. Consequently, it can be clearly seen from these results that the decreasing rate of the correlation time for sea clutter tends to have a smaller range than those of the targets statistically. Furthermore, the more various samples of this correlation feature can be obtained for sea clutter. We can first obtain the R r (m) from Eq. (5) and then use the Eq. (11) to obtain the correlation property; the calculation cost of the rth range cell is only (m r +1)(N−m r /2). For the different range cells, the computational cost changes with the correlation times. According to Fig. 3, we can say that the computational cost of our detector is less than the detector based on the consistency factor [34]. Thus, γ r is considered to be one of the most effective features for target detection.

Fig. 4
figure 4

Statistical results of the decreasing rate of the correlation time for the sea clutter and targets

Full size image

2.3 Correlation feature-based detector

Since the binary integration detector is easy to implement, it is widely applied to detect the range distributed target as a quasi-optimum integration CFAR detection scheme. In terms of the differences of the correlation characteristics between the sea clutter and the range distributed target, a correlation feature-based detector is developed for the detection of range distributed target in sea clutter. This detector can be regarded as a modified binary integration detector. Succinctly, it is comprised of an initial binary detector on each individual range cell for a set of consecutive pulses (within a coherent processing interval) and a followed binary accumulator across range to extract targets with sufficient range extent. Figure 5 illustrates the overall operation of the proposed detection algorithm.

Fig. 5
figure 5

Flowchart of correlation feature-based detector

Full size image

Following the experimental results in Fig. 4, we naturally exploit the decreasing rate of the correlation time of the received signal as the detection feature to implement the binary detector. For each individual range cell under test, we use Eq. (5) to estimate the autocorrelation function of the received signal, and then use Eq. (11) to obtain the decreasing rate of correlation time. The decreasing rate of correlation time for the rth range cell is denoted as γ r . Thus, the detection rule of the binary detector for each individual range cell can be usually set as

$$ \left[ {{\gamma_{r}} \begin{array}{*{20}{c}} \ge \\ < \end{array}{\eta_{1}}} \right] \mapsto d_{r}^{(1)},r = 1, \ldots,L, $$
(12)

where η1 is the detection threshold of the binary detector. The detector outputs \(d_{r}^{(1)}\mathrm {s}\) with the decreasing rate of the correlation time γ r surpassing the detector threshold η1 are set to 1 while all others are set to 0. After accomplishing the binary detection for all range cells under test, these outputs of the binary detector, \(d_{r}^{(1)}\mathrm {s}\), are inputted into the binary accumulator. Then, the hypothesis that a range distributed target is present is tested as follows

$$ \left[ {P = \sum\limits_{r = 1}^{L} {d_{r}^{(1)}} \begin{array}{*{20}{c}} \ge \\ < \end{array}M} \right] \mapsto {d^{(2)}}, $$
(13)

where M is the second detection threshold. If P≥M, d(2)=1, this indicates the presence of a range distributed target in sea clutter; otherwise d(2)=0, this indicates only the presence of sea clutter.

To guarantee the CFAR property of the proposed detector and achieve a good detection performance, the strategies of η1 and M selections need to be derived. In [38], the sparse factor α is defined as h e /A, where h e is the number of range cells occupied by the strong scatterers of the range distributed target and A is the total number of scattering centers. The overall false alarm probability of the binary integration detector is set as 10−6, the total detection probability is set as 90%, and the optimal number of the range resolution cell (Nopt) equals to A. By calculating the optimal selection of M (Mopt) under different values of α, then using the linear fit to find the relationship between Mopt, Nopt, and α, the authors of [38] finally obtain the empirical equation as

$$ {M_{\text{opt}}} \approx \text{ceil}\left[{0.55\alpha{N_{\text{opt}}}}\right]=\text{ceil}\left[ {0.55{h_{e}}} \right], $$
(14)

where \(\text {ceil}\left [ x \right ]\) denotes the nearest integer which is greater than or equal to x. Thus, the Mopt is determined only by the number of strong scatterers of the range distributed target.

Generally, h e is unknown and varies with time for a range distributed target. To solve this shortcoming, a method based on modified entropy is used to adaptively estimate the value of h e [39]. The estimations of the decreasing rate of the correlation time, \(\left \{ {{\gamma _{r}}|r = 1, \cdots,L} \right \}\), are sorted by the decreasing value, and the sorted estimations are denoted as \(\left \{ {{\gamma _{(r)}}|r = 1, \cdots,L} \right \}\). It is assumed that the number of range cells occupied by the target strong scatterers is h. The sorted estimations can then be divided into two sub-sequences \(\left \{ {{\gamma _{(1)}}, \cdots,{\gamma _{(h)}}} \right \}\) and \(\left \{ {{\gamma _{(h + 1)}}, \cdots,{\gamma _{(L)}}} \right \}\), and these two sub-sequences are respectively normalized as

$$ \left\{ \begin{array}{l} {e_{i}} = \cfrac{{\left| {{\gamma_{(i)}}} \right|}}{{\sum\limits_{r = 1}^{h} {\left| {{\gamma_{(r)}}} \right|} }},i = 1, \cdots,h,\\ {g_{i}} = \cfrac{{\left| {{\gamma_{(i)}}} \right|}}{{\sum\limits_{r = h + 1}^{L} {\left| {{\gamma_{(r)}}} \right|} }},i = h + 1, \cdots,L. \end{array} \right. $$
(15)

Thus, the modified entropy of the normalized estimations for the hypotheses number h can be calculated by the following formula

$$ H(h) = \left\{ \begin{array}{l} \cfrac{1}{L} - \cfrac{{L - 1}}{{L\lg \left({L - 1} \right)}}\sum\limits_{j = 2}^{L} {{g_{j}}} \lg \left({{g_{j}}} \right),h = 1,\\ - \cfrac{{L - 1}}{{L\lg \left(h \right)}}\sum\limits_{j = 1}^{h} {{e_{j}}\lg \left({{e_{j}}} \right)} + \cfrac{1}{L},h = L - 1,\\ - \cfrac{1}{{\lg \left(h \right)}}\sum\limits_{j = 1}^{L} {{e_{j}}\lg \left({{e_{j}}} \right)},h = L,\\ - \cfrac{h}{{L\lg \left(h \right)}}\sum\limits_{j = 1}^{h} {{e_{j,n}}\lg \left({{e_{j}}} \right)} - B, \text{others}. \end{array} \right. $$
(16)

where \(B = \cfrac {{L - h}}{{L\lg \left ({L - h} \right)}}\sum \limits _{j = h + 1}^{L} {{g_{j}}} \lg \left ({{g_{j}}} \right)\). Equation (16) shows that for different values of h, the modified entropy has different values. The number of range cells occupied by the strong scatterers of the range distributed target can be searched by

$$ {h_{e}} = \mathop {\arg \max }\limits_{h} H(h),h = 1, \cdots,L. $$
(17)

Then, the optimal selection of M can be determined by Eq. (14).

The overall false alarm probability of the binary integration detector, P fa , can be expressed as

$$ {P_{fa}} = \sum\limits_{m = M}^{L} {C_{L}^{m}{{\left({{P_{fa1}}} \right)}^{m}}{{\left({1 - {P_{fa1}}} \right)}^{L - m}}}, $$
(18)

where Pfa1 is false alarm probability of the binary detector. \(C_{L}^{m}\) is the number of combinations of L items taken m at a time. When P fa is given and M is obtained, Pfa1 can be calculated by Eq. (18). The analytical formula for the test statistic in Eq. (12) can be not deduced.

In our proposed detector, P fa is set as a constant value. Because the first order of detector has no analytic expression, we cannot obtain the accurate value of the first detection threshold η1 by calculation, but it can be obtained by the widely used Monte-Carlo tests on the pure clutter for the false alarm probability Pfa1. Also, due to the pulse sampling, the correlation time of return fluctuate extracted from sea clutter are discrete values. We define the γ r in order to increase the number of samples; however, the Monte-Carlo tests only provide the “discrete-approximate” value. As a result, there can appear some difference between the P fa obtained from the detector and the P fa which we set at the very beginning. Therefore, we provide the numerical simulation results of comparison between actual P fa obtained from the detector and given P fa .

Figure 6 shows that the actual P fa has some difference with our given P fa , but those small errors are acceptable; therefore, it is assumptive that our proposed detection approach has CFAR-ity.

Fig. 6
figure 6

Comparison between actual P fa and given P fa , a L=1,M=1; b L=10,M=5; c L=100,M=5; d L=100,M=20; e L=100,M=40

Full size image

3 Results and discussion

In this section, the effectiveness of the proposed detector is evaluated by the experiment results with the measured radar data.

We put the clutter returns with the same number of range cells into the target returns. The amplitudes of the target returns are adjusted according to the different signal-to-clutter ratio (SCR). The SCR is defined as

$$ SCR = 10{\log_{10}}\left({{{{\sum\nolimits}_{r = 1}^{L} {{S_{r}}}} / {{\sum\nolimits}_{r = 1}^{L} {{C_{r}}} }}} \right), $$
(19)

where S r and C r are the average powers of the target and clutter in the rth range cell, respectively. L is the number of the range cells occupied by the target. According to the above results, L is set to 130 for target 1 and 150 for target 2. In simulation, due to the short observation time, the length of collected data only allow us to set the number of Monte Carlos as 200; therefore, the P fa is set to be 0.01, but it is enough for us to verify wether our detector is useful or not.

3.1 Detection performance of proposed detector under different values of M

As an extension of the binary integration detector, the proposed detector will exhibit different detection performances when the second detection threshold M has different values. The results of this experiment are shown in Fig. 7. Here, the 128 successive pulses are used, which correspond to a test with 0.128 observation time. We consider two main cases for the value of M: the constant value case and the adaptive estimation case. For the constant value case, the values of M are set to 3, 5, 22, and 44. It is worth pointing out that in adaptive estimation case, the detection threshold of the binary detector, η1, is obtained by the online Monte-Carlo tests due to the online estimation of M. This results in an increase in the computational complexity of the proposed detector. Nevertheless, according to the simulation results, the detection performance of the proposed detector with the adaptive estimation of M is superior to those with the constant values of M for both two targets. This demonstrates that even if there is no any prior knowledge of target’s scatterers, the proposed detector can effectively improve its performance and robustness by using the radar observations to adaptively estimate the number of strong scatterers of targets. In addition, in the constant value case of M, the proposed detector is optimized when M=5, and its detection performance is even close to that in the adaptive estimation case of M. Therefore, when the prior knowledge of strong scatterers of target is known, we can use this prior knowledge to obtain η1 by the offline Monte-Carlo tests. This not only maintains the suboptimum performance of the proposed detector but also reduces its computational complexity.

Fig. 7
figure 7

Detection performance of proposed detector with different second detection thresholds. a target 1. b target 2

Full size image

3.2 Comparison of detection performance between proposed detector and prior arts

In the following experiment, the detection performance of the proposed detector is compared with the fractal-based detector [29] and the feature-based detector [34]. Herein, both the fractal-based detector and the feature-based detector firstly operate on each individual range cell returns to obtain the binary outputs, and then the binary accumulator operates on those binary-detected outputs to determinate the presence of a target. The 128 successive pulses are used. For the feature-based detector, the time samples of each range cell are reshaped into 64 consecutive vectors and each vector has 2 elements. The corresponding average time interval is \(\left [17, 48\right ]\). For three detectors, their first-stage detection thresholds are designed by the Monte Carlo tests to the pure clutter, and their second-stage decision thresholds are both set to a same value (i.e., M=5 for both two targets). Figure 8 presents the detection probabilities of the three detectors. It can be seen that the proposed detector significantly outperforms the compared ones in detection performance for both two targets. Due to the short observation time, the correlation feature between sea clutter and the target is not quite obvious; therefore, the fractal-based detector in [29] suffer from a sharp degradation in the detection performance. The feature-based detector proposed in [34] ignores the nonstationary properties of sea clutter and uses only 128 successive pulses. Comparing with both detectors in [29, 34], the significant improvement in detection performance provided by the proposed detector demonstrates that the proposed detector is more effective to eliminate the effect of the nonstationary texture by using the correlation feature. Therefore, it can be concluded that the significant difference in correlation features between the pure clutter and that with target is helpful for the target detection.

Fig. 8
figure 8

Performance comparison of three detectors for target 1 and target 2. a target 1; b target 2

Full size image

3.3 Detection performance of proposed detector under different numbers of integrated pulses

In the experiment below, the evaluation of the detection performance of the proposed detector with different numbers of integrated pulses is demonstrated. Figure 9 shows the detection performance of two targets for N=32, 64, 128, 256, and 512. It is shown in Fig. 9 that the detection performance of the proposed detector tends to have an improvement as N increases. However, as shown in Fig. 1a and b, for the targets in realistic sea environment, the amplitudes of their returns fluctuate with time so that their correlation times are limited. On the other hand, during a long coherent processing interval, the range migration of target returns can not be ignored and the echo energy from the same target scatterers may be dispersed within different range cells. Therefore, for target 1, the detection performance of the proposed detector for N=128 is very close to that for N=256 and is superior to that for N=512. For target 2, the performance improvement gain is not notable by doubling integrated pulses when N>256. The results for the case N=512 are also different between Fig. 9a and b. Precisely, Fig. 9 shows that N=512 has the best P d when SNR is low, while Fig. 9a highlights that N=512 is less than N=128 and 256. On the one hand, we assume that the return fluctuate which comes from the same scattering unit of the target locates in the same range cell of the coherent processing interval. While verifying our proposed method by simulation, we choose the actual data of return fluctuate from two different targets, the two targets have different moving speed (both targets is moving slowly during the experiment). For the second target, the return fluctuate which comes from the same scattering unit of the target locates in the same range cell through the whole coherent processing interval ; therefore, with the increasing coherent processing time, the correlation feature becomes stronger, the performance about the detector becomes better. But for the first target, when \(N\geqslant 256\), the return fluctuate is dispersed in different rang cells (shown in Fig. 1b); in this situation, with the increasing coherent processing time, the correlation feature will decrease and that can lead to the decrease of detection performance.

Fig. 9
figure 9

Detection performance of proposed detector for N=32,64,128,256, and 512. a target 1. b target 2

Full size image

3.4 Comparison of computational cost between proposed detector and prior arts

In applications, the computational cost of a detector must be considered. It is measured by the number of multiplications/divisions of the detector. Here, we mainly discuss the computational costs for the proposed detector, the fractal-based detector [29], and the feature-based detector [34]. When these three detectors are applied in the above experiments, the only difference among them is the implementation method of the binary detector. Therefore, the main concern is the computational cost to calculate the feature in each detector. As stated in [34], for each range cell, the cost of the fractal-based detector is \((N + 4)\left ({{{\log }_{2}}N - 4} \right)\) due to the calculation of the Hurst exponent, and that of the feature-based detector is approximate to 0.5N2 due to the calculation of the consistency factor. We assume that m r is the correlation time of the received signals in the rth range cell. In the practical applications of the proposed detector, in view of the definition of the decreasing rate of the correlation time, the correlation coefficients are computed by Eq. (5) only for m=0,…,m r and the correlation feature can then be calculated by Eq. (11). Consequently, in the proposed detector, the computational cost for the rth range cell is \(({m_{r}} + 1)\left ({N - {{{m_{r}}} / 2}} \right)\). For different range cells, the costs vary with the changing correlation time. The shorter the correlation time is, the lower are the computational cost. According to the statistical results of the correlation time shown in Fig. 3, it is possible to conclude that the proposed detector has the lower computational cost than the feature-based detector does.

Summarizing all above considerations, it is implied that the correlation-based detector here remains a good choice for detecting the range distributed targets in sea clutter.

4 Conclusions

In this paper, we deal with the problem of detecting the range-distributed target embedded in sea clutter. To this end, the correlation characteristic of the received signals is considered and the decreasing rate of the correlation time is defined as a correlation feature to describe them. By analyzing the real radar data, the disparity of these correlation features of the target and sea clutter is illustrated clearly. Therefore, it is natural to design a novel detector based on these correlation features for the detection of the range-distributed target in sea clutter. This detector can be regarded as an extension of the binary integration detector. It is worth mentioning that by using the correlation feature, the proposed detector can effectively eliminate the negative effect of the nonstationary texture on the detection performance. Furthermore, in the detector, the number of target’s scatterers is adaptively estimated by using the modified entropy of the correlation feature, so the proposed detector is able to work well without any prior knowledge of the target’s scattering density. In comparison with the existing detectors including the fractal-based detector and the feature-based detector, the proposed detector exhibits the superiority in detection performance, which is verified by the record radar data. Moreover, the proposed detector has lower computational complexity than the feature-based detector does.

As a final remark, we highlight that possible future research tracks might include the possibility to account for oversampled data at the receiver side to improve detection performance for partially homogeneous environments [40, 41].