Additive-multiplicative hazards regression models for interval-censored semi-competing risks data with missing intermediate events

Abstract

Background

In clinical trials and survival analysis, participants may be excluded from the study due to withdrawal, which is often referred to as lost-to-follow-up (LTF). It is natural to argue that a disease would be censored due to death; however, when an LTF is present it is not guaranteed that the disease has been censored. This makes it important to consider both cases; the disease is censored or not censored. We also note that the illness process can be censored by LTF. We will consider a multi-state model in which LTF is not regarded as censoring but as a non-fatal event.

Methods

We propose a multi-state model for analyzing semi-competing risks data with interval-censored or missing intermediate events. More precisely, we employ the additive and multiplicative hazards model with log-normal frailty and construct the conditional likelihood to estimate the transition intensities among states in the multi-state model. Marginalization of the full likelihood is accomplished using adaptive importance sampling, and the optimal solution of the regression parameters is achieved through the iterative quasi-Newton algorithm.

Results

Simulation is performed to investigate the finite-sample performance of the proposed estimation method in terms of the relative bias and coverage probability of the regression parameters. The proposed estimators turned out to be robust to misspecifications of the frailty distribution. PAQUID data have been analyzed and yielded somewhat prominent results.

Conclusions

We propose a multi-state model for semi-competing risks data for which there exists information on fatal events, but information on non-fatal events may not be available due to lost to follow-up. Simulation results show that the coverage probabilities of the regression parameters are close to a nominal level of 0.95 in most cases. Regarding the analysis of real data, the risk of transition from a healthy state to dementia is higher for women; however, the risk of death after being diagnosed with dementia is higher for men.

Background

In classical time-to-event or survival analysis, subjects are under risk for one fatal event. However, subjects do not fail from just one certain type of event in some applications, but are under risk of failing from two or more mutually exclusive types of events. When an individual is under risk of failing from two different types of event, these different event types are called competing risks. One of the events censors the other, and vice versa, in these competing risks frameworks [1–3]. However, many clinical trials have revealed that a subject can experience both a non-fatal event (e.g., a disease or relapse) and a fatal event (e.g., death), where the fatal event censors the non-fatal event but not vice versa. We call these types of data semi-competing risks data [4–6].

In clinical trials, the occurrence of a non-fatal event can be detected in conjunction with possibly incessant monitoring during periodic follow-up. For illustration purposes of our methodologies, a dataset named PAQUID (Personnes Agées Quid) is analyzed to investigate the meaningful prognostic factors associated with dementia. These data were initially analyzed by [7] using the conventional Cox model [8, 9]. Complete descriptions of the PAQUID data can be found in Conclusions section. In this paper, we employ a semi-competing risks model where death may occur after dementia has occurred (i.e., been diagnosed), but death censors the disease. An illness-death model [10] is perhaps one of the most commonly and frequently used semi-competing risks models. Many studies have been conducted under semi-competing risks frameworks [4, 5, 11].

As shown in the PAQUID data, dementia can be censored informatively by death. Furthermore, an additional informative censoring process can also occur. That is, participants may be excluded from the study due to withdrawal, which is often referred to as lost-to-follow-up (LTF). It is clear that dementia would be censored due to death; however, when an LTF is present it is not guaranteed that dementia has been censored. This makes it important to consider both cases; dementia is censored or not censored. We also note that the illness process (dementia) can be censored by LTF. This forces us to consider a multi-state model in which LTF is not regarded as censoring but as a non-fatal event. Considerable studies have utilized this multi-state model. For example, [12] proposed a nonparametric method to estimate the survival function associated with disease occurrences, while [6, 13] used the Cox proportional hazards model [8, 9] to estimate regression coefficients.

In the meantime, most non-fatal events are observed periodically. That is, the event time is not observed exactly but lies on an interval of the form (L,R], where L is the last time a subject visited without possessing a disease and R is the first time that the subject was diagnosed with a disease. This type of censoring is called interval censoring. We could emulate what [6] did and assume that a non-fatal event of a subject occurs uniformly on the interval (L,R]. However, using the methods proposed by [14, 15], we instead partition the interval (L,R] into a few sub-intervals, in which a non-fatal event can occur. Ultimately, different weights can be assigned to each sub-interval. Thus, the former method corresponds to an unconditional probability approach with equal weight on all of the sub-intervals, whereas the latter utilizes a conditional probability approach with a specific weight, depending on the sub-interval.

In our study, we use the latter method to deal with non-fatal events that are interval-censored on an interval. In addition, we propose an additive-multiplicative model by combining the Cox proportional hazards model with the additive risk model of [16], in accordance with a multi-state model. The additive-multiplicative model was initially introduced by [17] and has since been developed by a number of researchers. Scheike and Zhang [19] incorporated time-varying covariates for the additive part and time-independent covariates for the multiplicative part. On the other hand, [18] estimated relevant parameters by considering time-varying covariates for both additive and multiplicative parts. We also consider the frailty effect as a latent variable to incorporate possible connections between events; this is done because each individual is exposed to several events, including the occurrence of illness, LTF, and death.

The rest of the paper is organized as follows. First, we explain notations and procedures for parameter estimation along with the proposed models. Second, extensive simulation studies are presented to investigate the model performances in terms of the relative bias and coverage probability of the proposed estimates. We also provide the results of real data analysis. Finally, we present a summary and concluding remarks, including some of the drawbacks of the proposed models and directions for future research.

Methods

Models

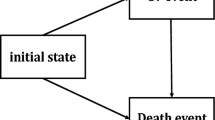
As depicted in Fig. 1, the proposed model in this study consists of five states: healthy (H), non-fatal (NF), fatal (F), lost-to-follow-up (LTF), and unobserved non-fatal (NF(LTF)). Each state is denoted by numbers 0 through 4, respectively. A total of seven possible transitions exists in the model: 0→1, 0→2, 0→3, 1→2, 3→2, 3→4, and 4→2. However, among these transitions, both 3→4 and 4→2 (displayed as dotted lines in Fig. 1 are unobservable and should be regarded as potential transitions.

Fig. 1

Five-state model

Let t be the time from study entry. Additionally, S_t is defined as the state that each subject can take at t≥0. Then, S_t∈{0,1,2,3,4}. Let $\mathcal {A}=\{(r,s):(r,s)=(0,1), (0,2), (0,3), (1,2), (3,2), (3,4), (4,2)\}$. Also, define λ_rs(t) to be the transition intensity from states r to s at time t. That is,

$$\begin{array}{@{}rcl@{}} \lambda_{rs}(t)={\lim}_{dt\rightarrow0}\frac{\Pr(S_{t+dt}=s|S_{t}=r)}{dt}\ \ \text{for }\ \ (r,s)\in\mathcal{A}, \end{array} $$

and λ_rs(t)=0 for $(r,s)\notin \mathcal {A}$. As mentioned above, the data corresponding to transitions 3→4 and 4→2 are not observable, requiring the following assumptions for λ₃₄(t) and λ₄₂(t):

$$\begin{array}{*{20}l} \lambda_{34}(t) &=& \lambda_{01}(t), \ t\ge0, \end{array} $$

(1)

$$\begin{array}{*{20}l} \lambda_{42}(t) &=& \lambda_{12}(t),\ t\ge0. \end{array} $$

(2)

Assumptions (1) and (2) imply that the transition intensities of H to NF and NF to F may be the same, irrespective of the occurrence of LTF. As mentioned in Background section, given covariates z=(z₁,z₂,…,z_p)^′ and w=(w₁,w₂,…,w_d)^′, along with frailty u, we consider additive and multiplicative models defined as

$$ {\begin{aligned} \lambda_{rs}(t|{\boldsymbol{z}},{\boldsymbol{w}},u)=\eta \left({\boldsymbol{\beta}}_{rs}^{\prime}{\boldsymbol{z}} + \exp \left({\boldsymbol{\alpha}}_{rs}^{\prime}{\boldsymbol{w}}\right)\theta_{rs}\gamma_{rs}t^{\gamma_{rs} - 1}\right)\ \ \text{for }\ \ (r,s)\in\mathcal{A}, \end{aligned}} $$

(3)

where θ_rs(>0) and γ_rs(>0) are the scale and shape parameters of a Weibull distribution, respectively, and β_rs and α_rs are vectors of the regression coefficients for the additive and multiplicative parts, respectively. Moreover, η= exp(u) is the frailty for a log-normal distribution and u is assumed to follow a normal distribution with a mean of zero and variance σ². Thus, we use a Weibull distribution as a baseline transition intensity and impose a multiplicative frailty effect on the transition intensities. Since the parameters θ₃₄,θ₄₂,γ₃₄,γ₄₂,α₃₄,α₄₂,β₃₄, and β₄₂ related to transitions 3→4 and 4→2 should satisfy the assumptions in (1) and (2), the parameter vector estimated for the model in (3) is ζ=(θ^∗,γ^∗,α^∗,β^∗,σ²)^′, where θ^∗=(θ₀₁,θ₀₂,θ₀₃,θ₁₂,θ₃₂), γ^∗=(γ₀₁,γ₀₂,γ₀₃,γ₁₂,γ₃₂), ${\boldsymbol {\alpha }}^{*} =\left ({\boldsymbol {\alpha }}_{01}^{\prime }, {\boldsymbol {\alpha }}_{02}^{\prime }, {\boldsymbol {\alpha }}_{03}^{\prime }, {\boldsymbol {\alpha }}_{12}^{\prime }, {\boldsymbol {\alpha }}_{32}^{\prime }\right)$, and ${\boldsymbol {\beta }}^{*} = \left ({\boldsymbol {\beta }}_{01}^{\prime }, {\boldsymbol {\beta }}_{02}^{\prime }, {\boldsymbol {\beta }}_{03}^{\prime }, {\boldsymbol {\beta }}_{12}^{\prime }, {\boldsymbol {\beta }}_{32}^{\prime }\right)$. According to the model in (3), the cumulative hazard functions H_k(t₁,t₂) (k=0,1,3,4) for leaving state k between t₁ and t₂ can be represented as

$$\begin{array}{@{}rcl@{}} H_{0}(t_{1},t_{2}|{\boldsymbol{z}},{\boldsymbol{w}},u) &=& \int_{t_{1}}^{t_{2}}\{ \lambda_{01}(s|{\boldsymbol{z}},{\boldsymbol{w}},u) + \lambda_{02}(s|{\boldsymbol{z}},{\boldsymbol{w}},u) + \lambda_{03}(s|{\boldsymbol{z}},{\boldsymbol{w}},u)\} ds\\ &=& \sum_{r=1}^{3} \eta\left\{ \left({\boldsymbol{\beta}}_{0r}^{\prime}{\boldsymbol{z}}\right)(t_{2} - t_{1}) + \exp \left({\boldsymbol{\alpha}}_{0r}^{\prime}{\boldsymbol{w}}\right)\theta_{0r}\left(t_{2}^{\gamma_{0r}} - t_{1}^{\gamma_{0r}}\right)\right\}\!,\\ H_{1}(t_{1},t_{2}|{\boldsymbol{z}},{\boldsymbol{w}},u) &=& \int_{t_{1}}^{t_{2}} \lambda_{12}(s|{\boldsymbol{z}},{\boldsymbol{w}},u) ds\\ &=& \eta\left\{ \left({\boldsymbol{\beta}}_{12}^{\prime}{\boldsymbol{z}}\right)(t_{2} - t_{1}) + \exp \left({\boldsymbol{\alpha}}_{12}^{\prime}{\boldsymbol{w}}\right)\theta_{12}\left(t_{2}^{\gamma_{12}} - t_{1}^{\gamma_{12}}\right)\right\}, \end{array} $$

$$ \begin{aligned} H_{3}(t_{1},t_{2}|{\boldsymbol{z}},{\boldsymbol{w}},u) &= \int_{t_{1}}^{t_{2}}\{\lambda_{32}(s|{\boldsymbol{z}},{\boldsymbol{w}},u) + \lambda_{34}(s|{\boldsymbol{z}},{\boldsymbol{w}},u) \}ds \\ &= \eta\big\{ \left({\boldsymbol{\beta}}_{32}^{\prime}{\boldsymbol{z}}\right)(t_{2} - t_{1}) + \exp \left({\boldsymbol{\alpha}}_{32}^{\prime}{\boldsymbol{w}}\right)\theta_{32}\left(t_{2}^{\gamma_{32}} - t_{1}^{\gamma_{32}}\right) \\ &\quad+ \left({\boldsymbol{\beta}}_{34}^{\prime}{\boldsymbol{z}}\right)(t_{2} - t_{1}) + \exp \left({\boldsymbol{\alpha}}_{34}^{\prime}{\boldsymbol{w}}\right)\theta_{34}\left(t_{2}^{\gamma_{34}} - t_{1}^{\gamma_{34}}\right) \big\},\\ H_{4}(t_{1},t_{2}|{\boldsymbol{z}},{\boldsymbol{w}},u) &= \int_{t_{1}}^{t_{2}} \lambda_{42}(s|{\boldsymbol{z}},{\boldsymbol{w}},u) ds\\ &= \eta\left\{ \left({\boldsymbol{\beta}}_{42}^{\prime}{\boldsymbol{z}}\right)(t_{2} - t_{1}) + \exp \left({\boldsymbol{\alpha}}_{42}^{\prime}{\boldsymbol{w}}\right)\theta_{42}\left(t_{2}^{\gamma_{42}} - t_{1}^{\gamma_{42}}\right)\right\}. \end{aligned} $$

Based on Assumptions (1) and (2), we note that β₃₄=β₀₁, β₄₂=β₁₂, α₃₄=α₀₁, α₄₂=α₁₂, θ₃₄=θ₀₁, θ₄₂=θ₁₂, γ₃₄=γ₀₁, and γ₄₂=γ₁₂ in the equations of H₃ and H₄.

Parameter estimation

As shown in Fig. 1, a total of six routes can be experienced by a subject from the beginning to the end of the study. These are route 1 (0 → 0), route 2 (0 → 2), route 3 (0 → 1), route 4 (0 → 1 → 2), route 5 (0 → 3), and route 6 (0 → 3 → 2). In particular, route 5 can be classified into two paths, i.e., 0 → 3 and 0 → 3 → 4, depending on whether or not a subject experiences the unobservable NF state. Similarly, route 6 can be classified into two paths: 0 → 3 → 2 and 0 → 3 → 4 → 2. We introduce notations to define the likelihood associated with each route. Consider three random variables R, L, and T, each of which represents a time from the start of the study until the occurrence of a non-fatal event, LTF, and a fatal event, respectively. Furthermore, let $\mathcal {H}_{0}(s)$ be the set of subjects staying in state 0 at time s. That is,

$$\begin{array}{@{}rcl@{}} \mathcal{H}_{0}(s)=\{R\wedge L\wedge T>s\}. \end{array} $$

Let $\mathcal {H}_{3,f}(s)$ be the set of subjects who have already experienced LTF at time f and remain in state 3 at time s. Then,

$$\begin{array}{@{}rcl@{}} \mathcal{H}_{3,f}(s)=\{L=f,R\wedge T>s, f\le s\}. \end{array} $$

Now, let e_i be the entry time of study, a_i be the last time the i^th subject visited before a non-fatal event was observed, and b_i be the first time a non-fatal event is observed by the i^th subject for i=1,2,…,n. Consider an indicator function I_ij, which is 1 if subject i follows route j and zero otherwise for j=1,2,…,6. Let $\mathcal {B}_{j}=\{i:I_{ij}=1\}$. For subject $i\in \mathcal {B}_{1}\cup \mathcal {B}_{2}$, we have a_i,b_i≥t_i; this is the case because a non-fatal event has not been observed before time t_i. For subject $i\in \mathcal {B}_{3}\cup \mathcal {B}_{4}$, we have a_i<b_i≤t_i; this is the case because a non-fatal event has occurred between a_i and b_i. When subject i is a member of $\mathcal {B}_{5}\cup \mathcal {B}_{6}$, LTF has occurred at time a_i, which yields a_i<t_i; however, b_i<t_i or b_i≥t_i, depending on whether an unobservable non-fatal event has occurred. Thus, t_i would be a censoring time for $i\in \mathcal {B}_{1}\cup \mathcal {B}_{3}\cup \mathcal {B}_{5}$, whereas it would be a time of death for $i\in \mathcal {B}_{2}\cup \mathcal {B}_{4}\cup \mathcal {B}_{6}$. Therefore, likelihood functions Q₁ and Q₂ can be constructed for routes 1 and 2, respectively. These are given as follows:

$$\begin{array}{@{}rcl@{}} Q_{i1} &=& \Pr\left(R_{i}\wedge L_{i}\wedge T_{i}>t_{i}|\mathcal{H}_{0}(e_{i}),{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}\right) \\ &=& \exp\{-H_{0}(e_{i},t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\}, \ i\in\mathcal{B}_{1}. \end{array} $$

(4)

$$\begin{array}{@{}rcl@{}} Q_{i2} &=& \Pr(T=t_{i}, R\wedge L>t_{i}|\mathcal{H}_{0}(e_{i}),{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ &=& Q_{i1}\times\lambda_{02}(t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}),\ i\in\mathcal{B}_{2}. \end{array} $$

(5)

Likelihood functions can also be constructed for routes 3 and 4:

$$\begin{array}{@{}rcl@{}} Q_{i3}^{*} &=& \Pr(R_{i}\in(a_{i},b_{i}],L_{i}>t_{i},T_{i}>t_{i}|\mathcal{H}_{0}(e_{i}), {\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ &=&\int_{a_{i}}^{b_{i}}\bigg[\exp\{-H_{0}(e_{i},s|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\}\lambda_{01}(s|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\\ &&\quad\times\exp\{-H_{1}(s,t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\}\bigg]ds. \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} Q_{i4}^{*}&\!=& \Pr(R_{i}\!\in\!(a_{i},b_{i}],L_{i}\!>\!t_{i},R_{i}\!<T_{i}=t_{i}|\mathcal{H}_{0}(e_{i}), {\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ &\!=& Q_{i3}^{*}\times\lambda_{12}(t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}),\ i\in\mathcal{B}_{4}. \end{array} $$

(7)

Equations (6) and (7) are derived by assuming that a non-fatal event of subject i in the set $\mathcal {B}_{3}\cup \mathcal {B}_{4}$ can occur uniformly on the interval (a_i,b_i] [6]. However, we partition the interval (a_i,b_i] into several sub-intervals where non-fatal events could occur and assign different weights to each interval [15].

• Let $R_{i^{\prime }}\in (a_{i^{\prime }},b_{i^{\prime }}]$ be an interval for the occurrence of non-fatal events associated with subjects in routes 3 or 4. Let s₁ be the smallest value among all $b_{i^{\prime }}$’s for subjects in the set $\mathcal {B}_{3}\cup \mathcal {B}_{4}$. Let s₂ be the smallest value among all $b_{i^{\prime }}$’s corresponding to subjects having $a_{i^{\prime }}$ greater than or equal to s₁. This process is repeated until we have no subjects with $a_{i^{\prime }}$ greater than or equal to s_m (m=1,2,…). Thus, we can have a refined set of time points

  $$\begin{array}{@{}rcl@{}} 0=s_{0}< s_{1}< s_{2}<\cdots< s_{l}< s_{l+1}=\infty. \end{array} $$

• We can define the weight $w_{i^{\prime }m}$ at time s_m (m=1,2,…) for subject i^′ in the set $\mathcal {B}_{3}\cup \mathcal {B}_{4}:$

  $$ {\begin{aligned} w_{i^{\prime}m} = \frac{d_{i^{\prime}m}\exp\left\{-H_{0}\left(e_{i^{\prime}},s_{m}|{\boldsymbol{w}}_{i^{\prime}}, {\boldsymbol{z}}_{i^{\prime}}, u_{i^{\prime}}\right)\right\}\lambda_{01}(s_{m}|{\boldsymbol{w}}_{i^{\prime}}, {\boldsymbol{z}}_{i^{\prime}}, u_{i^{\prime}})}{\sum_{m^{\prime}=1}^{l} d_{i^{\prime}m^{\prime}}\exp\left\{-H_{0}(e_{i^{\prime}},s_{m^{\prime}}|{\boldsymbol{w}}_{i^{\prime}}, {\boldsymbol{z}}_{i^{\prime}}, u_{i^{\prime}})\right\}\lambda_{01}(s_{m^{\prime}}|{\boldsymbol{w}}_{i^{\prime}}, {\boldsymbol{z}}_{i^{\prime}}, u_{i^{\prime}})}, \end{aligned}} $$

  (8)

where $d_{i^{\prime }m} = I(s_{m}\in (a_{i^{\prime }},b_{i^{\prime }}])$. Subsequently, likelihood functions incorporated with weight $w_{i^{\prime }m}$ in (8) for routes 3 and 4 are given by

$$ {\begin{aligned} Q_{i3}=& \sum_{m=1}^{l}d_{im}w_{im}\exp\{-H_{0}(e_{i},s_{m}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\}\lambda_{01}(s_{m}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\\ & \times \exp\{-H_{1}(s_{m}, t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\},\ i\in\mathcal{B}_{3}. \end{aligned}} $$

(9)

$$\begin{array}{@{}rcl@{}} Q_{i4} = Q_{i3}\times\lambda_{12}(t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}),\ i\in\mathcal{B}_{4}. \end{array} $$

(10)

Finally, likelihood functions for routes 5 and 6 are given by

$$\begin{array}{@{}rcl@{}} Q_{i5}&=& \Pr(R_{i}\wedge T_{i}>t_{i}|\mathcal{H}_{3,a_{i}}(a_{i}),{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ &&+ \Pr(R_{i}\in(a_{i},t_{i}], T_{i}>t_{i}|\mathcal{H}_{3,a_{i}}(a_{i}),{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ &=& \exp\{-H_{0}(e_{i},a_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\}\lambda_{03}(a_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\\ &&\times \bigg[ \exp\{-H_{3}(a_{i},t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\} \\ &&+ \int_{a_{i}}^{t_{i}}\exp\{-H_{3}(a_{i},s|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\}\lambda_{34}(s|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ &&\times \exp\{-H_{4}(s,t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\} ds \bigg], \ i\in\mathcal{B}_{5}, \end{array} $$

(11)

$$ {\begin{aligned} Q_{i6}=&\Pr(R_{i}>T_{i},\ T_{i}=t_{i}|\ \mathcal{H}_{3,\ a_{i}}(a_{i}),{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ &+ \Pr(R_{i} \in(a_{i},\ t_{i}],\ R_{i}<T_{i}=t_{i}|\mathcal{H}_{3,a_{i}}(a_{i}),{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ =& \exp\{-H_{0}(e_{i},a_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\}\lambda_{03}(a_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\\ &\times\bigg [ \exp\{-H_{3}(a_{i},t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\} \lambda_{32}(t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\\ &+\bigg\{\int_{a_{i}}^{t_{i}}\exp\{-H_{3}(a_{i},s|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i})\}\lambda_{34}(s|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \\ &\times \exp\{-H_{4}(s,t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \} ds \bigg\} \lambda_{42}(t_{i}|{\boldsymbol{z}}_{i}, {\boldsymbol{w}}_{i}, u_{i}) \bigg],\ i\in\mathcal{B}_{6}. \end{aligned}} $$

(12)

Therefore, based on Eqs. (4)-(5) and (9)-(12), the likelihood function for the parameter vector ζ is

$$\begin{array}{@{}rcl@{}} L({\boldsymbol{\zeta}})=\prod_{i=1}^{n}\left\{\prod_{j=1}^{6}Q_{ij}^{I_{ij}}\right\} \phi\left(0,\sigma^{2};u_{i}\right), \end{array} $$

(13)

where ϕ(·) is the probability density function of a normal distribution with a mean of zero and variance σ². In our analysis, we use the NLMIXED procedure of the SAS software to estimate ζ. For the sake of parameter estimation procedures, we define the marginal likelihood as

$$\begin{array}{@{}rcl@{}} m({\boldsymbol{\zeta}})=\int\cdots\int L({\boldsymbol{\zeta}}){du}_{1}\cdots {du}_{n}. \end{array} $$

Then, we find the value of ζ that minimizes f(ζ)=− logm(ζ), which is referred to as $\hat {{\boldsymbol {\zeta }}}$. Consequently, the inverse of the Hessian matrix evaluated at $\hat {{\boldsymbol {\zeta }}}$ is defined as the estimated variance-covariance matrix of $\hat {{\boldsymbol {\zeta }}}$. Numerical integration is required for the frailty distribution. For this purpose, we use the adaptive importance sampling [20]. Finally, we employ quasi-Newton optimization, which utilizes the gradient vector and the Hessian matrix of f(ζ), to achieve the optimal solution of ζ.

Results

Simulation studies

Extensive simulation is performed to investigate the finite-sample properties of the estimators proposed in Methods section. As mentioned earlier, we assume a Weibull distribution with a shape parameter of γ_rs=1 as the baseline transition intensity and a log-normal distribution for frailty η= exp(u), where u is generated from a normal distribution with a mean of zero and a variance of 0.01. Furthermore, we use a binary covariate for z (generated from a Bernoulli trial with a success probability of 0.5) and a continuous covariate for w (generated from a standard normal distribution). We fix the sample size n at 200 and the censoring time C at 365. A total of 500 replications is used in our simulations. The following presents the details related to the generation of random variates for the i^th (i=1,2,…,n) subject.

• Step 0: We may allow the total number of occurrences for non-fatal events to be 24 times in a 12-month period, such as 15,31,…,349,365 days. However, the actual visiting time of each subject can be different from the designated times. Hence, we add random numbers, generated from a normal distribution with a mean of zero and a variance of 9, to each designated time point. Subsequently, the actual observed time points will be defined as

  $$\begin{array}{@{}rcl@{}} 0= l_{0} < l_{1i} < \cdots < l_{23,i} < l_{24}=366. \end{array} $$

  Let u_01i, u_02i, and u_03i be random numbers generated from a uniform distribution on the interval (0,1). Additionally, let R_i, T_i, and L_i be, respectively, the roots s of the equations:

  $$\begin{array}{*{20}l} \Lambda_{01}(s|z_{i}, w_{i},u_{i}) + \log(1-u_{01i})&=0,\\ \Lambda_{02}(s|z_{i}, w_{i},u_{i}) + \log(1-u_{02i})&=0,\\ \text{and} \Lambda_{03}(s|z_{i}, w_{i},u_{i}) + \log(1-u_{03i})&=0, \end{array} $$

  where

  $$\begin{array}{@{}rcl@{}} \Lambda_{0j}(s|z_{i}, w_{i},u_{i}) = \eta_{i}\left[\left(\beta_{0j} z_{i}\right) s + \exp\{\alpha_{0j} w_{i}\} \theta_{0j} s^{\gamma_{0j}}\right]\ \text{for}\ j=1,2,3. \end{array} $$

• Step 1: If C≤R_i∧T_i∧L_i, then the i^th subject is defined as being censored without experiencing a non-fatal event, i.e., $i \in \mathcal {B}_{1}$. If T_i=R_i∧T_i∧L_i, then the i^th subject is defined as being dead without experiencing a non-fatal event, i.e., $i \in \mathcal {B}_{2}$. However, if R_i=R_i∧T_i∧L_i, proceed to Step 2, and if L_i=R_i∧T_i∧L_i, proceed to Step 3.

• Step 2: Let u_12i be a random number generated from a uniform distribution on the interval (1− exp{Λ₁₂(R_i|z_i,w_i,u_i)},1), where

  $$\begin{array}{@{}rcl@{}} \Lambda_{12}(s|z_{i},w_{i},u_{i})=\eta_{i}\left[(\beta_{12} z_{i}) s + \exp\{\alpha_{12}w_{i}\} \theta_{12}s^{\gamma_{12}}\right]. \end{array} $$

  Redefine T_i as the root s of the equation,

  $$\begin{array}{@{}rcl@{}} \Lambda_{12}(s|z_{i},w_{i},u_{i}) + \log(1-u_{12i})=0. \end{array} $$

  If C≤T_i, then the i^th subject is defined as being censored after experiencing a non-fatal event, i.e., $i \in \mathcal {B}_{3}$. Otherwise, the i^th subject is defined as being dead at time T_i after experiencing a non-fatal event, i.e., $i \in \mathcal {B}_{4}$. Moreover,

  - If R_i∈(0,l_1i), let a_i=0 and b_i=l_1i. If R_i∈(l_k−1,i,l_ki), let a_i=l_k−1,i and b_i=l_ki for k=2,3,…,23.

  - However, if R_i∈(l_23,i,C), the type of path should be redefined because a non-fatal event for the subject did not occur before the time of the last observation. Thus, if C≤T_i, the i^th subject is defined as being censored without experiencing a non-fatal event, i.e., $i \in \mathcal {B}_{1}$. Otherwise, the i^th subject is defined as being dead at time T_i without experiencing a non-fatal event, i.e., $i \in \mathcal {B}_{2}$.

• Step 3: Let u_32i and u_34i be random numbers generated from uniform distributions on the intervals (1− exp{Λ₃₂(L_i|z_i,w_i,u_i)},1) and (1− exp{Λ₃₄(L_i|z_i,w_i,u_i)},1), respectively, where

  $$\begin{array}{@{}rcl@{}} \Lambda_{3j}(s|z_{i},w_{i},u_{i})=\eta_{i}\left[(\beta_{3j} z_{i}) s + \exp\{\alpha_{3j}w_{i}\} \theta_{3j}s^{\gamma_{3j}}\right],\ \text{for}\ j=2,4. \end{array} $$

  Now redefine R_i and T_i as the roots s of the equations:

  $$\begin{array}{*{20}l} \Lambda_{32}(s|z_{i},w_{i},u_{i}) + \log(1-u_{32i})&=0 \\ \text{and} \Lambda_{34}(s|z_{i},w_{i},u_{i}) + \log(1-u_{34i})&=0, \end{array} $$

  respectively. If C≤R_i∧T_i, the i^th subject is defined as being censored without experiencing a non-fatal event after LTF, i.e., $i \in \mathcal {B}_{5}$. If T_i≤R_i, then the i^th subject is defined as being dead without experiencing a non-fatal event after LTF, i.e., $i \in \mathcal {B}_{6}$. However, if R_i<T_i, move to Step 4.

• Step 4: Let u_42i be a random number generated from a uniform distribution on the interval (1− exp{Λ₄₂(R_i|z_i,w_i,u_i)},1), where

  $$\begin{array}{@{}rcl@{}} \Lambda_{42}(s|z_{i},w_{i},u_{i})=\eta_{i}\left[(\beta_{42} z_{i}) s + \exp\{\alpha_{42}w_{i}\} \theta_{42}s^{\gamma_{42}}\right]. \end{array} $$

  Redefine T_i as the root s of the equation,

  $$\begin{array}{@{}rcl@{}} \Lambda_{42}(s|z_{i},w_{i},u_{i}) + \log(1-u_{42i})=0. \end{array} $$

  If C≤T_i, then the i^th subject is defined as being censored at time C after experiencing LTF and a non-fatal event, i.e., $i \in \mathcal {B}_{5}$. Otherwise, the i^th subject is defined as being dead at time T_i after experiencing LTF and a non-fatal event, i.e., $i \in \mathcal {B}_{6}$.

In the simulation settings, we consider three types of regression coefficients (i.e., ‘even’, accelerated (‘acc’), and decelerated (‘dec’)) as well as three types of LTF proportions (i.e., ‘low’, ‘moderate’, and ‘high’). For the ‘even’ type, there are no differences in the effects of the covariates on the hazard rate of death before and after experiencing a non-fatal event. That is, α₀₂=α₁₂=0.01 and β₀₂=β₁₂=0.004. Meanwhile, for ‘acc’ and ‘dec’, increasing and decreasing effects are noted on the hazard rates of death, respectively. That is, α₀₂=0.01, α₁₂=0.0125, β₀₂=0.004, and β₁₂=0.005 for ‘acc’, whereas α₀₂=0.02, α₁₂=0.01, β₀₂=0.008, and β₁₂=0.004 for ‘dec’. For the rest of the regression coefficients, we set β₀₁=β₀₃=β₃₂=0.004 and α₀₁=α₀₃=α₃₂=0.01. Moreover, we set θ₀₃=0.00075, θ₀₃=0.002, and θ₀₃=0.004 for the ‘low’, ‘moderate’, and ‘high’ types, respectively. The remaining shape parameters of the baseline transition intensities were set as θ₀₁=θ₃₂=0.002 and θ₀₂=0.001. Tables 1, 2, and 3 provide the relative bias (‘r.Bias’), standard deviation (‘SD’), average of the standard errors (‘SEM’), and coverage probability (‘CP’) of 95% confidence intervals for the regression parameters and the variance estimate of the frailty distribution, respectively, according to the three LTF proportions. For comparison purposes with the proposed approach (‘proposed’), each table also displays the results obtained by simply assuming that a non-fatal event occurred at the end of the right endpoint of the interval (‘imputed-by-the-right-endpoint’). When the type of the regression coefficients is fixed at ‘even’, ‘acc’, or ‘dec’, the CPs of the regression parameters corresponding to the ‘proposed’ case are close to a nominal level of 0.95 irrespective of the LTF proportions, whereas those of the regression parameters such as b₀₁ and b₀₃, are much smaller than 0.95 for the ‘imputed-by-the-right-endpoint’ case. For the results based on the ‘proposed’ method, as the proportion of LTF increases, the mean squared error (MSE) for estimates of some regression parameters (e.g., a₀₃,a₃₂, and b₃₂) decreases, while the MSE of other regression parameters (e.g., a₀₂,b₀₂, and b₀₃) increases, regardless of the type of regression coefficients.

Table 1 Empirical results for the averages of the relative bias (r.Bias) and standard errors (SEM), standard deviation (SD), and coverage probability (CP) for the regression parameters and variance parameter of the log-normal frailty based on the ‘imputed-by-the-right-endpoint’ and ‘proposed’ methods when the type of regression coefficients is ‘even’ under three types of LTF proportions (‘low’, ‘moderate’, and ‘high’)

Table 2 Empirical results for the averages of the relative bias (r.Bias) and standard errors (SEM), standard deviation (SD), and coverage probability (CP) for the regression parameters and variance parameter of the log-normal frailty based on the ‘imputed-by-the-right-endpoint’ and ‘proposed’ methods when the type of regression coefficients is ‘dec’ under three types of LTF proportions (‘low’, ‘moderate’, and ‘high’)

Table 3 Empirical results for the averages of the relative bias (r.Bias) and standard errors (SEM), standard deviation (SD), and coverage probability (CP) for the regression parameters and variance parameter of the log-normal frailty based on the ‘imputed-by-the-right-endpoint’ and ‘proposed’ methods when the type of regression coefficients is ‘acc’ under three types of LTF proportions (‘low’, ‘moderate’, and ‘high’)

Sensitivity analysis is also conducted to investigate how the estimator of the parameter behaves with different frailty distributions. For simplicity of computation, we consider only the ‘even’ case for the regression parameters and the ‘moderate’ LTF proportion. Three different frailty distributions are used, along with a normal distribution with a mean of zero and a variance of 0.01. These are uniform, double exponential, and gamma distributions with specific parameter value(s), for which the mean and variance of each distribution are the same as those of the normal distribution. Simulation results are provided in Table 4. We compare the results of the three distributions with those of the normal distribution. The uniform and double exponential distributions are symmetric, like the normal distribution. However, the uniform distribution has thinner tails than the normal distribution, while the double exponential distribution has heavier tails than the normal distribution. Alternatively, unlike the normal distribution, the gamma distribution is an asymmetric distribution. Overall, there are no differences in the values of r.Bias and CP between the three distributions and the normal distribution. This implies that the proposed estimators are robust to misspecifications of the frailty distribution.

Table 4 Sensitivity analysis of the ‘proposed’ method depending on the underlying frailty distribution in terms of the averages of the relative bias (r.Bias) as well as the standard errors (SEM) and coverage probability (CP) when the type of the regression coefficients is ‘even’ and the LTF proportion is ‘moderate’

Illustrative data analysis

PAQUID data were collected to investigate the effects of dementia on mortality. Samples were taken from community residents of two southwestern regions (Gironde and Dordogne) of France [7]. The population consists of elderly people of ages 65 or above, between 1988 and 1990, whose socio-demographic characteristics and mental health status were recorded every two to three years. A total of 3675 persons was selected to participate in the study; among these individuals, 832 (22.6%) were diagnosed with dementia, 639 of whom died. The remaining 2843 participants (77.4%) did not experience dementia but 2298 of them died.

In this article, we performed an analysis based on ‘paq1000’ data, which included 1000 randomly selected observations from the PAQUID data [21]. The paq1000 data consist of several pieces of information, such as the mental health status (diagnosed with dementia or dementia-free), dead or alive status, age (including a n’s age at the start of study, their age at the last dementia-free visit, their age when they were diagnosed with dementia, their age at their time of death, and their age at censoring), gender, and educational background (educated or non-educated in terms of graduation of elementary school, say certificate). When a person who was not diagnosed with dementia at their last visit has not been traced for more than four years, this person is assigned to the LTF category. Table 5 shows summary statistics to briefly grasp the subjects’ characteristics including ages at entry, at dementia diagnosis, at death after dementia, at death without dementia, and at death after LTF. A total of 231 persons was categorized as LTF; among these, 159 (68.8%) died. Moreover, 127 (68.3%) persons out of the 186 who experienced dementia died, and 438 (75.1%) persons out of the 583 dementia-free persons died. Moreover, age at dementia diagnosis is higher for women than for men regardless of the education group (with certificate or without certificate). The same trend is observed both at age after dementia and at age without dementia. Meanwhile, age at death after LTF is a bit higher for women than for men.

Table 5 Patients’ characteristics of ages at entry, at demensia (DM) diagnosis, at death after DM, at death without DM, and at death after LTF

First, we check to see whether each covariate satisfies the proportional hazards assumption by using the test procedure of [22] and the Schoenfeld residual [23]. Figure 2 shows diagnostic (scattered) plots of the scaled Schoenfeld residual versus age. In each plot, we mark a spline smoother (solid line) as well as two standard deviation bands (dashed lines). In the curve showing the effect of gender, there is a decreasing trend on transitions 0→1 and 0→2, an increasing trend on 1→2 and 3→2, and a quite steady pattern for 0→3. In the curve showing the effect of certificate, there is a prominent decreasing trend for transition 0→2, while the other transitions show steady patterns. Table 6 provides the p-values for the test results [11]. For the gender effect, only the p-value for transition 0→3 is greater than 0.1, which seems to violate the proportional hazards assumption. Alternatively, the p-values for all transitions for the certificate effect, with the exception of 0→2, are greater than 0.1. This seems to satisfy the proportional hazards assumption. Thus, we put ‘gender’ into the additive side and ‘certificate’ into the multiplicative side for future analyses:

$$\begin{array}{@{}rcl@{}} \lambda_{rs}(t|z&=&\text{gender},w=\text{certificate},u)\\&=&\exp(u)\left\{\beta_{rs}z+\exp(\alpha_{rs}w)\theta_{rs}\gamma_{rs}t^{\gamma_{rs}-1}\right\} \end{array} $$

Fig. 2

Diagnostic plots showing the constancy of the coefficients in the PAQUID data. Each plot shows a component of the time-varying coefficient against the ordered time. A spline smoother (solid line) is shown together with the ±2 standard deviation bands (dashed lines)

Table 6 P-values of the test used to check the proportional hazard assumption for each transition model

for $(r,s)\in \mathcal {A}.$

Table 7 shows a summary of the estimation procedures. We provide the estimates of the regression coefficients along with their standard errors and p-values. For the transition from H to LTF (0→3), the intensities for women are larger than for men, with a value of 0.00849 (849 out of 100000 persons). However, this turned out to be insignificant with a p-value of 0.439. For the intensity of the 3→2 transition, a reversed outcome was obtained, with a value of 0.00619 for men with a very significant p-value of less than 0.001. For the 0→1 transition, women showed a larger intensity than men with a value of 0.0156, yielding a non-significant result with a p-value of 0.245. For the 1→2 transition, the intensity for men is similar to that for women, with a value of 0.0101 and a p-value of 0.961. Finally, for the 0→2 transition, the intensity for men is larger than for women with a value of 0.0295 along with a significant p-value of 0.038. Meanwhile, all transition intensities of the non-educated group are similar to those of the educated group. Finally, the estimate for the variance σ² on the common frailty is 0.999 with a highly significant p-value less than 0.001, showing non-homogeneity between clusters classified by the age at entry. Figure 3 shows five transition intensities over age by gender and certificate and estimated normal frailties of each cluster. As presented in Fig. 3, the transition intensities of 0→1 and 0→3 are higher for women than for men over age regardless of the education group, while these trends are reversed for the 0→2 and 3→2 transitions. For the transition 1→2, no difference is observed between women and men, but there is a significantly monotone increasing trend over age. These are consistent with the results in Table 7.

Fig. 3

Five transition intensities over age by gender and certificate: 0→1, 0→2, 1→2, 0→3, 3→2 transitions and estimated normal frailties of each cluster classified by age at entry

Table 7 Regression parameter estimates (Est) with the accompanying standard errors (SE) and p-values (P)

Conclusions

We considered a multi-state model for semi-competing risks data, for which there exists information on fatal events, but information on non-fatal events may not be available due to lost to follow-up. More precisely, we proposed an additive and multiplicative random effect model by combining the additive risk model [16] with the proportional hazards model [8, 9] in order to derive the conditional likelihood function. An adjusted importance sampling method was used to compute the marginal likelihood function, where the MLEs for the regression coefficients were obtained by an iterative quasi-Newton algorithm. The proposed model was illustrated using PAQUID data and yielded several promising results. The risk of transition from a healthy state to dementia is higher for women. However, the risk of death is higher for men regardless whether a subject is diagnosed with dementia or not. Meanwhile, the risk of transition from a healthy state to dementia is higher for the educated group. The risk of death after being diagnosed with dementia is higher for the educated group; however, a reversed result is observed for non-diagnosed subjects. Furthermore, we conducted simulations with finite-sample sizes to investigate the efficiency of the proposed estimators. In particular, we considered nine combinations of three different types of regression coefficients and three different types of LTF proportions. In general, the coverage probabilities of the regression parameters are close to a nominal level of 0.95 in most cases. Moreover, according to a referee’s suggestion, we investigated influence of parameter estimation when LTF is omitted (not censoring) in our simulation studies. Finally, we performed simulations with the same realizations generated from each configuration included in Tables 1, 2, and 3. Based on the results not reported here, the CP of parameter β₀₁ is extremely lower than a nominal level of 0.95 for all configurations. In addition, when the type of regression coefficients is ‘dec’, the CP of parameter β₀₂ is much smaller than 0.95 regardless of types of LTF proportions. Moreover, compared to each table, namely, Tables 1, 2, and 3, the relative bias of β₀₁ increases around ten times for all configurations. This is the reason omitting LTF results in route changes of subjects included in routes 5 and 6 at the data generation stage, i.e., from route 5 to 1 (when the fatal event is censored) or from route 6 to 2 (when the fatal event is observed) according to the fatal status of subjects.

The proposed model has some drawbacks. At the initial stage of this research, as developed in [8, 9, 16], we intended to consider a semi-parametric model incorporating five transition intensity models. However, it was quite difficult to handle nonparametric estimation procedures for the baseline transition intensity associated with the nuisance parameter because the total number of parameters is proportional to the number of subjects. Rather, we assumed a Weibull distribution for the baseline transition intensity; further research should be carried out to avoid the use of this specific distribution. To circumvent arbitrariness, it is necessary to calculate the Nelson-Aalen estimators for the cumulative baseline transition intensity [8, 9, 16] and extend this method to semi-competing risks models based on the profile likelihood function. Another plausible remedy would be to apply a spline smoothing method on the baseline transition intensity proposed by [24, 25]. In the additive and multiplicative hazards model with frailty, one could use a semi-parametric Bayesian approach by assuming a prior distribution on the log-normal frailty. Subsequently, conventional Markov Chain Monte Carlo computation would be proceeded for the full conditional distribution on the frailty [26, 27].