Abstract
Background
One of evolutionary molecular biology fundamental issues is to discover genomic duplication events and their correspondence to the species tree. Such events can be reconstructed by clustering single gene duplications inferred by reconciling a set of gene trees with a species tree.
Results
Here we propose the first solutions to the genomic duplication problem in which every reconciliation with the minimal number of single gene duplications is allowed and the method of clustering called minimum episodes under the assumption that input gene trees are unrooted.
Conclusions
We showed new theoretical properties of unrooted reconciliation for the duplication cost and apply them to design several exact and heuristic algorithms for solving the problem. Our evaluation study on empirical dataset confirmed several genomic duplication events from the literature and demonstrate that algorithms can be successfully applied.
Similar content being viewed by others
Background
The phenomenon of genomic duplication is fundamental to understand the evolution of life on Earth [1–5]. The research in phylogenetics focus on the way how the gene families and genomes evolve by discovering the locations of gene duplications. Multiple gene duplications occur when large parts of a genome are duplicated. In particular, the whole-genome duplication occurred for numerous species and had a crucial impact on the evolution of crops [6–9]. The studies of this phenomenon focus on detecting its occurrences as well as its influence on introgressing novel metabolic traits [10] or its association with periods of increased environmental stress [11]. The methods of detecting whole-genome duplications can be divided into three categories based on synteny and colinearity comparison of genomes [1, 12, 13], the estimation of the age distribution of paralogous gene pairs [3, 14], and phylogenetic tree inference [15–17].
The reconstruction of the evolution of individual genes has been thoroughly studied [18–22] also with the focus on gene trees [23–26], networks [27, 28], from the perspective of population genetics [29] or the evolution of entities (which can be genes, gene domains, or parts of genes) [30].
The reconciliation model, introduced by Goodman [31] and formalized by Page [18], interprets the differences between a gene tree and its species tree [32–34]. In this model, each node from a rooted gene family tree is mapped into the species tree and classified as a single gene duplication or related to a speciation event. In our work, we model a biologically consistent scenario as the embedding of a gene tree into a species tree which represents the location of evolutionary events in the species tree [35]. Identification of such a scenario is made by a function called duplication mapping that assigns a gene tree node, interpreted as a duplication event, to a node of a species tree [20, 36–43]. Reconciliation becomes complex when considering multiple gene duplications. The general formulation is as follows: given a set of gene trees and a species treefind evolutionary scenarios for the collection of gene trees that yields the minimal number of multiple gene duplication events [44]. Two fundamental issues arise when dealing with multiple gene duplications: a model of allowed evolutionary scenarios [20, 44, 45] and the rules of clustering gene duplications from gene trees into multiple duplication events. We distinguish three variants of problems depending on the clustering: episode clustering (EC) [20, 37, 38], gene duplication clustering (GD) [45], and minimum episodes (ME). EC is to find scenarios having the minimal number of locations of duplication episodes in a species tree. EC for rooted gene trees has a linear time solution [42], while for unrooted trees an FPT algorithm is known [36]. GD is similar to EC with the difference that a cluster cannot have two gene duplications from the same tree. In ME a duplication and its ancestor duplication cannot be clustered together [20, 38]. The first polynomial time algorithm for ME with rooted gene trees, called RME, under the model from [20] was proposed in [38], whereas the optimal linear time algorithm in [41, 42]. The concept of assigning every duplication to an interval of allowed locations in a species tree was introduced in [46] in a more general framework without the requirement that the intervals induce a biologically consistent scenario. The naïve implementation of the iterative algorithm from [46] has cubic time complexity. The solution to RME for a variety of models was presented in [44]. In particular, the algorithm proposed in [44] solves RME in linear time.
Our contribution. We propose the solution to the unrooted minimum episodes problem, UME, in which allowed scenarios have the minimal number of gene duplications [36]. According to our knowledge, the complexity of UME is unknown. We expanded the theory of unrooted reconciliation by presenting new properties of the plateau which is the subtree of an unrooted gene tree containing edges whose rootings have the minimal duplication cost. Next, we show that these properties lead to a decomposition of an unrooted gene tree that allows limiting the possible search space significantly. We show that every instance of UME can be transformed into at most 5k “simpler” instances that can be solved in linear time, where k is bounded above by special cases of S2 stars [47] in input trees. Next, we propose two linear time algorithms for computing bounds of the score. Finally, for the case when k is large, we propose an efficient heuristic algorithm, which in practice allows solving exactly empirical instances consisting of thousands of unrooted gene trees. Also, we present an evaluation of several empirical datasets.
Methods
Basic notation
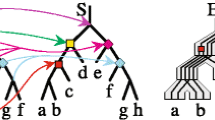
Let S denote a species tree which is a rooted binary tree with leaves uniquely labeled by the names of species. We assume that S is fixed throughout this work. A rooted gene tree is a rooted binary tree with leaves labeled by the names of species. The rooted tree (T1,T2) has two subtrees T1 and T2 whose roots are the children of the tree root. Additionally, for nodes a and b, we write \(a \preceq b\) when a and b are on the same path from the root, with b being closer to the root than a. Notation \(a \prec b\) means that \(a \preceq b\) and a≠b. The root of a tree T we denote by root(T). By T v , we denote the subtree of T rooted at v. A cluster for a node v is the set of all species present in T v .
Let T=〈V T ,E T 〉 be a rooted gene tree such that the set of species present in T is a subset of the set of species present in S. The least common ancestor (lca) mapping, M T :V T →V S , is defined as follows. If v is a leaf in T then M T (v) is the leaf in S labeled by the label of v. For an internal node v in T having two children a and b, mapping M T (v) is the least common ancestor of M T (a) and M T (b) in S. An internal node g∈V T is called a duplication if M T (g)=M T (a) for a child a of g. The duplication cost, the total number of duplications in T, is denoted by D(T,S). Every non-duplication node of T we call a speciation (including leaves).
Evolutionary scenarios
Here, we present the model of DLS trees [35] that will be used to represent evolutionary scenarios. A DLS tree is a binary tree having two types of internal nodes, that denote speciation and duplication events, and two types of leaves that denote gene loss and gene sequences. DLS trees are defined as follows [44]:
-
1
a is a single-noded DLS tree denoting a gene sequence from the species a,
-
2
A- is a single-noded DLS tree denoting a lost gene lineage, where A is a non-empty set of species,
-
3
(R1,R2)+ is a DLS tree whose root is a duplication node and its children are DLS trees R1 and R2 such that the set of species present in R1 and the set of species present in R2 are equal,
-
4
(R1,R2)∼ is a DLS tree whose root represents a speciation and its children are DLS trees R1 and R2 such that the set of species present in R1 and the set of species present in R2 are disjoint.
Let T be a DLS-tree with at least one gene sequence. A gene tree can be extracted from T by contracting nodes of degree 2 from the smallest subgraph of T containing all gene sequences. Such an operation will be denoted by gt(T).
We say that a DLS-tree T is a scenario for a gene tree G and a species tree S if gt(T)=G, and T is compatible with S, that is, every cluster of T is present in S. In such a case, every node g in G uniquely corresponds to a node in T denoted by ξ(g). We can define mappings \(\xi \colon G \rightarrow T\) and \(F_{T} \colon G \rightarrow S\), such that F T (g) is the node in S whose cluster equals the cluster of ξ(g). An example is depicted in Fig. 1.
Unrooted reconciliation
The unrooted gene tree is an undirected acyclic connected graph in which each internal node has degree 3, and the leaves are labeled by the names of species. The rooting of an unrooted gene tree U=〈V U ,E U 〉 obtained from U by placing the root on an edge e∈E U is denoted by U e . Such a rooting induces the duplication cost D(U e ,S). An edge e is called optimal if D(U e ,S) is minimal in the set of all rootings of U. It is known that the set of optimal edges, called the plateau, is a full subtree of U [47, 48]. In this article, the notion of the plateau is used exclusively with the duplication cost. In literature, it is often called D-plateau in order to distinguish between plateaus for other costs, e.g. DL-plateau [48]. In this work, the subtree induced by the set of all optimal edges will be denoted by U∗. For X, the set of edges of unrooted tree U, by U| X we denote the smallest subgraph of U containing all edges from X.
Without loss of generality, we assume that every root of a gene tree is mapped into the root of S, and both trees are non-trivial. An edge e=〈v,w〉 of U can be classified as one of three following types: (a) empty if the root of U e is a speciation, i.e., M e (v)≠root(S)≠M e (w), (b) double if M e (v)=root(S)=M e (w), and (c) single otherwise, where M e is the lca-mapping between U e and S. Let v be an internal node of U, then a star with the centerv consists of three edges, sharing v. There are five possible types of stars present in unrooted gene trees [47, 48], however, in this article we only use the star called S2 having one empty edge. In such a case the remaining edges are single, and by using the notation from Fig. 2, for x∈{a,b} we have that \(\mathsf {M}_{U_{\langle {v,x}\rangle }}(x) \neq \mathsf {root}(S) = \mathsf {M}_{U_{\langle {v,x}\rangle }}(v)\).
It follows from unrooted reconciliation that plateau has either exactly one empty edge or at least one double edge [47]. We say that a node is a super-duplication (respectively, a super-speciation) if it is a duplication (respectively, a speciation) in every rooting with the minimal duplication cost.
Lemma 1
[adapted from [36]] Assume that an unrooted tree has a double edge. Then, every leaf of the plateau is a super-speciation, and every internal node of the plateau is a super-duplication.
On the other hand, when there is an empty edge in an unrooted tree, we have:
Lemma 2
Let U be an unrooted gene tree with an empty edge e. A node incident to e is a speciation in U e if and only if it is a leaf of the plateau.
Proof
We use the notation from Fig. 2 where e is 〈v,c〉. We may assume that c is an internal node of U; otherwise, we have a trivial case where c is a leaf in the rooting of U which is a speciation. Thus, we have two S2 stars sharing the empty edge. \((\Leftarrow)\) Without loss of generality, we may assume that v is a leaf of U∗. If v is not a speciation in U〈v,c〉 then it is a duplication. From the definition of the empty edge, the root of U〈v,c〉 and v in U〈v,a〉 are speciation nodes. Moreover, the node v in U〈v,a〉 is mapped to root(S) thus the root of U〈v,a〉 is a duplication. Both rootings U〈v,c〉 and U〈v,a〉, have the same number of duplications having the same setting of duplications in subtrees T a ,T b and T c as indicated in Fig. 2. Hence, 〈v,a〉 is a U∗ edge, a contradiction. \((\Rightarrow)\) The proof is similar to the first case. □
The conclusion from the above Lemma 2 is that either only empty edge or the whole S2 star is included in the plateau. Moreover, we can describe the plateau having an empty edge by the following lemma:
Lemma 3
If the unrooted gene tree has an empty edge then every leaf of the plateau is a super-speciation, and every internal node of the plateau not incident to an empty edge is a super-duplication.
Proof
For the first part of the proof, let assume that v is a leaf of U∗ which consists of 〈v,c〉 edge. Assume that v is a duplication in some plateau rooting. Then, the subtree T v in this rooting is also a subtree in all plateau rootings because v is a leaf of U∗. Hence, v is a super-duplication. If 〈v,c〉 is an empty edge we have a contradiction from Lemma 2. Assume that 〈v,c〉 is non-empty. The edge 〈v,a〉 does not belong to U∗. Therefore, the rooting U〈v,a〉 has more duplications than U〈v,c〉. Hence, U〈v,a〉 has two duplications in v and in the root. Therefore, the root of U〈v,c〉 is not a duplication. However, this is possible only when T a and T v are mapped below the root(S), thus the 〈v,c〉 is an empty edge, a contradiction. For the next part of the proof, if U∗ consists of exactly one empty edge then the property holds trivially. Let assume that the U∗ has more than one edge. We show that every internal node v of U∗, that is, not incident to an empty edge is a super-duplication. Let us consider a path \(p = v_{1}, v_{2}, \dots, v_{n}\) (n>1) consisting of nodes not incident with the empty edge connecting v=v1 with a leaf v n of U∗. Hence, when rooting on p, v is mapped to root(S) as it is the ancestor of nodes incident with the empty edge. Moreover, when rooting on 〈vn−1,v n 〉, we have n gene duplications: for \(v_{1}, v_{2}, \dots, v_{n-1}\) and one for the root. All edges from p are elements of U∗, thus moving the root to other edges on p will preserve the total number of gene duplications. We showed that the first n−1 nodes on p are duplications for every rooting placed on this path. If v is incident to an empty edge, it is a speciation mapped to the root(S) when rooting on p. When rooting on an empty edge, the root is a speciation. Moreover, from Lemma 2 a child of the root is a duplication if it is an internal node of U∗. Hence, all plateau rootings have the same number of duplications equalling the number of internal nodes of U∗. When rooting on an empty edge, the root is a speciation and all internal nodes of U∗ are duplications. Otherwise, if we place the root on the edge from U∗, the root is a duplication node and the only speciation is that node among nodes incident to an empty edge which is an ancestor to the other. □
Clustering Duplications: Minimum Episodes Problems
We define the cost determining the number of multiple gene duplication episodes for a set of evolutionary scenarios. Let \(\mathcal {R}\) be a set of scenarios compatible with S. We say that duplications d and \(d^{\prime }\) from \(\mathcal R\) are clusterable, denoted \(d \ \sim _{c}\ d^{\prime }\), iff (1) d and \(d^{\prime }\) have the same cluster and (2) if d and \(d^{\prime }\) are present in the same DLS-tree then either d and \(d^{\prime }\) are incomparable or equal. Then, the minimum number of duplication episodes for \(\mathcal {R}\), denoted \(\mathsf {MES}({\mathcal R},S)\), is the size of the smallest partition of the set of all duplication nodes from \(\mathcal R\) induced by an equivalence relation contained in ∼ c .
It can be shown that for a collection \(\mathcal {R}\) of scenarios compatible with a species tree S,
where duppath(T,v) is the maximal (node) length of the path in T that consists of all comparable duplication nodes whose cluster equals the cluster of v [44].
Let \(\mathcal {A}(G, S)\) be the set of all scenarios for a rooted gene tree G and a species tree S having the minimal number of gene duplications. Every element of \(\mathcal {A}(G, S)\) will be referred to as an allowed scenario. Here, allowed scenarios are defined as in [36], for the comprehensive overview see [44]. Now, we formulate the general problem in which the input consists of mixed types of gene trees: rooted and unrooted.
Problem 1
[General Minimum Episodes, GME] Given a collection of gene trees (rooted or not) \(\mathcal {U}=\left \{U^{1},U^{2},\dots,U^{n}\right \}\) and a species tree S. Computeminimum episodes score\(\mathsf {ME}(\mathcal {U},S)\), or ME score, as the minimal value of \(\mathsf {MES}(\{ R_{i} \}_{i=1,2,\dots,n},S)\) in the sets of scenarios R i such that \(R_{i} \in \mathcal {A}(U^{i},S)\) if Ui is rooted or \(R_{i} \in \mathcal {A}\left (U^{i}_{e},S\right)\) if Ui is unrooted, where e is an optimal edge.
Observe that we allow only scenarios that preserve the minimal number of gene duplications. We distinguish two variants of GME Problem: unrooted minimum episodes (UME) and rooted minimum episodes (RME) in which the instances consist entirely of unrooted and rooted gene trees, respectively. RME Problem has a linear time and space solution [44]. See also [38, 42] for more details on RME Problem.
Unrooted tree decomposition
In this section, we show that every unrooted gene tree can be decomposed into a set of trees having at most one unrooted tree with a simplified structure allowing to solve UME more efficiently. We start with the following observation.
Lemma 4
Let U be an unrooted gene tree and T be a rooted subtree of U rooted at v. Let \(X \subseteq U^{*}\) such that
-
X is disjoint with V T ∖{v},
-
v is a speciation in every scenario from \(\mathcal {A}(U_{e},S)\) for all e∈E X .
Then, for any set of scenarios \(\mathcal {X}\):
where \(U^{\prime }_{e}\) is the unrooted tree obtained from U by replacing T with S(M(v)).
Proof
In every allowed scenario R from the left side, \(F_{U_{e}}(v)\) is a speciation node. Thus, scenarios \(R^{\prime }\) and \(R^{\prime \prime }\) can be obtained from R as follows: \(R^{\prime \prime }\) is the subtree rooted at \(F_{U_{e}}(v)\) in R, while \(R^{\prime }\) is obtained from R by replacing the subtree with the copy of S(M(v)), where every internal node is a speciation. Such a transformation is a bijection that preserves the clusterability of duplication nodes. We omit technical details. □
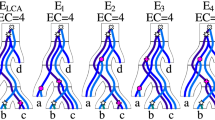
Given a species tree S and a rooted tree G by \(\widetilde {G}\) we denote the set of all \(\preceq \)-maximal elements in the set of all non-root speciation nodes from G. Lets ∼ be a relation on edges of U∗ for an unrooted gene tree U such that \(e \sim e^{\prime }\) if \(\widetilde {U}_{e} = \widetilde {U}_{e^{\prime }}\). It should be clear that ∼ is an equivalence relation. The set of equivalence classes of this relation we denote by U∗ /∼. An example is depicted in Fig. 3.
Equivalence relation ∼. An example of an unrooted gene tree U with one S2 star and all plateau rootings reconciled with a species tree S = (((a,b),(c,d)),e). U∗ contains five edges and induces three ∼-equivalence classes. The first consists of an empty edge 〈e,v〉, the second of 〈d,v〉 while the last class consists of the remaining three edges. These three classes induce rootings {G1}, {G5} and {G2,G3,G4}, respectively. Observe, that \(\widetilde {G}_{2} = \widetilde {G}_{3} = \widetilde {G}_{4}\) consist of a subset of U∗ leaves and a speciation (different for each class) at node v which is a center of S2 star
Lemma 5
If an empty edge is present in an unrooted gene tree then every plateau edge present in S2 star uniquely defines one ∼-equivalence class. Otherwise, the tree has exactly one ∼-equivalence class.
Proof
Let U be an unrooted gene tree. We have two cases: (a) either U has a double edge or (b) U has an empty edge. In the case (a), it follows from Lemma 1, that \(\widetilde {U}_{e}\) consists of all U∗ leaves for every e from U∗. Thus, we have one equivalence class consisting of all U∗ edges. Let use the notation from Fig. 2. For the case (b), from the proof of Lemma 3 we conclude that for the empty edge 〈v,c〉 the set \(\widetilde {U}_{\langle {v,c}\rangle }\) consists of all U∗ leaves. Moreover, from the conclusion from the proof of Lemma 2, there are 0,2 or 4 single edges in U∗ present in S2 stars. Let 〈v,a〉 be such an edge. The set \(\widetilde {U}_{\langle {v,a}\rangle }\) consists of: (a) v which is the root of the subtree T v =(T b ,T c ) and thus it is a speciation (it maps to root(S) and both its children map below the root(S)) and (b) all leaves of U∗ present in T a . From Lemma 3 for every edge e of U∗ present in T a , we have \(\widetilde {U}_{e} = \widetilde {U}_{\langle {v,a}\rangle }\). Summing up there can be 1,3 or 5 ∼-equivalence classes uniquely defined by every edge of U∗ present in S2 star (see Fig. 3). □
If an empty edge is an element of a class X∈U∗/∼, X will be called plain. Otherwise, we call Xcomplex.
Lemma 6
If X∈U∗/∼ is complex then the leaves from U| X are speciations in every tree U e for every e in X.
Proof
U has either an empty or a double edge. The leaves of U∗ are super-speciations from Lemmas 1 and 3. If U has a double edge, then there is only one ∼-equivalence class (Lemma 5) and every leaf v of U| X is also a leaf in U∗. If U has an empty edge, say e, then there are 0, 2 or 4 classes X disjoint with {e}. For all of them the set of the leaves of U| X consists of a subset of the leaves of U∗ (disjoint with subsets corresponding to other classes see Fig. 3) and a node v which is the center of a star S2 and a speciation when rooting on edges from X (see the proof of Lemma 5). □
Definition 1
[Unrooted Decomposition] Let U be an unrooted gene tree, and X∈U∗/∼, then:
-
If X has an empty edge e then Δ(U,X)={U e }.
-
Otherwise, Δ(U,X) is the set of all maximal subtrees T v of U such that v is a leaf of U| X and \(T_{v} \cap U|_{X} = \{v\}\).
For a complex class X, UX denotes a tree obtained from U| X by replacing every leaf v with the subtree S(M(root(T v ))). For example, for the largest class X from Fig. 3, we have: \(\Delta (U,X) = \{ c,\ (d,e),\ \left ((a,b),b),((c,d),d)\right) \}\) and UX=((((a,b),(c,d)),e),((a,b),(c,d)),c).
The intuition is that Δ(U,X) is the set of rooted trees T induced by X with the following properties: (a) the root of T is a speciation, and (b) T is a subtree present in all rootings induced by X. For example, when we consider an empty class there is only one possible rooting U e . Lemma 6 describes the properties of Δ(U,X) for a complex class X. Finally, for an unrooted tree U we have the following formula:
Lemma 7
[Decomposition Lemma] For a given set of input gene trees \(\mathcal {G}\), an input unrooted gene tree U and a species tree S we have, \(\mathsf {ME}(\mathcal {G} \cup \{ U\},S) = \min _{X \in U{*}/_{\sim }} \left \{\begin {array}{cc} \mathsf {ME}(\mathcal {G} \cup \{U_{e}\}) & \\ & {} \text {if}\ X=\{e\}\ \text {and}\ e\ \text {is empty,}\\ \min _{e \in X} \mathsf {ME}(\mathcal {G} & \hspace {-10pt} \cup \left \{ U^{X}_{e} \right \} \cup \Delta (U,X), S) \\ & {\kern -2.4cm} otherwise. \end {array}\right.\)
Proof
Let us consider the set of allowed DLS scenarios induced by rootings of edges from each X∈U∗/∼. If X is plain, then the set is \(\mathcal {A}(U_{e},S)\). If X is complex, then by Lemma 6, X and every leaf v from U| X , satisfies assumptions from Lemma 4. Thus, the subtree of U disjoint with X∖{v} can be detached and replaced by S(M(v)) in U. By Lemma 4 the MES score is preserved. The rest follows by induction on the set of leaves v, where we show that the unrooted tree after all transformations is UX and the set of detached subtrees is Δ(U,X). □
Algorithms
Solution to RME
We start with the linear time algorithm for RME from [44] adapted to the model of allowed scenarios presented here.

For the input consisting of rooted gene trees, every duplication d is associated with the interval consisting of all possible locations of d in the species tree. Our model of allowed scenarios is equivalent to the model from [44], in which I(d) is an interval defined by a pair 〈M(d),s〉, where s≽M(d) is the child of M(g) such that g is the lowest speciation satisfying g≻d, or s is the root if such a speciation does not exist. Algorithm 1 is a greedy bottom-up algorithm that iteratively assigns duplications to the top-end of intervals. In every step, it finds the lowest top node s of available intervals and assigns to s all duplications d having \(\max \mathsf {I}(d)\) equal to s. Additionally, the algorithm assigns other duplications to s but only if the ME score is not increased, which is controlled by λ(s). For details please refer to [44].
Exact solution to UME
A naïve solution to UME is to run RME algorithm for every combination of plateau rootings from input gene trees. In many cases the plateau can be large, hence, the time complexity of such a solution is \(O(\prod _{i}|U_{i}|(\sum _{i}|U_{i}|+|S|))\). Here, we propose an algorithm based on Lemma 7 to limit the cases that have to be checked to the number of classes of ∼ relation.

Lemma 8
[Correctness of gnaw] Let U be an unrooted gene tree and X be a complex class. Let \(\mathcal {X}_{r}\) be a set of rooted gene trees T such that the root of every T is a speciation. Let me(u,v)=〈s,n〉, in a call of gnaw with UX and \(\mathcal {X}_{r}\), such that v is internal in X. Then,
-
for every rooting \(U^{X}_{e}\) such that e∈X, and having v below the root, if Algorithm 1 (RME) is executed for \(\mathcal {X}_{r} \cup \ \left \{U^{X}_{e}\right \}\), then v is assigned to a node s and n=level s (d),
-
the call of gnaw returns \(\min _{e \in X} ME\left (\mathcal {X}_{r} \cup \left \{U^{X}_{e}\right \}\right)\).
Proof
First, observe that every call of gnaw satisfies the assumptions (see Def. 1). Assume that e∈X. Then, by the properties of a complex class X, we have in \(U^{X}_{e}\) that the root and all internal nodes of X, are duplications, while all leaves of X are speciations. Let \(X^{\prime }_{e}\) be the set of duplication nodes from X including the root. Thus, for every \(d \in X^{\prime }_{e}\), we have I(d)=〈M e (v),root(S)〉, where M e is the lca-mapping from \(U^{X}_{e}\) to S. Hence, all duplications from \(\mathcal {X}_{r}\) have the top interval node below the root, therefore, if Algorithm 1 (RME) would be called with the input consisting of \(\mathcal {X}_{r} \cup \ \left \{U^{X}_{e}\right \}\), then, for v being the root of S (in line 2 of Algorithm 1), all \(\mathcal {X}_{r}\) duplications are already processed. Additionally, a duplication d from \(X^{\prime }_{e}\) can be assigned earlier to a node v≽M e (d) only in step 5, if the condition is satisfied. Thus, we can separate the process of RME computation for \(\mathcal {X}_{r}\) (line 7 of Algorithm 2) and the rootings of UX. Furthermore, processing UX can be done collectively for all rootings from X, by using a dynamic programming that jointly executes the assignment operation. Note, that in line 11 the first elements of me(x,u) and me(y,u) are comparable (i.e., u is a duplication), therefore, \(\max \) is well defined by using lexicographical order. The proof of the first part follows by induction, in which a node in a rooted subtree of UX is assigned to the first next free “slot” in a species node. Such a slot can be located by using next. When all slots of non-root nodes are occupied then duplications have to be assigned to the root. Such assignments create new episode events. Thus, the score of every rooting placed on e={u,v} can be easily computed by verifying if such additional episodes were created. This information is stored for the two subtrees of the root in me(u,v) and me(v,u), respectively, i.e., if me(u,v)=〈root(S),n〉, then n additional episodes are required. This value for both subtrees is stored in m e . Note that, \(\max \) in line 12 is well defined, otherwise, X cannot be complex. Additionally, the root of \(U^{X}_{e}\) creates one more episode. Therefore, the score returned by gnaw consists of r (from rooted trees), the minimal value of m e (the contribution of X) and 1 (the root duplication). An example is depicted in Fig. 4. □
Illustration of gnaw for U with a double edge. Here, τ denotes the root of S. Assume that S has two positive lambda’s computed in line 7 by Algorithm 1: λ(α)=2 and λ(β)=1. Every edge e=〈u,v〉 of the plateau is split into two directed edges: 〈u,v〉 and 〈v,u〉. Each directed edge 〈u,v〉 is decorated with the lca-mapping M〈u,v〉(v) and me(u,v). For example, τ6 denotes the lca-mapping to τ and me(u,v)=〈τ,6〉. Here, gnaw returns 3+1+3 induced by the marked edge
Lemma 9
[Correctness] Given a collection of unrooted gene trees \(\mathcal U\) and a species tree S, Algorithm 2 returns \(\mathsf {ME}(\mathcal {U},S)\).
Proof
The proof follows from Decomposition Lemma 4 and Lemma 8. □
Lemma 10
[Complexity of Exact UME] Algorithm 2 requires \(O\left (\left (|S|+\sum _{i}|U_{i}|\right)5^{k}\right)\) time and \(O\left (\sum _{i}|U_{i}|+|S|\right)\) space, where k is the number of gene trees with S2 star having more than one class of U∗/∼.
Proof
Time: The number of iterations of the main loop is bounded above by 5k. Locating classes of ∼ and transforming trees can be done in linear time. Each call of function gnaw requires \(O\left (\sum _{T \in \mathcal {X}_{r}}|T|+|U^{X}|\right)\) time. Space: It follows from the complexity of Algorithm 1 and gnaw. □
Solving hard instances
In this section, we propose several alternative solutions to our problem designed to cope with hard instances of ME Problem. For example, when the input consists of thousands of trees, it is more likely that k is large enough (e.g., for k≥20) to prohibit applications of Algorithm 2.
The first approach, presented in Algorithms 3 and 4, is to decrease the search space by introducing the lower and upper bounds on the optimal solution in a similar way that we proposed in [44]. In these algorithms we define function gnawrooting, being a variant of gnaw from Algorithm 2., that instead of the minimal score it returns the corresponding optimal rooting of the input gene tree.

Lemma 11
Algorithm 3 computes the lower bound of ME score in \(O\left (|S|+\sum _{i}|U_{i}|\right)\) time and space.
Proof
Algorithm 3 computes the score from a set of input gene trees as follows. For each gene tree U:
-
If U∗/∼ contains exactly one class then decompose the tree similarly to Algorithm 2, i.e., incorporate all duplications from U into the clustering space.
-
Otherwise, ignore every duplication located in the plateau. In other words, to preserve all non-plateau duplications, it is sufficient to extract all (rooted) subtrees of U obtained from U by removing all internal nodes of the plateau.
Having this, we conclude that the size of the clustering computed by Algorithm 3 is less or equal to the size of the clustering from Algorithm 2.
The function gnawrooting processes all edges of the input tree in linear time, thus, the time complexity of the loop from line 11 is equal to \(O(\sum _{i}|U_{i}|)\). A similar property has the decomposition from lines 7-9. The ME score for rooted trees is computed by Algorithm 1 two times: in line 10 and in line 12. Hence, the time and space complexity of Algorithm 2 is \(O\left (|S|+\sum _{i}|U_{i}|\right)\). □

Lemma 12
Algorithm 4 computes the upper bound of ME score in \(O(|S|+\sum _{i}|U_{i}|)\) time and space.
Proof
Algorithm 4 returns the number of episodes computed for exactly one set of rootings that uniquely corresponds to an element from the product of classes \(U^{\ast }_{1}/_{\sim } \times U^{\ast }_{2}/_{\sim } \times \dots \times U^{\ast }_{n}/_{\sim }\). Hence, this number of episodes is evaluated in \(\max \)-formula in line 4 of Algorithm 2. Therefore, the ME score computed by Algorithm 2 is bounded above by output of Algorithm 4. The class of the maximal size for a gene tree G can be found in O(|G|) time, therefore, the complexity of the decomposition from lines 3-6 is \(O\left (\sum _{i}|U_{i}|\right)\). □
Algorithm 4 is a greedy heuristic in which the method of class selection can be replaced in several ways, e.g., by using a random class, the minimal size class or the class with the minimal value of gnaw. Moreover, it could be further refined to obtain a feasible algorithm similar to one presented in [36].
Finally, we present Algorithm 5. It is a heuristic solution to UME Problem having a quadratic time complexity. Algorithm 5 is designed to utilize the following property: if the input consists of thousands of trees, then it is more likely that clustering of duplications from all non-plateau rooted subtrees is sufficient to approximate, or even to provide, the exact ME score. Therefore, Algorithm 5 first solves computationally simple instances of RME extracted from the input gene trees and, then if the solution is not found, it proceeds to complex unrooted parts. In the next Section (see Table 1), we observe a surprising performance of Algorithm 5 allowing to solve exactly hard instances containing a large number of complex classes with runtimes counted in seconds. Also, when the ‘rooted’ part of an instance is small (see the Guigó dataset with 53 trees), the runtime could be much worse than for the large and potentially hard datasets (e.g., Génolevures with 4144 trees).

Lemma 13
Algorithm 5 is a heuristic solution to UME that runs in \(O\left (\left (|S|+\sum _{i}|U_{i}|\right)^{2}\right)\) time and \(O(|S|+\sum _{i}|U_{i}|)\) space.
Proof
The first part of Algorithm 5 consists of two phases. The first phase (lines 10-11) has a linear time complexity (see Lemmas 11 and 12). In the second phase (lines 12-24) it may provide an exact solution in quadratic time due to the calls of gnaw.
In the second part of Algorithm 5, depending on the size of \(\mathcal {E}\) it is either computing an exact solution by applying Algorithm 2, or it returns a heuristic solution that has quadratic worst-time complexity. This part of the heuristic is similar to Algorithm 4, however, instead of selecting the largest class we choose the class with the minimal ME score (see line 20).
Observe, that some duplications, which are included in Algorithm 5 in line 12 and corresponding to Algorithm 3 line 9 in Algorithm 5 are included for the second time. Note, the ME score will remain the same, because all of them have a plateau leaf ancestor. □
Implementation
Our algorithms are implemented in a prototype computer program written in C++ and python. Additionally, for a more detailed output, all score computing algorithms are extended with a routine for the reconstruction of gene duplication clusters (episodes) with their location in the species tree. The software is available on request.
Results and discussion
In this section we present the result of evaluation of three datasets: Guigó dataset [20], Génolevures [49] and TreeFam [50]. Datasets properties including the size of classes and the runtime are depicted in Table 1.
Datasets
Guigó dataset is a collection of 53 rooted gene trees from 16 Eucaryotes [20]. Multiple gene duplication events were inferred for two species trees: S1 from [51] and S2 from [20]. The comparison of the results for RME [44] and Algorithm 2 is shown in Fig. 5, where the original rooting of each gene tree was ignored in UME.
Génolevures consists of 4144 gene families from nine yeast genomes [49]. We used the corresponding gene family trees inferred by the authors of [52] using tools from Phylip [53]. The gene trees were reconciled with the species trees from [54] and [55]. The summary of duplication episodes found by our algorithms is depicted in Fig. 6.
Left: a summary of 100 duplication episodes found in Génolevures dataset [49] by Algorithm 5 for the species trees from [54]. Right: 91 duplication episodes found in the species tree from [55]. D2 and D2∗ denote one whole genome duplication (WGD) event suggested in [58, 59], while D1 and D1∗ denote one WGD event from [57]. The number of episodes assigned to a single edge is presented on the side (blue italic), for example, our algorithm found 13 duplication episodes in the rooting edge in both trees. A gray histogram (the right side of a node) denotes the frequency of gene trees (Y axis) being involved into exactly x (X-axis starting from 1) episodes located on the corresponding node. The number above the highest bar denotes the maximal number of such gene trees. For example, the gray histogram in the left tree with the second bar of the size 960 denotes that there are 960 gene trees contributing to exactly 2 episodes at the current node. Bars of frequency lower that 10 are not shown. A red bar on the left of a node denotes the number of gene trees having at least one duplication event mapped to this node, i.e., the sum of bars of the corresponding gray histogram
TreeFam consists of 1274 unrooted gene family trees [50] sampled from 28 mostly animal species. The species tree is based on NCBI taxonomy [56]. The summary of duplication episodes found by our algorithms is depicted in Fig. 7.
Two hundred twenty seven duplication episodes found by Algorithm 5 for the TreeFam dataset. The upper and lower bounds returned by our algorithms are the same, therefore, 227 is the exact solution. Please refer to Fig. 6 for the description of numbers and histograms. Two consecutive WGD events at D1 and one WGD event at D2 are reported in [60–62]
Discussion
Guigó dataset: The clustering for the species tree S1 indicates that UME algorithm found a better scenario than RME, i.e., 5 episodes vs. 6. Additionally, the duplication locations are generally in agreement with the solution to the unrooted variant of episode clustering (see more in [36]). Next, the result of RME for S2 is consistent with [20, 38]. However, in [37] authors suggested a different evolutionary scenario having more duplication episodes. The results differ, i.e., for the gene tree for β-nerve growth factor precursor (NGF) of topology (rept,(mamm,(amph,aves))) in the placement of two duplications inferred by that gene tree and S2. In the optimal solution from UME algorithm, the rooting of NGF gene tree is (aves,((mamm,rept),amph)) and it infers one duplication with S2.
Génolevures: We locate two genomic duplication events spanning a large number of gene trees in the left species tree: one situated at D1 (2638 trees) and the other above D2 (1064 trees). While in the right tree, we have three such events: at D1∗ (2228 trees) and the children of D1∗. There is a definite correspondence between the events located above D2 and D2∗. Next, we observe at least 960 trees participating in two duplication clusters at D1. Therefore, we postulate that D1 has at least two large genomic duplications. Also, they seem to correspond to two events from the right tree located at D1∗ and the left child of D1∗.
In comparison to the literature, we claim that the peaks at D1 and D1∗ match the whole genome duplication that was a direct consequence of ancient interspecies hybridization [57]. The location of a WGD event at D2 and D2∗ [58, 59] is not supported by our analysis. Based on UME clustering, the most likely location of such an event is their parent, i.e., the root of (ZYRO,(CAGL,SACE)).
TreeFam: The episode clustering (see Fig. 7) indicates several genomic duplications located at D1, D2, D3, D4 and D5. The dataset have only two plant genomes so it is inadequate to study WGD in plants. The same applies to yeasts (2 species), worms (2 species) and insects (6 species). The major part of TreeFam consists of Chordates, for which various studies [60–62] suggest the existence of two consecutive WGDs located at D1 as well as one WGD event at D2. Both are partially supported by our analysis by the presence of relatively large number of gene trees contributing to gene duplication events at these two nodes. The genomic duplication at D3 spans almost every tree from the dataset suggesting one WGD event, however, we did not find any evidence of such an event in the literature.
Conclusions
In this article, we proposed the first solution to the problem of minimum episodes clustering for the case when input gene trees are unrooted. We showed new properties of unrooted reconciliation for the duplication cost. Then, we proposed a decomposition of an unrooted gene tree that allows transforming a gene tree into a set of rooted trees and a simplified unrooted tree. Based on the tree decomposition, we designed several exact and heuristic algorithms for solving the problem. From the application point of view, the most important is an efficient heuristic algorithm, which in practice allows solving exactly empirical instances consisting of thousands of unrooted gene trees. Our evaluation on empirical datasets confirmed several genomic duplication events from the literature.
Future Work
Future work will focus on the open question of the complexity of UME (we conjecture that UME is intractable). Moreover, we plan to research on the applications of the developed theory to infer genomic duplication events from simulated and empirical datasets of unrooted gene trees including a comparative study of other models of duplication intervals [36].
Abbreviations
- D:
-
Gene duplication
- DL:
-
Gene duplication and loss
- lca:
-
Least common ancestor
- ME:
-
Minimum episodes clustering for rooted gene trees
- UME:
-
Minimum episodes clustering for unrooted gene trees
References
Kellis M, Birren BW, Lander ES. Proof and evolutionary analysis of ancient genome duplication in the yeast Saccharomyces cerevisiae. Nature. 2004; 428:617–24.
Guyot R, Keller B. Ancestral genome duplication in rice. Genome. 2004; 47(3):610–14.
Vision TJ, Brown DG, Tanksley SD. The origins of genomic duplications in Arabidopsis. Science. 2000; 290(5499):2114–7.
Costantino L, Sotiriou SK, Rantala JK, Magin S, et al. Break-induced replication repair of damaged forks induces genomic duplications in human cells. Science. 2014; 343(6166):88–91.
Cui L, Wall PK, Leebens-Mack JH, Lindsay BG, et al. Widespread genome duplications throughout the history of flowering plants. Genome Res. 2006; 16(6):738–49.
Aury JM, Jaillon O, Duret L, Noel B, et al. Global trends of whole-genome duplications revealed by the ciliate Paramecium tetraurelia. Nature. 2006; 444(7116):171–8.
Van de Peer Y, Maere S, Meyer A. The evolutionary significance of ancient genome duplications. Nat Rev Genet. 2009; 10(10):725–32.
Vandepoele K, Simillion C. Van de Peer Y. Evidence that rice and other cereals are ancient aneuploids. Plant Cell. 2003; 15(9):2192–202.
Sato S, Tabata S, Hirakawa H, Asamizu E, et al. The tomato genome sequence provides insights into fleshy fruit evolution. Nature. 2012; 485(7400):635–41.
Scossa F, Brotman Y, de Abreu e Lima F, et al. Genomics-based strategies for the use of natural variation in the improvement of crop metabolism. Plant Sci. 2016; 242:47–64.
Vanneste K, Maere S, Van de Peer Y. Tangled up in two: a burst of genome duplications at the end of the Cretaceous and the consequences for plant evolution. Philos Trans R Soc Lond B Biol Sci. 2014; 369(1648):17:1–17:12.
Tang H, Bowers JE, Wang X, Ming R, et al. Synteny and Collinearity in Plant Genomes. Science. 2008; 320(5875):486–8.
Holloway P, Swenson K, Ardell D, El-Mabrouk N. Ancestral Genome Organization: An Alignment Approach. J Comput Biol. 2013; 20(4):280–95.
Blanc G, Wolfe KH. Widespread paleopolyploidy in model plant species inferred from age distributions of duplicate genes. Plant Cell. 2004; 16(7):1667–78.
Bowers JE, Chapman BA, Rong J, Paterson AH. Unravelling angiosperm genome evolution by phylogenetic analysis of chromosomal duplication events. Nature. 2003; 422(6930):433–8.
Jiao Y, Wickett NJ, Ayyampalayam S, Chanderbali AS, et al. Ancestral polyploidy in seed plants and angiosperms. Nature. 2011; 473(7345):97–100.
Rabier CE, Ta T, Ané C. Detecting and locating whole genome duplications on a phylogeny: a probabilistic approach. Mol Biol Evol. 2014; 31(3):750–62.
Page RDM. Maps between trees and cladistic analysis of historical associations among genes, organisms, and areas. Syst Biol. 1994; 43(1):58–77.
Mirkin B, Muchnik I, Smith TF. A Biologically Consistent Model for Comparing Molecular Phylogenies. J Comput Biol. 1995; 2(4):493–507.
Guigó R, Muchnik IB, Smith TF. Reconstruction of ancient molecular phylogeny. Mol Phylogenet Evol. 1996; 6(2):189–213.
Arvestad L, Berglund AC, Lagergren J, Sennblad B. Bayesian gene/species tree reconciliation and orthology analysis using MCMC. Bioinformatics. 2003; 19 Suppl 1:i7–15.
Bonizzoni P, Della Vedova G, Dondi R. Reconciling a gene tree to a species tree under the duplication cost model. Theor Comput Sci. 2005; 347(1-2):36–53.
Noutahi E, Semeria M, Lafond M, Seguin J, et al. Efficient Gene Tree Correction Guided by Genome Evolution. PLoS ONE. 2016; 11(8):1–22.
Lafond M, Ouangraoua A, El-Mabrouk N. Reconstructing a SuperGeneTree minimizing reconciliation. BMC Bioinformatics. 2015; 16(14):S4.
Dondi R, Mauri G, Zoppis I. Orthology Correction for Gene Tree Reconstruction. Theor Exp Results Procedia Comput Sci. 2017; 108:1115–24.
Scornavacca C, Jacox E, Szöllősi GJ. Joint amalgamation of most parsimonious reconciled gene trees. Bioinformatics. 2014; 31(6):841–8.
Nakhleh L. Computational approaches to species phylogeny inference and gene tree reconciliation. Trends Ecol Evol. 2013; 28(12):719–28.
Zhu Y, Lin Z, Nakhleh L. Evolution after whole-genome duplication: a network perspective. G3: Genes, Genomes. Genetics. 2013; 3(11):2049–57.
Zheng Y, Zhang L. Effect of incomplete lineage sorting on tree-reconciliation-based inference of gene duplication. IEEE/ACM Trans Comput Biol Bioinform. 2014; 11(3):477–85.
Duchemin W, Anselmetti Y, Patterson M, Ponty Y, et al. DeCoSTAR: Reconstructing the ancestral organization of genes or genomes using reconciled phylogenies. Genome Biol Evol. 2017; 9(5):1312–9.
Goodman M, Czelusniak J, Moore GW, Romero-Herrera AE, et al. Fitting the Gene Lineage into its Species Lineage, a Parsimony Strategy Illustrated by Cladograms Constructed from Globin Sequences. Syst Zool. 1979; 28(2):132–63.
Doyon JP, Chauve C, Hamel S. Space of gene/species tree reconciliations and parsimonious models. J Comput Biol. 2009; 16(10):1399–418.
Ma B, Li M, Zhang L. From Gene Trees to Species Trees. SIAM J Comput. 2000; 30(3):729–52.
Stolzer M, Lai H, Xu M, et al. Inferring duplications, losses, transfers and incomplete lineage sorting with nonbinary species trees. Bioinformatics. 2012; 28(18):i409—i15.
Górecki P, DLS-trees TiurynJ. A model of evolutionary scenarios. Theor Comput Sci. 2006; 359(1-3):378–99.
Paszek J, Górecki P. Genomic duplication problems for unrooted gene trees. BMC Genomics. 2016; 17(1):165–75.
Page RDM, Cotton JA. Vertebrate phylogenomics: reconciled trees and gene duplications. Pac Symp Biocomput. 2002;:536–47.
Bansal MS, Eulenstein O. The multiple gene duplication problem revisited. Bioinformatics. 2008; 24(13):i132—8.
Burleigh JG, Bansal MS, Wehe A, Eulenstein O. Locating Multiple Gene Duplications through Reconciled Trees. Recomb LNCS. 2008; 4955:273–84.
Nøjgaard N, Geiß M, Merkle D, Stadler PF, et al. Forbidden Time Travel: Characterization of Time-Consistent Tree Reconciliation Maps In: Schwartz R, Reinert K, editors. 17th International Workshop on Algorithms in Bioinformatics, WABI 2017, August 21-23, 2017, Boston, MA, USA. vol. 88 of LIPIcs. Wadern: Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik: 2017. p. 17:1–17:12.
Mettanant V, Fakcharoenphol J. A Linear-Time Algorithm for the Multiple Gene Duplication Problem. NCSEC. 2008;:198–203.
Luo CW, Chen MC, Chen YC, Yang RWL, et al. Linear-Time Algorithms for the Multiple Gene Duplication Problems. IEEE/ACM Trans Comput Biol Bioinform. 2011; 8(1):260–5.
Burleigh JG, Bansal MS, Eulenstein O, Vision TJ. Inferring Species Trees from Gene Duplication Episodes. ACM BCB. 2010;:198–203.
Paszek J, Górecki P. Efficient Algorithms for Genomic Duplication Models; APBC 2017. IEEE/ACM Trans Comput Biol Bioinform. https://doi.org/10.1109/TCBB.2017.2706679.
Fellows M, Hallet M, Stege U. On the Multiple Gene Duplication Problem. ISAAC. LNCS. 1533; 1998:347–56.
Czabarka E, Székely L, Vision T. Minimizing the number of episodes and Gallai’s theorem on intervals; 2012. arXiv:12095699.
Górecki P, Tiuryn J. Inferring phylogeny from whole genomes. Bioinformatics. 2007; 23(2):e116—e22.
Górecki P, Eulenstein O, Tiuryn J. Unrooted Tree Reconciliation: A Unified Approach. IEEE/ACM Trans Comput Biol Bioinform. 2013; 10(2):522–36.
Sherman DJ, Martin T, Nikolski M, Cayla C, et al. Génolevures: protein families and synteny among complete hemiascomycetous yeast proteomes and genomes. Nucleic Acids Res. 2009; 37(suppl 1):D550—D4.
Ruan J, Li H, Chen Z, Coghlan A, et al. TreeFam: 2008 Update. Nucleic Acids Res. 2008; 36:D735—40.
Page RDM, Charleston MA. Reconciled trees and incongruent gene and species trees. DIMACS 96 Math Hierarchies Biol. 1997; 37:57–70.
Górecki P, Eulenstein O. Algorithms: simultaneous error-correction and rooting for gene tree reconciliation and the gene duplication problem. BMC Bioinformatics. 2012; 13(Suppl 10):S14.
Felsenstein J. PHYLIP. http://evolution.genetics.washington.edu/phylip.html.
Dujon B. Yeasts illustrate the molecular mechanisms of eukaryotic genome evolution. Trends Genet. 2006; 22(7):375–87.
Shen XX, Zhou X, Kominek J, Kurtzman CP, et al. Reconstructing the Backbone of the Saccharomycotina Yeast Phylogeny Using Genome-Scale Data. G3 (Bethesda). 2016; 6(12):3927–39.
Wheeler DL, Barrett T, Benson DA, Bryant SH, et al. Database resources of the National Center for Biotechnology Information. Nucleic Acids Res. 2007; 35(Database issue):5–12.
Marcet-Houben M, Gabaldón T. Beyond the Whole-Genome Duplication: Phylogenetic Evidence for an Ancient Interspecies Hybridization in the Baker’s Yeast Lineage. PLoS Biol. 2015; 13(8):1–26.
Capra JA, Pollard KS, Singh M. Novel genes exhibit distinct patterns of function acquisition and network integration. Genome Biol. 2010; 11(12):R127.
Hudson CM, Conant GC. Polyploidy and Genome Evolution In: Soltis PS, Soltis DE, editors. Yeast as a Window into Changes in Genome Complexity Due to Polyploidization. Berlin: Springer Berlin Heidelberg: 2012. p. 293–308.
Hufton AL, Groth D, Vingron M, Lehrach H, et al. Early vertebrate whole genome duplications were predated by a period of intense genome rearrangement. Genome Res. 2008; 18(10):1582–91.
Inoue J, Sato Y, Sinclair R, Tsukamoto K, et al. Rapid genome reshaping by multiple-gene loss after whole-genome duplication in teleost fish suggested by mathematical modeling. Proc Natl Acad Sci USA. 2015; 112(48):14918–23.
Braasch I, Postlethwait JH. Polyploidy and Genome Evolution In: Soltis PS, Soltis DE, editors. Polyploidy in Fish and the Teleost Genome Duplication. Berlin: Springer Berlin Heidelberg: 2012. p. 341–83.
Acknowledgements
We would like to thank the three reviewers for their detailed comments that allowed us to improve our paper. We thank Michał A. Ciach for helpful comments and discussion. JP was supported by the grant of National Science Centre NCN #2015/19/N/ST6/01193. JP and PG were supported by the grant of National Science Centre NCN #2015/19/B/ST6/00726.
Funding
The publication costs for this article were funded by the grant of National Science Centre NCN #2015/19/N/ST6/01193.
Availability of data and materials
The software is available on request.
About this supplement
This article has been published as part of BMC Genomics Volume 19 Supplement 5, 2018: Proceedings of the 15th Annual Research in Computational Molecular Biology (RECOMB) Comparative Genomics Satellite Workshop: genomics. The full contents of the supplement are available online at https://bmcgenomics.biomedcentral.com/articles/supplements/volume-19-supplement-5.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Additional information
Author’s contributions
JP and PG contributed equally to the writing of the paper. Both authors read and approved the final manuscript. JP implemented algorithms and performed all computational experiments.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver(http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Paszek, J., Górecki, P. Inferring duplication episodes from unrooted gene trees. BMC Genomics 19 (Suppl 5), 288 (2018). https://doi.org/10.1186/s12864-018-4623-z
Published:
DOI: https://doi.org/10.1186/s12864-018-4623-z