Background

The ultimate breeding goal of most Warmblood studbooks is to breed top sport horses, i.e. horses that are successful at the highest level in competitions [1]. Being successful in competitions implies being highly ranked and also participating in the most difficult competitions. Consequently, many breeding organizations use performance in competitions as the main trait in their breeding program. However, no common performance trait has ever been adopted by the different Warmblood studbooks [2]. In fact, since there is no gold standard, several breeding organizations have developed their own genetic evaluation for show jumping performance using custom phenotypes (Table 1). Some organizations use elementary performances (performances in a single competition), such as ranking in competitions, penalty points or earnings, which in some cases are transformed into more normally distributed variables [2]. Estimates of heritabilities are rather low (0.01–0.17) for these traits (Table 1). Summarized performances are an interpretation of multiple elementary performances of a horse over a year, over several years or over a lifetime. Such summarized performances show moderate heritabilities (0.31, 0.12–0.28 and 0.10–0.36, respectively) and represent the advantage of having only one observation per horse (Table 1). However, compared to a summarized phenotype, repeated measures may be more informative to estimate the genetic merit since some effects, such as the rider(s) and the other competitors in the events, can be taken into account.

Table 1 Review of reported heritability estimates for show jumping performance traits used in Europe
Full size table

Nevertheless, defining a precise phenotype solely does not guarantee the quality of a genetic evaluation since the inclusion of other non-genetic factors can heavily affect the outcome. In the equestrian world, there is debate on the rider effect [15, 19, 23,24,25,26]. First, show jumping horses cannot perform without a rider, and second, performance in competitions does not merely rely on a horse’s capacity but also on the quality of the rider and the relationship between horse and rider. Previous studies have shown that the rider effect accounts for a significant proportion of the variance (up to 37%) in genetic evaluations for performance in competitions [15, 19, 23,24,25]. However, this effect can be difficult to estimate when the number of horses per rider is small or when many horses are ridden by only one rider, since it can be confounded with the quality (genetic + permanent environment effects) of the horse. The Belgian model, currently used by the Belgian Warmblood horse (BWP) studbook [3], does not consider a rider effect.

To account for both the ranking (intra-competition variability) and the competition level (inter-competition variability) i.e. to differentiate the intra- from the inter-competition variability, two strategies are used in sport horse breeding. The first one uses a rank-based phenotype [3,4,5,6,7,8,9,10,11,12,13] and corrects for competition level in the genetic model by adding an event effect. A rank does not reflect competition level as there will always be a winner in competitions, regardless of the difficulty. Adding an event effect allows taking competition level into account by measuring the level of the competitors, i.e. their results in other competitions. The second strategy is to develop a phenotype based on arbitrary points that depend on ranking and competition level (Table 1). The number of these assigned points differs across countries (Table 1).

Here, we initiated a study to assess simultaneously the choice of the phenotype and the importance of the rider effect in order to generate an optimal model to evaluate the genetic merit of show jumpers. To this end, we developed a non-arbitrary method to distinguish the intra- from the inter- competition variability of performances by defining a new precise show jumping performance trait based on elementary performances from competition data, i.e. “adjusted fence height” (AFH). Then, we compared this model with other models that are based on elementary performances (Blom-transformed ranking (BTR)) or on a summarized performance (highest level achieved (HL)) to define the most suitable genetic model for show jumping performance in the Belgian Warmblood studbooks.

Methods

Datasets

Three datasets were provided by K.B.R.S.F. (Royal Belgian Sport Equestrian Federation). The first dataset contained competition results: ranking of the horse, its sport number (a unique number given by the organization), the  fault(s), the time of the rounds, the rider identification number and the competition identification number. The second dataset included event information: the identification number, date, and location of the competition, and the fence height. The third dataset consisted of horse information: the sport number of the horse, its Universal Equine Life Number (UELN), name and sex. In total, 2,436,461 show jumping competition records, reflecting individual placings of horses within the complete ranking of each competition, from events held between 2004 and 2019, were used in this study. Occurrences of horses per rider and riders per horse are given in Table 2. An integrated pedigree [27] containing BWP and Zangersheide (Z) pedigree information such as the UELN of the horses and of their parents and the birth dates (393,719 records) was used for the genetic analyses. Among those 393,719 pedigree records, 80,897 were informative i.e. for horses with show jumping performances or relatives of horses with own performances. The following criteria were used to link the data between datasets and to clean the data using custom R scripts [28]: (i) competition records that could not be linked to an event, with impossible ranking or with missing fence height (79,426 records), (ii) records that could not be linked to a sport number (131,775 records), (iii) records of horses that could not be linked to the pedigree via the UELN due to incomplete recording of UELN or presence of foreign horses (1,379,547 records), (iv) records of horses that were younger than 4 years or older than 18 years (21,670 records), and (v) records of riders that had competed with only one horse (149,516 records) were discarded, resulting in a final number of 674,527 records retained for further analysis. These competition records referred to 50,913 unique competitions, 26,351 different horses and 8410 unique riders.

Table 2 Occurrences of horses per rider and riders per horse in the initial dataset (n = 2,436,461 records)
Full size table

Models for analysis


First, a Blom transformation [29] was applied, which is an approximation of the “normal score” of ranks and depends on the rank and number of competitors. It was used on rankings from elementary performances resulting in Blom-transformed rankings:

$$Blom-transformed \, ranking={\Upphi}^{-1}\left(\frac{r - \frac{3}{8}}{n+ \frac{1}{4}}\right),$$

where \({\Upphi}^{-1}\) is the inverse standard cumulative normal distribution; \(r\) is the rank of an observation and \(n\) is the number of competitors in a competition. Blom-transformed rankings were limited to [− 2.76, + 2.76] in our data because there were, at most, 216 competitors in the same competition.

In addition to the frequently-used Blom-transformed ranking, a new phenotype “AFH” was defined using a non-arbitrary method to distinguish the intra- from the inter-competition variability of performances. For that purpose, the ranking and the competition level (defined here as fence height) were scaled by using a linear regression on the differences in fence height and the differences in Blom-transformed ranking. The differences were calculated within horses from consecutive performances in competitions (Table 3) resulting in the following regression line (r2 = 0.04):

Table 3 Descriptive statistics of differences in fence height and in Blom-transformed ranking
Full size table
$$\varDelta (Fence \, height) = -1.32 \times \varDelta (Blom{\text{-}}transformed \, ranking)+0.44.$$

We used the absolute value of the regression coefficient obtained to convert the differences in rankings, expressed as Blom-transformed rankings into the scale “fence height” in cm resulting in the following formula used to express AFH:

$$\mathrm{AFH}=\mathrm{Fence \, height}+ 1.32 \times \mathrm{Blom}\mathrm{-transformed \, ranking}.$$

AFH was then calculated for each elementary performance. In addition to the two rank-based phenotypes previously described, we constructed a summarized and career-linked trait as used in several countries and/or studbooks [16,17,18,19,20,21,22], i.e. the highest level achieved (HL). For each horse (n = 26,351), the highest AFH obtained during its career was extracted. Thus, in summary, three phenotypes were used in our study: two obtained from elementary performances (BTR and AFH) and one from a summarized performance (HL).

Variance components and breeding values for BTR, AFH and HL were estimated using univariate models with the remlf90 program, which is a part of the blupf90 family of programs [30]. Assessment of goodness-of-fit of the different models was based on Akaike’s information criterion (AIC) [31].

Genetic parameters for BTR, AFH and HL were estimated with the following models:


M1_BTR: \({y}_{ijkl}= \mu +{sex}_{i}+{age}_{j}+{animal}_{k}+{c}_{k}+{event}_{l}+{e}_{ijkl}\),


M2_BTR: \({y}_{ijklm}= \mu +{sex}_{i}+{age}_{j}+{animal}_{k}+{c}_{k}+{event}_{l}{+ rider}_{m}+{e}_{ijklm}\),


M1_AFH: \({y}_{ijk}= \mu +{sex}_{i}+{age}_{j}+{animal}_{k}+{c}_{k}+{e}_{ijk}\),


M2_AFH: \({y}_{ijkm}= \mu +{sex}_{i}+{age}_{j}+{animal}_{k}+{c}_{k}+{rider}_{m}+{e}_{ijkm}\),


M1_HL: \({y}_{ijk}= \mu +{sex}_{i}+{age}_{j}+{animal}_{k}+{e}_{ijk}\),


where \({y}_{ijkl}\) is the value of the trait (BTR, AFH or HL) for the kth animal; \(\mu\) is the population mean; \({sex}_{i}\) is the fixed effect of the sex of the horse (M, F, G); \({age}_{j}\) is the fixed effect of its age (from 4 to 18); \({animal}_{k}\) is the random additive genetic effect (from 1 to 80,897); \({c}_{k}\) is the permanent environment effect linked to animal \(k\), \({event}_{l}\) is the fixed effect of the event (from 1 to 50,913); \({rider}_{m}\) is the random effect of the rider (from 1 to 8410) and \({e}_{ijklm}\), \({e}_{ijkm}\), or \({e}_{ijk}\) is the random residual effect.

The influence of the rider effect was assessed by comparing the models M1_BTR with M2_BTR and M1_AFH with M2_AFH. Genetic correlations between the five models M1_BTR, M2_BTR, M1_AFH, M2_AFH and M1_HL were estimated using bivariate analyses.

Validation of the most suitable model

Two different groups of stallions were studied to validate the most suitable model for selection on success in show jumping competitions: (1) the approved stallions that meet the criteria for publication of their estimated breeding values (EBV), which for stallions in Belgium are currently: having an accuracy of EBV higher than 0.70 and having at least five offspring with own performances; and (2) the young stallions that were 4 to 5 years old with own performances but without offspring. Dubois et al. [32] showed that the optimal selection age was around 4 or 5 years old for males with own performances in competitions or in station test. The most appropriate/fitting models for BTR, AFH and HL were used to compare the two groups of stallions (1) and (2) in terms of: number of approved stallions that meet the criteria for EBV publication per model, number of young stallions that reach an EBV accuracy of at least 0.70, descriptive statistics for each group per model and Spearman rank correlations between EBV.

Results

The descriptive statistics and their distributions for BTR, AFH and HL are in Table 4 and Fig. 1. Values for BTR ranged from − 2.76 to 2.76 with a mean of 0.00 and those for AFH and HL ranged from 62.90 to 162.30 with means of 115.15 and 119.46, respectively.

Table 4 Descriptive statistics for BTR, AFH and HL
Full size table
Fig. 1
figure 1

Distributions of BTR, AFH and HL in show jumping competitions: a Blom-transformed ranking; b adjusted fence height; and c highest level

Full size image

The AIC values and estimated variance components for the different models applied to BTR, AFH and HL are in Table 5. The estimates of the heritabilities (h2) for BTR ranged from 0.06 to 0.09. The best-fit model for BTR was M2_BTR with an estimated heritability of 0.06. The estimates of the heritabilities for AFH ranged from 0.12 to 0.36. According to the AIC values, M2_AFH was the best-fit model. An intermediate heritability was found for HL (h2 = 0.39).

Table 5 AIC values and variance components of the models performed for BTR, AFH and HL
Full size table

When the model accounted for the rider effect (M2_BTR and M2_AFH), the AIC decreased for BTR and AFH, which means that including this effect improved the model fit, and their heritability estimate also decreased (0.09 ± 0.0051 vs 0.06 ± 0.0041 and 0.36 ± 0.0130 vs 0.12 ± 0.0061, respectively). For M2_BTR, the proportion of variance due to the rider effect was similar to that due to the permanent environment effect (0.08). Both these effects had a larger influence on M2_BTR than the additive genetic effect (0.08 ± 0.0033 > 0.06 ± 0.0041). For M2_AFH, the largest proportion of the variance was due to the rider effect (0.51): nearly four times that due to the permanent environment effect or the additive genetic effect. The permanent environment effect accounted for a slightly larger proportion of the variance than the additive genetic effect (0.14 ± 0.0048 > 0.12 ± 0.0061). Hence, both rider and environment effects had a larger influence on M2_AFH than the additive genetic effect.

The heritability estimated with the most appropriate/fitting model (M2_AFH, M1_HL, and M2_BTR) differed for the three performance traits, i.e. it was highest with M1_HL (h2 = 0.39), lowest with M2_BTR (h2 = 0.06) and low to moderate with M2_AFH (h2 = 0.12).

The estimated genetic correlations between M2_AFH, M1_HL and M2_BTR ranged from 0.60 to 0.99 (Table 6) and were highest between M1_AFH and M1_HL and between M2_AFH and M1_HL, and lowest between M2_AFH and M1_BTR. The estimated correlations of the permanent environment effects ranged from 0.73 between M2_BTR and M1_AFH to 0.99 between M1_BTR and M2_BTR.

Table 6 Estimated genetic correlations (rg) between models
Full size table

Table 7 shows the descriptive statistics for the two groups of stallions per model: proven stallions with an EBV that can be published and young stallions (4–5 years old) with own performances but without offspring. Since the stallions that meet publication criteria had more own records and more offspring than the young stallions, their mean EBV accuracy was higher for all the models (0.82–0.83 vs 0.60–0.70) and they were within the same range. However, their mean EBV was lower than that for the young stallions for all the models. Nevertheless, a smaller mean number of offspring was found for M2_AFH compared to the two other models. Young stallions reached the highest mean EBV accuracy with M2_AFH (0.70) and the lowest with M2_BTR (0.60).

Table 7 Descriptive statistics for the two groups of stallions
Full size table

The number of animals that reach an EBV accuracy higher than 0.70 per group of stallions and per model is shown in Fig. 2. More stallions met the publication criteria (accuracy ≥ 0.70 and at least five offspring) for M2_AFH (n = 841, 8.1% of all stallions) compared to M2_BTR and M1_HL with 654 (6.3% of all stallions) and 766 stallions (7.4% of all stallions), respectively. The same held for the young stallions, with 586 young stallions reaching an EBV accuracy of 0.70 or more for M2_AFH compared to only 514 and 52 for M1_HL and M2_BTR, respectively).

Fig. 2
figure 2

Number of stallions that reach an accuracy of estimated breeding value higher than 0.70: a stallions for which EBV can be published and b young stallions (4 to 5 years old). Publication criteria: having an accuracy of estimated breeding value ≥ 0.70 and at least five offspring with own performances

Full size image

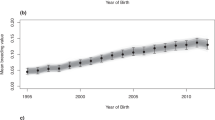
The range of birth years of the approved stallions that meet publication criteria did not differ (1949 to 2011) between traits (Fig. 3). However, regarding year of birth, stallions tended to be younger for M2_AFH and M1_HL (Fig. 4).

Fig. 3
figure 3

Number of stallions for which EBV can be published per birth year and per model. Publication criteria: having an accuracy of estimated breeding value ≥ 0.70 and at least five offspring with own performances

Full size image
Fig. 4
figure 4

Relationship between year of birth of stallions and their EBV for the a M2_BTR, b M2_AFH, and c M1_HL models

Full size image

Differences in Spearman rank correlations between EBV of approved stallions (that meet publication criteria) were also observed between models (Table 8), with values ranging from 0.69 to 0.88 and being highest (0.88) between M1_HL and M2_AFH and lowest (0.69) between M2_BTR and M1_HL and between M2_BTR and M2_AFH. Table 8 shows that the results obtained for the group of young stallions are similar to those of the approved stallions although their Spearman rank correlations were lower (r = 0.49–0.71 vs 0.69–0.88). The highest correlation was between M2_AFH and M1_HL and the lowest between M2_AFH and M2_BTR.

Table 8 Spearman rank correlations between EBV of approved stallions and young stallions
Full size table

Discussion

Ideally, genetic evaluations are based on EBV derived from informative phenotypes that can efficiently improve the breeding goal. In the case of show jumping, no single trait can be used to translate “success in competitions” into a measurable trait and several countries have developed their own custom phenotype since no gold standard has ever been adopted by the Warmblood studbooks. However, the same difficulty is encountered by any organization that aims at selecting for “success in competitions”, i.e. how can the intra-competition variability be differentiated from the inter-competition variability? Two different strategies are used in sport horse breeding for that purpose: (i) using a rank-based phenotype and correcting for the competition level by adding an event effect, or (ii) developing a phenotype based on (partly) arbitrary points that are assigned based on the ranking and competition level. Here, we studied BTR as a rank-based phenotype and developed a new phenotype AFH based on a non-arbitrary method that combines information from Blom-transformed rankings (ranking i.e. intra-competition variability) and fence height (competition difficulty i.e. inter-competition variability). In the genetic model used for BTR, an event effect was added to account for the inter-competition variability. However, in show jumping competitions, horses that compete in the same event(s) are not grouped at random i.e. they are pre-selected based on their level. Hence, adding an event effect is not sufficient because it cannot be estimated correctly and thus leads to biased EBV as shown in Ricard and Legarra [33]. Therefore, to account for intra- and inter-competition variability, it is better to use a phenotype such as AFH that measures directly ranking and competition difficulty from the data.

The use of traits based on elementary performances such as BTR and AFH allows the model to account for effects that are specific to each competition. Success in competitions is not only due to the horse’s jumping ability but also to the skills of the rider [34], thus accounting for a rider effect in the genetic model is relevant. Here, by comparing M1_BTR to M2_BTR and M1_AFH to M2_AFH, we showed that including a rider effect in the model improved the model fit according to the AIC values, which confirms previous studies in different equine disciplines: show jumping, dressage or trotting races [4, 15, 19, 23, 25]. Our estimated rider effect for AFH accounts for a larger proportion of the variance (0.51) than that cited in these papers, which may be due to a larger variation in riders’ skills and/or a larger number of riders in our data. In addition, by construction, we considered a zero correlation between rider effect and genetic effect. However, the comparison of M1_BTR with M2_BTR and of M1_AFH with M2_AFH showed that accounting for a rider effect decreased the residual variance and the sum of the genetic and permanent environment effects, which suggests that rider effect could be correlated with the genetic and permanent environment effects. Developing a model that includes an interaction between genetic and permanent environment effects could help dealing with this issue although convergence problems may occur. To alleviate this, we decided to filter the data by removing the records of horses that were ridden by only one rider (i.e. 6.1% of the total number of removed records). If these single rider performances are retained, distinguishing the rider effect from the horse effect would be more difficult and could lead to confounding effects as shown by Albertsdóttir et al. [35]. Contrary to traits based on elementary performances, a trait based on a summarized performance such as HL, does not allow accounting for differences between riders or only partly, when horses are ridden by several riders which is often the case in a horse career.

In this study, we evaluated two traits based on elementary performances (BTR and AFH) and one trait based on a summarized performance (HL). The heritability estimates for M2_AFH and M2_BTR (the best-fit models for AFH and BTR) are low but similar to those reported for traits related to jumping performance based on elementary performances (Table 1). For BTR, the heritability estimates range from 0.06 to 0.09 and are consistent with those reported for Belgian sport horses by Janssens et al. [3], which range from 0.02 to 0.10 although neither Z horses nor a rider effect were included (Table 1). M2_AFH presents a higher heritability estimate (0.12) than M2_BTR but it is still lower than the estimate obtained with M1_HL (0.39). With M1_HL the heritability estimate is a little higher than the range of estimates for the “highest level achieved in a career” traits found in the literature (from 0.10 to 0.36, see Table 1). The genetic correlations estimated between the models were high (0.60) to very high (0.99) (Table 6). The highest genetic correlations (rg = 0.99) were found between M1_AFH and M1_HL and between M2_AFH and M1_HL. The fact that M1_BTR and M2_BTR differentiate the intra- from the inter-competition variability only because an event effect was added to account for the level of competitors may be the reason why they generally had lower genetic correlations with M1_AFH (rg = 0.68 and 0.69), M2_AFH (rg = 0.60 and 0.72) and M1_HL (rg = 0.68 and 0.92). The Spearman rank correlations between the stallions’ EBV (approved and young stallions) (0.88 and 0.71 for M2_AFH and M1_HL and only 0.69 and 0.49 for M2_AFH and M2_BTR) also show that taking fence height and not only ranking into consideration results in a higher correlation between EBV for M2_AFH and M1_HL compared to the (lower) correlations with the EBV for M2_BTR.

In Belgium, two criteria are used to publish the EBV of stallions: having an EBV accuracy higher than 0.70 and at least five offspring with own performances. Published EBV are of great interest for breeders to help make mating choices. However, both the choice of the performance trait and the structure of the model have an impact on the list of stallions that meet the criteria. The use of M2_AFH would result in the largest number of stallions (841) (Fig. 3). Hence, this model returns more information to the breeders for making mating choices than M1_HL (766) or M2_BTR (654). The stallions for which EBV can be published based on M2_AFH and M1_HL also tend to be younger than the stallions based on M2_BTR, which indicates that the EBV of the stallions reach an accuracy of 0.70 at a younger age, hence with less own performances and/or fewer offspring with own performances. Moreover, more young stallions (4 to 5 years old with own performances but without offspring) reached an EBV accuracy of 0.70 with M2_AFH than with the other models (Fig. 2). Thus, our proposed AFH model will promote the use of younger stallions, which will impact generation interval and hence genetic progress.

Extending the current model by including a rider effect and using AFH presents substantial advantages to improve a selection program. As an axis for future research, including international competition records and not only national data could be interesting to assess the reproducibility of AFH and the added value of international data to the genetic evaluation.

Conclusions

In this paper, we propose and evaluate a novel phenotype, i.e. adjusted fence height, for the genetic evaluation of show jumping performance in Warmblood horses. This phenotype combines the fence height used in a competition with the final ranking of horses in this competition, and thus differentiates the intra- from the inter-competition variability by using a novel non-arbitrary method that can be extended to any show jumping competition dataset. This new trait, used in a model that includes a rider effect is moderately correlated with the Blom-transformed ranking and strongly correlated with lifetime success (highest level achieved). In addition, the use of this phenotype results in more approved stallions with publishable EBV, more young males reaching an EBV accuracy of 0.70 and thus more information for the breeders. A revision of the current Belgian model for show jumping performance is therefore advocated.