Application of a bending vibration method without weighing specimens to the practical wooden members conditions

Abstract

A vibration test to measure the mass of a specimen without weighing it using the difference between the resonance frequency with an additional mass and that without it (vibration method with additional mass, VAM) was applied to small, clear, and wooden specimens assuming practical situations. An apparatus that provided various end conditions by compressing the ends of the specimens was used in the tests. Bending vibration tests were performed on the specimens installed in the apparatus with/without an additional mass. Because the mass ratio (estimated mass by VAM/measured mass), namely, M_VAM/M₀, which represents the estimation accuracy of VAM, was stable when the compressive strength was sufficiently large, VAM could be adequately used when the specimen was properly installed in the apparatus. The end condition at maximum compressive stress by the apparatus was an imperfect fixed condition. The M_VAM/M₀ value greatly deviated from 1 in the specimens with a large height. The deviation in M_VAM/M₀ from 1 was due to the introduction of the measured resonance frequencies with/without a concentrated mass into the frequency equation that required resonance frequencies under an ideal fixed–fixed condition. A correction method for M_VAM/M₀ was then proposed.

Introduction

Vibration test is a simple and nondestructive testing method for measuring the Young’s modulus. Density is needed to calculate the Young’s modulus. Weighing a specimen requires much time in some cases, such as weighing of each piled lumber and each round bar that is fixed to a post of a timber guardrail.

The mass of a specimen can be measured without weighing the specimen using the difference between the resonance frequency with an additional mass and that without it [1,2,3,4,5]. In the present study, this method is referred to as the “vibration method with additional mass (VAM)”.

To analyze the potential practical application of VAM, a series of parameters was investigated, including the suitable mass ratio (additional mass/specimen) [6], connection between the additional mass and specimen [6], crossers’ position of piled lumber [7], moisture content of specimen [8], bending vibration generation method [9], and effects of shear and rotatory inertia in bending [10]. VAM can be applied to a timber guardrail cross-beam [11], piled lumber [12], and piled round bars [13].

The end conditions of the specimens in the abovementioned studies were simply supported, free, and fixed. However, the end conditions of actual wooden members do not represent these “ideal” conditions. For example, the end condition of a timber guardrail cross-beam is believed to be between the simply supported and fixed conditions, i.e., semi-rigid [14, 15]. Although the accurate mass of a timber guardrail cross-beam, which can reflect its deterioration, can be estimated using VAM when its attachment to the post is loose [11], the deterioration of the timber guardrail cross-beam can be more efficiently assessed without loosening the attachment. In addition, the underground end condition of wooden piles is semi-rigid [16]. The simply supported–simply supported condition has been used to estimate the density in traditional timber buildings using nondestructive tests [17].

The effect of the non-ideal conditions of specimens on VAM should be clarified for applying VAM to the wooden members that are practically used. This matter was examined by changing end conditions of specimens during vibration tests.

Theory

The bending vibrations under the simply supported–simply supported and fixed–fixed conditions are considered. In the case of a thin beam with a constant cross section, the effect of deflections due to shear and rotatory inertia involved in the bending vibrational deflection is negligible, and the Euler–Bernoulli elementary theory of bending can be applied to the bending vibration.

The resonance frequency, which is denoted by f_n0 (n refers to the resonance mode number and “0” denotes the value without an additional mass), can be expressed as follows:

$${f}_{n0}=\frac{1}{2\uppi }{\left(\frac{{m}_{n0}}{l}\right)}^{2}\sqrt{\frac{EI}{\rho A},}$$

(1)

where l, E, ρ, I, and A are the span, Young’s modulus, density, second moment of area, and cross-sectional area, respectively. m_n0 is a constant, which is expressed as follows:

$${m}_{n0}=n\uppi \left(\mathrm{simply\, supported}-\mathrm{simply\, supported \,condition}\right),$$

(2a)

$${m}_{10}=4.730, {m}_{20}=7.853, {m}_{30}=10.996, {m}_{n0}=\frac{1}{2}\left(2n+1\right)\uppi \left(n>3\right) \left(\mathrm{fixed}-\mathrm{fixed \,condition}\right).$$

(2b)

The resonance frequency is experimentally reduced by attaching an additional mass while the dimensions, density, and Young’s modulus are not altered. Hence, we can state that m_n0 changes to m_n. Thus, the resonance frequency after attachment of the additional mass is expressed as follows:

$${f}_{n}=\frac{1}{2\uppi }{\left(\frac{{m}_{n}}{l}\right)}^{2}\sqrt{\frac{EI}{\rho A}.}$$

(3)

Equations (1) and (3) yield

$${m}_{n}=\sqrt{\frac{{f}_{n}}{{f}_{n0}}}{m}_{n0}.$$

(4)

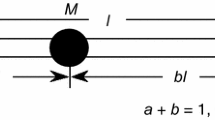
The frequency equation for the bending vibration with concentrated mass M placed at position x = al (x: distance along the bar, 0 ≤ a ≤ 1, a + b = 1) on a bar (Fig. 1) can be expressed as follows:

Fig. 1

Beam with an additional mass

$$\mathrm{sin}{m}_{n}\mathrm{sinh}{m}_{n}-\frac{1}{2}\mu {m}_{n}\left(\mathrm{sinh}{m}_{n}\mathrm{sin}a{m}_{n}\mathrm{sin}b{m}_{n}-\mathrm{sin}{m}_{n}\mathrm{sinh}{am}_{n}\mathrm{sinh}{bm}_{n}\right)=0\, \left(\mathrm{simply \,supported}-\mathrm{simply\, supported}\right),$$

(5a)

[18].

$$\left(\mathrm{cos}{m}_{n}\mathrm{cosh}{m}_{n}-1\right)-\frac{1}{2}\mu {m}_{n}\left\{\left(\mathrm{cos}{am}_{n}\mathrm{cosh}a{m}_{n}-1\right)\left(\mathrm{sin}b{m}_{n}\mathrm{cosh}{bm}_{n}-\mathrm{cos}b{m}_{n}\mathrm{sinh}{bm}_{n}\right)+\left(\mathrm{cos}{bm}_{n}\mathrm{cosh}b{m}_{n}-1\right)\left(\mathrm{sin}a{m}_{n}\mathrm{cosh}{am}_{n}-\mathrm{cos}a{m}_{n}\mathrm{sinh}{am}_{n}\right)\right\}=0 \left(\mathrm{fixed}-\mathrm{fixed}\right),$$

(5b)

where μ is the ratio of the concentrated mass to the mass of the bar and can be defined as follows:

$$\mu =\frac{M}{\rho Al}.$$

(6)

To calculate m_n, the measured resonance frequencies (f_n0 and f_n) are substituted into Eq. (4). Calculated m_n is substituted into Eqs. (5a) and (5b) to calculate μ. The specimen mass and density can be obtained by substituting calculated μ, the concentrated mass, and dimensions of the bar into Eq. (6). The Young’s modulus can be calculated by substituting the estimated density, resonance frequency without a concentrated mass, and dimensions of the bar into Eq. (1) [1,2,3,4,5]. The specimen mass is not required in these calculations.

These calculations illustrate the VAM procedure. In the present study, the estimation accuracy of VAM is expressed by the ratio of the specimen mass estimated using VAM (M_VAM) to the measured specimen mass (M₀). Here, M_VAM represents the product of the estimated mass using the VAM process and length-to-span ratio. The estimation accuracy of VAM in this study is considered to be sufficiently high at 0.9 ≤ M_VAM/M₀ ≤ 1.1.

Materials and methods

Specimens

Sitka spruce (Picea sitchensis Carr.) rectangular bars with a width of 25 mm (radial direction, R), heights of 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, and 25 mm (tangential direction, T), and a length of 300 mm (longitudinal direction, L) were used as specimens. The surface of each specimen was finished using a tip saw. Three specimens at each dimension were used. The specimens were conditioned at 20 °C and 65% relative humidity until weight became constant. All tests were conducted under the same conditions.

Free–free bending vibration test

To obtain the Young’s modulus by bending, free–free flexural vibration tests were conducted according to the following procedure [19]. The test bar was suspended using two threads at the nodal positions of the free–free vibration corresponding to its resonance mode. The bending vibration was initiated by hitting the LR-plane of the specimen at one end using a wooden hammer (hammer head size: 5 mm × 6 mm × 10 mm, 0.85 g), whereas the bar motion was monitored using a microphone (PRECISION SOUND LEVEL METER 2003, NODE Co., Ltd., Tokyo, Japan) at the other end. The signal was processed using a fast Fourier transform (FFT) digital signal analyzer (Multi-Purpose FFT Analyzer CF-5220, Ono-Sokki, Co., Ltd., Yokohama, Japan) to obtain high-resolution resonance frequencies (Fig. 2).

Fig. 2

Schematic diagram of the experimental setup for the free–free bending vibration test

A vibration test was conducted on a specimen without a concentrated mass, and the resonance frequencies in the 1st to 6th modes were measured. Young’s modulus (E_TGH) and shear modulus of the LT-plane (G_LT) were calculated using the Goens–Hearmon regression method based on the Timoshenko theory of bending (TGH method) [20,21,22]. The Young’s modulus in the absence of the effects of shear and rotatory inertia and shear modulus could be obtained using the TGH method for bending vibration.

Bending vibration test under a semi-rigid condition

The bending vibration tests under the semi-rigid condition were conducted according to the following procedure [14]. The apparatus (Takachiho Seiki Co., Ltd., End condition controller KS-200) shown in Fig. 3 was used to provide different end conditions. The 25 mm (L) × 25 mm (R) regions from both ends were supported by the posts of the apparatus whose cross section was 25 mm × 25 mm. Consequently, the span was 250 mm. The test bar was compressed by screwing a bolt attached to a load cell. It is thought that the vertical displacement was almost 0 and the rotation was partially restrained at both ends. The compression load was measured by the load cell and recorded using a data logger. Bending vibration was initiated by hitting the LR-plane of the specimen in the vertical direction at the center part using the aforementioned wooden hammer. The bar motion was detected by the aforementioned microphone installed at the center part. The signal was processed using the aforementioned FFT digital signal analyzer to generate high-resolution resonance frequencies. Because the stress relaxation was observed for each set compressive stress, the vibration test was conducted when the load change became sufficiently small.

Fig. 3

Schematic diagram of the experimental setup for the bending vibration test under various end conditions

Vibration tests were conducted on the specimen with and without a steel plate, which was used as the concentrated mass (1.29–7.55 g, as listed in Table 1) and the resonance frequency of the 1st mode was measured. The steel plate was bonded at x = 0.5 l on the LR-plane using a double-sided tape. The bending vibration test was performed using the same specimen without the concentrated mass during the increase in the compressive stress. After the bending vibration test at maximum compressive stress, which means the stress when loading was stopped in this study, the stress was reduced to 0. Subsequently, the concentrated mass was attached to the same specimen, and the bending vibration test was performed using the same specimen with the concentrated mass during the increase in the compressive stress. The compressive stress during the resonance frequency measurement with the concentrated mass and that without the concentrated mass were made to have the same value as much as possible.

Table 1 Concentrated masses (steel plates) attached to the specimens

Results and discussion

The mean and standard deviation of the density were 411 and 26 kg/m³, respectively, whereas those of the Young’s modulus and shear modulus of the LT-plane according to the TGH method were 11.52 and 0.97 GPa, 0.78 and 0.15 GPa, respectively.

Figure 4 shows an example of the changes in the estimation accuracy of VAM during the increase in compressive stress. The changes in M_VAM/M₀ were large at the early stage of loading specimens and M_VAM/M₀ became stable under the larger compressive stress. Because the compression set caused by the partial compression around the ends of the specimens was observed in the case of specimens with a larger height during the preliminary experiments, the maximum compressive stress for the specimens with a larger height was smaller than that for the specimens with a smaller height.

Fig. 4

Example of the changes in the estimation accuracy of VAM during the increase in compressive stress

Figure 5 shows an example of the changes in the measured resonance frequency without the concentrated mass (f_10M) during the increase in the compressive stress. The f_10M value increased with the increase in compressive stress and approached the value of ideal fixed ends for the 1st resonance mode (f_FF) (subscript FF: fixed–fixed). Here, f_FF was calculated by introducing E_TGH into Eq. (1).

Fig. 5

Example of the changes in the measured resonance frequency without the concentrated mass during the increase in compressive stress

Comparing Fig. 4 with Fig. 5, when M_VAM/M₀ was stable (larger than 0.5 MPa for height = 5 mm, larger than 1.7 MPa for height = 25 mm), f_10M was stable. In other words, VAM could not be adequately used when the specimen was not properly installed in the apparatus. Hence, M_VAM/M₀ at the maximum compressive strength was discussed hereafter.

Because f_10M was close to f_FF and was less than f_FF in the case of the specimen with a smaller height as shown in Fig. 5, the end condition was considered as an imperfect fixed condition in this study. Hence, the frequency equation under the fixed–fixed end condition, i.e., Eq. (5b) was used to estimate the specimen mass by VAM hereafter.

According to Fig. 6, M_VAM/M₀ increased with the increase in the specimen height (h), i.e., greatly deviated from 1 in the specimens with a larger height. The M_VAM/M₀ value was experimentally approximated as follows:

Fig. 6

Change in the mass ratio (estimated specimen mass by VAM/measured specimen mass) that indicates the estimation accuracy of VAM with respect to the specimen height

$$\frac{{M}_{\mathrm{VAM}}}{{M}_{0}}=0.0078927{h}^{2}-0.095749h+1.3336 \left(\mathrm{coefficient\, of\, determination}\hspace{0.17em}=\hspace{0.17em}0.98395\right).$$

(7)

We assume that the increase in M_VAM/M₀ shown in Fig. 6 is related to the result of f_10M < f_FF shown in Fig. 5. It is thought that f_10M < f_FF was caused by the deflections due to shear and rotatory inertia involved in the apparent deflection in the bending vibration [20] and semi-rigid condition.

The frequency equation taking into account the effects of shear and rotatory inertia under the fixed–fixed condition for a rectangular bar without the concentrated mass is expressed by Eq. (8) based on the boundary condition [23]:

$$2\left(\mathrm{cos}\beta {k}_{n0}\mathrm{cosh}\beta {k}_{n0}-1\right)+\left(\frac{\alpha \eta }{\beta \varepsilon }-\frac{\beta \varepsilon }{\alpha \eta }\right)\mathrm{sin}\beta {k}_{n0}\mathrm{sinh}\beta {k}_{n0}=0,$$

(8)

$$\alpha =\sqrt{\sqrt{{B}_{\mathrm{t}}^{2}{k}_{n0}^{4}+1}-{A}_{\mathrm{t}}{k}_{n0}^{2},}$$

(9)

$$\beta =\sqrt{\sqrt{{B}_{\mathrm{t}}^{2}{k}_{n0}^{4}+1}+{A}_{\mathrm{t}}{k}_{n0}^{2},}$$

(10)

$$\varepsilon =\sqrt{{B}_{\mathrm{t}}^{2}{k}_{n0}^{4}+1}+{B}_{\mathrm{t}}{k}_{n0}^{2},$$

(11)

$$\eta =\sqrt{{B}_{\mathrm{t}}^{2}{k}_{n0}^{4}+1}-{B}_{\mathrm{t}}{k}_{n0}^{2},$$

(12)

$${A}_{\mathrm{t}}=\frac{I}{2A{l}^{2}}\left(\frac{sE}{G}+1\right),$$

(13)

$${B}_{\mathrm{t}}=\frac{I}{2A{l}^{2}}\left(\frac{sE}{G}-1\right).$$

(14)

k_n and s are a constant and shear factor (= 1.2 for rectangular cross section). Substituting the measured E_TGH, G_LT and l/h into Eq. (8), k_n can be obtained. Mathematica 10.4J software (Wolfram Research Co., Ltd.) was used in the calculation. The relationship of Eq. (15) exists.

$${f}_{n0\mathrm{SR}}=\frac{1}{2\uppi }{\left(\frac{{k}_{n0}}{l}\right)}^{2}{\sqrt{\frac{EI}{\rho A}}\, \left(\mathrm{subscript\ SR}:\mathrm{ shear \,and\, rotatory\, inertia}\right).}$$

(15)

From Eqs. (1) and (15),

$$\frac{{f}_{n0\mathrm{SR}}}{{f}_{\mathrm{FF}}}={\left(\frac{{k}_{n0}}{{m}_{n0}}\right)}^{2}.$$

(16)

The frequency ratios of f_10SR/f_FF and f_10M/f_FF were plotted against l/h in Fig. 7. The f_10M/f_FF value was smaller than f_10SR/f_FF. It is thought that the difference between f_10SR/f_FF and f_10M/f_FF were caused by the semi-rigid condition at the end. The difference increased with the decrease in l/h.

Fig. 7

Change in the frequency ratio without the concentrated mass with respect to the span-to-height ratio

In the previous study, M_VAM/M₀ decreased with the decrease in l/h under the free–free condition [10] while the opposite tendency is observed in Fig. 6. We think that semi-rigid condition more strongly affected M_VAM/M₀ rather than the effects due to shear and rotatory inertia.

The M_VAM/M₀ value that was larger than 1 was discussed. The VAM procedure expressed by Eqs. (1)–(5) are based on the assumption that a specimen is under the ideal conditions, however, the measured resonance frequencies with and without the concentrated mass subjected to the effect of the non-ideal condition (f_1M, f_10M) were used as f₁ and f₁₀ for VAM (Eq. (4)), respectively, in the “Results and discussion” Section. Because m₁₀ = 4.73 for the ideal condition was substituted into Eq. (4), the resonance frequency ratio f_1M/f_10M was discussed.

The relationship between f_n/f_n0 and f_nM/f_n0M was experimentally investigated. Ideal m_n/m_n0 could be calculated by substituting the measured mass ratio = (measured concentrated mass)/(measured specimen mass) into Eq. (5b). Mathematica 10.4J software was used in the calculation. By substituting the obtained m_n/m_n0 into Eq. (4), ideal f_n/f_n0 can be calculated.

Here, degree of ideality (DI) was defined as:

$$DI=\frac{{f}_{10\mathrm{M}}}{{f}_{\mathrm{FF}}}\left(\le 1\right),$$

(17)

where DI = 1 indicates the ideal condition of specimens and DI < 1 indicates that a specimen deviates from the ideal condition. According to Fig. 7, DI was experimentally approximated as follows:

$$DI=-3.9223\times {10}^{-7}{\left(\frac{l}{h}\right)}^{4}+5.837\times {10}^{-5}{\left(\frac{l}{h}\right)}^{3}-0.0033909{\left(\frac{l}{h}\right)}^{2}+0.095073\frac{l}{h}-0.18954 \left(\mathrm{coefficient\, of\, determination}\hspace{0.17em}=\hspace{0.17em}0.99639\right).$$

(18)

The ratio (f_1M/f_10M)/(f₁/f₁₀) was plotted against DI (Fig. 8), and a liner relationship existed at 1% significance level as follows:

Fig. 8

Change in the frequency ratio (measured value/theoretical value) with respect to the degree of ideality

$$\frac{{f}_{1\mathrm{M}}/{f}_{10\mathrm{M}}}{{f}_{1}/{f}_{10}}=-0.1806DI+1.1675 \left(\mathrm{correlation \,coefficient }= 0.96386\right).$$

(19)

Since f_1M/f_10M > f₁/f₁₀ as shown in Fig. 8, m₁ obtained by substituting f_1M/f_10M into Eq. (4) was larger than m₁ under the ideal condition. According to the previous study [4], m_n theoretically decreases with the increase in μ under the fixed–fixed condition. The M_VAM value increases with the decrease in μ from Eq. (6). Therefore, M_VAM/M₀ under the non-ideal condition was larger than that under the ideal condition.

The M_VAM value could be corrected by according to the following procedure. Measured l/h was substituted into Eq. (18) to estimate DI. Substitution of the estimated DI and the measured f_1M and f_10M into Eq. (19) yielded the estimation of f₁/f₁₀. The m₁ value was estimated by substituting the estimated f₁/f₁₀ and m₁₀ = 4.73 into Eq. (4). The μ value was estimated by substituting the estimated m₁ and the position of the concentrated mass into Eq. (5b). The M_VAM value was corrected with the substitution of the estimated μ into Eq. (6). The corrected M_VAM/M₀ is shown in Fig. 9. Many results could be improved using this correction method.

Fig. 9

Corrected mass ratio (estimated specimen mass by VAM/measured specimen mass) at various span-to-height ratios

Conclusions

VAM was applied to small clear specimens under conditions where wooden members are expected to be practically used, and the following results were obtained:

• 1. VAM could not be adequately used when the specimen was not properly installed in the apparatus.

• 2. Because f_10M was close to f_FF and was less than f_FF in the case of the specimen with a smaller height, the end condition at the maximum stress was considered as an imperfect fixed condition in this study.

• 3. M_VAM/M₀ increased with the increase in the specimen height and greatly deviated from 1 in specimen with a larger height.

• 4. The deviation in M_VAM/M₀ from 1 was due to the substitution of the measured resonance frequencies into the frequency equation that required the resonance frequencies under the ideal fixed–fixed condition.

• 5. A correction method for M_VAM/M₀ was subsequently proposed.