1 Introduction

Suspension system performs the significant influence on vehicle ride comfort. The design of new suspension configurations and matching of corresponding structural parameters is very important to attenuate the vibration excitation from the roads, and to maintain tire-road contact [1]. Due to significant load changes and complex driving conditions, commercial vehicles have higher requirements for suspension. Pneumatic suspension is a kind of suspension with a non-linear stiffness and a low natural frequency [2], which is widely used in commercial vehicles and passenger vehicles [3]. For past decades, according to the vibration isolation theory [4], the non-linear characteristics of pneumatic suspensions have an extremely complex effect on the overall vehicle performance and have attracted researchers’ attention [5, 6]. Compared with the traditional metal suspension system, the vehicle equipped with pneumatic suspension system can adjust the vehicle height in real time with the change of driving conditions. Further, the pneumatic suspension system with quasi-zero stiffness structural characteristics can not only ensure the original load-bearing capacity, but also further reduce the natural frequency and improve the comprehensive vibration isolation performance of the vehicle [7], especially the low frequency and ultra-low frequency vibration isolation performance [8]. The advantage of quasi-zero stiffness in vehicle vibration isolation has led to a continuous increase in attention in this field.

The scope of research on quasi-zero stiffness is very extensive and has been going through a considerable period of time. Molyneux [9] first introduced the concept of Quasi-zero Stiffness (QZS) with one spring placed vertically and two springs placed horizontally, which is the most typical structure: the three-spring QZS suspension system. Based on this, Carrella et al. studied characteristics of such QZS systems, including static analysis [10], static optimization [11], and force transmissibility analysis [12]. This structure has low dynamic stiffness and high static stiffness which is widely used in practice. However, this structure cannot change the positive and negative stiffness and is only suitable for systems with constant isolation mass. Hao et al. [13] conducted a comprehensive dynamic analysis about the force transmissibility of the QZS suspension system through an exact motion equation model. Further, they proposed a two-sided damping constraint control strategy for QZS isolator, which can effectively isolate shock and swiftly stabilize the transient state into the steady state response [14]. The above researches are all studies on the inherent characteristics of quasi-zero stiffness isolators, and have not yet been applied to specific objects. Inspired by the three-spring isolator, researchers explore additional implementation structures for QZS-based vibration isolation theory. More realistically, they started putting QZS isolators into specific application scenarios. Complex ways to realize the negative stiffness like cam-roller-spring [15], magnetic spring [16], cylinders [17] were implemented. They applied the magnetic one in a conceptually designed platform [18], which can achieve 6-DOF low-frequency vibration isolation. Sun et al. [19] utilized magnetic spring as a negative stiffness component and analyzed the effective isolation band. Meanwhile, they applied this structure to the Stewart platforms to improve its isolation performances in all six directions [20]. However, the existing quasi-zero stiffness isolation systems are mostly applied to fixed high-precision instruments, and the range of vibration isolation is small, which is more difficult to apply to mobile vehicles.

Generally, QZS isolators are applied to mechanical or electromechanical structures and most were designed based on a constant sprung mass. Although there have been some studies on the application of quasi-zero stiffness isolators in vehicle suspensions, they are also designed based on load invariance. However, the load of commercial vehicles significantly and frequently changes [21]. This leads to insufficient vibration isolation frequency bands for traditional commercial vehicle suspensions based on fixed load design, which cannot adapt to load changes from unloaded to fully loaded. Therefore, this article proposes a new type of GIQZSPS to improve the vibration isolation performance of commercial vehicle suspension systems under frequent load changes. Pipes are used to connect air chambers between positive stiffness pneumatic suspension and negative stiffness cylinders. By controlling the solenoid valve on pipelines, the working state of the system can be adjusted to adapt to frequently changing loads. The static and dynamic characteristics of GIQZSPS system are analyzed in different states. The main contributions of this paper are summarized as follows.

  1. (1)

    A new semi-active structure of GIQZSPS system is realized by controlling the solenoid valves, which can obtain different dynamic characteristics for vehicles’ different driving conditions.

  2. (2)

    GIQZSPS structure parameters influencing the dynamic stiffness characteristics and comprehensive vibration isolation performance are analyzed.

  3. (3)

    A dimensionless model of GIQZSPS system is proposed, and non-linear dynamics characteristics of both two operating states are analyzed by numerical simulation.

The rest of this paper is organized as follows. A mathematical model of GIQZSPS system in the disconnected and the connected states are developed in Section 2. In Section 3, the effect of load and damping on the dynamic characteristics of GIQZSPS system is given using the frequency response. The experimental set-up and results are presented in Section 4, followed by the conclusions in Section 5.

2 Nonlinear Modelling of GIQZSPS System

2.1 Structure Description of GIQZSPS

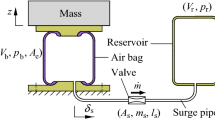
The proposed GIQZSPS is composed of an air spring, two pairs of double-direction acting cylinders, connection pipelines and solenoid valves. The air spring provides positive stiffness force to support system load. Double-direction acting cylinders are arranged in both sides of air spring to provide negative stiffness force. The position shown in Figure 1 is the static equilibrium position. By precisely designing structure parameters, the dynamic stiffness can approach quasi-zero. Furthermore, solenoid valves are applied to regulate the opening or closing of the pipeline connecting the air chambers between the positive and negative stiffness components.

Figure 1
figure 1

Schematic of configuration of GIQZSPS system

Full size image

2.2 Nonlinear Modelling of GIQZSPS in the Disconnected State

The dynamic model of GIQZSPS system in disconnected state includes the model of air spring and cylinders. Figure 2 shows the motion of GIQZSPS system with all solenoid valves closed, where the pneumatic suspension is in a disconnected state with double-direction acting cylinders. Due to external excitation such as road profile, the pneumatic suspension restoring force \(F_{r}\), in the vertical direction can be expressed as

$$F_{r} = F_{s} - 4F_{PLA} \sin \theta,$$
(1)

where \(F_{s}\) is the vertical spring force, and \(F_{PLA}\) is the force generated by a pair of double-direction pneumatic cylinders.

Figure 2
figure 2

QZS pneumatic isolator diagram

Full size image

For the positive stiffness system, the stiffness model of pneumatic suspension can be derived explicitly as

$$K = n(P_{0a} + P_{a} )\frac{{A_{e}^{2} }}{{(V_{0} - A_{e} z)}},$$
(2)

where K is the pneumatic suspension stiffness, \(n\) is the gas polytropic index, this value depends on the gas flow rate inside the air spring. \(n\) is generally chosen as 1.3–1.4, and it can be regarded as an adiabatic process, \(P_{0a}\) is the initial air pressure of the air spring, \(P_{a}\) is atmospheric pressure, \(P_{0c}\) is the initial air pressure of the negative stiffness cylinder, \(A_{e}\) is the effective area of the pneumatic actuator piston, \(V_{0}\) is the initial volume in the air spring, and \(z\) is the displacement of the sprung mass relative to the initial position.

As illustrated in Figure 3, the global static stiffness characteristics of this isolator depends on the air spring initial pressure \(P_{0c}\), atmosphere \(P_{a}\) and the angular deviation \(\theta\) of cylinders from its horizontal reference. In the equilibrium position, the distance between two hinged points is \(L_{0}\). When the sprung mass moves z, the cylinder turns an angle \(\theta\). The distance of piston moves inside the cylinder is d. The relationship between those parameters can be expressed as

$$\theta { = }\arctan \left( {\frac{{z - z_{0} }}{{L_{0} }}} \right).$$
(3)
Figure 3
figure 3

Double-direction pneumatic cylinder diagram

Full size image

Correspondingly, the piston moves \(d\):

$$d = \sqrt {L_{0}^{2} + (z - z_{0} )^{2} } - L_{0}.$$
(4)

The vertical restoring force can be rewritten as follows:

$$\begin{aligned} F_{r} & = n(P_{0A} + P_{a} )\frac{{A_{e}^{2} }}{v}z \\ & \quad - 4A\left[ {P_{0c} \left( {\frac{{d_{0} }}{{d_{0} + \sqrt {L_{0}^{2} + z^{2} } - L_{0} }}} \right)^{n} - P_{a} } \right]\text{sin}\theta. \\ \end{aligned}$$
(5)

In the formula, A is the cross-sectional area of the double-direction pneumatic cylinder, and v is the volume of the air spring after being stretched or compressed. Define the following dimensionless coefficients as

$$\begin{aligned} \varphi & = \frac{\alpha }{{\alpha - 1 + \sqrt {1 - \gamma^{2} } }} \cdots \beta_{0} = \frac{{P_{0a} }}{{P_{a} }}...\beta_{1} = \frac{{P_{0c} }}{{P_{a} }} \cdots \\ \alpha & = \frac{{d_{0} }}{{L_{0} }} \cdots \gamma = \frac{z}{{L_{0} }} \cdots \lambda = \frac{A}{{A_{e} }} \cdots \varepsilon = \frac{{V_{0} }}{{A_{e} L_{0} }}. \\ \end{aligned}$$

In term of dimensionless form, Eq. (5) is rewritten as

$$\begin{aligned} F_{{\text{r}}} & = F_{S} - F_{N} = n(\beta_{0} + 1)\frac{\delta }{\varepsilon - \delta } \\ & \quad - 4\lambda \left[ {\beta_{1} \left( {\frac{\alpha }{{\alpha + \sqrt {1 + \delta^{2} } - 1}}} \right)^{n} - 1} \right]\frac{\delta }{{\sqrt {1 + \delta^{2} } }}. \\ \end{aligned}$$
(6)

By differentiating Eq. (6) with respect to the dimensionless displacement \(\delta\), the dimensionless non-linear stiffness \(\hat{K}_{r}\) of GIQZSPS system in the disconnected state is obtained as

$$\begin{aligned} \hat{K}_{r} & = n(\beta_{0} + 1)\frac{\varepsilon }{{(\varepsilon - \delta )^{2} }} - 4\lambda \beta_{1} \left[ {\varphi^{n} \frac{1}{{(1 + \delta^{2} )^{\frac{3}{2}} }}} \right. \\ & \quad \left. - n\frac{{\delta^{2} }}{{\alpha (1 + \delta^{2} )}}\varphi^{n + 1} \right] - 4\lambda \frac{1}{{(1 + \delta^{2} )^{\frac{3}{2}} }}. \\ \end{aligned}$$
(7)

To analyze dynamic characteristics of the quasi-zero stiffness system, the structure parameters should satisfy some quantitative equations [22]. The quasi-zero stiffness is supposed to occurs near the equilibrium [23]. That means the stiffness \(\hat{K}_{r} = 0\) when \(\delta = 0\). By incorporating this equation into Eq. (7), it can be calculated that the necessary condition for the system stiffness to achieve quasi-zero can be obtained as follows:

$$n(\beta_{0} + 1)\frac{1}{\varepsilon } - 4\lambda \beta_{1} - 4\lambda = 0.$$
(8)

As shown in Eq. (8), it can be found that system stiffness \(\hat{K}_{r}\) is influenced by parameters \(P_{0c}\), \(L_{0}\) and \(d_{0}\).

2.3 Nonlinear Modelling of GIQZSPS in the Connected State

In connected state, the air spring and four double-direction acting cylinders are linked by pipelines. As shown in Figure 4, when valve 1 and 2 are open, the gas flow between the cylinders and the air spring is allowed to exchange. And connecting pipeline diagram is shown in Figure 5. The systematic analysis reveals that the pressure, volume and mass of the cylinders changes dramatically. GIQZSPS can be regarded as an adiabatic process without heat exchange between the gas and the external environment [24,25,26]. Based on the above assumptions, the GIQZSPS composed of air spring, pipelines and double-direction acting cylinders can be divided into three parts. It includes mathematical model of state parameters of air spring and double-direction acting cylinders, pipeline model and mass exchange model. According to the process of suspension compression, the mathematical model of GIQZSPS system is established theoretically. The modeling process is as follows.

Figure 4
figure 4

GIQZSPS system in connected state

Full size image
Figure 5
figure 5

Connecting pipeline diagram

Full size image

Then, the gas state can be expressed as follows:

$$p\left( \frac{V}{m} \right)^{k} = cons.$$
(9)

The instantaneous mass and volume of air in each chamber is calculated as

$$m = m_{0} + \int_{0}^{t} {\dot{m}\text{d}t},$$
(10)
$$V = V_{0} - A_{e} \cdot d.$$
(11)

Compressed gas exchange between the air spring and double-direction cylinders mainly depends on the flow characteristics of the pipe. Therefore, the accurate mathematical description of the flow can better reflect the dynamic characteristics.

Two ends of the pipe are simplified into two throttling holes with the same cross-sectional area. Therefore, flow area \(S_{{\text{e}}}\) can be calculated by multiplying the square of pipeline inner diameter \(D\). The mass flow rate of gas flowing through the pipeline can be expressed as

$$q_{m} = \left\{ {\begin{array}{*{20}c} { - S_{e} P_{1} \sqrt {\frac{k}{{RT_{1} }}\left( {\frac{2}{k + 1}} \right)^{{\frac{k + 1}{{k - 1}}}} } }, & {\frac{{P_{2} }}{{P_{1} }} \le b}, \\ { - S_{e} P_{1} \sqrt {\frac{2k}{{(k - 1)RT_{1} }}\left[ {\left( {\frac{{P_{2} }}{{P_{1} }}} \right)^{\frac{2}{k}} - \left( {\frac{{P_{2} }}{{P_{1} }}} \right)^{{\frac{k}{k + 1}}} } \right]} }, & {b < \frac{{P_{2} }}{{P_{1} }} \le {1}}. \\ \end{array} } \right.$$
(12)

Among them, \(P_{1}\) is the gas pressure at the pipeline inlet, \(P_{2}\) is the gas pressure at the pipeline outlet, \(T_{1}\) is the gas temperature at the pipeline inlet, \(R\) is the gas related parameter, and its value is \(R = 287\,\,\text{N} \cdot \text{m}/(\text{kg} \cdot \text{K)}\). Where b is critical pressure ratio. The disconnected state can be seen as a special situation with the area of throttle orifice zero, \(S_{e} = 0\). Meanwhile, considering the pipe length, internal friction and other factors, the dynamic distribution model of pipe flow is used to reflect the pressure loss along the pipe and the hysteresis of air transmission [27], so that the model can be more accurately described as

$$\dot{m}_{p} (l,t) = \left\{ {\begin{array}{*{20}c} 0, & {t{ < }\frac{l}{a}}, \\ {e^{{ - \frac{{RR_{t} T_{{2}} l}}{{2P_{{2}} }}\frac{l}{a}}} \dot{m}_{p} \left( {0,t - \frac{l}{a}} \right)}, & {t > \frac{l}{a}}. \\ \end{array} } \right.$$
(13)

In the formula, l is the length of the pipeline; a is the speed of sound, taken as 345.2 m/s and t is the time for gas to flow through the pipeline. In addition, gas mass exchange will occur in the suspension system when air chambers are connected. In the process of vehicle vibration, there is a certain pressure difference between the air spring and the double-direction acting cylinder due to the different internal gas pressure change speed. Because of the existence of pipeline, the two can exchange mass. The mass exchange between the air spring and the double-direction acting cylinder is shown in Figure 6.

Figure 6
figure 6

Gas Mass exchange of the connected state

Full size image

In fact, the connected state is to use the pipeline to realize the mass exchange of gas in the positive and negative stiffness air chamber. During the vibration process, the mass parameters of the air spring and the double-direction acting cylinder model also need to be changed in time. When the system is connected, the positive and negative stiffness elements of each suspension generate gas flow and exchange through the pipeline. With the central air spring as the reference point, the instantaneous mass of gas in each air chamber is as follows:

$$\left\{ \begin{aligned} m_{a} & = m_{a0} + \int_{0}^{t} {\dot{m}_{ac1} } \text{d}t + \int_{0}^{t} {\dot{m}_{ac2} } \text{d}t + \int_{0}^{t} {\dot{m}_{ac3} } \text{d}t + \int_{0}^{t} {\dot{m}_{ac4} } \text{d}t, \\ m_{c1} & = m_{c10} - \int_{0}^{t} {\dot{m}_{ac1} \text{d}t}, \\ m_{c2} & = m_{c20} - \int_{0}^{t} {\dot{m}_{ac2} \text{d}t}, \\ m_{c3} & = m_{c30} - \int_{0}^{t} {\dot{m}_{ac3} \text{d}t}, \\ m_{c4} & = m_{c40} - \int_{0}^{t} {\dot{m}_{ac4} \text{d}t}, \\ \end{aligned} \right.$$
(14)

where \(\dot{m}_{aci}\) is the mass flow of pipeline gas when the gas in the negative stiffness chamber \(i\) flows to the air spring. Combined with the state model of air and double-direction acting cylinder and the pipeline mass flow model mentioned above, the corresponding simulation model is built in the MATLAB/Simulink environment, as shown in Figure 7.

Figure 7
figure 7

MATLAB/Simulink model

Full size image

3 Nonlinear Dynamic Analysis of GIQZSPS System

3.1 Frequency Response of GIQZSPS

The stiffness characteristic is a part of the dynamic characteristic of the system. Dynamic analysis is an important means of exploring system characteristics. The force displacement relationship of the quasi-zero stiffness vibration isolation system can be approximated as a cubic polynomial which is shown in Figure 3. The restoring force in the disconnected state can be approximately obtained by Taylor series expansion [28] at \(z = 0\) and push to

$$\begin{aligned} F & = \left( {k - 4A[P_{{0{\text{c}}}} - P_{a} ]\frac{1}{{\sqrt {L_{0}^{2} + z^{2} } }}} \right)z \\ & \quad + \left( {2A[P_{{0{\text{c}}}} - P_{a} ]\frac{1}{{\left( {\sqrt {L_{0}^{2} + z^{2} } } \right)^{3} }}} \right)z^{3}. \\ \end{aligned}$$
(15)

In the complex connected state of GIQZSPS system, the force-displacement fitting cubic term is used to simplify the calculation as follows:

$$F_{{}} = k_{1} z + k_{2} z^{3}.$$
(16)

The quasi-zero stiffness vibration isolation system is shown in Figure 8. It includes the mass m on the spring and the external damper with damping coefficient is \(c\). The GIQZSPS system composed of vertically placed air springs and two pairs of horizontally fixed double-direction acting cylinders, as well as the connecting rod and other mechanisms. Under the action of simple harmonic exciting force \(f = F\cos \omega t\), the mass vibrates up and down near the equilibrium position. The force acting on the ground by the system is \(f_{t}\).

Figure 8
figure 8

QZS isolator force transfer structure diagram

Full size image

Under the action of external harmonic excitation force \(f = F\cos \omega t\), the mass oscillates up and down near the equilibrium position. The dimensionless form of the system dynamics equation can be changed to

$$\ddot{\hat{x}} + 2\xi \omega_{0} \dot{\hat{x}} + \omega_{0}^{2} (\hat{x} + \varepsilon \hat{x}^{3} ) = \hat{F}\text{cos}\omega^{{}} t.$$
(17)

In the formula, \(\xi = \frac{c}{{2\sqrt {k_{1} m} }}\), \(\omega_{0} = \sqrt {\frac{{k_{1} }}{m}}\), \(\varepsilon = \frac{{k_{2} }}{{k_{1} }}\). The periodic response of the system can be written as:

$$\hat{x}(t) = A\cos (\omega t + \varphi ).$$
(18)

Substituting Eq. (18) into Eq. (17) yields:

$$\begin{aligned} & (\omega_{0}^{2} - \omega^{2} )A\text{cos}(\omega t + \varphi ) - 2\xi \omega_{0} \omega A\text{sin}(\omega t + \varphi ) \\ & \quad + \varepsilon \omega_{0}^{2} A^{3} \text{cos}^{3} (\omega t + \varphi ) = \hat{F}\text{cos}\omega t. \\ \end{aligned}$$
(19)

By ignoring higher-order harmonic terms, the coefficients of the second and third terms equal to zero. Therefore, the following equation can be obtained

$$\left\{ \begin{gathered} (\omega_{0}^{2} - \omega^{2} )A + \frac{3}{4}\varepsilon \omega_{0}^{2} A^{3} = \hat{F}\text{cos}\varphi, \\ - 2\xi \omega_{0} \omega A = \hat{F}\text{sin}\varphi. \\ \end{gathered} \right.$$
(20)

The system amplitude frequency response function can be obtained by subtracting the phase from Eq. (20) as follows:

$$\left[ {(\omega_{0}^{2} - \omega^{2} )A + \frac{3}{4}\varepsilon \omega_{0}^{2} A^{3} } \right]^{2} + \left( { - 2\xi \omega_{0} \omega A} \right)^{2} = \hat{F}^{2}.$$
(21)

Simplify Eq. (21) as follows:

$$\left[ {(1 - \Omega^{2} )A + \frac{3}{4}\gamma A^{3} } \right]^{2} + \left( { - 2\xi \Omega A} \right)^{2} = \hat{F}^{2},$$
(22)

where \(\Omega = \frac{\omega }{{\omega_{0} }},\gamma = \frac{\varepsilon }{{\omega_{0} }}.\)

The frequency bifurcation phenomenon is shown in Figure 9. It bends the resonant peak toward higher frequencies. The equilibrium point exists when the external excitation \(\Omega < \Omega_{u}\) or \(\Omega > \Omega_{d}\) in system disconnected state. When the external excitation is within this interval, GIQZSPS has two stable states. The upper branch is the vibration with larger amplitude and the lower branch is the vibration state with relatively smaller amplitude. The amplitude changes up or down to another branch when the excitation frequency is further increased or decreased, resulting in the instability of GIQZSPS system. Obviously, compared to the disconnected state, the frequency bifurcation range of connected state is decreased which makes GIQZSPS system more stable. However, the maximum amplitude of the upper branch increases significantly, which makes the isolation performance worse.

Figure 9
figure 9

Frequency response in two working states

Full size image

Eq. (22) consists of a quadratic equation in \(\Omega^{2}\) solving the above quadratic equation for \(\Omega^{2}\) gives

$$\Omega_{1,2} = \sqrt {\left( {1 - \frac{3}{4}\gamma A^{2} + 2\xi^{2} } \right) \pm \frac{{\sqrt {A^{2} \left( {4\xi^{4} - 3\gamma A^{2} + 4\xi^{2} - 3\xi^{2} \gamma A^{2} } \right) + \hat{F}^{2} } }}{A}}.$$
(23)

In case of \(\Omega_{1} = \Omega_{2}\):

$$A^{2} (4\xi^{4} - 3\gamma A^{2} + 4\xi^{2} - 3\xi^{2} \, \gamma A^{2} ) + \hat{F}^{2} { = 0}.$$
(24)

The maximum amplitude corresponding to the jump frequency can be obtained as

$$A_{\max } = \sqrt {\frac{{2(\xi^{4} + \xi^{2} ) + \sqrt {4(\xi^{4} + \xi^{2} )^{2} + \hat{F}^{2} (3\gamma + 3\xi^{2} \gamma )} }}{{3\gamma + 3\xi^{2} \gamma }}}.$$
(25)

If \(4(\xi^{4} + \xi^{2} )^{2} < < F^{2} (3\gamma + 3\xi^{2} \gamma )\), the equation above can be simplified as

$$A_{\max } = \sqrt[{4}]{{\frac{{\hat{F}^{2} }}{{3\gamma + 3\xi^{2} \, \gamma }}}}.$$
(26)

Jump-up frequency \(\Omega_{u}\) and jump-down frequency \(\Omega_{d}\) can be obtained by combining Eq. (23) and Eq. (26). It illustrates that excitation force amplitude \(F\), stiffness \(\gamma\) and damping ratio \(\xi\) impact the isolation performance of GIQZSPS. \(\gamma\) mainly depends on the system mass. \(\xi\) mainly depends on the system damping coefficient.

The frequency bifurcation phenomenon of GIQZSPS system always exists in the absence of a damper. The frequency response curve of system bends to right owing to the non-linear stiffness characteristics. Figure 10 show the influence of load on frequency response. The increase of sprung mass will enlarge the jump frequency interval, which is not conducive to the stability of GIQZSPS system.

Figure 10
figure 10

Amplitude-frequency response of GIQZSPS under different loads

Full size image

Through analysis Figure 10, it can be found that the stability of the system is mainly affected by the system load and damping ratio. The larger the load, the smaller the damping ratio, and the poorer the stability of the system. A larger damping ratio can eliminate the jumping phenomenon of the system and ensure its stability. Compared to others, the stability of quasi zero stiffness non connected states is more sensitive to parameter changes.

Figure 11 shows the relationship between the jumping frequency \(\Omega_{u}\), \(\Omega_{d}\) and the dynamic stiffness \(\gamma\) under different sprung mass \(m_{s}\). Apparently, the impact of load on the jump-down frequency \(\Omega_{d}\) of GIQZSPS system is much greater than that on jump-up frequency \(\Omega_{u}\). In addition, the disconnected state is more sensitive to sprung mass. For example, when \(\gamma = 6\), the frequency interval of the disconnected state is 1.386. And the frequency interval in connected state is 1.108. In Eq. (23), the jump-down frequency \(\Omega_{d}\) contains higher sub-term of stiffness \(\gamma\) than the jump-down frequency \(\Omega_{u}\). Meanwhile, the value of stiffness \(\gamma\) in the disconnected state is larger. Therefore, the jump interval in the disconnected state is larger than that in connected state.

Figure 11
figure 11

Effect of stiffness on jump frequency \(\Omega_{u}\), \(\Omega_{d}\) in connected and disconnected state

Full size image

Figure 12 shows the effect of the damping ratio \(\xi\) on the amplitude-frequency response. For a small damping ratio \(\xi = 0.00015\), the jumping phenomenon still occurs when the excitation frequency fluctuates up and down throughout the frequency domain. As the damping ratio \(\xi\) increases, the maximum amplitude \(A_{\max }\) decreases which lead to the system more stable. The jump-up frequency \(\Omega_{u}\) is constant because the effect of the damping ratio \(\xi\) can be neglected in the calculation. In Figure 13(a) and (b), when the damping ratio \(\xi < 0.05\), the jump-down frequency \(\Omega_{d}\) decreases rapidly with the increase of the damping ratio \(\xi\). When the damping ratio reaches to a certain position, the jump interval is equal to zero, and the jump phenomenon disappears, and the damping ratio \(\xi\) at this time is the critical damping ratio of GIQZSPS system. The main difference between the two states lies in the critical damping ratio. The critical damping ratio of connected state is around 0.1, while the disconnected state is less stable and requires a larger critical damping ratio of 0.124.

Figure 12
figure 12

Amplitude-frequency responses of connected state and disconnected state

Full size image
Figure 13
figure 13

Amplitude-frequency response of connected state and disconnected state with different damper

Full size image

3.2 Force Transmissibility of GIQZSPS

To compare the vibration isolation performance of the suspension, the force transmissibility of GIQZSPS system is calculated. The force transmitted to the unsprung mass through the quasi-zero stiffness suspension is

$$F_{t} = c\dot{z} + F_{r},$$
(27)
$$\hat{F}_{t} = \sqrt {\left( {A + \frac{3}{4}\gamma A^{3} } \right)^{2} + (2\xi \omega A)^{2} }.$$
(28)

The force transmissibility is derived as

$$T = \sqrt {\frac{{\left( {A + \frac{3}{4}\gamma A^{3} } \right)^{2} + (2\xi \omega A)^{2} }}{{F^{2} }}}.$$
(29)

Obviously, the force transmissibility of GIQZSPS system in connected and disconnected states are function of damping ratio, stiffness and excitation force amplitude. Whereas the force transmissibility of the linear system only depends on damping ratio.

Figure 14 presents the force transmissibility of GIQZSPS system in connected and disconnected states and the air spring. The natural frequency and resonance peak of GIQZSPS system in the disconnected state are the smallest, and the vibration isolation performance is better. GIQZSPS system in the connected state has similar natural frequency in the disconnected state. However, its resonance peak without load is much higher than that in the disconnected state, which results in worse isolation effect.

Figure 14
figure 14

Force transmissibility of GIQZSPS and pneumatic suspension

Full size image

Through analyzing the effect of load on the isolation performance, different loads in connected state can be compared. As shown in Figure 15, GIQZSPS system in connected state is sensitive to the system load. As the load increases, the resonance peak decreases obviously, resulting in a better isolation performance.

Figure 15
figure 15

Force transmissibility of connected state in different loads

Full size image

4 Experiment and Validation

4.1 Experimental Apparatus

Figure 16 shows the experimental setup of the proposed system. This servo system includes mainly a hydraulic cylinder controlled by a servo valve and controller. A single-channel servo hydraulic system is used to create kinds of ideal excitations such as sinusoidal exciton and random exciton. Experiments are divided into dynamic experiments with sinusoidal signals and dynamic experiments with random exciton. A motion sensor is installed to measure the vertical relative displacement between the excitation stage and the sprung mass, while two acceleration sensors are glued on the excitation stage and sprung mass.

Figure 16
figure 16

Experimental setup of GIQZSPS

Full size image

4.2 Frequency Responses with Sin Road Profile

To maintain consistency, a sinusoidal excitation with the same amplitude as a single channel servo hydraulic system is given. Frequency is controlled within 0.5–10 Hz. According to the simulation of Model-in-the-Loop (MiL), the natural frequency of GIQZSPS system in two working states is about 0.6 Hz. In order to study the characteristics of GIQZSPS and traditional air suspension, we conducted the following comparative experiments. The comparison model adopted includes: (1) GIQZSPS system in connected state (2) GIQZSPS system in disconnected state and (3) pneumatic suspension. The pneumatic suspension is a single air spring without an additional air chamber. Initial pressure of air spring and cylinders of each system are given in Table 1.

Table 1 Initial pressure of air spring and cylinders
Full size table

The time-domain response is measured by acceleration sensors located on the sprung and unsprung mass. Response relationships between acceleration and time under three system working states when low (0.5 Hz) and high frequency (5 Hz) signals are input which are shown in Figure 17. When the air pressure of air chambers on both sides are 0, GIQZSPS system can be regarded as an ordinary air spring. Generally, GIQZSPS system shows no isolation effect at 0.5 Hz near the natural frequency. The acceleration amplitude of the sprung mass is larger than that of unsprung mass. Vibration isolation effectiveness is obvious at high frequency. In the experiment, the force transfer rate is the ratio of the root mean square value of the acceleration of the mass block to the root mean square value of the acceleration of the excitation table. By converting the acceleration responses of the system under synchronous frequency excitation into root mean square values, the force transfer rate of the system under different frequency conditions is calculated. The results are shown in Figure 18.

Figure 17
figure 17

Time-domain response in empty load with sinusoidal input

Full size image
Figure 18
figure 18

Force transmissibility of different states under empty load

Full size image

After processing time-domain response at different frequencies, Root Mean Square (RMS) of acceleration is obtained. The force transmissibility in the experiment is obtained by the ratio between the RMS of sprung mass and unsprung mass.

Test results of GIQZSPS system are compared with the simulation in Figure 19. There still exists a difference between the theoretical and test results especially within the 1–3 Hz frequency. It is assumed that the mass oscillation is in a steady state with small amplitude near the static equilibrium position. Furthermore, the natural frequency of the experimental bench itself will have an impact on the overall effect, which cannot be simulated in the theoretical derivation. However, the natural frequency attained from the theoretical solution are essentially the same as those obtained from the experiments.

Figure 19
figure 19

Comparison between simulation and experimental results of GIQZSPS under connected and disconnected state

Full size image

In addition to the no-load case, experiments under full load are also conducted to investigate the effect of load variation on the damping performance under different system states. Three different states of GIQZSPS system under empty and full load are shown in Figure 20.

Figure 20
figure 20

Force transmissibility of different suspension system

Full size image

Under different two load cases, the vibration isolation effect of each state of GIQZSPS system varies significantly. As load increases, the vibration isolation performance improved obviously. At low frequency, the increase of load has a serious effect on the resonance peak at the natural frequency and effective vibration isolation frequency also decreases as well. It is noteworthy that a peak around 3 Hz appears under heavy load, where the force transmissibility is distinctly higher than that in natural frequency. And force transmissibility around 3 Hz under light load will also be improved. However, it is still far below the value in the natural frequency.

GIQZSPS system is sensitive to sprung mass. Compare to the simulation, the most obvious difference in the experimental results lies in the attenuation of force transmissibility in the middle frequency band (1–3 Hz). The simulation results show that the force transmissibility in the mid-frequency band gradually decays from higher values to lower values. It is evident from the experiments that there is a smaller decrease or even an increase in the force transmissibility in the mid-frequency band. The possible reason is that the natural frequency of the bench itself is close to the transmission rate of suspension force in this frequency band, resulting in the diffusion of single point resonance as regional resonance. This may have prevented the force transmission rate from declining as it should have.

5 Conclusions

This article aims to establish a brand-new air suspension system to solve the problem of significant load changes in current commercial vehicles. Furthermore, characteristics of GIQZSPS in connected and disconnected states can reflect its advantages and disadvantages compared to traditional air suspension. The findings clearly indicate that stiffness characteristics of GIQZSPS can be influenced by structural parameters, cylinder pressure and sprung mass. Main conclusions were summarized as follows:

  1. (1)

    A static analysis of the influence with different structural parameters on GIQZSPS stiffness was performed. The analysis points out that when air spring stiffness is constant, the air pressure in cylinders has the greatest influence on the system stiffness.

  2. (2)

    The pipeline model and the influence of parameters on the stiffness of the system are introduced. The analysis shows that the length of pipeline is positively correlated with the frequency band of stiffness change, while the diameter of pipeline is negatively correlated with that.

  3. (3)

    The influence of stiffness and damping ratio on the frequency response in the two states is also analyzed. The simulating results show that the natural frequency of GIQZSPS in disconnected state is small, the resonance peak is low, and the vibration isolation performance is better. The frequency bifurcation phenomenon is more obvious, the critical damping is relatively large, and the stability is relatively poor.

  4. (4)

    The validity of GIQZSPS system is verified through bench experiments. The experimental results clearly show that GIQZSPS has excellent isolation performance in the two states. However, the experimental results also show that the force transmissibility of GIQZSPS in the two states has two resonance peaks, which means that GIQZSPS is more susceptible to the influence of the natural frequency of the experimental bench.