1 Introduction

The sea surface recovery platform is constantly moving and swaying, thereby leading to the tilting of the recovery spacecraft and causing the spacecraft recovery mission to fail. Currently, only NASA has successfully developed a surface recovery platform for spacecraft; the first stage of the “Falcon 9” carrier rocket landed vertically on the sea platform in April 2016 [1]. For some dynamic balancing devices, only the condition of the vertically launched instantaneous missile is suitable [2, 3]. However, during the spacecraft recovery process, the dynamic balancing device needs to be constantly balanced under a large variable load impact. Therefore, the existing dynamic balancing device of the ship-borne missile launch is not suitable for the surface recovery platform of spacecraft. Parallel mechanisms are increasingly used in applications where precision is of great importance [4,5,6]. To take advantage of the parallel mechanism by applying it to the surface recovery platform, a 5-prismatical–spherical–spherical (PSS)/ universal–prismatical–universal (UPU) parallel mechanism is proposed as a dynamic balancing device [7] in this paper. To reduce the load on the device and improve its driving ability, all the drives are placed on the frame. The position adjustment of five degrees of freedom of the moving platform can be realized through the real–time drive control of each active branch, and the dynamic balance can be maintained.

Under the condition of high speed and heavy load, the elastic deformation of each component will have a certain influence on the motion accuracy of the moving platform and the positioning accuracy of the load [8,9,10,11,12,13]. Therefore, to reduce the influence of elastic deformation on the moving platform and improve its output accuracy, the research on the elastic dynamics modeling and dynamic characteristics of the 5-PSS/UPU mechanism are absolutely necessary [14,15,16]. Liu et al. [17] established an elastic dynamics modeling of a flexible 3-RRS parallel robot using the simplified KED (kineto-elastodynamics) method and analyzed its dynamic characteristics in detail. Fattah et al. [18] obtained the whole mechanism dynamic equation of the 3-RRS parallel mechanism using the natural orthogonal complement method, and the influence of the output precision of the moving platform with flexible links was studied. Zhao et al. [19] established the elastic dynamic equations of each moving member based on the idea of substructure, and the dynamic equations of three-degrees-of-freedom translational parallel mechanism was obtained using the displacement coordination. Xie et al. [20] considered the parallel moving platform and active branched chains as a spatial beam element modeling, and an overall dynamic equation was established based on the motion constraints. Furthermore, the Newmark numerical method was used, and the elastic dynamic model was solved discretely. Zhao et al. [21] investigated the elastic dynamic characteristics of the 6-PSS and 8-PSS parallel robots, and the result shows that the redundant 8-PSS parallel robots have higher natural frequencies and better dynamic characteristics. Shan et al. [22] established the elastic dynamics modeling of a novel 2 (3HUS + U) parallel hip joint simulator, and the natural frequency and stiffness of the mechanism in its working space were analyzed. As mentioned above, the investigations on the parallel mechanism are mainly limited to the simple planar or three-degrees-of-freedom parallel mechanism, and only a few studies have been reported on the dynamic characteristics of parallel mechanism with complex structure, especially the five-degrees-of-freedom parallel mechanism.

In this study, a novel five-degrees-of-freedom parallel mechanism—5-PSS/UPU parallel mechanism—is proposed [23, 24], considering the moving platform, and the active branching chains and screw slider as the spatial beam element and plane beam element modeling, respectively. Next, according to the kinematic coupling relationship of each component, the dynamic equation of the parallel mechanism is constructed. Finally, the natural frequency distribution of the 5-PSS/UPU parallel mechanism in the working space and the elastic displacement of the moving platform are obtained.

2 Dynamic Equations

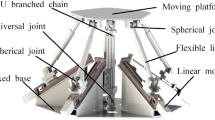
The basic structure of the parallel mechanism is shown in Figure 1. It consists of a fixed base and a moving platform connected using six branched chains. The six branches include five PSS joint branches and one UPU joint branch. The two ends of five PSS joint branch chain are respectively connected to the moving platform and linear module through two spherical joints, and the linear module is fixed on the base. The UPU joint branch chain is connected to the geometric center of the moving platform and fixed base through a universal joint. The power input is the moving pair of five PSS joint branches,and the UPU joint branch chains only provide constraints to institutions.

Figure 1
figure 1

General 5-PSS/UPU parallel mechanism

Full size image

As shown in Figure 2, the rigid moving pentagon platform is \(a_{1} a_{2} a_{3} a_{4} a_{5}\), and the radius of the circumscribed circle is r. The fixed pentagon base \(B_{1} B_{2} B_{3} B_{4} B_{5}\) is assumed rigid, and the radius of the circumscribed circle is R. Each active branched chain contains a link and a linear motor. The active branched chains are connected to moving platform \(a_{1} a_{2} a_{3} a_{4} a_{5}\) through spherical joints and coupled to the slider through spherical joints at \(b_{i}\), where i = 1, 2, 3, 4, 5. The UPU branched chain is connected to moving platform \(a_{1} a_{2} a_{3} a_{4} a_{5}\) through the universal joint and coupled to the fixed base through the universal joint. The length of link \(a_{i} b_{i}\) is L.

Figure 2
figure 2

Sketch of 5-PSS/UPU parallel mechanism

Full size image

The basal Cartesian coordinate frame, designated as the \(o {-} xyz\) frame, is fixed at the center of the base platform, with the z-axis pointing vertically upward and x-axis pointing towards joint \(B_{1}\). Similarly, a coordinate frame \(p {-} x_{p} y_{p} z_{p}\) is assigned to the center of the moving platform, with the \(z_{p}\)-axis normal to the platform and \(x_{p}\)-axis pointing towards joint\(a_{1}\). The local frame \(w_{i} {-} x_{i} y_{i} z_{i}\) (i = 1, 2, 3, 4, 5) is fixed on the base platform joint \(B_{i}\), with \(y_{i}\)-axis pointing from \(B_{i}\) to \(b_{i}\) and \(x_{i}\)-axis pointing vertically to x-axis. The parallel mechanism has five degrees of freedom and five linear motors to drive the actuated joints.

To analyze the characteristics of the 5-PSS/UPU with elastically active branched chains, the dynamics modeling of the parallel mechanism was investigated based on the finite element theory. To ensure the accuracy of the analysis and reduce the complexity of modeling, the following assumptions are made:

  1. 1.

    The deformation of the flexible components is very small and can be regarded as a small elastic deformation. Thus, the actual movement of the member can be regarded as a linear superposition of the elastic and rigid displacement.

  2. 2.

    Considering that the UPU chain is composed of an electric cylinder and universal joints, its elastic deformation is relatively small compared to the active branch chains. Thus, considering the moving platform, peripheral bracket, and UPU branched chains as rigid, the torsional deformation of active branched chains (including flexible link and linear motor) is mainly considered.

2.1 Flexible Link Dynamic Equation

As shown in Figure 3, the flexible link is considered a spatial flexible beam element for elastic dynamic modeling. \(\varvec{\delta}_{li} = [\delta_{1} ,\delta_{2} , \ldots ,\delta_{18} ]^{\text{T}}\) represents the vector of generalized coordinates of beam elements, where \(\delta_{1} {-} \delta_{3}\) and \(\delta_{10} {-} \delta_{12}\), \(\delta_{4} {-} \delta_{6}\) and \(\delta_{13} {-} \delta_{15}\), and \(\delta_{7} {-} \delta_{9}\) and \(\delta_{16} {-} \delta_{18}\) represent the axial or transverse displacements, rotary angles, and curvatures at nodes \(b_{i}\) and \(a_{i}\), respectively. It is supported that a spatial flexible beam element is subjected to axial, lateral, and torsional deformational. A point in the element has elastic displacement in the direction of \(u_{i} v_{i} w_{i}\)-axes.

Figure 3
figure 3

Schematic of spatial flexible beam element

Full size image

According to the deformation characteristics and requirement of the flexible components, the lateral elastic, axial elastic, and elastic angular displacements around \(w_{i}\)-axis of beam elements are expressed using the quintic Hermite, linear, and cubic interpolation functions, respectively. Next, the functions can be obtained based on the set of boundary conditions of the flexible beam element as follows:

$$\varPhi_{ui} = \varvec{N}_{ui}\varvec{\delta}_{li} ;\;\varPhi_{vi} = \varvec{N}_{vi}\varvec{\delta}_{li} ;\;\varPhi_{wi} = \varvec{N}_{wi}\varvec{\delta}_{li} ;\;\varPhi_{\varphi i} = \varvec{N}_{\varphi i}\varvec{\delta}_{li} ,$$
(1)

where \(\varPhi_{ui}\), \(\varPhi_{vi}\), \(\varPhi_{wi}\), and \(\varPhi_{\varphi i}\) are interpolation vectors, and the functions of w. The expressions are specified as follows [25]:

$$\begin{aligned} \varvec{N}_{\varphi i} & = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & {n_{7} } & 0 & 0 & {n_{8} } & 0 & 0 & 0 & 0 & 0 & {n_{9} } & 0 & 0 & {n_{10} } \\ \end{array} } \right]^{\text{T}} , \\ \varvec{N}_{wi} & = \left[ {\begin{array}{*{20}c} 0 & 0 & {1 - e} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{\text{T}} , \\ \varvec{N}_{vi} & = \left[ {\begin{array}{*{20}c} 0 & {n_{1} } & 0 & {n_{2} } & 0 & 0 & {n_{3} } & 0 & 0 & 0 & {n_{4} } & 0 & {n_{5} } & 0 & 0 & {n_{6} } & 0 & 0 \\ \end{array} } \right]^{\text{T}} , \\ \varvec{N}_{ui} & = \left[ {\begin{array}{*{20}c} {n_{1} } & 0 & 0 & 0 & {n_{2} } & 0 & 0 & {n_{3} } & 0 & {n_{4} } & 0 & 0 & 0 & {n_{5} } & 0 & 0 & {n_{6} } & 0 \\ \end{array} } \right]^{\text{T}} , \\ e & = \frac{w}{L};n_{1} = 1 - 10e^{3} + 15e^{4} - 6e^{5} ;n_{2} = L\left( {e - 6e^{3} + 8e^{4} - 3e^{5} } \right);n_{3} = \frac{{L^{2} }}{2}\left( {e^{2} - 3e^{3} + 3e^{4} - e^{5} } \right), \\ n_{4} & = 10e^{3} - 15e^{4} + 6e^{5} ;n_{5} = L\left( { - 4e^{3} + 7e^{4} - 3e^{5} } \right);n_{6} = \frac{{L^{2} }}{2}\left( {e^{3} - 2e^{4} + e^{5} } \right);n_{7} = 1 - 3e^{2} + 2e^{3} , \\ n_{8} & = L\left( {e - 2e^{2} + e^{3} } \right);n_{9} = 3e^{2} - 2e^{3} ;n_{10} = L\left( { - e^{2} + e^{3} } \right), \\ \end{aligned}$$
(2)

where \(n_{i} \, (i = 1,2, \ldots ,\;10)\) is the type function of displacement of elements and \(w\) is the axial displacement of elements.

The absolute acceleration at a random point on the beam element is considered to be the sum of the acceleration of the movement of rigid body and the acceleration of elastic deformation. Hence, the velocity of the random point with the coordinates of w on beam element is shown as follows:

$$\left\{ \begin{aligned} &\dot{\varvec{\varPhi }}_{aui} = \dot{\varvec{\varPhi }}_{rui} + \dot{\varvec{\varPhi }}_{ui} = \varvec{N}_{ui} (\dot{\varvec{\delta }}_{li} + \dot{\varvec{\delta }}_{rl} ), \hfill \\ &\dot{\varvec{\varPhi }}_{avi} = \dot{\varvec{\varPhi }}_{rvi} + \dot{\varvec{\varPhi }}_{vi} = \varvec{N}_{vi} (\dot{\varvec{\delta }}_{li} + \dot{\varvec{\delta }}_{rl} ), \hfill \\ &\dot{\varvec{\varPhi }}_{awi} = \dot{\varvec{\varPhi }}_{rwi} + \dot{\varvec{\varPhi }}_{wi} = \varvec{N}_{wi} (\dot{\varvec{\delta }}_{li} + \dot{\varvec{\delta }}_{rl} ), \hfill \\& \dot{\varvec{\varPhi }}_{a\varphi i} = \dot{\varvec{\varPhi }}_{r\varphi i} + \dot{\varvec{\varPhi }}_{\varphi i} = \varvec{N}_{\varphi i} (\dot{\varvec{\delta }}_{li} + \dot{\varvec{\delta }}_{rl} ), \hfill \\ \end{aligned} \right.$$
(3)

where \(\dot{\varvec{\varPhi }}_{aui}\), \(\dot{\varvec{\varPhi }}_{avi}\), and \(\dot{\varvec{\varPhi }}_{awi}\) are the absolute velocities of a given point on beam element along the u-, v-, and w-axes, respectively; \(\dot{\varvec{\varPhi }}_{rui}\), \(\dot{\varvec{\varPhi }}_{rvi}\), and \(\dot{\varvec{\varPhi }}_{rwi}\) are the velocities of the moving rigid body along u-, v-, and w-axes, respectively; \(\dot{\varvec{\varPhi }}_{ui}\), \(\dot{\varvec{\varPhi }}_{vi}\), and \(\dot{\varvec{\varPhi }}_{wi}\) are the velocities of elastic deformation of a given point on beam element along the u-, v-, and w-axes, respectively; \(\dot{\varvec{\varPhi }}_{a\varphi i}\), \(\dot{\varvec{\varPhi }}_{r\varphi i}\), and \(\dot{\varvec{\varPhi }}_{\varphi i}\) are the absolute angular velocity, angular velocity of the rigid body, and angular velocity of elastic deformation around w-axis of a given point on beam element, respectively; and \(\dot{\varvec{\delta }}_{rl}\) represents the vector of generalized coordinates of the rigid body.

The kinetic energy of the spatial flexible beam element is expressed as follows:

$$\begin{aligned} T & = \frac{1}{2}\int_{0}^{L} {\rho_{ab} S_{ab} } \left[ {\left( {\frac{{{\text{d}}\varvec{\varPhi}_{aui} }}{{{\text{d}}t}}} \right)^{2} + \left( {\frac{{{\text{d}}\varvec{\varPhi}_{avi} }}{{{\text{d}}t}}} \right)^{2} + \left( {\frac{{{\text{d}}\varvec{\varPhi}_{awi} }}{{{\text{d}}t}}} \right)^{2} } \right]{\text{d}}\delta_{{w_{i} }} \\ & \quad + \frac{1}{2}\int_{0}^{L} {\rho_{ab} I_{p} } \left( {\frac{{{\text{d}}\varvec{\varPhi}_{a\varphi i} }}{{{\text{d}}t}}} \right)^{2} {\text{d}}\delta_{{w_{i} }} = \frac{1}{2}\text{(}\dot{\varvec{\delta }}_{l} + \dot{\varvec{\delta }}_{rl} \text{)}^{\text{T}} \varvec{M}_{abi} \text{(}\dot{\varvec{\delta }}_{li} + \dot{\varvec{\delta }}_{rl} \text{),} \\ \end{aligned}$$
(4)

where L and \(\rho_{ab}\) are the length and mass density of beam element, respectively; \(I_{p}\) is the polar moment of inertia of cross sections of beam element about w-axis; \(S_{ab}\) is the cross-sectional area of beam element; and \(\delta_{{w_{i} }}\) is the \(w_{i}\)-axial displacement. Moreover, \(\varvec{M}_{abi}\) is the function of the mass distribution of beam element:

$$\varvec{M}_{abi} = \rho_{ab} S_{ab} \int_{0}^{L} {\varvec{N}_{li}^{\text{T}} \varvec{N}_{li} } {\text{d}}\delta_{wi} + \rho_{ab} I_{p} \int_{0}^{L} {\varvec{N}_{\varphi } \varvec{N}_{\varphi i}^{\text{T}} } {\text{d}}\delta_{wi} ,$$
(5)

where \(\varvec{N}_{li} = [N_{wi} ,N_{ui} ,N_{vi} ]^{\text{T}}\).

Ignoring the shear deformation of the beam element and coupling between the axial displacement and lateral displacement, the potential energy of the branched component is expressed as follows:

$$\begin{aligned} V & = \frac{1}{2}E_{ab} \int_{0}^{L} {S_{ab} } \\ & \quad \times \left[ {\left( {\frac{{\partial \varPhi_{wi} }}{{\partial \delta_{wi} }}} \right)^{2} + I_{abiu} \left( {\frac{{\partial^{2} \varPhi_{ui} }}{{\partial \delta^{2}_{wi} }}} \right)^{2} + I_{abiv} \left( {\frac{{\partial^{2} \varPhi_{vi} }}{{\partial \delta^{2}_{wi} }}} \right)^{2} } \right]{\text{d}}\delta_{wi} \\ & \quad + \frac{1}{2}\int_{0}^{L} {G_{ab} } I_{p} \left( {\frac{{\partial \varPhi_{\varphi i} }}{{\partial \delta_{wi} }}} \right){\text{d}}\delta_{wi} = \frac{1}{2}\varvec{\delta}_{li}^{\text{T}} \varvec{K}_{abi}\varvec{\delta}_{li} , \\ \end{aligned}$$
(6)

where \(E_{ab}\) and \(G_{ab}\) are the elastic modulus of tension/compression and shearing modulus of elasticity of the material, respectively. \(I_{abiu}\) and \(I_{abiv}\) are the principal moments of inertia of cross sections of beam element to u- and v-axes, respectively. Moreover, \(\varvec{K}_{abi}\) is the function of rigidity of beam element:

$$\begin{aligned} \varvec{K}_{abi} & = E_{ab} \int_{0}^{L} {(S_{ab} } {N_{wi}^{\prime}} {N_{wi}^{\prime}}^{\text{T}} + I_{abiu} {N_{ui}^{\prime\prime}} {N_{ui}^{\prime\prime}}^{\text{T}} \\ & \quad + I_{abiv} {N_{vi}^{\prime\prime}} {N_{vi}^{\prime\prime}}^{\text{T}} ){\text{d}}\delta_{wi} + G_{ab} I_{abiw} \int_{0}^{L} {{N_{\varphi i} ^{\prime}}{N_{\varphi i}^{\prime}}^{\text{T}} } {\text{d}}\delta_{wi} , \\ \end{aligned}$$
(7)

where \(\varvec{N^{\prime}}_{wi} = \frac{{\partial \varvec{N}_{wi} }}{{\partial \delta_{wi} }}\); \(\varvec{N^{\prime\prime}}_{ui} = \frac{{\partial^{2} \varvec{N}_{ui} }}{{\partial \delta^{2}_{wi} }}\); \(\varvec{N^{\prime\prime}}_{vi} = \frac{{\partial^{2} \varvec{N}_{vi} }}{{\partial \delta^{2}_{wi} }}\); \(\varvec{N^{\prime}}_{\varphi i} = \frac{{\partial \varvec{N}_{\varphi i} }}{{\partial \delta_{wi} }}\).

By substituting Eqs. (4) and (6) into the Lagrange’s equation, the flexible link dynamic equation in the terms of \(b_{i} - u_{i} v_{i} w_{i}\) frame is expressed as follows:

$$\varvec{M}_{abi} \varvec{\ddot{\delta }}_{li} + \varvec{K}_{abi}\varvec{\delta}_{li} = \varvec{F}_{abi} + \varvec{F}_{ebai} - \varvec{M}_{abi} \varvec{\delta^{\prime\prime}}_{rli} ,$$
(8)

where \(\varvec{F}_{abi}\) is the array of the generalized force of external load of beam element, \(\varvec{F}_{ebai}\) is the array of forces on the studied beam element exerted by other beam elements connected with the studied one, and \(\varvec{\delta^{\prime\prime}}_{rli}\) is the acceleration of rigid bodies.

Because two end nodes of the branched link are spherical joints, the curvature in three directions is zero. Consequently, the generalized coordinates (Figure 4) of the branch can be expressed in the global coordinates as follows:

$$\varvec{u}_{li}^{o} = [u_{{\text{o}1}} , \ldots ,u_{{\text{o6}}} ,0,0,0,u_{{\text{o7}}} , \ldots ,u_{{\text{o12}}} ,0,0,0]^{\text{T}} ,$$
(9)

then

$$\begin{aligned}\varvec{\delta}_{li} & = \varvec{R}_{abi} \varvec{u}_{li}^{o} , \\ \varvec{R}_{abi} & = {\text{diag}}(\varvec{R}_{li}^{ - 1} ,\varvec{R}_{li}^{ - 1} ,\varvec{R}_{li}^{ - 1} ,\varvec{R}_{li}^{ - 1} ,\varvec{R}_{li}^{ - 1} ,\varvec{R}_{li}^{ - 1} ), \\ \end{aligned}$$
(10)

where \(\varvec{R}_{li}^{{}}\) is the transformation matrix of the element coordinate system to the global coordinate system.

Figure 4
figure 4

Finite element model of flexible link: a element coordinates; b global coordinates

Full size image

The element equations are expressed in terms of the O–XYZ frame as follows:

$$\varvec{M}_{abi}^{o} \varvec{\ddot{u}}_{li}^{o} + \varvec{K}_{abi}^{o} \varvec{u}_{li}^{o} = \varvec{F}_{abi}^{o} + \varvec{F}_{eabi}^{o} - \varvec{M}_{abi}^{o} \varvec{\ddot{u}}_{lri}^{o} ,$$
(11)

where \(\varvec{M}_{abi}^{o} = \varvec{R}_{abi}^{\text{T}} \varvec{M}_{abi} \varvec{R}_{abi}\); \(\varvec{K}_{abi}^{o} = \varvec{R}_{abi}^{\text{T}} \varvec{K}_{abi} \varvec{R}_{abi}\); \(\varvec{F}_{abi}^{o} = \varvec{R}_{abi}^{\text{T}} \varvec{F}_{abi}\); \(\varvec{F}_{eabi}^{o} = \varvec{R}_{abi}^{\text{T}} \varvec{F}_{ebai}\); \(\varvec{\ddot{u}}_{lri}^{o} = \varvec{R}_{abi} \varvec{\delta}_{ri}^{\prime\prime}.\)

2.2 Linear Motor Dynamic Equation

Because the linear module only performs linear motion in a fixed plane, the linear motor is considered a plane beam element model for elastic dynamic modeling. The linear motor is divided into two units. The joint of the coupling and the screw at the position slider \(b_{i}\) is the first unit, and the position of the slider at the end of the screw bearing is the second unit.

Each node has then three degrees of freedom, and generalized coordinates (Figure 5) of the linear motor can be expressed as follows:

$$\varvec{u}_{Li}^{\prime} = \left[ {u_{{Li\varvec{1}}} ,\;u_{{Li\varvec{2}}} ,\;u_{{Li\varvec{3}}} ,\;u_{{Li\varvec{4}}} ,\;u_{{Li\varvec{5}}} ,\;u_{{Li\varvec{6}}} ,\;u_{{Li\varvec{7}}} ,\;u_{{Li\text{8}}} ,\;u_{{Li\text{9}}} } \right]^{\text{T}} .$$
(12)

With the boundary constraints, the transverse displacements and rotary angles of the linear motor in the element coordinates can be expressed as follows:

$$\begin{aligned} \varvec{u}_{Li} & = [\varvec{u}_{{L\text{1}i}} ;\varvec{u}_{{L\text{2}i}} ]^{\text{T}} \\ & = [0,\;0,\;u_{{L\varvec{3}}} ,\;u_{{L\varvec{4}}} ,\;u_{{L\varvec{5}}} ,\;u_{{L\varvec{6}}} ,\;u_{{L\text{7}}} ,\;0,\;0]^{\text{T}} . \\ \end{aligned}$$
(13)
Figure 5
figure 5

Finite element model of linear motor: a first unit; b second unit

Full size image

Considering the dynamic accuracy design requirements of the moving platform, the lateral elastic displacement and axial elastic displacement of elements are expressed using the quintic Hermite interpolation function and linear interpolation function, respectively.

$$\left\{ \begin{aligned} u_{Ljxi} &= \varvec{N}_{Lx} \varvec{u}_{Li} , \hfill \\ u_{Ljyi} &= \varvec{N}_{Ly} \varvec{u}_{Li} , \hfill \\ \end{aligned} \right.$$
(14)

where \(\varvec{N}_{Lx}\) and \(\varvec{N}_{Ly}\) are the vectors of interpolation polynomials. The expressions are expressed as follows [26]:

$$\left\{ \begin{array}{l} {l_{1}} = 1 - e;l_{2} = e;{l_{3}} = 1 - 10e^{3} + 15e^{4} - 6e^{5} ;\\ {l_{4}} = L_{sj} (e - 6e^{3} + 8e^{4} - 3e^{5} );{l_{5}} = 10e^{3} - 15e^{4} + 6e^{5} ; \\ {l_{6}} = L_{sj} ( - 4e^{3} + 7e^{4} - 3e^{5} );e = {y_{i} /L_{sj}} ; \\ \end{array} \right.$$
(15)

where \(y_{i}\) and \(L_{sj}\) are axial displacement and axial length of the element, respectively.

According to the kinetic energy of the linear motor element unit, the mass matrix can be obtained as follows:

$$\varvec{M}_{Lji} = \rho_{L} S_{L} \int_{0}^{Lsj} {(N_{Lx} } N_{Lx}^{\text{T}} + N_{{L\text{y}}} N_{{L\text{y}}}^{\text{T}} ){\text{d}}u_{Ljyi} ,$$
(16)

where \(\rho_{L}\), \(S_{L}\), and \(L_{sj}\) are the mass density, cross–sectional area, and slider displacement of linear motor element, respectively.

With the boundary conditions of the element unit, the overall mass matrix \(\varvec{M}_{Li9 \times 9}\) of the linear motor is assembled.

The shear deformation of the beam element, and the coupling between the axial displacement and lateral displacement are ignored. Consequently, the function of rigidity of beam element \(\varvec{K}_{{Lj\text{6} \times \text{6}}}\) can be expressed as follows:

$$\left\{ \begin{aligned} \varvec{K}_{Lji} &= E_{L} S_{L} \int_{0}^{Lsj} {\varvec{N^{\prime}}_{Ly} \varvec{N^{\prime}}_{Ly}^{\text{T}} } {\text{d}}u_{Ljyi} + E_{L} \text{I}_{Lx} \int_{0}^{Lsj} {\varvec{N^{\prime\prime}}_{Lx} \varvec{N^{\prime\prime}}_{Lx}^{\text{T}} } {\text{d}}u_{Ljyi} , \hfill \\ \varvec{N^{\prime}}_{Ly} &= \frac{{\partial \varvec{N}_{Ly} }}{{\partial u_{Ljyi} }};\varvec{N^{\prime\prime}}_{Lx} = \frac{{\partial^{2} \varvec{N}_{Lx} }}{{\partial u_{Ljyi}^{2} }}, \hfill \\ \end{aligned} \right.$$
(17)

where \(E_{L}\) is the elastic modulus of tension/compression of the material, and \(I_{Lx}\) is the principal moments of inertia of the cross sections of linear motor element along \(x_{i}\)-axes.

With the boundary conditions of the element unit, the overall stiffness matrix \(K_{Li9 \times 9}\) of the linear motor is assembled.

The linear motor dynamic equation in the terms of local coordinate can be obtained as follows:

$$\varvec{M}_{Li} \varvec{\ddot{u}}_{Li} + \varvec{K}_{Li} \varvec{u}_{Li} = \varvec{F}_{Li} + \varvec{F}_{Lei} - \varvec{M}_{Li} \varvec{\ddot{u}}_{Lri} ,$$
(18)

where \(\varvec{F}_{Li}\) is the array of generalized force of external load of linear motor element, \(\varvec{F}_{Lei}\) is the array of forces on the studied linear motor element exerted by other elements connected with the studied one, and \(\varvec{\ddot{u}}_{Lri}\) is the acceleration of rigid bodies.

In the global coordinates, the generalized coordinates of the linear motor can be expressed as follows:

$$\varvec{u}_{Li}^{o} = \left[ {u_{L1}^{o} ,\;u_{{L\text{2}}}^{o} ,\;u_{{L\text{3}}}^{o} ,\;u_{{L\text{4}}}^{o} ,\;u_{{L\text{5}}}^{o} ,\;u_{{L\text{6}}}^{o} ,\;u_{{L\text{7}}}^{o} ,\;u_{{L\text{8}}}^{o} ,\;u_{{L\text{9}}}^{o} ,\;u_{L10}^{o} ,\;u_{L11}^{o} ,\;u_{L12}^{o} } \right]^{\text{T}} ,$$
(19)

where \(\varvec{u}_{Li} = \varvec{R}_{Li(5 \times 12)}^{o} \varvec{u}_{Li}^{o}\), \(\varvec{R}_{Li}^{o} = {\text{diag}}(\varvec{R}_{1Li} ,\varvec{R}_{2Li} ,\varvec{R}_{3Li} ,\varvec{R}_{4Li} )\), \(\varvec{R}_{1Li} = \varvec{R}_{Li} (3{:})\), \(\varvec{R}_{2Li} = \varvec{R}_{Li} (1,2{:})\), \(\varvec{R}_{3Li} = \varvec{R}_{Li} (3{:})\), \(\varvec{R}_{4Li} = \varvec{R}_{Li} (3{:})\), and \(\varvec{R}_{Li}\) is the rotation matrix of the base coordinate system to the global coordinate system of the linear motor element.

Next, the element equations are expressed in terms of the O–XYZ frame as follows:

$$\varvec{M}_{Li}^{o} \varvec{\ddot{u}}_{Li}^{o} + \varvec{K}_{Li}^{o} \varvec{u}_{Li}^{o} = \varvec{F}_{Li}^{o} + \varvec{F}_{Lei}^{o} - \varvec{M}_{Li}^{o} \varvec{\ddot{u}}_{Lri}^{o} ,$$
(20)

where \(\varvec{M}_{Li}^{o} = \varvec{R}_{Li}^{{o\text{T}}} \varvec{M}_{Li} \varvec{R}_{Li}^{o}\), \(\varvec{K}_{Li}^{o} = \varvec{R}_{{\text{L}i}}^{{o\text{T}}} \varvec{K}_{Li} \varvec{R}_{{\text{L}i}}^{o}\), \(\varvec{F}_{Li}^{o} = \varvec{R}_{{\text{L}i}}^{{o\text{T}}} \varvec{F}_{Li}\), \(\varvec{F}_{Lei}^{o} = \varvec{R}_{Li}^{{o\text{T}}} \varvec{F}_{Lei}\), and \(\varvec{\ddot{u}}_{Lri}^{o} = \varvec{R}_{Li}^{o} \varvec{\ddot{u}}_{Lri}\).

2.3 Kinematic Constraint Equations

As shown in Figure 6, the elastic deformation of the moving platform is much smaller than that of the branched chains; hence, it can be regarded as a rigid body [27]. The displacement of the moving platform and the displacements of the joints of each chain are not independent. Due to the elastic deformation of the branched chains, the displacement of the moving platform displacement is consistent with the displacement of the point where chains and moving platform are jointed.

Figure 6
figure 6

Coordination and constraint relationship between moving platform and branched chains

Full size image

We suppose that the elastic deformation of point \(a_{i}\) (i = 1, 2, 3, 4, 5) in the global system \(O {-} XYZ\)is \(\varvec{u}_{ai} = [\Delta x_{ai} ,\Delta y_{ai} ,\Delta z_{ai} ,\Delta \alpha_{ai} ,\Delta \beta_{ai} ,\Delta \gamma_{ai} ]^{\text{T}}\), and the kinematic position of the moving platform is at point p. The actual position changes slightly for the elastic deformation of the components of branched chains in the system. \(\varvec{u}_{p} = [\Delta x_{p} ,\Delta y_{p} ,\Delta z_{p} ,\Delta \alpha_{p} ,\Delta \beta_{p} ,\Delta \gamma_{p} ]^{\text{T}}\), and finally moves to point P′. The z–y–x Euler angle of the moving platform is \((\alpha ,\beta ,\gamma )\), and the coordinate of point p in coordinate system O–xyz is \((p_{x} ,p_{y} ,p_{z} )^{\text{T}}\). The transformation matrix of coordinate system \(p {-} xyz\) to the global coordinate system \(O {-} XYZ\) is \(R_{p}^{o}\), the transformation matrix of coordinate system \(p^{\prime} - x^{\prime}y^{\prime}z^{\prime}\) to the global coordinate system \(O {-} XYZ\) is \(R_{{p^{\prime}}}^{o}\), and the transformation matrix of coordinate system \(p^{\prime} - x^{\prime}y^{\prime}z^{\prime}\) to the coordinate system \(p {-} xyz\) is \(R_{{p^{\prime}}}^{p}\).

Based on small deformation, the approximate expression of transformation matrix \(R_{{p^{\prime}}}^{p}\) is defined as follows:

$$\varvec{R}_{{p^{\prime}}}^{p} = \left[ {\begin{array}{*{20}c} 1 & { - \Delta \alpha_{p} } & {\Delta \beta_{p} } & {\Delta x_{p} } \\ {\Delta \alpha_{p} } & 1 & { - \Delta \gamma_{p} } & {\Delta y_{p} } \\ { - \Delta \beta_{p} } & {\Delta \gamma_{p} } & 1 & {\Delta z_{p} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right].$$
(21)

Next, the transformation matrix \(R_{p}^{o}\) can be expressed as follows:

$$\varvec{R}_{{p^{\prime}}}^{o} = \varvec{R}_{{p^{\prime}}}^{p} \varvec{R}_{p}^{o} .$$
(22)

In this case, the elastic line displacement at the end of the branched chains \(a_{i}\) can be obtained as follows:

$$\begin{aligned} \left[ {\Delta x_{ai} ,\Delta y_{ai} ,\Delta z_{ai} ,1} \right]^{\text{T}} &= \varvec{R}_{{p^{\prime}}}^{o} \left[ {\varvec{a}_{i}^{p} ,1} \right]^{\text{T}} - \varvec{R}_{p}^{o} \left[ {\varvec{a}_{i}^{p} ,1} \right]^{\text{T}} \\ &= (\varvec{R}_{{p^{\prime}}}^{p} - \varvec{I})\left[ {\varvec{a}_{i}^{o} ,1} \right]^{\text{T}} , \\ \end{aligned}$$
(23)

where \(\varvec{a}_{i}^{p}\) and \(\varvec{a}_{i}^{o}\)are the displacement vectors of branched chain nodes \(a_{i}\)in \(p - xyz\) and \(O - XYZ\), respectively.

Next, by substituting Eq. (22) into Eq. (23), the following formula is obtained:

$$\left[ {\Delta x_{ai} ,\Delta y_{ai} ,\Delta z_{ai} } \right]^{\text{T}} = [\varvec{I} ,\varvec{T}_{pi} ]\Delta \varvec{p}\text{,}$$
(24)

where

$$\varvec{T}_{pi} = \left[ {\begin{array}{*{20}c} 0 & {a_{iz}^{o} } & { - a_{iy}^{o} } \\ { - a_{iz}^{o} } & 0 & {a_{ix}^{o} } \\ {a_{iy}^{o} } & { - a_{ix}^{o} } & 0 \\ \end{array} } \right].$$

The angular displacement at the end of the branched chains is equal to the angular displacement of the moving platform, \(\left[ {\Delta \alpha_{ai} ,\Delta \beta_{ai} ,\Delta \gamma_{ai} } \right]^{\text{T}} = \left[ {\Delta \alpha_{p} ,\Delta \beta_{p} ,\Delta \gamma_{p} } \right]^{\text{T}}\). Next, the functional relationship between the displacement of the moving platform and point \(a_{i}\) can be obtained. The result is shown as follows after arrangement.

$$\Delta \varvec{a}_{i} = \varvec{J}_{pi} \Delta \varvec{p}\text{,}$$
(25)

where \(\varvec{J}_{pi} = \left[ {\begin{array}{*{20}c} \varvec{I} & {\varvec{T}_{pi} } \\ {\mathbf{0}} & \varvec{I} \\ \end{array} } \right]\).

The elastic displacement of joint \(b_{i}\) between the linear motor and slider can be expressed as follows:

$$\Delta S_{i} = u_{li4} + \frac{p}{{2\uppi}}u_{li6} = \varvec{R}_{si} \left[ {\begin{array}{*{20}c} {u_{li4} } & {\begin{array}{*{20}c} {u_{li5} } & {u_{li6} } \\ \end{array} } \\ \end{array} } \right]^{\text{T}} ,$$
(26)

where \(p\) is the lead for the screw and \(\varvec{R}_{si} = \left[ {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} 0 & {\frac{p}{{2\uppi}}} \\ \end{array} } \\ \end{array} } \right]\).

The elastic displacement of the slider is the same as the elastic displacement of the end of the branched chains in yi axial direction of wi–xiyizi, \(\Delta S_{i} = \delta_{3i}\).

2.4 Dynamic Model of 5-PSS/UPU Parallel Mechanism

Based on the above analysis, the generalized coordinates of the 5-PSS/UPU parallel mechanism system are as follows:

$$\varvec{U}_{i} = \left[ {u_{L1}^{o} ,u_{{L\text{2}}}^{o} , \ldots ,u_{{L\text{12}}}^{o} ,u_{{\text{o}1}} ,u_{{\text{o2}}} , \ldots ,u_{{\text{o6}}} ,\Delta x_{p} ,\Delta y_{p} ,\Delta z_{p} ,\Delta \alpha_{p} ,\Delta \beta_{p} ,\Delta \gamma_{p} } \right]^{\text{T}} .$$
(27)

In the generalized coordinates of the system, the generalized coordinates of the branched chains can be expressed as follows:

$$\varvec{u}_{li}^{ * } = \varvec{R}_{ * }^{li} \varvec{U}_{i} ,$$
(28)

where \({\varvec{R}}_{ * }^{li} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{6 \times 12} } & {\varvec{E}_{6} } & {{\mathbf{0}}_{6 \times 6} } \\ {{\mathbf{0}}_{6 \times 12} } & {{\mathbf{0}}_{6 \times 6} } & {\varvec{T}_{pi} } \\ \end{array} } \right]\).

By substituting Eq. (28) into Eq. (11), the mass matrix and function of the rigidity of beam element in the generalized coordinate can be obtained as follows:

$$\varvec{M}_{abi}^{ * } = \text{(}\varvec{R}_{ * }^{li} {)}^{\text{T}} \varvec{M}_{abi}^{o} \text{(}\varvec{R}_{ * }^{li} {);}\;\varvec{K}_{abi}^{ * } = \text{(}\varvec{R}_{ * }^{li} {)}^{\text{T}} \varvec{K}_{abi}^{o} \text{(}\varvec{R}_{ * }^{li} {)}$$
(29)

In the generalized coordinates of the system, the generalized coordinates of the linear motor can be expressed as follows:

$$\varvec{u}_{Li}^{ * } = \varvec{R}_{ * }^{Li} \varvec{U}_{i} ,$$
(30)

where \(\varvec{R}_{ * }^{Li} = \left[ {\begin{array}{*{20}c} {\varvec{E}_{12 \times 12} } & {\varvec{0}_{12 \times 12} } \\ \end{array} } \right]\).

By substituting Eq. (30) into Eq. (19), the mass matrix and function of linear motor in the generalized coordinate can be obtained as follows:

$$\varvec{M}_{Li}^{ * } = \text{(}\varvec{R}_{ * }^{li} \text{)}^{\text{T}} \varvec{M}_{Li}^{o} \text{(}\varvec{R}_{ * }^{li} \text{);}\;\varvec{K}_{Li}^{ * } = \text{(}\varvec{R}_{ * }^{li} \text{)}^{\text{T}} \varvec{K}_{Li}^{o} \text{(}\varvec{R}_{ * }^{li} \text{)}.$$
(31)

The generalized coordinates of the slider can be expressed as follows:

$$\Delta S_{i}^{ * } = \varvec{R}_{ * }^{Si} \varvec{U}_{i} ,$$
(32)

where \(\varvec{R}_{ * }^{Si} = \left[ {\begin{array}{*{20}c} {\varvec{0}_{1 \times 3} } & {\varvec{R}_{si} \varvec{R}_{Li} } & {\varvec{0}_{1 \times 18} } \\ \end{array} } \right]\).

In this case, the mass matrix of slider in the generalized coordinate can be obtained as follows:

$$\varvec{M}_{Si}^{ * } = \text{(}\varvec{R}_{ * }^{Si} {)}^{\text{T}} m_{si} \text{(}\varvec{R}_{ * }^{Si} {)}$$
(33)

Therefore, based on the above analysis, the total mass matrix and stiffness matrix of the single branch of the 5-PSS/UPU parallel mechanism in the generalized system coordinates are expressed as follows:

$$\begin{aligned} \varvec{M}_{i}^{ * } & = \varvec{M}_{abi}^{ * } + \varvec{M}_{Li}^{ * } + \varvec{M}_{Si}^{ * } = \left[ {\begin{array}{*{20}c} {\left[ {\varvec{M}_{i}^{11} } \right]_{18 \times 18} } & {\left[ {\varvec{M}_{i}^{12} } \right]_{18 \times 6} } \\ {\left[ {\varvec{M}_{i}^{21} } \right]_{6 \times 18} } & {\left[ {\varvec{M}_{i}^{22} } \right]_{6 \times 6} } \\ \end{array} } \right]; \\ \varvec{K}_{i}^{ * } & = \varvec{K}_{abi}^{ * } + \varvec{K}_{Li}^{ * } = \left[ {\begin{array}{*{20}c} {\left[ {\varvec{K}_{i}^{11} } \right]_{18 \times 18} } & {\left[ {\varvec{K}_{i}^{12} } \right]_{18 \times 6} } \\ {\left[ {\varvec{K}_{i}^{21} } \right]_{6 \times 18} } & {\left[ {\varvec{K}_{i}^{22} } \right]_{6 \times 6} } \\ \end{array} } \right]. \\ \end{aligned}$$
(34)

The moving platform is considered a rigid body. Therefore, in coordinate system O–xyz, the kinematic equation of the moving platform can be obtained as follows:

$$\varvec{M}_{p} \varvec{\ddot{u}}_{p} = \varvec{T}_{p} + \varvec{T}_{ep} - \varvec{M}_{p} \varvec{\ddot{u}}_{rp} ,$$
(35)

where \(\varvec{M}_{p}\) is the mass matrix of the moving platform, \(\varvec{T}_{p}\) is the array of forces exerted on the studied moving platform by branched chains with the studied one, \(\varvec{T}_{ep}\) is the array of generalized force of external load of the moving platform, and \(\varvec{\ddot{u}}_{rp}\) is the acceleration of rigid bodies.

It is supposed that the \(\varvec{U}\) is the array of generalized coordinates of the 5-PSS/UPU parallel mechanism system, which is expressed as follows:

$$\varvec{U} = \left[ {\begin{array}{*{20}c} {\varvec{U}_{1}^{ * } } & {\varvec{U}_{2}^{ * } } & {\varvec{U}_{3}^{ * } } & {\varvec{U}_{4}^{ * } } & {\varvec{U}_{5}^{ * } } & {\varvec{u}_{p} } \\ \end{array} } \right]^{\text{T}} ,$$
(36)

where \(\varvec{U}_{i}^{ * } = \left[ {u_{L1}^{o} ,u_{{L\text{2}}}^{o} , \cdots ,u_{{L\text{12}}}^{o} ,u_{{\text{o}1}} ,u_{{\text{o2}}} , \cdots ,u_{{\text{o6}}} } \right]\) and \(\varvec{u}_{p} = \left[ {\Delta x_{p} ,\Delta y_{p} ,\Delta z_{p} ,\Delta \alpha_{p} ,\Delta \beta_{p} ,\Delta \gamma_{p} } \right]\).

The dynamic equation of the parallel mechanism with rigid and flexible couplings can be obtained by assembling differential equations of motion of kinematic chains, and combining the kinematic and dynamics constraint equations:

$$\varvec{M\ddot{U}} + \varvec{C\dot{U}} + \varvec{KU} = \varvec{F} - \varvec{M\ddot{U}}_{r} ,$$
(37)

where U is the array of generalized coordinates of the 5-PSS/UPU parallel mechanism system. M and K are the mass matrix and rigidity matrix, respectively. \(\varvec{C = }\lambda_{1} \varvec{M} + \lambda_{2} \varvec{K}\) is the damping matrix of the system, and \(\lambda_{1}\) and \(\lambda_{2}\) are the Rayleigh damping coefficients. \(\varvec{F}\) is the array of generalized forces. \(\varvec{\ddot{U}}_{r}\) is the array of the accelerations of rigid bodies, which can be obtained through the kinematic analysis of the rigid body of the 5-PSS/UPU parallel mechanism.

$$\begin{aligned} \varvec{M} & \varvec{ = }\left[ {\begin{array}{*{20}c} {\varvec{M}_{1}^{11} } & {} & {} & {} & {} & {\varvec{M}_{1}^{12} } \\ {} & {\varvec{M}_{2}^{11} } & {} & {} & {} & {\varvec{M}_{2}^{12} } \\ {} & {} & {\varvec{M}_{3}^{11} } & {} & {} & {\varvec{M}_{3}^{12} } \\ {} & {} & {} & {\varvec{M}_{4}^{11} } & {} & {\varvec{M}_{4}^{12} } \\ {} & {} & {} & {} & {\varvec{M}_{5}^{11} } & {\varvec{M}_{5}^{12} } \\ {\varvec{M}_{1}^{21} } & {\varvec{M}_{2}^{21} } & {\varvec{M}_{3}^{21} } & {\varvec{M}_{4}^{21} } & {\varvec{M}_{5}^{21} } & {\sum\limits_{i = 1}^{5} {\varvec{M}_{i}^{22} + M_{p} } } \\ \end{array} } \right], \\ \varvec{K} & \varvec{ = }\left[ {\begin{array}{*{20}c} {\varvec{K}_{1}^{11} } & {} & {} & {} & {} & {\varvec{K}_{1}^{12} } \\ {} & {\varvec{K}_{2}^{11} } & {} & {} & {} & {\varvec{K}_{2}^{12} } \\ {} & {} & {\varvec{K}_{3}^{11} } & {} & {} & {\varvec{K}_{3}^{12} } \\ {} & {} & {} & {\varvec{K}_{4}^{11} } & {} & {\varvec{K}_{4}^{12} } \\ {} & {} & {} & {} & {\varvec{K}_{5}^{11} } & {\varvec{K}_{5}^{12} } \\ {\varvec{K}_{1}^{21} } & {\varvec{K}_{2}^{21} } & {\varvec{K}_{3}^{21} } & {\varvec{K}_{4}^{21} } & {\varvec{K}_{5}^{21} } & {\sum\limits_{i = 1}^{5} {\varvec{K}_{i}^{22} } } \\ \end{array} } \right]. \\ \end{aligned}$$
(38)

3 Numerical Simulation

3.1 Analysis of Natural Frequency Characteristics

To prevent the resonance of parallel mechanism caused by impact load [28] and reduce its effects on the dynamic accuracy of the moving platform, it is necessary to analyze the natural frequency characteristics of the 5-PSS/UPU parallel mechanism. Table 1 shows the parameters of the 5-PSS/UPU parallel mechanism.

Table 1 Parameters of the 5-PSS/UPU parallel mechanism
Full size table

Neglecting the damp term from Eq. (37), we obtain the main vibration equation of the system and its characteristic equation as follows:

$$\left\{ \begin{aligned} &A( - \varvec{M}\omega_{n}^{2} + \varvec{K}) = 0, \hfill \\ &\left| {\varvec{M}^{ - 1} \varvec{K} - \omega_{n}^{2} \varvec{E}} \right| = 0, \hfill \\ \end{aligned} \right.$$
(39)

where \(\omega_{n}\) denotes the natural frequency. The natural frequency with respect to the 5-PSS/UPU parallel mechanism can be achieved using Eq. (38) during the simulation, which is very significant to realize the dynamic decoupling of the parallel mechanism [29].

Next, we can obtain the distribution of the natural frequency of the 5-PSS/UPU parallel mechanism in the position space at zp= 0 and the distribution under the attitude working space.

Figure 7 shows the natural frequency of the 5-PSS/UPU parallel mechanism positional space with consideration of elastically active branched chains candidates. It can be observed that the variations in each natural frequency in the position working space are [2.19, 20.89] Hz, [23.49, 64.64] Hz, and [65.31, 100.33] Hz. The first-order natural frequency and the third-order natural frequency are relatively large at the center position (X = 0; Y = 0), and the natural frequency is relatively small at the working edge position. The second-order natural frequency is small at the center position (X = 0; Y = 0), and the natural frequency is large at the working edge position [30].

Figure 7
figure 7

Natural frequency distribution of the 5-PSS/UPU parallel mechanism positional space

Full size image

Figure 8 shows the natural frequency of the 5-PSS/UPU parallel mechanism attitude space with consideration of elastically active branched chains candidates. It can be observed that the variations in each natural frequency in the attitude working space are [3.89, 20.89] Hz, [23.49, 69.48] Hz, and [37.49, 100.33] Hz. The first-order natural frequency and the third-order natural frequency are relatively large at the center position (\(\alpha = 0^{\text{o}} ;\beta = 0^{\text{o}}\)), and the natural frequency is relatively small at the working edge position. The second-order natural frequency is small at the center position (\(\alpha = 0^{\text{o}} ;\beta = 0^{\text{o}}\)), and the natural frequency is large at the working edge position.

Figure 8
figure 8

Natural frequency distribution of the 5-PSS/UPU parallel mechanism attitude space

Full size image

In addition, it can be observed through the above natural frequency numerical analysis that the natural frequency of the 5-PSS/UPU parallel mechanism in the moving working space is greater than its operating frequency of 0.5 Hz; hence, the system does not cause resonance.

3.2 Elastic Displacement of Moving Platform

During simulation, the moving platform is set to move on a trajectory given as follows:

$$\left\{ \begin{aligned} & x = y = 10\text{sin}(0.4\uppi{t}), \hfill \\ & z = 0, \hfill \\ \end{aligned} \right.\;\;\left\{ \begin{aligned} \alpha = 7.5\text{sin}(0.4\uppi{t}), \hfill \\ \beta = 7.5\text{sin}(0.4\uppi{t}). \hfill \\ \end{aligned} \right.$$
(40)

Using the Newmark method [31] to solve Eq. (36), the displacement errors of the moving platform in the global frame O-XYZ are obtained. Figure 9 illustrates the displacement errors of the moving platform in the global frame O-XYZ, where εX, εY, and εZ refer to the position errors in directions X, Y, and Z, respectively. εγ and εβ refer to the orientation errors around X-axis and Y-axis, respectively. With these preconditions, it is found that the maximum position error is − 0.096 mm in direction Y, and the maximum orientation error is − 0.29° around X-axis. Hence, the influence of elastic links should not be ignored, especially when the moving platform moves at a relatively high speed. It is necessary to analyze the displacement errors of the flexible 5-PSS/UPU parallel mechanism.

Figure 9
figure 9

Displacement errors of moving platform: a Position error in direction X; b Position error in direction Y; c Position error in direction Z; d Orientation error around X-axis; e Orientation error around Y-axis

Full size image

4 Conclusions

A novel five-degree-of-freedom parallel mechanism is proposed as the dynamic balance device in the spacecraft recovery research filed because of its simple structure, better dynamic, and stiffness qualities.

According to the method of the finite element theory and Lagrange, the dynamics modeling of flexible branched links and linear motors are investigated, and the 5-PSS/UPU parallel mechanism according to the kinematic coupling relationship between each components of parallel mechanism is obtained.

The natural frequency and accuracy of the moving platform of 5-PSS/UPU parallel mechanism by considering elastically active branched chains are investigated through numerical simulation. The results show that the natural frequency of the system in the moving working space is greater than its operating frequency, the maximum position errors in direction of X-axis, Y-axis, and Z-axis are − 0.084 mm, − 0.096 mm, and 0.018 mm, respectively, and the maximum orientation errors around X-axis and Y-axis are − 0.29° and 0.26°, respectively. It is of great significance to improve the kinematics performance of the parallel mechanism.