Abstract
Let A be an Artinian Gorenstein algebra over a field k of characteristic zero with dimk A>1. To every such algebra and a linear projection π on its maximal ideal  with range equal to the socle Soc(A) of A, one can associate a certain algebraic hypersurface
with range equal to the socle Soc(A) of A, one can associate a certain algebraic hypersurface  , which is the graph of a polynomial map P
π
: kerπ→Soc(A)≃k. Recently, the following surprising criterion has been obtained: two Artinian Gorenstein algebras A and
, which is the graph of a polynomial map P
π
: kerπ→Soc(A)≃k. Recently, the following surprising criterion has been obtained: two Artinian Gorenstein algebras A and  are isomorphic if and only if any two hypersurfaces S
π
and
are isomorphic if and only if any two hypersurfaces S
π
and  arising from A and
arising from A and  , respectively, are affinely equivalent. In the present paper, we focus on the cases
, respectively, are affinely equivalent. In the present paper, we focus on the cases  and
and  and explain how in these situations the above criterion can be derived by complex-analytic methods. The complex-analytic proof for
and explain how in these situations the above criterion can be derived by complex-analytic methods. The complex-analytic proof for  has not previously appeared in print but is foundational for the general result. The purpose of our paper is to present this proof and compare it with that for
has not previously appeared in print but is foundational for the general result. The purpose of our paper is to present this proof and compare it with that for  , thus highlighting a curious connection between complex analysis and commutative algebra.
, thus highlighting a curious connection between complex analysis and commutative algebra.
Mathematics Subject Classification
13H10; 32V40
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper concerns a result in commutative algebra but is intended mainly for experts in complex analysis and CR-geometry. The background required for understanding the algebraic content is rather minimal and is given in Section 2.
We consider Artinian local commutative associative algebras over a field k. Such an algebra A is Gorenstein if and only if the socle Soc(A) of A is a one-dimensional vector space over k. Gorenstein algebras frequently occur in various areas of mathematics and its applications to physics (see, e.g., [1],[12]). In the case when the field k has characteristic zero, in articles [6],[11], a surprising criterion for isomorphism of Artinian Gorenstein algebras was found. The criterion is given in terms of a certain algebraic hypersurface S
π
in the maximal ideal  of A associated to a linear projection π on
of A associated to a linear projection π on  with range Soc(A), where we assume that dimk A>1. The hypersurface S
π
passes through the origin and is the graph of a polynomial map P
π
: kerπ→Soc(A)≃k. It is shown in [6],[11] that two Artinian Gorenstein algebras A and
with range Soc(A), where we assume that dimk A>1. The hypersurface S
π
passes through the origin and is the graph of a polynomial map P
π
: kerπ→Soc(A)≃k. It is shown in [6],[11] that two Artinian Gorenstein algebras A and  are isomorphic if and only if any two hypersurfaces S
π
and
are isomorphic if and only if any two hypersurfaces S
π
and  arising from A and
arising from A and  , respectively, are affinely equivalent, that is, there exists a bijective affine map
, respectively, are affinely equivalent, that is, there exists a bijective affine map  such that
such that  .
.
Currently, there are two different proofs of the above criterion. The one given in [11] is purely algebraic, whereas the one proposed in [6] reduces the case of an arbitrary field to that of  . A proof of the criterion in the latter case is contained in our earlier article [7] and, quite surprisingly, is based on a complex-analytic argument. It turns out that one can give an independent complex-analytic proof of the criterion for
. A proof of the criterion in the latter case is contained in our earlier article [7] and, quite surprisingly, is based on a complex-analytic argument. It turns out that one can give an independent complex-analytic proof of the criterion for  as well. This proof has not been previously published and is derived from ideas developed in paper [5], which never appeared in print (see Remark 4.1). However, the argument utilized in the case
as well. This proof has not been previously published and is derived from ideas developed in paper [5], which never appeared in print (see Remark 4.1). However, the argument utilized in the case  is rather important as it inspired our proof for the case
is rather important as it inspired our proof for the case  in [7] and therefore laid the foundation of the general result for an arbitrary field. Thus, the purpose of the present article is to provide a complex-analytic proof of the criterion for
in [7] and therefore laid the foundation of the general result for an arbitrary field. Thus, the purpose of the present article is to provide a complex-analytic proof of the criterion for  and to compare it with that for
and to compare it with that for  given in [7]. These proofs emphasize an intriguing connection between complex analysis and commutative algebra. In each of the two cases, the idea is to consider certain tube submanifolds in complex space associated to the algebras in question and utilize their CR-automorphisms. In fact, as stated in Remark 5.1, there is a deep relationship between Artinian Gorenstein algebras for
given in [7]. These proofs emphasize an intriguing connection between complex analysis and commutative algebra. In each of the two cases, the idea is to consider certain tube submanifolds in complex space associated to the algebras in question and utilize their CR-automorphisms. In fact, as stated in Remark 5.1, there is a deep relationship between Artinian Gorenstein algebras for  and tube hypersurfaces locally CR-equivalent to Levi non-degenerate hyperquadrics. We believe that this relationship has much to offer if fully understood.
and tube hypersurfaces locally CR-equivalent to Levi non-degenerate hyperquadrics. We believe that this relationship has much to offer if fully understood.
The paper is organized as follows. Section 2 contains algebraic preliminaries and the precise statement of the criterion in Theorem 2.1. The proof of the necessity implication of Theorem 2.1 is given in Section 3. This part of the proof has no relation to complex analysis and is only included for the completeness of our exposition. Further, Sections 4 and 5 contain the complex-analytic proofs of the sufficiency implications for  and
and  , respectively. Finally, in Section 6, we demonstrate how powerful our criterion can be in applications. Namely, we apply it to a one-parameter family A
t
of 15-dimensional Gorenstein algebras. While directly finding all pairwise isomorphic algebras in the family A
t
seems to be quite hard, this problem is easily solved with the help of Theorem 2.1
, respectively. Finally, in Section 6, we demonstrate how powerful our criterion can be in applications. Namely, we apply it to a one-parameter family A
t
of 15-dimensional Gorenstein algebras. While directly finding all pairwise isomorphic algebras in the family A
t
seems to be quite hard, this problem is easily solved with the help of Theorem 2.1
2 Preliminaries
Let A be a commutative associative algebra over a field k. We assume that A is unital and denote by 1 its multiplicative identity element. Further, we assume that A is local, that is, (i) A has a unique maximal ideal (which we denote by  ), and (ii) the natural injective homomorphism
), and (ii) the natural injective homomorphism  is in fact an isomorphism. In this case, one has the vector space decomposition
is in fact an isomorphism. In this case, one has the vector space decomposition  , where 〈·〉 denotes linear span. Furthermore, A is isomorphic to the unital extension of its maximal ideal
, where 〈·〉 denotes linear span. Furthermore, A is isomorphic to the unital extension of its maximal ideal  , which is the direct sum
, which is the direct sum  endowed with an operation of multiplication in the obvious way. For example, the algebra
endowed with an operation of multiplication in the obvious way. For example, the algebra  of germs of holomorphic functions at the origin in
of germs of holomorphic functions at the origin in  is a complex local algebra whose maximal ideal consists of all germs vanishing at 0. Clearly, every element of
is a complex local algebra whose maximal ideal consists of all germs vanishing at 0. Clearly, every element of  is the sum of the germ of a constant function and a germ vanishing at the origin.
is the sum of the germ of a constant function and a germ vanishing at the origin.
Next, we suppose that dimk A>1 and that A is Artinian, i.e., dimk A<∞. In addition, we let A to be Gorenstein, which means that the socle of A, defined as  , is a one-dimensional vector space over k (see, e.g., [9]). For example, if I is the ideal in
, is a one-dimensional vector space over k (see, e.g., [9]). For example, if I is the ideal in  generated by the germs of
generated by the germs of  , then
, then  is a complex Artinian Gorenstein algebra with
is a complex Artinian Gorenstein algebra with  and
and  spanned by the element of
spanned by the element of  represented by the germ of z
1
z
2.
represented by the germ of z
1
z
2.
We now assume that the field k has characteristic zero and consider the exponential map


where x
0:=1. By Nakayama’s lemma (see, e.g., Theorem 2.2 on p. 8 in [13]),  is a nilpotent algebra, and therefore the above sum is in fact finite, with the highest-order term corresponding to m=ν, where ν≥1 is the socle degree of A, i.e., the largest among all integers μ for which
is a nilpotent algebra, and therefore the above sum is in fact finite, with the highest-order term corresponding to m=ν, where ν≥1 is the socle degree of A, i.e., the largest among all integers μ for which  . Observe that
. Observe that  . The map exp is bijective with the inverse given by the polynomial transformation
. The map exp is bijective with the inverse given by the polynomial transformation

Fix a linear projection π on A with range Soc(A) and kernel containing 1 (we call such projections admissible). Set  and let S
π
be the hypersurface in
and let S
π
be the hypersurface in  given as the graph of the polynomial map
given as the graph of the polynomial map  of degree ν defined as follows:
of degree ν defined as follows:

(note that for dimk A=2, one has P
π
=0). Observe that the Soc(A)-valued quadratic part of P
π
is non-degenerate on  since the Soc(A)-valued bilinear form
since the Soc(A)-valued bilinear form

is non-degenerate on A (see, e.g., p. 11 in [8]). Numerous examples of hypersurfaces S π explicitly computed for particular algebras can be found in [2],[6],[7] (see also Section 6 below).
We will now state the criterion for isomorphism of Artinian Gorenstein algebras obtained in [6],[11].
Theorem 2.1.
Let A and  be Gorenstein algebras of finite vector space dimension greater than 1 over a field of characteristic zero and π and
be Gorenstein algebras of finite vector space dimension greater than 1 over a field of characteristic zero and π and  admissible projections on A and
admissible projections on A and  , respectively. Then A and
, respectively. Then A and  are isomorphic if and only if the hypersurfaces S
π
and
are isomorphic if and only if the hypersurfaces S
π
and  are affinely equivalent.
are affinely equivalent.
Remark 2.2.
For every hypersurface S
π
, we let  be the graph over
be the graph over  of the polynomial map -P
π
(see (2.2)). Observe that
of the polynomial map -P
π
(see (2.2)). Observe that

Clearly, S
π
and  are affinely equivalent if and only if
are affinely equivalent if and only if  and
and  are affinely equivalent. Therefore, in order to prove Theorem 2.1, it is sufficient to obtain its statement with
are affinely equivalent. Therefore, in order to prove Theorem 2.1, it is sufficient to obtain its statement with  and
and  in place of S
π
and
in place of S
π
and  , respectively. The hypersurfaces
, respectively. The hypersurfaces  and
and  are easier to work with, and we utilize them instead of S
π
and
are easier to work with, and we utilize them instead of S
π
and  in our proofs below.
in our proofs below.
3 Proof of the necessity implication
First of all, we explain how the necessity implication of Theorem 2.1 is derived. As stated in the introduction, this part of the proof has no relation to complex analysis and is only included in the paper for the completeness of our exposition. The proof below works for any field of characteristic zero. The idea is to show that if π
1 and π
2 are admissible projections on A, then  for some
for some  . Clearly, the necessity implication is a consequence of this fact (cf. [7]).
. Clearly, the necessity implication is a consequence of this fact (cf. [7]).
For every  , let M
y
be the multiplication operator from A to
, let M
y
be the multiplication operator from A to  defined by a↦y a and set
defined by a↦y a and set  . The correspondence
. The correspondence  defines a linear map
defines a linear map  from
from  into the space
into the space  of linear maps from
of linear maps from  to Soc(A). Since for every admissible projection π the form b
π
defined in (2.3) is non-degenerate on A and since
to Soc(A). Since for every admissible projection π the form b
π
defined in (2.3) is non-degenerate on A and since  , it follows that
, it follows that  is an isomorphism.
is an isomorphism.
Next, let λ:=π
2-π
1 and observe that λ(1)=0, λ(Soc(A))=0. Clearly,  lies in
lies in  , and therefore there exists
, and therefore there exists  such that
such that  . We then have
. We then have  everywhere on A, hence
everywhere on A, hence

for x
0:= log(1+y
0), which implies  as claimed. □
as claimed. □
4 Proof of the sufficiency implication for 
By assumption,  , and we denote this common dimension by N. If N=2, then A and
, and we denote this common dimension by N. If N=2, then A and  are clearly isomorphic, and thus, from now on, we suppose that N>2.
are clearly isomorphic, and thus, from now on, we suppose that N>2.
Let  be the complexification of the real algebra A. Then
be the complexification of the real algebra A. Then  , and
, and  is a complex Artinian Gorenstein algebra with maximal ideal
is a complex Artinian Gorenstein algebra with maximal ideal  . Next, we denote by
. Next, we denote by  the complex-linear extension of π to
the complex-linear extension of π to  and by
and by  the conjugation on
the conjugation on  defining the real form A, for all
defining the real form A, for all  , with x,y∈A. Then
, with x,y∈A. Then  is a
is a  -valued Hermitian form on
-valued Hermitian form on  that coincides with b
π
on A (see (2.3)). Since the bilinear form b
π
is non-degenerate on A, the Hermitian form h is non-degenerate on
that coincides with b
π
on A (see (2.3)). Since the bilinear form b
π
is non-degenerate on A, the Hermitian form h is non-degenerate on  .
.
Consider the following real Levi non-degenerate hyperquadric in the complex projective space  :
:

where [z] denotes the point of  represented by
represented by  . We think of
. We think of  as the affine part of
as the affine part of  and of
and of

as the affine part of the hyperquadric  . One can choose complex coordinates w
1,…,w
N-1 in
. One can choose complex coordinates w
1,…,w
N-1 in  so that, upon identification of
so that, upon identification of  with
with  , the affine quadric
, the affine quadric  is given by the equation
is given by the equation

where w:=(w
1,…,w
N-2) and H is a non-degenerate Hermitian form on  .
.
Next, consider the following real tube hypersurface in  :
:

Let  be the exponential map associated to
be the exponential map associated to  . It is straightforward to check that the biholomorphic transformation from
. It is straightforward to check that the biholomorphic transformation from  to
to  given by
given by

maps T onto  .
.
Analogously, for the algebra  , we obtain a Hermitian
, we obtain a Hermitian  -valued form
-valued form  on
on  , a real Levi non-degenerate hyperquadric
, a real Levi non-degenerate hyperquadric  in
in  , the corresponding affine hyperquadric
, the corresponding affine hyperquadric  in
in  , and a tube hypersurface
, and a tube hypersurface  in
in  .
.
Now, let  be a bijective affine map that establishes equivalence between
be a bijective affine map that establishes equivalence between  and
and  . We extend it to a complex affine map
. We extend it to a complex affine map  . Clearly,
. Clearly,  transforms T into
transforms T into  . Consider the biholomorphism from
. Consider the biholomorphism from  to
to  defined as follows:
defined as follows:

where  and
and  is the exponential map associated to
is the exponential map associated to  . Observe that Φ maps
. Observe that Φ maps  onto
onto  .
.
We will now show that, upon identification of  with
with  and
and  with
with  , the map Φ is affine. Indeed, since
, the map Φ is affine. Indeed, since  and
and  are biholomorphically equivalent, the signatures of their Levi forms coincide. Therefore, one can choose complex coordinates
are biholomorphically equivalent, the signatures of their Levi forms coincide. Therefore, one can choose complex coordinates  in
in  so that, upon identification of
so that, upon identification of  with
with  , the affine quadric
, the affine quadric  is given by the equation
is given by the equation

where  (cf. (4.1)). Thus, when written in the coordinates (w,w
N-1),
(cf. (4.1)). Thus, when written in the coordinates (w,w
N-1),  , the map Φ becomes an automorphism of
, the map Φ becomes an automorphism of  preserving quadric (4.1). It is well-known that every such transformation has the form
preserving quadric (4.1). It is well-known that every such transformation has the form

where  satisfies H(U w,U w)≡σ H(w,w),
satisfies H(U w,U w)≡σ H(w,w),  ,
,  , λ>0, σ=±1, and σ may be equal to -1 only if the numbers of positive and negative eigenvalues of H are equal. In particular, Φ is an affine map as claimed.
, λ>0, σ=±1, and σ may be equal to -1 only if the numbers of positive and negative eigenvalues of H are equal. In particular, Φ is an affine map as claimed.
By formulas (2.1) and (4.3), for  we have
we have

where x
0:=f(0), g:=f-x
0 is the linear part of f, and  is the exponential map associated to
is the exponential map associated to  . Since Φ is affine, formula (4.4) implies g(x)2=g(x
2) for all
. Since Φ is affine, formula (4.4) implies g(x)2=g(x
2) for all  , which is equivalent to the statement that
, which is equivalent to the statement that  is an algebra isomorphism. Therefore,
is an algebra isomorphism. Therefore,  and
and  are isomorphic, hence A and
are isomorphic, hence A and  are also isomorphic as required. □
are also isomorphic as required. □
Remark 4.1.
The method utilized in the above proof can be extracted, in principle, from ideas contained in paper [5] (which should be read in conjunction with [4]), but is by no means explicitly articulated there.
5 Proof of the sufficiency implication for 
The argument that follows is contained in [7] and is included in this paper for comparison with the proof in the case  given in Section 4.
given in Section 4.
By assumption,  , and we denote this common dimension by N. If N=2, then A and
, and we denote this common dimension by N. If N=2, then A and  are isomorphic, and thus, from now on, we suppose that N>2.
are isomorphic, and thus, from now on, we suppose that N>2.
Consider the maximal ideal  of A. We will now forget the complex structure on
of A. We will now forget the complex structure on  and treat it as a real algebra. Let
and treat it as a real algebra. Let  be the (real) unital extension of
be the (real) unital extension of  (see Section 2) and 1 the multiplicative identity element in
(see Section 2) and 1 the multiplicative identity element in  . Observe that
. Observe that  is not Gorenstein since
is not Gorenstein since  . We now consider the complexification
. We now consider the complexification  of
of  . Then
. Then  , and
, and  is a complex Artinian local algebra with maximal ideal
is a complex Artinian local algebra with maximal ideal  . The complex algebra
. The complex algebra  is not Gorenstein since
is not Gorenstein since  .
.
Next, let  be the extension of
be the extension of  to
to  defined by the condition
defined by the condition  and denote by
and denote by  the complex-linear extension of
the complex-linear extension of  to
to  . Further, denote by
. Further, denote by  the conjugation on
the conjugation on  defining the real form
defining the real form  , for all
, for all  , with
, with  . Then
. Then  is a
is a  -valued Hermitian form on
-valued Hermitian form on  that coincides on
that coincides on  with the
with the  -valued bilinear form
-valued bilinear form  defined analogously to (2.3).
defined analogously to (2.3).
Consider the following subset of the complex projective space  :
:

where [z] denotes the point of  represented by
represented by  . We think of
. We think of  as the affine part of
as the affine part of  and of
and of

as the affine part of  . Observe that
. Observe that  is a real-analytic Levi non-degenerate CR-submanifold of
is a real-analytic Levi non-degenerate CR-submanifold of  of real codimension 2. In fact, one can choose complex coordinates w
1,…,w
2N-2 in
of real codimension 2. In fact, one can choose complex coordinates w
1,…,w
2N-2 in  so that, upon identification of
so that, upon identification of  with
with  , the affine quadric
, the affine quadric  is given by the equations
is given by the equations

This can be seen by choosing coordinates in  (regarded as a complex algebra) in which the restriction of the Soc(A)-valued bilinear form b
π
to
(regarded as a complex algebra) in which the restriction of the Soc(A)-valued bilinear form b
π
to  is given by the identity matrix.
is given by the identity matrix.
Next, consider the following real tube codimension 2 submanifold in  :
:

Let  be the exponential map associated to
be the exponential map associated to  . It is straightforward to check that the biholomorphic transformation from
. It is straightforward to check that the biholomorphic transformation from  to
to  given by
given by

maps T onto  .
.
Analogously, for the algebra  , we obtain algebras
, we obtain algebras  and
and  , a Hermitian
, a Hermitian  -valued form
-valued form  on
on  , a real Levi non-degenerate codimension 2 affine quadric
, a real Levi non-degenerate codimension 2 affine quadric  in
in  , the corresponding coordinates
, the corresponding coordinates  in
in  , and a tube hypersurface
, and a tube hypersurface  in
in  .
.
Now, let  be a bijective affine map that establishes equivalence between
be a bijective affine map that establishes equivalence between  and
and  . We treat f as a real affine map and extend it to a complex affine map
. We treat f as a real affine map and extend it to a complex affine map  . Notice that
. Notice that  transforms T into
transforms T into  . Consider the biholomorphism from
. Consider the biholomorphism from  to
to  defined as follows:
defined as follows:

where  and
and  is the exponential map associated to
is the exponential map associated to  . Observe that Φ maps
. Observe that Φ maps  onto
onto  .
.
We claim that, upon identification of  with
with  and
and  with
with  , the map Φ is affine. Indeed, when written in the coordinates w
1,…,w
2N-2,
, the map Φ is affine. Indeed, when written in the coordinates w
1,…,w
2N-2,  , the map Φ becomes an automorphism of
, the map Φ becomes an automorphism of  preserving quadric (5.1). The fact that Φ is affine now follows from a description of CR-automorphism of this quadric (see the elliptic case on pp. 37–38 in [3]).
preserving quadric (5.1). The fact that Φ is affine now follows from a description of CR-automorphism of this quadric (see the elliptic case on pp. 37–38 in [3]).
By formulas (2.1) and (5.2), for  we have
we have

where x
0:=f(0), g:=f-x
0 is the linear part of f, and  is the exponential map associated to
is the exponential map associated to  . Since Φ is affine, formula (5.3) implies g(x)2=g(x
2) for all
. Since Φ is affine, formula (5.3) implies g(x)2=g(x
2) for all  , i.e.,
, i.e.,  is an algebra isomorphism. Therefore,
is an algebra isomorphism. Therefore,  and
and  are isomorphic, hence A and
are isomorphic, hence A and  are also isomorphic as required. □
are also isomorphic as required. □
Remark 5.1.
The proofs of Theorem 2.1 for the cases  presented in this paper are based on considering real tube submanifolds in complex space CR-equivalent to Levi non-degenerate affine quadrics. For
presented in this paper are based on considering real tube submanifolds in complex space CR-equivalent to Levi non-degenerate affine quadrics. For  , we utilized hypersurfaces, whereas for
, we utilized hypersurfaces, whereas for  , codimension 2 submanifolds were required. The former are called spherical tube hypersurfaces (see [10]), and there is in fact an intriguing relationship between them and real and complex Artinian Gorenstein algebras. This relationship was outlined in [5] (see also Section 9.2 in [10] for a brief survey). It turns out that
, codimension 2 submanifolds were required. The former are called spherical tube hypersurfaces (see [10]), and there is in fact an intriguing relationship between them and real and complex Artinian Gorenstein algebras. This relationship was outlined in [5] (see also Section 9.2 in [10] for a brief survey). It turns out that
-
to every real Artinian Gorenstein algebra of dimension greater than 2 and to every complex Artinian Gorenstein algebra one can associate a (closed) spherical tube hypersurface, where in the real case one obtains exactly hypersurfaces with bases (2.4) as in (4.2);
-
any two such hypersurfaces are affinely equivalent if and only if the corresponding algebras are isomorphic (one way to obtain the necessity implication in the real case is to proceed as in Section 4);
-
in a certain sense, all spherical tube hypersurfaces can be obtained by combining hypersurfaces of these two types.
We note that no higher-codimensional analogues of spherical tube hypersurfaces were considered in [5]. However, as the proof of Theorem 2.1 for  suggests, analogues of this kind are related to Artinian Gorenstein algebras as well. We believe that the curious connection between complex analysis and commutative algebra manifested through tube submanifolds CR-equivalent to affine quadrics deserves further investigation.
suggests, analogues of this kind are related to Artinian Gorenstein algebras as well. We believe that the curious connection between complex analysis and commutative algebra manifested through tube submanifolds CR-equivalent to affine quadrics deserves further investigation.
6 Example of application of Theorem 2.1
Theorem 2.1 is particularly useful when at least one of the hypersurfaces S
π
and  is affinely homogeneous (recall that a subset S of a vector space V is called affinely homogeneous if for every pair of points p,q∈S there exists a bijective affine map g of V such that g(S)=S and g(p)=q). In this case, the hypersurfaces S
π
and
is affinely homogeneous (recall that a subset S of a vector space V is called affinely homogeneous if for every pair of points p,q∈S there exists a bijective affine map g of V such that g(S)=S and g(p)=q). In this case, the hypersurfaces S
π
and  are affinely equivalent if and only if they are linearly equivalent. Indeed, if, for instance, S
π
is affinely homogeneous and
are affinely equivalent if and only if they are linearly equivalent. Indeed, if, for instance, S
π
is affinely homogeneous and  is an affine equivalence between S
π
and
is an affine equivalence between S
π
and  , then f∘g is a linear equivalence between S
π
and
, then f∘g is a linear equivalence between S
π
and  , where g is an affine automorphism of S
π
such that g(0)=f
-1(0). Clearly, in this case,
, where g is an affine automorphism of S
π
such that g(0)=f
-1(0). Clearly, in this case,  is affinely homogeneous as well.
is affinely homogeneous as well.
The proof of Theorem 2.1 in [11] shows that every linear equivalence f between S
π
and  has the block-diagonal form with respect to the decompositions
has the block-diagonal form with respect to the decompositions  and
and  , where
, where  , that is, there exist linear isomorphisms
, that is, there exist linear isomorphisms  and
and  such that f(x+y)=f
1(x)+f
2(y), with
such that f(x+y)=f
1(x)+f
2(y), with  , y∈Soc(A). Therefore, for the corresponding polynomial maps P
π
and
, y∈Soc(A). Therefore, for the corresponding polynomial maps P
π
and  (see (2.2)), we have
(see (2.2)), we have

where  and
and  are the homogeneous components of degree m of P
π
and
are the homogeneous components of degree m of P
π
and  , respectively.
, respectively.
Thus, Theorem 2.1 yields the following corollary (cf. Theorem 2.11 in [7]).
Corollary 6.1
Let A and  be Gorenstein algebras of finite vector space dimension greater than 1 over a field of characteristic zero and π and
be Gorenstein algebras of finite vector space dimension greater than 1 over a field of characteristic zero and π and  admissible projections on A and
admissible projections on A and  , respectively.
, respectively.
-
(i)
If A and
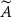 are isomorphic and at least one of S
π
and
are isomorphic and at least one of S
π
and 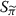 is affinely homogeneous, then for some linear isomorphisms
is affinely homogeneous, then for some linear isomorphisms  and
and  identity (6.1) holds. In this case, both S
π
and
identity (6.1) holds. In this case, both S
π
and 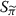 are affinely homogeneous.
are affinely homogeneous. -
(ii)
If for some linear isomorphisms
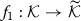 and
and 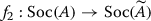 identity (6.1) holds, then the hypersurfaces S
π
and
identity (6.1) holds, then the hypersurfaces S
π
and 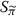 are linearly equivalent, and therefore the algebras A and
are linearly equivalent, and therefore the algebras A and 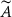 are isomorphic.
are isomorphic.
In [11] (see also Corollary 4.10 in [6]), we found a criterion for the affine homogeneity of some (hence every) hypersurface S
π
arising from an Artinian Gorenstein algebra A. Namely, S
π
is affinely homogeneous if and only if the action of the automorphism group of the algebra  on the set of all hyperplanes in
on the set of all hyperplanes in  complementary to Soc(A) is transitive. Furthermore, we showed (see also Corollary 4.11 in [6]) that this condition is satisfied if A is non-negatively graded in the sense that it can be represented as a direct sum
complementary to Soc(A) is transitive. Furthermore, we showed (see also Corollary 4.11 in [6]) that this condition is satisfied if A is non-negatively graded in the sense that it can be represented as a direct sum

where A
j are linear subspaces of A, with A
0=k (in this case  and Soc(A)=A
d for d:= max{j:A
j≠0}). It then follows that part (i) of Corollary 6.1 applies in the situation when one (hence the other) of the algebras A and
and Soc(A)=A
d for d:= max{j:A
j≠0}). It then follows that part (i) of Corollary 6.1 applies in the situation when one (hence the other) of the algebras A and  is non-negatively graded (see also [7] for the case
is non-negatively graded (see also [7] for the case  ). Note, however, that the existence of a non-negative grading on A is not a necessary condition for the affine homogeneity of S
π
(see, e.g., Remark 2.6 in [7]). Also, as shown in Section 8.2 in [6], the hypersurface S
π
need not be affinely homogeneous in general.
). Note, however, that the existence of a non-negative grading on A is not a necessary condition for the affine homogeneity of S
π
(see, e.g., Remark 2.6 in [7]). Also, as shown in Section 8.2 in [6], the hypersurface S
π
need not be affinely homogeneous in general.
To demonstrate how our method works, we will now apply Corollary 6.1 to a one-parameter family of non-negatively graded Artinian Gorenstein algebras. As before, let k be a field of characteristic zero. For t∈k, t≠±2, define

It is straightforward to verify that every A t is a Gorenstein algebra of dimension 15. We will prove the following proposition.
Proposition 6.2
A r and A s are isomorphic if and only if r=±s.
Proof.
The sufficiency implication is trivial (just replace y by -y). For the converse implication, consider the following monomials in k[x,y]:

Let e 0=1,e 1,…,e 14, respectively, be the vectors in A t arising from these monomials (to simplify the notation, we do not indicate the dependence of e j on t). They form a basis of A t . Define

where, as before, 〈·〉 denotes linear span. It is straightforward to check that the subspaces  form a non-negative grading on A
t
.
form a non-negative grading on A
t
.
Next, denote by  the maximal ideal of A
t
and let π
t
be the projection on A
t
with range
the maximal ideal of A
t
and let π
t
be the projection on A
t
with range  and kernel 〈e
0,…,e
13〉. Denote by w
1,…,w
14 the coordinates in
and kernel 〈e
0,…,e
13〉. Denote by w
1,…,w
14 the coordinates in  with respect to the basis e
1,…,e
14. In these coordinates the corresponding polynomial map
with respect to the basis e
1,…,e
14. In these coordinates the corresponding polynomial map  is written as
is written as

Suppose that for some r≠s the algebras A r and A s are isomorphic. By part (i) of Corollary 6.1, there exist C∈GL(13,k) and c∈k ∗ such that

where w:=(w 1,…,w 13). Since 0 is the only value of t for which P t has degree 7, we have r,s≠0. Comparing the terms of order 7 in identity (6.2), we obtain that the second row in the matrix C has the form (0,μ,0,…,0), and

Next, comparing the terms of order 6 in (6.2), we see that the first row in the matrix C has the form (σ,ρ,0,…,0), and

Further, comparing the terms of order 5 in (6.2) that do not involve  , we obtain
, we obtain

Now, (6.3), (6.4), and (6.5) yield r 2=s 2 as required. □
References
Bass H: On the ubiquity of Gorenstein rings. Math. Z 1963, 82: 8–28. 10.1007/BF01112819
Eastwood MG, Isaev AV: Extracting invariants of isolated hypersurface singularities from their moduli algebras. Math. Ann 2013, 356: 73–98. 10.1007/s00208-012-0836-7
Ezhov V, Schmalz G: A matrix Poincaré formula for holomorphic automorphisms of quadrics of higher codimension. Real associative quadrics. J. Geom. Anal 1998, 8: 27–41. 10.1007/BF02922107
Fels G, Kaup W: Local tube realizations of CR-manifolds and maximal Abelian subalgebras. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 2011, 10: 99–128.
Fels G, Kaup W: Classification of commutative algebras and tube realizations of hyperquadrics. preprint, available from http://arxiv.org/pdf/0906.5549v2
Fels G, Kaup W: Nilpotent algebras and affinely homogeneous surfaces. Math. Ann 2012, 353: 1315–1350. 10.1007/s00208-011-0718-4
Fels G, Isaev A, Kaup W, Kruzhilin N: Isolated hypersurface singularities and special polynomial realizations of affine quadrics. J. Geom. Analysis 2011, 21: 767–782. 10.1007/s12220-011-9223-y
Hertling C: Frobenius Manifolds and Moduli Spaces for Singularities. Cambridge: Cambridge Tracts in Mathematics 151, Cambridge University Press; 2002.
Huneke C: Hyman Bass and ubiquity: Gorenstein rings. Algebra, K-theory, Groups, and Education (New York, 1997), Contemp. Math. 243, Amer. Math. Soc., Providence, RI (1999)
Isaev AV: Spherical Tube Hypersurfaces. Lecture Notes in Mathematics 2020. Berlin: Springer; 2011.
Isaev AV: On the affine homogeneity of algebraic hypersurfaces arising from Gorenstein algebras. Asian J. Math 2011, 15: 631–640. 10.4310/AJM.2011.v15.n4.a7
Lurie J: On the classification of topological field theories. In Current Developments in Mathematics, 2008. Somerville, MA: Int. Press; 2009.
Matsumura H: Commutative Ring Theory. Cambridge: Cambridge Studies in Advanced Mathematics 8, Cambridge University Press; 1986.
Acknowledgements
This work is supported by the Australian Research Council.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Isaev, A. A complex-analytic proof of a criterion for isomorphism of Artinian Gorenstein algebras. Complex Analysis and its Synergies 1, 1 (2015). https://doi.org/10.1186/2197-120X-1-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2197-120X-1-1






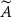 are isomorphic and at least one of S
π
and
are isomorphic and at least one of S
π
and 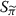 is affinely homogeneous, then for some linear isomorphisms
is affinely homogeneous, then for some linear isomorphisms  and
and  identity (6.1) holds. In this case, both S
π
and
identity (6.1) holds. In this case, both S
π
and 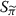 are affinely homogeneous.
are affinely homogeneous.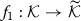 and
and 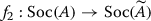 identity (6.1) holds, then the hypersurfaces S
π
and
identity (6.1) holds, then the hypersurfaces S
π
and 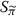 are linearly equivalent, and therefore the algebras A and
are linearly equivalent, and therefore the algebras A and 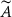 are isomorphic.
are isomorphic.