Two species competitive model with the Allee effect

Abstract

We consider the following system of difference equations: $x_{n+1}=\frac{a{x}_n^2}{1+x_n^2+c{y}_n}$, $y_{n+1}=\frac{b{y}_n^2}{1+y_n^2+d{x}_n}$, $n=0,1,\dots$ , where a, b, c, d are positive constants and $x_0,y_0\ge 0$ are initial conditions. This system has interesting dynamics and can have up to nine equilibrium points. The most complex and perhaps most interesting case is the case of nine equilibrium points, four of which are local attractors, four of which are saddle points, and one of which is a repeller. Using recent results of Kulenović and Merino we are able to characterize the basins of attractions of all local attractors and thus to describe the global dynamics of this system. This case can be considered as a two-dimensional version of the Allee effect for competitive systems.

MSC:39A10, 39A30, 37G35.

1 Introduction

The following difference equation is known as the Beverton-Holt model:

$$x_{n+1}=\frac{a{x}_n}{1+x_n},n=0,1,\dots ,$$

(1)

where $a>0$ is the rate of change (growth or decay) and $x_n$ is the size of the population at the n th generation.

This model was introduced by Beverton and Holt in 1957. It depicts density dependent recruitment of a population with limited resources which are not shared equally. The model assumes that the per capita number of offspring is inversely proportional to a linearly increasing function of the number of adults. In other words (1) can be considered as an equation of the form

$$x_{n+1}=x_{n}f(x_n),n=0,1,\dots ,$$

(2)

where $f(u)=a/(1+u)$ is inversely proportional to the linear function $A+Bu$, $A,B>0$, which can be normalized to be $1+u$.

The Beverton-Holt model is well studied and understood. It exhibits the following properties.

Theorem 1 Equation (1) has the two equilibrium points 0 and $a-1$ when $a>1$.

• (a) All solutions of (1) are monotonic (increasing or decreasing) sequences.

• (b) If $a\le 1$, then the zero equilibrium is a global attractor, that is, ${lim}_{n\to \mathrm{\infty }}{x}_n=0$, for all $x_0\ge 0$.

• (c) If $a>1$, then the equilibrium point $a-1$ is a global attractor, that is, ${lim}_{n\to \mathrm{\infty }}{x}_n=a-1$, for all $x_0>0$.

• (d) Both equilibrium points are globally asymptotically stable in the corresponding regions of parameters $a\le 1$ and $a>1$, that is, they are global attractors with the property that small changes of initial condition $x_0$ result in small changes of the corresponding solution $\{x_n\}$.

Furthermore, (1) can be solved explicitly and has the following solution:

$$\begin{array}{r}{x}_n=\frac{1}{1/(a-1)+(1/x_0-1/(a-1))1/a^n}\text{if }a\ne 1,\\ x_n=\frac{1}{n+1/x_0}\text{if }a=1,\end{array}$$

(3)

which can be used to prove all the preceding properties. See [1–4].

The Allee effect is a phenomenon in biology characterized by a positive correlation between population density and per capita growth rate. The Allee effect was first written on extensively by its namesake Warder Clyde Allee. The general idea of the Allee effect is that for smaller populations, the reproduction and survival rates of individuals decrease. This effect usually saturates or disappears as populations get larger. The Allee effect has been detected in a number of discrete models; see [4–7].

The effect may be due to any number of causes. In some species, reproduction (finding a mate in particular) may be increasingly difficult as the population density decreases.

In mathematics, when the basin of attraction of the zero equilibrium of a system contains an open set, we consider the system to exhibit the Allee effect. See [4, 5].

In view of Theorem 1 the Beverton-Holt model does not exhibit the Allee effect.

1.1 Beverton-Holt type model that exhibits the Allee effect

The difference equation

$$x_{n+1}=\frac{a{x}_n^2}{1+x_n^2},n=0,1,\dots ,$$

(4)

which was introduced by Thompson [8] as a depensatory generalization of the Beverton-Holt stock-recruitment relationship, was used to develop a set of constraints designed to safeguard against overfishing. This model has been used in the study of fish population dynamics, particularly when overfishing is present; see [7] for further references. In view of the sigmoid shape of the function $f(u)=\frac{a{u}^2}{1+u^2}$, (4) is called the sigmoid Beverton-Holt model. A very important feature of the sigmoid Beverton-Holt model is that it exhibits the Allee effect. We can see this from the following result, the proof of which is an immediate consequence of a stair-step diagram analysis.

Theorem 2 The global dynamics of Equation (4) is as follows:

• (a) Equation (4) has only a zero equilibrium when $a<2$.

• (b) Equation (4) has a zero equilibrium and the positive equilibrium $\overline{x}=1/2$, when $a=2$.

• (c) There exists a zero equilibrium and two positive equilibria, ${\overline{x}}_{-}$ and ${\overline{x}}_{+}$, when $a>2$.

• (d) All solutions of (4) are monotonic (increasing or decreasing) sequences.

• (e) If $a<2$, then the equilibrium point 0 is a global attractor, that is, ${lim}_{n\to \mathrm{\infty }}{x}_n=0$ for all $x_0\ge 0$.

• (f) If $a=2$, then the equilibrium point 0 is a global attractor, with the basin of attraction $B(0)=(0,\overline{x})$ and $\overline{x}=1/2$ is a non-hyperbolic equilibrium point with the basin of attraction $B(\overline{x})=[\overline{x},\mathrm{\infty })$.

• (g) If $a>2$, then we have zero equilibrium and ${\overline{x}}_{+}$ are locally asymptotically stable, while ${\overline{x}}_{-}$ is a repeller and the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(0)=\{x_0:0\le x_0<{\overline{x}}_{-}\},\hfill \\ B({\overline{x}}_{+})=\{x_0:{\overline{x}}_{-}<x_0<\mathrm{\infty }\}.\hfill \end{array}$$

In other words, the smaller positive equilibrium serves as the boundary between two basins of attraction. The zero equilibrium has the basin of attraction $B(0)$ and the model exhibits the Allee effect.

• (h) The equilibrium points 0 and ${\overline{x}}_{+}$ are globally asymptotically stable in the corresponding basins of attractions $B(0)$ and $B({\overline{x}}_{+})$.

1.2 Competitive model in two dimensions that exhibits the Allee effect

We will now consider the two-dimensional analog of (4) which is the uncoupled system

$$\begin{array}{r}{x}_{n+1}=\frac{a{x}_n^2}{1+x_n^2},\\ y_{n+1}=\frac{b{y}_n^2}{1+y_n^2},n=0,1,\dots ,\end{array}$$

(5)

where a and b are positive parameters. System (5) can have at most nine nonnegative equilibrium points:

$$\begin{array}{c}{E}_0(0,0),E_{{\overline{y}}_{-}}(0,{\overline{y}}_{-}),E_{{\overline{y}}_{+}}(0,{\overline{y}}_{+}),\hfill \\ E_{{\overline{x}}_{-}}({\overline{x}}_{-},0),E_{{\overline{x}}_{+}}({\overline{x}}_{+},0),E_{-}({\overline{x}}_{-},{\overline{y}}_{-}),\hfill \\ E_{-+}({\overline{x}}_{-},{\overline{y}}_{+}),E_{+-}({\overline{x}}_{+},{\overline{y}}_{-}),E_{+}({\overline{x}}_{+},{\overline{y}}_{+}).\hfill \end{array}$$

The dynamics of system (5) is partially described in the following theorem, with complete visual interpretation in Figure 1 can be derived from Theorem 2. Since there are three dynamics scenarios for each of two equations in (5), there are nine dynamic scenarios for system (5), which are visualized in Figure 1.

Figure 1

Global dynamics of uncoupled two-dimensional model (5) with nine dynamics scenarios.

Theorem 3 System (5) has the following properties:

• (a) All solutions $(x_n,y_n)$ of system (5) are component-wise monotonic and bounded, that is, both sequences $\{x_n\}$ and $\{y_n\}$ are monotonic and bounded.

• (b) If $a<2$ and $b<2$, then there exists only a zero equilibrium, which is a global attractor.

• (c) If $a<2$, $b>2$, then the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):0\le x_0<\mathrm{\infty },0\le y_0<{\overline{y}}_{-}\},\hfill \\ B(E_{{\overline{y}}_{+}}(0,{\overline{y}}_{+}))=\{(x_0,y_0):0\le x_0<\mathrm{\infty },{\overline{y}}_{-}<y_0<\mathrm{\infty }\}.\hfill \end{array}$$

• (d) If $a>2$, $b<2$, then the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):0\le x_0<{\overline{x}}_{-},0\le y_0<\mathrm{\infty }\},\hfill \\ B(E_{{\overline{x}}_{+}}({\overline{x}}_{+},0))=\{(x_0,y_0):{\overline{x}}_{-}<x_0<\mathrm{\infty },0\le y_0<\mathrm{\infty }\}.\hfill \end{array}$$

• (e) If $a>2$, $b>2$, then the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):0\le x_0<{\overline{x}}_{-},0\le y_0<{\overline{y}}_{-}\},\hfill \\ B(E_{{\overline{x}}_{+}}({\overline{x}}_{+},0))=\{(x_0,y_0):{\overline{x}}_{-}<x_0<\mathrm{\infty },0\le y_0<{\overline{y}}_{-}\},\hfill \\ B(E_{{\overline{y}}_{+}}(0,{\overline{y}}_{+}))=\{(x_0,y_0):0\le x_0<{\overline{x}}_{-},{\overline{y}}_{-}<y_0<\mathrm{\infty }\},\hfill \\ B(E_{++}({\overline{x}}_{+},{\overline{y}}_{+}))=\{(x_0,y_0):{\overline{x}}_{-}<x_0<\mathrm{\infty },{\overline{y}}_{-}<y_0<\mathrm{\infty }\},\hfill \\ B(E_{{\overline{x}}_{-}}({\overline{x}}_{-},0))=\{({\overline{x}}_{-},y_0):0\le y_0<{\overline{y}}_{-}\},\hfill \\ B(E_{{\overline{y}}_{-}}(0,{\overline{y}}_{-}))=\{(x_0,{\overline{y}}_{-}):0\le x_0<{\overline{x}}_{-}\},\hfill \\ B(E_{+-})=\{(x_0,{\overline{y}}_{-}):{\overline{x}}_{-}<x_0<\mathrm{\infty }\},B(E_{-+})=\{({\overline{x}}_{-},y_0):{\overline{y}}_{-}<y_0<\mathrm{\infty }\}.\hfill \end{array}$$

• (f) If $a=2$, $b<2$, then the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):0\le x_0<\overline{x},0\le y_0<\mathrm{\infty }\},\hfill \\ B(E_{\overline{x}}(\overline{x},0))=\{(x_0,y_0):\overline{x}\le x_0<\mathrm{\infty },0\le y_0<\mathrm{\infty }\}.\hfill \end{array}$$

• (g) If $a<2$, $b=2$, then the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):0\le x_0<\mathrm{\infty },0\le y_0<\overline{y}\},\hfill \\ B(E_{\overline{y}}(0,\overline{y}))=\{(x_0,y_0):0\le x_0<\mathrm{\infty },\overline{y}\le y_0<\mathrm{\infty }\}.\hfill \end{array}$$

• (g) If $a=2$, $b=2$, then the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):0\le x_0<\overline{x},0\le y_0<\overline{y}\},\hfill \\ B(E_{\overline{x}}(\overline{x},0))=\{(x_0,y_0):\overline{x}\le x_0<\mathrm{\infty },0\le y_0<\overline{y}\},\hfill \\ B(E_{\overline{y}}(0,\overline{y}))=\{(x_0,y_0):0\le x_0<\overline{x},\overline{y}\le y_0<\mathrm{\infty }\},\hfill \\ B(E)=\{(x_0,y_0):\overline{x}\le x_0,\overline{y}\le y_0\}.\hfill \end{array}$$

• (h) If $a=2$, $b>2$, then the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):0\le x_0<\overline{x},0\le y_0<{\overline{y}}_{-}\},\hfill \\ B(E_{\overline{x}}(\overline{x},0))=\{(x_0,y_0):\overline{x}\le x_0<\mathrm{\infty },0\le y_0<{\overline{y}}_{-}\},\hfill \\ B(E_{{\overline{y}}_{+}})=\{(x_0,y_0):0\le x_0<\overline{x},{\overline{y}}_{-}\le y_0<\mathrm{\infty }\},\hfill \\ B(E_{+}(\overline{x},{\overline{y}}_{+}))=\{(x_0,y_0):\overline{x}\le x_0,{\overline{y}}_{-}<y_0\}.\hfill \end{array}$$

• (i) Case $a>2$, $b=2$, is symmetric to the case $a=2$, $b>2$.

Two species can interact in several different ways through competition, cooperation, or predator-prey interactions. For each of these interactions, we obtain variations of system (5), all of which may require a different mathematical analysis.

The following coupled system is a variation of system (5) that exhibits competitive interactions:

$$\begin{array}{r}{x}_{n+1}=\frac{a{x}_n^2}{1+x_n^2+c{y}_n},\\ y_{n+1}=\frac{b{y}_n^2}{1+y_n^2+d{x}_n},n=0,1,\dots ,\end{array}$$

(6)

where $a,b,c,d>0$. This system will be considered in the remainder of this paper. We will show that system (6) has similar but more complex dynamics than system (5). We will see that like system (5) the coupled system (6) may possess one, three, five, seven or nine equilibrium points in the hyperbolic case and two, four, six or eight equilibrium points in the non-hyperbolic case. In each of these cases we will show that the Allee effect is present and we will precisely describe the basins of attraction of all equilibrium points. We will show that the boundaries of the basins of attraction of the equilibrium points are the global stable manifolds of the saddle or the non-hyperbolic equilibrium points. See [9–15] for related results. An interesting feature of our results is that the size of the basin of attraction of the zero equilibrium decreases as a function of the number of the equilibrium points. The biological interpretation of our results is given in [16, 17] and a similar system is treated in [18]. However, no details of the proofs are provided in [16, 17] and non-hyperbolic cases were not treated there. Here we give the detailed proofs of all dynamic scenarios and provide the explicit algebraic conditions for the existence of one through nine equilibrium points, which was also missing in [16, 17]. A specific feature of our results is that no equilibrium point in the interior of the first quadrant is computable and so our analysis is based on the geometry of the equilibrium curves.

2 Preliminaries

Our proofs use some recent general results for competitive systems of difference equations of the form

$$\{\begin{array}{l}{x}_{n+1}=f(x_n,y_n),\\ y_{n+1}=g(x_n,y_n),\end{array}$$

(7)

where f and g are continuous functions and $f(x,y)$ is non-decreasing in x and non-increasing in y and $g(x,y)$ is non-increasing in x and non-decreasing in y in some domain A.

Competitive systems of the form (7) were studied by many authors in [14, 15, 19–37] and others.

Here we give some basic notions as regards monotonic maps in a plane.

We define a partial order ${⪯}_{\mathrm{se}}$ on ${\mathbf{R}}^2$ (the so-called southeast ordering) so that the positive cone is the fourth quadrant, i.e., this partial order is defined by

$$\left(\begin{array}{c}{x}^1\\ y^1\end{array}\right){⪯}_{\mathrm{se}}\left(\begin{array}{c}{x}^2\\ y^2\end{array}\right)\iff \{\begin{array}{c}{x}^1⩽x^2,\\ y^1⩾y^2.\end{array}$$

(8)

Similarly, we define northeast ordering as

$$\left(\begin{array}{c}{x}^1\\ y^1\end{array}\right){⪯}_{\mathrm{ne}}\left(\begin{array}{c}{x}^2\\ y^2\end{array}\right)\iff \{\begin{array}{c}{x}^1⩽x^2,\\ y^1⩽y^2.\end{array}$$

(9)

A map F is called competitive if it is non-decreasing with respect to ${⪯}_{\mathrm{se}}$, that is, if the following holds:

$$\left(\begin{array}{c}{x}^1\\ y^1\end{array}\right)⪯\left(\begin{array}{c}{x}^2\\ y^2\end{array}\right)\Rightarrow F\left(\begin{array}{c}{x}^1\\ y^1\end{array}\right)⪯F\left(\begin{array}{c}{x}^2\\ y^2\end{array}\right).$$

(10)

For each $\mathbf{v}=(v^1,v^2)\in {\mathbf{R}}_{+}^2$, define ${\mathcal{Q}}_i(\mathbf{v})$ for $i=1,\dots ,4$ to be the usual four quadrants based at v and numbered in a counterclock-wise direction, e.g., ${\mathcal{Q}}_1(\mathbf{v})=\{(x,y)\in {\mathbf{R}}_{+}^2:v^1\le x,v^2\le y\}$.

For $S\subset R_{+}^2$ let $S^{\circ }$ denote the interior of S.

The following definition is from [35].

Definition 1 Let R be a nonempty subset of ${\mathbb{R}}^2$. A competitive map $T:R\to R$ is said to satisfy condition (O+) if for every x, y in R, $T(x){⪯}_{\mathrm{ne}}T(y)$ implies $x{⪯}_{\mathrm{ne}}y$, and T is said to satisfy condition (O−) if for every x, y in R, $T(x){⪯}_{\mathrm{ne}}T(y)$ implies $y{⪯}_{\mathrm{ne}}x$.

The following theorem was proved by de Mottoni-Schiaffino [38] for the Poincaré map of a periodic competitive Lotka-Volterra system of differential equations. Smith generalized the proof to competitive and cooperative maps [34, 39].

Theorem 4 Let R be a nonempty subset of ${\mathbb{R}}^2$. If T is a competitive map for which (O+) holds then for all $x\in R$, $\{T^n(x)\}$ is eventually component-wise monotone. If the orbit of x has compact closure, then it converges to a fixed point of T. If instead (O−) holds, then for all $x\in R$, $\{T^{2n}\}$ is eventually component-wise monotone. If the orbit of x has compact closure in R, then its omega limit set is either a period-two orbit or a fixed point.

It is well known that a stable period-two orbit and a stable fixed point may coexist; see Hess [40].

A non-hyperbolic equilibrium point E of a competitive or cooperative map T is called non-hyperbolic point of stable type (resp. of unstable type) if the second characteristic value of the Jacobian matrix $J_T(E)$ is in interval $(-1,1)$ (resp. outside of interval $[-1,1]$).

The following result is from [35], with the domain of the map specialized to be the Cartesian product of intervals of real numbers. It gives a sufficient condition for conditions (O+) and (O−).

Theorem 5 Let $R\subset {\mathbb{R}}^2$ be the Cartesian product of two intervals in ℝ. Let $T:R\to R$ be a $C^{\prime }$ competitive map. If T is injective and $det{J}_T(x)>0$ for all $x\in R$ then T satisfies (O+). If T is injective and $det{J}_T(x)<0$ for all $x\in R$ then T satisfies (O−).

Theorems 4 and 5 are quite applicable as we have shown in [41], in the case of competitive systems in the plane consisting of linear fractional equations.

The following result is from [13], which generalizes the corresponding result for hyperbolic case from [30]. Related results have been obtained by Smith in [34].

Theorem 6 Let ℛ be a rectangular subset of ${\mathbb{R}}^2$ and let T be a competitive map on ℛ. Let $\overline{x}\in \mathcal{R}$ be a fixed point of T such that $({\mathcal{Q}}_1(\overline{x})\cup {\mathcal{Q}}_3(\overline{x}))\cap \mathcal{R}$ has nonempty interior (i.e., $\overline{x}$ is not the NW or SE vertex of ℛ).

Suppose that the following statements are true.

• (a) The map T is strongly competitive on $int(({\mathcal{Q}}_1(\overline{x})\cup {\mathcal{Q}}_3(\overline{x}))\cap \mathcal{R})$.

• (b) T is $C^2$ on a relative neighborhood of $\overline{x}$.

• (c) The Jacobian of T at $\overline{x}$ has real eigenvalues λ, μ such that $|\lambda |<\mu$, where λ is stable and the eigenspace $E^{\lambda }$ associated with λ is not a coordinate axis.

• (d) Either $\lambda \ge 0$ and

  $$T(x)\ne \overline{x}\mathit{\text{and}}T(x)\ne x\mathit{\text{for all }}x\in int(({\mathcal{Q}}_1(\overline{x})\cup {\mathcal{Q}}_3(\overline{x}))\cap \mathcal{R}),$$

or $\lambda <0$ and

$$T^2(x)\ne x\mathit{\text{for all }}x\in int(({\mathcal{Q}}_1(\overline{x})\cup {\mathcal{Q}}_3(\overline{x}))\cap \mathcal{R}).$$

Then there exists a curve $\mathcal{C}$ in ℛ such that:

• (i) $\mathcal{C}$ is invariant and a subset of ${\mathcal{W}}^s(\overline{x})$.

• (ii) The endpoints of $\mathcal{C}$ lie on $\partial \mathcal{R}$.

• (iii) $\overline{x}\in \mathcal{C}$.

• (iv) $\mathcal{C}$ the graph of a strictly increasing continuous function of the first variable.

• (v) $\mathcal{C}$ is differentiable at $\overline{x}$ if $\overline{x}\in int(\mathcal{R})$ or one sided differentiable if $\overline{x}\in \partial \mathcal{R}$, and in all cases $\mathcal{C}$ is tangential to $E^{\lambda }$ at $\overline{x}$.

• (vi) $\mathcal{C}$ separates ℛ into two connected components, namely

  $${\mathcal{W}}_{-}:=\{x\in \mathcal{R}:\mathrm{\exists }y\in \mathcal{C}\mathit{\text{ with }}x⪯y\}$$

  and

  $${\mathcal{W}}_{+}:=\{x\in \mathcal{R}:\mathrm{\exists }y\in \mathcal{C}\mathit{\text{ with }}y⪯x\}.$$

• (vii) ${\mathcal{W}}_{-}$ is invariant, and $dist(T^n(x),{\mathcal{Q}}_2(\overline{x}))\to 0$ as $n\to \mathrm{\infty }$ for every $x\in {\mathcal{W}}_{-}$.

• (viii) ${\mathcal{W}}_{+}$ is invariant, and $dist(T^n(x),{\mathcal{Q}}_4(\overline{x}))\to 0$ as $n\to \mathrm{\infty }$ for every $x\in {\mathcal{W}}_{+}$.

The next results from [42] give the existence and uniqueness of invariant curves emanating from a non-hyperbolic point of unstable type, that is, a non-hyperbolic point where the second eigenvalue is outside the interval $[-1,1]$. See also [43].

Theorem 7 Let $\mathcal{R}=(a_1,a_2)\times (b_1,b_2)$, and let $T:\mathcal{R}\to \mathcal{R}$ be a strongly competitive map with a unique fixed point $\overline{\mathbf{x}}\in \mathcal{R}$, and such that T is continuously differentiable in a neighborhood of $\overline{\mathbf{x}}$. Assume further that at the point $\overline{\mathbf{x}}$ the map T has associated characteristic values μ and ν satisfying $1<\mu$ and $-\mu <\nu <\mu$.

Then there exist curves ${\mathcal{C}}_1$, ${\mathcal{C}}_2$ in ℛ and there exist ${\mathbf{p}}_1,{\mathbf{p}}_2\in \partial \mathcal{R}$ with ${\mathbf{p}}_1{\ll }_{\mathrm{se}}\overline{\mathbf{x}}{\ll }_{\mathrm{se}}{\mathbf{p}}_2$ such that:

• (i) For $\ell =1,2$, ${\mathcal{C}}_{\ell }$ is invariant, northeast strongly linearly ordered, such that $\overline{\mathbf{x}}\in {\mathcal{C}}_{\ell }$ and ${\mathcal{C}}_{\ell }\subset {\mathcal{Q}}_3(\overline{\mathbf{x}})\cup {\mathcal{Q}}_1(\overline{\mathbf{x}})$; the endpoints ${\mathbf{q}}_{\ell }$, ${\mathbf{r}}_{\ell }$ of ${\mathcal{C}}_{\ell }$, where ${\mathbf{q}}_{\ell }{⪯}_{\mathrm{ne}}{\mathbf{r}}_{\ell }$, belong to the boundary of ℛ. For $\ell ,j\in \{1,2\}$ with $\ell \ne j$, ${\mathcal{C}}_{\ell }$ is a subset of the closure of one of the components of $\mathcal{R}\setminus {\mathcal{C}}_j$. Both ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ are tangential at $\overline{\mathbf{x}}$ to the eigenspace associated with ν.

• (ii) For $\ell =1,2$, let $B_{\ell }$ be the component of $\mathcal{R}\setminus {\mathcal{C}}_{\ell }$ whose closure contains ${\mathbf{p}}_{\ell }$. Then $B_{\ell }$ is invariant. Also, for $\mathbf{x}\in B_1$, $T^n(\mathbf{x})$ accumulates on ${\mathcal{Q}}_2({\mathbf{p}}_1)\cap \partial \mathcal{R}$, and for $x\in B_2$, $T^n(\mathbf{x})$ accumulates on ${\mathcal{Q}}_4({\mathbf{p}}_2)\cap \partial \mathcal{R}$.

• (iii) Let ${\mathcal{D}}_1:={\mathcal{Q}}_1(\overline{\mathbf{x}})\cap \mathcal{R}\setminus ({\mathcal{B}}_1\cup {\mathcal{B}}_2)$ and ${\mathcal{D}}_2:={\mathcal{Q}}_3(\overline{\mathbf{x}})\cap \mathcal{R}\setminus ({\mathcal{B}}_1\cup {\mathcal{B}}_2)$. Then ${\mathcal{D}}_1\cup {\mathcal{D}}_2$ is invariant.

Corollary 1 Let a map T with fixed point $\overline{\mathbf{x}}$ be as in Theorem  7. Let ${\mathcal{D}}_1$, ${\mathcal{D}}_2$ be the sets as in Theorem  7. If T satisfies (O+), then for $\ell =1,2$, ${\mathcal{D}}_{\ell }$ is invariant, and for every $\mathbf{x}\in {\mathcal{D}}_{\ell }$, the iterates $T^n(\mathbf{x})$ converge to $\overline{\mathbf{x}}$ or to a point of $\partial \mathcal{R}$. If T satisfies (O−), then $T({\mathcal{D}}_1)\subset {\mathcal{D}}_2$ and $T({\mathcal{D}}_2)\subset {\mathcal{D}}_1$. For every $\mathbf{x}\in {\mathcal{D}}_1\cup {\mathcal{D}}_2$, the iterates $T^n(\mathbf{x})$ either converge to $\overline{\mathbf{x}}$, or converge to a period-two point, or to a point of $\partial \mathcal{R}$.

3 Main results

The main results of this paper depend on the number of interior equilibrium points of system (6). So first we give the explicit algebraic conditions in terms of the parameters for system (6) to have zero-five interior equilibrium points. Next, we present the local stability analysis of the equilibrium points and then the results on the global dynamics. It is interesting to note that the local stability analysis is the most difficult part of our analysis.

3.1 Equilibrium points

The equilibrium points of system (6) satisfy the following system of equations:

$$\begin{array}{r}\overline{x}=\frac{a{\overline{x}}^2}{1+{\overline{x}}^2+c\overline{y}},\\ \overline{y}=\frac{b{\overline{y}}^2}{1+{\overline{y}}^2+d\overline{x}},n=0,1,\dots .\end{array}$$

(11)

All solutions of system (11) with at least one zero component are given as $E_0(0,0)$, $E_{\overline{x}}(\overline{x},0)$ where $\overline{x}=1$, $E_{\overline{y}}(0,\overline{y})$ where $\overline{y}=1$, $E_{{\overline{x}}_{\pm }}(0,{\overline{x}}_{\pm })$ where ${\overline{x}}_{\pm }=\frac{a\pm \sqrt{a^2-4}}{2}$, and $E_{{\overline{y}}_{\pm }}(0,{\overline{y}}_{\pm })$ where ${\overline{y}}_{\pm }=\frac{b\pm \sqrt{b^2-4}}{2}$. $E_0(0,0)$ exists in all cases. $E_{\overline{x}}(\overline{x},0)$ and $E_{\overline{y}}(0,\overline{y})$ exist when $a=2$ and $b=2$, respectively. $E_{{\overline{x}}_{\pm }}(0,{\overline{x}}_{\pm })$ and $E_{{\overline{y}}_{\pm }}(0,\overline{y_{\pm }})$ exist when $a>2$ and $b>2$, respectively.

The equilibrium points with strictly positive coordinates satisfy the following system of equations:

$$\begin{array}{r}-ax+cy+x^2+1=0,\\ -by+dx+y^2+1=0.\end{array}$$

(12)

From (12) one can see that all positive solutions of system (12) satisfy the quartic equation:

$$x^4-2a{x}^3+x^2(a^2+bc+2)+x(c^{2}d-a(bc+2))+bc+c^2+1=0.$$

(13)

Lemma 1 Let

$$\begin{array}{c}{\mathrm{\Delta }}_3=-4a(b^2-4)d(-4(a^2-4)bc+{(a^2-4)}^2-2(b^2-12)c^2)\hfill \\ \phantom{{\mathrm{\Delta }}_3=}-4a{c}^2{d}^3(a^2-18(bc+2))+2d^2(4a^4(bc+2)-a^2(c(b(31bc+64)-60c)+64)\hfill \\ \phantom{{\mathrm{\Delta }}_3=}-2(bc+2)((b^2-36)c^2-32bc-32))\hfill \\ \phantom{{\mathrm{\Delta }}_3=}+{(b^2-4)}^2(a^4-4a^2(bc+2)+16(c(b+c)+1))-27c^4{d}^4,\hfill \end{array}$$

(14)

$${\mathrm{\Delta }}_2=(b^2-4)(a^2-2bc-4)-2ad(a^2-2bc-4)-9c^2{d}^2$$

(15)

and

$${\mathrm{\Delta }}_1=a^2-2bc-4.$$

Then the following holds:

• (a) If ${\mathrm{\Delta }}_3>0$, ${\mathrm{\Delta }}_2>0$, and ${\mathrm{\Delta }}_1>0$, then (13) has four simple real roots.

• (b) If ${\mathrm{\Delta }}_3>0$ and ${\mathrm{\Delta }}_2\le 0\vee ({\mathrm{\Delta }}_2>0\wedge {\mathrm{\Delta }}_1\le 0)$ then (13) has no real roots.

• (c) If ${\mathrm{\Delta }}_3<0$ then (13) has two simple real roots.

• (d) If ${\mathrm{\Delta }}_3=0$ and ${\mathrm{\Delta }}_2<0$ then (13) has one real double root.

• (e) If ${\mathrm{\Delta }}_3=0$ and ${\mathrm{\Delta }}_2>0$ then (13) has two real simple roots and one real double root.

• (f) If ${\mathrm{\Delta }}_3=0$, ${\mathrm{\Delta }}_2=0$ and ${\mathrm{\Delta }}_1>0$ then (13) has two real double roots.

• (g) If ${\mathrm{\Delta }}_3=0$, ${\mathrm{\Delta }}_2=0$ and ${\mathrm{\Delta }}_1<0$ then (13) has no real roots.

• (h) If ${\mathrm{\Delta }}_3=0$, ${\mathrm{\Delta }}_2=0$ and ${\mathrm{\Delta }}_1=0$ then (13) has one real root of multiplicity four.

Proof The discrimination matrix [44] of $\tilde{f}$ and ${\tilde{f}}^{\prime }$ is given by

$$\begin{array}{c}Discr(\tilde{f})\hfill \\ =\left(\begin{array}{cccccccc}1& -2a& a^2+bc+2& c^{2}d-a(bc+2)& c^2+bc+1& 0& 0& 0\\ 0& 4& -6a& 2(a^2+bc+2)& c^{2}d-a(bc+2)& 0& 0& 0\\ 0& 1& -2a& a^2+bc+2& c^{2}d-a(bc+2)& c^2+bc+1& 0& 0\\ 0& 0& 4& -6a& 2(a^2+bc+2)& c^{2}d-a(bc+2)& 0& 0\\ 0& 0& 1& -2a& a^2+bc+2& c^{2}d-a(bc+2)& c^2+bc+1& 0\\ 0& 0& 0& 4& -6a& 2(a^2+bc+2)& c^{2}d-a(bc+2)& 0\\ 0& 0& 0& 1& -2a& a^2+bc+2& c^{2}d-a(bc+2)& c^2+bc+1\\ 0& 0& 0& 0& 4& -6a& 2(a^2+bc+2)& c^{2}d-a(bc+2)\end{array}\right),\hfill \end{array}$$

where

$$\tilde{f}(x)=x^4-2a{x}^3+x^2(a^2+bc+2)+x(c^{2}d-a(bc+2))+bc+c^2+1.$$

Let $D_k$ denote the determinant of the submatrix of $Discr(\tilde{f})$, formed by the first 2k rows and the first 2k columns, for $k=1,2,3,4$. So, by straightforward calculation one can see that $D_1=4$, $D_2=4{\mathrm{\Delta }}_1$, $D_3=4c^2{\mathrm{\Delta }}_2$, and $D_4=c^4{\mathrm{\Delta }}_3$. The rest of the proof follows in view of [[44], Theorem 1]. □

3.2 Local stability of equilibrium points

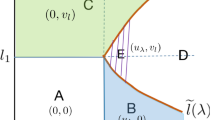
Geometrically the solutions of system (12) are intersections of two orthogonal parabolas that satisfy the equations

$$\begin{array}{r}y=-\frac{1}{c}{(x-\frac{a}{2})}^2+\frac{a^2-4}{4c},\\ x=-\frac{1}{d}{(y-\frac{b}{2})}^2+\frac{b^2-4}{4d},\end{array}$$

(16)

with respective vertices $(\frac{a}{2},\frac{a^2-4}{4c})$ and $(\frac{b^2-4}{4d},\frac{b}{2})$. See Figure 2.

Figure 2

Equilibrium curves.

Consequently when $a>2$ and $b>2$, in addition to the five equilibrium points on the axes, system (6) may have one, two, three or four positive equilibrium points. We will refer to these equilibrium points as $E_{\mathrm{SW}}(\overline{x},\overline{y})$ (southwest), $E_{\mathrm{SE}}(\overline{x},\overline{y})$ (southeast), $E_{\mathrm{NW}}(\overline{x},\overline{y})$ (northwest), and $E_{\mathrm{NE}}(\overline{x},\overline{y})$ (northeast) where

$$E_{\mathrm{NW}}{⪯}_{\mathrm{se}}{E}_{\mathrm{NE}}{⪯}_{\mathrm{se}}{E}_{\mathrm{SE}},E_{\mathrm{SW}}{⪯}_{\mathrm{ne}}{E}_{\mathrm{NW}}.$$

When a positive equilibrium point is non-hyperbolic we will refer to it as $E_N(\overline{x},\overline{y})$.

The map associated with system (6) has the form

$$T\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}\frac{a{x}^2}{1+x^2+cy}\\ \frac{b{y}^2}{1+y^2+dx}\end{array}\right).$$

(17)

The Jacobian matrix of T is

$$J_T(x,y)=\left(\begin{array}{cc}\frac{2ax(cy+1)}{{(x^2+cy+1)}^2}& -\frac{ac{x}^2}{{(x^2+cy+1)}^2}\\ -\frac{bd{y}^2}{{(y^2+dx+1)}^2}& \frac{2by(dx+1)}{{(y^2+dx+1)}^2}\end{array}\right).$$

(18)

The Jacobian matrix of T evaluated at an equilibrium $E(\overline{x},\overline{y})$ with positive coordinates has the form

$$J_T(\overline{x},\overline{y})=\left(\begin{array}{cc}\frac{2(c\overline{y}+1)}{a\overline{x}}& -\frac{c}{a}\\ -\frac{d}{b}& \frac{2(d\overline{x}+1)}{b\overline{y}}\end{array}\right).$$

(19)

The determinant and trace of (19) are

$$\begin{array}{r}det{J}_T(\overline{x},\overline{y})=\frac{2(c\overline{y}+1)}{a\overline{x}}\frac{2(d+1)}{b\overline{y}}-\frac{d}{b}\frac{c}{a}=\frac{4c\overline{y}+4d\overline{x}+3cd\overline{x}\overline{y}+4}{a\overline{x}b\overline{y}},\\ tr{J}_T(\overline{x},\overline{y})=\frac{2(c\overline{y}+1)}{a\overline{x}}+\frac{2(d\overline{x}+1)}{b\overline{y}}.\end{array}$$

(20)

It is worth noting that $det{J}_T(\overline{x},\overline{y})$ and $tr{J}_T(\overline{x},\overline{y})$ of (19) are both positive.

Using the equilibrium condition (12), we may rewrite the determinant and trace as

$$\begin{array}{r}det{J}_T(\overline{x},\overline{y})=\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{d}{b}\frac{c}{a},\\ tr{J}_T(\overline{x},\overline{y})=\frac{2(a-\overline{x})}{a}+\frac{2(b-\overline{y})}{b}.\end{array}$$

(21)

We will use both (20) and (21) in our proofs to follow.

The characteristic equation of the matrix (19) is

$${\lambda }^2-tr{J}_T(\overline{x},\overline{y})\lambda +det{J}_T(\overline{x},\overline{y})=0,$$

(22)

of which the solutions are the eigenvalues

$$\begin{array}{r}\lambda =\frac{tr{J}_T(\overline{x},\overline{y})-\sqrt{{(tr{J}_T(\overline{x},\overline{y}))}^2-4det{J}_T(\overline{x},\overline{y})}}{2},\\ \mu =\frac{tr{J}_T(\overline{x},\overline{y})+\sqrt{{(tr{J}_T(\overline{x},\overline{y}))}^2-4det{J}_T(\overline{x},\overline{y})}}{2}.\end{array}$$

(23)

The eigenvalues of (19) are therefore

$$\begin{array}{r}\lambda =\frac{(\frac{2(c\overline{y}+1)}{a\overline{x}}+\frac{2(d\overline{x}+1)}{b\overline{y}})-\sqrt{{(\frac{2(c\overline{y}+1)}{a\overline{x}}-\frac{2(d\overline{x}+1)}{b\overline{y}})}^2+4\frac{dc}{ba}}}{2},\\ \mu =\frac{(\frac{2(c\overline{y}+1)}{a\overline{x}}+\frac{2(d\overline{x}+1)}{b\overline{y}})+\sqrt{{(\frac{2(c\overline{y}+1)}{a\overline{x}}-\frac{2(d\overline{x}+1)}{b\overline{y}})}^2+4\frac{dc}{ba}}}{2},\end{array}$$

(24)

with corresponding eigenvectors

$$\begin{array}{r}{E}_{\lambda }=(-\frac{b}{d}(\frac{(c\overline{y}+1)}{a\overline{x}}-\frac{(d\overline{x}+1)}{b\overline{y}}-\frac{\sqrt{{(\frac{2(c\overline{y}+1)}{a\overline{x}}-\frac{2(d\overline{x}+1)}{b\overline{y}})}^2+4\frac{dc}{ba}}}{2}),1),\\ E_{\mu }=(-\frac{b}{d}(\frac{(c\overline{y}+1)}{a\overline{x}}-\frac{(d\overline{x}+1)}{b\overline{y}}+\frac{\sqrt{{(\frac{2(c\overline{y}+1)}{a\overline{x}}-\frac{2(d\overline{x}+1)}{b\overline{y}})}^2+4\frac{dc}{ba}}}{2}),1).\end{array}$$

(25)

Using the equilibrium condition (12), we may rewrite the eigenvalues and eigenvectors as

$$\begin{array}{r}\lambda =\frac{(\frac{2(a-\overline{x})}{a}+\frac{2(b-\overline{y})}{b})-\sqrt{{(\frac{2(a-\overline{x})}{a}-\frac{2(b-\overline{y})}{b})}^2+4\frac{dc}{ba}}}{2},\\ \mu =\frac{(\frac{2(a-\overline{x})}{a}+\frac{2(b-\overline{y})}{b})+\sqrt{{(\frac{2(a-\overline{x})}{a}-\frac{2(b-\overline{y})}{b})}^2+4\frac{dc}{ba}}}{2},\end{array}$$

(26)

$$\begin{array}{r}{E}_{\lambda }=(-\frac{b}{d}(\frac{(a-\overline{x})}{a}-\frac{(b-\overline{y})}{b}-\frac{\sqrt{{(\frac{2(a-\overline{x})}{a}-\frac{2(b-\overline{y})}{b})}^2+4\frac{dc}{ba}}}{2}),1),\\ E_{\mu }=(-\frac{b}{d}(\frac{(a-\overline{x})}{a}-\frac{(b-\overline{y})}{b}+\frac{\sqrt{{(\frac{2(a-\overline{x})}{a}-\frac{2(b-\overline{y})}{b})}^2+4\frac{dc}{ba}}}{2}),1).\end{array}$$

(27)

We will now consider two lemmas that will be used to prove the local stability character of the positive equilibrium points of system (6). The nonzero coordinates, $(\overline{x},\overline{y})$, of all equilibrium points will subsequently be designated with the subscripts: r (repeller), a (attractor), s, $s_1$, $s_2$ (saddle point), $n{s}_1$, $n{s}_2$ (non-hyperbolic of the stable type), and nu (non-hyperbolic of the unstable type).

Lemma 2 The following conditions hold for the coordinates of the positive equilibrium points, $E(\overline{x},\overline{y})$, of system (6).

• (i) For $E_{\mathrm{SW}}({\overline{x}}_r,{\overline{y}}_r)$

  $$\overline{x}<\frac{a}{2}<\frac{b^2-4}{4d}\mathit{\text{and}}\overline{y}<\frac{b}{2}<\frac{a^2-4}{4c}.$$

  (28)

• (ii) For $E_{\mathrm{NW}}({\overline{x}}_{s_1},{\overline{y}}_{s_1})$,

  $$\overline{x}<\frac{a}{2}<\frac{b^2-4}{4d}\mathit{\text{and}}\frac{b}{2}<\overline{y}<\frac{a^2-4}{4c}.$$

  (29)

• (iii) For $E_{\mathrm{NE}}({\overline{x}}_a,{\overline{y}}_a)$,

  $$\frac{a}{2}<\overline{x}<\frac{b^2-4}{4d}\mathit{\text{and}}\frac{b}{2}<\overline{y}<\frac{a^2-4}{4c}.$$

  (30)

• (iv) For $E_{\mathrm{SE}}({\overline{x}}_{s_2},{\overline{y}}_{s_2})$,

  $$\frac{a}{2}<\overline{x}<\frac{b^2-4}{4d}\mathit{\text{and}}\overline{y}<\frac{b}{2}<\frac{a^2-4}{4c}.$$

  (31)

• (v) For $E_N({\overline{x}}_{ns1},{\overline{y}}_{ns1})$ and $E_N({\overline{x}}_{ns2},{\overline{y}}_{ns2})$,

  $$\frac{a}{2}\le \overline{x}<\frac{b^2-4}{4d}\mathit{\text{and}}\frac{b}{2}<\overline{y}\le \frac{a^2-4}{4c}.$$

  (32)

• (vi) For $E_N({\overline{x}}_{nu},{\overline{y}}_{nu})$,

  $$\overline{x}<\frac{b^2-4}{4d}<\frac{a}{2}\mathit{\text{and}}\overline{y}<\frac{a^2-4}{4c}<\frac{b}{2}.$$

  (33)

Proof This is clear from the geometry. See Figure 3.  □

Figure 3

Local stability.

Lemma 3 The following conditions hold for the coordinates of the positive equilibrium points, $E(\overline{x},\overline{y})$, of system (6).

• (i) For $E_{\mathrm{SW}}({\overline{x}}_r,{\overline{y}}_r)$ and $E_{\mathrm{NW}}({\overline{x}}_{s_1},{\overline{y}}_{s_1})$,

  $$cd<(a-2\overline{x})(b-2\overline{y}).$$

  (34)

• (ii) For $E_{\mathrm{NE}}({\overline{x}}_a,{\overline{y}}_a)$ and $E_{\mathrm{SE}}({\overline{x}}_{s_2},{\overline{y}}_{s_2})$,

  $$cd>(a-2\overline{x})(b-2\overline{y}).$$

  (35)

• (iii) For $E_N({\overline{x}}_{ns1},{\overline{y}}_{ns1})$, $E_N({\overline{x}}_{ns2},{\overline{y}}_{ns2})$, and $E_N({\overline{x}}_{nu},{\overline{y}}_{nu})$,

  $$cd=(a-2\overline{x})(b-2\overline{y}).$$

  (36)

Proof (i) Let $m_{P1}$ be the slope of the tangent line to parabola $P_1$ at $E(\overline{x},\overline{y})=E_{\mathrm{SW}}({\overline{x}}_r,{\overline{y}}_r)$ and let $m_{P2}$ be the slope of the tangent line to parabola $P_2$ at $E(\overline{x},\overline{y})=E_{\mathrm{SW}}({\overline{x}}_r,{\overline{y}}_r)$. It is clear from the geometry that

$$m_{P1}>m_{P2}>0.$$

See Figure 3. It follows that

$${\frac{dy}{dx}|}_{P_1}(\overline{x},\overline{y})>{\frac{dx}{dy}|}_{P_2}(\overline{x},\overline{y})>0$$

and in turn

$$\frac{a-2\overline{x}}{c}>\frac{d}{b-2\overline{y}}>0.$$

Therefore

$$cd<(a-2\overline{x})(b-2\overline{y}).$$

The proofs for cases (ii) and (iii) are similar and will be omitted. □

Theorem 8 The following conditions hold for the equilibrium points $E(\overline{x},\overline{y})$ of system (6).

• (i) $E_0(0,0)$ is locally asymptotically stable.

• (ii) $E_{\overline{x}}({\overline{x}}_{ns},0)$ and $E_{\overline{y}}(0,{\overline{y}}_{ns})$ are non-hyperbolic of the stable type.

• (iii) $E_{{\overline{x}}_{+}}({\overline{x}}_{+a},0)$ is locally asymptotically stable and $E_{{\overline{x}}_{-}}({\overline{x}}_{-s},0)$ is a saddle point.

• (iv) $E_{{\overline{y}}_{+}}(0,{\overline{y}}_{+a})$ is locally asymptotically stable and $E_{{\overline{y}}_{-}}(0,{\overline{y}}_{-s})$ is a saddle point.

• (v) $E_{\mathrm{SW}}({\overline{x}}_r,{\overline{y}}_r)$ is a repeller.

• (vi) $E_{\mathrm{NW}}({\overline{x}}_{s_1},{\overline{y}}_{s_1})$ and $E_{\mathrm{SE}}({\overline{x}}_{s_2},{\overline{y}}_{s_2})$ are saddle points.

• (vii) $E_{\mathrm{NE}}({\overline{x}}_a,{\overline{y}}_a)$ is locally asymptotically stable.

• (viii) $E_N({\overline{x}}_{ns1},{\overline{y}}_{ns1})$ and $E_N({\overline{x}}_{ns2},{\overline{y}}_{ns2})$ are non-hyperbolic of the stable type.

• (ix) $E_N({\overline{x}}_{nu},{\overline{y}}_{nu})$ is non-hyperbolic of the unstable type.

Proof

• (i) The eigenvalues of (18), evaluated at $E_{\overline{x}}(0,0)$, are $\lambda =0$ and $\mu =0$.

• (ii) The eigenvalues of (18), evaluated at $E_{\overline{x}}({\overline{x}}_{ns},0)$, are $\lambda =0$ and $\mu =1$ when $a=2$. The eigenvalues of (18), evaluated at $E_{\overline{y}}(0,{\overline{y}}_{ns})$, are $\lambda =0$ and $\mu =1$ when $b=2$.

• (iii) The eigenvalues of (18), evaluated at $E_{{\overline{x}}_{+}}({\overline{x}}_{+a},0)$ and $E_{{\overline{x}}_{-}}({\overline{x}}_{-s},0)$, respectively, are $\lambda =0$ and ${\mu }_{\pm }=\frac{2a(\frac{a\pm \sqrt{a^2-4}}{2})}{{(\frac{a\pm \sqrt{a^2-4}}{2})}^4+2{(\frac{a\pm \sqrt{a^2-4}}{2})}^2+1}$ when $a>2$.

  • (a) Note that when $a>2$,

    $$\begin{array}{rl}{\mu }_{+}& =\frac{2a(\frac{a+\sqrt{a^2-4}}{2})}{{(\frac{a+\sqrt{a^2-4}}{2})}^4+2{(\frac{a+\sqrt{a^2-4}}{2})}^2+1}\\ =\frac{4a+4\sqrt{a^2-4}}{4a+4\sqrt{a^2-4}+a^2\sqrt{a^2-4}+{(a^2-4)}^{\frac{3}{2}}+2a(a^2-4)}\\ <\frac{4a+4\sqrt{a^2-4}}{4a+4\sqrt{a^2-4}}=1.\end{array}$$

  • (b) Note that when $a>2$,

    $$\begin{array}{rl}{\mu }_{-}& =\frac{2a(\frac{a-\sqrt{a^2-4}}{2})}{{(\frac{a-\sqrt{a^2-4}}{2})}^4+2{(\frac{a-\sqrt{a^2-4}}{2})}^2+1}\\ =\frac{4a-4\sqrt{a^2-4}}{4a-4\sqrt{a^2-4}-a^2\sqrt{a^2-4}-\sqrt{{(a^2-4)}^3}+2a^3-8a}.\end{array}$$

    It can be shown that

    $$-a^2\sqrt{a^2-4}-\sqrt{{(a^2-4)}^3}+2a^3-8a=2a(a^2-4)(1-\sqrt{1+\frac{4}{a^2(a^2-4)}})<0.$$

    Therefore,

    $${\mu }_{-}>\frac{4a-4\sqrt{a^2-4}}{4a-4\sqrt{a^2-4}}=1.$$

    In both cases, the conclusion follows.

• (iv) The eigenvalues of (18), evaluated at $E_{{\overline{y}}_{+}}(0,{\overline{y}}_{+a})$ and $E_{{\overline{y}}_{-}}(0,{\overline{y}}_{-s})$, respectively, are $\lambda =0$ and ${\mu }_{\pm }=\frac{2b(\frac{b\pm \sqrt{b^2-4}}{2})}{{(\frac{b\pm \sqrt{b^2-4}}{2})}^4+2{(\frac{b\pm \sqrt{b^2-4}}{2})}^2+1}$ when $b>2$.

  The proof of (iv) is similar to the proof of (iii) and will be omitted.

• (v) We need to show that $|tr{J}_T(\overline{x},\overline{y})|<|1+det{J}_T(\overline{x},\overline{y})|$ and $|det{J}_T(\overline{x},\overline{y})|>1$ when $E(\overline{x},\overline{y})=E_{\mathrm{SW}}({\overline{x}}_r,{\overline{y}}_r)$. Since $tr{J}_T(\overline{x},\overline{y})$ and $det{J}_T(\overline{x},\overline{y})$ are both positive, our conditions become $tr{J}_T(\overline{x},\overline{y})<1+det{J}_T(\overline{x},\overline{y})$ and $det{J}_T(\overline{x},\overline{y})>1$. We will first show that $det{J}_T(\overline{x},\overline{y})>1$. By (34) we have

  $$\begin{array}{c}det(J_T(\overline{x},\overline{y}))-1\hfill \\ =\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{d}{b}\frac{c}{a}-1\hfill \\ >\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{(a-2\overline{x})(b-2\overline{y})}{ab}-1\hfill \\ =2(1-\frac{\overline{y}}{b}-\frac{\overline{x}}{a}).\hfill \end{array}$$

By (28) we have

$$1-\frac{\overline{y}}{b}-\frac{\overline{x}}{a}>0.$$

Therefore $det(J_T(\overline{x},\overline{y}))>1$. We will next show that $tr(J_T(\overline{x},\overline{y}))<1+det(J_T(\overline{x},\overline{y}))$. By (34) we have

$$\begin{array}{c}1+det(J_T(\overline{x},\overline{y}))-1\hfill \\ =1+\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{d}{b}\frac{c}{a}-1\hfill \\ >1+\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{(a-2\overline{x})(b-2\overline{y})}{ab}-1\hfill \\ =tr(J_T(\overline{x},\overline{y}))-1.\hfill \end{array}$$

Therefore $tr(J_T(\overline{x},\overline{y}))<1+det(J_T(\overline{x},\overline{y}))$.

• (vi) We need to show that $|trJ(\overline{x},\overline{y})|>|1+det{J}_T(\overline{x},\overline{y})|$ when $E(\overline{x},\overline{y})=E_{\mathrm{NW}}({\overline{x}}_{s_1},{\overline{y}}_{s_1})$. Since $tr{J}_T(\overline{x},\overline{y})$ and $det{J}_T(\overline{x},\overline{y})$ are both positive, our condition becomes $tr{J}_T(\overline{x},\overline{y})>1+det{J}_T(\overline{x},\overline{y})$. By (34) we have

  $$\begin{array}{c}1+det(J_T(\overline{x},\overline{y}))\hfill \\ =1+\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{d}{b}\frac{c}{a}\hfill \\ <1+\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{(a-2\overline{x})(b-2\overline{y})}{ab}\hfill \\ =\frac{2(a-\overline{x})}{a}+\frac{2(b-\overline{y})}{b}\hfill \\ =tr(J_T(\overline{x},\overline{y})).\hfill \end{array}$$

Therefore $tr{J}_T(\overline{x},\overline{y})>1+det{J}_T(\overline{x},\overline{y})$. The proof that $E_{\mathrm{SE}}({\overline{x}}_{s_2},{\overline{y}}_{s_2})$ is a saddle point is similar and will be omitted.

• (vii) We need to show that $|tr{J}_T(\overline{x},\overline{y})|<1+det{J}_T(\overline{x},\overline{y})$ and $det{J}_T(\overline{x},\overline{y})<1$ when $E(\overline{x},\overline{y})=E_{\mathrm{NE}}({\overline{x}}_a,{\overline{y}}_a)$. Since $tr{J}_T(\overline{x},\overline{y})$ and $det{J}_T(\overline{x},\overline{y})$ are both positive, our conditions become $tr{J}_T(\overline{x},\overline{y})<1+det{J}_T(\overline{x},\overline{y})$ and $det{J}_T(\overline{x},\overline{y})<1$. We will first show that $det{J}_T(\overline{x},\overline{y})<1$. By (35) we have

  $$det(J_T(\overline{x},\overline{y}))-1=\frac{2(c\overline{y}+1)}{a\overline{x}}\frac{2(d\overline{x}+1)}{b\overline{y}}-\frac{d}{b}\frac{c}{a}-1.$$

By (30) we have

$$\begin{array}{r}\frac{2(c\overline{y}+1)}{a\overline{x}}\frac{2(d\overline{x}+1)}{b\overline{y}}-\frac{d}{b}\frac{c}{a}-1\\ <\frac{2(\frac{a^2}{4})}{a\overline{x}}\frac{2(\frac{b^2}{4})}{b\overline{y}}-\frac{d}{b}\frac{c}{a}-1=\frac{ab}{4\overline{x}\overline{y}}-\frac{d}{b}\frac{c}{a}-1.\end{array}$$

By (30) again we have

$$\frac{ab}{4\overline{x}\overline{y}}-\frac{d}{b}\frac{c}{a}-1<1-\frac{d}{b}\frac{c}{a}-1=-\frac{d}{b}\frac{c}{a}<0.$$

Therefore $det(J_T(\overline{x},\overline{y}))<1$. We will next show that $1+det(J_F(\overline{x},\overline{y}))>tr(J_F(\overline{x},\overline{y}))$.

By (35) we have

$$\begin{array}{c}1+det(J_F(\overline{x},\overline{y}))-tr(J_F(\overline{x},\overline{y}))\hfill \\ =1+\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{d}{b}\frac{c}{a}-\frac{2(a-\overline{x})}{a}-\frac{2(b-\overline{y})}{b}\hfill \\ >1+\frac{2(a-\overline{x})}{a}\frac{2(b-\overline{y})}{b}-\frac{(a-2\overline{x})(b-2\overline{y})}{ab}-\frac{2(a-\overline{x})}{a}-\frac{2(b-\overline{y})}{b}=0.\hfill \end{array}$$

Therefore $1+det(J_F(\overline{x},\overline{y}))>tr(J_F(\overline{x},\overline{y}))$.

• (viii) By (26) and (36), we have

  $$\begin{array}{c}\lambda =3-\frac{2y}{b}-\frac{2x}{a},\hfill \\ \mu =1.\hfill \end{array}$$

By (32), we have $\lambda <1$. The conclusion follows.

• (ix) The proof of (ix) is similar to the proof of (viii) and will be omitted. □

3.3 Global results

In this section we combine the results from Sections 2 and 3.2 to prove the global results for system (6). First, we prove that the map T which corresponds to system (6) is injective and it satisfies (O+).

Theorem 9 The map T which corresponds to system (6) is injective.

Proof Indeed,

$$T\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)=T\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)\iff \left(\begin{array}{c}\frac{a{x}_1^2}{1+x_1^2+c{y}_1}\\ \frac{b{y}_1^2}{1+y_1^2+d{x}_1}\end{array}\right)=\left(\begin{array}{c}\frac{a{x}_2^2}{1+x_2^2+c{y}_2}\\ \frac{b{y}_2^2}{1+y_2^2+d{x}_2}\end{array}\right),$$

which is equivalent to

$$x_1^2-x_2^2=c(x_2^2{y}_1-x_1^2{y}_2),$$

(37)

$$y_1^2-y_2^2=d(y_2^2{x}_1-y_1^2{x}_2).$$

(38)

Now we will prove that $x_1=x_2$, which immediately implies $y_1=y_2$.

First, assume $x_1>x_2$. Then $x_2^2{y}_1-x_1^2{y}_2>0$ and $x_2^2{y}_1>x_1^2{y}_2$ which in view of (37) implies $y_1>y_2$. In view of (38), $y_2^2{x}_1-y_1^2{x}_2>0$, that is, $x_1{y}_2\cdot y_2>x_2{y}_1\cdot y_1$, which implies $x_1{y}_2>x_2{y}_1$ and $x_1^2{y}_2>x_1{x}_2{y}_1>x_2^2{y}_1$ and in view of (37) we obtain $x_1<x_2$, which is a contradiction.

Second, assume $x_1<x_2$. Then $x_2^2{y}_1<x_1^2{y}_2$, which implies $y_2>y_1$ and $y_2^2{x}_1-y_1^2{x}_2<0$ and $x_1{y}_2\cdot y_2<x_2{y}_1\cdot y_1$, which is equivalent to $x_1{y}_2<x_2{y}_1$ and $x_2^2{y}_1>x_1{x}_2{y}_1>x_1^2{y}_2$. In view of (37) we obtain $x_1>x_2$, which is a contradiction.

Thus $x_1=x_2$ and T is injective. □

Theorem 10 The map T which corresponds to system (6) satisfies (O+). All solutions of system (6) converge to an equilibrium point.

Proof Assume that

$$T\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right){\le }_{\mathrm{ne}}T\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)\iff \left(\begin{array}{c}\frac{a{x}_1^2}{1+x_1^2+c{y}_1}\\ \frac{b{y}_1^2}{1+y_1^2+d{x}_1}\end{array}\right)\le \left(\begin{array}{c}\frac{a{x}_2^2}{1+x_2^2+c{y}_2}\\ \frac{b{y}_2^2}{1+y_2^2+d{x}_2}\end{array}\right).$$

The last inequality is equivalent to

$$\begin{array}{c}{x}_1^2-x_2^2\le c(x_2^2{y}_1-x_1^2{y}_2),\hfill \\ y_1^2-y_2^2\le d(y_2^2{x}_1-y_1^2{x}_2).\hfill \end{array}$$

First we prove that $x_1\le x_2$. Otherwise $x_1>x_2$.

Then

$$x_2^2{y}_1>x_1^2{y}_2,$$

(39)

which implies $y_1>y_2\Rightarrow y_2^2{x}_1-y_1^2{x}_2>0$, which is equivalent to $x_1{y}_2\cdot y_2-x_2{y}_1\cdot y_1>0$ and implies $x_1{y}_2>x_2{y}_1$, which in turn implies $x_1^2{y}_2>x_1{x}_2{y}_1>x_2^2{y}_1$, which contradicts (39). Consequently $x_1\le x_2$.

Next we prove that $y_1\le y_2$. Otherwise $y_1>y_2$.

Then $x_1{y}_2^2>x_2{y}_1^2$, which implies $x_1>x_2$, which is impossible in view of $x_1\le x_2$.

Thus $\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right){\le }_{\mathrm{ne}}\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)$.

Thus we conclude that all solutions of (6) are eventually monotonic for all values of parameters. Furthermore it is clear that all solutions are bounded. Indeed every solution of (6) satisfies

$$x_n\le a,y_n\le b,n=1,2,\dots .$$

(40)

Consequently, all solutions converge to an equilibrium point. □

Theorem 11 Assume that $a<2$ and $b<2$. Then the zero equilibrium of (6) is globally asymptotically stable.

Proof It follows immediately from Theorem 10. □

Theorem 12

• (a) If $a=2$, $b<2$, then system (6) has two equilibrium points, $E_0$, $E_{\overline{x}}$, where $E_0$ is locally asymptotically stable and $E_{\overline{x}}$ is non-hyperbolic of the stable type. The basins of attraction of the two equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):\mathit{\text{points above }}{\mathcal{W}}^s(E_{\overline{x}})\},\hfill \\ B(E_{\overline{x}})=\{(x_0,y_0):\mathit{\text{points below }}{\mathcal{W}}^s(E_{\overline{x}})\},\hfill \end{array}$$

  where ${\mathcal{W}}^s(E)$ denotes the global stable manifold guaranteed by Theorem  6.

• (b) Similarly, if $a<2$, $b=2$, the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):\mathit{\text{points below }}{\mathcal{W}}^s(E_{\overline{y}})\},\hfill \\ B(E_{\overline{y}})=\{(x_0,y_0):\mathit{\text{points above }}{\mathcal{W}}^s(E_{\overline{y}})\}.\hfill \end{array}$$

Proof We will present the proof of (a) since the proof of (b) uses analogous arguments. Local stability of the equilibrium points follows from Theorem 8. Furthermore, the existence of the stable manifold ${\mathcal{W}}^s(E_{\overline{x}})$ follows from Theorem 6. By immediate checking one can see that if $x_0>\overline{x}$ then $T^n(x_0,0)\to E_x$ as $n\to \mathrm{\infty }$ and if $x_0<\overline{x}$ then $T^n(x_0,0)\to E_0$ as $n\to \mathrm{\infty }$. Let $(x_0,y_0)$ be an arbitrary point below ${\mathcal{W}}^s(E_{\overline{x}})$. Then $(x_0,y_W){⪯}_{\mathrm{se}}(x_0,y_0){⪯}_{\mathrm{se}}(x_0,0)$ where $y_W$ denotes the y coordinate of the point on ${\mathcal{W}}^s(E_{\overline{x}})$. Consequently $T^n((x_0,y_W)){⪯}_{\mathrm{se}}{T}^n((x_0,y_0)){⪯}_{\mathrm{se}}{T}^n((x_0,0))$, which in view of $T^n((x_0,y_W))\to E_{\overline{x}}$ and $T^n((x_0,0))\to E_{\overline{x}}$ as $n\to \mathrm{\infty }$ implies that $T^n((x_0,y_0))\to E_{\overline{x}}$ as $n\to \mathrm{\infty }$.

Let $(x_0,y_0)$ be an arbitrary point above ${\mathcal{W}}^s(E_{\overline{x}})$. If $x_0\ge \overline{x}$, then $(0,y_0){⪯}_{\mathrm{se}}(x_0,y_0){⪯}_{\mathrm{se}}(x_0,y_W)$ where $y_W$ denotes the y coordinate of the point on ${\mathcal{W}}^s(E_{\overline{x}})$. Consequently, $T^n((0,y_0)){⪯}_{\mathrm{se}}{T}^n((x_0,y_0)){⪯}_{\mathrm{se}}{T}^n((x_0,y_W))$, which in view of $T^n((x_0,y_W))\to E_{\overline{x}}$ and $T^n((0,y_0))\to E_0$ as $n\to \mathrm{\infty }$ implies that $T^n((x_0,y_0))\to (x,0)$, $x<\overline{x}$ as $n\to \mathrm{\infty }$. Thus $T^n((x_0,y_0))\to E_0$ as $n\to \mathrm{\infty }$. If $x_0<\overline{x}$, then $(0,y_0){⪯}_{\mathrm{se}}(x_0,y_0){⪯}_{\mathrm{se}}(x_0,0)$, which implies $T^n((0,y_0)){⪯}_{\mathrm{se}}{T}^n((x_0,y_0)){⪯}_{\mathrm{se}}{T}^n((x_0,0))$, which in view of $T^n((x_0,0))\to E_0$ and $T^n((0,y_0))\to E_0$ as $n\to \mathrm{\infty }$ implies that $T^n((x_0,y_0))\to E_0$ as $n\to \mathrm{\infty }$.

Another proof of this result follows from Theorem 6, which guarantees the existence and uniqueness of ${\mathcal{W}}^s(E_{\overline{x}})$ and the invariance of the regions below and above ${\mathcal{W}}^s(E_{\overline{x}})$ and Theorem 10, which guarantees that all solutions converge to an equilibrium point. □

Theorem 13

• (a) If $a<2$, $b>2$, then system (6) has three equilibrium points, $E_0$, $E_{{\overline{y}}_{+}}$, $E_{{\overline{y}}_{-}}$, where the first two are locally stable and the third is a saddle point. The basins of attraction of the three equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):\mathit{\text{points below }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\},\hfill \\ B(E_{{\overline{y}}_{+}}(0,{\overline{y}}_{+}))=\{(x_0,y_0):\mathit{\text{points above }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\},\hfill \end{array}$$

where ${\mathcal{W}}^s(E)$ denotes the global stable manifold guaranteed by Theorem  6.

• (b) Similarly, if $a>2$, $b<2$, the basins of attraction of the equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):\mathit{\text{points above }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\},\hfill \\ B(E_{{\overline{x}}_{+}}({\overline{x}}_{+},0))=\{(x_0,y_0):\mathit{\text{points below }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\}.\hfill \end{array}$$

• (c) If $a=b=2$, then system (6) has three equilibrium points, $E_0$, $E_{\overline{x}}$, $E_{\overline{y}}$, where $E_0$ is locally stable and the remaining two are non-hyperbolic of stable type. The basins of attraction of three equilibrium points are given as

  $$\begin{array}{c}B(E_0(0,0))=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{\overline{x}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{\overline{y}})\},\hfill \\ B(E_{\overline{y}})=\{(x_0,y_0):\mathit{\text{points above }}{\mathcal{W}}^s(E_{\overline{y}})\},\hfill \\ B(E_{\overline{x}})=\{(x_0,y_0):\mathit{\text{points below }}{\mathcal{W}}^s(E_{\overline{x}})\},\hfill \end{array}$$

where ${\mathcal{W}}^s(E)$ denotes corresponding global stable manifold.

Proof We present the proof in case (a) only. The proof in case (b) is similar.

Local stability of the equilibrium points follows from Theorem 8.

In view of Theorem 10 all solutions converge to an equilibrium solution. Furthermore, all conditions of Theorem 6 are satisfied, which guarantee the existence of the manifold ${\mathcal{W}}^s(E_{{\overline{y}}_{-}})$, which is the graph of a continuous increasing function and such that both regions, below and above it are invariant. In addition the basin of attraction of $E_{{\overline{y}}_{-}}$ is exactly ${\mathcal{W}}^s(E_{{\overline{y}}_{-}})$. Thus, both regions, below and above ${\mathcal{W}}^s(E_{{\overline{y}}_{-}})$ are invariant and contain exactly one equilibrium point and all solutions there are convergent. Consequently the conclusion of the theorem follows.

Let us consider case (c). The existence and the properties of the manifolds ${\mathcal{W}}^s(E_{\overline{y}})$ and ${\mathcal{W}}^s(E_{\overline{x}})$, as well as the invariance of the regions above ${\mathcal{W}}^s(E_{\overline{y}})$, between ${\mathcal{W}}^s(E_{\overline{y}})$ and ${\mathcal{W}}^s(E_{\overline{x}})$ and below ${\mathcal{W}}^s(E_{\overline{x}})$ is guaranteed by Theorem 6. Since the regions above ${\mathcal{W}}^s(E_{\overline{y}})$ and below ${\mathcal{W}}^s(E_{\overline{x}})$ contains only one equilibrium point in view of Theorem 10 all solutions that start in those regions converge to $E_{\overline{y}}$ and $E_{\overline{x}}$, respectively.

Now, let $(x_0,y_0)$ be an arbitrary point between ${\mathcal{W}}^s(E_{\overline{y}})$ and ${\mathcal{W}}^s(E_{\overline{x}})$. First assume that $x_0<\overline{x}$, $y_0<\overline{y}$. Then $(0,y_0){⪯}_{\mathrm{se}}(x_0,y_0){⪯}_{\mathrm{se}}(x_0,0)$ which implies $T^n(0,y_0){⪯}_{\mathrm{se}}{T}^n(x_0,y_0){⪯}_{\mathrm{se}}{T}^n(x_0,0)$. In view of $T^n(0,y_0)\to E_0$, $T^n(0,x_0)\to E_0$ as $n\to \mathrm{\infty }$ we conclude that $T^n(x_0,y_0)\to E_0$ as $n\to \mathrm{\infty }$. Next assume that $x_0<\overline{x}$, $y_0<\overline{y}$ is not satisfied. Then there exist points $(x_l,y_l)\in {\mathcal{W}}^s(E_{\overline{y}})$, $(x_u,y_u)\in {\mathcal{W}}^s(E_{\overline{x}})$ such that $(x_l,y_l){⪯}_{\mathrm{se}}(x_0,y_0){⪯}_{\mathrm{se}}(x_u,y_u)$ which implies $T^n(x_l,y_l){⪯}_{\mathrm{se}}{T}^n(x_0,y_0){⪯}_{\mathrm{se}}{T}^n(x_u,y_u)$. Since $T^n(x_l,y_l)\to E_{\overline{y}}$, $T^n(x_u,y_u)\to E_{\overline{x}}$ as $n\to \mathrm{\infty }$ we conclude that $T^n(x_0,y_0)$ eventually enters the ordered interval $I(E_{\overline{y}},E_{\overline{x}})=\{(x,y):0\le x\le \overline{x},0\le y\le \overline{y}\}$. Since the map T is strongly competitive it will eventually enter the interior of $I(E_{\overline{y}},E_{\overline{x}})$ and then, as we just showed, will converge to $E_0$. □

See Figure 4 for visual illustration of Theorems 11-13.

Figure 4

Global stability and basins of attraction of system ( 6 ) in cases of one, two, and three equilibrium points.

Theorem 14

• (a) If $a>2$, $b=2$, then system (6) has four equilibrium points, $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{x}}_{-}}$, $E_{\overline{y}}$, where the first two are locally asymptotically stable, the third is a saddle point and the fourth is non-hyperbolic of the stable type. The basins of attraction of the four equilibrium points are given as

  $$\begin{array}{c}B(E_0)=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{\overline{y}})\},\hfill \\ B(E_{\overline{y}})=\{(x_0,y_0):\mathit{\text{points above }}{\mathcal{W}}^s(E_{\overline{y}})\},\hfill \\ B(E_{{\overline{x}}_{+}})=\{(x_0,y_0):\mathit{\text{points below }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\},\hfill \\ B(E_{{\overline{x}}_{-}})={\mathcal{W}}^s(E_{{\overline{x}}_{-}}),\hfill \end{array}$$

where ${\mathcal{W}}^s(E)$ denotes the global stable manifold guaranteed by Theorem  6.

• (b) Similarly, if $a=2$, $b>2$, then system (6) has four equilibrium points $E_0$, $E_{{\overline{y}}_{+}}$, $E_{{\overline{y}}_{-}}$, $E_{\overline{x}}$, where the first two are locally asymptotically stable, the third is a saddle point and the fourth one is non-hyperbolic of the stable type. The basins of attraction are given as

  $$\begin{array}{c}B(E_0)=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{\overline{x}})\},\hfill \\ B(E_{\overline{x}})=\{(x_0,y_0):\mathit{\text{points below }}{\mathcal{W}}^s(E_{\overline{x}})\},\hfill \\ B(E_{{\overline{y}}_{+}})=\{(x_0,y_0):\mathit{\text{points above }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\},\hfill \\ B(E_{{\overline{y}}_{-}})={\mathcal{W}}^s(E_{{\overline{y}}_{-}}).\hfill \end{array}$$

Proof We present the proof in case (a) only. The proof in case (b) is similar. Local stability of the equilibrium points follows from Theorem 8. The proof for the basin of attraction $B(E_{\overline{y}})$ is identical to the proof of the corresponding part of Theorem 12. Let $(x_0,y_0)$ be an arbitrary point below ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$. Then $(x_0,y_W){⪯}_{\mathrm{se}}(x_0,y_0){⪯}_{\mathrm{se}}(x_0,0)$ where $y_W$ denotes the y coordinate of the point on ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$. Consequently $T^n((x_0,y_W)){⪯}_{\mathrm{se}}{T}^n((x_0,y_0)){⪯}_{\mathrm{se}}{T}^n((x_0,0))$, which in view of $T^n((x_0,y_W))\to E_{{\overline{x}}_{-}}$ and $T^n((x_0,0))\to E_{{\overline{x}}_{+}}$ as $n\to \mathrm{\infty }$ implies that $T^n((x_0,y_0))\to E_{{\overline{x}}_{+}}$ as $n\to \mathrm{\infty }$. We also used the fact that the stable manifold ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$ is unique and represents the basin of attraction of the point $E_{{\overline{x}}_{-}}$.

Finally, let $(x_0,y_0)$ be an arbitrary point between ${\mathcal{W}}^s(E_{\overline{y}})$ and ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$. First assume that $x_0<{\overline{x}}_{-}$, $y_0<\overline{y}$. Then $(0,y_0){⪯}_{\mathrm{se}}(x_0,y_0){⪯}_{\mathrm{se}}(x_0,0)$ which implies $T^n(0,y_0){⪯}_{\mathrm{se}}{T}^n(x_0,y_0){⪯}_{\mathrm{se}}{T}^n(x_0,0)$. In view of $T^n(0,y_0)\to E_0$, $T^n(0,x_0)\to E_0$ as $n\to \mathrm{\infty }$ we conclude that $T^n(x_0,y_0)\to E_0$ as $n\to \mathrm{\infty }$. Next assume that $x_0<{\overline{x}}_{-}$, $y_0<\overline{y}$ is not satisfied. Then there exist points $(x_l,y_l)\in {\mathcal{W}}^s(E_{\overline{y}})$, $(x_u,y_u)\in {\mathcal{W}}^s(E_{{\overline{x}}_{-}})$ such that $(x_l,y_l){⪯}_{\mathrm{se}}(x_0,y_0){⪯}_{\mathrm{se}}(x_u,y_u)$ which implies $T^n(x_l,y_l){⪯}_{\mathrm{se}}{T}^n(x_0,y_0){⪯}_{\mathrm{se}}{T}^n(x_u,y_u)$. Since $T^n(x_l,y_l)\to E_{\overline{y}}$, $T^n(x_u,y_u)\to E_{{\overline{x}}_{-}}$ as $n\to \mathrm{\infty }$ we conclude that $T^n(x_0,y_0)$ eventually enters the ordered interval $I(E_y,E_{{\overline{x}}_{-}})=\{(x,y):0\le x\le {\overline{x}}_{-},0\le y\le \overline{y}\}$. Since the map T is strongly competitive it will eventually enters the interior of $I(E_{\overline{y}},E_{{\overline{x}}_{-}})$ and then, as we just showed, will converge to $E_0$. □

Theorem 15 Assume that $a>2$, $b>2$ and that system (6) has five equilibrium points. Three of these equilibrium points are locally asymptotically stable, $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$, and two are saddle points, $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$.

The basins of attraction of the equilibrium points are given as

$$\begin{array}{c}B(E_0)=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\},\hfill \\ B(E_{{\overline{x}}_{+}})=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\mathit{\text{ and the }}x\text{-}\mathit{\text{axis}}\},\hfill \\ B(E_{{\overline{y}}_{+}})=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\mathit{\text{ and the }}y\text{-}\mathit{\text{axis}}\}.\hfill \end{array}$$

The basins of attraction of the saddle equilibrium points E are the corresponding stable manifolds ${\mathcal{W}}^s(E)$.

Proof Local stability of the equilibrium points follows from Theorem 8. Furthermore, the existence of the stable manifolds ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$ and ${\mathcal{W}}^s(E_{{\overline{y}}_{-}})$ with the mentioned properties follows in the same way as in Theorem 13. The three regions $B(E_0)$, $B(E_{{\overline{x}}_{+}})$, $B(E_{{\overline{y}}_{+}})$ are invariant by Theorem 6 and in view of Theorem 10 every solution converges to an equilibrium point. Since the equilibrium points $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$ are locally asymptotically stable and $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$ are saddle points, the result follows. □

Theorem 16 Assume that $a>2$, $b>2$ and that system (6) has six equilibrium points. Three of these equilibrium points are locally asymptotically stable, $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$, two are saddle points, $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$, and one interior point, $E_{nu}$, is non-hyperbolic of the unstable type. There exist two invariant curves ${\mathcal{C}}_u$ and ${\mathcal{C}}_l$ emanating from $E_{nu}$ which are graphs of continuous non-decreasing functions such that ${\mathcal{C}}_u$ is above ${\mathcal{C}}_l$.

The basins of attraction of the equilibrium points are given as

$$\begin{array}{c}B(E_0)=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\},\hfill \\ B(E_{{\overline{x}}_{+}})=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\cup {\mathcal{C}}_l\mathit{\text{ and the }}x\text{-}\mathit{\text{axis}}\},\hfill \\ B(E_{{\overline{y}}_{+}})=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\cup {\mathcal{C}}_u\mathit{\text{ and the }}y\text{-}\mathit{\text{axis}}\},\hfill \\ B(E_{nu})=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{C}}_l\mathit{\text{ and }}{\mathcal{C}}_u\}.\hfill \end{array}$$

The basins of attraction of the saddle equilibrium points $B(E_{{\overline{x}}_{-}})$ and $B(E_{{\overline{y}}_{-}})$ are the corresponding stable manifolds ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$ and ${\mathcal{W}}^s(E_{{\overline{y}}_{-}})$, respectively.

Proof Local stability of the equilibrium points follows from Theorem 8. Furthermore, the existence of the stable manifolds ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$ and ${\mathcal{W}}^s(E_{{\overline{y}}_{-}})$ with the mentioned properties follows from Theorem 6. The region $B(E_0)$ is invariant by Theorem 6 and in view of Theorem 10 every solution which starts in that region converges to $E_0$. The existence and the properties of the curves ${\mathcal{C}}_l$ and ${\mathcal{C}}_u$ follow from Corollary 1. Thus the regions $B(E_{{\overline{x}}_{+}})$ and $B(E_{{\overline{y}}_{+}})$ are both invariant and so by Theorem 10 every solution which starts in those regions converges to $E_{{\overline{x}}_{+}}$ and $E_{{\overline{y}}_{+}}$, respectively, since these equilibrium points are locally asymptotically stable. Finally, the set $B(E_{nu})$ is invariant by Theorem 7 and by Theorem 10 every solution which starts in that region converges to $E_{nu}$. □

Conjecture 1 Based on our numerical experiments we believe that ${\mathcal{C}}_l={\mathcal{C}}_u$ in Theorem  16 holds.

Theorem 17 Assume that $a>2$, $b>2$ and that system (6) has seven equilibrium points. Three of these equilibrium points are locally asymptotically stable, $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$, three are saddle points, $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$, $E_{\mathrm{NW}}$ or $E_{\mathrm{SE}}$, and one is a repeller, $E_{\mathrm{SW}}$.

The basins of attraction of the equilibrium points are given as

$$\begin{array}{c}B(E_0)=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\},\hfill \\ B(E_{{\overline{x}}_{+}})=\{(x_0,y_0):\mathit{\text{region below }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\cup {\mathcal{W}}^s(E_{\mathrm{NW}})\},\hfill \\ B(E_{{\overline{y}}_{+}})=\{(x_0,y_0):\mathit{\text{region above }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\cup {\mathcal{W}}^s(E_{\mathrm{NW}})\}.\hfill \end{array}$$

The basins of attraction of the saddle equilibrium points E are the corresponding stable manifolds ${\mathcal{W}}^s(E)$.

Proof Local stability of all equilibrium points $E_0$, $E_{{\overline{x}}_{\pm }}$, $E_{{\overline{y}}_{\pm }}$ follows from Theorem 8.

Three regions $B(E_0)$, $B(E_{{\overline{x}}_{+}})$, $B(E_{{\overline{y}}_{+}})$ are invariant by Theorem 6 and in view of Theorem 10 every solution converges to an equilibrium. Since the equilibrium points $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$ are locally asymptotically stable and $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$, $E_{\mathrm{NW}}$ or $E_{\mathrm{SE}}$ are saddle points, the result follows. □

See Figure 5 for visual illustration of Theorems 14-17.

Figure 5

Global stability and basins of attraction of system ( 6 ) in cases of four, five, six and seven equilibrium points.

Theorem 18 Assume that $a>2$, $b>2$ and that system (6) has eight equilibrium points. Three of these equilibrium points are locally asymptotically stable, $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$, three are saddle points, $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$, $E_{\mathrm{NW}}$ or $E_{\mathrm{SE}}$, one is a repeller, $E_{\mathrm{SW}}$, and one is non-hyperbolic of the stable type $E_{ns}$.

The basins of attraction of the equilibrium points are given as

$$\begin{array}{c}B(E_0)=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\},\hfill \\ B(E_{{\overline{x}}_{+}})=\{(x_0,y_0):\mathit{\text{region below }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\cup {\mathcal{W}}^s(E_{\mathrm{SE}})\},\hfill \\ B(E_{{\overline{y}}_{+}})=\{(x_0,y_0):\mathit{\text{region above }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\cup {\mathcal{W}}^s(E_{ns})\},\hfill \\ B(E_{ns})=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{\mathrm{SE}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{ns})\}.\hfill \end{array}$$

The basins of attraction of the saddle equilibrium points E are the corresponding stable manifolds ${\mathcal{W}}^s(E)$.

The same result holds if $E_{\mathrm{SW}}$ is replaced with $E_{\mathrm{NE}}$.

Proof Local stability of the equilibrium points follows from Theorem 8. The existence and the properties of four manifolds ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$, ${\mathcal{W}}^s(E_{{\overline{y}}_{-}})$, ${\mathcal{W}}^s(E_{\mathrm{SE}})$, ${\mathcal{W}}^s(E_{ns})$ follow from Theorem 6.

The four regions $B(E_0)$, $B(E_{{\overline{x}}_{+}})$, $B(E_{{\overline{y}}_{+}})$, $B(E_{ns})$ are invariant by Theorem 6 and in view of Theorem 10 every solution converges to an equilibrium point. Since the equilibrium points $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$ are locally asymptotically stable, $E_{ns}$ is non-hyperbolic of stable type and $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$, $E_{\mathrm{SE}}$ are saddle points, the result follows. □

Theorem 19 Assume that $a>2$, $b>2$ and that system (6) has nine equilibrium points. Four of these equilibrium points are locally asymptotically stable, $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$, $E_{\mathrm{NE}}$, four are saddle points, $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$, $E_{\mathrm{NW}}$, $E_{\mathrm{SE}}$, and one is a repeller, $E_{\mathrm{SW}}$.

The basins of attraction of the equilibrium points are given as

$$\begin{array}{c}B(E_0)=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\},\hfill \\ B(E_{{\overline{x}}_{+}})=\{(x_0,y_0):\mathit{\text{region below }}{\mathcal{W}}^s(E_{{\overline{x}}_{-}})\cup {\mathcal{W}}^s(E_{\mathrm{SE}})\},\hfill \\ B(E_{{\overline{y}}_{+}})=\{(x_0,y_0):\mathit{\text{region above }}{\mathcal{W}}^s(E_{{\overline{y}}_{-}})\cup {\mathcal{W}}^s(E_{\mathrm{NW}})\},\hfill \\ B(E_{\mathrm{NE}})=\{(x_0,y_0):\mathit{\text{region bounded by }}{\mathcal{W}}^s(E_{\mathrm{SE}})\mathit{\text{ and }}{\mathcal{W}}^s(E_{\mathrm{NW}})\}.\hfill \end{array}$$

The basins of attraction of the saddle equilibrium points E are the corresponding stable manifolds ${\mathcal{W}}^s(E)$.

Proof Local stability of the equilibrium points follows from Theorem 8. The existence and the properties of four manifolds ${\mathcal{W}}^s(E_{{\overline{x}}_{-}})$, ${\mathcal{W}}^s(E_{{\overline{y}}_{-}})$, ${\mathcal{W}}^s(E_{\mathrm{SE}})$, ${\mathcal{W}}^s(E_{\mathrm{NW}})$ follow from Theorem 6.

The four regions $B(E_0)$, $B(E_{{\overline{x}}_{+}})$, $B(E_{{\overline{y}}_{+}})$, $B(E_{\mathrm{NE}})$ are invariant by Theorem 6 and in view of Theorem 10 every solution converges to an equilibrium point. Since the equilibrium points $E_0$, $E_{{\overline{x}}_{+}}$, $E_{{\overline{y}}_{+}}$, $E_{\mathrm{NE}}$ are locally asymptotically stable and $E_{{\overline{x}}_{-}}$, $E_{{\overline{y}}_{-}}$, $E_{\mathrm{NW}}$, and $E_{\mathrm{SE}}$ are saddle points, the result follows. □

See Figure 6 for visual illustration of Theorems 18, 19.

Figure 6

Global stability and basins of attraction of system ( 6 ) in cases of eight and nine equilibrium points.