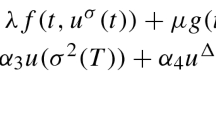Abstract
In this paper, we consider a class of boundary value problems for third-order p-Laplacian functional dynamic equations on time scales, some existence criteria of at least three positive solutions are established. The main tool used in this paper is the fixed point theorem due to Avery and Peterson (Comput. Math. Appl. 42:313-322, 2001).
MSC:39K10, 34B15.
Similar content being viewed by others
1 Introduction
Recently, some authors have paid much attention to the existence of positive solutions for functional dynamic equations on time scales [1–8], especially for the p-Laplacian functional dynamic equations on time scales [1, 3–8]. For convenience, throughout this paper we denote by the p-Laplacian operator, i.e., , , , .
In [2], Kaufmann and Raffoul considered a nonlinear functional dynamic equation on time scales and obtained sufficient conditions for the existence of positive solutions. In [5], by using a double fixed point theorem due to Avery et al. [9], Song and Gao considered the existence of at least twin positive solutions to the following p-Laplacian functional dynamic equations on time scales:
where , −r, 0, .
In [8], Wang and Guan considered the existence of positive solutions to problem (1.1) by applying the well-known Leggett-Williams fixed point theorem [10].
Motivated by [2, 5] and [8], we shall show that problem (1.1) has at least three positive solutions by means of the fixed point theorem due to Avery and Peterson [11].
In this article, we always assume that:
(C1) is continuous;
(C2) is left dense continuous (i.e., ) and does not vanish identically on any closed subinterval of , where denotes the set of all left dense continuous functions from T to ;
(C3) is continuous and ;
(C4) is continuous, for all t;
(C5) is a continuous function defined on ℝ and satisfies that there exist and such that
Remark 1.1 Although the Banach space in this paper is the same as that of [8], i.e., with , the hypotheses utilized in the existence theorem in this paper differ from those of [8] where the effect of was imposed.
Throughout this work, we assume the knowledge of time scales and time-scale notation, first introduced by Hilger [12]. For more on time scales, please see the texts by Bohner and Peterson [13, 14].
In the remainder of this section, we state the following theorem which is crucial to our proof.
Let γ and θ be nonnegative continuous convex functions on P, α be a nonnegative continuous concave function on P, and ψ be a nonnegative continuous function on P. Then, for positive real numbers a, b, c and d, we define the following convex sets:
and a closed set
To prove our main results, we need the following fixed point theorem due to Avery and Peterson in [11].
Theorem 1.1 Let P be a cone in a real Banach space E. Let γ and θ be nonnegative continuous convex functionals on P, α be a nonnegative continuous concave functional on P and ψ be a nonnegative continuous functional on P satisfying for , such that for some positive numbers h and d,
for all . Suppose that
is completely continuous and there exist positive numbers a, b and c with such that:
-
(i)
and for ;
-
(ii)
for with ;
-
(iii)
and for with .
Then F has at least three fixed points such that
2 Main result
In this section we consider the existence of three positive solutions for problem (1.1).
We say that u is concave on if for .
We note that is a solution of problem (1.1) if and only if
Let with , . So E is a Banach space with the norm and P is a cone in E. For each , extend to with for .
Define by
It is well known that this operator F is completely continuous.
We seek a fixed point of F in the cone P. Define
Then denotes a positive solution of problem (1.1).
Lemma 2.1 If , then
-
(i)
, i.e., .
-
(ii)
, .
-
(iii)
is decreasing on .
Proof This is easy, so we omit it here. □
Let be fixed such that , and set
Throughout this paper, we assume and .
Define the nonnegative continuous concave functional α, the nonnegative continuous convex functionals θ, γ, and the nonnegative continuous functional ψ on the cone P, respectively, as
In addition, by Lemma 2.1, we have for each .
For convenience, we define
We now state growth conditions on f so that BVP (1.1) has at least three positive solutions.
Theorem 2.1 Let , , and suppose that f satisfies the following conditions:
(H1) if uniformly in ; if , ,
(H2) if uniformly in ,
(H3) if uniformly in ; if , .
Then BVP (1.1) has at least three positive solutions of the form
where for , , with and .
Proof We first assert that .
Let , then , consequently, for .
From (H1), we have
Therefore , i.e., .
Secondly, we assert that and for .
Let with , then and . Furthermore, by we have . Let , then .
Moreover, , we have , .
From (H2), we see that
as required.
Thirdly, we assert that for with .
with , from Lemma 2.1 we have
So,
This implies that for with .
Finally, we assert that and for with .
As , we have . with , by Lemma 2.1 we have for .
From (H3), we have
which shows that condition (iii) of Theorem 1.1 is fulfilled.
Thus, all the conditions of Theorem 1.1 are satisfied. Hence, F has at least three fixed points , , satisfying
Let
which are three positive solutions of BVP (1.1) □
References
Guan W: Three positive solutions for p -Laplacian functional dynamic equations on time scales. Electron. J. Qual. Theory Differ. Equ. 2008, 28: 1-7. http://www.math.u-szeged.hu/ejqtde/
Kaufmann ER, Raffoul YN: Positive solutions for a nonlinear functional dynamic equation on a time scale. Nonlinear Anal. 2005, 62: 1267-1276. 10.1016/j.na.2005.04.031
Song CX, Xiao CT: Positive solutions for p -Laplacian functional dynamic equations on time scales. Nonlinear Anal. 2007, 66: 1989-1998. 10.1016/j.na.2006.02.036
Song CX, Weng PX: Multiple positive solutions for p -Laplacian functional dynamic equations on time scales. Nonlinear Anal. 2008, 68: 208-215. 10.1016/j.na.2006.10.043
Song CX, Gao XJ: Positive solutions for third-order p -Laplacian functional dynamic equations on time scales. Bound. Value Probl. 2011., 2011: Article ID 585378
Wang DB: Three positive solutions for p -Laplacian functional dynamic equations on time scales. Electron. J. Differ. Equ. 2007, 2007(95):1-9.
Wang DB, Guan W: Multiple positive solutions for p -Laplacian functional dynamic equations on time scales. Taiwan. J. Math. 2008, 12: 2327-2340.
Wang DB, Guan W: Multiple positive solutions for third-order p -Laplacian functional dynamic equations on time scales. Adv. Differ. Equ. 2014. 10.1186/1687-1847-2014-145
Avery RI, Chyan CJ, Henderson J: Twin solutions of boundary value problems for ordinary differential equations and finite difference equations. Comput. Math. Appl. 2001, 42: 695-704. 10.1016/S0898-1221(01)00188-2
Leggett RW, Williams LR: Multiple positive fixed points of nonlinear operators on ordered Banach spaces. Indiana Univ. Math. J. 1979, 28: 673-688. 10.1512/iumj.1979.28.28046
Avery RI, Peterson AC: Three positive fixed points of nonlinear operators on ordered Banach spaces. Comput. Math. Appl. 2001, 42: 313-322. 10.1016/S0898-1221(01)00156-0
Hilger S: Analysis on measure chains - a unified approach to continuous and discrete calculus. Results Math. 1990, 18: 18-56. 10.1007/BF03323153
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston; 2001.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston; 2003.
Acknowledgements
The author thanks the referees and the editors for their helpful comments and suggestions. Research was supported by the Natural Science Foundation of Gansu Province of China (Grant no. 1310RJYA080).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that she has no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Guan, W. Existence of multiple positive solutions for third-order p-Laplacian functional dynamic equations on time scales. Adv Differ Equ 2014, 242 (2014). https://doi.org/10.1186/1687-1847-2014-242
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-242