Synchronization of a class of uncertain stochastic discrete-time delayed neural networks

Abstract

The global asymptotical synchronization problem is discussed for a general class of uncertain stochastic discrete-time neural networks with time delay in this paper. Time delays include time-varying delay and distributed delay. Based on the drive-response concept and the Lyapunov stability theorem, a linear matrix inequality (LMI) approach is given to establish sufficient conditions under which the considered neural networks are globally asymptotically synchronized in the mean square. Therefore, the global asymptotical synchronization of the stochastic discrete-time neural networks can easily be checked by utilizing the numerically efficient Matlab LMI toolbox. Moreover, the obtained results are dependent not only on the lower bound but also on the upper bound of the time-varying delays, that is, they are delay-dependent. And finally, a simulation example is given to illustrate the effectiveness of the proposed synchronization scheme.

1 Introduction

Since Chua and Yang in [1, 2] proposed the theory and applications of cellular neural networks, the dynamical behaviors of neural networks have attracted a great deal of research interest in the past two decades. Those attentions have mainly concentrated on the stability and the synchronization problems of neural networks (see [3–28]). Especially after synchronization problems of chaotic systems had been studied by Pecora and Carroll in [29, 30], in which they proposed the drive-response concept, the control and synchronization problems of chaotic systems have been thoroughly investigated [5–8, 14–18, 31–35]. And many applications of such systems have been found in different areas, particularly in engineering fields such as creating secure communication systems (see [33–35]). As long as we can reasonably design the receiver so that the state evolution of the response system synchronize to that of the driven system, the message obtained by the receiver can be hidden in a chaotic signal, hence, secure communication can be implemented.

It is well known that neural networks, including Hopfield neural networks (HNNs) and cellular neural networks (CNNs), are large-scale and complex nonlinear high-dimensional systems composed of a large number of interconnected neurons. And they have also been found effective applications in many areas such as image processing, optimization problems, pattern recognition, and so on. Therefore, it is not easy to achieve the control and synchronization of these systems. In [8, 16, 19, 22], by drive-response method, some results are given for different type neural networks to guarantee the synchronization of drive system and response system in the models discussed. It is easy to apply those results to real neural networks. And in [5–7, 18], synchronization in an array of linearly or nonlinearly coupled networks has been analyzed in details. The authors studied the global asymptotic or exponential synchronization of a complex dynamical neural networks through constructing a synchronous manifold and showed that it is globally asymptotically or exponentially stable. To the best of our knowledge, up till now, most of the synchronization methods of chaotic systems (especially neural networks) are of drive-response type (which is also called a master-slave system).

At the same time, most of the papers mentioned above are concerned with continuous-time neural networks. When implementing these networks for practical use, discrete-time types of models should be formulated. The readers may refer to [3, 23] for more details as regards the significance of investigating discrete-time neural networks. Therefore, it is important to study the dynamical behaviors of discrete-time neural networks. On the other hand, because the synaptic transmission is probably a noisy process brought about by random fluctuations from the release of neurotransmitters, and a stochastic disturbance must be considered when formulating real artificial neural networks. Recently, the stability and synchronization analysis problems for stochastic or discrete-time neural networks have been investigated; see e.g. [3, 10–13, 19–21, 23], and references therein. So, in this paper, based on drive-response concept and Lyapunov functional method, some different decentralized control laws will be given for global asymptotical synchronization of a general class of discrete-time delayed chaotic neural networks with stochastic disturbance. In the neural network model, the parameter uncertainties are norm-bounded, the neural networks are subjected to stochastic disturbances described in terms of a Brownian motion, and the delay includes time-varying delay and distributed delay. Up to now, to the best of our knowledge, there are few works about the synchronization problem of discrete-time neural networks with distributed delay. And the master-slave system’s synchronization problem for the uncertain stochastic discrete-time neural networks with distributed delay is little investigated.

This paper is organized as follows. In Section 2, model formulation and some preliminaries are presented for our main results. In Section 3, based on the drive-response concept and the Lyapunov functional method, we discuss global asymptotical synchronization in mean square for uncertain stochastic discrete-time delayed neural networks with mixed delays. A numerical example is given to illustrate the effectiveness and feasibility of our results in Section 4. And finally, in Section 5, we give the conclusions.

Notations Throughout this paper, ℝ, ${\mathbb{R}}^n$, and ${\mathbb{R}}^{n\times m}$ are used to denote, respectively, the real number field, the real vector space of dimension n, and the set of all $n\times m$ real matrices. And $E_n$ denotes a n-dimensional identity matrix. The set of all integers on the closed interval $[a,b]$ is denoted as $\mathbb{N}[a,b]$, where a, b are integers and $a<b$. We use ℕ to denote the set of all positive integers. Also, we assume that $C(\mathbb{N}[a,b],\mathbb{R})$ represents the set of all functions $\varphi :\mathbb{N}[a,b]\to \mathbb{R}$. The superscript ‘T’ represents the transpose of a matrix or a vector, and the notation $X⩾Y$ (respectively, $X>Y$) means that $X-Y$ is a positive semi-definite matrix (respectively, a positive definite matrix) where X and Y are symmetric matrices. The notation $|\cdot |$ denotes the Euclidian norm of a vector and $E_m$ refers to an m-dimensional identity matrix. Let $(\mathrm{\Omega },\mathcal{F},\mathcal{P})$ be a complete probability space with a natural filtration ${\{{\mathcal{F}}_t\}}_{t⩾0}$ satisfying the usual conditions (i.e., the filtration contains all -null sets and is right continuous) and generated by Brownian motion $\{\omega (s):0⩽s⩽t\}$. $\mathbb{E}\{\cdot \}$ stands for the mathematical expectation operator with respect to the given probability measure . The asterisk ∗ in a matrix is used to denote the term that is induced by symmetry. Usually, if not explicitly specified, matrices are always assumed to have compatible dimensions.

2 Model formulation and preliminaries

It is well known that most of the synchronization methods of chaotic systems are of the master-slave (drive-response) type. The system, which is called a slave system or a response system, can be driven by another system, which is called a master system or drive system, so that the behavior of the slave system can be influenced by the master system, i.e., the master system is independent to the slave system but the slave system is driven by the master system. In this paper, our aim is to design the controller reasonably such that the behavior of the slave system synchronizes to that of the master system.

Now, let us consider a general class of n-neuron discrete-time neural networks with time-varying and distributed delays which is described by the following difference equations:

$$\begin{array}{rcl}x(k+1)& =& (A+\mathrm{\Delta }A(k))x(k)+(\tilde{A}+\mathrm{\Delta }\tilde{A}(k))x(k-\tau (k))+(B+\mathrm{\Delta }B(k))\tilde{f}(x(k))\\ +(\tilde{B}+\mathrm{\Delta }\tilde{B}(k))\tilde{g}\left(x(k-\tau (k))\right)+(C+\mathrm{\Delta }C(k))\sum _{s=1}^{\tau (k)}\tilde{h}(x(k-s))+I(k),\end{array}$$

(1)

that is,

$$\begin{array}{rl}{x}_i(k+1)=& (a_i+\mathrm{\Delta }{a}_i(k))x_i(k)+({\tilde{a}}_i+\mathrm{\Delta }{\tilde{a}}_i(k))x_i(k-\tau (k))\\ +\sum _{j=1}^n(b_{ij}+\mathrm{\Delta }{b}_{ij}(k)){\tilde{f}}_j(x_j(k))+\sum _{j=1}^n({\tilde{b}}_{ij}+\mathrm{\Delta }{\tilde{b}}_{ij}(k)){\tilde{g}}_j\left(x_{ij}(k-\tau (k))\right)\\ +\sum _{s=1}^{\tau (k)}\sum _{j=1}^n(c_{ij}+\mathrm{\Delta }{c}_{ij}(k)){\tilde{h}}_j(x_{ij}(k-s))+I_i(k),i=1,2,\dots ,n,\end{array}$$

where $x(k)={(x_1(k),x_2(k),\dots ,x_n(k))}^T\in {\mathbb{R}}^n$ is the state vector associated with the n neurons. The positive integer $\tau (k)$ corresponds to the time-varying delay satisfying

$$1⩽{\tau }_m⩽\tau (k)⩽{\tau }_M,k\in \mathbb{N},$$

(2)

where ${\tau }_m$ and ${\tau }_M$ are known positive integers. $A=diag(a_1,a_2,\dots ,a_n)$ and $\tilde{A}=diag({\tilde{a}}_1,{\tilde{a}}_2,\dots ,{\tilde{a}}_n)$ are real diagonal constant matrices (corresponding to the state feedback and the delayed state-feedback coefficient matrices, respectively) with $|a_i|<1$, $|{\tilde{a}}_i|<1$, $i=1,2,\dots ,n$, $B={[b_{ij}]}_{n\times n}$, $\tilde{B}={[{\tilde{b}}_{ij}]}_{n\times n}$, and $C={[c_{ij}]}_{n\times n}$ are the connection weight matrix, the discretely delayed connection weight matrix and the distributively delayed connection weight matrix, respectively. The functions $\tilde{f}(x(k))={({\tilde{f}}_1(x_1(k)),{\tilde{f}}_2(x_2(k)),\dots ,{\tilde{f}}_n(x_n(k)))}^T$, $\tilde{g}(x(k-\tau (k)))={({\tilde{g}}_1(x_1(k-\tau (k))),{\tilde{g}}_2(x_2(k-\tau (k))),\dots ,{\tilde{g}}_n(x_n(k-\tau (k))))}^T$ and $\tilde{h}(x(k))={({\tilde{h}}_1(x_1(k)),{\tilde{h}}_2(x_2(k)),\dots ,{\tilde{h}}_n(x_n(k)))}^T$ in ${\mathbb{R}}^n$ denote the neuron activation functions. The real vector $I(k)={(I_1(k),I_2(k),\dots ,I_n(k))}^T$ is the exogenous input.

Remark 1 The term of the distributed time delays, ${\sum }_{s=1}^{\tau (k)}\tilde{h}(x(k-s))$, in the discrete-time form, is included in the model (1). It can be interpreted as the discrete analog of the following well-discussed continuous-time complex network with time-varying and distributed delays:

$$\dot{x}=Ax(t)+Bf(x(t))+Cg\left(x(t-\tau (t))\right)+D{\int }_{t-\tau (t)}^{t}h(x(s))ds+I(t).$$

Obviously, such a distributed delay term will bring about an additional difficulty in our analysis.

For the activation functions in the model (1), we have the following assumptions:

Assumption 1 The activation functions ${\tilde{f}}_i(\cdot )$, ${\tilde{g}}_i(\cdot )$, and ${\tilde{h}}_i(\cdot )$ ($i=1,2,\dots ,n$) in model (1) are all continuous and bounded.

Assumption 2 [10, 21, 23, 26]

The activation functions ${\tilde{f}}_i(\cdot )$, ${\tilde{g}}_i(\cdot )$, and ${\tilde{h}}_i(\cdot )$ ($i=1,2,\dots ,n$) in model (1) satisfy

$${\theta }_i^{-}⩽\frac{{\tilde{f}}_i(s_1)-{\tilde{f}}_i(s_2)}{s_1-s_2}⩽{\theta }_i^{+},\mathrm{\forall }{s}_1,s_2\in \mathbb{R},$$

(3)

$${\iota }_i^{-}⩽\frac{{\tilde{g}}_i(s_1)-{\tilde{g}}_i(s_2)}{s_1-s_2}⩽{\iota }_i^{+},\mathrm{\forall }{s}_1,s_2\in \mathbb{R},$$

(4)

$${\delta }_i^{-}⩽\frac{{\tilde{h}}_i(s_1)-{\tilde{h}}_i(s_2)}{s_1-s_2}⩽{\delta }_i^{+},\mathrm{\forall }{s}_1,s_2\in \mathbb{R},$$

(5)

where ${\theta }_i^{-}$, ${\theta }_i^{+}$, ${\iota }_i^{-}$, ${\iota }_i^{+}$, ${\delta }_i^{-}$, ${\delta }_i^{+}$ are some constants.

Remark 2 The constants ${\theta }_i^{-}$, ${\theta }_i^{+}$, ${\iota }_i^{-}$, ${\iota }_i^{+}$, ${\delta }_i^{-}$, ${\delta }_i^{+}$ in Assumption 2 are allowed to be positive, negative or zero. So, the activation functions in this paper are less conservative than the usual sigmoid functions.

The time-varying matrices $\mathrm{\Delta }A(k)$, $\mathrm{\Delta }\tilde{A}(k)$, $\mathrm{\Delta }B(k)$, $\mathrm{\Delta }\tilde{B}(k)$, and $\mathrm{\Delta }C(k)$ in model (1) represent the parameter uncertainties, which are generated by the modeling errors and are assumed satisfying the following admissible condition:

$$\begin{array}{r}\left[\begin{array}{ccccc}\mathrm{\Delta }A(k)& \mathrm{\Delta }\tilde{A}(k)& \mathrm{\Delta }B(k)& \mathrm{\Delta }\tilde{B}(k)& \mathrm{\Delta }C(k)\end{array}\right]\\ =MH(k)[\begin{array}{ccccc}{W}_1& W_2& W_3& W_4& W_5\end{array}],\end{array}$$

(6)

in which M and $W_i$ ($i=1,2,\dots ,5$) are known real constant matrices, and $H(k)$ is the unknown time-varying matrix-valued function subject to the following condition:

$$H^T(k)H(k)⩽E_n,\mathrm{\forall }k\in \mathbb{N}.$$

(7)

Also, the initial conditions of model (1) are given by

$$x_i(s)={\varphi }_i(s)\in C(\mathbb{N}[-{\tau }_M,0],\mathbb{R})(i=1,2,\dots ,n).$$

(8)

In this paper, we consider model (1) as the master system. And the response system is

$$\begin{array}{rcl}y(k+1)& =& (A+\mathrm{\Delta }A(k))y(k)+(\tilde{A}+\mathrm{\Delta }\tilde{A}(k))y(k-\tau (k))+(B+\mathrm{\Delta }B(k))\tilde{f}(y(k))\\ +(\tilde{B}+\mathrm{\Delta }\tilde{B}(k))\tilde{g}\left(y(k-\tau (k))\right)+(C+\mathrm{\Delta }C(k))\sum _{s=1}^{\tau (k)}\tilde{h}(y(k-s))+I(k)\\ +u(k)+\sigma (k,e(k),e(k-\tau (k)))\omega (k),\end{array}$$

(9)

namely,

$$\begin{array}{rl}{y}_i(k+1)=& (a_i+\mathrm{\Delta }{a}_i(k))y_i(k)+({\tilde{a}}_i+\mathrm{\Delta }{\tilde{a}}_i(k))y_i(k-\tau (k))\\ +\sum _{j=1}^n(b_{ij}+\mathrm{\Delta }{b}_{ij}(k)){\tilde{f}}_j(y_j(k))+\sum _{j=1}^n({\tilde{b}}_{ij}+\mathrm{\Delta }{\tilde{b}}_{ij}(k)){\tilde{g}}_j\left(y_{ij}(k-\tau (k))\right)\\ +\sum _{s=1}^{\tau (k)}\sum _{j=1}^n(c_{ij}+\mathrm{\Delta }{c}_{ij}(k)){\tilde{h}}_j(y_{ij}(k-s))+I_i(k)\\ +u_i(k)+\sum _{j=1}^n{\sigma }_{ij}(k,e_i(k),e_i(k-\tau (k))){\omega }_j(k),i=1,2,\dots ,\end{array}$$

where the related parameters and the activation functions are all same as model (1), $u(k)$ is the controller which is to be designed later, this is also our main aim. $e(k)={(e_1(k),e_2(k),\dots ,e_n(k))}^T\in {\mathbb{R}}^n$ is the error state, $\omega (k)=({\omega }_1(k),{\omega }_2(k),\dots ,{\omega }_n(k))$ is a n-dimensional Brownian motion defined on a complete probability space $(\mathrm{\Omega },\mathcal{F},\mathcal{P})$ with

$$\mathbb{E}\{\omega (k)\}=0,\mathbb{E}\{{\omega }^2(k)\}=1,\mathbb{E}\{\omega (i)\omega (j)\}=0(\text{for }i\ne j)$$

(10)

and $\sigma :{\mathbb{R}}^n\times {\mathbb{R}}^n\times \mathbb{R}\to \mathbb{R}$ is a continuous function with $\sigma (\cdot ,0,0)=0$ and

$${\sigma }^T(k,x,y)\sigma (k,x,y)⩽{\rho }_1{x}^{T}x+{\rho }_2{y}^{T}y,\mathrm{\forall }x,y\in {\mathbb{R}}^n,$$

(11)

where ${\rho }_1>0$ and ${\rho }_2>0$ are known constant scalars.

The initial conditions of the slave system model (9) are given by

$$y_i(s)={\psi }_i(s)\in L_{{\mathcal{F}}_0}^2(\mathbb{N}[-{\tau }_M,0],\mathbb{R});$$

(12)

here $L_{{\mathcal{F}}_0}^2([-{\tau }_M,0],\mathbb{R})$ denotes the family of all ${\mathcal{F}}_0$-measurable $C([-{\tau }_M,0],\mathbb{R})$-valued random variables satisfying ${sup}_{-{\tau }_M\le s\le 0}\mathbb{E}\{{\parallel {\psi }_i(s)\parallel }^2\}<\mathrm{\infty }$.

Now let us define the error state $e(k)$ as $e(k)=y(k)-x(k)$, subtracting (9) from (1), it yields the error dynamical systems as follows:

$$\begin{array}{rcl}e(k+1)& =& (A+\mathrm{\Delta }A(k))e(k)+(\tilde{A}+\mathrm{\Delta }\tilde{A}(k))e(k-\tau (k))+(B+\mathrm{\Delta }B(k))f(e(k))\\ +(\tilde{B}+\mathrm{\Delta }\tilde{B}(k))g\left(e(k-\tau (k))\right)+(C+\mathrm{\Delta }C(k))\sum _{s=1}^{\tau (k)}h(e(k-s))\\ +u(k)+\sigma (k,e(k),e(k-\tau (k)))\omega (k),\end{array}$$

(13)

where $f(e(k))=\tilde{f}(e(k)+x(k))-\tilde{f}(x(k))$, $g(e(k-\tau (k)))=\tilde{g}(e(k-\tau (k))+x(k-\tau (k)))-\tilde{g}(x(k-\tau (k)))$, $h(e(k-\tau (k)))=\tilde{h}(e(k-\tau (k))+x(k-\tau (k)))-\tilde{h}(x(k-\tau (k)))$. Denoted the error state vector as $e(k)={(e_1(k),e_2(k),\dots ,e_n(k))}^T\in {\mathbb{R}}^n$. Correspondingly, from (8) and (12), the initial condition of error system (12) is $\phi (s)=\psi (s)-\varphi (s)={({\psi }_1(s)-{\varphi }_1(s),\dots ,{\psi }_n(s)-{\varphi }_n(s))}^T$. Here it is necessary to assume that $\phi (s)\in L_{{\mathcal{F}}_0}^2(\mathbb{N}[-{\tau }_M,0],\mathbb{R})$.

Now, we firstly give the definition of the globally robust asymptotical synchronization in mean square of the master system (1) and the slave system (9) as follows.

Definition 1 System (1) and system (9) are said to be globally asymptotically synchronized in the mean square if all parameter uncertainties satisfying the admissible condition (6) and (7), and the trajectories of system (1) and system (9) satisfy

$$\underset{k\to +\mathrm{\infty }}{lim}\mathbb{E}\left\{|y(k)-x(k)|\right\}=0.$$

That is, if the error system (13) is globally robustly asymptotically stable in the mean square, then system (1) and system (9) are robustly globally asymptotically synchronized in the mean square.

Remark 3 Assumption 1 and Assumption 2 can derive that the error system (13) has at least an equilibrium point. Our main aim is to design the controller $u(k)$ reasonably such that the equilibrium point of the error system (13) is robustly globally asymptotically stable in the mean square.

In many real applications, we are interested in designing a memoryless state-feedback controller as

$$u(k)=Ge(k),$$

(14)

where $G\in {\mathbb{R}}^{n\times n}$ is a constant gain matrix.

However, as a special case where the information on the size of time-varying delay $\tau (k)$ is available, we can also consider a discretely delayed-feedback controller of the following form:

$$u(k)=Ge(k)+G_{\tau }e(k-\tau (k)).$$

(15)

Moreover, we can design a more general form of a delayed-feedback controller as

$$u(k)=Ge(k)+G_{\tau }e(k-\tau (k))+G_z\sum _{s=1}^{\tau (k)}e(k-s),$$

(16)

Although a memoryless controller (14) has the advantage of easy implementation, its performance cannot be better than a discretely delayed-feedback controller which utilizes the available information of the size of time-varying delay. Therefore, in this respect, the controller (16) could be considered as a compromise between the performance improvement and the implementation simplicity.

Now, let $u(k)=Ge(k)+G_{\tau }e(k-\tau (k))+G_z{\sum }_{s=1}^{\tau (k)}e(k-s)$, and substituting it into (13), and denoting

$$\begin{array}{r}A(k)=G+A+\mathrm{\Delta }A(k),\tilde{A}(k)=G_{\tau }+\tilde{A}+\mathrm{\Delta }\tilde{A}(k),\\ B(k)=B+\mathrm{\Delta }B(k),\tilde{B}(k)=\tilde{B}+\mathrm{\Delta }\tilde{B}(k),C(k)=C+\mathrm{\Delta }C(k),\end{array}$$

(17)

it follows that

$$\begin{array}{rcl}e(k+1)& =& A(k)e(k)+\tilde{A}(k)e(k-\tau (k))+B(k)f(e(k))+\tilde{B}(k)g\left(e(k-\tau (k))\right)\\ +G_z\sum _{s=1}^{\tau (k)}e(k-s)+C(k)\sum _{s=1}^{\tau (k)}h(e(k-s))+\sigma (k,e(k),e(k-\tau (k)))\omega (k).\end{array}$$

(18)

To complete this particular issue, we still need several lemmas to be used later.

Lemma 1 Let , , and H be real matrices of appropriate dimensions with H satisfying $H^{T}H⩽E$. Then the following inequality:

$$\mathcal{P}H\mathcal{Q}+{(\mathcal{P}H\mathcal{Q})}^T⩽{\mu }^{-1}\mathcal{P}{\mathcal{P}}^T+\mu {\mathcal{Q}}^T\mathcal{Q}$$

holds for any scalar $\mu >0$.

Lemma 2 (Schur complement)

Given constant matrices , , ℛ, where ${\mathcal{P}}^T=\mathcal{P}$, ${\mathcal{Q}}^T=\mathcal{Q}$, then

$$\left[\begin{array}{cc}\mathcal{P}& \mathcal{R}\\ {\mathcal{R}}^T& -\mathcal{Q}\end{array}\right]<0$$

is equivalent to the following conditions:

$$\mathcal{Q}>0,\mathcal{P}+\mathcal{R}{\mathcal{Q}}^{-1}{\mathcal{R}}^T<0.$$

Lemma 3 [27, 28]

Let $\mathcal{M}\in {\mathbb{R}}^{n\times n}$ be a positive semi-definite matrix. If the series concerned are convergent, we have the following inequality:

$${\left(\sum _{i=1}^m{\alpha }_i{x}_i\right)}^T\mathcal{M}\left(\sum _{i=1}^m{\alpha }_i{x}_i\right)⩽\left(\sum _{i=1}^m{\alpha }_i\right)\sum _{i=1}^m{\alpha }_i{x}_i^T\mathcal{M}{x}_i$$

holds for any $x_i\in {\mathbb{R}}^n$ and ${\alpha }_i⩾0$ ($i=1,2,\dots ,m$).

3 Main results and proofs

In this section, some sufficient criteria are presented for the globally asymptotically synchronization in the mean square of the neural networks (1) and (9).

Before our main work, for presentation convenience, in the following, we denote

$$\begin{array}{r}{\mathrm{\Theta }}_1=diag({\theta }_1^{-}{\theta }_1^{+},{\theta }_2^{-}{\theta }_2^{+},\dots ,{\theta }_n^{-}{\theta }_n^{+}),\\ {\mathrm{\Theta }}_2=diag(-\frac{{\theta }_1^{-}+{\theta }_1^{+}}{2},-\frac{{\theta }_2^{-}+{\theta }_2^{+}}{2},\dots ,-\frac{{\theta }_n^{-}+{\theta }_n^{+}}{2}),\end{array}$$

(19)

$${\mathrm{\Upsilon }}_1=diag({\iota }_1^{-}{\iota }_1^{+},{\iota }_2^{-}{\iota }_2^{+},\dots ,{\iota }_n^{-}{\iota }_n^{+}),{\mathrm{\Upsilon }}_2=diag(-\frac{{\iota }_1^{-}+{\iota }_1^{+}}{2},-\frac{{\iota }_2^{-}+{\iota }_2^{+}}{2},\dots ,-\frac{{\iota }_n^{-}+{\iota }_n^{+}}{2}),$$

(20)

$$\begin{array}{r}{\mathrm{\Sigma }}_1=diag({\delta }_1^{-}{\delta }_1^{+},{\delta }_2^{-}{\delta }_2^{+},\dots ,{\delta }_n^{-}{\delta }_n^{+}),\\ {\mathrm{\Sigma }}_2=diag(-\frac{{\delta }_1^{-}+{\delta }_1^{+}}{2},-\frac{{\delta }_2^{-}+{\delta }_2^{+}}{2},\dots ,-\frac{{\delta }_n^{-}+{\delta }_n^{+}}{2}).\end{array}$$

(21)

Then, along the same line as with [21, 23], from Assumption 2, we can easily get, for $i=1,2,\dots ,n$,

$$\begin{array}{c}{(f(e(k))-{\theta }_i^{-}e(k))}^T(f(e(k))-{\theta }_i^{+}e(k))⩽0,\hfill \\ {(g\left(e(k-\tau (k))\right)-{\iota }_i^{-}e(k-\tau (k)))}^T(g\left(e(k-\tau (k))\right)-{\iota }_i^{+}e(k-\tau (k)))⩽0,\hfill \\ {(h(e(k))-{\delta }_i^{-}e(k))}^T(f(e(k))-{\delta }_i^{+}e(k))⩽0,\hfill \end{array}$$

which are equivalent to

$${\left[\begin{array}{c}e(k)\\ f(e(k))\end{array}\right]}^T\left[\begin{array}{cc}{\theta }_i^{-}{\theta }_i^{+}{e}_i{e}_i^T& -\frac{{\theta }_i^{-}+{\theta }_i^{+}}{2}{e}_i{e}_i^T\\ -\frac{{\theta }_i^{-}+{\theta }_i^{+}}{2}{e}_i{e}_i^T& e_i{e}_i^T\end{array}\right]\left[\begin{array}{c}e(k)\\ f(e(k))\end{array}\right]⩽0,$$

(22)

$${\left[\begin{array}{c}e(k-\tau (k))\\ g(e(k-\tau (k)))\end{array}\right]}^T\left[\begin{array}{cc}{\iota }_i^{-}{\iota }_i^{+}{e}_i{e}_i^T& -\frac{{\iota }_i^{-}+{\iota }_i^{+}}{2}{e}_i{e}_i^T\\ -\frac{{\iota }_i^{-}+{\iota }_i^{+}}{2}{e}_i{e}_i^T& e_i{e}_i^T\end{array}\right]\left[\begin{array}{c}e(k-\tau (k))\\ g(e(k-\tau (k)))\end{array}\right]⩽0,$$

(23)

$${\left[\begin{array}{c}e(k)\\ h(e(k))\end{array}\right]}^T\left[\begin{array}{cc}{\delta }_i^{-}{\delta }_i^{+}{e}_i{e}_i^T& -\frac{{\delta }_i^{-}+{\delta }_i^{+}}{2}{e}_i{e}_i^T\\ -\frac{{\delta }_i^{-}+{\delta }_i^{+}}{2}{e}_i{e}_i^T& e_i{e}_i^T\end{array}\right]\left[\begin{array}{c}e(k)\\ h(e(k))\end{array}\right]⩽0,$$

(24)

where $i=1,2,\dots ,n$ and $e_i$ represents the unit column vector having ‘1’ as the element on its i th row and zeros elsewhere.

Multiplying both sides of (22), (23), and (24) by ${\lambda }_i$, ${\gamma }_i$, and ${\nu }_i$, respectively, and summing up from 1 to n with respect to i, it will follow that

$${\left[\begin{array}{c}e(k)\\ f(e(k))\end{array}\right]}^T\left[\begin{array}{cc}\mathrm{\Lambda }{\mathrm{\Theta }}_1& \mathrm{\Lambda }{\mathrm{\Theta }}_2\\ \mathrm{\Lambda }{\mathrm{\Theta }}_2& \mathrm{\Lambda }\end{array}\right]\left[\begin{array}{c}e(k)\\ f(e(k))\end{array}\right]⩽0,$$

(25)

$${\left[\begin{array}{c}e(k-\tau (k))\\ g(e(k-\tau (k)))\end{array}\right]}^T\left[\begin{array}{cc}\mathrm{\Gamma }{\mathrm{\Upsilon }}_1& \mathrm{\Gamma }{\mathrm{\Upsilon }}_2\\ \mathrm{\Gamma }{\mathrm{\Upsilon }}_2& \mathrm{\Gamma }\end{array}\right]\left[\begin{array}{c}e(k-\tau (k))\\ g(e(k-\tau (k)))\end{array}\right]⩽0,$$

(26)

$${\left[\begin{array}{c}e(k)\\ h(e(k))\end{array}\right]}^T\left[\begin{array}{cc}\mathrm{\Xi }{\mathrm{\Sigma }}_1& \mathrm{\Xi }{\mathrm{\Sigma }}_2\\ \mathrm{\Xi }{\mathrm{\Sigma }}_2& \mathrm{\Xi }\end{array}\right]\left[\begin{array}{c}e(k)\\ h(e(k))\end{array}\right]⩽0.$$

(27)

The main results are as follows.

Theorem 1 Under Assumptions 1 and 2, the discrete-time neural networks (1) and (9) are globally robustly asymptotically synchronized in the mean square if there exist three positive definite matrices P, Q, and R, three diagonal matrices $\mathrm{\Lambda }=diag\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}>0$, $\mathrm{\Gamma }=diag\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\}>0$, and $\mathrm{\Xi }=diag\{{\nu }_1,{\nu }_2,\dots ,{\nu }_n\}>0$, and two scalars ${\lambda }^{\ast }>0$ and $\mu >0$ such that the following LMIs hold:

$$P<{\lambda }^{\ast }{E}_n,$$

(28)

and

$$\mathrm{\Phi }:=\left[\begin{array}{ccccccccc}{\mathrm{\Pi }}_1& \mu W_1^T{W}_2& 0& {\mathrm{\Omega }}_1& \mu W_1^T{W}_4& -\mathrm{\Xi }{\mathrm{\Sigma }}_2& \mu W_1^T{W}_5& {(G+A)}^{T}P& 0\\ \ast & {\mathrm{\Pi }}_2& 0& \mu W_2^T{W}_3& {\mathrm{\Omega }}_2& 0& \mu W_2^T{W}_5& {(G_{\tau }+\tilde{A})}^{T}P& 0\\ \ast & \ast & 0& 0& 0& 0& 0& G_z^{T}P& 0\\ \ast & \ast & \ast & {\mathrm{\Pi }}_3& \mu W_3^T{W}_4& 0& \mu W_3^T{W}_5& B^{T}P& 0\\ \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_4& 0& \mu W_4^T{W}_5& {\tilde{B}}^{T}P& 0\\ \ast & \ast & \ast \ast & \ast & {\mathrm{\Pi }}_5& 0& 0& 0\\ \ast & \ast & \ast \ast & \ast & \ast & {\mathrm{\Pi }}_6& C^{T}P& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -P& PM\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & -\mu E_n\end{array}\right]<0,$$

(29)

where

$$\begin{array}{r}{\mathrm{\Pi }}_1=-P+({\tau }_M-{\tau }_m+1)Q+{\lambda }^{\ast }{\rho }_1{E}_n-\mathrm{\Lambda }{\mathrm{\Theta }}_1-\mathrm{\Xi }{\mathrm{\Sigma }}_1+\mu W_1^T{W}_1,\\ {\mathrm{\Pi }}_2=-Q+{\lambda }^{\ast }{\rho }_2{E}_n-\mathrm{\Gamma }{\mathrm{\Upsilon }}_1+\mu W_2^T{W}_2,\\ {\mathrm{\Pi }}_3=-\mathrm{\Lambda }+\mu W_3^T{W}_3,{\mathrm{\Pi }}_4=-\mathrm{\Gamma }+\mu W_4^T{W}_4,\\ {\mathrm{\Pi }}_5=-\mathrm{\Xi }+{\tau }_M({\tau }_M-{\tau }_m+1)R,{\mathrm{\Pi }}_6=-\frac{1}{{\tau }_M}R+\mu W_5^T{W}_5,\\ {\mathrm{\Omega }}_1=-\mathrm{\Lambda }{\mathrm{\Theta }}_2+\mu W_1^T{W}_3{\mathrm{\Omega }}_2=-\mathrm{\Gamma }{\mathrm{\Upsilon }}_2+\mu W_2^T{W}_4.\end{array}$$

(30)

Proof To verify that the neural networks (1) and (9) are globally asymptotically synchronized in the mean square, a Lyapunov-Krasovskii function V is defined as follows:

$$V(k)=V_1(k)+V_2(k)+V_3(k)+V_4(k)+V_5(k),$$

(31)

where

$$V_1(k)=e^T(k)Pe(k),$$

(32)

$$V_2(k)=\sum _{i=k-\tau (k)}^{k-1}{e}^T(i)Qe(i),$$

(33)

$$V_3(k)=\sum _{j={\tau }_m+1}^{{\tau }_M}\sum _{i=k-j+1}^{k-1}{e}^T(i)Qe(i),$$

(34)

$$V_4(k)=\sum _{j=1}^{\tau (k)}\sum _{i=k-j}^{k-1}{h}^T(e(i))Rh(e(i)),$$

(35)

$$V_5(k)=\sum _{s={\tau }_M+1}^{{\tau }_M}\sum _{j=k-{\tau }_m+1}^{k-1}\sum _{i=j}^{k-1}{h}^T(e(i))Qh(e(i)).$$

(36)

Calculating the difference of $V(k)$ along the trajectory of the model (18) and taking the mathematical expectation, one obtains

$$\mathbb{E}\{\mathrm{\Delta }V(k)\}=\mathbb{E}\{\mathrm{\Delta }{V}_1(k)\}+\mathbb{E}\{\mathrm{\Delta }{V}_2(k)\}+\mathbb{E}\{\mathrm{\Delta }{V}_3(k)\}+\mathbb{E}\{\mathrm{\Delta }{V}_4(k)\},$$

(37)

where

$$\begin{array}{r}\mathbb{E}\{\mathrm{\Delta }{V}_1(k)\}\\ =\mathbb{E}\{V_1(k+1)-V_1(k)\}\\ =\mathbb{E}\left\{\right[A(k)e(k)+\tilde{A}(k)e(k-\tau (k))+B(k)f(e(k))\\ {+\tilde{B}(k)g\left(e(k-\tau (k))\right)+G_z\sum _{s=1}^{\tau (k)}e(k-s)+C(k)\sum _{s=1}^{\tau (k)}h(e(k-s))]}^T\\ \times P[A(k)e(k)+\tilde{A}(k)e(k-\tau (k))+B(k)f(e(k))\\ +\tilde{B}(k)g\left(e(k-\tau (k))\right)+G_z\sum _{s=1}^{\tau (k)}e(k-s)+C(k)\sum _{s=1}^{\tau (k)}h(e(k-s))]\\ +{\sigma }^T(k,e(k),e(k-\tau (k)))P\sigma (k,e(k),e(k-\tau (k)))-e^T(k)Pe(k)\},\end{array}$$

(38)

$$\begin{array}{r}\mathbb{E}\{\mathrm{\Delta }{V}_2(k)\}\\ =\mathbb{E}\{V_2(k+1)-V_2(k)\}\\ =\mathbb{E}\{\sum _{i=k+1-\tau (k+1)}^k{e}^T(i)Qe(i)-\sum _{i=k-\tau (k)}^{k-1}{e}^T(i)Qe(i)\}\\ =\mathbb{E}\{e^T(k)Qe(k)-e^T(k-\tau (k))Qe(k-\tau (k))+\sum _{i=k+1-\tau (k+1)}^{k-1}{e}^T(i)Qe(i)\\ -\sum _{i=k+1-\tau (k)}^{k-1}{e}^T(i)Qe(i)\}\\ =\mathbb{E}\{e^T(k)Qe(k)-e^T(k-\tau (k))Qe(k-\tau (k))+\sum _{i=k+1-{\tau }_m}^{k-1}{e}^T(i)Qe(i)\\ +\sum _{i=k+1-\tau (k+1)}^{k-{\tau }_m}{e}^T(i)Qe(i)-\sum _{i=k+1-\tau (k)}^{k-1}{e}^T(i)Qe(i)\}\\ ⩽\mathbb{E}\{e^T(k)Qe(k)-e^T(k-\tau (k))Qe(k-\tau (k))+\sum _{i=k-{\tau }_M+1}^{k-{\tau }_m}{e}^T(i)Qe(i)\},\end{array}$$

(39)

$$\begin{array}{r}\mathbb{E}\{\mathrm{\Delta }{V}_3(k)\}\\ =\mathbb{E}\{V_3(k+1)-V_3(k)\}\\ =\mathbb{E}\{\sum _{j={\tau }_m+1}^{{\tau }_M}\sum _{i=k-j+2}^k{e}^T(i)Qe(i)-\sum _{j={\tau }_m+1}^{{\tau }_M}\sum _{i=k-j+1}^{k-1}{e}^T(i)Qe(i)\}\\ =\mathbb{E}\left\{\sum _{j={\tau }_m+1}^{{\tau }_M}[e^T(k)Qe(k)-e^T(k-j+1)Qe(k-j+1)]\right\}\\ =\mathbb{E}\{({\tau }_M-{\tau }_m)e^T(k)Qe(k)-\sum _{i={\tau }_m+1}^{{\tau }_M}{e}^T(k-i+1)Qe(k-i+1)\}\\ =\mathbb{E}\{({\tau }_M-{\tau }_m)e^T(k)Qe(k)-\sum _{i=k-{\tau }_M+1}^{k-{\tau }_m}{e}^T(i)Qe(i)\},\end{array}$$

(40)

$$\begin{array}{r}\mathbb{E}\{\mathrm{\Delta }{V}_4(k)\}\\ =\mathbb{E}\{V_4(k+1)-V_4(k)\}\\ =\mathbb{E}\{\sum _{j=1}^{\tau (k+1)}\sum _{i=k-j+1}^k{h}^T(e(i))Rh(e(i))-\sum _{j=1}^{\tau (k)}\sum _{i=k-j}^{k-1}{h}^T(e(i))Rh(e(i))\}\\ ⩽\mathbb{E}\{\sum _{j=1}^{{\tau }_M}\sum _{i=k-j+1}^k{h}^T(e(i))Rh(e(i))-\sum _{j=1}^{\tau (k)}\sum _{i=k-j}^{k-1}{h}^T(e(i))Rh(e(i))\}\\ ⩽\mathbb{E}\{\sum _{j=1}^{{\tau }_M}{h}^T(e(k))Rh(e(k))+\sum _{j={\tau }_m+1}^{{\tau }_M}\sum _{i=k-j+1}^{k-1}{h}^T(e(i))Rh(e(i))\\ -\sum _{j=1}^{\tau (k)}{h}^T(e(k-j))Rh(e(k-j))\}\\ ⩽\mathbb{E}\{{\tau }_M{h}^T(e(k))Rh(e(k))+\sum _{j={\tau }_m+1}^{{\tau }_M}\sum _{i=k-{\tau }_M+1}^{k-1}{h}^T(e(i))Rh(e(i))\\ -\frac{1}{{\tau }_M}{\left(\sum _{j=1}^{\tau (k)}h(e(k-j))\right)}^{T}R\left(\sum _{j=1}^{\tau (k)}h(e(k-j))\right)\},\end{array}$$

(41)

and

$$\begin{array}{r}\mathbb{E}\{\mathrm{\Delta }{V}_5(k)\}\\ =\mathbb{E}\{V_3(k+1)-V_3(k)\}\\ =\mathbb{E}\{\sum _{s={\tau }_m+1}^{{\tau }_M}\sum _{j=k-{\tau }_M+2}^k\sum _{i=j}^k{h}^T(e(i))Rh(e(i))\\ -\sum _{s={\tau }_m+1}^{{\tau }_M}\sum _{j=k-{\tau }_M+1}^{k-1}\sum _{i=j}^{k-1}{h}^T(e(i))Rh(e(i))\}\\ =\mathbb{E}\{\sum _{s={\tau }_m+1}^{{\tau }_M}\sum _{j=k-{\tau }_M+1}^k\sum _{i=j+1}^k{h}^T(e(i))Rh(e(i))-\sum _{s={\tau }_m+1}^{{\tau }_M}\sum _{j=k-{\tau }_M+1}^{k-1}\sum _{i=j}^{k-1}{h}^T(e(i))Rh(e(i))\}\\ =\mathbb{E}\left\{\sum _{j={\tau }_m+1}^{{\tau }_M}\sum _{i=k-{\tau }_M+1}^{k-1}[h^T(e(k))Rh(e(k))-h^T(e(i))Rh(e(i))]\right\}\\ =\mathbb{E}\{{\tau }_M({\tau }_M-{\tau }_m)h^T(e(k))Rh(e(k))-\sum _{j={\tau }_m+1}^{{\tau }_M}\sum _{i=k-{\tau }_M+1}^{k-1}{h}^T(e(i))Rh(e(i))\}.\end{array}$$

(42)

The above inequality (41) results by Lemma 3.

On the other hand, from (11) and (28), we have

$$\begin{array}{r}{\sigma }^T(k,e(k),e(k-\tau (k)))P\sigma (k,e(k),e(k-\tau (k)))\\ ⩽{\lambda }_{max}(P){\sigma }^T(k,e(k),e(k-\tau (k)))\sigma (k,e(k),e(k-\tau (k)))\\ ⩽{\lambda }^{\ast }({\rho }_1{e}^T(k)e(k)+{\rho }_2{e}^T(k-\tau (k))e(k-\tau (k))).\end{array}$$

(43)

Substituting (38)-(43) into (37) yields

$$\mathbb{E}\{\mathrm{\Delta }V(k)\}⩽\mathbb{E}\{{\eta }^T(k){\mathrm{\Phi }}_1\eta (k)+{\eta }^T(k){\mathfrak{L}}^T(k)P\mathfrak{L}(k)\eta (k)\},$$

(44)

where

$$\begin{array}{r}\begin{array}{rl}\eta (k)=& [e^T(k),e^T(k-\tau (k)),{(\sum _{j=1}^{\tau (k)}e(k-j))}^T,f^T(e(k)),\\ {g^T\left(e(k-\tau (k))\right),h^T(e(k)),{\left(\sum _{j=1}^{\tau (k)}h(e(k-j))\right)}^T]}^T,\end{array}\\ \mathfrak{L}(k)=[A(k),\tilde{A}(k),G_z,B(k),\tilde{B}(k),0,C(k)],\\ {\mathrm{\Phi }}_1=\left[\begin{array}{ccccccc}{\hat{\mathrm{\Pi }}}_1& 0& 0& 0& 0& 0& 0\\ \ast & {\hat{\mathrm{\Pi }}}_2& 0& 0& 0& 0& 0\\ \ast & \ast & 0& 0& 0& 0& 0\\ \ast & \ast & \ast & 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\hat{\mathrm{\Pi }}}_3& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -\frac{1}{{\tau }_M}R\end{array}\right],\end{array}$$

with ${\hat{\mathrm{\Pi }}}_1=-P+({\tau }_M-{\tau }_m+1)Q+{\lambda }^{\ast }{\rho }_1{E}_n$, ${\hat{\mathrm{\Pi }}}_2=-Q+{\lambda }^{\ast }{\rho }_2{E}_n$, ${\hat{\mathrm{\Pi }}}_3={\tau }_M({\tau }_M-{\tau }_m+1)R$.

From (25), (26), and (27), it follows that

$$\begin{array}{r}\mathbb{E}\{\mathrm{\Delta }V(k)\}\\ ⩽\mathbb{E}\{{\eta }^T(k){\mathrm{\Phi }}_1\eta (k)+{\eta }^T(k){\mathfrak{L}}^T(k)P\mathfrak{L}(k)\eta (k)\\ -{\left[\begin{array}{c}e(k)\\ f(e(k))\end{array}\right]}^T\left[\begin{array}{cc}\mathrm{\Lambda }{\mathrm{\Theta }}_1& \mathrm{\Lambda }{\mathrm{\Theta }}_2\\ \mathrm{\Lambda }{\mathrm{\Theta }}_2& \mathrm{\Lambda }\end{array}\right]\left[\begin{array}{c}e(k)\\ f(e(k))\end{array}\right]-{\left[\begin{array}{c}e(k)\\ h(e(k))\end{array}\right]}^T\left[\begin{array}{cc}\mathrm{\Xi }{\mathrm{\Sigma }}_1& \mathrm{\Xi }{\mathrm{\Sigma }}_2\\ \mathrm{\Xi }{\mathrm{\Sigma }}_2& \mathrm{\Xi }\end{array}\right]\left[\begin{array}{c}e(k)\\ h(e(k))\end{array}\right]\\ -{\left[\begin{array}{c}e(k-\tau (k))\\ g(e(k-\tau (k)))\end{array}\right]}^T\left[\begin{array}{cc}\mathrm{\Gamma }{\mathrm{\Upsilon }}_1& \mathrm{\Gamma }{\mathrm{\Upsilon }}_2\\ \mathrm{\Gamma }{\mathrm{\Upsilon }}_2& \mathrm{\Gamma }\end{array}\right]\left[\begin{array}{c}e(k-\tau (k))\\ g(e(k-\tau (k)))\end{array}\right]\}\\ =\mathbb{E}\{{\eta }^T(k)[{\mathrm{\Phi }}_2+{\mathfrak{L}}^T(k)P\mathfrak{L}(k)]\eta (k)\},\end{array}$$

(45)

where

$${\mathrm{\Phi }}_2=\left[\begin{array}{ccccccc}{\varkappa }_1& 0& 0& -\mathrm{\Lambda }{\mathrm{\Theta }}_2& 0& -\mathrm{\Xi }{\mathrm{\Sigma }}_2& 0\\ \ast & {\varkappa }_2& 0& 0& -\mathrm{\Gamma }{\mathrm{\Upsilon }}_2& 0& 0\\ \ast & \ast & 0& 0& 0& 0& 0\\ \ast & \ast & \ast & -\mathrm{\Lambda }& 0& 0& 0\\ \ast & \ast & \ast & \ast & -\mathrm{\Gamma }& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\varkappa }_3& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -\frac{1}{{\tau }_M}R\end{array}\right]$$

with ${\varkappa }_1=-P+({\tau }_M-{\tau }_m+1)Q+{\lambda }^{\ast }{\rho }_1{E}_n-\mathrm{\Lambda }{\mathrm{\Theta }}_1-\mathrm{\Xi }{\mathrm{\Sigma }}_1$, ${\varkappa }_2=-Q+{\lambda }^{\ast }{\rho }_2{E}_n-\mathrm{\Gamma }{\mathrm{\Upsilon }}_1$, and ${\varkappa }_3=-\mathrm{\Xi }+{\tau }_M({\tau }_M-{\tau }_m+1)R$.

Denote

$${\hat{\mathrm{\Phi }}}_1(k)={\mathrm{\Phi }}_2+{\mathfrak{L}}^T(k)P\mathfrak{L}(k)={\mathrm{\Phi }}_3+\mathrm{\Delta }{\mathrm{\Phi }}_3(k),$$

(46)

where

$$\begin{array}{r}{\mathrm{\Phi }}_3=\left[\begin{array}{cccccccc}{\varkappa }_1& 0& 0& -\mathrm{\Lambda }{\mathrm{\Theta }}_2& 0& -\mathrm{\Xi }{\mathrm{\Sigma }}_2& 0& {(G+A)}^{T}P\\ \ast & {\varkappa }_2& 0& 0& -\mathrm{\Gamma }{\mathrm{\Upsilon }}_2& 0& 0& {(G_{\tau }+\tilde{A})}^{T}P\\ \ast & \ast & 0& 0& 0& 0& 0& G_z^{T}P\\ \ast & \ast & \ast & -\mathrm{\Lambda }& 0& 0& 0& B^{T}P\\ \ast & \ast & \ast & \ast & -\mathrm{\Gamma }& 0& 0& {\tilde{B}}^{T}P\\ \ast & \ast & \ast & \ast & \ast & {\varkappa }_3& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -\frac{1}{{\tau }_M}R& C^{T}P\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -P\end{array}\right],\\ \mathrm{\Delta }{\mathrm{\Phi }}_3(k)=\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& \mathrm{\Delta }{A}^T(k)P\\ \ast & 0& 0& 0& 0& 0& 0& \mathrm{\Delta }{\tilde{A}}^T(k)P\\ \ast & \ast & 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & 0& 0& 0& 0& \mathrm{\Delta }{B}^T(k)P\\ \ast & \ast & \ast & \ast & 0& 0& 0& \mathrm{\Delta }{\tilde{B}}^T(k)P\\ \ast & \ast & \ast & \ast & \ast & 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & 0& \mathrm{\Delta }{C}^T(k)P\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & 0\end{array}\right].\end{array}$$

(47)

Let

$$\begin{array}{r}\mathcal{P}={[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& P\end{array}]}^T,\\ \mathcal{L}(k)=\left[\begin{array}{cccccccc}\mathrm{\Delta }{A}^T(k)& \mathrm{\Delta }{\tilde{A}}^T(k)& 0& \mathrm{\Delta }{B}^T(k)& \mathrm{\Delta }{\tilde{B}}^T(k)& 0& \mathrm{\Delta }{C}^T(k)& 0\end{array}\right],\\ \mathcal{W}=[\begin{array}{cccccccc}{W}_1& W_2& 0& W_3& W_4& 0& W_5& 0\end{array}].\end{array}$$

It follows easily from (6) and Lemma 1 that

$$\begin{array}{rl}\mathrm{\Delta }{\mathrm{\Phi }}_3(k)& =\mathcal{P}\mathcal{L}(k)+{\mathcal{L}}^T(k){\mathcal{P}}^T\\ =\mathcal{P}MH(k)\mathcal{W}+{\mathcal{W}}^T{H}^T(k)M^T{\mathcal{P}}^T\\ ⩽\mu {\mathcal{W}}^T\mathcal{W}+{\mu }^{-1}\mathcal{P}M{M}^T{\mathcal{P}}^T.\end{array}$$

(48)

Substituting (47) and (48) into (46), one obtains

$${\hat{\mathrm{\Phi }}}_1(k)⩽{\hat{\mathrm{\Phi }}}_2(k)+{\mu }^{-1}\mathcal{P}M{M}^T{\mathcal{P}}^T,$$

(49)

where

$${\hat{\mathrm{\Phi }}}_2(k)=\left[\begin{array}{cccccccc}{\mathrm{\Pi }}_1& \mu W_1^T{W}_2& 0& {\mathrm{\Omega }}_1& \mu W_1^T{W}_4& -\mathrm{\Xi }{\mathrm{\Sigma }}_2& \mu W_1^T{W}_5& {(G+A)}^{T}P\\ \ast & {\mathrm{\Pi }}_2& 0& \mu W_2^T{W}_3& {\mathrm{\Omega }}_2& 0& \mu W_2^T{W}_5& {(G_{\tau }+\tilde{A})}^{T}P\\ \ast & \ast & 0& 0& 0& 0& 0& G_z^{T}P\\ \ast & \ast & \ast & {\mathrm{\Pi }}_3& \mu W_3^T{W}_4& 0& \mu W_3^T{W}_5& B^{T}P\\ \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_4& 0& \mu W_4^T{W}_5& {\tilde{B}}^{T}P\\ \ast & \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_5& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_6& C^{T}P\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -P\end{array}\right],$$

and ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$, ${\mathrm{\Pi }}_3$, ${\mathrm{\Pi }}_4$, ${\mathrm{\Pi }}_5$, ${\mathrm{\Pi }}_6$, ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ are defined in (30).

By Lemma 2, we have

$${\hat{\mathrm{\Phi }}}_2(k)+{\mu }^{-1}\mathcal{P}M{M}^T{\mathcal{P}}^T=\mathrm{\Phi }.$$

(50)

Therefore, it is not difficult from (29), (45), (46), (49), and (50) to get

$$\mathbb{E}\{\mathrm{\Delta }V(k)\}⩽\mathbb{E}\{{\eta }^T(k)\mathrm{\Phi }\eta (k)\}⩽{\lambda }_{max}(\mathrm{\Phi })\mathbb{E}\left\{{|e(k)|}^2\right\},$$

(51)

with ${\lambda }_{max}(\mathrm{\Phi })<0$.

Let N be a positive integer. Summing up both sides of (51) from 1 to N with respect to k, it easily follows that

$$\mathbb{E}\{V(N)-V(0)\}⩽{\lambda }_{max}(\mathrm{\Phi })\sum _{k=1}^N\mathbb{E}\left\{{|e(k)|}^2\right\},$$

which implies that

$$-{\lambda }_{max}(\mathrm{\Phi })\sum _{k=1}^N\mathbb{E}\left\{{|e(k)|}^2\right\}⩽\mathbb{E}\{V(0)\}.$$

By letting $N\to +\mathrm{\infty }$, it can be seen that the series ${\sum }_{k=1}^{+\mathrm{\infty }}\mathbb{E}\{{|e(k)|}^2\}$ is convergent, and therefore we have

$$\underset{k\to +\mathrm{\infty }}{lim}\mathbb{E}\left\{|e(k)|\right\}=\underset{k\to +\mathrm{\infty }}{lim}\mathbb{E}\left\{|y(k)-x(k)|\right\}=0.$$

According to Definition 1, it can be deduced that the master system (1) and the slave system (9) are globally robustly asymptotically synchronized in the mean square, and the proof is then completed. □

In the following, we will consider four special cases. Firstly, we can consider a state-feedback controller $u(k)=Ge(k)+G_{\tau }e(k-\tau (k))$, and the slave system model (9) can then be rewritten to

$$\begin{array}{rcl}y(k+1)& =& (A+\mathrm{\Delta }A(k))y(k)+(\tilde{A}+\mathrm{\Delta }\tilde{A}(k))y(k-\tau (k))+(B+\mathrm{\Delta }B(k))\tilde{f}(y(k))\\ +(\tilde{B}+\mathrm{\Delta }\tilde{B}(k))\tilde{g}\left(y(k-\tau (k))\right)+(C+\mathrm{\Delta }C(k))\sum _{s=1}^{\tau (k)}\tilde{h}(y(k-s))+I(k),\\ +Ge(k)+G_{\tau }e(k-\tau (k))+\sigma (k,e(k),e(k-\tau (k)))\omega (k).\end{array}$$

(52)

Corollary 1 Under Assumptions 1 and 2, the discrete-time neural networks (1) and (52) are globally robustly asymptotically synchronized in the mean square if there exist three positive definite matrices P, Q, and R, three diagonal matrices $\mathrm{\Lambda }=diag\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}>0$, $\mathrm{\Gamma }=diag\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\}>0$, and $\mathrm{\Xi }=diag\{{\nu }_1,{\nu }_2,\dots ,{\nu }_n\}>0$, and two scalars ${\lambda }^{\ast }>0$ and $\mu >0$ such that the following LMIs hold:

$$P<{\lambda }^{\ast }{E}_n,$$

(53)

and

$$\left[\begin{array}{cccccccc}{\mathrm{\Pi }}_1& \mu W_1^T{W}_2& {\mathrm{\Omega }}_1& \mu W_1^T{W}_4& -\mathrm{\Xi }{\mathrm{\Sigma }}_2& \mu W_1^T{W}_5& {(G+A)}^{T}P& 0\\ \ast & {\mathrm{\Pi }}_2& \mu W_2^T{W}_3& {\mathrm{\Omega }}_2& 0& \mu W_2^T{W}_5& {(\tilde{A}+G_{\tau })}^{T}P& 0\\ \ast & \ast & {\mathrm{\Pi }}_3& \mu W_3^T{W}_4& 0& \mu W_3^T{W}_5& B^{T}P& 0\\ \ast & \ast & \ast & {\mathrm{\Pi }}_4& 0& \mu W_4^T{W}_5& {\tilde{B}}^{T}P& 0\\ \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_5& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_6& C^{T}P& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -P& PM\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -\mu E_n\end{array}\right]<0,$$

(54)

where ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$, ${\mathrm{\Pi }}_3$, ${\mathrm{\Pi }}_4$, ${\mathrm{\Pi }}_5$, ${\mathrm{\Pi }}_6$, ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ are defined in (30).

This corollary is very easily accessible from Theorem 1.

Secondly, if the considered model is without stochastic disturbance, the response system (9) will be specialized to

$$\begin{array}{rcl}y(k+1)& =& (A+\mathrm{\Delta }A(k))y(k)+(\tilde{A}+\mathrm{\Delta }\tilde{A}(k))y(k-\tau (k))+(B+\mathrm{\Delta }B(k))\tilde{f}(y(k))\\ +(\tilde{B}+\mathrm{\Delta }\tilde{B}(k))\tilde{g}\left(y(k-\tau (k))\right)+(C+\mathrm{\Delta }C(k))\sum _{s=1}^{\tau (k)}\tilde{h}(y(k-s))+I(k)\\ +Ge(k)+G_{\tau }e(k-\tau (k))+G_z\sum _{s=1}^{\tau (k)}e(k-s).\end{array}$$

(55)

Corollary 2 Under Assumptions 1 and 2, the discrete-time neural networks (1) and (55) are globally robustly asymptotically synchronized if there exist three positive definite matrices P, Q, and R, three diagonal matrices $\mathrm{\Lambda }=diag\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}>0$, $\mathrm{\Gamma }=diag\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\}>0$, and $\mathrm{\Xi }=diag\{{\nu }_1,{\nu }_2,\dots ,{\nu }_n\}>0$, and two scalars ${\lambda }^{\ast }>0$ and $\mu >0$ such that the following LMIs hold:

$$P<{\lambda }^{\ast }{E}_n,$$

(56)

and

$$\left[\begin{array}{ccccccccc}{\tilde{\mathrm{\Pi }}}_1& \mu W_1^T{W}_2& 0& {\mathrm{\Omega }}_1& \mu W_1^T{W}_4& -\mathrm{\Xi }{\mathrm{\Sigma }}_2& \mu W_1^T{W}_5& {(G+A)}^{T}P& 0\\ \ast & {\tilde{\mathrm{\Pi }}}_2& 0& \mu W_2^T{W}_3& {\mathrm{\Omega }}_2& 0& \mu W_2^T{W}_5& {(G_{\tau }+\tilde{A})}^{T}P& 0\\ \ast & \ast & 0& 0& 0& 0& 0& G_z^{T}P& 0\\ \ast & \ast & \ast & {\mathrm{\Pi }}_3& \mu W_3^T{W}_4& 0& \mu W_3^T{W}_5& B^{T}P& 0\\ \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_4& 0& \mu W_4^T{W}_5& {\tilde{B}}^{T}P& 0\\ \ast & \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_5& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_6& C^{T}P& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -P& PM\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & -\mu E_n\end{array}\right]<0,$$

(57)

where ${\tilde{\mathrm{\Pi }}}_1=-P+({\tau }_M-{\tau }_m+1)Q-\mathrm{\Lambda }{\mathrm{\Theta }}_1-\mathrm{\Xi }{\mathrm{\Sigma }}_1+\mu W_1^T{W}_1$, ${\tilde{\mathrm{\Pi }}}_2=-Q-\mathrm{\Gamma }{\mathrm{\Upsilon }}_1+\mu W_2^T{W}_2$, and ${\mathrm{\Pi }}_3$, ${\mathrm{\Pi }}_4$, ${\mathrm{\Pi }}_5$, ${\mathrm{\Pi }}_6$, ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ are defined in (30).

Thirdly, let us consider the uncertainty-free case, that is, there are no parameter uncertainties in the models. Then the master system (1) and the response system (9) can be reduced, respectively, to the following models:

$$\begin{array}{rcl}x(k+1)& =& Ax(k)+\tilde{A}x(k-\tau (k))+B\tilde{f}(x(k))\\ +\tilde{B}\tilde{g}\left(x(k-\tau (k))\right)+C\sum _{s=1}^{\tau (k)}\tilde{h}(x(k-s))+I(k)\end{array}$$

(58)

and

$$\begin{array}{rcl}y(k+1)& =& Ay(k)+\tilde{A}y(k-\tau (k))+B\tilde{f}(y(k))+\tilde{B}\tilde{g}\left(y(k-\tau (k))\right)\\ +C\sum _{s=1}^{\tau (k)}\tilde{h}(y(k-s))+I(k)+Ge(k)+G_{\tau }e(k-\tau (k))\\ +G_z\sum _{s=1}^{\tau (k)}e(k-s)+\sigma (k,e(k),e(k-\tau (k)))\omega (k).\end{array}$$

(59)

Corollary 3 Under Assumptions 1 and 2, the discrete-time neural network (58) and (59) are globally robustly asymptotically synchronized in the mean square if there exist three positive definite matrices P, Q, and R, three diagonal matrices $\mathrm{\Lambda }=diag\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}>0$, $\mathrm{\Gamma }=diag\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\}>0$, and $\mathrm{\Xi }=diag\{{\nu }_1,{\nu }_2,\dots ,{\nu }_n\}>0$, and a scalar ${\lambda }^{\ast }>0$ such that the following LMIs hold:

$$P<{\lambda }^{\ast }{E}_n,$$

(60)

and

$$\left[\begin{array}{cccccccc}{\mathrm{\Pi }}_1^{\ast }& 0& 0& -\mathrm{\Lambda }{\mathrm{\Theta }}_2& 0& -\mathrm{\Xi }{\mathrm{\Sigma }}_2& 0& {(G+A)}^{T}P\\ \ast & {\mathrm{\Pi }}_2^{\ast }& 0& 0& -\mathrm{\Gamma }{\mathrm{\Upsilon }}_2& 0& 0& {(G_{\tau }+\tilde{A})}^{T}P\\ \ast & \ast & 0& 0& 0& 0& 0& G_z^{T}P\\ \ast & \ast & \ast & -\mathrm{\Lambda }& 0& 0& 0& B^{T}P\\ \ast & \ast & \ast & \ast & -\mathrm{\Gamma }& 0& 0& {\tilde{B}}^{T}P\\ \ast & \ast & \ast & \ast & \ast & {\mathrm{\Pi }}_5& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -\frac{1}{{\tau }_M}R& C^{T}P\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -P\end{array}\right]<0,$$

(61)

with ${\mathrm{\Pi }}_1^{\ast }=-P+({\tau }_M-{\tau }_m+1)Q+{\lambda }^{\ast }{\rho }_1{E}_n-\mathrm{\Lambda }{\mathrm{\Theta }}_1-\mathrm{\Xi }{\mathrm{\Sigma }}_1$, ${\mathrm{\Pi }}_2^{\ast }=-Q+{\lambda }^{\ast }{\rho }_2{E}_n-\mathrm{\Gamma }{\mathrm{\Upsilon }}_1$, and ${\mathrm{\Pi }}_5$ is defined as (30).

Moreover, in this case, if the stochastic disturbance in the response system (59) is ${\sigma }_i(k,e(k),e(k-\tau (k)))=0$ ($i=1,2,\dots ,n$), then we need only rewrite ${\mathrm{\Pi }}_1^{\ast }$ and ${\mathrm{\Pi }}_2^{\ast }$ as ${\mathrm{\Pi }}_1^{\ast \ast }=-P+({\tau }_M-{\tau }_m+1)Q-\mathrm{\Lambda }{\mathrm{\Theta }}_1-\mathrm{\Xi }{\mathrm{\Sigma }}_1$ and ${\mathrm{\Pi }}_2^{\ast \ast }=-Q-\mathrm{\Gamma }{\mathrm{\Upsilon }}_1$, and the corollary will still be true.

The proofs of Corollary 2 and Corollary 3 are similar to that of Theorem 1 and are therefore omitted.

Finally, we consider the systems without the distributed delay influence. The master system (1) and the response system (9) will become, respectively, the following difference equations:

$$\begin{array}{rcl}x(k+1)& =& (A+\mathrm{\Delta }A(k))x(k)+(\tilde{A}+\mathrm{\Delta }\tilde{A}(k))x(k-\tau (k))+(B+\mathrm{\Delta }B(k))\tilde{f}(x(k))\\ +(\tilde{B}+\mathrm{\Delta }\tilde{B}(k))\tilde{g}\left(x(k-\tau (k))\right)+I(k)\end{array}$$

(62)

and

$$\begin{array}{rcl}y(k+1)& =& (A+\mathrm{\Delta }A(k))y(k)+(\tilde{A}+\mathrm{\Delta }\tilde{A}(k))y(k-\tau (k))+(B+\mathrm{\Delta }B(k))\tilde{f}(y(k))\\ +(\tilde{B}+\mathrm{\Delta }\tilde{B}(k))\tilde{g}\left(y(k-\tau (k))\right)+Ge(k)+G_{\tau }e(k-\tau (k))\\ +I(k)+\sigma (k,e(k),e(k-\tau (k)))\omega (k).\end{array}$$

(63)

Then the error system is

$$\begin{array}{rcl}e(k+1)& =& (G+A+\mathrm{\Delta }A(k))e(k)+(G_{\tau }+\tilde{A}+\mathrm{\Delta }\tilde{A}(k))e(k-\tau (k))\\ +(B+\mathrm{\Delta }B(k))f(e(k))+(\tilde{B}+\mathrm{\Delta }\tilde{B}(k))g\left(e(k-\tau (k))\right)\\ +Ge(k)+G_{\tau }e(k-\tau (k))+\sigma (k,e(k),e(k-\tau (k)))\omega (k).\end{array}$$

(64)

In this case, we will show that the neural networks (62) and (63) are not only globally, robustly, and asymptotically synchronized in the mean square, but also globally, robustly, and exponentially synchronized in the mean square. The definition of the globally robustly exponentially synchronization in the mean square is given firstly in the following.

Definition 2 Systems (62) and (63) are said to be globally exponentially synchronized in the mean square if all parameter uncertainties satisfy the admissible condition (6) and (7), and if there exist two constants $\beta >0$ and $0<\epsilon <1$, and a big enough positive integer N, such that the following inequality:

$$\mathbb{E}\left\{{|y(k)-x(k)|}^2\right\}⩽\beta {\epsilon }^k\underset{s\in \mathbb{N}[-{\tau }_M,0]}{max}\mathbb{E}\left\{{|\psi (s)-\varphi (s)|}^2\right\}$$

holds for $\phi (s)=\psi (s)-\varphi (s)\in L_{{\mathcal{F}}_0}^2(\mathbb{N}[-{\tau }_M,0],\mathbb{R})$ and all $k>N$.

Then we have the following theorem.

Theorem 2 Under Assumptions 1 and 2, the discrete-time neural networks (62) and (63) are globally robustly exponentially synchronized in the mean square if there exist two positive definite matrices P and Q, two diagonal matrices $\mathrm{\Lambda }=diag\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}>0$ and $\mathrm{\Gamma }=diag\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\}>0$, and two scalars ${\lambda }^{\ast }>0$ and $\mu >0$ such that the following LMIs hold:

$$P<{\lambda }^{\ast }{E}_n,$$

(65)

and

$$\mathrm{\Psi }:=\left[\begin{array}{cccccc}{\mathrm{\Pi }}_7& \mu W_1^T{W}_2& {\mathrm{\Omega }}_1& \mu W_1^T{W}_4& {(G+A)}^{T}P& 0\\ \ast & {\mathrm{\Pi }}_2& \mu W_2^T{W}_3& {\mathrm{\Omega }}_2& {(G_{\tau }+\tilde{A})}^{T}P& 0\\ \ast & \ast & {\mathrm{\Pi }}_3& \mu W_3^T{W}_4& B^{T}P& 0\\ \ast & \ast & \ast & {\mathrm{\Pi }}_4& {\tilde{B}}^{T}P& 0\\ \ast & \ast & \ast & \ast & -P& PM\\ \ast & \ast & \ast & \ast & \ast & -\mu E_n\end{array}\right]<0,$$

(66)

where ${\mathrm{\Pi }}_7=-P+({\tau }_M-{\tau }_m+1)Q+{\lambda }^{\ast }{\rho }_1{E}_n-\mathrm{\Lambda }{\mathrm{\Theta }}_1+\mu W_1^T{W}_1$ and ${\mathrm{\Pi }}_2$, ${\mathrm{\Pi }}_3$, ${\mathrm{\Pi }}_4$, ${\mathrm{\Pi }}_5$, ${\mathrm{\Pi }}_6$, ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ are defined in (30).

Proof A Lyapunov-Krasovskii function $V(k)$ is needed to guarantee that the neural networks (62) and (63) are globally exponentially synchronized in the mean square:

$$V(k)=V_1(k)+V_2(k)+V_3(k),$$

(67)

where $V_1(k)$, $V_2(k)$, and $V_3(k)$ are similar to (32), (33), and (34).

Then, along a similar line to the proof of Theorem 1, one can obtain

$$\mathbb{E}\{\mathrm{\Delta }V(k)\}⩽\mathbb{E}\{{\zeta }^T(k)\mathrm{\Psi }\zeta (k)\}⩽{\lambda }_{max}(\mathrm{\Psi })\mathbb{E}\left\{{|e(k)|}^2\right\},$$

(68)

where ${\lambda }_{max}(\mathrm{\Psi })<0$, and

$$\zeta (k)={[e^T(k),e^T(k-\tau (K)),f^T(e(k)),g^T\left(e(k-\tau (k))\right)]}^T.$$

Now, we are in a position to establish the robust global exponential stability in the mean square of the error system (64).

First, from the definition of function $V(k)$, it is easy to see that

$$\mathbb{E}\{V(k)\}⩽\mathbb{E}\{{\overline{\lambda }}_P{|e(k)|}^2+{\overline{\lambda }}_Q\sum _{i=k-{\tau }_M}^{k-1}{|e(i)|}^2\},$$

(69)

$$\mathbb{E}\{V(k)\}⩾{\lambda }_{min}(P)\mathbb{E}\left\{{|e(k)|}^2\right\},$$

(70)

where

$${\overline{\lambda }}_P={\lambda }_{max}(P),{\overline{\lambda }}_Q=({\tau }_M-{\tau }_m+1){\lambda }_{max}(Q).$$

For any $\epsilon >1$, inequalities (68) and (69) imply that

$$\begin{array}{rcl}\mathbb{E}\left\{\mathrm{\Delta }({\epsilon }^{k}V(k))\right\}& =& \mathbb{E}\{{\epsilon }^{k+1}V(k+1)-{\epsilon }^{k}V(k)\}=\mathbb{E}\{{\epsilon }^{k+1}\mathrm{\Delta }V(k)+{\epsilon }^k(\epsilon -1)V(k)\}\\ ⩽& \mathbb{E}\{{\omega }_1(\epsilon ){\epsilon }^k{|e(k)|}^2+{\omega }_2(\epsilon )\sum _{i=k-{\tau }_M}^{k-1}{\epsilon }^k{|e(i)|}^2\},\end{array}$$

(71)

where

$${\omega }_1(\epsilon )={\lambda }_{max}(\mathrm{\Psi })\epsilon +(\epsilon -1){\overline{\lambda }}_P,{\omega }_2(\epsilon )=(\epsilon -1){\overline{\lambda }}_Q.$$

Let N be a sufficient big positive integer satisfying $N>{\tau }_M+1$. Summing up both sides of the inequality (71) from 0 to $N-1$ with respect to k, one can obtain

$$\mathbb{E}\{{\epsilon }^{N}V(N)-V(0)\}⩽\mathbb{E}\{{\omega }_1(\epsilon )\sum _{k=0}^{N-1}{\epsilon }^k{|e(k)|}^2+{\omega }_2(\epsilon )\sum _{k=0}^{N-1}\sum _{i=k-{\tau }_M}^{k-1}{\epsilon }^k{|e(i)|}^2\},$$

(72)

while for ${\tau }_M⩾1$,

$$\begin{array}{rcl}\sum _{k=0}^{N-1}\sum _{i=k-{\tau }_M}^{k-1}{\epsilon }^k\mathbb{E}\left\{{|e(i)|}^2\right\}& ⩽& (\sum _{i=-{\tau }_M}^{-1}\sum _{k=0}^{i+{\tau }_M}+\sum _{i=0}^{N-{\tau }_M-1}\sum _{k=i+1}^{i+{\tau }_M}+\sum _{i=N-{\tau }_M}^{N-1}\sum _{k=i+1}^{N-1}){\epsilon }^k\mathbb{E}\left\{{|e(i)|}^2\right\}\\ ⩽& {\tau }_M\sum _{i=-{\tau }_M}^{-1}{\epsilon }^{i+{\tau }_M}\mathbb{E}\left\{{|e(i)|}^2\right\}+{\tau }_M\sum _{i=0}^{N-{\tau }_M-1}{\epsilon }^{i+{\tau }_M}\mathbb{E}\left\{{|e(i)|}^2\right\}\\ +{\tau }_M\sum _{i=N-{\tau }_M-1}^{N-1}{\epsilon }^{i+{\tau }_M}\mathbb{E}\left\{{|e(i)|}^2\right\}\\ ⩽& {\tau }_M^2{\epsilon }^{{\tau }_M}\underset{-{\tau }_M⩽i⩽0}{max}\mathbb{E}\left\{{|e(i)|}^2\right\}+{\tau }_M{\epsilon }^{{\tau }_M}\sum _{i=0}^{N-1}{\epsilon }^i\mathbb{E}\left\{{|e(i)|}^2\right\}.\end{array}$$

(73)

Then, it follows from (72) and (73) that

$$\begin{array}{rcl}{\epsilon }^N\mathbb{E}\{V(N)\}& ⩽& \mathbb{E}\{V(0)\}+{\omega }_2(\epsilon ){\tau }_M^2{\epsilon }^{{\tau }_M}\underset{-{\tau }_M⩽i⩽0}{max}\mathbb{E}\left\{{|e(i)|}^2\right\}\\ +[{\omega }_1(\epsilon )+{\omega }_2(\epsilon ){\tau }_M{\epsilon }^{{\tau }_M}]\sum _{i=0}^{N-1}{\epsilon }^i\mathbb{E}\left\{{|e(i)|}^2\right\}.\end{array}$$

(74)

Considering ${\omega }_1(1)={\lambda }_{max}(\mathrm{\Psi })<0$, ${\omega }_2(1)=0$, and ${\omega }_2(\epsilon )>0$ for $\epsilon >1$, it can be verified that there exists a scalar ${\epsilon }_0>1$ such that ${\omega }_1({\epsilon }_0)+{\omega }_2({\epsilon }_0){\tau }_M{\epsilon }_0^{{\tau }_M}=0$. So, it is not difficult to derive

$${\epsilon }_0^N\mathbb{E}\{V(N)\}⩽\mathbb{E}\{V(0)\}+{\omega }_2({\epsilon }_0){\tau }_M^2{\epsilon }_0^{{\tau }_M}\underset{-{\tau }_M⩽i⩽0}{max}\mathbb{E}\left\{{|e(i)|}^2\right\}.$$

(75)

On the other hand, it also follows easily from (69) that

$$\mathbb{E}\{V(0)\}⩽\vartheta \underset{-{\tau }_M⩽i⩽0}{max}\mathbb{E}\left\{{|e(i)|}^2\right\},$$

(76)

where $\vartheta =max\{{\overline{\lambda }}_P,{\overline{\lambda }}_Q\}$. Therefore, from (70), (75), and (76), one has

$$\mathbb{E}\left\{{|e(N)|}^2\right\}⩽\frac{1}{{\lambda }_{min}(P)}[\vartheta +{\omega }_2({\epsilon }_0){\tau }_M^2{\epsilon }_0^{{\tau }_M}]{\left(\frac{1}{{\epsilon }_0}\right)}^N\underset{-{\tau }_M⩽i⩽0}{max}\mathbb{E}\left\{{|e(i)|}^2\right\}.$$

According to Definition 2, this completes the proof. □

Remark 4 Based on the drive-response concept, synchronization problems of discrete-time neural networks are little investigated. To the best of our knowledge, for master-slave systems, the synchronization analysis problem for stochastic neural networks with parameter uncertainties, especially distributed delay, is for the first time discussed.

4 Numerical example

In this section, an example will be illustrated to show the feasibility of our results.

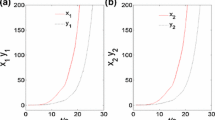
Example 1 Consider the drive system (1) and the response system (9) with the following parameters:

$$\begin{array}{r}A=\left[\begin{array}{ccc}0.6& 0& 0\\ 0& 0.2& 0\\ 0& 0& 0.4\end{array}\right],\tilde{A}=\left[\begin{array}{ccc}0.3& 0& 0\\ 0& 0.5& 0\\ 0& 0& -0.1\end{array}\right],B=\left[\begin{array}{ccc}0.4& -0.3& 0\\ 0.1& -0.2& -0.3\\ 0.2& 0& 0.1\end{array}\right],\\ \tilde{B}=\left[\begin{array}{ccc}0.5& 0& -0.2\\ 0.1& 0.2& 0.1\\ -0.1& 0.3& 0.2\end{array}\right],C=\left[\begin{array}{ccc}-0.2& 0.2& 0\\ 0.1& 0.2& -0.1\\ 0& 0.1& 0.2\end{array}\right],M=\left[\begin{array}{c}-0.1\\ 0.1\\ 0.2\end{array}\right],\\ \tilde{f}(x(k))=\tilde{g}(x(k))=\tilde{h}(x(k))=\left[\begin{array}{c}tanh(0.8x_1(k))\\ tanh(-0.4x_1(k))\\ tanh(0.6x_1(k))\end{array}\right],\\ W_1=W_3=W_4=W_5=[\begin{array}{ccc}-0.2& 0.1& 0.1\end{array}],W_2=[\begin{array}{ccc}0& 0& 0\end{array}],\\ \tau (k)=4+{(-1)}^k,d_k=2^{-k},{\rho }_1={\rho }_2=0.1,I(k)=0.\end{array}$$

Therefore, it can be derived that $d^{\ast }=1$, ${\tau }_m=3$, ${\tau }_M=5$, and the activation functions satisfy Assumption 2 with

$${\mathrm{\Theta }}_1={\mathrm{\Upsilon }}_1={\mathrm{\Sigma }}_1=diag\{0,0,0\},{\mathrm{\Theta }}_2={\mathrm{\Upsilon }}_2={\mathrm{\Sigma }}_2=diag\{0.4,-0.2,0.3\}.$$

We design a delayed-feedback controller as $u(k)=Ge(k)+G_{\tau }e(k-\tau (k))$, that is, the distributed delayed controller is omitted. By using the Matlab LMI Toolbox, LMI (28) and (29) can be solved and the feasible solutions are obtained as follows:

$$\begin{array}{r}P=\left[\begin{array}{ccc}10.7271& 0.4759& 0.2023\\ \ast & 7.3604& -0.6581\\ \ast & \ast & 10.0764\end{array}\right],Q=\left[\begin{array}{ccc}2.2544& 0.0658& -0.0473\\ \ast & 1.4303& -0.1111\\ \ast & \ast & 2.1584\end{array}\right],\\ R=\left[\begin{array}{ccc}2.3904& -0.5966& 0.5486\\ \ast & 3.3556& 0.4730\\ \ast & \ast & 3.0583\end{array}\right],\mathrm{\Lambda }=diag\{9.4695,18.7205,10.4127\},\\ \mathrm{\Gamma }=diag\{6.3622,3.0023,9.8068\},\mathrm{\Xi }=diag\{4.9624,8.1531,7.3455\},\\ {\lambda }^{\ast }=10.9097,\mu =6.4636,\end{array}$$

and

$$G=\left[\begin{array}{ccc}-4.8030& -0.2974& 0.5754\\ -1.0704& -1.2260& 0.2636\\ 0.1993& 0.4936& -3.8391\end{array}\right],G_{\tau }=\left[\begin{array}{ccc}-1.0885& -0.4761& -0.2475\\ 0.0031& -3.9716& 0.5437\\ -0.9665& 0.1146& 1.5992\end{array}\right].$$

Then Corollary 1 proves that the response system (9) and the drive system (1) with the given parameters can achieve globally robustly asymptotically synchronization in the mean square.

5 Conclusions

In this paper, based on Lyapunov stability theorem and drive-response concept, the globally asymptotically synchronization has been discussed for a general class of uncertain stochastic discrete-time neural networks with mixed time delays which consist of time-varying discrete and infinite distributed time delays. The proposed controller is robust to a stochastic disturbance and to the parameter uncertainties. In comparison with previous literature, the distributed delay is taken into account in our models, which are few investigated in the discrete-time complex networks. By using the linear matrix inequality (LMI) approach, several easy-to-verify sufficient criteria have been established to ensure the uncertain stochastic discrete-time neural networks to be globally robustly asymptotically synchronized in the mean square. The LMI-based criteria obtained are dependent not only on the lower bound, but also on the upper bound of the time-varying delay, and they can be solved efficiently via the Matlab LMI Toolbox. Also, the proposed synchronization scheme is easy to implement in practice.

Authors’ information

Zhong Chen (1971-), male, native of Xingning, Guangdong, M.S.D., engages in the groups theory and differential equation.