Joint source and relay design for MIMO multi-relay systems using projected gradient approach

Abstract

In this paper, we develop the optimal source precoding matrix and relay amplifying matrices for non-regenerative multiple-input multiple-output (MIMO) relay communication systems with parallel relay nodes using the projected gradient (PG) approach. We show that the optimal relay amplifying matrices have a beamforming structure. Exploiting the structure of relay matrices, an iterative joint source and relay matrices optimization algorithm is developed to minimize the mean-squared error (MSE) of the signal waveform estimation at the destination using the PG approach. The performance of the proposed algorithm is demonstrated through numerical simulations.

1 Introduction

Recently, multiple-input multiple-output (MIMO) relay communication systems have attracted much research interest and provided significant improvement in terms of both spectral efficiency and link reliability [1–17]. Many works have studied the optimal relay amplifying matrix for the source-relay-destination channel. In [2, 3], the optimal relay amplifying matrix maximizing the mutual information (MI) between the source and destination nodes was derived, assuming that the source covariance matrix is an identity matrix. In [4–6], the optimal relay amplifying matrix was designed to minimize the mean-squared error (MSE) of the signal waveform estimation at the destination.

A few research has studied the joint optimization of the source precoding matrix and the relay amplifying matrix for the source-relay-destination channel. In [7], both the source and relay matrices were jointly designed to maximize the source-destination MI. In [8, 9], source and relay matrices were developed to jointly optimize a broad class of objective functions. The author of [10] investigated the joint source and relay optimization for two-way MIMO relay systems using the projected gradient (PG) approach. The source and relay optimization for multi-user MIMO relay systems with single relay node has been investigated in [11–14].

All the works in [1–14] considered a single relay node at each hop. In general, joint source and relay precoding matrices design for MIMO relay systems with multiple relay nodes is more challenging than that for single-relay systems. The authors of [15] developed the optimal relay amplifying matrices with multiple relay nodes. A matrix-form conjugate gradient algorithm has been proposed in [16] to optimize the source and relay matrices. In [17], the authors proposed a suboptimal source and relay matrices design for parallel MIMO relay systems by first relaxing the power constraint at each relay node to the sum relay power constraints at the output of the second-hop channel and then scaling the relay matrices to satisfy the individual relay power constraints.

In this paper, we propose a jointly optimal source precoding matrix and relay amplifying matrices design for a two-hop non-regenerative MIMO relay network with multiple relay nodes using the PG approach. We show that the optimal relay amplifying matrices have a beamforming structure. This new result is not available in [16]. It generalizes the optimal source and relay matrices design from a single relay node case [8] to multiple parallel relay nodes scenarios. Exploiting the structure of relay matrices, an iterative joint source and relay matrices optimization algorithm is developed to minimize the MSE of the signal waveform estimation. Different to [17], in this paper, we develop the optimal source and relay matrices by directly considering the transmission power constraint at each relay node. Simulation results demonstrate the effectiveness of the proposed iterative joint source and relay matrices design algorithm with multiple parallel relay nodes using the PG approach.

The rest of this paper is organized as follows. In Section 2, we introduce the model of a non-regenerative MIMO relay communication system with parallel relay nodes. The joint source and relay matrices design algorithm is developed in Section 3. In Section 4, we show some numerical simulations. Conclusions are drawn in Section 5.

2 System model

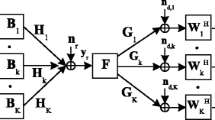
In this section, we introduce the model of a two-hop MIMO relay communication system consisting of one source node, K parallel relay nodes, and one destination node as shown in Figure 1. We assume that the source and destination nodes have N_s and N_d antennas, respectively, and each relay node has N_r antennas. The generalization to systems with different number of antennas at each relay node is straightforward. Due to its merit of simplicity, a linear non-regenerative strategy is applied at each relay node. The communication process between the source and destination nodes is completed in two time slots. In the first time slot, the N_b×1(N_b≤N_s) modulated source symbol vector s is linearly precoded as

$$\mathbf{x}=\mathbf{B}\mathbf{s},$$

(1)

Figure 1

Block diagram of a parallel MIMO relay communication system.

where B is an N_s×N_b source precoding matrix. We assume that the source signal vector satisfies $\mathrm{E}\left[\mathbf{s}{\mathbf{s}}^H\right]={\mathbf{I}}_{N_{\mathrm{b}}}$, where I _n stands for an n×n identity matrix, (·)^H is the matrix (vector) Hermitian transpose, and E [·] denotes statistical expectation. The precoded vector x is transmitted to K parallel relay nodes. The N_r×1 received signal vector at the i th relay node can be written as

$${\mathbf{y}}_{\mathrm{r},i}={\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{x}+{\mathbf{v}}_{\mathrm{r},i},i=1,\cdots ,K,$$

(2)

where H_sr,i is the N_r×N_s MIMO channel matrix between the source and the i th relay nodes and v_r,i is the additive Gaussian noise vector at the i th relay node.

In the second time slot, the source node is silent, while each relay node transmits the linearly amplified signal vector to the destination node as

$${\mathbf{x}}_{\mathrm{r},i}={\mathbf{F}}_i{\mathbf{y}}_{\mathrm{r},i},i=1,\cdots ,K,$$

(3)

where F _i is the N_r×N_r amplifying matrix at the i th relay node. The received signal vector at the destination node can be written as

$${\mathbf{y}}_{\mathrm{d}}=\sum _{i=1}^K{\mathbf{H}}_{\mathrm{r}\mathrm{d},i}{\mathbf{x}}_{\mathrm{r},i}+{\mathbf{v}}_{\mathrm{d}},$$

(4)

where H_rd,i is the N_d×N_r MIMO channel matrix between the i th relay and the destination nodes, and v_d is the additive Gaussian noise vector at the destination node.

Substituting (1) to (3) into (4), we have

$$\begin{array}{ll}{\mathbf{y}}_{\mathrm{d}}& =\sum _{i=1}^K({\mathbf{H}}_{\mathrm{r}\mathrm{d},i}{\mathbf{F}}_i{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}\mathbf{s}+{\mathbf{H}}_{\mathrm{r}\mathrm{d},i}{\mathbf{F}}_i{\mathbf{v}}_{\mathrm{r},i})+{\mathbf{v}}_{\mathrm{d}}\\ ={\mathbf{H}}_{\mathrm{r}\mathrm{d}}\mathbf{F}{\mathbf{H}}_{\mathrm{s}\mathrm{r}}\mathbf{B}\mathbf{s}+{\mathbf{H}}_{\mathrm{r}\mathrm{d}}\mathbf{F}{\mathbf{v}}_{\mathrm{r}}+{\mathbf{v}}_{\mathrm{d}}\triangleq \tilde{\mathbf{H}}\mathbf{s}+\tilde{\mathbf{v}},\end{array}$$

(5)

where ${\mathbf{H}}_{\mathrm{s}\mathrm{r}}\triangleq {\left[{\mathbf{H}}_{\mathrm{s}\mathrm{r},1}^T,{\mathbf{H}}_{\mathrm{s}\mathrm{r},2}^T,\cdots ,{\mathbf{H}}_{\mathrm{s}\mathrm{r},K}^T\right]}^T$ is a K N_r×N_s channel matrix between the source node and all relay nodes, ${\mathbf{H}}_{\mathrm{r}\mathrm{d}}\triangleq \left[{\mathbf{H}}_{\mathrm{r}\mathrm{d},1},{\mathbf{H}}_{\mathrm{r}\mathrm{d},2},\cdots ,{\mathbf{H}}_{\mathrm{r}\mathrm{d},K}\right]$ is an N_d×K N_r channel matrix between all relay nodes and the destination node, $\mathbf{F}\triangleq \mathrm{b}\mathrm{d}[{\mathbf{F}}_1,{\mathbf{F}}_2,\cdots ,{\mathbf{F}}_K]$ is the K N_r×K N_r block diagonal equivalent relay matrix, ${\mathbf{v}}_{\mathrm{r}}\triangleq \left[\right.{\mathbf{v}}_{\mathrm{r},1}^T,{\mathbf{v}}_{\mathrm{r},2}^T,\cdots ,{\mathbf{v}}_{\mathrm{r},K}^T{}^T$ is obtained by stacking the noise vectors at all the relays, $\tilde{\mathbf{H}}\triangleq {\mathbf{H}}_{\mathrm{r}\mathrm{d}}\mathbf{F}{\mathbf{H}}_{\mathrm{s}\mathrm{r}}\mathbf{B}$ is the effective MIMO channel matrix of the source-relay-destination link, and $\tilde{\mathbf{v}}\triangleq {\mathbf{H}}_{\mathrm{r}\mathrm{d}}\mathbf{F}{\mathbf{v}}_{\mathrm{r}}+{\mathbf{v}}_{\mathrm{d}}$ is the equivalent noise vector. Here, (·)^T denotes the matrix (vector) transpose, bd [ ·] constructs a block-diagonal matrix. We assume that all noises are independent and identically distributed (i.i.d.) Gaussian noise with zero mean and unit variance. The transmission power consumed by each relay node (3) can be expressed as

$$\begin{array}{ll}\mathrm{E}\left[\mathrm{t}\mathrm{r}\left({\mathbf{x}}_{\mathrm{r},i}{\mathbf{x}}_{\mathrm{r},i}^H\right)\right]& =\text{tr}\left({\mathbf{F}}_i\left[{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}{\mathbf{B}}^H{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}^H+{\mathbf{I}}_{N_{\mathrm{r}}}\right]{\mathbf{F}}_i^H\right),\\ i& =1,\cdots ,K,\end{array}$$

(6)

where tr(·) stands for the matrix trace.

Using a linear receiver, the estimated signal waveform vector at the destination node is given by $\widehat{\mathbf{s}}={\mathbf{W}}^H{\mathbf{y}}_{\mathrm{d}}$, where W is an N_d×N_b weight matrix. The MSE of the signal waveform estimation is given by

$$\begin{array}{ll}\text{MSE}& =\mathrm{t}\mathrm{r}\left(\mathrm{E}\left[\left(\widehat{\mathbf{s}}-\mathbf{s}\right){\left(\widehat{\mathbf{s}}-\mathbf{s}\right)}^H\right]\right)\\ =\mathrm{t}\mathrm{r}\left(\left({\mathbf{W}}^H\tilde{\mathbf{H}}-{\mathbf{I}}_{N_{\mathrm{b}}}\right){\left({\mathbf{W}}^H\tilde{\mathbf{H}}-{\mathbf{I}}_{N_{\mathrm{b}}}\right)}^H+{\mathbf{W}}^H\tilde{\mathbf{C}}\mathbf{W}\right),\end{array}$$

(7)

where $\tilde{\mathbf{C}}$ is the equivalent noise covariance matrix given by $\tilde{\mathbf{C}}=\mathrm{E}\left[\tilde{\mathbf{v}}{\tilde{\mathbf{v}}}^H\right]={\mathbf{H}}_{\mathrm{r}\mathrm{d}}\mathbf{F}{\mathbf{F}}^H{\mathbf{H}}_{\mathrm{r}\mathrm{d}}^H+{\mathbf{I}}_{N_{\mathrm{d}}}$. The weight matrix W which minimizes (7) is the Wiener filter and can be written as

$$\mathbf{W}={(\tilde{\mathbf{H}}{\tilde{\mathbf{H}}}^H+\tilde{\mathbf{C}})}^{-1}\tilde{\mathbf{H}},$$

(8)

where (·)^-1 denotes the matrix inversion. Substituting (8) back into (7), it can be seen that the MSE is a function of F and B and can be written as

$$\text{MSE}=\mathrm{t}\mathrm{r}\left({\left[{\mathbf{I}}_{N_{\mathrm{b}}}+{\tilde{\mathbf{H}}}^H{\tilde{\mathbf{C}}}^{-1}\tilde{\mathbf{H}}\right]}^{-1}\right).$$

(9)

3 Joint source and relay matrix optimization

In this section, we address the joint source and relay matrix optimization problem for MIMO multi-relay systems with a linear minimum mean-squared error (MMSE) receiver at the destination node. In particular, we show that optimal relay matrices have a general beamforming structure. Based on (6) and (9), the joint source and relay matrices optimization problem can be formulated as

$$\begin{array}{ll}\underset{\left\{{\mathbf{F}}_i\right\},\mathbf{B}}{min}\text{tr}& \left({\left[{\mathbf{I}}_{N_{\mathrm{b}}}+{\tilde{\mathbf{H}}}^H{\tilde{\mathbf{C}}}^{-1}\tilde{\mathbf{H}}\right]}^{-1}\right)\end{array}$$

(10)

$$\begin{array}{ll}\text{s.t.}\text{tr}& \left(\mathbf{B}{\mathbf{B}}^H\right)\le P_{\mathrm{s}}\end{array}$$

(11)

$$\begin{array}{ll}\text{tr}& \left({\mathbf{F}}_i\left[{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}{\mathbf{B}}^H{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}^H+{\mathbf{I}}_{N_{\mathrm{r}}}\right]{\mathbf{F}}_i^H\right)\\ \le P_{\mathrm{r},i},i=1,\cdots ,K,\end{array}$$

(12)

where $\left\{{\mathbf{F}}_i\right\}\triangleq \{{\mathbf{F}}_i,i=1,\cdots ,K\}$, (11) is the transmit power constraint at the source node, while (12) is the power constraint at each relay node. Here, P_s>0 and P_r,i>0, i=1,⋯,K, are the corresponding power budget. Obviously, to avoid any loss of transmission power in the relay system when a linear receiver is used, there should be N_b≤min(K N_r,N_d). The problem (10)-(12) is non-convex, and a globally optimal solution of B and {F _i } is difficult to obtain with a reasonable computational complexity. In this paper, we develop an iterative algorithm to optimize B and {F _i }. First, we show the optimal structure of {F _i }.

3.1 Optimal structure of relay amplifying matrices

For given source matrix B satisfying (11), the relay matrices {F _i } are optimized by solving the following problem:

$$\begin{array}{ll}\underset{\left\{{\mathbf{F}}_i\right\}}{min}\text{tr}& \left({\left[{\mathbf{I}}_{N_{\mathrm{b}}}+{\tilde{\mathbf{H}}}^H{\tilde{\mathbf{C}}}^{-1}\tilde{\mathbf{H}}\right]}^{-1}\right)\end{array}$$

(13)

$$\begin{array}{ll}\text{s.t.}\text{tr}& \left({\mathbf{F}}_i\left[{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}{\mathbf{B}}^H{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}^H+{\mathbf{I}}_{N_{\mathrm{r}}}\right]{\mathbf{F}}_i^H\right)\le P_{\mathrm{r},i},i=1,\cdots ,\mathrm{K.}\end{array}$$

(14)

Let us introduce the following singular value decompositions (SVDs):

$${\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}={\mathbf{U}}_{\mathrm{s},i}{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H,{\mathbf{H}}_{\mathrm{r}\mathrm{d},i}={\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{V}}_{\mathrm{r},i}^H,i=1,\cdots ,K,$$

(15)

where Λ_s,i and Λ_r,i are R_s,i×R_s,i and R_r,i×R_r,i diagonal matrices, respectively. Here, $R_{\mathrm{s},i}\triangleq \text{rank}\left({\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}\right)$, $R_{\mathrm{r},i}\triangleq \text{rank}\left({\mathbf{H}}_{\mathrm{r}\mathrm{d},i}\right)$, i=1,⋯,K, and rank(·) denotes the rank of a matrix. Based on the definition of matrix rank, R_s,i≤ min(N_r,N_b) and R_r,i≤ min(N_r,N_d). The following theorem states the structure of the optimal {F _i }.

Theorem 1.

Using the SVDs of (15), the optimal structure of F_i as the solution to the problem (13)-(14) is given by

$${\mathbf{F}}_i={\mathbf{V}}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{U}}_{\mathrm{s},i}^H,i=1,\cdots ,K,$$

(16)

where A _i is an R_r,i×R_s,i matrix, i=1,⋯,K.

Proof

See Appendix 1.

The remaining task is to find the optimal A_i, i=1,⋯,K. From (31) and (32) in Appendix 1, we can equivalently rewrite the optimization problem (13)-(14) as

$$\begin{array}{ll}\underset{\left\{{\mathbf{A}}_i\right\}}{min}\text{tr}& \left(\left[{\mathbf{I}}_{N_{\mathrm{b}}}+\sum _{i=1}^K{\mathbf{V}}_{\mathrm{s},i}{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H\right.\right.\\ \times {\left(\sum _{i=1}^K{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H+{\mathbf{I}}_{N_{\mathrm{d}}}\right)}^{-1}\\ \left.{\left.\times \sum _{i=1}^K{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right]}^{-1}\right)\end{array}$$

(17)

$$\begin{array}{ll}\text{s.t.}\text{tr}& \left({\mathbf{A}}_i({\mathbf{\Lambda }}_{\mathrm{s},i}^2+{\mathbf{I}}_{R_{\mathrm{s},i}}){\mathbf{A}}_i^H\right)\le P_{\mathrm{r},i},i=1,\cdots ,\mathrm{K.}\end{array}$$

(18)

Both the problem (13)-(14) and the problem (17)-(18) have matrix optimization variables. However, in the former problem, the optimization variable F _i is an N_r×N_r matrix, while the dimension of A _i is R_r,i×R_s,i, which may be smaller than that of F _i . Thus, solving the problem (17)-(18) has a smaller computational complexity than solving the problem (13)-(14). In general, the problem (17)-(18) is non-convex, and a globally optimal solution is difficult to obtain with a reasonable computational complexity. Fortunately, we can resort to numerical methods, such as the projected gradient algorithm [18] to find (at least) a locally optimal solution of (17)-(18).

Theorem 2.

Let us define the objective function in (17) as f(A _i ). Its gradient ∇f(A_i) with respect to A _i can be calculated by using results on derivatives of matrices in [19] as

$$\begin{array}{ll}\nabla f\left({\mathbf{A}}_i\right)& =2\left({\mathbf{R}}_i^H{\mathbf{M}}_i^H\left({\mathbf{E}}_i{\mathbf{S}}_i^H+{\mathbf{D}}_i^H\right)-{\mathbf{R}}_i^H{\mathbf{G}}_i^{-H}{\mathbf{E}}_i{\mathbf{S}}_i^H\right),\\ i& =1,\cdots ,K,\end{array}$$

(19)

where M _i , R _i , S _i , D _i , E _i , and G _i are defined in Appendix 2.

Proof

See Appendix 2.

In each iteration of the PG algorithm, we first obtain ${\tilde{\mathbf{A}}}_i={\mathbf{A}}_i-s_n\nabla f\left({\mathbf{A}}_i\right)$ by moving A _i one step towards the negative gradient direction of f(A _i ), where s _n >0 is the step size. Since ${\tilde{\mathbf{A}}}_i$ might not satisfy the constraint (18), we need to project it onto the set given by (18). The projected matrix ${\bar{\mathbf{A}}}_i$ is obtained by minimizing the Frobenius norm of ${\bar{\mathbf{A}}}_i-{\tilde{\mathbf{A}}}_i$ (according to [18]) subjecting to (18), which can be formulated as the following optimization problem:

$$\begin{array}{ll}\underset{{\bar{\mathbf{A}}}_i}{min}\text{tr}& \left(({\bar{\mathbf{A}}}_i-{\tilde{\mathbf{A}}}_i){({\bar{\mathbf{A}}}_i-{\tilde{\mathbf{A}}}_i)}^H\right)\end{array}$$

(20)

$$\begin{array}{ll}\text{s.t.}\text{tr}& \left({\bar{\mathbf{A}}}_i\left({\mathbf{\Lambda }}_{\mathrm{s},i}^2+{\mathbf{I}}_{R_{\mathrm{s},i}}\right){{\bar{\mathbf{A}}}_i}^H\right)\le P_{\mathrm{r},i}.\end{array}$$

(21)

Obviously, if $\mathrm{t}\mathrm{r}\left({\tilde{\mathbf{A}}}_i\left({\mathbf{\Lambda }}_{\mathrm{s},i}^2+{\mathbf{I}}_{R_{\mathrm{s},i}}\right){{\tilde{\mathbf{A}}}_i}^H\right)\le P_{\mathrm{r},i}$, then ${\bar{\mathbf{A}}}_i={\tilde{\mathbf{A}}}_i$. Otherwise, the solution to the problem (20)-(21) can be obtained by using the Lagrange multiplier method, and the solution is given by

$${\bar{\mathbf{A}}}_i={\tilde{\mathbf{A}}}_i{\left[(\lambda +1){\mathbf{I}}_{R_{\mathrm{s},i}}+\lambda {\mathbf{\Lambda }}_{\mathrm{s},i}^2\right]}^{-1},$$

where λ>0 is the solution to the non-linear equation of

$$\begin{array}{ll}\mathrm{t}\mathrm{r}& \left({\tilde{\mathbf{A}}}_i{\left[(\lambda +1){\mathbf{I}}_{R_{\mathrm{s},i}}+\lambda {\mathbf{\Lambda }}_{\mathrm{s},i}^2\right]}^{-1}({\mathbf{\Lambda }}_{\mathrm{s},i}^2+{\mathbf{I}}_{R_{\mathrm{s},i}})\right.\\ \times \left.{\left[(\lambda +1){\mathbf{I}}_{R_{\mathrm{s},i}}+\lambda {\mathbf{\Lambda }}_{\mathrm{s},i}^2\right]}^{-1}{\tilde{\mathbf{A}}}_i^H\right)=P_{\mathrm{r},i}.\end{array}$$

(22)

Equation (22) can be efficiently solved by the bisection method [18].

The procedure of the PG algorithm is listed in Algorithm 1, where (·)⁽ⁿ⁾ denotes the variable at the n th iteration, δ _n and s _n are the step size parameters at the n th iteration, ∥·∥ denotes the maximum among the absolute value of all elements in the matrix, and ε is a positive constant close to 0. The step size parameters δ _n and s _n are determined by the Armijo rule [18], i.e., s _n =s is a constant through all iterations, while at the n th iteration, δ _n is set to be ${\gamma }^{m_n}$. Here, m _n is the minimal non-negative integer that satisfies the following inequality $f\left({\mathbf{A}}_i^{(n+1)}\right)-f\left({\mathbf{A}}_i^{\left(n\right)}\right)\le \alpha {\gamma }^{m_n}\mathrm{t}\mathrm{r}\left({\left(\nabla f\left({\mathbf{A}}_i^{\left(n\right)}\right)\right)}^H\left({\bar{\mathbf{A}}}_i^{\left(n\right)}-{\mathbf{A}}_i^{\left(n\right)}\right)\right)$, where α and γ are constants. According to [18], usually α is chosen close to 0, for example, α∈[10^-5,10^-1], while a proper choice of γ is normally from 0.1 to 0.5.

3.2 Optimal source precoding matrix

With fixed {F _i }, the source precoding matrix B is optimized by solving the following problem:

$$\begin{array}{ll}\underset{\mathbf{B}}{min}\text{tr}& \left({\left[{\mathbf{I}}_{N_{\mathrm{b}}}+{\mathbf{B}}^H\mathbf{\Psi }\mathbf{B}\right]}^{-1}\right)\end{array}$$

(23)

$$\begin{array}{ll}\text{s.t.}\text{tr}& \left(\mathbf{B}{\mathbf{B}}^H\right)\le P_{\mathrm{s}},\end{array}$$

(24)

$$\begin{array}{ll}\text{tr}& \left({\mathbf{F}}_i{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}{\mathbf{B}}^H{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}^H{\mathbf{F}}_i^H\right)\le {\breve{P}}_{\mathrm{r},i},i=1,\cdots ,K,\end{array}$$

(25)

where $\mathbf{\Psi }\triangleq {\mathbf{H}}_{\mathrm{s}\mathrm{r}}^H{\mathbf{F}}^H{\mathbf{H}}_{\mathrm{r}\mathrm{d}}^H{\left({\mathbf{H}}_{\mathrm{r}\mathrm{d}}\mathbf{F}{\mathbf{F}}^H{\mathbf{H}}_{\mathrm{r}\mathrm{d}}^H+{\mathbf{I}}_{N_{\mathrm{d}}}\right)}^{-1}{\mathbf{H}}_{\mathrm{r}\mathrm{d}}\mathbf{F}{\mathbf{H}}_{\mathrm{s}\mathrm{r}}$, and ${\breve{P}}_{\mathrm{r},i}\triangleq P_{\mathrm{r},i}-\mathrm{t}\mathrm{r}\left({\mathbf{F}}_i{\mathbf{F}}_i^H\right)$, i=1,⋯,K. Let us introduce $\mathbf{\Omega }\triangleq \mathbf{B}{\mathbf{B}}^H$, and a positive semi-definite (PSD) matrix X with $\mathbf{X}\succcurlyeq {\left({\mathbf{I}}_{N_{\mathrm{s}}}+{\mathbf{\Psi }}^{\frac{1}{2}}\mathbf{\Omega }{\mathbf{\Psi }}^{\frac{1}{2}}\right)}^{-1}$, where A≽B means that A-B is a PSD matrix. By using the Schur complement [20], the problem (23)-(25) can be equivalently converted to the following problem:

$$\begin{array}{ll}\underset{\mathbf{X},\mathbf{\Omega }}{min}& \text{tr}\left(\mathbf{X}\right)-N_{\mathrm{s}}+N_{\mathrm{b}}\end{array}$$

(26)

$$\begin{array}{ll}\text{s.t.}& \left(\begin{array}{ll}\mathbf{X}& {\mathbf{I}}_{N_{\mathrm{s}}}\\ {\mathbf{I}}_{N_{\mathrm{s}}}& {\mathbf{I}}_{N_{\mathrm{s}}}+{\mathbf{\Psi }}^{\frac{1}{2}}\mathbf{\Omega }{\mathbf{\Psi }}^{\frac{1}{2}}\end{array}\right)\succcurlyeq 0,\end{array}$$

(27)

$$\begin{array}{l}\mathrm{t}\mathrm{r}\left(\mathbf{\Omega }\right)\le P_{\mathrm{s}},\mathbf{\Omega }\succcurlyeq 0,\end{array}$$

(28)

$$\begin{array}{l}\mathrm{t}\mathrm{r}\left({\mathbf{F}}_i{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{\Omega }{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}^H{\mathbf{F}}_i^H\right)\le {\breve{P}}_{\mathrm{r},i},i=1,\cdots ,\mathrm{K.}\end{array}$$

(29)

The problem (26)-(29) is a convex semi-definite programming (SDP) problem which can be efficiently solved by the interior point method [20]. Let us introduce the eigenvalue decomposition (EVD) of $\mathbf{\Omega }={\mathbf{U}}_{\Omega }{\mathbf{\Lambda }}_{\Omega }{\mathbf{U}}_{\Omega }^H$, where Λ _Ω is a R _Ω ×R _Ω eigenvalue matrix with R _Ω =rank(Ω). If R _Ω =N_b, then from Ω=B B^H, we have $\mathbf{B}={\mathbf{U}}_{\Omega }{\mathbf{\Lambda }}_{\Omega }^{\frac{1}{2}}$. If R _Ω >N_b, the randomization technique [21] can be applied to obtain a possibly suboptimal solution of B with rank N_b. If R _Ω <N_b, it indicates that the system (channel) cannot support N_b independent data streams, and thus, in this case, a smaller N_b should be chosen in the system design.

Now, the original joint source and relay optimization problem (10)-(12) can be solved by an iterative algorithm as shown in Algorithm 2, where (·)^(m) denotes the variable at the m th iteration. This algorithm is first initialized at a random feasible B satisfying (11). At each iteration, we first update {F _i } with fixed B and then update B with fixed {F _i }. Note that the conditional updates of each matrix may either decrease or maintain but cannot increase the objective function (10). Monotonic convergence of {F _i } and B towards (at least) a locally optimal solution follows directly from this observation. Note that in each iteration of this algorithm, we need to update the relay amplifying matrices according to the procedure listed in Algorithm 1 at a complexity order of $\mathcal{O}\left(K\left(N_{\mathrm{d}}^3+N_{\mathrm{r}}^3+N_{\mathrm{b}}^3\right)\right)$ and update the source precoding matrix through solving the SDP problem (26)-(29) at a complexity cost that is at most $\mathcal{O}\left({\left(N_{\mathrm{s}}^2+K+1\right)}^{3.5}\right)$ using interior point methods [22]. Therefore, the per-iteration computational complexity order of the proposed algorithm is $\mathcal{O}\left(K\left(N_{\mathrm{d}}^3+N_{\mathrm{r}}^3+N_{\mathrm{b}}^3\right)+{\left(N_{\mathrm{s}}^2+K+1\right)}^{3.5}\right)$. The overall complexity of this algorithm depends on the number of iterations until convergence, which will be studied in the next section.

4 Simulations

In this section, we study the performance of the proposed jointly optimal source and relay matrix design for MIMO multi-relay systems with linear MMSE receiver. All simulations are conducted in a flat Rayleigh fading environment where the channel matrices have zero-mean entries with variances ${\sigma }_{\mathrm{s}}^2/N_{\mathrm{s}}$ and ${\sigma }_{\mathrm{r}}^2/\left({\mathit{\text{KN}}}_{\mathrm{r}}\right)$ for H_sr and H_rd, respectively. For the sake of simplicity, we assume P_r,i=P_r, i=1,⋯,K. The BPSK constellations are used to modulate the source symbols, and all noises are i.i.d. Gaussian with zero mean and unit variance. We define ${\text{SNR}}_{\mathrm{s}}={\sigma }_{\mathrm{s}}^2{P}_{\mathrm{s}}K{N}_{\mathrm{r}}/N_{\mathrm{s}}$ and ${\text{SNR}}_{\mathrm{r}}={\sigma }_{\mathrm{r}}^2{P}_{\mathrm{r}}{N}_{\mathrm{d}}/\left({\mathit{\text{KN}}}_{\mathrm{r}}\right)$ as the signal-to-noise ratio (SNR) for the source-relay link and the relay-destination link, respectively. We transmit 1000N_s randomly generated bits in each channel realization, and all simulation results are averaged over 200 channel realizations. In all simulations, we set N_b=N_s=N_r=N_d=3, and the MMSE linear receiver in (8) is employed at the destination for symbol detection.

In the first example, a MIMO relay system with K=3 relay nodes is simulated. We compare the normalized MSE performance of the proposed joint source and relay optimization algorithm using the projected gradient (JSR-PG) algorithm in Algorithm 2, the optimal relay-only algorithm using the projected gradient (ORO-PG) algorithm in Algorithm 1 with $\mathbf{B}=\sqrt{P_{\mathrm{s}}/N_{\mathrm{s}}}{\mathbf{I}}_{N_{\mathrm{s}}}$, and the naive amplify-and-forward (NAF) algorithm. Figure 2 shows the normalized MSE of all algorithms versus SNR_s for SNR_r= 20 dB. While Figure 3 demonstrates the normalized MSE of all algorithms versus SNR_r for SNR_s fixed at 20 dB. It can be seen from Figures 2 and 3 that the JSR-PG and ORO-PG algorithms have a better performance than the NAF algorithm over the whole SNR_s and SNR_r range. Moreover, the proposed JSR-PG algorithm yields the lowest MSE among all three algorithms.

Figure 2

Example 1. Normalized MSE versus SNR_s with K=3, SNR_r=20 dB.

Figure 3

Example 1. Normalized MSE versus SNR_r with K=3, SNR_s=20 dB.

The number of iterations required for the JSR-PG algorithm to converge to ε=10^-3 in a typical channel realization are listed in Table 1, where we set K=3 and SNR_r=20 dB. It can be seen that the JSR-PG algorithm converges within several iterations, and thus, it is realizable with the advancement of modern chip design.

Table 1 Iterations required until convergence in the JSR-PG algorithm

In the second example, we compare the bit error rate (BER) performance of the proposed JSR-PG algorithm in Algorithm 2, the ORO-PG algorithm in Algorithm 1, the suboptimal source and relay matrix design in [17], the one-way relay version of the conjugate gradient-based source and relay algorithm in [16], and the NAF algorithm. Figure 4 displays the system BER versus SNR_s for a MIMO relay system with K=3 relay nodes and fixed SNR_r at 20 dB. It can be seen from Figure 4 that the proposed JSR-PG algorithm has a better BER performance than the existing algorithms over the whole SNR_s range.

Figure 4

Example 2. BER versus SNR_s with K=3, SNR_r=20 dB.

In the third example, we study the effect of the number of relay nodes to the system BER performance using the JSR-PG and ORO-PG algorithms. Figure 5 displays the system BER versus SNR_s with K=2, 3, and 5 for fixed SNR_r at 20 dB. It can be seen that at BER = 10^-2, for both the ORO-PG algorithm and JSR-PG algorithm, we can achieve approximately 3-dB gain by increasing from K=2 to K=5. It can also be seen that the performance gain of the JSR-PG algorithm over the ORO-PG algorithm increases with the increasing number of relay nodes.

Figure 5

Example 3. BER versus SNR_s for different K, SNR_r=20 dB.

5 Conclusions

In this paper, we have derived the general structure of the optimal relay amplifying matrices for linear non-regenerative MIMO relay communication systems with multiple relay nodes using the projected gradient approach. The proposed source and relay matrices minimize the MSE of the signal waveform estimation. The simulation results demonstrate that the proposed algorithm has improved the MSE and BER performance compared with existing techniques.

Appendices

Appendix 1

Proof of Theorem 1

Without loss of generality, F _i can be written as

$${\mathbf{F}}_i=\left[\begin{array}{ll}{\mathbf{V}}_{\mathrm{r},i}& {\mathbf{V}}_{\mathrm{r},i}^{\perp }\end{array}\right]\left[\begin{array}{ll}{\mathbf{A}}_i& {\mathbf{X}}_i\\ {\mathbf{Y}}_i& {\mathbf{Z}}_i\end{array}\right]\left[\begin{array}{l}{\mathbf{U}}_{\mathrm{s},i}^H\\ {\left({\mathbf{U}}_{\mathrm{s},i}^{\perp }\right)}^H\end{array}\right],i=1,\cdots ,K,$$

(30)

where ${\mathbf{V}}_{\mathrm{r},i}^{\perp }{\left({\mathbf{V}}_{\mathrm{r},i}^{\perp }\right)}^H={\mathbf{I}}_{N_{\mathrm{r}}}-{\mathbf{V}}_{\mathrm{r},i}{\mathbf{V}}_{\mathrm{r},i}^H$, ${\mathbf{U}}_{\mathrm{s},i}^{\perp }{\left({\mathbf{U}}_{\mathrm{s},i}^{\perp }\right)}^H={\mathbf{I}}_{N_{\mathrm{r}}}-{\mathbf{U}}_{\mathrm{s},i}{\mathbf{U}}_{\mathrm{s},i}^H$, such that ${\bar{\mathbf{V}}}_{\mathrm{r},i}\triangleq \left[{\mathbf{V}}_{\mathrm{r},i},{\mathbf{V}}_{\mathrm{r},i}^{\perp }\right]$ and ${\bar{\mathbf{U}}}_{\mathrm{s},i}\triangleq \left[{\mathbf{U}}_{\mathrm{s},i},{\mathbf{U}}_{\mathrm{s},i}^{\perp }\right]$ are N_r×N_r unitary matrices. Matrices A _i ,X _i ,Y _i ,Z _i are arbitrary matrices with dimensions of R_r,i×R_s,i, R_r,i×(N_r-R_s,i), (N_r-R_r,i)×R_s,i, (N_r-R_r,i)×(N_r-R_s,i), respectively. Substituting (15) and (30) back into (13), we obtain that ${\mathbf{H}}_{\mathrm{r}\mathrm{d},i}{\mathbf{F}}_i{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}={\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H$ and ${\mathbf{H}}_{\mathrm{r}\mathrm{d},i}{\mathbf{F}}_i{{\mathbf{F}}_i}^H{\mathbf{H}}_{\mathrm{r}\mathrm{d},i}^H={\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}\left({\mathbf{A}}_i{\mathbf{A}}_i^H+{\mathbf{X}}_i{\mathbf{X}}_i^H\right){\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H$. Thus, we can rewrite (13) as

$$\begin{array}{ll}\text{MSE}\text{tr}& \left(\left[{\mathbf{I}}_{N_{\mathrm{b}}}+\sum _{i=1}^K{\mathbf{V}}_{\mathrm{s},i}{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H\right.\right.\\ \times {\left(\sum _{i=1}^K{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}\left({\mathbf{A}}_i{\mathbf{A}}_i^H+{\mathbf{X}}_i{\mathbf{X}}_i^H\right){\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H+{\mathbf{I}}_{N_{\mathrm{d}}}\right)}^{-1}\\ \left.{\left.\times \sum _{i=1}^K{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right]}^{-1}\right).\end{array}$$

(31)

It can be seen that (31) is minimized by ${\mathbf{X}}_i={\mathbf{0}}_{R_{\mathrm{r},i}\times (N_{\mathrm{r}}-R_{\mathrm{s},i})}$, i=1,⋯,K.

Substituting (15) and (30) back into the left-hand side of the transmission power constraint (14), we have

$$\begin{array}{l}\text{tr}\left({\mathbf{F}}_i\left[{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}\mathbf{B}{\mathbf{B}}^H{\mathbf{H}}_{\mathrm{s}\mathrm{r},i}^H+{\mathbf{I}}_{N_{\mathrm{r}}}\right]{\mathbf{F}}_i^H\right)\\ =\text{tr}\left({\mathbf{A}}_i\left({\mathbf{\Lambda }}_{\mathrm{s},i}^2+{\mathbf{I}}_{R_{\mathrm{s},i}}\right){\mathbf{A}}_i^H+{\mathbf{Y}}_i\left({\mathbf{\Lambda }}_{\mathrm{s},i}^2+{\mathbf{I}}_{R_{\mathrm{s},i}}\right){\mathbf{Y}}_i^H\right.\\ \left.+{\mathbf{X}}_i{\mathbf{X}}_i^H+{\mathbf{Z}}_i{\mathbf{Z}}_i^H\right),i=1,\cdots ,\mathrm{K.}\end{array}$$

(32)

From (32), we find that ${\mathbf{X}}_i={\mathbf{0}}_{R_{\mathrm{r},i}\times (N_{\mathrm{r}}-R_{\mathrm{s},i})}$, ${\mathbf{Y}}_i={\mathbf{0}}_{(N_{\mathrm{r}}-R_{\mathrm{r},i})\times R_{\mathrm{s},i}}$, and ${\mathbf{Z}}_i={\mathbf{0}}_{(N_{\mathrm{r}}-R_{\mathrm{r},i})\times (N_{\mathrm{r}}-R_{\mathrm{s},i})}$ minimize the power consumption at each relay node. Thus, we have ${\mathbf{F}}_i={\mathbf{V}}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{U}}_{\mathrm{s},i}^H,i=1,\cdots ,K$.

Appendix 2

Proof of Theorem 2

Let us define ${\mathbf{Z}}_i\triangleq \sum _{j=1,j\ne i}^K{\mathbf{U}}_{\mathrm{r},j}{\mathbf{\Lambda }}_{\mathrm{r},j}{\mathbf{A}}_j{\mathbf{\Lambda }}_{\mathrm{s},j}{\mathbf{V}}_{\mathrm{s},j}^H$ and ${\mathbf{Y}}_i\triangleq \sum _{j=1,j\ne i}^K{\mathbf{U}}_{\mathrm{r},j}{\mathbf{\Lambda }}_{\mathrm{r},j}{\mathbf{A}}_j{\mathbf{A}}_j^H{\mathbf{\Lambda }}_{\mathrm{r},j}{\mathbf{U}}_{\mathrm{r},j}^H+{\mathbf{I}}_{N_{\mathrm{d}}}$. Then, f(A _i ) can be written as

$$\begin{array}{ll}f\left({\mathbf{A}}_i\right)=& \mathrm{t}\mathrm{r}\left(\left[{\mathbf{I}}_{N_{\mathrm{b}}}+\left({\mathbf{Z}}_i^H+{\mathbf{V}}_{\mathrm{s},i}{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H\right)\right.\right.\\ \times {\left({\mathbf{Y}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H\right)}^{-1}\\ \left.{\left.\times \left({\mathbf{Z}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right)\right]}^{-1}\right).\end{array}$$

(33)

Applying ${\left({\mathbf{I}}_{N_{\mathrm{b}}}+{\mathbf{A}}^H{\mathbf{C}}^{-1}\mathbf{A}\right)}^{-1}={\mathbf{I}}_{N_{\mathrm{b}}}-{\mathbf{A}}^H{(\mathbf{A}{\mathbf{A}}^H+\mathbf{C})}^{-1}\mathbf{A}$, (33) can be written as

$$\begin{array}{ll}f\left({\mathbf{A}}_i\right)=& \mathrm{t}\mathrm{r}\left({\mathbf{I}}_{N_{\mathrm{b}}}-\left({\mathbf{Z}}_i^H+{\mathbf{V}}_{\mathrm{s},i}{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H\right)\right.\\ \times \left[\left({\mathbf{Z}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right)\right.\\ \times \left({\mathbf{Z}}_i^H+{\mathbf{V}}_{\mathrm{s},i}{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H\right)\\ {\left.+{\mathbf{Y}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H\right]}^{-1}\\ \left.\times \left({\mathbf{Z}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right)\right).\end{array}$$

(34)

Let us now define ${\mathbf{E}}_i\triangleq {\mathbf{Z}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H$, ${\mathbf{K}}_i\triangleq {\mathbf{Y}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H$, and ${\mathbf{G}}_i\triangleq {\mathbf{E}}_i{\mathbf{E}}_i^H+{\mathbf{K}}_i$. We can rewrite (34) as

$$f\left({\mathbf{A}}_i\right)=\mathrm{t}\mathrm{r}\left({\mathbf{I}}_{N_{\mathrm{b}}}-{\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}{\mathbf{E}}_i\right)=\mathrm{t}\mathrm{r}\left({\mathbf{I}}_{N_{\mathrm{b}}}-{\mathbf{E}}_i{\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}\right).$$

(35)

The derivative of f(A _i ) with respect to A _i is given by

$$\begin{array}{ll}\frac{\mathrm{\partial f}\left({\mathbf{A}}_i\right)}{\partial {\mathbf{A}}_i}=& -\frac{\partial }{\partial {\mathbf{A}}_i}\mathrm{t}\mathrm{r}\left({\mathbf{E}}_i{\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}\right)\\ =\frac{\partial }{\partial {\mathbf{A}}_i}\mathrm{t}\mathrm{r}\left({\mathbf{G}}_i^{-1}{\mathbf{E}}_i{\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}\left(\left({\mathbf{Z}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right){\mathbf{E}}_i^H\right.\right.\\ +\left.\left.{\mathbf{Y}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H\right)\right)\\ -\frac{\partial }{\partial {\mathbf{A}}_i}\mathrm{t}\mathrm{r}\left({\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right).\end{array}$$

(36)

Defining ${\mathbf{M}}_i\triangleq {\mathbf{G}}_i^{-1}{\mathbf{E}}_i{\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}$, ${\mathbf{R}}_i\triangleq {\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}$, ${\mathbf{S}}_i\triangleq {\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H$, and ${\mathbf{D}}_i\triangleq {\mathbf{A}}_i^H{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{U}}_{\mathrm{r},i}^H$, we can rewrite (36) as

$$\begin{array}{ll}\frac{\mathrm{\partial f}\left({\mathbf{A}}_i\right)}{\partial {\mathbf{A}}_i}=& \frac{\partial }{\partial {\mathbf{A}}_i}\mathrm{t}\mathrm{r}\left({\mathbf{M}}_i\left({\mathbf{Z}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right){\mathbf{E}}_i^H\right.\\ +\left.{\mathbf{M}}_i\left({\mathbf{Y}}_i+{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}{\mathbf{A}}_i{\mathbf{D}}_i\right)\right)\\ -{\left({\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}{\mathbf{U}}_{\mathrm{r},i}{\mathbf{\Lambda }}_{\mathrm{r},i}\right)}^T{\left({\mathbf{\Lambda }}_{\mathrm{s},i}{\mathbf{V}}_{\mathrm{s},i}^H\right)}^T\end{array}$$

(37)

$$\begin{array}{ll}=& \frac{\partial }{\partial {\mathbf{A}}_i}\mathrm{t}\mathrm{r}\left({\mathbf{M}}_i{\mathbf{R}}_i{\mathbf{A}}_i{\mathbf{S}}_i{\mathbf{E}}_i^H+{\mathbf{M}}_i{\mathbf{R}}_i{\mathbf{A}}_i{\mathbf{D}}_i\right)\\ -{\left({\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}{\mathbf{R}}_i\right)}^T{\mathbf{S}}_i^T.\end{array}$$

(38)

Finally, the gradient of f(A _i ) is given by

$$\begin{array}{ll}\nabla f\left({\mathbf{A}}_i\right)& =2{\left(\frac{\mathrm{\partial f}\left({\mathbf{A}}_i\right)}{\partial {\mathbf{A}}_i}\right)}^{\ast }\\ =2{\left({\left({\mathbf{M}}_i{\mathbf{R}}_i\right)}^T{\left({\mathbf{S}}_i{\mathbf{E}}_i^H\right)}^T+{\left({\mathbf{M}}_i{\mathbf{R}}_i\right)}^T{\mathbf{D}}_i^T-{\left({\mathbf{E}}_i^H{\mathbf{G}}_i^{-1}{\mathbf{R}}_i\right)}^T{\mathbf{S}}_i^T\right)}^{\ast }\\ =2\left({\mathbf{R}}_i^H{\mathbf{M}}_i^H\left({\mathbf{E}}_i{\mathbf{S}}_i^H+{\mathbf{D}}_i^H\right)-{\mathbf{R}}_i^H{\mathbf{G}}_i^{-H}{\mathbf{E}}_i{\mathbf{S}}_i^H\right)\end{array}$$

(39)

where (·)^∗ stands for complex conjugate.