1 Introduction

Charm physics plays a unique role in modern flavor physics. Modern experimental facilities, the flavor factories, produce immense quantities of charm quarks, making available for studies the rarest transition channels. Charm decay and production experiments provide valuable checks and supporting measurements for studies of CP-violation in measurements of CKM parameters. Different theoretical methods that make use of various symmetries of the QCD Lagrangian, however, need to be adapted for their applications to the charm system.

Here we will discuss the surprises that the charm quark brings fifty years after its discovery, starting from spectroscopy of the states containing charm quark and ending with CP-violation and mixing phenomena that the charm quark system exhibits.

2 Spectroscopy

Meson spectroscopy has experienced a resurgence in the last twenty years. Ever since the surprise discovery of \(\chi _{c1}(3872)\), which at the time was known as X(3872), Nature presented us with new “gifts”every year. Since then, over fifty new states have been observed (see Fig. 1), with most containing one or more charmed quarks. Most of those states could be classified as “exotic.”

What states can be called exotic? The definition of exotic states is mainly driven by quark models: the exotic states are defined as those whose quantum numbers are not allowed in a simple picture of \(q\bar{q}\) or qqq states. Often, those states require more than 2 or 3 (constituent) quarks to realize the observed quantum numbers. The crypto-exotic states are usually defined as those whose mass/width do not fit in meson or baryon spectra or those whose production or decay properties are incompatible with those of the “ordinary”states. In practice, such distinction is not emphasized, so the crypto-exotic states are also referred to as the exotic ones.

Fig. 1
figure 1

Level diagram for charmonium-like states. Dashed and dotted lines denote di-hadron mass thresholds (from the presentation of R. Lebed at FPCP 2023 [1])

Full size image

Experimental and theoretical studies of meson and baryon spectra provide an important pathway for understanding quark confinement. In particular, mesons containing one heavy quark can provide valuable information about the structure of the heavy quark symmetry, as spectroscopic considerations simplify significantly in the limit of the infinitely heavy charm quark, \(m_c/\Lambda \rightarrow \infty\), where \(\Lambda\) represents a typical scale of hadronic interactions. In this limit, the spin degrees of freedom of the heavy quark decouple, so the total angular momentum of the light degrees of freedom \(J_l^p\) becomes a “good” quantum number. As the parity of a meson can be obtained by knowing the angular momentum quantum number l as \((-1)^{l+1}\), the heavy meson states appear as degenerate parity doublets classified by the total angular momentum of the light degrees of freedom,

$$\begin{aligned} S^p=J_l^p\pm \frac{1}{2}. \end{aligned}$$
(1)

As charm quark is not particularly heavy, the subleading \(1/m_c\) corrections lift this degeneracy.

It is interesting to point out that many new states depicted in Fig. 1 exhibit masses whose values are close to various di-hadron thresholds. This might indicate that their main hadronic components are molecular states,Footnote 1 but there could be other explanations. In fact, the mass of the \(\chi _{c1}(3872)\) suggests that its main component is a molecular state with tiny binding energy, \(m_{\chi _{c1}(3872)} - m_{D^0} - m_{D^{*0}} = -40 \pm 90\) keV [2,3,4], but it is not the only possible explanation [5, 6]. Some exotic states exhibit features that allow for a nice description within an effective field theory framework [7, 8]. For a recent review of the discoveries of the QCD exotic states, see [1].

3 Rare decays of charmed mesons

A conventional definition of the rare decays of the charmed states involves quark flavor-changing neutral current (FCNC) transitions in the charm quark sector, i.e., those generated by the quark transition \(c \rightarrow u\bar{\ell }\ell ^\prime\), where \(\{\ell ,\ell ^\prime \} = \{e,\mu ,\tau \}\). Such transitions are only possible at the loop level in the Standard Model (SM), which makes them, at least as a matter of principle, suitable probes of the beyond-the-SM (BSM) physics.

Theoretical predictions for the FCNC effects in the charm sector of the SM are rather uncertain. This is mainly because while the Glashow–Iliopoulos–Maiani (GIM) mechanism ensures that the dominant contribution is (naively) proportional to the mass squared of the heaviest down-type quark, the b-quark, its effects are largely diminished by a combination of the corresponding Cabbibo–Kobayashi–Maskawa (CKM) matrix elements, \(V_{ub} V_{cb}^*\). The remaining effects are proportional to the difference between the strange and the down quark contributions [9], which vanish in the flavor \(SU(3)_F\) limit. Then, poorly controlled long-distance QCD effects might spoil unambiguous identifications of the BSM effects [9, 10]. Those long-distance effects could be ultimately brought under theoretical control by employing lattice or other nonperturbative methods.

3.1 Rare decays with lepton flavor conservation

The ultimate goal of BSM physics studies at low energies involves a careful determination of the Wilson coefficients of the Standard Model Effective Field Theory (SM EFT) Lagrangian [11, 12], which encapsulate all heavy BSM degrees of freedom. The SM EFT Lagrangian could be further matched to a low-energy effective Lagrangian that describes rare charm transitions governed by the \(c \rightarrow u \ell ^+ \ell ^-\) current,

$$\begin{aligned} {{ }L}_{\textrm{BSM}}^{\textrm{rare}} = - \frac{1}{\Lambda ^2} \sum _{i=1}^{10} \widetilde{C}_i (\mu ) ~ \widetilde{Q}_i, \end{aligned}$$
(2)

where \(\mathrm{\widetilde{C}}_i\) are Wilson coefficients, \(\widetilde{Q}_i\) are the effective operators, and \(\Lambda\) represents the energy scale of BSM interactions that generate \(\widetilde{Q}_i\) operators. There are only ten of these operators with canonical dimension six. The first five can be listed as

$$\begin{aligned} \begin{array}{l} \widetilde{Q}_1 = (\overline{\ell }_L \gamma _\mu \ell _L) (\overline{u}_L \gamma ^\mu c_L)\, \qquad \widetilde{Q}_4 = (\overline{\ell }_R \ell _L) (\overline{u}_R c_L) \, \\ \widetilde{Q}_2 = (\overline{\ell }_L \gamma _\mu \ell _L) (\overline{u}_R \gamma ^\mu c_R)\, \qquad \widetilde{Q}_5 = (\overline{\ell }_R \sigma _{\mu \nu } \ell _L) ( \overline{u}_R \sigma ^{\mu \nu } c_L)\, \\ \widetilde{Q}_3 = (\overline{\ell }_L \ell _R) \ (\overline{u}_R c_L) \, \end{array} \end{aligned}$$
(3)

and five additional operators \(\widetilde{Q}_6, \dots , \widetilde{Q}_{10}\) obtained from those in Eq. (3) by interchanging \(L \leftrightarrow R\), e.g. \(\widetilde{Q}_6 = (\overline{\ell }_R \gamma _\mu \ell _R) (\overline{u}_R \gamma ^\mu c_R)\), \(\widetilde{Q}_7 = (\alpha /4) (\overline{\ell }_R \gamma _\mu \ell _R) (\overline{u}_L \gamma ^\mu c_L)\), etc.

The effective Lagrangian of Eq. (2) is quite general, and thus it also contains the SM contribution. The Wilson coefficients in Eq. (2) can be computed using the conventional methods [9]. Other rare decays, such as rare radiative \(D \rightarrow \rho \gamma\) transitions, receive significant SM contributions, which are often difficult to calculate [13].

3.2 Rare leptonic decays

The experimentally simplest rare decay is a purely leptonic transition of a neutral D-meson into a lepton pair, \(D^0 \rightarrow \ell ^+ \ell ^-\). The most general \(D^0 \rightarrow \ell ^+ \ell ^-\) decay amplitude can be written

$$\begin{aligned} {{ }A} (D^0 \rightarrow \ell ^+\ell ^-) = {\overline{u}}(p_-, s_-) \left[ A + \gamma _5 B\right] v(p_+, s_+)\,, \end{aligned}$$
(4)

where \(u(p_-, s_-)\) and \(v(p_+, s_+)\) are the spinors for the lepton states, and A and B are the (complex) amplitudes that depend on the short-distance Wilson coefficients of Eq. (2) and long-distance parameters. It is essential to point out that all non-perturbative QCD effects in that transition can be parameterized by a single D-meson decay constant, which can be computed numerically with lattice QCD or other nonperturbative methods,

$$\begin{aligned} \left| A\right|= & {} \frac{f_D M_D^2}{4 \Lambda ^2 m_c} \left[ \widetilde{C}_{3-8} + \widetilde{C}_{4-9}\right] \nonumber \\ \left| B\right|= & {} \frac{f_D}{4 \Lambda ^2} \left[ 2 m_\ell \left( \widetilde{C}_{1-2} + \widetilde{C}_{6-7}\right) \right. + \left. \frac{M_D^2}{m_c} \left( \widetilde{C}_{4-3} + \widetilde{C}_{9-8}\right) \right] , \end{aligned}$$
(5)

with \(\widetilde{C}_{i-k} \equiv \widetilde{C}_i-\widetilde{C}_k\). It is worth noting that matrix elements of some operators in Eq. (3) or their linear combinations vanish in the calculation of \({{ }B} (D^0\rightarrow \ell ^+\ell ^-)\). For example, \(\langle \ell ^+ \ell ^- | \widetilde{Q}_5 | D^0 \rangle = \langle \ell ^+ \ell ^- | \widetilde{Q}_{10} | D^0 \rangle = 0\) vanish identically, while \(\langle \ell ^+ \ell ^- | Q_9 | D^0 \rangle \equiv (\alpha /4) \langle \ell ^+ \ell ^- | (\widetilde{Q}_1 + \widetilde{Q}_7) | D^0 \rangle = 0\) due to vector current conservation, etc.

The amplitude of Eq. (4) results in the following branching fractions for the lepton flavor-diagonal decays,

$$\begin{aligned} {{ }B} (D^0 \rightarrow \ell ^+\ell ^-) = \frac{M_D}{8 \pi \Gamma _{\textrm{D}}} \sqrt{1-\frac{4 m_\ell ^2}{M_D^2}} \ \left[ \left( 1-\frac{4 m_\ell ^2}{M_D^2}\right) \left| A\right| ^2 + \left| B\right| ^2 \right] , \end{aligned}$$
(6)

Any NP model that contributes to \(D^0 \rightarrow \ell ^+ \ell ^-\) can be constrained by bounds on the Wilson coefficients appearing in Eq. (5). We note that because of helicity suppression, studies of lepton universality in \(D^0 \rightarrow \mu ^+ \mu ^-\) vs \(D^0 \rightarrow e^+ e^-\) are very challenging experimentally. These decays were studied experimentally by Belle [14] and BaBar [15] collaborations. The best constraints on those decays are currently provided by the LHCb collaboration [16],

$$\begin{aligned} {{ }B}(D^0 \rightarrow \mu ^+\mu ^-)< & {} 6.2 \times 10^{-9}, \nonumber \\ {{ }B}(D^0 \rightarrow e^+ e^-)< & {} 7.9 \times 10^{-8}, \end{aligned}$$
(7)

An exciting alternative to studies of \(c \rightarrow u e^+ e^-\) in leptonic D decays is to measure the corresponding production process \(e^+e^- \rightarrow D^*(2007)\). The process, shown in Fig. 2, was proposed in [17]. This is possible at an \(e^+e^-\) collider that is tuned to run at the center-of-mass energy corresponding to the mass of the \(D^*\) meson, \(\sqrt{s} \approx 2007\) MeV. Such machines exist, e.g., BEPCII or VEPP-2000. They have already explored that energy region in measuring the \(e^+e^- \rightarrow\) hadrons for R(s).

The technique calls for the searches for the produced \(D^{*0}\) resonance, tagged by a single charmed particle in the final state, that decay strongly (\(D^{*0} \rightarrow D^0\pi ^0\)) or electromagnetically (\(D^{*0}\rightarrow D^0\gamma\)) with branching fractions of \((61.9\pm 2.9)\%\) and \((38.1\pm 2.9)\%\) respectively. This process, albeit very rare, has clear advantages for BSM studies compared to the \(D^0 \rightarrow e^+e^-\) decay: the helicity suppression is absent, and a richer set of effective operators can be probed. It is also interesting to note that contrary to other rare decays of charmed mesons, long-distance SM contributions are under theoretical control and contribute at the same order of magnitude as the short-distance ones.

The first studies of this process in the production mode were performed by the CMD-3 Collaboration [18] and resulted in an upper limit reported as a branching ratio of the decays of the \(D^{0*}(2007)\),

$$\begin{aligned} {{ }B}(D^{0*}(2007) \rightarrow e^+ e^-) < 1.7 \times 10^{-6}. \end{aligned}$$
(8)

Alternatively, the decays \(D^{0*}(2007) \rightarrow \mu ^+\mu ^-)\) or \(D^{0*}(2007) \rightarrow e^+ e^-)\) can be searched for by analyzing \(B^- \rightarrow \pi ^- \mu ^+\mu ^-\) decays with \(B^- \rightarrow \pi ^- D^{0*} (\rightarrow \mu ^+\mu ^-)\). Recently, LHCb collaboration posted an upper limit [19],

$$\begin{aligned} {{ }B}(D^{0*}(2007) \rightarrow \mu ^+\mu ^-) < 2.6 \times 10^{-8}. \end{aligned}$$
(9)

Similar opportunities exist for B-decays as well [17, 20]. Studying the BSM contributions to rare decays in charm can be advantageous to study correlations of various processes, for example, \(D^0-\overline{D}{}^0\) mixing and rare decays [21]. In general, one cannot predict the rare decay rate by knowing just the mixing rate, even if both it and \({{ }B}(D^0 \rightarrow \ell ^+\ell ^-)\) are dominated by a single operator contribution. It is, however, possible to do so for a restricted subset of NP models [21, 22].

Fig. 2
figure 2

Probing the \(c\bar{u}\rightarrow e^+ e^-\) vertex with the \(D^*(2007)^0\) resonance production in \(e^+e^-\) collisions (from [17])

Full size image

3.3 Rare decays without lepton flavor conservation

If lepton-flavor nonconserved decays are allowed, the amplitude of Eq. (4) also results in the following branching fractions for the lepton off-diagonal decays,

$$\begin{aligned} {{ }B} (D^0 \rightarrow \mu ^+e^-) = \frac{M_D}{8 \pi \Gamma _{\textrm{D}}} \left( 1-\frac{ m_\mu ^2}{M_D^2} \right) ^2 \ \left[ \left| A\right| ^2 + \left| B\right| ^2 \right] \,. \end{aligned}$$
(10)

In this expression, A and B are also related to the Wislon coefficients of an effective Lagrangian, and the electron mass is safely neglected. Experimental limits on \({{ }B}(D^0 \rightarrow \mu ^+e^-)\) [23]

$$\begin{aligned} {{ }B}(D^0 \rightarrow \mu ^+e^-) < 1.3 \times 10^{-8}, \end{aligned}$$
(11)

give constraints on lepton-flavor-violating interactions via Eq. (11). Similar limits can also be obtained from two-body charmed quarkonium decays [24].

3.4 Rare decays into invisible states

High-luminosity \(e^+e^-\) flavor factories, such as SuperKEKb or the Super Tau-Charm Facility (STCF), provide an excellent opportunity to search for the rare processes where D mesons decay into the final states that leave no traces in a detector, or invisible final states. Such searches require high purity of the final states achievable at \(e^+e^-\) colliders.

Such invisible final states could represent feebly-interacting light new physics particles such as dark photons or axion-like particles (ALPs). Depending on their masses and couplings to the SM particles, they might or might not be dark matter candidates. If those particles decay after leaving a detector, their experimental signature (or the absence thereof) is like the neutrinos.

Thus, the only irreducible SM background with the same experimental signature is heavy meson decays into the final states containing only neutrinos. Transitions of a \(B^0_q (D^0)\) meson into such final states are described by an effective Lagrangian,

$$\begin{aligned} {{ }L}_{\textrm{eff}} = -\frac{4 G_F}{\sqrt{2}}\frac{\alpha }{2\pi \sin ^2\theta _W} \ \sum _{l=e,\mu ,\tau } \sum _{k} \lambda _k X^l(x_k) \left( J_{Qq}^\mu \right) \left( \overline{\nu }^l_L \gamma _\mu \nu ^l_L\right) , \end{aligned}$$
(12)

where \(J_{Qq}^\mu =\overline{u}_L \gamma ^\mu c_L\) for charm transitions. The functions \(\lambda _k X^l(x_k)\) are combinations of the CKM factors and Inami-Lim functions. For the charm FCNC \(c \rightarrow u\) transitions we keep the contributions from both internal b and s-quarks in these functions,

$$\begin{aligned} \sum _{k} \lambda _k X^l(x_k) = V_{cs}^* V_{us} X^l(x_s)+V_{cb}^* V_{ub} X^l(x_b), \end{aligned}$$
(13)

where \(X^l(x_q) = \overline{D}(x_q,y_l)/2\) with \(y_l=m_l^2/m_W^2\) are related to the Inami-Lim functions defined in [25],

$$\begin{aligned}{} {} \overline{D}(x_q,y_l) & = \frac{1}{8}\frac{x_q y_l}{x_q-y_l} \left( \frac{y_l-4}{y_l-1}\right) ^2 \ln y_l + \frac{x_q}{4} -\frac{3}{8}\left( 1+3\frac{1}{y_l-1}\right) \frac{x_q}{x_q-1} + \frac{x_q}{8} \left[ \frac{x_q}{y_l-x_q}\left( \frac{x_q-4}{x_q-1}\right) ^2+1+\frac{3}{(x_q-1)^2}\right] \ln {x_q}. \end{aligned}$$

Given this, one can easily estimate branching ratios for \(D( \text{ or }~B_q) \rightarrow \nu \overline{\nu }\) decays. One can immediately notice that the left-handed structure of the Lagrangian results in helicity suppression of these decays because the initial state is a spin-0 meson. The branching ratio is therefore proportional to a tiny factor \(x_\nu ^2= m^2_\nu /M^2_D\) [26],

$$\begin{aligned} {{ }B}(D\rightarrow \nu \overline{\nu })= \frac{G_F^2\alpha ^2f_{D}^2 M_{D}^3}{16 \pi ^3 \sin ^4 \theta _W\Gamma _{D}} \left| \sum _{k} \lambda _k X^l(x_k)\right| ^2 x_\nu ^2 , \end{aligned}$$
(14)

where we summed over all possible neutrino states. Here \(\Gamma _{D}=1/\tau _{D}\) is the total width of the D meson. A similar formula for B-decays can be obtained by substituting relevant quantities.

As can be seen from Eq. (14), the branching ratio is exactly zero in the minimal standard model with massless neutrinos. For neutrino masses \(m_\nu \sim \sum _i m_{\nu _i} < 1\) eV, where \(m_{\nu _i}\) is the mass of one of the neutrinos, Eq. (14) yields the branching ratios of \({{ }B}_{th}(D^0 \rightarrow \nu \bar{\nu }) \simeq 1\times 10^{-30}\), which is practically unobservable! It is instructive to point out that the relevant branching ratios for B-decays are also small, \({{ }B}_{th}(B_{s}^0 \rightarrow \nu \bar{\nu }) \simeq 3 \times 10^{-24}\), and \({{ }B}_{th}(B_{d}^0 \rightarrow \nu \bar{\nu }) \simeq 1\times 10^{-25}\). Thus, transitions to invisible final states constitute almost background-free modes for searches for new light particles.

To complete the argument, we must point out that, experimentally, the \(\nu \bar{\nu }\) final state does not constitute a good representation of the invisible width of \(D^0\) or \(B^0\) mesons in the Standard Model. Indeed, in the SM, the final state that is not detectable at a collider contains an arbitrary number of neutrino pairs [27],

$$\begin{aligned} \mathcal {B}\left( D\rightarrow E\!\!\!\!/\right) =\mathcal {B}\left( D\rightarrow \nu \bar{\nu }\right) +\mathcal {B}\left( D\rightarrow \nu \bar{\nu }\nu \bar{\nu }\right) +\dots . \end{aligned}$$
(15)

As can be seen from the Eq. (14)), the decay to \(\nu \bar{\nu }\) final state is helicity-suppressed. The four-neutrino final state, however, is not. Thus, it is expected to have a considerably larger branching ratio,

$$\begin{aligned} \frac{\mathcal {B}\left( D\rightarrow \nu \bar{\nu }\nu \bar{\nu }\right) }{\mathcal {B}\left( D\rightarrow \nu \bar{\nu } \right) } \sim \frac{G_F^2 M_D^4}{16 \pi ^2 x_{\nu }^{2}} \gg 1. \end{aligned}$$
(16)

Still, a result of a calculation shows [27] that the SM result for the invisible width of a heavy meson is still tiny, the largest branching ratio of the \(B_s\) decay is still \({{ }O}(10^{-27})\) Therefore, \(D(B) \rightarrow {\rm invisible}\) is still an excellent channel to search for invisible decays into NP particles.

The decays of the \(D^0\)-mesons into invisible states \({{ }B}(D^0 \rightarrow {\rm invisible})\) have been performed by Belle collaboration [28],

$$\begin{aligned} {{ }B}(D^0 \rightarrow \rm invisible) < 9.4 \times 10^{-5}, \end{aligned}$$
(17)

which provides constraints on the couplings of the invisible light states to the D-meson state.

Branching fractions for the heavy meson states decaying into \(\chi _s \overline{\chi }_s\) and \(\chi _s \overline{\chi }_s\gamma\), where \(\chi _s\) is a DM particle of spin s, can be calculated in the EFT framework. Since the production of scalar \(\chi _0\) states avoid helicity suppression, the decay of a \(D^0\) state into the final state containing a pair of the \(\chi _s\) state can provide good constraints on their interaction properties.

A generic effective Lagrangian for scalar \(\chi _0\) interactions with the \(c \rightarrow u\) current has a simple form [26]

$$\begin{aligned} {{ }L}_{\textrm{eff}} = -2 \sum _i \frac{C_i}{\Lambda ^2} O_i, \end{aligned}$$
(18)

where \(C_i\) are the Wilson coefficients. The effective operators \(O_i\) contain a heavy quark \(Q=\{b,c\}\) and a light quark q of the same electric charge as Q and can be written as

$$\begin{aligned} O_1 \, = \, & {} m_Q (\overline{q}_R Q_L)(\chi _0^* \chi _0), \qquad O_3 = (\overline{q}_L \gamma ^{\mu } Q_L)(\chi _0^* {\mathop {\partial }\limits ^{\leftrightarrow }}_{\mu }\chi _0), \nonumber \\ O_2\, =\, & {} m_Q (\overline{q}_L Q_R)(\chi _0^* \chi _0), \qquad O_4 = (\overline{q}_R \gamma ^{\mu } Q_R)(\chi _0^* {\mathop {\partial }\limits ^{\leftrightarrow }}_{\mu }\chi _0), \end{aligned}$$
(19)

where \({\mathop {\partial }\limits ^{\leftrightarrow }} = ({\mathop {\partial }\limits ^{\rightarrow }}-{\mathop {\partial }\limits ^{\leftarrow }})/2\) and the light new anti-particle \(\overline{\chi }_0\) may or may not coincide with \(\chi _0\). The branching fraction for the two-body decay \(D^0_q \rightarrow \chi _0 \bar{\chi }_0\) is

$$\begin{aligned}{} {} {{ }B} (D^0 \rightarrow \chi _0 \bar{\chi }_0) & = \frac{\left( C_1-C_2\right) ^2}{4\pi m_{D^0} \Gamma _{D^0}} \left[ \frac{f_{P} m_{D^0}^2 m_c}{\Lambda ^2 (m_c +m_u)}\right] ^2 \sqrt{1-4 x_\chi ^2}, \end{aligned}$$
(20)

where \(x_\chi = {m_\chi }/{m_{D^0}}\) is a rescaled mass of the light BSM particle \(\chi _0\). This rate is not helicity-suppressed, so it could allow us to study properties of \(\chi _0\) states at an \(e^+e^-\) flavor factory. Using the formalism above, the photon energy distribution and the decay width of the radiative transition \(D^0_q \rightarrow \chi _0\,\chi _0\,\gamma\) can be calculated [26].

The decays to the “invisible”+ “visible”final states, such as \(D \rightarrow \pi + {\rm invisible}\), can also be studied. In particular, theoretical predictions show [29] that such final states are quite sensitive to BSM models [30].

There are many possible rare decays of D mesons and charmed baryons that can be studied. For a more comprehensive recent review of such decays, see [13].

4 Nonleptonic decays of charmed mesons

Studies of non-leptonic decays of charmed mesons constitute a primary method of investigation into direct CP-violation in that system. Even though the experimental precision for studying D decays has steadily improved over the past decade, theory calculations have faced severe challenges. Precise numerical predictions of CP-violating observables are not possible at the moment due to significant non-perturbative contributions from strong interactions affecting weak-decay amplitudes. A way out in such a situation involves phenomenological fits of decay amplitudes to experimentally measured decay widths of charmed mesons. Predictions are possible if the number of fit parameters is smaller than the number of experimentally measured observables. Such fits require a defined procedure on how to parametrize complex-valued decay amplitudes [31].

One way to approach the problem is to note that the light-quark operators in the weak effective Hamiltonian governing heavy-quark decays, and the initial and final states form product representations of a flavor \(SU(3)_F\) group. These product representations can be reduced with the help of the Wigner-Eckart theorem. This way, a basis is chosen to expand all decay amplitudes in terms of the reduced matrix elements. The \(SU(3)_F\) analysis of decay amplitudes cannot predict their absolute values. However, one can relate transition amplitudes for different decays within this approach, which is helpful for experimental analysis, at least in the symmetry limit.

Alternatively, a topological flavor-flow approach can be used. The flavor-flow approach postulates a basis of universal flavor topologies for various decay amplitudes. \(SU(3)_F\) symmetry can be used to relate decay amplitudes, as both the light-quark final states and initial D-mesons transform under it.

It is helpful to classify the nonleptonic decay amplitudes according to their weak suppression with respect to \(\lambda \equiv \sin \theta _C \simeq V_{us}\). For example, the Cabibbo-favored amplitudes (CF) are the ones with a decay amplitude proportional to \(\lambda ^0 \sim 1\), the singly-Cabibbo-suppressed amplitudes (SCS) are the ones with a decay amplitude proportional to \(\lambda ^1\), and doubly-Cabibbo suppressed transitions (DCS) are the ones with the decay amplitude proportional to \(\sin \theta _C^2 \sim \lambda ^2\).

4.1 Amplitudes: \(SU(3)_F\) flavor symmetry

In the flavor-symmetry approach, all particles involved in the decay process are labeled by how they transform under flavor \(SU(3)_F\). As charm quarks transform as singlets under flavor \(SU(3)_F\), the transformation of \(D_q\) mesons and charmed baryons are governed by the flavor of the light quark q. The fundamental representation of \(SU(3)_F\) is a triplet, 3, so the light quarks \(q=u\), d, and s belong to this representation with \((1,2,3)=(u,d,s)\). Thus, D mesons containing light quarks (u, d, s) form triplets and can be written as vectors,

$$\begin{aligned} D_i = \left( D^0, D^+, D_s\right) . \end{aligned}$$
(21)

Let us look into the decay amplitudes of a charmed meson into a pair of light pseudoscalar mesons. The octet of such mesons formed by the light quarks q can be represented by a \(3 \times 3\) matrix \(M^i_j\), where the upper index of \(M^i_j\) represents the quarks, while the lower index represents the antiquarks,

$$\begin{aligned} M = \left( \begin{array}{l@{\quad}l@{\quad}l} \dfrac{\pi ^0}{\sqrt{2}} + \dfrac{\eta _8}{\sqrt{6}} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\dfrac{\pi ^0}{\sqrt{2}} + \dfrac{\eta _8}{\sqrt{6}} &{} K^0 \\ K^- &{} \overline{K}^0&{} -\sqrt{\dfrac{2}{3}}\eta _8 \end{array} \right) \end{aligned}$$
(22)

Decays into the higher spin light quark states can be represented similarly. One must note that some physical states, such as \(\eta\) and \(\eta ^\prime\) are formed by mixing with an \(SU(3)_F\) singlet, \(\eta _1\) for pseudoscalars and \(\omega _1\) for the vector mesons.

To describe nonleptonic charm decays, one needs to write a transition Hamiltonian. The \(\Delta C=-1\) part of this Hamiltonian has the flavor structure \((\bar{q}_ic)(\bar{q}_jq_k)\), so its matrix representation is written with a fundamental index and two antifundamentals, \(H^{ij}_k\). This Hamiltonian can be decomposed into the sum of irreducible representations according to \(\textbf{3} \times \mathbf{\overline{3}} \times \mathbf{\overline{3}} =\mathbf{\overline{15}} + \textbf{6} + \textbf{3} + \mathbf{\overline{3}}\). The Hamiltonian \(H^{ij}_k\) is also traceless, so only the \(\mathbf{\overline{15}}\) (symmetric on i and j) and \(\textbf{6}\) (antisymmetric on i and j) representations appear, \({1\over 2} ({{ }O}_{\mathbf{\overline{15}}} + {{ }O}_{\textbf{6}})\), where [32]

$$\begin{aligned} {{ }O}_{\mathbf{\overline{15}}} \,= \, & {} (\bar{s}c)(\bar{u}d) + (\bar{u}c)(\bar{s}d) + s_1(\bar{d}c)(\bar{u}d) + s_1(\bar{u}c)(\bar{d}d) - s_1(\bar{s}c)(\bar{u}s) - s_1(\bar{u}c)(\bar{s}s) - s_1^2(\bar{d}c)(\bar{u}s) - s_1^2(\bar{u}c)(\bar{d}s) , \nonumber \\ {{ }O}_{\textbf{6}} \, =\, & {} (\bar{s}c)(\bar{u}d) - (\bar{u}c)(\bar{s}d) + s_1(\bar{d}c)(\bar{u}d) - s_1(\bar{u}c)(\bar{d}d) - s_1(\bar{s}c)(\bar{u}s) + s_1(\bar{u}c)(\bar{s}s) - s_1^2(\bar{d}c)(\bar{u}s) + s_1^2(\bar{u}c)(\bar{d}s) , \end{aligned}$$
(23)

where \(s_1=\sin \theta _C\approx 0.22\). The matrix representations \(H(\mathbf{\overline{15}})^{ij}_k\) and \(H(\textbf{6})^{ij}_k\) have nonzero elements as shown in Eq. (24).

$$\begin{aligned} \begin{array}{lll} H(\mathbf{\overline{15}})^{ij}_k: &{} H^{13}_2 = H^{31}_2=1 &{} H^{12}_2 = H^{21}_2 = s_1\\ &{} ~H^{13}_3 = H^{31}_3 = -s_1 &{} H^{12}_3 = H^{21}_3=-s_1^2 \\ H(\textbf{6})^{ij}_k: &{} H^{13}_2 = -H^{31}_2=1 &{} H^{12}_2 = -H^{21}_2 = s_1 \\ &{} ~H^{13}_3 = -H^{31}_3 = -s_1 &{} H^{12}_3 = -H^{21}_3 = -s_1^2 \end{array} \end{aligned}$$
(24)

In the \(SU(3)_F\) limit, the effective Hamiltonian for the hadronic decays to two pseudoscalars \(D \rightarrow PP\) can be written as

(25)

Here \(a_{\mathbf{\overline{15}}}\), \(b_{\mathbf{\overline{15}}}\), and \(c_{\textbf{6}}\) are the reduced matrix elements that correspond to different \(SU(3)_F\) representations and is an \(SU(3)_F\)-breaking term. Several amplitude relations can be obtained from Eq. (25). For example, in \(SU(3)_F\) limit, there is a relation between the \(A_{D^0 \rightarrow K^+ K^-}\) and \(A_{D^0 \rightarrow \pi ^+ \pi ^-}\) decay amplitudes that can be obtained from Eq. (25),

$$\begin{aligned} A(D^0 \rightarrow K^+ K^-) \, = \, & {} s_1 \left( -a_{\mathbf{\overline{15}}}-b_{\mathbf{\overline{15}}} + c_{\textbf{6}} \right) , \nonumber \\ A(D^0 \rightarrow \pi ^+ \pi ^-) \, =\, & {} s_1 \left( a_{\mathbf{\overline{15}}}+b_{\mathbf{\overline{15}}} - c_{\textbf{6}} \right) , \end{aligned}$$
(26)

so it appears that \(A(D^0 \rightarrow K^+ K^-) = -A(D^0 \rightarrow \pi ^+ \pi ^-)\). Experimental measurements of \(D^0 \rightarrow K^+ K^-\) and \(D^0 \rightarrow \pi ^+ \pi ^-\) transitions give [33]

$$\begin{aligned} {{ }B}(D^0 \rightarrow K^+ K^-)\, = \, & {} \left( 4.08 \pm 0.06\right) \times 10^{-3}, \nonumber \\ {{ }B}(D^0 \rightarrow \pi ^+ \pi ^-)\,=\, & {} \left( 1.454 \pm 0.024\right) \times 10^{-3} \end{aligned}$$
(27)

which shows that accounting for the phase space corrections, the amplitude relation is not satisfied, indicating the need to include \(SU(3)_F\) symmetry-breaking corrections.

Such corrections can be taken into account perturbatively, assuming that they are proportional to light quark masses suppressed by a typical hadronic scale \(\Lambda _{\textrm{had}} \sim 1\) GeV. Since the quark mass operator belongs to the matrix representation \(M^i_j=\textrm{diag}(m_u,m_d,m_s)\), transforms as \(\textbf{8} + \textbf{1}\). Retaining the strange quark mass only, the breaking is parameterized in

$$\begin{aligned} \gamma = \frac{m_s}{3 \Lambda _{\textrm{had}}} \left( {\begin{array}{c@{\quad}c@{\quad}c} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array} } \right) + \frac{m_s}{3 \Lambda _{\textrm{had}}} \left( {\begin{array}{c@{\quad}c@{\quad}c} -1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 2 \\ \end{array} } \right) \end{aligned}$$
(28)

where the first term transforms as a singlet and thus can be absorbed into the reduced matrix elements of the \(SU(3)_F\) conserving amplitudes. The second term gives rise to \(SU(3)_F\) breaking. A complete analysis with broken \(SU(3)_F\) is possible [12, 32].

The \(SU(3)_F\) breaking part of the Hamiltonian of Eq. (25) reads,

(29)

where the two triplets have one non-zero component, each with

$$\begin{aligned} H_1(\mathbf{\overline{3}}^{(1)}) = -s_1, \quad H_1(\mathbf{\overline{3}}^{(2)}) = s_1, \end{aligned}$$
(30)

so that the relations of Eq. (26) are modified as to

$$\begin{aligned} A_{D^0 \rightarrow K^+ K^-}= & {} s_1 \left( -a_{\mathbf{\overline{15}}}-b_{\mathbf{\overline{15}}} + c_{\textbf{6}} - 2 \frac{m_s}{\Lambda _{\textrm{had}}} d_{\mathbf{\overline{3}}} - \frac{m_s}{\Lambda _{\textrm{had}}} e_{\mathbf{\overline{3}}} \right) , \nonumber \\ A_{D^0 \rightarrow \pi ^+ \pi ^-}= & {} s_1 \left( a_{\mathbf{\overline{15}}}+b_{\mathbf{\overline{15}}} - c_{\textbf{6}} - 2 \frac{m_s}{\Lambda _{\textrm{had}}} d_{\mathbf{\overline{3}}} - \frac{m_s}{\Lambda _{\textrm{had}}} e_{\mathbf{\overline{3}}} \right) . \end{aligned}$$
(31)

As can be seen from Eq. (31) the breaking term contributes equally to \(A(D^0 \rightarrow K^+ K^-)\) and \(A(D^0 \rightarrow \pi ^+ \pi ^-)\), but since the leading terms are of opposite sign, the amount of symmetry breaking needed to explain the factor of three difference between \(\Gamma (D^0 \rightarrow K^+ K^-)\) and \(\Gamma (D^0 \rightarrow \pi ^+ \pi ^-)\) could be quite modest. The above discussion is important for a proper understanding of the observed CP violation in D decays to \(\pi \pi\) and KK final states.

4.2 Amplitudes: flavor-flow (topological) diagrams

Expansion of the decay amplitudes in terms of the universal parameters using the Wigner-Eckart theorem is not a unique method of parameterizing nonleptonic decay amplitudes. Any approach that relies on experimental data to fix the “basis parameters”would be equivalent to the \(SU(3)_F\) amplitude method. Another popular approach dubbed the flavor-flow or topological SU(3) approach, has been rather popular. This approach involves a set of “quark diagrams”, which shows the flow of flavor in usual Feynman diagrams. The application of this method to D-decays was developed in [34, 35]. In the case of linear \(SU(3)_F\)-breaking, this basis was shown to be equivalent to the basis based on the reduced amplitudes described above [36].

In the topological flavor-flow approach, each decay amplitude is parametrized according to the topology of Feynman diagrams driving the decay amplitudes. It is, however, understood that only the flow of flavor is described by those graphs; the amplitudes are not computed but taken as non-perturbative parameters forming the basis of the expansion and fitted to experimental data. The decays topologies are conventionally chosen as follows: a color-favored tree amplitude (usually denoted by T), a color-suppressed tree amplitude (C), an exchange amplitude (E), a penguin amplitude (P), an annihilation amplitude (A), and a penguin annihilation amplitude (PA). The diagrams are depicted in Fig. 3. One can use flavor \(SU(3)_F\) relations to relate various decay amplitudes, similar to those derived in the previous section. Often, the following phase conventions are used [34],

Fig. 3
figure 3

Flavor-flow diagrams representing the contributions of various decay topologies (from [12])

Full size image
  1. 1.

    Charmed mesons: \(D^0 = -c \overline{u}\), \(D^+ = c \overline{d}\), and \(D_s = c \overline{s}\).

  2. 2.

    Pseudoscalar mesons: \(\pi ^+ = u \overline{d}\), \(\pi ^0 = \left( u \overline{u} - d \overline{d}\right) /\sqrt{2}\), \(\pi ^- = -d \overline{u}\), \(K^+ = u \overline{s}\), \(K^0 = d \overline{s}\), \(\overline{K}^0 = s \overline{d}\), \(K^- = - s \overline{u}\), \(\eta = \left( s \overline{s} - u \overline{u} - d \overline{d}\right) /\sqrt{3}\), and \(\eta ^\prime = \left( u \overline{u} + d \overline{d} - 2\,s \overline{s}\right) /\sqrt{6}\).

  3. 3.

    Vector mesons: \(\rho ^+ = u \overline{d}\), \(\rho ^0 = \left( u \overline{u} - d \overline{d}\right) /\sqrt{2}\), \(\rho ^- = -d \overline{u}\), \(\omega ^0 = \left( u \overline{u} + d \overline{d}\right) /\sqrt{2}\), \(K^{*+} = u \overline{s}\), \(K^{*0} = d \overline{s}\), \(\overline{K}^{*0} = s \overline{d}\), \(K^{*-} = - s \overline{u}\), and \(\phi = s \overline{s}\).

The color-allowed amplitude T is usually taken to be real. As with the \(SU(3)_F\) approach, this method does not provide absolute predictions for the branching fractions in D-meson decays. However, it provides relations among several decay amplitudes by matching the quark-level “flavor topology” graphs with the final states defined above. For example, a DCS decays \(D^0 \rightarrow K^+\pi ^-\) can proceed via a tree-level amplitude \(T (c \rightarrow u \overline{s} d)\) and an exchange amplitude \(E (c \overline{u} \rightarrow \overline{s} d)\). Matching those with the initial state meson \(D^0 = -c \overline{u}\) and final state mesons \(K^+ = u \overline{s}\) and \(\pi ^- = -d \overline{u}\), one obtains the following amplitude relation,

$$\begin{aligned} A(D^0 \rightarrow K^+\pi ^-) = T+E \equiv \frac{G_F}{\sqrt{2}} V_{ud} V_{cs}^* \left( {{ }T} + {{ }E}\right) , \end{aligned}$$
(32)

where we use calligraphic notation for the amplitudes with \(G_F/\sqrt{2}\) and CKM-factors removed. Similarly, for other transitions, one obtains

$$\begin{aligned} A(D^0 \rightarrow K^0 \pi ^0)\, = \, & {} \frac{1}{\sqrt{2}} (C-E) = \frac{1}{\sqrt{2}} \frac{G_F}{\sqrt{2}} V_{us} V_{cd}^* \ ({{ }C}^{\prime \prime }- {{ }E}^{\prime \prime }), \nonumber \\ A(D^0 \rightarrow \overline{K}^0 \pi ^0)\, =\, & {} \frac{1}{\sqrt{2}} (C-E) = \frac{1}{\sqrt{2}} \frac{G_F}{\sqrt{2}} V_{ud} V_{cs}^* \ ({{ }C}- {{ }E}), \nonumber \\ A(D^+ \rightarrow K^0 \pi ^+)\, =\, & {} C+A = \frac{G_F}{\sqrt{2}} V_{us} V_{cd}^* \ ({{ }C}^{\prime \prime } + {{ }A}^{\prime \prime }), \nonumber \\ A(D^+ \rightarrow \overline{K}^0 \pi ^+)\, =\, & {} T+C = \frac{G_F}{\sqrt{2}} V_{ud} V_{cs}^* \ ({{ }T}+ {{ }C}), \nonumber \\ A(D^0 \rightarrow K^0 \eta )\, =\, & {} \frac{1}{\sqrt{3}} C = \frac{1}{\sqrt{3}} \frac{G_F}{\sqrt{2}} V_{us} V_{cd}^* \ {{ }C}^{\prime \prime }, \end{aligned}$$
(33)

and so on. Note that in Eq. (33), we denoted DCS amplitudes with double primes, while SCS amplitudes are conventionally denoted by a single prime. The resulting parameterizations can be fitted separately to CF, SCS, and DCS nonleptonic D-decays. The sample recent fits and their time progression are shown in Table 1 (see also [31]).

No penguin amplitudes contribute to CF or DCS decays, which is reflected in Eq. (33). The structure of SCS decay amplitudes is richer, involving P or PA amplitudes. Considering the final state interaction, it might not be easy to introduce such amplitudes unambiguously.

One reason for the employed phase convention is a requirement that \(SU(3)_F\) sum rules are satisfied. For example, for transitions \(D^+ \rightarrow K^+\pi ^0\), \(D^+ \rightarrow K^+\eta\), and \(D^+ \rightarrow K^+\eta ^\prime\), a sum rule

$$\begin{aligned} 3 \sqrt{2} A(K^+\pi ^0) + 4 \sqrt{3} A(K^+\eta )+\sqrt{6} A(K^+\eta ^\prime ) = 0 \end{aligned}$$
(34)

can be written. With the flavor-flow parameterization,

$$\begin{aligned} A(D^+ \rightarrow \overline{K}^+ \pi ^0)\, =\, & {} \frac{1}{\sqrt{2}} \left( T-A\right) , \nonumber \\ A(D^+ \rightarrow \overline{K}^+ \eta )= & {} - \frac{1}{\sqrt{3}} \ T \nonumber \\ A(D^+ \rightarrow \overline{K}^+ \eta ^\prime )\, =\, & {} \frac{1}{\sqrt{6}} \left( T + 3A\right) \end{aligned}$$
(35)

the above sum rule gives \(3(T-A)-4T+(T+3A)=0\).

Table 1 The timeline of extraction of the topological amplitudes extracted from the CF \(D\rightarrow PP\) decays in units of \(10^{-6}\) GeV for the fits obtained in 2010 [37], 2019 [38], and 2023 [39]. The fit is performed for two values of the \(\eta -\eta ^\prime\) mixing angle \(\theta\) (the table is reproduced from [39])
Full size table

Thus, provided that a sufficient number of decay modes is measured, one can predict both branching fractions and amplitude phases for several transitions. Still, no prediction for absolute branching ratios is possible in this approach. Yet, the obtained results can be used to predict the decay rates and CP-violating asymmetries.

4.3 Amplitudes: QCD light-cone sum rules

It has been recently shown that the framework of light-cone sum rules (LCSR) can be successfully used to compute the nonleptonic D-meson decay amplitudes and predict CP-violating asymmetries [40,41,42]. The computation is based on the light cone operator product expansion (OPE) for the \(x^2,y^2 \approx 0\) of the correlation function,

$$\begin{aligned}{} & {} F_\mu (p,q) = i^2 \int d^4 x e^{-i p\cdot x} d^4 y e^{i q\cdot y} \langle K(p-q)| T \left\{ j_5^D(x), O_1^s (0), j_\mu ^K(y)\right\} |0\rangle , \end{aligned}$$
(36)

where \(j_5^D=i m_c \bar{c} \gamma _5 u\) represents an interpolating current with the D-meson quantum numbers, \(O_1\) is the weak effective operator, and \(j_\mu ^K=\bar{s} \gamma _\mu \gamma _5 u\) is the interpolating current with kaon quantum numbers for the \(D \rightarrow KK\) computation [40,41,42]. The result of the OPE can then be linked to the relevant matrix element via dispersion relations and other machinery of the LCSRs.

The obtained results can be used to predict CP-violating asymmetries in \(D \rightarrow K^+K^-\) and \(D \rightarrow \pi ^+\pi ^-\). While [40] used the sum rules to mainly predict the ratio of the “penguin”to “tree”matrix elements, fitting the tree amplitude to the experimental data (see also [43]), [42] use LCSRs also to predict the tree amplitudes. The results are in remarkable agreement with the experimental data.

5 Phenomenology of new physics

Phenomenological studies of new physics with CP-violation in charm decays are quite different from the conventional analysis of the CKM unitarity triangle in b-quark transitions. This is because while overconstraining the CKM triangle is possible in charm decays, it is challenging because charm CKM triangles are squished. Indeed, the “charm” CKM triangle is [44]

$$\begin{aligned} V^*_{us} V_{cs} + V^*_{ub} V_{cb} + V^*_{ud} V_{cd} = 0, \end{aligned}$$
(37)

whose sides scale very differently with the Wolfenstein parameter \(\lambda\),

$$\begin{aligned} V^*_{us} V_{cs} \sim {{ }O}(\lambda ), \quad V^*_{ud} V_{cd} \sim {{ }O}(\lambda ), \quad V^*_{ub} V_{cb} \sim {{ }O}(\lambda ^5). \end{aligned}$$
(38)

This implies that other, more direct methods of searches for BSM physics are preferable. Indeed, the area of the “charmed” CKM triangle should be the same as that of any other CKM triangle due to the singular source of CP-violation in the Standard Model.

5.1 CP-violation and CP-violating observables

Charmed quark systems allow for high-statistics studies of CP-violation. While the most compelling signals of CP-violation have been observed in nonleptonic transitions, strong interaction effects make it challenging to make precise predictions of such signals. The methods of dealing with such decay amplitudes were discussed above.

Useful experimental observables and sources of CP-violation allow it to classify them in three different categories,

  1. (I)

    CP violation in the meson-antimeson mixing matrix (or “indirect” CP violation). It is known that introduction of \(\Delta c = 2\) transitions, either via SM or BSM one-loop or a tree-level NP amplitudes lead to non-diagonal entries in the meson-antimeson mass matrix,

    $$\begin{aligned} \left[ M - i \frac{\Gamma }{2} \right] _{ij} = \left( \begin{array}{c@{\quad}c} A &{} p^2 \\ q^2 &{} A \end{array} \right) \end{aligned}$$
    (39)

    This type of CP violation is manifest when \(R_m^2=\left| p/q\right| ^2=(2 M_{12}-i \Gamma _{12})/(2 M_{12}^*-i \Gamma _{12}^*) \ne 1\).

  2. (II)

    CP violation in the \(\Delta C =1\) decay amplitudes (or “direct” CP-violation). This type of CP violation occurs when the absolute value of the decay amplitude for a meson or baryon state to decay to a final state f (\(A_f\)) is different from the one of the corresponding CP-conjugated amplitude (“direct CP-violation”). This can happen if the decay amplitude can be broken into at least two parts associated with different weak and strong phases,

    $$\begin{aligned} A_f = \left| A_1\right| e^{i \delta _1} e^{i \phi _1} + \left| A_2\right| e^{i \delta _2} e^{i \phi _2}, \end{aligned}$$
    (40)

    where \(\phi _i\) represent weak phases (\(\phi _i \rightarrow -\phi _i\) under CP-transormation), and \(\delta _i\) represents strong phases (\(\delta _i \rightarrow \delta _i\) under CP-transformation). This ensures that the CP-conjugated amplitude, \(\overline{A}_{\overline{f}}\) would differ from \(A_f\).

  3. (III)

    CP violation in the interference of decays with and without mixing. This type of CP violation is possible for a subset of final states to which both neutral meson and antimeson can decay.

One of the most common observables for CP violation is CP-violating asymmetry. While CPT invariance requires the total widths of D and \(\overline{D}\) to be the same, the partial decay widths \(\Gamma (D \rightarrow f)\) and \(\Gamma ({\overline{D}} \rightarrow {\overline{f}})\) could be different in the presence of CP-violation, which would be signaled by a non-zero value of the asymmetry

$$\begin{aligned} a_f=\frac{\Gamma (D \rightarrow f)-\Gamma ({\overline{D}} \rightarrow {\overline{f}})}{ \Gamma (D \rightarrow f)+\Gamma ({\overline{D}} \rightarrow {\overline{f}})}, \end{aligned}$$
(41)

which can be generated by both \(\Delta C =1\) and \(\Delta C =2\) interactions. This asymmetry is non-zero only if there are at least two different amplitudes with different weak and strong phases are present,

$$\begin{aligned} A(D\rightarrow f) \equiv A_f = |A_{f1}| e^{i\delta _1} e^{i\phi _1} + |A_{f2}| e^{i\delta _2} e^{i\phi _2} \end{aligned}$$
(42)

We can now compute CP-violating asymmetry \(a_f\) for the final state f,

$$\begin{aligned} a_f \sim \sin (\phi _1-\phi _2) \sin (\delta _1-\delta _2). \end{aligned}$$
(43)

It is important to realize that the extraction of the fundamental parameters of CP violation from Eq. (41) is complicated because the final states are built from strongly interacting hadrons. Several methods could be used to compute those non-leptonic decay amplitudes.

Contrary to the case of bottom quarks, standard model interactions do not produce a large CP-violating signal in the charmed system. This argument stems from the fact that all quarks that build up initial and final hadronic states in weak decays of charm mesons or baryons belong to the first two generations. This implies that, at the tree level, those transitions are governed by a \(2\times 2\) Cabibbo quark mixing matrix. This matrix is real, so no CP-violation is possible in the dominant tree-level diagrams describing decay amplitudes.

Asymmetries of Eq. (41) can be introduced for both charged and neutral D-mesons. In the latter case, a much richer structure becomes available due to the interplay of CP-violating contributions to decay and mixing amplitudes, which can play the role of a “second pathway”for the CP-asymmetry

$$\begin{aligned} a_f \, = \, & {} a_f^d + a_f^m + a_f^i, \nonumber \\ a_f^m\, =\, & {} - R_f \frac{y'}{2} \left( R_m - R_m^{-1}\right) \cos \phi , \nonumber \\ a_f^i\, =\, & {} R_f \frac{x'}{2} \left( R_m + R_m^{-1}\right) \sin \phi , \end{aligned}$$

where \(a_f^d\), \(a_f^m\), and \(a_f^i\) represent CP-violating contributions from decay, mixing, and interference between decay and mixing amplitudes, respectively. Note that for the final states that are also CP-eigenstates \(f = \overline{f}\) and \(y' = y\).

The combined asymmetry, formed as a difference of CP-asymmetries in \(\pi ^+\pi ^-\) and \(K^+K^-\) channels,

$$\begin{aligned} \Delta A_{CP} = a_{KK} - a_{\pi \pi }, \end{aligned}$$
(44)

is actually approximately double of the individual asymmetries due to \(a_{KK} = - a_{\pi \pi }\) in the flavor \(SU(3)_F\) limit. A proper interpretation of \(\Delta A_{CP}\) in terms of fundamental CP-violating parameters is needed.

A recent measurement of direct CP-violating asymmetry \(A_{CP}\) in \(D^0 \rightarrow K^+K^-\) by the LHCb collaboration [45] provided a big boost to studies of CP violation in charm. The data collected in Run 2 indicates that

$$\begin{aligned} a_{KK} = (7.7 \pm 5.7) \times 10^{-4}\,. \end{aligned}$$
(45)

The LHCb collaboration used this result in combination with their earlier measurement of \(\Delta A_{CP}\) from Eq. (44) [46], to present the first observation of CP violation in a given decay channel \(D^0 \rightarrow \pi ^+\pi ^-\) in a charmed quark system [45],

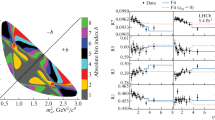
$$\begin{aligned} a_{\pi \pi } = (23.2 \pm 6.1) \times 10^{-4}\,, \end{aligned}$$
(46)

As the results for \(a_{\pi \pi }\) and \(a_{KK}\) are highly correlated, graphical representation is useful and presented in Fig. 4.

Fig. 4
figure 4

The two-dimensional confidence regions in the \(a_{\pi \pi }\) vs \(a_{KK}\) plane. The figure is from [45]

Full size image

The theoretical interpretation of this result is quite non-trivial and is subject to intense theoretical scrutiny. Naively, as discussed above, the flavor \(SU(3)_F\) symmetry (or even its subgroup, the U-spin) limit ensures that \(a_{KK}=-a_{\pi \pi }\), so it was expected that the asymmetries in those channels would be of a different sign. Surprisingly, experimental data seems to suggest a strong breaking of a U-spin symmetry relation [47], currently at the \(2.7\sigma\) level [45]. Is the result compatible with the SM, or is it a sign of BSM physics?

Theoretical predictions for \(\Delta A_{CP}\), as well as separately for \(a_{KK}\) and \(a_{\pi \pi }\), draw different conclusions based on the method used in the predictions of the amplitudes. In particular, agreement with the Standard Model is mostly found with the methods based on different variants of the amplitude fits of experimental data discussed in sections 4.2 and 4.1, as discussed in [38, 48, 48, 49] or approaches that model amplitude enhancements due to final state interactions [50,51,52] (see also [53]). On the contrary, methods that attempt computation of the relevant amplitudes with QCD-based methods (see section 4.3) tend to find the smaller values of CP-violating asymmetries [40,41,42], implying that a BSM contribution is needed to explain the observed data.

This issue still needs to be settled, with all methods having weak points in the discussion. On one hand, if BSM contributions are present, fits to the experimental decay amplitudes also include these BSM effects as parts of the fit. Therefore, it is not possible to claim that the resulting CP-violating asymmetries are due to the SM effects only. Moreover, experimental precision of some decay rates used in the fits might not justify the precision claimed in the predictions of \(\Delta A_{CP}\), as well as \(a_{KK}\) and \(a_{\pi \pi }\). On the other hand, LCSR computations rely on quark-hadron duality, violations of which, if present, are challenging to quantify.

5.2 \(D^0-\overline{D}{}^0\) mixing

The \(\Delta C = 2\) interactions, generated either at one loop level in the Standard Model (or maybe even by new physics particles), mix a \(D^0\) state into a \(\overline{D}{}^0\) state, which results in physical (measurable) mass and lifetime differences between new mass eigenstates [12],

$$\begin{aligned} x_D \equiv \frac{m_2-m_1}{\Gamma }, ~~ y_D \equiv \frac{\Gamma _2 - \Gamma _1}{2 \Gamma }, \end{aligned}$$
(47)

where \(m_{1,2}\) and \(\Gamma _{1,2}\) are the masses and widths of \(D_{1,2}\) and the mean width and mass are \(\Gamma =(\Gamma _1+\Gamma _2)/2\) and \(m=(m_1+m_2)/2\). The mass eigenstates themselves are usually defined as

$$\begin{aligned} | D_{^1_2} \rangle = p | D^0 \rangle \pm q | \bar{D}^0 \rangle , \end{aligned}$$
(48)

where the complex parameters p and q are obtained from diagonalizing the \(D^0-\overline{D}{}^0\) mass matrix in Eq. (39). The mass and lifetime differences introduced above can be calculated as absorptive and dispersive parts of a certain correlation function,

$$\begin{aligned}{} {} x_D &\, = \, \frac{1}{M_D\Gamma _D} \text{ Re } \Biggl [ 2 \langle \overline{D}{}^0 | {{ }H}_w^{|\Delta C| = 2} | D^0\rangle + \langle \overline{D}{}^0 | i \int d^4x ~\text{ T }\left\{ {{ }H}_w^{|\Delta C|=1} (x) {{ }H}_w^{|\Delta C|=1} (0)\right\} | D^0\rangle \Biggr ], \nonumber \\{} & {} \quad y_D = \frac{1}{M_D\Gamma _D} \text{ Im } \left[ \langle \overline{D}{}^0 | i \int d^4x ~\text{ T }\left\{ {{ }H}_w^{|\Delta C|=1} (x) {{ }H}_w^{|\Delta C|=1} (0)\right\} | D^0\rangle \right] . \end{aligned}$$
(49)

Only those quarks whose masses are lighter than \(m_D\) can go on mass shells in Eq. (49) generate the lifetime difference \(y_D\).

The charm system is unique because \(x_D\) is not dominated by the contribution of the \(\Delta C = 2\) operator that is local at the charm scale. It is very different from the case of B-mixing, where the top quark contribution completely dominates x. Since Glashow-Iliopoulos-Maiani guarantees that the mixing amplitude is proportional to the power of intrinsic quark mass running in the box diagram, suppressions due to a combination of CKM greatly diminishes the contribution due to b-quark, the only heavy quark intermediate state possible in \(D^0-\overline{D}{}^0\) mixing. Thus, it is essential to calculate the contribution due to the correlation functions in Eq. (49) with light intermediate s and d quarks [54].

The most challenging problem in charm mixing is appropriately evaluating the integrals in the above equations. This can be done in several ways, depending on whether one considers the decaying particle heavy or light compared to the QCD’s scale \(\Lambda _{QCD}\). Since \(m_c \simeq 1.3\) GeV, both approaches are possible for D-decays and mixing calculations.

If the decaying particle is heavy, it is possible to show [55] that the integrals in Eq. (49) are dominated by short distances, so a short-distance operator product expansion (OPE) can be used to evaluate the products of \(|\Delta C|=1\) Hamiltonians. Similar approaches worked very well for calculating lifetime differences of \(B_s\) mesons [56]. Such an approach has been applied to compute mixing parameters in the charm system, including the subleading corrections [57].

If the decaying particle is considered light, no short-distance expansion of operator products is possible, as long distances dominate the integrals. However, only a few open channels are available for such light particles, so the calculations can be done by explicitly summing over each channel’s contributions. This approach worked well for kaon physics.Footnote 2 The number of available decay channels is quite large, but some predictions can be made.

It is possible to prove that \(D^0-\overline{D}{}^0\) mixing arises only at second order in the SU(3) violating parameter \(m_s\) [58], in the Standard Model x and y are generated only at second order in \(SU(3)_F\) breaking,

$$\begin{aligned} x\,,\, y \sim \sin ^2\theta _C \times [SU(3) \text{ breaking}]^2\,, \end{aligned}$$
(50)

where \(\theta _C\) is the Cabibbo angle. This result should be reproduced in all explicit calculations of \(D^0-\overline{D}{}^0\) mixing parameters, as explained below (based on [12]).

The use of the OPE relies on local quark-hadron duality and on expansion parameter \(\Lambda /m_c\) being small enough to allow truncation of the series after the first few terms. Let us see what one can expect at leading order in \(1/m_c\) expansion, i.e., assuming that the integrals in Eq. (49) are dominated by the short distances. The leading-order result is then generated by calculating the usual box diagram with intermediate s and d quarks.

Unitarity of the CKM matrix assures that the leading-order, mass-independent contribution due to s-quark is completely canceled by the corresponding contribution due to a d-quark. A non-zero contribution can be obtained if the mass insertions are added on each quark line in the box diagram. However, adding only one mass insertion flips the chirality of the propagating quarks from being left-handed to right-handed. This does not contribute to the resulting amplitude, as right-handed quarks do not participate in the weak interaction. Thus, a second mass insertion is needed on each quark line. Neglecting \(m_d\) compared to \(m_s\), we see that the resulting contribution to \(x_D\) is \({{ }O}(m_s^2\times m_s^2) \sim {{ }O}(m_s^4)\)! It is easy to convince yourself that \(y_D\) has additional \(m_s^2\) suppression due to on-shell propagation of left-handed quarks emitted from a spin-zero meson, which brings total suppression of \(y_D\) to \({{ }O}(m_s^6)\)! An explicit calculation of the leading order mixing amplitude and perturbative QCD corrections to it [54] agrees precisely with the hand-waving arguments above. Clearly, leading order contribution in \(1/m_c\) gives “too much” of \(SU(3)_F\) suppression [58].

Somewhat surprisingly, the resolution of this paradox follows from considerations of higher-order corrections in \(1/m_c\). Among many higher-dimensional operators that encode \(1/m_c\) corrections to the leading four-fermion operator contribution, there exists a class of operators that result from chirality-flipping interactions with background quark condensates. These interactions do not bring additional powers of light quark mass but are suppressed by powers of \(\Lambda _{QCD}/m_c\), which is not a very small number. The leading \({{ }O}(m_s^2)\) order of \(SU(3)_F\) breaking is obtained from matrix elements of dimension twelve operators that are suppressed by \((\Lambda _{QCD}/m_c)^6\) compared to the parametrically-leading contribution in \(1/m_c\) expansion! As usual in OPE calculation, the proliferation of the number of operators at higher orders (over 20) makes it difficult to pinpoint the precise value of the effect.

It is possible to calculate \(D^0-\overline{D}{}^0\) mixing rates by dealing explicitly with hadronic intermediate states which result from every common decay product of \(D^0\) and \(\overline{D}{}^0\) [58]. In the \(SU(3)_F\) limit, these contributions cancel when one sums over complete SU(3) multiplets in the final state. The cancellations depend on \(SU(3)_F\) symmetry in the decay matrix elements and the final state phase space. While there are \(SU(3)_F\)-breaking corrections to both of these make it difficult to compute the symmetry-breaking effects in the matrix elements in a model-independent manner. As experimental data on nonleptonic decay rates becomes better and better, it is possible to use it to calculate \(y_D\) by directly inputting it into Eq. (49),

$$\begin{aligned} y = {1\over \Gamma } \sum _n \int [\mathrm{P.S.}]_n\, \langle \overline{D}{}^0|\,{{ }H}_w\,|n \rangle \langle n|\,{{ }H}_w\,|D^0 \rangle \,, \end{aligned}$$
(51)

where the sum is over distinct final states n and the integral is over the phase space for state n.

One can see that \(y_D\) on the order of a few percent is entirely natural and that any smaller order of magnitude would require significant cancellations, which do not appear naturally in this framework. The normalized mass difference, \(x_D\), can be calculated via a dispersion relation.

$$\begin{aligned} x_D = - \frac{1}{\pi }\ \text{ P } \int _{2 m_\pi }^\infty dE \frac{y_D(E)}{E-m_D} \end{aligned}$$
(52)

that additionally contain guesses on the off-shell behavior of hadronic form factors in \(y_D(E)\) [58]. Here, P denotes the principal value. The result of the calculation yields \(x_D \sim {{ }O}(1\%)\) [58].

\(D^0\) decay processes that are easier to study experimentally contain all charged particles in the final state. Some of the most interesting ones include the doubly-Cabibbo-suppressed \(D^0\rightarrow K^+\pi ^-\) decay, the singly-Cabibbo-suppressed \(D^0\rightarrow K^+K^-\) decay, the Cabibbo-favored \(D^0\rightarrow K^-\pi ^+\) decay, and their three CP-conjugate decay processes. Let us now write down approximate expressions for the time-dependent decay rates that are valid for times \(t\sim 1/\Gamma\). We take into account the experimental information that x, y, and \(\lambda\) are small and expand each of the rates only to the order that is relevant to experimental measurements:

$$\begin{aligned}{} {} \Gamma [D^0(t)\rightarrow K^+\pi ^-]\ & =\ e^{-\Gamma t}|\bar{A}_{K^+\pi ^-}|^2 |q/p|^2 \left[ |\lambda _{K^+\pi ^-}^{-1}|^2+ [\Re (\lambda ^{-1}_{K^+\pi ^-})y +\Im (\lambda ^{-1}_{K^+\pi ^-})x]\Gamma t +{1\over 4}(y^2+x^2)(\Gamma t)^2\right] , \nonumber \\{} {} \quad \Gamma [\overline{D}{}^0(t)\rightarrow \ K^-\pi ^+]\ & = \ e^{-\Gamma t}|A_{K^-\pi ^+}|^2 |p/q|^2 \left[ |\lambda _{K^-\pi ^+}|^2+[\Re (\lambda _{K^-\pi ^+})y +\Im (\lambda _{K^-\pi ^+})x] \Gamma t+{1\over 4}(y^2+x^2)(\Gamma t)^2\right] , \nonumber \\{} & {} \quad \Gamma [D^0(t)\rightarrow K^+K^-]\ =\ e^{-\Gamma t}|A_{K^+K^-}|^2 \left[ 1+[\Re (\lambda _{K^+K^-})y-\Im (\lambda _{K^+K^-})x]\Gamma t\right] ,\ \nonumber \\{} & {} \quad \Gamma [\overline{D}{}^0(t)\rightarrow K^+K^-]\ =\ e^{-\Gamma t}|\bar{A}_{K^+K^-}|^2 \left[ 1+[\Re (\lambda ^{-1}_{K^+K^-})y-\Im (\lambda ^{-1}_{K^+K^-})x] \Gamma t\right] , \nonumber \\{} & {} \quad \Gamma [D^0(t)\rightarrow \ K^-\pi ^+]\ = \ e^{-\Gamma t}|A_{K^-\pi ^+}|^2, \nonumber \\{} & {} \quad \Gamma [\overline{D}{}^0(t)\rightarrow \ K^+\pi ^-]\ = \ e^{-\Gamma t}|\bar{A}_{K^+\pi ^-}|^2. \end{aligned}$$
(53)

where \(\lambda _f = (q/p)(\bar A_{f}/ A_f)\) for \(f = K\pi\) and KK. In particular, as \(\left| q/p\right| = R_m\),

$$\begin{aligned} \lambda _{K^-\pi ^+} = \sqrt{R} R_m e^{-i(\delta -\phi )}. \end{aligned}$$
(54)

Studies of time-dependent rates of Eq. (53) allow us to measure several exciting quantities. First, mixing parameters x and y can be determined,

$$\begin{aligned}{} & {} \Gamma [D^0(t) \rightarrow K^+ \pi ^-] = e^{-\Gamma t}|A_{K^-\pi ^+}|^2 ~\left[ R+\sqrt{R}R_m(y'\cos \phi -x'\sin \phi )\Gamma t+ \frac{R_m^2}{4}(y^2+x^2)(\Gamma t)^2 \right] ,~~~ \end{aligned}$$
(55)

where R is the ratio of DCS and Cabibbo favored (CF) decay rates. Since x and y are small, the best constraint comes from the linear terms in t that are also linear in x and y. A direct extraction of x and y from Eq. (55) is not possible due to unknown relative strong phase \(\delta _D\) of DCS and CF amplitudes,

$$\begin{aligned} x'= & {} x\cos \delta _D+y\sin \delta _D, \nonumber \\ y'= & {} y\cos \delta _D-x\sin \delta _D \end{aligned}$$
(56)

This strong phase can be measured independently, for instance, at BES III or, in the future, at STCF. The most recent value is from BESIII [59]

$$\begin{aligned} \delta _D = ({187.6^{+8.9}_{-9.7}}^{+5.4}_{-6.4})^o. \end{aligned}$$
(57)

Alternatively, its value can also be determined as a parameter of a global fit, along with the CP-violating phase \(\phi\), as commonly done in LHCb analyses.

There is also an update on the measurement of y from the \(K\pi\) final states [60]

$$\begin{aligned} y-y_{K\pi } = (6.96\pm 0.26 \pm 0.13) \times 10^{-3}, \end{aligned}$$
(58)

Note that the difference of \(y_{CP}\) and y also indicates the presence of CP violation.

Finally, a fit provided by the Heavy Flavor Averaging Group (HFLAV) [61] to a combination of measurements, allowing for the presence of CP-violation provides the most up-to-date constraints on the \(D^0-\overline{D}{}^0\) mixing parameters,

$$\begin{aligned} x \,=\, & {} (0.407 \pm 0.044)\%, \nonumber \\ y\,= \,& {} (0.645^{+0.024}_{-0.023})\%, \nonumber \\ \phi\,= \,& {} (-2.6^{+1.1}_{-1.2}), \nonumber \\ |q/p|\,=\, & {} 0.995^{+0.016}_{-0.015} \end{aligned}$$
(59)

The calculation of \(D^0-\overline{D}{}^0\) mixing is a challenging theoretical exercise. It is unclear if brute-force improvements of the calculations would result in much more precise results. However, a glimpse of hope for yet another approach has recently been identified. It remains to be seen if multichannel generalizations of Lellouch-Luscher methods [62] to calculations of weak matrix elements will be successful in calculating non-leptonic decay rates of charm mesons [63]. Yet, this approach will undoubtedly impact charm physics, particularly calculations of \(D^0-\overline{D}{}^0\) mixing rate.

6 Conclusions

Discovered 50 years ago, in November of 1974, charmed quark started a series of breakthroughs now collectively known as the November Revolution. Upon its discovery, many questions about the Standard Model found their natural resolution: new narrow states (\(J/\psi\)), Glashow-Iliopoulos-Maiani mechanism to solve kaon decay puzzles, etc. Astonishingly, fifty years after its discovery, in 2024, the charm quark continues to bring surprises and offer new solutions, hopefully paving the way to a new Standard Model.