Multi-pulse chaotic dynamics and global dynamics analysis of circular mesh antenna with three-degree-of-freedom system

Abstract

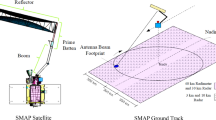
In the complex space environment, the antenna of the running satellite may cause large amplitude nonlinear vibrations. In scientific experiments, it is difficult to simulate the state for the operation of the antenna. To study the nonlinear dynamic behaviors of the circular mesh antenna, the dynamic models and dynamic equations are established. First, the circular mesh antenna is simplified to an equivalent cylindrical shell structure. Then, the high-dimensional nonlinear dynamic equation is derived. The dynamic equations of the circular mesh antenna are discrete by the third-order Galerkin method. The breathing vibration nonlinear equations with three-degree-of-freedom are obtained. The nonlinear ordinary equations are simplified to be a topological equivalent nonlinear equation. The topological equivalent nonlinear equation under the conditions of the unperturbed and perturbed situations is analyzed, respectively. Based on the energy phase method of Haller and Wiggins, this theory for the six-dimensional system is extended and improved. The multi-pulse chaotic motion of the circular mesh antenna system is verified by the extended energy phase method. The geometric structure of the three jumping pulses in the six-dimensional phase space is described in the first time. Finally, numerical simulation is used to verify the theoretical analysis.

Appendix A

The nonlinear transformations in Eq. (18) are presented as follows:

$$\begin{aligned} x_{\text{1 }}= & {} -\frac{\text{3 }}{16}\alpha _{14} y_{1} ^{\text{3 }}-\frac{\text{9 }}{8}\alpha _{14} y_{1} y_{2} ^{\text{2 }}-\frac{\text{1 }}{4}\alpha _{21} y_{1} y_{3}^{\text{2 }}\nonumber \\&-\frac{\text{1 }}{4}\alpha _{21} y_{1} y_{4} ^{\text{2 }}-\frac{\text{1 }}{4}\alpha _{25} y_{1} y_{5} ^{\text{2 }}-\frac{\text{1 }}{4}\alpha _{25} y_{1} y_{6}^{\text{2 }}, \end{aligned}$$

(A1)

$$\begin{aligned} x_{2}= & {} \frac{9}{16}\alpha _{14} y_{1}^{2}y_{2} , \end{aligned}$$

(A2)

$$\begin{aligned} x_{\text{3 }}= & {} -\frac{\text{9 }\beta _{15} }{32\sigma _{2} }y_{3} ^{\text{3 }}+\frac{\text{9 }\beta _{15} }{32\sigma _{2} }y_{4} ^{\text{3 }}\nonumber \\&-\frac{\text{3 }\beta _{24} }{4\left( {3\sigma _{2} -2\sigma _{3} } \right) }y_{1}^{2}y_{5} +\frac{\text{3 }\beta _{24} y_{2}^{2}y_{5} }{4}\left[ {\left( {81\sigma _{2}^{4}} \right. } \right. -72\sigma _{2} ^{2}\sigma _{3}^{2}\nonumber \\&+16\sigma _{3}^{4}-129\sigma _{2}^{3}+864\sigma _{2}^{2}\sigma _{3} -576\sigma _{2} \sigma _{3}^{2}+384\sigma _{3}^{3}\nonumber \\&\quad +10368\sigma _{2} ^{2}+13824\sigma _{2} \sigma _{3}\nonumber \\&\left. +4608\sigma _{3}^{2} \right) /\left( 234\sigma _{2}^{5}-162\sigma _{2}^{4}\sigma _{3} \nonumber \right. \\&-216\sigma _{2}^{3}\sigma _{3}^{2} \nonumber \\&+144\sigma _{2}^{2}\sigma _{3}^{3}-162\sigma _{2}^{4}\sigma _{3}\nonumber \\&-216\sigma _{2}^{3}\sigma _{3}^{2}+144\sigma _{2} ^{2}\sigma _{3}^{3}\nonumber \\&\left. \left. +48\sigma _{2} \sigma _{3}^{4}-32\sigma _{3}^{5} \right) \right] +\frac{8\beta _{24} y_{2} y_{3}^{2}}{9\sigma _{2} ^{2}}+\frac{9\beta _{15} y_{3}^{2}y_{4} }{16\sigma _{2} }\nonumber \\&-\frac{8\beta _{24} y_{2} y_{\text{4 }}^{2}}{9\sigma _{2}^{2}}-\frac{9\beta _{15} y_{3} y_{4}^{2}}{16\sigma _{2} }+\frac{\beta _{23} y_{3} y_{5} ^{2}}{4\sigma _{2} }\nonumber \\&-\frac{\beta _{23} y_{4} y_{5}^{2}}{4\sigma _{2} }+\frac{\beta _{23} y_{3} y_{6}^{2}}{4\sigma _{2} }-\frac{\beta _{23} y_{4} y_{6}^{2}}{4\sigma _{2} } \nonumber \\&-\frac{\beta _{20} y_{1} y_{2} y_{4} }{16}+\frac{\beta _{24} y_{1} y_{3} y_{4} }{6\sigma _{2} }\nonumber \\&+\frac{\text{3 }\left( {\text{3 }\sigma _{2} \sigma _{\text{3 }} -2\sigma _{3}^{2}-36\sigma _{2} -24\sigma _{3} } \right) \beta _{24} y_{1} y_{2} y_{6} }{27\sigma _{2}^{3}-18\sigma _{2}^{2}\sigma _{3} -12\sigma _{2} \sigma _{3}^{2}+8\sigma _{3}^{3}}, \end{aligned}$$

(A3)

$$\begin{aligned} x_{\text{4 }}= & {} -\frac{\text{27 }\beta _{15} }{32\sigma _{2} }y_{3} ^{\text{3 }}-\frac{\text{27 }\beta _{15} }{32\sigma _{2} }y_{\text{4 }} ^{\text{3 }}\nonumber \\&-\frac{\text{3 }\beta _{24} }{4\left( {3\sigma _{2} -2\sigma _{3} } \right) }y_{1}^{2}y_{\text{6 }}\nonumber \\&+\frac{\text{3 }\beta _{24} y_{2} ^{2}y_{\text{6 }} }{4}\left[ {\left( {81\sigma _{2}^{4}-72\sigma _{2} ^{2}\sigma _{3}^{2}} \right. } \right. \nonumber \\&-\text{1728 }\sigma _{2}^{2}\sigma _{3} \nonumber \\&+1152\sigma _{2} \sigma _{3} ^{2}+10368\sigma _{2}^{2}\nonumber \\&\left. +13824\sigma _{2} \sigma _{3} +4608\sigma _{3} ^{2} \right) /\left( {243} \right. \sigma _{2}^{5} \quad -162\sigma _{2}^{4}\sigma _{3} \nonumber \\&-216\sigma _{2}^{3}\sigma _{3}^{2}+144\sigma _{2}^{2}\sigma _{3}^{3}\nonumber \\&\left. \left. +48\sigma _{2} \sigma _{3} ^{4}-32\sigma _{3}^{5} \right) \right] \nonumber \\&-\frac{\beta _{24} y_{1} y_{3} ^{2}}{6\sigma _{2} }+\frac{\beta _{24} y_{1} y_{4}^{2}}{6\sigma _{2} } \nonumber \\&+\frac{\beta _{20} y_{1} y_{2} y_{3} }{16}-\frac{\text{9 }\left( {\text{3 }\sigma _{2}^{2}-2\sigma _{2} \sigma _{3} -24\sigma _{2} -16\sigma _{3} } \right) \beta _{24} y_{1} y_{2} y_{5} }{2\left( {27\sigma _{2} ^{3}-18\sigma _{2}^{2}\sigma _{3} -12\sigma _{2} \sigma _{3}^{2}+8\sigma _{3}^{3}} \right) }\nonumber \\&+\frac{20\beta _{24} y_{2} y_{3} y_{4} }{9\sigma _{2} ^{2}}, \end{aligned}$$

(A4)

$$\begin{aligned} x_{\text{5 }}= & {} -\frac{\text{9 }\gamma _{1\text{6 }} }{32\sigma _{\text{3 }} }y_{\text{5 }}^{\text{3 }}+\frac{\gamma _{\text{20 }} }{\text{2 }\left( {3\sigma _{2} -2\sigma _{3} } \right) }y_{1}^{2}y_{\text{3 }} \nonumber \\&+\frac{\gamma _{\text{20 }} }{\text{96 }}y_{1}^{2}y_{\text{6 }} -\frac{\gamma _{\text{20 }} y_{2}^{2}y_{3} }{2}\left[ {\left( {81\sigma _{2}^{4}-72\sigma _{2} ^{2}\sigma _{3}^{2}} \right. } \right. \nonumber \\&+16\sigma _{3}^{4}-864\sigma _{2}^{2}\sigma _{3} +576\sigma _{2} \sigma _{3}^{2}-384\sigma _{3}^{3}\nonumber \\&+10368\sigma _{2}^{2}+13824\sigma _{2} \sigma _{3} +1296\sigma _{2}^{3} \nonumber \\&\quad \left. +4608\sigma _{3}^{2} \right) /\left( {243} \right. \sigma _{2} ^{5}-162\sigma _{2}^{4}\sigma _{3} -216\sigma _{2}^{3}\sigma _{3} ^{2}+144\sigma _{2}^{2}\sigma _{3}^{3}\nonumber \\&+48\sigma _{2} \sigma _{3} ^{4}\left. {\left. {-32\sigma _{3}^{5}} \right) } \right] \nonumber \\&-\frac{1296\gamma _{16} \sigma _{2} \sigma _{3} y_{2}^{2}y_{4} }{81\sigma _{2}^{4}-72\sigma _{2}^{2}\sigma _{3}^{2}+16\sigma _{3} ^{4}}\nonumber \\&-\frac{3\gamma _{20} y_{2}^{2}y_{\text{6 }} }{2\sigma _{3} ^{2}}\nonumber \\&+\frac{9\gamma _{16} y_{1} y_{2} y_{3} }{9\sigma _{2}^{2}-4\sigma _{3} ^{2}}-\frac{9\gamma _{16} y_{5} y_{6}^{2}}{16\sigma _{3} } \nonumber \\&+\frac{\gamma _{20} y_{1} y_{2} y_{5} }{8\sigma _{3} }-\frac{\gamma _{24} y_{1} y_{2} y_{6} }{24}\nonumber \\&-\frac{\text{3 }\left( {\text{3 }\sigma _{2} ^{2}-2\sigma _{2} \sigma _{3} +24\sigma _{2} +16\sigma _{3} } \right) \gamma _{20} y_{1} y_{2} y_{4} }{27\sigma _{2}^{3}-18\sigma _{2}^{2}\sigma _{3} -12\sigma _{2} \sigma _{3}^{2}+8\sigma _{3}^{3}}, \end{aligned}$$

(A5)

$$\begin{aligned} x_{\text{6 }}= & {} -\frac{\text{27 }\gamma _{1\text{6 }} }{32\sigma _{\text{3 }} }y_{\text{6 }}^{\text{3 }}+\frac{\gamma _{\text{20 }} }{\text{2 }\left( {3\sigma _{2} -2\sigma _{3} } \right) }y_{1}^{2}y_{\text{4 }} -\frac{\gamma _{\text{20 }} }{\text{96 }}y_{1}^{2}y_{\text{5 }} \nonumber \\&+\frac{108\left( {3\sigma _{2}^{2}+4\sigma _{3}^{2}} \right) \gamma _{16} y_{2}^{2}y_{3} }{81\sigma _{2}^{4}-72\sigma _{2}^{2}\sigma _{3}^{2}+16\sigma _{3}^{4}}\nonumber \\&-\frac{\gamma _{\text{20 }} y_{2}^{2}y_{4} }{2}\left[ {\left( {81\sigma _{2} ^{4}-72\sigma _{2}^{2}\sigma _{3}^{2}+16\sigma _{3}^{4}} \right. } \right. +1728\sigma _{2}^{2}\sigma _{3} \nonumber \\&\left. \left. -1152\sigma _{2} \sigma _{3} ^{2}+10368\sigma _{2}^{2}+13824\sigma _{2} \sigma _{3} +4608\sigma _{3}^{2} \right) \right] /\left( {243} \right. \sigma _{2}^{5}\nonumber \\&-162\sigma _{2} ^{4}\sigma _{3}-216\sigma _{2}^{3}\sigma _{3}^{2}+144\sigma _{2} ^{2}\sigma _{3}^{3}\nonumber \\&\left. {+48\sigma _{2} \sigma _{3}^{4}-32\sigma _{3}^{5}} \right) -\frac{\gamma _{20} y_{1} y_{2} y_{6} }{8\sigma _{3} }+\frac{27\sigma _{2} \gamma _{16} y_{1} y_{2} y_{4} }{2\left( {9\sigma _{2}^{2}-4\sigma _{3}^{2}} \right) }\nonumber \\&+\frac{\gamma _{24} y_{1} y_{2} y_{5} }{24} \nonumber \\&-\frac{\text{2 }\left( {3\sigma _{2} \sigma _{3} -2\sigma _{3}^{2}+36\sigma _{2} +24\sigma _{3} } \right) \gamma _{20} y_{1} y_{2} y_{3} }{27\sigma _{2} ^{3}-18\sigma _{2}^{2}\sigma _{3} -12\sigma _{2} \sigma _{3}^{2}+8\sigma _{3}^{3}}. \end{aligned}$$

(A6)