1 Introduction

For humanity, climate extremes have always been a challenge [1]. Due to their societal as well as economic impact, understanding the drivers and interplays between extreme events is still a central topic of climate research [2,3,4]. With the rise of computational power, studying the synchrony of extreme events has attracted increasing attention over the past decade [5,6,7]. Most of the corresponding studies have employed event synchronization (ES) [8] (a method that has originally been introduced to study EEG spike trains to quantify the synchrony of event time series) to examine the spatio-temporal characteristics of heavy rainfall [9,10,11]. Utilizing ES to construct functional network representations of the Earth’s climate system [12, 13] has led to substantial improvements in understanding global extreme rainfall patterns [14], predicting the Indian summer monsoon onset [15], and forecasting flood events in the Central Andes [9], to mention only a few examples.

Despite the success of the method, several recent studies [9, 16,17,18] have pointed out a methodological concern related to ES that can arise when working with events exhibiting marked clustering in time. While this potential drawback may have considerable consequences for the application of ES in functional climate networks, it does not render previous analysis results invalid, yet calls for some careful re-examination. In a recent publication [18], the dependence of ES based functional climate networks on event clustering in the underlying time series has been studied for two illustrative case studies on the South American monsoon system (SAMS), highlighting that a corresponding connectivity bias can be (at least partially) corrected for by employing a simple event declustering scheme [9].

As an alternative method to quantify the synchrony of events, event coincidence analysis (ECA) [19, 20] has been proposed, which is not prone to the aforementioned connectivity bias in the presence of temporally clustered events. In our recent work [18], we have compared the results of functional climate network analysis when employing either ES or ECA for characterizing event synchrony. In particular, we have discussed the impact of the declustering scheme to avoid paired extreme events on the results for the associated network representations based on the corrected and uncorrected versions of both event synchrony measures. However, this discussion has focused exclusively on the per-node degree patterns of the resulting networks as the probably simplest possible complex network characteristic, leaving aside the consideration of possibly distinct effects on higher-order structural as well as spatial network properties [18].

In this work, we expand this previous analysis by investigating patterns of the local clustering coefficient as an example for a higher-order network measure as well as the spatial characteristics of edge lengths in the geographically embedded climate networks obtained based on both event synchrony measures without and with employing a declustering scheme. Moreover, we also investigate the dependency of the different characteristics on the link density in the networks, which has been previously shown to potentially modify climate network properties not only quantitatively [21], but also qualitatively [22]. Unlike the present work, these earlier studies have utilized Pearson correlation to infer statistical association between time series. Here, we show that a corresponding crossover behavior associated with a qualitative reversal of the large-scale spatial pattern of certain local network characteristics like the node degree can also be observed in event synchrony based networks.

Accordingly, we structure our manuscript as follows: We first introduce the conceptual ideas and methodological details of functional climate network analysis, ES and ECA along with considerations on the temporal clustering of events and a simple declustering scheme. To underline the possible relevance of identifying and accounting for possible biases of event synchrony methods, we briefly summarize recent studies that have employed either ES or ECA to study spatio-temporal patterns of extreme events using complex network representations. Subsequently, we introduce the SAMS as a well-studied regional climate phenomenon that will be used in the following to illustrate the distinctive features of the networks based on the two event synchrony measures, along with a short description of the employed data set. Comparing and contrasting the behavior of ES and ECA based functional climate networks will be finally performed in three steps. First, we investigate the spatial patterns of three local (per-node) network measures for different values of the prescribed link density. Second, we examine the mutual dependency between the values of each measure obtained with the different methods along with the corresponding impact of local event clustering as measured by the so-called pairing coefficient [16]. Third, we illustrate how the interdependency between different network characteristics can contribute to analyzing the differences among the methods. We close our work by summarizing the main findings of our analysis.

2 Methods

2.1 Functional climate networks and their characteristics

Functional networks present a discrete way of encoding information on statistical associations among a commonly large set of time series and have been successfully employed in diverse fields of science such as neurophysiology [23,24,25], economics [26,27,28,29], seismology [30,31,32,33,34] and climatology [12, 13, 35, 36], to mention only a few. In the context of extreme (or just “extraordinary”) climate events as studied in the present work, such associations can be quantified by suitable event synchrony measures (see below). In the resulting functional climate networks, we can associate each individual time series with a node that is characterized by a specific location (i.e., of the corresponding grid point or measurement site), making the constructed networks being embedded in geographical space.

By measuring the strength of statistical interdependency between all pairs of time series, we identify the strongest mutual interrelationships among the analyzed set of series. Here, the concept of a strong interrelationship is commonly understood as a value of the employed pairwise association measure that exceeds a certain percentile of the corresponding empirical distribution obtained from all pairs, i.e., focusing on the \(\rho \cdot 100\%\) largest values. Identifying the presence (absence) of such a strong interrelationship with the presence (absence) of a link between the two corresponding nodes, we obtain an unweighted functional network representation of the underlying climate data set with a prescribed link density \(\rho \) (i.e., the fraction of possible edges that are actually present in the network). For the sake of simplicity, we will consider here only symmetric association measures, implying that the resulting network is also undirected (i.e., any link between a pair of nodes always describes a bidirectional association). The topology of such an unweighted and undirected network with N (i.e., the number of time series) nodes and E (\(=\rho N(N-1)/2\)) edges is conveniently summarized in the binary adjacency matrix \({\mathbf {A}}\). Its matrix elements \(a_{ij}\) equal 1 if node i is connected with node j, and 0 otherwise. Note that other methodological choices (e.g., fully or partially connected weighted networks [37], directed networks [37, 38], or networks based on a locally defined instead of a global threshold criterion [39]) are possible, but shall not be further studied in the context of the present work.

To quantify the individual connectivity properties of each node in the network, there exist a plethora of complementary topological (structural) as well as spatial (geometric) different network measures [40, 41], of which we will employ just a few examples in our present study. Before discussing those measures in detail, we note that in functional climate networks, nodes often represent differently sized fractions of the Earth’s surface. Accordingly, network measures can exhibit biased values according to their different represented area if not accounting for this heterogeneous placement of nodes on the approximately spherical surface of the Earth. To correct for such biases, Heitzig et al. [42] have introduced the concept of node-splitting invariance. Using the proposed strategy, suitable node weights are introduced to correct for the bias originating from the heterogeneous coverage of the available geographical space. Specifically, for a regular (latitude–longitude) grid on a spherical surface, the spatial node density increases with the inverse of the cosine of the latitude, which is why we will use here node weights corresponding to the cosine of the latitudinal position \(\lambda _i\) of each node (i.e., \(w_i= \cos \lambda _i)\). With this prerequisite, we can now proceed with defining the network properties of interest in this study.

The n.s.i. degree \(k_i\) of node i indicates the number of connections of node i to the other nodes in the network and is, therefore, defined as

$$\begin{aligned} k_i=\sum _{j=1}^N w_j a_{ij}, \end{aligned}$$
(1)

We further compute the n.s.i. local clustering coefficient [42, 43].

$$\begin{aligned} {\mathcal {C}}_i=\frac{1}{k_i^2}\sum _{j\ne k} w_j w_k a_{ij} a_{jk} a_{ki} \end{aligned}$$
(2)

and the average link distance

$$\begin{aligned} d_i=\frac{\sum _{j=1}^N a_{ij} d_{ij}}{\sum _{j=1}^N a_{ij}}, \end{aligned}$$
(3)

which is the per-node arithmetic mean of the spatial distances covered by all adjacent edges. For convenience, we will measure \(d_i\) as an angular distance in dimensionless units (rad). Note that unlike for the two other measures, the considered version of the average link distance does not include any n.s.i. node weights.

For the computation of the respective measures, we utilize the python package pyunicorn [44]. In employing the current version of this package, we have unfortunately encountered computational problems that did not allow us to estimate the complete field of n.s.i. local clustering coefficients for our large functional climate networks (\(N=48,400\) nodes, see Sect. 3) when operating at high link densities (\(\rho =0.05\)). Accordingly, only for this specific case, we will consider in the following an unweighted version of the local clustering coefficient (\(w_j=w_k=1\)). As for the average link distance, this appears justified by the fact that for the real-world example to be studied, we are operating far from the poles, where the n.s.i. node weights do not differ too much from 1 (\(\cos \lambda _i>0.75\)). Since even more, the majority of connected nodes in functional climate networks are commonly located at similar latitudes (close nodes are far more likely to be connected than distant ones), we expect the effects of including proper n.s.i. node weights on the overall patterns of \({\mathcal {C}}_i\) to be sufficiently small to be disregarded in this special case, which will be further supported by our obtained results (see Sect. 3).

With the aforementioned clarifications, we will omit the term n.s.i. for brevity in our discussions on node properties in the functional climate networks studied in the remainder of this paper.

2.2 Event synchronization

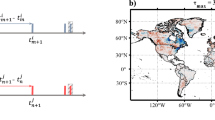
Event synchronization (ES), as established by Quiroga et al. [8], has originally been introduced to quantify the synchrony between EEG spike trains. In the last decade, this parameter-free method has also been utilized to construct functional climate networks (see Sect. 2.5). Using ES, two events l and m at nodes i and j, respectively, which occur at times \(t_l^i\) and \(t_m^j\) are considered synchronous if and only if their temporal distance is smaller than the local (dynamical) coincidence interval [17]

$$\begin{aligned} \tau _{lm}^{ij}=\frac{1}{2}\min \left\{ t_{l+1}^i - t_{l}^i, t_{l}^i-t_{l-1}^i, t_{m+1}^j-t_{m}^j, t_{m}^j - t_{m-1}^j \right\} . \end{aligned}$$
(4)

For the first and the last event of each time series, we cannot compute the temporal distance to the preceding or subsequent event, respectively. Therefore, we exclude these events in the following calculations [16]. For two event sequences with \(s_i\) and \(s_j\) events, l and m can therefore take values between \(l= 2,3,\ldots ,s_i-1\) and \(m=2,3,\ldots ,s_j-1\).

Using these dynamical coincidence intervals, we formulate the synchronization condition

$$\begin{aligned} \sigma _{lm}^{ij}= {\left\{ \begin{array}{ll}1,&{} \text {if } 0< t_l^i-t_m^j\le \tau _{lm}^{ij},\\ 0,&{} \text { otherwise,} \end{array}\right. } \end{aligned}$$
(5)

Here, we note that the dynamical coincidence interval \(\tau _{lm}^{ij}\) can be further restricted by an upper bound \(\tau _\mathrm{max}\) to avoid unrealistically large values, thereby introducing an otherwise omitted parameter to the method.

To obtain the total number of synchronous event pairs, we next compute

$$\begin{aligned} c(i|j)=\sum _{l=2}^{s_i-1}\sum _{m=2}^{s_j-1}J_{lm}^{ij}. \end{aligned}$$
(6)

using the indicator function [16]

$$\begin{aligned} J_{lm}^{ij}= {\left\{ \begin{array}{ll} 1, &{}\text {if}\ \sigma _{lm}^{ij}=1, \sigma _{m,l-1}^{ji}=0\ \text {and}\ \sigma _{m+1,l}^{ji}=0,\\ \frac{1}{2}, &{}\text {if either}\ t_l^i = t_m^j\\ &{}\text {or}\ \sigma _{lm}^{ij}=1\ \text {and}\ \left( \sigma _{m,l-1}^{ji}=1\ \text {or}\ \sigma _{m+1,l}^{ji}=1 \right) ,\\ 0, &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$
(7)

The above notion of event synchrony relies on the assumption that an event at node j precedes the correspondent event at node i. The rather complicated form of the employed indicator function is chosen precisely to prevent double counting of event pairs in both, c(j|i) and c(j|i) (with refers to the event synchrony in the opposite temporal order), and thereby ensure proper normalization of the resulting symmetric event synchronization strength defined as

$$\begin{aligned} Q_{ij}^{ES}=\frac{c\left( i|j\right) +c\left( j|i\right) }{\sqrt{\left( s_i-2\right) \left( s_j-2\right) }}. \end{aligned}$$
(8)

In the course of this work, we will utilize the symmetric matrix \({\varvec{Q}}^\mathrm{ES}=\left( Q_{ij}^\mathrm{ES}\right) \) to construct functional climate networks. For this purpose, we will threshold the elements of \({\varvec{Q}}^\mathrm{ES}\) at some suitable value such as to obtain a certain link density \(\rho \) which we will specify in the corresponding sections.

2.3 Event coincidence analysis

ECA is an alternative method to quantify synchrony between point processes, which is based on a similar yet somewhat simplified rationale as compared to ES. In contrast to ES where the local coincidence window is adaptively defined according to the timings of the previous and subsequent events, for ECA the corresponding coincidence window is a global parameter, the global (static) coincidence interval \(\varDelta T\).

Considering an identical setup as before, we consider two events at times \(t_l^i\) and \(t_m^j\) as synchronous, if they appear in a proper order with a mutual temporal distance smaller than \(\varDelta T\), i.e., \(0<t_l^i-t_m^j<\varDelta T\). On the one hand, this choice allows for faster computations, as the coincidence interval does not have to be computed individually for each pair of events. On the other hand, it provides the option of an analytical test for the significance of the resulting number of synchronous event pairs, at least in the limit of rare events [19, 20].

To quantify the synchrony of two time series, we estimate the event coincidence rate as the fraction of events in time series i which are preceded by at least one event in time series j within \(\varDelta T\),

$$\begin{aligned} r\left( i|j;\varDelta T\right) =\frac{1}{s_j-s_j'}\sum _{m=1}^{s_j-s_j'} \varTheta \Biggl \{ \sum _{l=1}^{s_i}1_{[0,\varDelta T]}\left( t_l^i- t_m^j\right) \Biggr \} \end{aligned}$$
(9)

with the indicator function

$$\begin{aligned} 1_I\left( x\right) ={\left\{ \begin{array}{ll}1, &{}\text {if } x \in I, \\ 0, &{}\text {otherwise,} \end{array}\right. } \end{aligned}$$
(10)

and the Heaviside step function \(\varTheta (\cdot )\) employed to avoid double counting of events. To correctly normalize the event coincidence rate [16], we have to subtract from the total number of events in time series j the number of events occurring between \(t_\mathrm{f}-\varDelta T\) and \(t_\mathrm{f}\), i.e.,

$$\begin{aligned} s_j'=\sum _{m=1}^{s_j} 1_{[t_\mathrm{f}-\varDelta T,t_\mathrm{f}]}\left( t_l^i\right) . \end{aligned}$$
(11)

As we are ultimately interested in obtaining an adjacency matrix that is based on the event synchrony between each pair of time series, we again construct a symmetric matrix by considering the arithmetic mean of any pair of event coincidence rates

$$\begin{aligned} Q_{ij}^\mathrm{ECA}= \frac{r\left( i|j;\varDelta T\right) +r\left( j|i;\varDelta T\right) }{2}. \end{aligned}$$
(12)

in full analogy to the case of ES. As a result, we can obtain a symmetric, binary adjacency matrix of the functional climate network by thresholding the similarity matrix \( {\varvec{Q}}^\mathrm{ECA}=\left( Q_{ij}^\mathrm{ECA}\right) \) at some value to obtain the desired link density.

We emphasize that there are two distinct algorithmic variants of event coincidence rates (referred to as trigger and precursor rates) that have been employed in recent works [20]. For the sake of simplicity and consistency with the definition of ES, we restrict our attention here to the so-called trigger rates corresponding to the definitions stated above. Moreover, it may be worth noticing that both, ES and ECA can be easily generalized to also account for delayed event occurrences by considering an additional time shift \(\tau \) between the two series of interest. As the latter is not of practical interest in the context of our present work, we will omit any further discussion on the implications of the corresponding additional parameter.

2.4 Effects of event clustering on synchrony measures

At it has been early recognized by [9] and others, events occurring in close temporal succession will lead to very short dynamical coincidence intervals of the ES, thereby possibly excluding actually close pairs of events in two series from being considered synchronous. Specifically, in the context of homogeneously sampled time series, events occurring at subsequent time steps would result in dynamical coincidence windows of \(\frac{1}{2}\) time step, allowing for counting only exactly simultaneous events. Recent work has focused on the practical implications of this effect, suggesting that a large number of temporally clustered events commonly lead to a downward bias of the estimated event synchronization strength, thereby missing possible links in a functional network construction. As a consequence, the degree of those nodes in functional networks that are characterized by strong temporal event clustering is commonly biased towards lower values [16,17,18] if not accounting for the latter effect. Notably, since ECA employs a fixed instead of adaptive coincidence interval, its values are not affected by the aforementioned mechanism.

To quantify the magnitude of temporal event clustering, we assign a simple statistical measure to each time series (i.e., each node of the functional network), the so-called pairing coefficient [16]. This property counts the fraction of events in a series that occur at subsequent time steps,

$$\begin{aligned} P_i= \frac{1}{s_i-1}\sum _{l=1}^{s_i-1}\delta \left[ \left( t_{l+1}^i-t_l^i \right) -1 \right] \end{aligned}$$
(13)

and takes values in the interval [0, 1] limited by the extreme cases with no event cluster (\(P_i=0\)) and all events occurring at subsequent time steps (\(P_i=1\)).

While having been quantitatively discussed only recently, some parts (yet not all) of the existing literature have already acknowledged the resulting effect of event clustering on ES and addressed this observation by a simple correction scheme [9, 14], which consists of removing all but the first events of each event cluster (consisting of two or more events observed at subsequent time steps) in all time series. This declustering approach prevents the described collapse of the dynamical coincidence interval to \(\frac{1}{2}\) time step and thereby avoids the clustering related bias, but comes on the cost of reducing the number of events in each affected series. The corresponding approach hence leads to a reduced sample size of events (and therefore an elevated variance of the obtained estimates of event synchrony measures, among other statistical characteristics) unless we employ an iterative (but commonly computationally expensive) procedure of successively lowering the threshold for defining additional events and declustering the resulting extended event sequences. In the context of the present work, the latter option will not be considered further.

Although the described correction scheme has been originally introduced to correct for the mentioned algorithmic shortcoming of the ES, it can also physically be motivated in the context of climate extremes. In time series including climatic extreme events, the appearance of events at subsequent time steps (e.g., days) can be caused by two different mechanisms. On the one hand, such subsequent events can be related to distinct weather systems or phenomena (which may still be interrelated physically, but could be counted as individual events). However, on the other hand (and potentially more frequently), subsequent extreme events are associated with one single (temporally and/or spatially persistent) weather system. Following this rationale, an application of the correction scheme can also be feasible along with functional climate networks constructed utilizing ECA [18]. From the latter reference, it follows that the degree patterns of ES based climate networks can be expected to be more strongly modified by event declustering than those of ECA based networks, while the results of both approaches become more similar to each other after declustering. In the context of the present work, we will further examine the role of link density in this process, along with corresponding effects on the spatial patterns of two additional local network measures as introduced in Sect. 2.1.

2.5 Previous work on event synchrony based functional climate networks

After the first corresponding proposal by Tsonis and co-workers in 2004 [35], complex networks have been increasingly demonstrated to provide prospective tools for studying the Earth’s climate variability. While early studies like [35, 36, 45, 46] had mostly considered the association between time series of seasonal anomalies by employing Pearson correlation or mutual information as similarity measures, a variety of subsequent works have focused on the timing of specific events. In the last decade, functional network analysis of synchronous heavy rainfall and closely related climate variables has led to several noticeable discoveries and advances. Among others, the Indian summer monsoon (ISM) and the South American monsoon system (SAMS) have intensively been studied using functional climate networks. Almost all of the corresponding studies have employed the ES concept to quantify the statistical association between the corresponding event time series.

Early studies focusing on the ISM [5, 10, 47] have not only described the spatial rainfall patterns but also identified different regions of coherent rainfall extremes and the emergence of characteristic network connectivity patterns around the onset and withdrawal of the monsoon. The effort of understanding the associated mechanisms has led to the development of a comprehensive onset and withdrawal prediction scheme for the ISM [15], which has performed impressively well since then. To investigate the interplay of the ISM with other large-scale climate variability modes such as the North Atlantic Oscillation (NAO) or the Pacific Decadal Oscillation (PDO), a wavelet-based multi-scale approach [48] has unraveled and characterized the respective spatial interdependency patterns across time-scales [49]. In addition to the ISM, some authors have also investigated other branches of the Asian monsoon system such as the East Asian monsoon system (EASM) [50]. In particular, the Baiu front as a key part of the EASM system has been characterized by quantifying its spatial pattern [51] and temporal evolution [52] in terms of complex network characteristics.

A plethora of other works have characterized different features of the SAMS. In a first study [53], the authors demonstrated that the main characteristic patterns can be highlighted using distinct event thresholds. A sequence of follow-up studies have addressed the propagation of heavy rainfall from South Eastern South America (SESA) to the Eastern Central Andes [9, 54], where frequent heavy rainfall events can lead to substantial flooding with large economic and societal effects. Southeastward moisture transport across South America via the South American low-level jet (SALLJ) towards SESA and South-East Brazil (SEBRA) results in the so-called South American rainfall dipole as the main continental pattern of rainfall variability. The interplay between this dipole and the other components of the SAMS has been comprehensively characterized by Boers et al. [55]. Another study [56] further quantified the influence of the El Niño–Southern Oscillation (ENSO) on extreme vertical moisture divergence in South America, demonstrating the relevance of including remote factors for understanding the SAMS characteristics by means of functional network analysis. Finally, a systematic inter-comparison between different rainfall data sets by means of complex networks [6] provided evidence that satellite-based gauged rainfall estimates allow for capturing rainfall events related to the SAMS correctly, while model-based data sets often missed certain functional dependencies between the different drivers of the SAMS.

Several more recent publications have extended the previous regional perspectives to other monsoon systems and a global realm. In this regard, a first characterization of the spatial pattern of heavy rainfall related to the Australian monsoon system (AMS) using functional climate networks has been presented recently [7]. In addition to the ongoing effort to studying phenomena related to the different regional monsoon systems, heavy rainfall patterns associated with tropical cyclones have also attracted considerable interest [11]. Last but not least, Boers et al. [14] achieved a major advance in investigating the interplay of heavy rainfall patterns across the whole globe. The latter work has highlighted the importance of Rossby waves as a major trigger and coupling mechanism that connects extreme rainfall events globally on spatial scales that by far exceed those of individual large-scale weather systems.

Next to the application of event synchrony to directly study the Earth’s complex climate variability, event synchrony measures have also been employed to understand and quantify the water resource distribution in hydrological applications. In particular, the role of an appropriate placement of measurement stations has been examined at the meso-scale by employing event synchrony and community detection methods [57, 58] and at the single-node level by proposing a new centrality measure [59].

Table 1 Overview on previous studies employing event synchrony measures to study functional connectivity in the Earth’s climate system based on rainfall data (as an exception, Boers et al. [56] employed vertically integrated moisture flux which can be considered as a quantity balancing between precipitation and evapotranspiration processes)
Full size table

3 Case study: the South American monsoon system

The South American monsoon system (SAMS) is controlled by moisture influx from the northern tropical Atlantic Ocean to the Amazon basin. While this moisture influx is mainly facilitated by the trade winds converging at the inter-tropical convergence zone (ITCZ) [60], precipitation is fostered all over the Amazon basin via moisture recycling mechanisms [61, 62]. Driven by the South American low-level jet (SALLJ) rainfall is further distributed along two different pathways. Depending on the Rossby wave phase [63], the SALLJ either transports moisture along the South American convergence zone (SACZ) to South East Brazil (SEBRA) [64, 65] or along the Eastern Central Andes to South Eastern South America (SESA) [65,66,67,68]. This dipolar behavior results in the major rainfall variability pattern in South America: the South American rainfall dipole. Due to the annual shift of the ITCZ, this regular precipitation pattern is most prominent in the period between December and February and leads to regular heavy precipitation along the described pathways [63, 66, 69].

For our analysis of the synchrony of heavy rainfall events in the SAMS, we employ daily rainfall estimates between December and February from the Tropical Rainfall Measuring Mission (TRMM, version 3B42 V7) [70]. This data set comprises the region from \(85\,^\circ \) W to \(30\,^\circ \) W and \(15\,^\circ \) N to \(40\,^\circ \) S at a spatial resolution of \(0.25\,^\circ \times 0.25\,^\circ \) in latitude and longitude (res ulting in \(N = 48,400\) grid points) and covers the period between 1998 and 2015. To apply event synchrony measures, we transform the daily rainfall time series of each grid point into binary event time series by thresholding each time series at the empirical \(90{\text {th}}\) percentile of each individual series. This leads to heterogeneous thresholds depending on the general distribution of rainfall at the different grid points. Dry spots with too few days of rainfall (most prominently in the continental shadow of the South American mainland west of the Andes mountain range) are not treated differently, and are, thus, underrepresented in the network. Due to their minor importance for the SAMS, we do not consider this as a drawback of our analysis.

To study the differences between the functional network characteristics for the SAMS obtained with the two event synchrony measures ES and ECA without and with temporal declustering, along with the influence of varying the link density \(\rho \), we consider an upper limit for the dynamic coincidence interval of the ES (\(\tau _\mathrm{max}=3\) days) and also choose a corresponding value of the ECA parameter as \(\varDelta T= 3\) days accordingly. These choices are not only in line with previous studies [18, 55], but also ensure that we analyze comparable time scales and characteristics with the two event synchrony measures. In what follows, we will present our main findings along with selected figures highlighting the most relevant points, while additional figures providing further details (e.g., patterns for different link densities) can be found in the Supplementary Material accompanying this manuscript.

3.1 Spatial patterns of local network measures

3.1.1 Node degree

By first examining the node degree pattern, we tie in with a recent publication [18] where the authors have conducted two case studies highlighting the similarities and differences between node degree patterns for the SAMS obtained using ES and ECA. Here, we show the corresponding pattern for two different values of the link density of \(\rho =0.005\) and \(\rho =0.05\) in Figs. 1 and 2, respectively, while the aforementioned earlier study [18] had utilized a link density of \(\rho = 0.02\) (reproduced in the Supplementary Fig. S1). The two cases shown here therefore illustrate two scenarios with decreased and increased link density, respectively.

Fig. 1
figure 1

Node degree patterns of the functional climate network representations of heavy rainfall events based on (a, b) ES and (c, d) ECA without (a, c) and with (b, d) incorporating the declustering scheme. All networks exhibit a link density of 0.005

Full size image

Figure 1 features the node degree pattern for ES (top) and ECA (bottom) without (left) and with (right) utilizing the correction scheme. In line with the findings presented earlier [18], the corrected versions of ES and ECA exhibit generally similar patterns, while the uncorrected versions differ regarding their respective placement of regions of elevated degree. In particular, we recover the previously found band of high degree north of the ITCZ over the Atlantic Ocean and only slightly elevated degree in SESA in the uncorrected ECA based network. In the uncorrected ES based network, the ITCZ is less highlighted but the South American rainfall dipole is well expressed. In the corrected ES based and ECA based networks, both the rainfall dipole as well as the ITCZ are characterized by elevated degree values, underlining that both features present large-scale precipitation systems which are however rather distinct. In addition, we observe two regions with an elevated degree in the northern Amazon basin. The moisture pathway along the Eastern Central Andes is however hardly visible in the degree pattern.

Fig. 2
figure 2

Same as in Fig. 1 but with a link density of 0.05

Full size image

As compared to Figs. 1 and 2 shows the degree pattern for a link density of \(\rho =0.05\) which is by a factor of 10 larger. Comparing the results for the uncorrected versions of ES and ECA (left panels), we find that the large-scale structures in the degree field appear like opposites of each other.

On the one hand, the ES based network now displays elevated degree in much of continental South America, especially in the southern part of the Amazon basin, along the Andes mountain range, and over SESA (along with those regions of the southwestern Atlantic ocean associated with the southern part of the rainfall dipole), while the ITCZ region and SEBRA do not exhibit prominently high degree values. Hence, the pattern has nearly switched as compared with the lower link density. To our best knowledge, a similar crossover behavior has not been described in ES based climate networks before, but was reported for the (scalar valued) global clustering coefficients of global surface air temperature networks established based on classical Pearson correlation [22]. Future work should further address this kind of transition behavior in network properties when increasing the density of connections, which has also been reported in other types of spatial networks [71,72,73,74] and could be related to a change in the structural complexity of the investigated network structures [21].

On the other hand, the general pattern for ECA based climate network still closely resembles those obtained with smaller link densities, presenting the highest degree values along the ITCZ, the northern Amazon basin, and SEBRA. While there are almost no regions highlighted along the Andes, the southern part of the South American rainfall dipole in SESA is marked by an intermediate degree.

For the corrected versions of ES and ECA, the degree patterns become more similar again. Hence, the temporal declustering of events affects the resulting network patterns even more strongly than for lower link densities. Despite the more similar appearance of the networks obtained with both event synchrony measures, there however remain certain quantitative differences between the respective degree patterns, especially regarding the separation of the two parts of the rainfall dipole, the low degree band along the ITCZ (i.e., a more clearly highlighted ITCZ in the ECA based network), and along the Andes (higher degree in the ES based network).

Fig. 3
figure 3

Average link distance patterns of the functional climate network representations of heavy rainfall events based on (a, b) ES and (c, d) ECA without (a, c) and with (b, d) incorporating the declustering scheme. All networks exhibit a link density of 0.005

Full size image

3.1.2 Average link distance

To complement the topological information on local network connectivity (in the sense of the number of connected neighbors) by spatial information, we now turn to the analysis for the average link distance. Notably, in combination with the node degree this measure allows distinguishing whether or not regions with elevated degree originate from particularly strong regional connectivity (e.g., locally increased spatial autocorrelation of the climate variable of interest) or the emergence of large-scale teleconnectivity [22, 75].

The link distance patterns obtained for the two event synchrony measures when employing a link density of \(\rho =0.005\) (shown in Fig. 3) closely resemble the corresponding degree patterns for the same link density. This statement does not only hold for the uncorrected versions of ECA and ES, but also for the link distance patterns based on the ES and ECA incorporating the declustering scheme. For larger link densities, we however also observe that degree and link distance appear qualitatively more and more similar between the uncorrected versions of ES and ECA as well (Supplementary Figs. S2 and S3). In general, we find that unlike for the node degree, an application of the declustering scheme is not as essential for obtaining spatial patterns which highlight the key features of the SAMS, while the general patterns of ECA and ES based networks again look almost identical after event declustering. We, therefore, conclude, that regardless of the specific link density, a larger degree indicates the presence of a higher number of long-distance connections and is thus accompanied by elevated values in the average link distance.

As a general result of the joint analysis of the node degree and link density patterns, we emphasize the great impact of the application of the correction scheme and the choice of the link density. While the differences between the respective local network measure patterns based on the uncorrected versions and the corrected versions have been slightly greater for ECA in the case of low link densities, ES experiences stronger effects of the correction scheme at higher link densities. Hence, based on the results obtained so far, we tentatively conclude that employing the correction scheme for temporally clustered events should be considered as a mandatory step for functional network applications of ES, while it calls for a somewhat different motivation in the context of ECA.

Fig. 4
figure 4

Spatial patterns of local clustering coefficients for the functional climate network representations of heavy rainfall events based on (a, b) ES and (c, d) ECA without (a, c) and with (b, d) incorporating the declustering scheme. All networks exhibit a link density of 0.02

Full size image

3.1.3 Local clustering coefficient

We finally discuss the spatial patterns of local clustering coefficients in the different functional climate network representations based on uncorrected and corrected ES and ECA. Other than node degree and average link distance, the local clustering coefficient does not exclusively assemble local information (in the sense of direct network connections) but considers connectivity information among the entire neighborhood of each node. In this spirit, it can be considered as a higher-order network characteristic as compared with degree and average link distance.

Figure 4 shows the local clustering coefficient patterns for a link density of \(\rho = 0.02\), revealing again notable differences between the ECA and ES based networks. While the clustering coefficient clearly exhibits lower values in the southern part of the Amazon basin in the ES based network, this effect is considerably more weakly developed in the ECA based network. In addition, we do not observe clearly expressed structures of elevated clustering coefficients along the eastern flank of the Andes in the ECA based network, especially when not employing the declustering scheme. In comparison to the degree, the application of the correction scheme seems to have fewer impact on the local clustering coefficient and does not lead to great similarity between the spatial patterns based on the two different event synchrony measures.

The reduced effect of prior declustering as compared to the other “first-order” network properties might be attributed to the role of the local clustering coefficient as a higher-order network measure. To better understand this, let us assume a relatively densely connected subgraph in a network. For nodes in this subgraph, we expect to obtain elevated values for the local clustering coefficient. The application of a correction scheme that affects the identification of edges in such a network can be expected to coherently influence the network’s degree distribution but, on average, retain similar characteristics for the neighborhood of each node. Since our results have shown such a behavior in the studied networks (i.e., a great impact of the correction scheme and high degree of similarity between corrected ES and ECA based networks for first-order network measures and less affected patterns for the higher-order network measure local clustering coefficient), we hypothesize that similar effects might also play a role in the networks studied in this work.

As compared to the other two local network characteristics, it is noticeable that at the considered intermediate link density of \(\rho =0.02\), the local clustering coefficient exhibits much smaller-scale spatial patterns, which is well in line with findings from previous studies [6, 53, 56]. When further reducing the link density (e.g., \(\rho = 0.005\), see Supplementary Fig. S4), the resulting patterns become very fine-scaled and appear not to allow for any meaningful interpretation. The reason for this is that especially in regions with low node degree, small random fluctuations in connectivity can cause large variation in the local clustering coefficient. As a result, the emergence of large-scale spatially coherent structures becomes increasingly unlikely with decreasing link density. Accordingly, we suggest that a meaningful estimation of higher-order network measures in functional climate networks calls for larger link densities, which is supported by our results obtained for the classical (non n.s.i. weighted) local clustering coefficient for \(\rho =0.05\) shown in Supplementary Fig. S5. Note that in our specific study region, the impact of n.s.i. weights on the spatial patterns of local clustering coefficients is indeed rather limited, which can be seen when comparing the corresponding results for \(\rho =0.02\) (Fig. 4 versus Supplementary Fig. S6) and \(\rho =0.005\) (Supplementary Figs. S4 versus S7) between n.s.i. and normal local clustering coefficients.

Fig. 5
figure 5

Values of (a, b) node degree \(k_i\), (c, d) local clustering coefficient \({\mathcal {C}}_i\) and (e, f) average link distance \(d_i\) for functional networks based on the two employed event synchrony measures. All results are shown for a link density of \(\rho = 0.005\). Panels a, c, e (b, d, f) show the properties of the networks obtained without (with) incorporating the declustering scheme. Each individual value is color-coded by the pairing coefficient of the event series associated with the corresponding node. The lines of identity are indicated as black dashed lines. Note that unlike node degree and average link distance, the local clustering coefficient is restricted to the interval [0, 1], which leads to saturation effects in the plot

Full size image
Fig. 6
figure 6

Same as Fig. 5 but for a link density of \(\rho = 0.02\)

Full size image

3.2 Node properties in different networks: role of the pairing coefficient

In the following, we further address the interrelationships between the values of the same local network property in ES versus ECA based climate networks along with the corresponding effect of event clustering as quantified by the pairing coefficient. We are particularly interested in the associated impact of the link density and the dependency on the declustering scheme. In Figs. 5 and 6, we show respective scatter plots of node degree, local clustering coefficient and average link distance for the same grid points in ES and ECA based networks for link densities of \(\rho =0.005\) and \(\rho =0.02\), respectively. Corresponding information for \(\rho =0.05\) can be found in Supplementary Fig. S8. To explicitly highlight the effect of the declustering scheme, we color each point in the scatter plot to encode the value of the pairing coefficient of the underlying event series.

As already stated above, the qualitative differences in the network properties based on ECA and ES are relatively minor for low link density (see Fig. 5). In line with the already discussed spatial pattern, we especially observe a better quantitative agreement (i.e., an alignment around the line of identity in the scatter plot) after the application of the correction scheme for both, node degree and average link distance. Without correction, we observe a clear misalignment with two relatively distinct groups of nodes. On the one hand, nodes with high pairing coefficient (strong event clustering) cover the whole range of degree values in the ECA based network while exhibiting only low to moderate values in the ES based network (i.e., they are located above the line of identity in the scatter plot). On the other hand, this negative connectivity bias for nodes with strong event clustering has to be compensated (due to the same, overall fixed link density) by other nodes with low pairing coefficient, which tend to have higher degrees in the ES based network than in that based on ECA. A similar behavior is observed for the average link distances. Here, nodes with very long average link distances are practically absent in the uncorrected ES based network, which is due to the fact that those nodes with the highest average link distances in the ECA based network almost all exhibit a high pairing coefficient. Thus, temporal clustering of events results in ES based networks missing especially the more distant (and, hence, probably often somewhat weaker) connections.

After applying the correction scheme, the node degrees and average link distances exhibit a much better agreement between ES and ECA based networks, while some residual differences remain. However, those differences necessarily emerge due to the fact that by their definitions, ECA counts all pairs of events as synchronous that appear within a temporal distance of 3 days or less, while ES most likely only counts some of them (depending on the respective local coincidence interval). In general, in good agreement with our observations for the corresponding spatial patterns, we conclude that ES and ECA based networks provide essentially the same information on the spatiotemporal patterns of heavy precipitation and their underlying dynamical mechanisms.

When increasing the link density, the separation between nodes with low and high pairing coefficient in terms of node agree and average link distance becomes even more distinct for networks obtained without event declustering (Fig. 6a, e). For both measures, the ES based network exhibits elevated values for nodes with low pairing coefficient, while the ECA leads to high degrees and large average link distances for nodes with high pairing coefficient. After application of our declustering scheme, the values for the degree are again much better aligned along the line of identity. For the average link density, this however does not apply.

As already seen for the spatial patterns of network properties, the distinction between ES and ECA based networks in terms of local clustering coefficients is much less obvious than for the other two considered network properties and does not change markedly when the correction scheme is applied or the link density is varied. As a general tendency, we however note that for larger link densities, nodes with higher pairing coefficient tend to display higher clustering coefficients than those with lower pairing coefficient in case of the ES based networks, while the corresponding effect is less pronounced for the ECA based networks. This observation might help further disentangling the mechanisms that are mapped by local clustering coefficients in functional climate networks in future more systematic research.

Fig. 7
figure 7

Relationship between node degree (n.s.i.) and local clustering coefficient (n.s.i.) for a link density of \(\rho = 0.02\). Panels a, c (b, d) show the network measures without (with) incorporating the declustering scheme. The values are color coded according to the pairing coefficient of each node

Full size image
Fig. 8
figure 8

Same as Fig. 7 but for the relationship between node degree and average link distance

Full size image

3.3 Statistical associations between different node properties

As a final step of our analysis, we take a look at the interrelationships between different local network characteristics. Figure 7 shows the scatter plots between node degree and local clustering coefficient for a link density of \(\rho =0.02\) without (left) and with (right) incorporating the declustering scheme. Corresponding results for \(\rho =0.005\) and 0.05 can be found in the Supplementary Figs. S9 and S10, respectively. As it can be seen, there is a general tendency of both properties to exhibit a negative correlation in all four networks, which is in line with previous findings for functional climate networks [22, 76] as well as other types of networks [77,78,79,80,81]. Besides this tendency, however, the overall scatter is fairly diffuse and appears to consist of different groups of nodes sharing a certain common behavior. To this end, we do not have a clear interpretation of this finding, but hypothesize that different combinations of atmospheric circulation regimes, orographic properties, or other key geographical features may contribute to the corresponding fragmentation of the scatter plots. Further disentangling these factors and thereby testing this general hypothesis is outlined as a possible subject of future work.

A much clearer picture is provided by Fig. 8 which shows the corresponding scatter plots between node degree and average link distance for \(\rho =0.02\) (corresponding results for \(\rho =0.005\) and 0.05 can be found in Supplementary Figs. S11 and S12, respectively). As expected from our previous findings, we observe a clear positive correlation (yet manifested as a not completely linear relationship) between both characteristics for both, ES and ECA based networks without and with event declustering. It is notable that this relationship is more distinct for the ECA based networks independent of whether or not declustering is applied, while the ES based networks show more nodes with higher than expected average link distance at a given node degree, pointing to a less homogeneous organization of network connectivity as compared to the ECA based networks. However, we find that the relationship becomes also more clearly expressed for the ES based networks in case of lower link densities (Supplementary Fig. S11) while getting blurred for both ES and ECA based networks when employing higher link densities (Supplementary Fig. S12).

For the sake of completeness, Supplementary Figs. S13–S15 also show the corresponding scatter plots between average link distance and local clustering coefficient for all three considered link densities, while essentially reflecting the already noted observations in terms of a generally negative yet nonlinear and rather diffuse relationship between both properties.

4 Conclusions

In this work, we have studied the characteristics of functional climate networks which have been obtained by quantifying event synchrony in terms of two different similarity measures, event synchronization (ES) and event coincidence analysis (ECA). Thereby, we have drawn upon the conclusions from a recent study [18] and expanded those previous results by comprehensively investigating three different local network properties encoding distinct features of the spatio-temporal organization of heavy rainfall during the South American monsoon season.

Beyond the setting of the aforementioned earlier work, we have first compared the spatial patterns of node degree in networks with different link densities. As a result, we have observed that the differences in the degree patterns in networks obtained based on ES and ECA become amplified when using denser networks. However, this effect can be suppressed if the underlying event sequences are declustered before the analysis, in which case we find very similar patterns under the considered comparable parameter setting of both methods.

In addition to the node degree, we have studied the spatial link distance patterns in networks derived utilizing the corrected and uncorrected versions of ES and ECA, respectively. We have found, that elevated link distances are intimately linked to larger node degrees in all studied network configurations. Although the link distance patterns are heavily affected when increasing the link density, the declustering scheme leads to similar patterns using ES and ECA.

To further examine the impact of declustering on higher-order network measures, we have also computed the local clustering coefficients. Our corresponding analysis has shown that the systematic difference between ES and ECA leads to distinct structures in the resulting climate networks. Notably, the structures that determine the local clustering coefficient are not as sensitive to the application of the declustering scheme as the first-order information captured by node degree and average link distance. As a consequence, the spatial patterns of the local clustering coefficient substantially differ between ES and ECA based networks even when incorporating the declustering scheme. This result is especially important since computing higher-order network measures typically requires larger link densities, which appear to amplify (as mentioned before) the structural differences between ES and ECA.

Finally, we have investigated the correlations between the values of each individual local network property in different networks, as well as those between different variables in the same network. First, the single variable correlations confirm the amplification of differences between the distributions of ES and ECA based network measures, especially for higher link densities. Additionally, our analysis has demonstrated the marked impact of the declustering scheme on the network degree and average link distance of ES based networks. By contrast, we have observed that the local clustering coefficients are less markedly affected by the correction scheme. Second, the inter-variable correlations have not only highlighted the distinct properties of ECA and ES but have also allowed analyzing further the characteristic features of the functional climate networks. This includes the general tendency that larger average link distances are typically associated with an elevated node degree. Furthermore, this analysis has revealed potential further biases of the event synchrony measures such as the tendency of high pairing coefficients coinciding with large average link distances in networks based on the uncorrected ES.

The central goal of this study has been to raise further awareness for possible methodological limitations of functional network construction based on event synchrony measures. In our study, we have illustrated that the choice of the methodological setup and the related parameters can have a substantial impact on the network topology and the conclusions drawn from the obtained results. In particular, we have shown that incorporating an event declustering scheme should be considered a mandatory preprocessing step especially when utilizing ES, and that the in theory rather minor methodological differences between the discussed event synchrony measures become increasingly important with rising link density and for higher-order network measures. In addition, a variation of the link density itself must be evaluated critically as we have demonstrated the existence of a crossover behavior in the large-scale spatial patterns of node degrees in one of the investigated settings.

To this end, we have not fully exploited the whole toolbox of higher-order complex network characteristics, disregarding, for example, the great variety of per-node network properties based on the concept of shortest paths like closeness, harmonic closeness, or betweenness. We outline further investigations on differences in those properties obtained for climate networks constructed using different event synchrony measures as a fruitful topic for future research. In a similar spirit, ES and ECA present two popular measures for event synchrony, but are not exclusive in their property of characterizing statistical associations between sequences of discrete events. Widening the scope of the present work also in this aspect might also be further addressed in upcoming studies.