Abstract
The potential of achieving computational hardware with quantum advantage depends heavily on the quality of quantum gate operations. However, the presence of imperfect two-qubit gates poses a significant challenge and acts as a major obstacle in developing scalable quantum information processors. Google’s Quantum AI and collaborators claimed to have conducted a supremacy regime experiment. In this experiment, a new two-qubit universal gate called the Sycamore gate is constructed and employed to generate random quantum circuits (RQCs), using a programmable quantum processor with 53 qubits. These computations were carried out in a computational state space of size \(9 \times 10^{15}\). Nevertheless, even in strictly-controlled laboratory settings, quantum information on quantum processors is susceptible to various disturbances, including undesired interaction with the surroundings and imperfections in the quantum state. To address this issue, we conduct both quantum state tomography (QST) and quantum process tomography (QPT) experiments on Google’s Sycamore gate using different artificial architectural superconducting quantum computer. Furthermore, to demonstrate how errors affect gate fidelity at the level of quantum circuits, we design and conduct full QST experiments for the five-qubit eight-cycle circuit, which was introduced as an example of the programability of Google’s Sycamore quantum processor. These quantum tomography experiments are conducted in three distinct environments: noise-free, noisy simulation, and on IBM Quantum’s genuine quantum computer. Our results offer valuable insights into the performance of IBM Quantum’s hardware and the robustness of Sycamore gates within this experimental setup. These findings contribute to our understanding of quantum hardware performance and provide valuable information for optimizing quantum algorithms for practical applications.
Similar content being viewed by others
1 Introduction
Traditional computers lack the capability to effectively simulate quantum mechanical systems. This is primarily due to the exponential growth in data requirements when attempting to comprehensively simulate quantum systems. In contrast, quantum computers [1] utilize the distinctive characteristics of quantum systems on which they are built to efficiently process vast amounts of information in a polynomial timeframe [2]. This allows them to handle exponentially larger quantities of data compared to classical counterparts.
Quantum processors are on the verge of fulfilling their transformative promise in revolutionizing the field of computing [1, 3–7]. Remarkable progress has been achieved in the development of quantum computers, particularly those utilizing superconducting qubits [8]. Among the most promising candidates are programmable processors based on superconducting qubits with Josephson junctions [9–14]. These processors offer the potential for scalable quantum computation on solid-state platforms, presenting an exciting avenue for advancement [15, 16].
One significant breakthrough lies in the utilization of superconducting transmon qubits [17–19], enabling Noisy intermediate-scale quantum (NISQ) architectures [20] to execute computations in a vast Hilbert space with a dimension of approximately 253 [21]. This represents an extraordinary leap forward, as quantum computers in the NISQ era can tackle computational challenges deemed impossible for classical counterparts [22]. The implications of this progress are profound, known as quantum supremacy regime [22–24], as it opens up new possibilities for tackling complex problems that were previously overwhelming, surpassing the limitations of classical systems and unlocking unprecedented computational power [22].
Random quantum circuits (RQCs) are considered challenging to simulate using classical systems. Achieving the ability to perform such simulations is a key milestone. In their work [21], Google’s Quantum AI and collaborators revealed that Sycamore, a programmable quantum processor consisting of 53 superconducting qubits, successfully executed a computation in a Hilbert space of dimension 253. This achievement claimed to surpass the capabilities of the Summit supercomputer, the most powerful classical supercomputer at that time. Initially estimated to take approximately 10,000 years on a conventional computer, the task purportedly was completed in just 200 seconds on Google’s quantum computer [21].
Soon after the publication, a debate erupted over the potential overestimation of the amount of time required to complete the same problem on a supercomputer. However, subsequent research demonstrated that an equivalent task could be simulated on classical computers, such as the Summit supercomputer, within a matter of days using classical simulation algorithms based on tensor networks [25–27]. During this debate, a significant issue was raised: whether there could be trustworthy techniques to precisely characterize the genuine quantum computing capabilities.
Today’s NISQ computers are capable of performing impressive algorithms. However, each quantum processor’s capability is limited by hardware errors. For example, errors such as drift [28, 29], coherent noise [30–32] and crosstalk [33]. These challenging errors make it difficult to reliably predict a processor’s capability and cause many programs to fail.
The ability to attain computational hardware with quantum advantage relies greatly on the quality of quantum gate operations. However, the existence of imperfect two-qubit gates presents a notable challenge and serves as a significant barrier in the advancement of scalable quantum information processors.
Quantum computing’s advancement hinges on our ability to accurately characterize quantum systems. Quantum state tomography and quantum process tomography play pivotal roles in this endeavor. QST allows us to fully describe the state of a quantum system, providing crucial insights into its properties and behavior. Meanwhile, QPT enables us to rigorously assess the performance of quantum gates and operations, shedding light on their effectiveness and fidelity. Together, these techniques empower researchers to understand, verify, and optimize quantum systems, driving progress towards realizing the transformative potential of quantum computing.
In this paper, we utilized a state-of-the-art superconducting quantum computer to conduct full quantum tomography experiments on a universal two-qubit gate known as the Sycamore gate. This gate was constructed and employed to generate random quantum circuits (RQCs) on 53 qubits, synonymous with a computational state-space of size \(9 \times 10^{15}\). The Sycamore gate belongs to a class of 2-qubit fermionic simulation gates [34]. Moreover, to demonstrate the impact of errors and their effects on gate fidelity at the level of quantum circuits, we conducted full QST experiments on the five-qubit eight-cycle circuit. This specific circuit was selected as an illustrative example of the programmability of Google’s Sycamore quantum processor. These QST experiments were conducted in three distinct environments: a noise-free setting, a noisy simulated environment, and on IBM Quantum’s genuine quantum computer.
Our findings shed light on the effectiveness of different implementations and the sources of errors, revealing fidelity results that are comparable to both theoretical (ideal) expectations and real-world experimental executions.
2 Sycamore RQCs
An astounding engineering achievement was introduced in [21], aiming to reach a quantum supremacy regime. A programmable superconducting processor was constructed, featuring a novel class of RQCs. These circuits consist of alternating layers of 1-qubit and 2-qubit gates. Additionally, fast, high-fidelity quantum gates capable of running simultaneously over a 2-dimensional qubit array were developed. The Sycamore processor is distinguished by its ability to perform high-fidelity one-qubit and two-qubit quantum gates, not only in isolation, but also while executing feasible computations with simultaneous gate operations on various qubits [21]. A full characterization of Google’s Quantum AI processor, Sycamore, has been presented in [35].
The Sycamore quantum computer employs transmon qubits [17], which can be considered as nonlinear superconducting resonators functioning at \(5\text{--}7\text{ GHz}\). The quantum bits are encoded as the resonant circuit’s two lowest quantum eigenstates. Additionally, each transmon has two controls: a microwave drive for excitation of the qubit and a magnetic flux control for frequency tuning. To read the qubit state, each qubit is associated with a linear resonator [12]. Moreover, every qubit is linked to its neighboring qubits via adjustable couplers [36, 37], as depicted in Fig. 1. Because of this coupler design, the coupling between qubits can be quickly tuned from totally off to 40 MHz. During the supremacy experiment, as one qubit was defective, the processor had 53-qubits as well as 86-couplers.
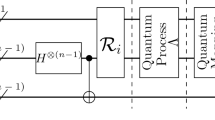
In every random circuit performed on the 53-qubit Sycamore quantum processor [21], each circuit consists of n cycles. Each “cycle” combines a single-qubit gate layer with a two-qubit gate layer, as depicted in Fig. 2. In these RQCs, three single-qubit gates are constructed and executed: the \(\sqrt{X}\), \(\sqrt{Y}\), and \(\sqrt{W}\) gates, such that
A schematic diagram illustrating an n-cycle circuit for the Sycamore 53-qubit Random Quantum Circuits (RQCs). Each cycle comprises two layers: one with randomly chosen 1-qubit gates from the set \(\{\sqrt{X}\text{ (in gray)}, \sqrt{Y} \text{ (in cyan)}, \sqrt{W}\text{ (in orange)}\}\), and another with 2-qubit gates labeled A, B, C, or D. For longer circuits, the layers follow the sequence A; B; C; D – C; D; A; B. Notably, the 1-qubit gates are not repeated sequentially, and an additional layer of 1-qubit gates precedes the measurements
In each cycle, there are two layers: one layer consists of randomly selected 1-qubit gates from the set \(\{\sqrt{X},\, \sqrt{Y},\, \sqrt{W} \}\), while the other layer consists of 2-qubit gates. The 1-qubit gates are not repeated in sequential order, and before the measurements, an additional layer of 1-qubit gates is applied. The 2-qubit gates in Google’s RQCs are not randomized. Instead, both the qubit pair and the cycle number contribute to determining the 2-qubit gates within the RQCs. These gates maintain the quantity of lower and excited states of the qubits.
The 2-qubit gates targeted for implementation in the quantum supremacy experiment are referred to as the fSim gates:
Equation (4) represents a family of two-qubit gates, known as “fSim” gates, which stands for fermionic simulation gates [34]. It can be expressed as the product of a two-qubit (iSWAP(£)) gate and a non-Clifford controlled phase gate (CPHASE(ϕ)).The experimental implementation of the entire space of gates described in Eq. (4) represents a long-term goal of Google Quantum AI and collaborators. [21]
In the supremacy experiment [21], the selected two-qubit gates are the Sycamore gates, which are equivalent to the fSim gate with the two-qubit gates tuned up near to a swap angle \(\pounds =\pi /2\) and a conditional phase \(\phi =\pi /6\) radians. That is, Sycamore \(\equiv \operatorname{fSim }(\pi /2,\pi /6)\). The fSim gate is defined to use a sign of £ different from that of the iSWAP gate [38]. Further insights into the 2-qubit gate strategy and the selection of implemented 2-qubit gates by Google Quantum AI and its collaborators can be found in [21]. Table 1 displays error measurements averaged over both \(|{0}\rangle \) and \(|{1}\rangle \) states [21]. The isolated readout error is detected to be 3.1%. Whereas, when running all qubit simultaneously, the readout error increases slightly to 3.8%.
The two-qubit Sycamore gate transforms the basis states as follows: \(|{0}\rangle _{A}\otimes |{0}\rangle _{B} \rightarrow |{0}\rangle _{A}\otimes |{0}\rangle _{B}\), \(|{0}\rangle _{A}\otimes |{1}\rangle _{B} \rightarrow - i \, |{1}\rangle _{A}\otimes |{0}\rangle _{B}\), \(|{1}\rangle _{A}\otimes |{0}\rangle _{B} \rightarrow -i \, |{0}\rangle _{A}\otimes |{1}\rangle _{B}\) and \(|{1}\rangle _{A}\otimes |{1}\rangle _{B} \rightarrow e^{(-i\pi /6)}|{1}\rangle _{A} \otimes |{1}\rangle _{B} \). Here, the subscripts A and B denote qubit A and qubit B, respectively. The matrix operator corresponding to Sycamore gate reads,
In the context of this paper, the two-qubit Sycamore gate is deconstructed into a set of 1-qubit gates combined with three controlled-X (CX) gates, as illustrated in Fig. 3. Additionally, Fig. 4 depicts the location of the Sycamore gate on the “Weyl chamber” [39, 40] in the \(m_{1} m_{2} m_{3}\) space, with respect to other two-qubit gates such as SWAP, iSWAP, and the two-qubit quantum Fourier transform (\(\mathrm{QFT} _{2}\)) [6].
The Sycamore gate located on the “Weyl chamber” in the \(m_{1} m_{2} m_{3}\) space. A tetrahedron whose vertices correspond to \(O(0,0,0)\), \(A_{1}(\pi ,0,0)\), \(A_{2}(\pi /2,\pi /2,0)\) and \(A_{3}(\pi /2,\pi /2,\pi /2)\). So that, every two qubit gate is associated with a point in the “Weyl chamber”. In this representation, orbits of locally equivalent unitary 2–qubit gates cross the Weyl chamber, constructing a tetrahedron in the cube of vectors \(m_{k}\). The polyhedron \(PQA_{2}RST\) represents the region of the perfect entanglers
It is worth clarifying that the Sycamore gate, in conjunction with single-qubit gates, constitutes a universal set, as is typical for most two-qubit gates [41]. Furthermore, it is pertinent to note that the broader class of fSim gates might achieve universality for the subset of Hamming-weight-preserving gates when utilized alongside Z-gates. However, the claim of universality asserted in this paper specifically addresses the Sycamore gate’s role in combination with single-qubit gates, rather than its standalone universality. The demonstration of universality as outlined by Google Quantum AI and collaborators in [21] is underpinned by establishing that the gate set consisting of CZ and SU(2) is universal [42, 43].
3 Full quantum tomography study of Sycamore gate
3.1 QPT experiments
Quantum process tomography (QPT) [44, 45] serves as a crucial method for validating quantum gates and discerning deficiencies in circuit configurations and gate designs. The principal aim of QPT is to derive a comprehensive characterization of the dynamical map, or quantum process, through a series of meticulously crafted experiments.
The theory of QPT is extensively elucidated in several seminal works, including those by Kraus [46], Chuang and Nielsen [44], Poyatos et al. [45], Mitchell et al. [47], and O’Brien et al. [48]. Additionally, the concept of stand-alone QPT, which obviates the need for QST, is expounded upon in [49].
In our investigation, we leverage the Choi-Jamiolkowski representation [50, 51] to provide a comprehensive characterization of our quantum operations via QPT experiments. The Choi representation offers a powerful framework wherein a quantum channel can be entirely described by a unique bipartite matrix known as the Choi matrix. This representation is achieved through the Choi-Jamiolkowski isomorphism [50, 51]. Further discussion on alternative representations for quantum channels can be found in the review by Wood et al. [52]. Nonetheless, the practical realization of full QPT has remained limited to exceedingly small-scale systems [44, 45]. For instance, in scenarios involving a system of N qubits, resulting in a formidable process matrix dimension of \(4^{N} \times 4^{N}\) [53].
To effectively visualize the quantum process of the Sycamore gate, we conducted QPT experiments focusing on the two-qubit gate. These experiments were carried out in three distinct environments: a noiseless setting, a simulated noisy environment, and on IBM Quantum’s quantum computer, ibm_oslo. In each environment, we executed the experiments by repeating the QPT process 4000 times for every measurement basis across all QPT circuits. The acquired experimental data were utilized to reconstruct the corresponding Choi matrices for each environment. Figure 5 depicts both the real (Re.(χ)) and imaginary (Im.(χ)) components of the Choi matrices for the Sycamore gate.
The real (Re.(χ)) and imaginary (Im.(χ)) components of the Choi matrices, derived from Quantum Process Tomography (QPT) experiments conducted on the two-qubit Sycamore gate, are examined. (a) The theoretical expectations for the ideal Choi matrix are considered. (b) QPT experiments are conducted in a noiseless environment. (c) QPT experiments are carried out in a simulated noisy environment. (d) QPT experiments are performed on IBM’s real quantum computer, ibm_oslo. These experiments entail 4000 repetitions in each environment. The resulting process fidelity (\({\mathcal{F}}_{P}\)) values are 0.9625, 0.6048, and 0.8102, respectively. In the Hinton diagram representation, positive elements are depicted as white squares, while negative elements are represented by black squares. The size of each square corresponds to the magnitude of its associated value, indicating its relative importance
To quantitatively assess the closeness of the measured Choi matrices to the ideal process, we computed the process fidelity \({\mathcal{F}}_{P}\) of the noisy quantum channels [54]. This allowed for meaningful comparisons across the different settings. The calculated process fidelities (\({\mathcal{F}}_{P}\)) for the noiseless, simulated noisy, and real-world ibm_oslo settings were found to be 0.9625, 0.6048, and 0.8102, respectively. These values provide insights into the efficacy of the Sycamore gate under various conditions.
3.2 QST experiments
Quantum state tomography entails reconstructing a system’s quantum state description from a series of quantum experiments. While a state vector characterizes the state of an ideal quantum system, a density matrix ρ delineates the state of an open quantum system. QST aims to rebuild or approximate this density matrix, through a consecutive set of repeated measurements.
To achieve this, the quantum state is initially prepared using a state preparation circuit, followed by a sequence of measurements corresponding to different operators. The resultant measurement data are utilized to approximate or reconstruct the state. Various techniques [55–59] have been developed to reconstruct a physically valid representation of the density matrix, reflecting the actual state obtained in the system, from the measured data. Additional studies of QST in noisy environments [60–63] have also provided valuable insights.
Here, we conduct QST experiments for the universal two-qubit Sycamore gate. The experiments are performed in three different environments: a noisy simulated environment, a noise-free, and on a real IBM Quantum’s quantum computer. For our experiments, we utilized the qasm_simulator [64] configured to simulate the perfect (noiseless) quantum computer. Additionally, we employed the 27-qubit IBM noisy simulator [64], which incorporates decoherence effects from earlier experimental implementations to compare with real (noisy) quantum computing architectures. Here, the input state of the Sycamore gate is prepared as the \(|{0}\rangle \otimes |{0}\rangle \) state. In the context of this paper, the notation xy serves as shorthand for the \(|{x}\rangle \otimes |{y}\rangle \) state, where x and y represent the binary values 0 or 1.
In these experiments, measurements of all qubits in the X, Y, and Z Pauli bases \(\{X,Y,Z\} \otimes \{X,Y,Z\} \) are added to the appended state preparation circuit of Sycamore gate. This necessitates the execution of nine measurement circuits for the two-qubit Sycamore gate. The resultant 36 measurement outcomes across all circuits, as depicted in Fig. 6, yield a tomographically overcomplete basis, facilitating the reconstruction of the quantum state.
Experimental measurements over all QST circuits for the two-qubit Sycamore gate. The experimental data were extracted from the nine measurement circuits performed in the QST experiments. Moreover, the ultimate outcomes encompass the 36 measurement results across all circuits and qubits within the Pauli bases \(\{XX,XY,XZ\}\), \(\{YX,YY,YZ\}\) and \(\{ZX,ZY,ZZ\} \) are presented. The experiments were run for 4000 repeated shots for each measurement basis, with a total running time of 13.8 s on the real IBM Quantum’s quantum machine, ibm_oslo
We utilize this data to reconstruct density matrices for the Sycamore gate, as illustrated in Fig. 7. This figure showcases both the real and imaginary components of the reconstructed density matrices derived from conducting QST experiments with 4000 repeated shots for each measurement basis. The state fidelity for two input states (density matrices) is computed as follows:
where \(\rho _{\mathrm{{ exper.}}}\) and \(\rho _{\mathrm{{ theor.}}}\) are experimental and theoretical density matrices, respectively. Our results demonstrate a state fidelity \({\mathcal{F}}_{S}\) of 94.65%, \(98.59\%0\) and 88.25% respectively, corresponding to QST experiments for Sycamore gate in a noisy simulated environment, noise-free, and on the ibm_oslo quantum computer.
Real (\(\mathrm{Re.}(\rho )\)) and imaginary (\(\mathrm{Im.}(\rho )\)) parts of the density matrices; reconstructed from QST experiments of the two-qubit Sycamore gate. (a) The ideal density matrix represents theoretical expectations. (b) QST experiments conducted in noise-free environment. (c) QST experiments implemented in a noisy simulated environment. (d) QST experiments executed on an IBM Quantum’s real quantum computer. These experiments were executed for 4000 repeated shots in each environment. The state fidelity \({\mathcal{F}}_{S}\) corresponding to the above-mentioned environments are 0.9859, 0.9465, and 0.8824, respectively. The experiments had a running time of 13.8 seconds
Table 2 provides details regarding qubit properties as well as the system experimental parameters during executing the QST experiment of the Sycamore gate on the ibm_oslo quantum computer. Figure 14 (appears in the Appendix) illustrates the machine’s performance during the execution of the QST experiments, including readout errors and parameter distributions for each qubit over the ibm_oslo quantum computer.
The running time for our QST experiments on the system was 13.8 second. Additionally, the average relaxation times T1 and T2 were found to be 103.819 μs and 90.417 μs, respectively. The qubit readout assignment error (ξ (Syc.)) averaged \(16.348 \times 10^{-3}\). The average readout length (λ) was measured to be 910.22 ns. Moreover, the average qubit frequency (\(\omega /2\pi \)) was determined to be 5.0779 GHz, while the average qubit anharmonicity (\(\gamma /2\pi \)) was calculated as \(-0.343\text{ GHz}\). Furthermore, the qubit flip probabilities from \(|{0}\rangle \) to \(|{1}\rangle \) (η) and from \(|{1}\rangle \) to \(|{0}\rangle \) (ζ) averaged \(16.28 \times 10^{-3}\) and \(16.42 \times 10^{-3}\), respectively.
The precision in determining the readout length and the gate error rates underscores our commitment to transparent reporting of experimental details. While we acknowledge the inherent challenges in achieving such levels of precision, it is important to clarify that these reported values serve to demonstrate the comprehensive characterization and meticulous control of experimental parameters in our study.
4 Full quantum state tomography of the five-qubit eight-cycle circuit
In this section, we aim to illustrate how errors manifest in gate fidelity at the level of quantum circuits. To achieve this, we design and conduct full QST experiments for the eight-cycles circuit, depicted in Fig. 2. This circuit, introduced in [21], serves as an illustration of the programmability of Google’s Sycamore quantum processor. The QST experiments are carried out in three environments: noise-free, noisy, and on an IBM Superconducting quantum computer.
It’s important to highlight that throughout these implementations, we configured the machine to adhere to Google’s layering configuration. This means that we instructed the quantum machine not to optimize or minimize the number of gates applied to each qubit in the original circuit. Instead, we allowed it to execute the circuit while maintaining the same structured layers as in Sycamore’s processor.
In doing so, we first execute the 5-qubit eight-cycle circuit on a qasm simulator and on two of IBM Quantum’s quantum computers: the five-qubit quantum machine ibmq_manila and the seven-qubit quantum machine ibm_oslo. Measurement outcomes from executing this circuit for \(20{,}000\) shots on these architectures are shown in Fig. 8.
Measurement outcomes for the experimental implementation of the 5-qubit 8-cycles circuit. Results were obtained from executing the circuit for \(20{,}000\) shots on a qasm simulator, as well as on two of IBM Quantum’s quantum computers: ibm_oslo and ibmq_manila. The vertical-axis represents the frequency (count) associated with each of the five-qubit computational basis states, which are labeled on the horizontal axis of the histogram. The quantum computation times on both ibm_oslo and ibmq_manila were recorded as 9.9 s and 9.4 s, respectively
Subsequently, we perform QST experiments on this 5-qubit 8-cycle quantum circuit in three different settings: noisy, noise-free, and on a real IBM quantum computer, ibmq_manila. This quantum computer is built based on a quantum processor of type Falcon r5.11L, which comprises five superconducting transmon qubits, produced by IBM Quantum [64].
In these full QST experiments, we include measurements of all qubits in the 5-qubit Pauli bases \(\{X,Y,Z\} ^{\otimes 5}\) to the appended state preparation circuit of the eight-cycles circuit. This results in a total of 243 measurement circuits (35) that must be executed for this five-qubit eight-cycles circuit. Furthermore, the culmination of the 7776 (65) measurement outcomes across all circuits furnishes a tomographically overcomplete basis, facilitating the reconstruction of the (targeted) quantum state. A random sample from the outputs of these quantum circuits is shown in Fig. 9 and Fig. 10.
Experimental results over a random subset of the 35 quantum state tomography measurement circuits. These circuits were randomly selected from a total of 243 measurement circuits executed in the QST experiments for the five-qubit eight-cycles circuit. These results include the final outcomes for the 7776 (\(6^{n}\)) measurement outcomes across all circuits of all qubits in the five qubit Pauli bases. The QST experiments were executed for 4000 repeated shots for each measurement basis on the real IBM Quantum’s quantum machine, ibmq_manila. The quantum computation running time was 4 minutes and 54 seconds. (Fig. 9 continued on the next page …)
(… Continued). The vertical-axis represents measurement outcomes associated with each of the five-qubit Pauli-basis states, that labeled on the horizontal axis of each histogram by numbers from 01 to 32. These numbers correspond respectively to the states: (00000, 01000, 01001, 01010, 01011, 01100, 01101, 01110, 01111, 00001, 10000, 10001, 10010, 10011, 10100, 10101, 10110, 10111, 11000, 11001, 11010, 11011, 11100, 11101, 11110, 11111, 00010, 00011, 00100, 00101, 00110, 00111)
We use these results to reconstruct density matrices for the five- qubit eight-cycles circuit, as depicted in Fig. 11. This figure displays both the real and the imaginary parts of the reconstructed density matrices obtained from running full QST experiments for 4000 repeated shots for each measurement basis. When performing QST in a noisy simulated environment, noise-free, and on the real IBM quantum computer, ibmq_manila, we demonstrate a state fidelity \({\mathcal{F}}_{S}\) of 0.5155, 0.9772, and 0.1595 respectively.
QST experiments conducted for the five-qubit eight-cycles circuit. Here, the real (\(\mathrm{Re.}(\rho )\)) and imaginary (\(\mathrm{Im.}( \rho )\)) parts of the density matrices are reconstructed from the 243 (35) measurement quantum circuits executed in the QST experiments for the 5-qubit 8 cycle circuit. These results include the final outcomes for the 7776 measurement across all circuits. (a) The ideal density matrix (theoretical expectations). (b) QST experiments performed in qasm_simulator. (c) QST experiments implemented with a noisy simulated environment. (d) QST experiments executed on an IBM’s real quantum computer ibmq_manila. These experiments were repeated for 4000 shot in each environment. The state fidelity \({\mathcal{F}}_{S}\) corresponding to the experimental implementations with qasm_simulator, noisy, and on the real quantum computer, ibmq_manila are 97.72%, 51.55% and 15.95% respectively
The discrepancy observed between noiseless simulations and real-world quantum device executions underscores the importance of understanding the impact of noise and imperfections in practical quantum computing environments. While noise-free simulations may provide valuable insights into theoretical performance, our experiments on real quantum hardware highlight the challenges and opportunities in optimizing quantum algorithms for real-world applications.
By conducting both QST and QPT analyses, we were able to gain insights into the performance of IBM Quantum’s hardware and the robustness of Sycamore gates, when implemented in this setup. These findings contribute to our understanding of quantum hardware performance and provide valuable information for optimizing quantum algorithms for practical applications.
Table 3 presents hardware performance, qubit properties as well as the system experimental parameters used during the execution of the full QST experiments of the eight-cycles circuit on the ibmq_manila quantum machine. The quantum computation time of running our QST experiments on the quantum computer ibmq_manila was 4 m 54 s. The average relaxation times T1 and T2 are respectively 151.791 μs and 57.119 μs. The qubit readout assignment error (\(\xi (8-\mathrm{cycle}.)\)) has an average of 0.02215. The average readout length (λ) is 5351.11 ns. The average qubit frequency (\(\omega /2\pi \)) is 4.971 GHz, and the average qubit anharmonicity (\(\gamma /2\pi \)) is \(-0.3436\text{ GHz}\). The qubit flip probabilities from \(|{0}\rangle \) to \(|{1}\rangle \) (η) and from \(|{1}\rangle \) to \(|{0}\rangle \) (ζ) have an average of 0.0145 and 0.0299, respectively. This study could extended further considering the per-round scrambling rate for the multi-round 8-cycle circuit tests.
Table 4 compares the state fidelities (\({\mathcal{F}}_{S}\)) and the process fidelities (\({\mathcal{F}}_{P}\)) obtained from conducting quantum experiments in different environments (noise-free, noisy-simulated, and on a physical quantum processor). While the fidelity observed in our noiseless simulations may be slightly below 1 compared to the ideal gate, this discrepancy is within an acceptable range considering the finite sampling and factors inherent to the simulation methodology, such as numerical precision errors and algorithmic approximations. We acknowledge that this deviation may impact the precision of other reported numbers and have taken this into consideration in our analysis.
The discrepancy observed in the performance between the QPT and QST experiments for the Sycamore gate is notable. It is remarkable that the simulated noisy environment performs better than the real IBM device in the QST experiments but fares poorly in the QPT experiment. While we currently lack a clear intuition regarding this observation, several factors may contribute to these differences. These factors include experimental variability, measurement sensitivity, and the complexity of QPT.
We acknowledge that employing bootstrapping methods to generate estimates of the uncertainty of the reported fidelities could further enhance the robustness of our analysis. This approach could provide a more comprehensive understanding of the precision to which the fidelities were determined, and we consider it as a valuable direction for future research.
5 Conclusion
The potential to attain computational hardware with quantum advantage relies significantly on the quality of quantum gate operations. However, the existence of imperfect two-qubit gates presents a notable challenge and serves as a significant barrier in the advancement of scalable quantum information processors.
In this study, we utilized state-of-the-art superconducting quantum computers to perform comprehensive quantum tomography experiments of a universal two-qubit gate. This gate falls within the category of 2-qubit fermionic simulation gates, specifically Google’s Sycamore gate, which played a crucial role in executing the random quantum circuits (RQCs) that led to the achievement of quantum supremacy regime using Google’s 53-qubits Sycamore Quantum AI.
Additionally, we aimed to demonstrate the influence of undesired operational interference on the fidelity of the Sycamore gate at the level of quantum circuits. To achieve this objective, we performed full QST experiments, specifically targeting the five-qubit eight-cycle circuit. This circuit was selected as an illustrative example to highlight the programmability of Google’s Sycamore quantum processor. These QST experiments were carried out in three different environments: a noise-free setting, a noisy simulated environment, and on IBM’s Quantum genuine quantum computers.
In our QPT experiments, the process fidelities (\({\mathcal{F}}_{P}\)) for the noiseless, simulated noisy, and real-world ibm_oslo settings were found to be 96.25%, 60.48%, and 81.02%, respectively. Moreover, in our QST experiments, results revealed that the Sycamore gate could maintain a relatively high state fidelity in these environments, with state fidelities 98.59%, 94.65% and 88.25%, respectively, when running our QST experiments for 4000 repeated shots for each measurement basis. However, at the level of quantum circuits, errors and other sources of unwanted operational interference significantly impact gate fidelity. We observed a state fidelity of 97.72%, 51.55% and 15.95% when running QST for the Sycamore gate within the 5-qubit 8-cycle circuit.
These findings highlight the Sycamore gate’s robustness and reliability as a component of a quantum computing system, suggesting its potential for diverse applications. However, it’s essential to acknowledge that the gate’s fidelity within a quantum circuit was notably lower in noisy and quantum computer environments compared to noise-free conditions. This indicates a need for continued efforts to improve the gate’s resilience to noise and external perturbations.
Future research could delve into identifying and mitigating the sources of these imperfections, aiming to enhance the overall performance of the Sycamore gate and other quantum computing elements.
Data availability
The datasets generated during and/or analyzed during the current study are included within this article.
Abbreviations
- RQCs:
-
Random quantum circuits
- QST:
-
Quantum state tomography
- QPT:
-
Quantum process tomography
- NISQ:
-
Noisy intermediate-scale quantum
- fSim:
-
Fermionic simulation
- £ :
-
A swap angle
- \(R_{Z}\) :
-
The rotation about z-axis
- CPHASE:
-
Controlled phase gate
- QFT:
-
Quantum Fourier transform
- Falcon r5.11L:
-
A quantum processor produced by IBM Quantum
- \({\mathcal{F}}_{S}\) :
-
The state fidelity
- ρ :
-
Density matrix
- \(\rho _{\mathrm{{exper.}}}\) :
-
Experimental density matrix
- \(\rho _{\mathrm{{theor.}}}\) :
-
Theoretical density matrix
- qasm:
-
Quantum assembly language
- \(Q_{i}\) :
-
The ith qubit
- CX:
-
The controlled-X gate
- Syc.:
-
Sycamore
- T1:
-
Relaxation time
- T2:
-
Dephasing time
- \(\omega /2\pi \) :
-
Qubit frequency
- \(\gamma /2\pi \) :
-
Qubit anharmonicity
- ξ :
-
The qubit readout assignment error
- ζ :
-
The qubit flip probabilities from \(|{1}\rangle \) to \(|{0}\rangle \)
- η :
-
The qubit flip probabilities from \(|{0}\rangle \) to \(|{1}\rangle \)
- λ :
-
Readout length
- Re.:
-
Real part
- Im.:
-
Imaginary Part
- GHz:
-
Giga hertz \(1 \text{ GHz} =1.0\times 10^{9}\) Hertz
- MHz:
-
Mega hertz \(1 \text{ MHz} =1.0\times 10^{6}\) Hertz
- μs:
-
Micro seconds, \(1~\mu \mathrm{s}=1.0\times 10^{-6}\) second
- ns:
-
Nano seconds, \(1~\mathrm{ns}=1.0\times 10^{-9}\) second
References
Ladd TD, Jelezko F, Laflamme R et al.. Quantum computers. Nature. 2010;464:45.
Feynman RP. Simulating physics with computers. Int J Theor Phys. 1982;21:467–88.
DiVincenzo DP. The physical implementation of quantum computation. Fortschr Phys. 2000;48:771–83.
Chuang I. Building the building blocks. Nat Phys. 2018;14:974.
Barenco A, Bennett CH, Cleve R et al.. Elementary gates for quantum computation. Phys Rev A. 1995;52:3457.
Nielsen MA, Chuang IL. Quantum computation and quantum information. 10th anniversary ed. Cambridge: Cambridge University Press; 2011.
AbuGhanem M, Homid A, Abdel-Aty M. Cavity control as a new quantum algorithms implementation treatment. Front Phys. 2018;13:1.
Castelvecchi D. Quantum computers ready to leap out of the lab in 2017. Nature. 2017;541:9–10.
Devoret MH, Martinis JM, Clarke J. Measurements of macroscopic quantum tunneling out of the zero-voltage state of a current-biased Josephson junction. Phys Rev Lett. 1985;55:1908.
Nakamura Y, Chen CD, Tsai JS. Spectroscopy of energy-level splitting between two macroscopic quantum states of charge coherently superposed by Josephson coupling. Phys Rev Lett. 1997;79:2328.
Mooij J et al.. Josephson persistent-current qubit. Science. 1999;285:1036–9.
Wallraff A et al.. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature. 2004;431:162–7.
You JQ, Nori F. Atomic physics and quantum optics using superconducting circuits. Nature. 2011;474:589–97.
AbuGhanem M, et al. Fast universal entangling gate for superconducting quantum computers. Elsevier, SSRN 4726035; 2024.
Wang T, Zhang Z, Xiang L et al.. The experimental realization of high-fidelity shortcut-to adiabaticity quantum gates in a superconducting Xmon qubit. New J Phys. 2018;20:065003.
AbuGhanem M. Properties of some quantum computing models. Master’s thesis. Ain Shams University; 2019.
Koch J et al.. Charge-insensitive qubit design derived from the Cooper pair box. Phys Rev A. 2007;76:042319.
Chow J, Gambetta J, Magesan E et al.. Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nat Commun. 2014;5:4015.
Barends R, Kelly J, Megrant A et al.. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature. 2014;508:500–3.
Preskill J. Quantum computing in the NISQ era and beyond. Quantum. 2018;2:79.
Arute F et al.. Quantum supremacy using a programmable superconducting processor. Nature. 2019;574:505–10.
AbuGhanem M, Eleuch H. NISQ computers: a path to quantum supremacy. arXiv preprint. 2023. arXiv:2310.01431 [quant-ph].
Preskill J. Quantum computing and the entanglement frontier. arXiv preprint. 2012. arXiv:1203.5813v3 [quant-ph].
Neill C et al.. A blueprint for demonstrating quantum supremacy with superconducting qubits. Science. 2018;360:195–9.
Huang C, et al. Classical simulation of quantum supremacy circuits. arXiv preprint. 2020. arXiv:2005.06787 [quant-ph].
Pan F, Chen K, Zhang P. Solving the sampling problem of the Sycamore quantum circuits. Phys Rev Lett. 2022;129:090502.
Pednault E, et al. Leveraging secondary storage to simulate deep 54-qubit Sycamore circuits. arXiv preprint. 2019. arXiv:1910.09534 [quant-ph].
Mavadia S et al.. Experimental quantum verification in the presence of temporally correlated noise. npj Quantum Inf. 2018;4:7.
Proctor T et al.. Detecting and tracking drift in quantum information processors. Nat Commun. 2020;11:5396.
Huang E, Doherty AC, Lammia S. Performance of quantum error correction with coherent errors. Phys Rev A. 2019;99:022313.
Kueng R, Long DM, Doherty AC, Flammia ST. Comparing experiments to the fault-tolerance threshold. Phys Rev Lett. 2016;117:170502.
Murphy DC, Brown KR. Controlling error orientation to improve quantum algorithm success rates. Phys Rev A. 2019;99:032318.
Sarovar M et al.. Detecting crosstalk errors in quantum information processors. Quantum. 2020;4:321.
Kivlichan ID et al.. Quantum simulation of electronic structure with linear depth and connectivity. Phys Rev Lett. 2018;120:110501.
AbuGhanem M, Eleuch H. Experimental characterization of Google’s Sycamore quantum AI on an IBM’s quantum computer. Elsevier, SSRN 4299338; 2023.
Chen Y et al.. Qubit architecture with high coherence and fast tunable coupling circuits. Phys Rev Lett. 2014;113:220502.
Yan F et al.. A tunable coupling scheme for implementing high-fidelity two-qubit gates. Phys Rev Appl. 2018;10:054062.
Bialczak RC et al.. Quantum process tomography of a universal entangling gate implemented with Josephson phase qubits. Nat Phys. 2010;6:409.
Kraus B, Cirac JI. Optimal creation of entanglement using a two-qubit gate. Phys Rev A. 2001;63:062309.
Zhang J, Vala J, Whaley KB, Sastry S. A geometric theory of non-local two-qubit operations. Phys Rev A. 2003;67:042313.
Lloyd S. Almost any quantum logic gate is universal. Phys Rev Lett. 1995;75:346.
Boykin P, Mor T, Pulver M, Roychowdhury V, Vatan F. On universal and fault-tolerant quantum computing. In: Proc. 40th annual symposium on foundations of computer science. Los Alamitos: IEEE Comput. Soc.; 1999.
DiVincenzo DP. Two-bit gates are universal for quantum computation. Phys Rev A. 1995;51:1015–22.
Chuang IL, Nielsen MA. Prescription for experimental determination of the dynamics of a quantum black box. J Mod Opt. 1997;44:2455.
Poyatos JF, Cirac JI, Zoller P. Complete characterization of a quantum process: the two-bit quantum gate. Phys Rev Lett. 1997;78:390.
Kraus K. States, effects, and operations. Berlin: Springer; 1983.
Mitchell MW et al.. Diagnosis, prescription, and prognosis of a Bell-State filter by quantum process tomography. Phys Rev Lett. 2003;91:120402.
O’Brien JL et al.. Quantum process tomography of a controlled-not gate. Phys Rev Lett. 2004;93:080502.
Merkel ST et al.. Self-consistent quantum process tomography. Phys Rev A. 2013;87:062119.
Choi MD. Completely positive linear maps on complex matrices. Linear Algebra Appl. 1975;10:285.
Jamiolkowski A. Linear transformations which preserve trace and positive semidefiniteness of operators. Rep Math Phys. 1972;3:275.
Wood CJ, Biamonte JD, Cory DG. Tensor networks and graphical calculus for open quantum systems. Quantum Inf Comput. 2015;15:0579.
AbuGhanem M. Full quantum process tomography of a universal entangling gate on an IBM’s quantum computer. arXiv preprint. 2024. arXiv:2402.06946.
Zhang J, Souza AM, Brandao FD, Suter D. Protected quantum computing: interleaving gate operations with dynamical decoupling sequences. Phys Rev Lett. 2014;112:050502.
James DF, Kwiat PG, Munro WJ, White AG. On the measurement of qubits. Phys Rev A. 2001;64:052312.
Teo YS et al.. Quantum-state reconstruction by maximizing likelihood and entropy. Phys Rev Lett. 2011;107:020404.
Smolin JA, Gambetta JM, Smith G. Efficient method for computing the maximum-likelihood quantum state from measurements with additive Gaussian noise. Phys Rev Lett. 2012;108:070502.
Qi B et al.. Adaptive quantum state tomography via linear regression estimation: theory and two-qubit experiment. npj Quantum Inf. 2017;3:19.
Bolduc E, Knee GC, Gauger EM, Leach J. Projected gradient descent algorithms for quantum state tomography. npj Quantum Inf. 2017;3:44.
Bogdanov YI, Bantysh BI, Bogdanova NA, Kvasnyy AB, Lukichev VF. Quantum state tomography with noisy measurement channels. In: Proc. SPIE. vol. 10224; 2016.
Ivanova-Rohling VN, Rohling N, Burkard G. Optimal quantum state tomography with noisy gates. EPJ Quantum Technol. 2023;10:25.
Rambach M et al.. Efficient quantum state tracking in noisy environments. Quantum Sci Technol. 2023;8:015010.
AbuGhanem M, Eleuch H. Two-qubit entangling gates for superconducting quantum computers. Results Phys. 2024;56:107236.
IBM Quantum. https://quantum-computing.ibm.com. 2023.
Acknowledgements
We sincerely thank the anonymous reviewers for their insightful feedback and constructive criticism on our paper. Their expertise and suggestions have undoubtedly improved the quality and clarity of our work. We acknowledge the use of IBM’s Superconducting quantum computers in this work. However, the views and conclusions expressed in this manuscript are solely those of the authors and do not necessarily represent the views of IBM Quantum or Google’s Quantum AI.
Funding
The authors declare that no funding, grants, or other forms of support were received at any point throughout this research work.
Author information
Authors and Affiliations
Contributions
M. AbuGhanem: Conceptualization, Methodology, Software, experimental implementations on IBM Quantum’s quantum computers, Data curation, Formal analysis, Visualization, Investigation, Validation, Writing, Reviewing and Editing. H. Eleuch: Investigation, Validation, Reviewing and Editing. All authors have approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
All authors have approved the publication. This research did not involve any human, animal or other participants.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Hardware performance
Appendix: Hardware performance
In this appendix, we offer comprehensive insights into the hardware characteristics of the IBM Quantum’s quantum computers utilized in our study, encompassing both the seven-qubit ibm_oslo and the five-qubit ibmq_manila systems. Figures 12 and 13 present the readout error map and layout of the ibm_oslo and ibmq_manila quantum computers, respectively. Detailed general specifications and coupling maps for both systems are provided in Tables 5, 6, 7, and 8.
The layout and the error map of the ibm_oslo quantum machine, presented by IBM Quantum. It comprises seven superconducting transmon qubits, with a minimum (maximum) qubit frequency of 4.925 (5.319) GHz, and a minimum (maximum) readout assignment error of \(0.710 \times 10^{-2}\) (\(2.870 \times 10^{-2}\)). The processor can execute up to 100 quantum circuits, with a maximum of 20,000 shots
Readout error map and layout of the ibmq_manila quantum machine. This quantum machine is based on a Falcon r5.11L quantum processor, produced by IBM Quantum. It consists of five superconducting transmon qubits, with a minimum (maximum) qubit frequency of 4.838 (5.065) GHz, and a minimum (maximum) readout assignment error of \(1.690\times 10^{-2}\) (\(3.920 \times 10^{-2}\)), with an average CNOT error rate of 0.817% and an average H error rate of 0.036%, with a median CNOT gate time of 344.889 ns. The processor can execute up to 100 quantum circuits, with a maximum of \(20{,}000\) shots
The quantum computer ibmq_manila have a minimum (maximum) qubit frequency of 4.838 (5.065) GHz, and a minimum (maximum) readout assignment error of \(1.690\times 10^{-2}\) (\(3.920 \times 10^{-2}\)), with a CNOT average error rate of 0.817% with, and an average H error rate of 0.036%, with median CNOT gate time 344.889 ns. This quantum computer can execute up to 100 quantum circuits, with \(20{,}000\) maximum shots. The basis gates of this device encompass the identity (I), the square root of NOT gate (\(\sqrt{X}\) or SX), the NOT gate (X), the rotation gate around the z-axis (RZ), and the 2-qubit controlled-NOT gate (CX). The coupling maps between its qubits are delineated as follows: CNOT:[\(Q_{0};Q_{1}\)], CNOT:[\(Q_{1};Q_{0}\)], CNOT:[\(Q_{1};Q_{2}\)], CNOT:[\(Q_{2};Q_{1}\)], CNOT:[\(Q_{2};Q_{3}\)], CNOT:[\(Q_{3};Q_{2}\)], CNOT:[\(Q_{3};Q_{4}\)] and CNOT:[\(Q_{4};Q_{3}\)].
The ibmq_manila quantum machine has the following median error rates and qubit parameters: Median CNOT error of \(7.296\times 10^{-3}\), median SX error of \(3.270\times 10^{-4}\), median readout error of \(2.640\times 10^{-2}\), median T1 of 134.7628 μs, and median T2 of 67.3 μs.
For each qubit of the ibm_oslo and ibmq_manila quantum computers during QST experiments, Figs. 14 and 15 showcase processor performance, parameter distribution, and readout errors. Finally, Figs. 16 and 17 represent the real (\(\mathrm{Re.}(\rho )\)) and imaginary (\(\mathrm{Im.}(\rho )\)) parts of the density matrices resulting from running QST for the five-qubit 8-cycle circuit, displayed as 2D (Hinton) diagrams.
The real (\(\mathrm{Re.}(\rho )\)) and imaginary (\(\mathrm{Im.}( \rho )\)) parts of the density matrices resulting from running QST for the five-qubit 8-cycle circuit are represented as Hinton diagrams. (a) The ideal density matrix representing theoretical expectations. (b) Quantum State Tomography (QST) experiments conducted on the qasm simulator. (Fig. 16 continued on the next page …)
(… Continued) The real (\(\mathrm{Re.}(\rho )\)) and imaginary (\(\mathrm{Im.}(\rho )\)) parts of the density matrices resulting from running QST for the five-qubit 8-cycle circuit are represented as a Hinton diagram. (c) QST experiments conducted in a noisy simulated environment. (d) QST experiments carried out on IBM Quantum’s real quantum computer, ibmq_manila
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
AbuGhanem, M., Eleuch, H. Full quantum tomography study of Google’s Sycamore gate on IBM’s quantum computers. EPJ Quantum Technol. 11, 36 (2024). https://doi.org/10.1140/epjqt/s40507-024-00248-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjqt/s40507-024-00248-8