1 Introduction

Rydberg atoms are neutral atoms whose valance electron is excited to a high-lying level, exhibiting great electric dipole moments and interacting strongly with ambient ones [1, 2]. Rydberg atoms have served as a potential platform for scalable quantum computing for a long time due to their relatively long coherent times [3–6]. The strong interaction between adjacent Rydberg atoms in a small volume with radius being several microns allows at most one of them to be excited to Rydberg states, which is called “Rydberg blockade”. This excitation blockade mechanism can induce many interacting atoms to form a Rydberg superatom and can further facilitate the mesoscopic quantum information processing with quantum information being stored in collective states of atomic ensembles [7]. Besides, the feature of preventing Rydberg transitions of more than one atom within the blockade radius can be extensively applied in constructing one-step multiqubit quantum gates [8–12], generating multiparticle entanglement [13–18], and achieving quantum sensing [19–24]. In addition to Rydberg blockade, Rydberg antiblockade is another important dynamics mechanism of Rydberg atom systems [25–28], which allows two or more atoms to be excited to Rydberg states simultaneously. Rydberg antiblockade can be yielded generally by simultaneous-driving–induced second-order resonant processes [29–31], sequential-driving–induced fast first-order processes [32, 33], or simultaneous-driving–induced fast first-order processes [12, 34], and this mechanism may be used for gaining the quantitative interaction strength information between atoms [25], constructing one-step quantum gates [35, 36], and generating steady entanglements [37–40].

For either Rydberg blockade or antiblockade mechanism, implementation of quantum gates on Rydberg atoms usually focuses on phase-shift or controlled-not (CNOT) gates [8, 12, 30–32, 35, 36, 41–45]. Although arbitrary gate operations may be constructed by combining a CNOT gate with several single-qubit gates (for example, one can form a SWAP gate by using three CNOT gates [46]), direct implementations of some certain gates can largely strengthen efficiency of processing lengthy quantum algorithms. As a nontrivial two-qubit gate, the SWAP gate is of great importance and applications in the field of quantum science and technologies, such as quantum computation [46], entanglement swapping [47], and quantum repeaters [48]. For SWAP gate schemes based on Rydberg blockade, multiple piecewise pulses involving two or more Rydberg states and three or more steps are needed to impose on single atoms [49–51], which inexorably increases complexity of quantum algorithms and also makes the system exposed to more decoherence. To this end, most recently there are one-step Rydberg-atom SWAP gate schemes proposed to decrease complexity of operations on atoms. For example, Wu et al. proposed a regime of unselective ground-state blockade in the context of Rydberg antiblockade to construct SWAP gates by using detuning [52] or amplitude-modulated [53] pulses without individual addressing of atoms. Li et al. proposed ground-state transport of Rydberg atoms by setting match between interatomic interaction strength and Rydberg pumping detunings [54]. However, these schemes of achieving SWAP gates have to depend on the slow dynamics using the second-order perturbation theory once or even twice.

In this work, we propose an efficient scheme of implementing SWAP gate on ground-state manifolds of Rydberg atoms, where the SWAP gate is not only implemented in one step but also dependent of undegraded dynamics without using the second-order perturbation theory. We apply lasers with amplitude modulation to drive ground-Rydberg state transitions, and the two-atom transitions from single-excitation states to the doubly-excited state can be obtained by elaborately matching the modulation frequency of one laser and interaction strength between atoms, which can then be described by dressed states formed with these single- and double-excitation states. Further, we modulate the amplitude of the other laser so as to yield constructive interference of two transitions to the single-excitation states from ground states \(|01\rangle \) and \(|10\rangle \) but destructive interference of transitions to the double-excitation state. In addition, we introduce soft quantum control [55] to manipulate the SWAP transformation, the rotating-wave approximation (RWA) can be satisfied well to restrain unwanted transitions, so the SWAP gate possesses relatively high fidelity. Compared with the recent Rydberg-atom SWAP schemes [52–54], the selective transition dynamics in the present scheme shows an interference-induced suppression of the doubly-excited Rydberg state, and two-atom transitions dependent of interference instead of the second-order perturbation theory make the SWAP gate cost shorter gate time, so we identify that the SWAP gate exhibits greater robustness against atomic decay and deviations in the interatomic interaction strengths related to the double-excitation state. Finally, we show some certain potential applications in quantum computation, entanglement swapping, and a quantum repeater.

2 Model and Hamiltonian

2.1 Description of the atom-laser interaction

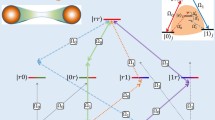
As depited in Fig. 1(a), we consider two neutral atoms 1 and 2 trapped in two optical lattices or microtraps with interatomic separation \(d\sim \mu\mathrm{m}\) [44, 45, 56–58], and the two atoms are assumed to interact with each other by the van der Waals (vdW) potential with strength \(V=C_{6}/d^{6}\) where \(C_{6}\) is the vdW dispersion coefficient. As shown in Fig. 1(b), two amplitude-modulated laser fields are imposed on two identical atoms to drive resonantly Rydberg transitions from two ground-state manifolds (computational states) \(|0\rangle \) and \(|1\rangle \) to a Rydberg state \(|r\rangle \), respectively, with modulated Rabi frequencies \(\Omega _{0}(t)=\Omega _{\mathrm{0m}}\cos (\omega _{0}t)\) and \(\Omega _{1}(t)=\Omega _{\mathrm{1m}}\cos (\omega _{1}t)\). \(\Omega _{\mathrm{0m}}\) (\(\Omega _{\mathrm{1m}}\)) and \(\omega _{0}\) (\(\omega _{1}\)) are the maximum and frequency of amplitude modulation for the laser driving transition \(|0(1)\rangle \leftrightarrow |r\rangle \), respectively. We can describe the interaction between the lasers and two atoms with the Hamiltonian in the interaction picture (using natural unit \(\hbar =1\))

$$ \hat{H}_{12}= \sum_{j=1}^{2} \sum_{k=0}^{1}\frac{\Omega _{k}(t)}{2} \bigl(|k\rangle _{j}\langle r|+|r\rangle _{j}\langle k| \bigr)+V|rr \rangle \langle rr|, $$
(1)

where \(|rr\rangle \equiv |r\rangle _{1}\otimes |r\rangle _{2}\) denotes the two-atom doubly-excited Rydberg pair state.

Figure 1
figure 1

Schematic for implementing a SWAP gate on ground-state manifolds of two Rydberg atoms. (a) Two neutral atoms confined in microtraps with separation \(d\sim{\mu\mathrm{m}}\) interact with each other through vdW interaction with strength \(V=C_{6}/d^{6}\). (b) Schematic of laser-induced atomic transitions from ground-state manifolds \(|0\rangle \) and \(|1\rangle \) to a Rydberg state \(|r\rangle \) with modulated Rabi frequencies \(\Omega _{0}(t)=\Omega _{\mathrm{0m}}\cos (\omega _{0}t)\) and \(\Omega _{1}(t)=\Omega _{\mathrm{1m}}\cos (\omega _{1}t)\), respectively

Full size image

This laser-atom interaction model is similar to that used in Ref. [53], with which when the parameter condition \(|\omega _{0}|\), \(|\omega _{1}|\), \(|V|\gg |\Omega _{0m}|/4\), \(|\Omega _{1m}|/4\) is considered, an effective Hamiltonian can be obtained with the second-order perturbation theory [53]

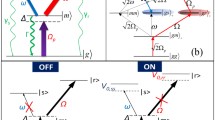
$$ \hat{H}_{e}=\frac{\Omega _{e}}{2} \bigl(|01\rangle \langle rr|+|10 \rangle \langle rr| \bigr)+{\mathrm{H.c.}}, $$
(2)

for which \(\Omega _{e}\) is a degraded effective Rabi frequency of the two-photon transition from ground state \(|01(10)\rangle \) towards the Rydberg pair state \(|rr\rangle \). For clarity, we visualize this kind of two-photon dynamics in Fig. 2(a). On one hand, compared with the reference transition rate \(\Omega _{0m(1m)}\) the effective frequency \(\Omega _{e}\) is degraded, which will increase the gate time. On the other hand, this two-photon dynamics depends on the attendance of Rydberg pair state \(|rr\rangle \), which is sensitive to deviations in the interatomic interaction strength. This two aspects of defect are also the common problems of hindering experimental realization of Rydberg-antiblockade-based quantum gates [30, 31, 34, 35, 59]. Therefore, here we intend to conceive an effective Hamiltonian involving transitions from \(|01\rangle \) and \(|10\rangle \) to a single- instead of double-excitation state. Besides, the effective Rabi frequencies are supposed to be originated from one-photon dynamics and thus be undegraded.

Figure 2
figure 2

Diagrams of effective dynamics for (a) the two-photon scheme in Ref. [53] with the second-order Rabi frequency \(\Omega _{e}\) and (b) the present one-photon scheme with the undegraded Rabi frequency \(\Omega _{\mathrm{0m}}\)

Full size image

2.2 Undegraded dynamics without the doubly-excited state

We transform the Hamiltonian Eq. (1) into a frame defined by the vdW interaction \(V|rr\rangle \langle rr|\) and expand it in the two-atom basis \(\{|mn\rangle \}\) (\(m,n=0,1,r\))

$$\begin{aligned} {\hat{H}}'_{12} =& \frac{\Omega _{\mathrm{0m}}}{2}\cos (\omega _{0}t) \bigl(|00 \rangle \langle r0|+|01\rangle \langle r1|\bigr)+ \frac{\Omega _{\mathrm{0m}}}{4} \bigl[e^{i(\omega _{0}-V)t}+e^{-i(\omega _{0}+V)t} \bigr]|0r\rangle \langle rr| \\ &{} +\frac{\Omega _{\mathrm{1m}}}{2}\cos (\omega _{1}t) \bigl(|10\rangle \langle r0|+|11 \rangle \langle r1|\bigr)+\frac{\Omega _{\mathrm{1m}}}{4} \bigl[e^{i(\omega _{1}-V)t}+e^{-i( \omega _{1}+V)t} \bigr]|1r\rangle \langle rr| \\ &{} +\frac{\Omega _{\mathrm{0m}}}{2}\cos (\omega _{0}t) \bigl(|00\rangle \langle 0r|+|10 \rangle \langle 1r|\bigr)+\frac{\Omega _{\mathrm{0m}}}{4} \bigl[e^{i(\omega _{0}-V)t}+e^{-i( \omega _{0}+V)t} \bigr]|r0\rangle \langle rr| \\ &{} +\frac{\Omega _{\mathrm{1m}}}{2}\cos (\omega _{1}t) \bigl(|01 \rangle \langle 0r|+|11 \rangle \langle 1r|\bigr)+\frac{\Omega _{\mathrm{1m}}}{4} \bigl[e^{i(\omega _{1}-V)t}+e^{-i( \omega _{1}+V)t} \bigr]|r1\rangle \langle rr| \\ &{} +{\mathrm{H.c.}} \end{aligned}$$
(3)

According to types of terms in Eq. (3) we can select desired transitions by setting parameter relations among \(\Omega _{\mathrm{0m(1m)}}\), \(\omega _{{0(1)}}\), and V. To this end, we specify \(V=\omega _{1}\gg \omega _{0},~\Omega _{\mathrm{0m(1m)}}/2\) so as to reduce \({\hat{H}}'_{12}\) by neglecting highly oscillating terms under RWA as follows

$$\begin{aligned} {\hat{H}}''_{12} =& \frac{\Omega _{\mathrm{0m}}}{2}\cos (\omega _{0}t) \bigl[|00 \rangle \bigl( \langle r0|+\langle 0r| \bigr)+|01\rangle \langle r1|+|10 \rangle \langle 1r| \bigr] \\ &{} +\frac{\Omega _{\mathrm{1m}}}{4} \bigl(|1r\rangle +|r1\rangle \bigr) \langle rr|+{\mathrm{H.c.}} \end{aligned}$$
(4)

From the expression of Eq. (4), we can easily find that the evolution of \(|11\rangle \) has be excluded. Further, because \(|00\rangle \) cannot be connected to the doubly-excited state \(|rr\rangle \), its evolution will become insignificant highly frequent oscillations and can also be excluded once we set the condition \(\omega _{0}\), \(\Omega _{\mathrm{1m}}/4\gg \Omega _{\mathrm{0m}}/2\). Then one can rewrite the effective Hamiltonian in the basis of dressed states induced by the interaction among excited states \(|1r\rangle \), \(|r1\rangle \), and \(|rr\rangle \)

$$\begin{aligned} {\hat{H}}_{\mathrm{dr}} =&\frac{\Omega _{\mathrm{0m}}}{4}\cos (\omega _{0}t) \bigl[|01\rangle \bigl(\langle \Psi _{+}|-\sqrt {2}\langle \Psi _{0}|+ \langle \Psi _{-}| \bigr) \\ &{} +|10\rangle \bigl(\langle \Psi _{+}|+\sqrt {2}\langle \Psi _{0}|+ \langle \Psi _{-}| \bigr)+{\mathrm{H.c.}} \bigr] \\ &{} +\frac{\sqrt {2}}{4}\Omega _{\mathrm{1m}} \bigl(|\Psi _{+} \rangle \langle \Psi _{+}|-|\Psi _{-}\rangle \langle \Psi _{-}| \bigr), \end{aligned}$$
(5)

for which the dressed states are defined as \(|\Psi _{\pm}\rangle = (|1r\rangle +|r1\rangle \pm \sqrt {2}|rr \rangle )/2\) and \(|\Psi _{0}\rangle =(|1r\rangle -|r1\rangle )/\sqrt {2}\). To more intuitively investigate the transitions between \(|01(10)\rangle \) and excited states, we move the Hamiltonian \({\hat{H}}_{\mathrm{dr}}\) into the frame defined by the diagonal terms \({\sqrt {2}}\Omega _{\mathrm{1m}} (|\Psi _{+}\rangle \langle \Psi _{+}|-| \Psi _{-}\rangle \langle \Psi _{-}| )/4\)

$$\begin{aligned} {\hat{H}}'_{\mathrm{dr}} =& \frac{\Omega _{\mathrm{0m}}}{8}|01\rangle \bigl\{ \langle \Psi _{+}| \bigl[e^{i(\omega _{0}-\sqrt {2}\Omega _{\mathrm{1m}}/4)t}+e^{-i( \omega _{0}+\sqrt {2}\Omega _{\mathrm{1m}}/4)t} \bigr]-2\sqrt {2}\langle \Psi _{0}|\cos (\omega _{0}t) \\ &{} +\langle \Psi _{-}| \bigl[e^{i(\omega _{0}+\sqrt {2}\Omega _{ \mathrm{1m}}/4)t}+e^{-i(\omega _{0}-\sqrt {2}\Omega _{\mathrm{1m}}/4)t} \bigr] \bigr\} \\ &{} +\frac{\Omega _{\mathrm{0m}}}{8}|10\rangle \bigl\{ \langle \Psi _{+}| \bigl[e^{i(\omega _{0}-\sqrt {2}\Omega _{\mathrm{1m}}/4)t}+e^{-i(\omega _{0}+2 \sqrt {2}\Omega _{\mathrm{1m}}/4)t} \bigr]+\sqrt {2}\langle \Psi _{0}|\cos ( \omega _{0}t) \\ &{} +\langle \Psi _{-}| \bigl[e^{i(\omega _{0}+\sqrt {2}\Omega _{ \mathrm{1m}}/4)t}+e^{-i(\omega _{0}-\sqrt {2}\Omega _{\mathrm{1m}}/4)t} \bigr] \bigr\} +{\mathrm{H.c.}} \end{aligned}$$
(6)

According to the consideration \(\omega _{0}\), \(\Omega _{\mathrm{1m}}/4\gg \Omega _{\mathrm{0m}}/2\), under RWA the Hamiltonian can be further simplified to an effective form of one-photon Raman resonance by setting \(\omega _{0}=\sqrt {2}\Omega _{\mathrm{1m}}/4\)

$$\begin{aligned} {\hat{H}}_{\mathrm{eff}} =&\frac{\Omega _{\mathrm{0m}}}{8}(|01\rangle +|10 \rangle ) \bigl(\langle \Psi _{+}|+\langle \Psi _{-}| \bigr)+{\mathrm{H.c.}} \\ =&\frac{\sqrt {2}}{8}\Omega _{\mathrm{0m}}\bigl(|01\rangle +|10 \rangle \bigr)\langle T|+{ \mathrm{H.c.}} \end{aligned}$$
(7)

for which we define a single-excitation state \(|T\rangle =(|1r\rangle +|r1\rangle )/\sqrt {2}\). The final effective Hamiltonian Eq. (7) does not involve the Rydberg pair state \(|rr\rangle \) but contains only a single-excitation superposition state \(|T\rangle \). This kind of selective dynamics of effective one-photon Raman transitions is originated from the destructive conference of \(|rr\rangle \) but constructive conference of single-excitation states in the term \((|\Psi _{+}\rangle +|\Psi _{-}\rangle )\), as visualized in Fig. 2(b). Besides, the Rabi frequencies of Raman transitions are of the same order of magnitude as the conference \(\Omega _{\mathrm{0m}}\), which will induce a fast SWAP gate.

3 Results

Based on the analysis above, under RWA conditions \(V=\omega _{1}\gg \omega _{0},~\Omega _{\mathrm{0m(1m)}}/2\) and \(\omega _{0}\), \(\Omega _{\mathrm{1m}}/4\gg \Omega _{\mathrm{0m}}/2\), the two-atom logical states \(|00\rangle \) and \(|11\rangle \) will remain invariant during evolution. As for \(|01\rangle \) and \(|10\rangle \), they participate in an effective Raman transition mediated by the single-excitation state \(|T\rangle \) governed by the effective Hamiltonian Eq. (7). Therefore, when we set the pulse area satisfying \(\int _{0}^{T}\Omega _{\mathrm{0m}}{\mathrm{d}}t=4\pi \) with T being the gate time to complete a period of Raman transition \(|01(10)\rangle \leftrightarrow |T\rangle \leftrightarrow |10(01) \rangle \), a SWAP gate operation \(\hat{U}_{\mathrm{SWAP}}=|00\rangle \langle 00|-|01\rangle \langle 10|-|10 \rangle \langle 01|+|11\rangle \langle 11|\) will be achieved.

3.1 Constant pulse

In order to execute a fast SWAP gate operation, in general a straightforward way is to impose a constant pulse with duration \(T = 4\pi /\Omega _{\mathrm{0m}}\). To ensure the degree of satisfying RWA conditions \(V=\omega _{1}\gg \omega _{0},~\Omega _{\mathrm{0m(1m)}}/2\) and \(\omega _{0}\), \(\Omega _{\mathrm{1m}}/4\gg \Omega _{\mathrm{0m}}/2\), we plot in Fig. 3(a) an initial-state-specified fidelity at the time \(T = 4\pi /\Omega _{\mathrm{0m}}\) for executing the SWAP gate \({\hat{U}}_{\mathrm{SWAP}}\) with different values of \(\omega _{0}/\Omega _{\mathrm{0m}}\) and \(\omega _{1}/\Omega _{\mathrm{0m}}\) (here we have set \(\Omega _{\mathrm{1m}}=2\sqrt {2}\omega _{0}\) and \(V=\omega _{1}\)). The initial-state-specified fidelity of the SWAP gate is defined as \(F(t)=|\langle \Psi (t)|{\hat{U}}_{\mathrm{SWAP}}|\Psi _{i}\rangle |^{2}\), where \(|\Psi (t)\rangle \) is the solution of Schrödinger equation \(i\partial |\Psi (t)\rangle /\partial t={\hat{H}}_{12}|\Psi (t) \rangle \) with \(|\Psi _{i}\rangle =(|01\rangle +|11\rangle )/\sqrt {2}\) being the initial state at instant \(t=0\). Figure 3(a) clearly shows the important impact of the RWA conditions \(V=\omega _{1}\gg \omega _{0},~\Omega _{\mathrm{0m(1m)}}/2\) and \(\omega _{0}\), \(\Omega _{\mathrm{1m}}/4\gg \Omega _{\mathrm{0m}}/2\) on the initial-state-specified fidelity of SWAP gate, from which we identify that within the range of \(\omega _{0}/\Omega _{\mathrm{0m}}\in [1,5]\) and \(\omega _{1}/\Omega _{\mathrm{0m}}\in [5,100]\), the parameter relation \(\omega _{0}/\Omega _{\mathrm{0m}}>1.5\cap \omega _{1}/\Omega _{\mathrm{0m}}>45\) guarantees \(F>0.99\) while \(\omega _{0}/\Omega _{\mathrm{0m}}>2.5\cap \omega _{1}/\Omega _{\mathrm{0m}}>70\) guarantees \(F>0.995\).

Figure 3
figure 3

(a) Initial-state-specified fidelity at the time \(T = 4\pi /\Omega _{\mathrm{0m}}\) for executing the SWAP gate \({\hat{U}}_{\text{SWAP}}\) with different values of \(\omega _{0}/\Omega _{\mathrm{0m}}\) and \(\omega _{1}/\Omega _{\mathrm{0m}}\) with \(\Omega _{\mathrm{1m}}=2\sqrt {2}\omega _{0}\) and \(V=\omega _{1}\). For clarity, we roughly plot contour lines of 0.99 (solid-blue) and 0.995 (dashed-red). (b) Initial-state-specified fidelity and populations of related states with evolution of time. \(\Omega _{\mathrm{0m}}/2\pi =1\text{ MHz}\), \(\omega _{0}/2\pi =2.5\text{ MHz}\), and \(d=4.8~\mu{\mathrm{m}}\) (\(C_{6}/2 \pi =858.4~{\text{GHz}}\cdot \mu{\mathrm{m}}^{6}\))

Full size image

Concretely, 87Rb atoms are assumed to be adopted in this work. We encode the computational states on the hyperfine ground-state manifolds \(|0\rangle =|5S_{1/2}, F=1, m_{F}=0\rangle \) and \(|1\rangle =|5S_{1/2}, F=2, m_{F}=0\rangle \). The Rydberg state is specified as \(|r\rangle =|70S_{1/2},J=1/2, m_{J}=-1/2\rangle \) corresponding to \(C_{6}/2\pi =858.4~{\mathrm{GHz}}\cdot \mu{\mathrm{m}}^{6}\). The excitation of 87Rb atoms from ground states to the Rydberg state with a principal quantum number \(n = 70\) has been experimentally demonstrated through two-photon processes [34, 44, 56, 60–62], and the vdW interaction strength between two Rydberg atoms can be achieved up to several dozens and even over one hundred of megahertz [62]. Here we set the interatomic separation \(d=4.8~\mu{\mathrm{m}}\) giving the interatomic interaction strength \(V/2\pi =70.2\text{ MHz}\). Accordingly, we set \(\Omega _{\mathrm{0m}}/2\pi =1\text{ MHz}\), \(\omega _{0}/2\pi =2.5\text{ MHz}\), \(\Omega _{\mathrm{1m}}=2\sqrt {2}\omega _{0}\) and \(\omega _{1}=V\) to see the system evolution during executing the SWAP gate by plotting the initial-state-specified fidelity and populations of several related states with evolution of time in Fig. 3(b). From Fig. 3(b) we can find a behavior of complete Raman-type transition between \(|01\rangle \) and \(|10\rangle \) mediated by the single-excitation state \(|T\rangle \), while \(|00\rangle \) and \(|11\rangle \) remain almost invariant and \(|rr\rangle \) is not involved in evolution of the two-atom system. Therefore, the initial-state-specified fidelity of the SWAP gate gradually increases with slight oscillations and finally reaches at \(F=0.998\).

3.2 Soft quantum control

Instead of the constant pulse of \(\Omega _{\mathrm{0m}}\), in order to satisfy RWA conditions \(V=\omega _{1}\gg \omega _{0},~\Omega _{\mathrm{0m(1m)}}/2\) and \(\omega _{0}\), \(\Omega _{\mathrm{1m}}/4\gg \Omega _{\mathrm{0m}}/2\) better for obtaining a more stable and higher fidelity, it is promising to adopt a temporal soft quantum control of \(\Omega _{\mathrm{0m}}\). By shaping \(\Omega _{\mathrm{0m}}(t)\) in time to start from and end at a zero amplitude, it will render transitions among desired levels to maintain on-resonant but suppress unwanted off-resonant transitions [55]. In this situation, the RWA conditions can be met more easily at most instants even when \(\max [\Omega _{\mathrm{0m}}(t)]\) is comparable to \(\omega _{0}\). The idea of quantum soft control has been introduced to many works to improve fidelities of tasks, such as implementing multi-qubit Rydberg-atom gates [63, 64], enantio-selective state transfer of chiral molecules [65, 66], and entanglement generation in superconducting circuits [67, 68].

In this work, we engineer the waveform of \(\Omega _{\mathrm{0m}}(t)\) with a temporal amplitude holding a single-period sin2 profile \(\Omega _{\mathrm{0m}}(t)={\bar{\Omega}}_{\mathrm{0m}}\sin ^{2}(\pi t/T)\). According to the condition of pulse area \(\int _{0}^{T}\Omega _{\mathrm{0m}}(t){\mathrm{d}}t=4\pi \), the gate time is determined as \(T=8\pi /{\bar{\Omega}}_{\mathrm{0m}}\). For showing the superiority of soft quantum control over the constant pulse, in Fig. 4(a) we consider the two cases of soft quantum control and constant pulse and plot the initial-state-specified fidelity of the SWAP gate at the finial time versus \({\bar{\Omega}}_{\mathrm{0m}}\) (here we set \(\Omega _{\mathrm{0m}}={\bar{\Omega}}_{\mathrm{0m}}\) in the case of constant pulse for convenience) with the same parameters as those in Fig. 3(b). Limited by the RWA conditions, in the case of constant pulse \(\Omega _{\mathrm{0m}}/2\pi \) is supposed to be less than 1.2 MHz to ensure \(F(T)>0.99\), but in the case of soft quantum control it is almost the whole range of \({\bar{\Omega}}_{\mathrm{0m}}/2\pi \in [0.2,~3]\text{ MHz}\) that can guarantee a high final fidelity \(F(T)>0.99\). For the sake of contrast, we choose \({\bar{\Omega}}_{\mathrm{0m}}/2\pi =2\text{ MHz}\) so that the gate time is equivalent for the two cases of pulse engineering. Even though the maximum \(\max [{\Omega}_{\mathrm{0m}}]\) in the case of soft quantum control is two times of that in the case of constant pulse, the extent of meeting RWA conditions is not degraded. To identify this, we see the system evolution during executing the SWAP gate by plotting the initial-state-specified fidelity and populations of several related states with evolution of time in Fig. 4(b), from which a behavior of complete Raman-type transition between \(|01\rangle \) and \(|10\rangle \) mediated by the single-excitation state \(|T\rangle \) is still accomplished. Accordingly, \(|00\rangle \) and \(|11\rangle \) have little changes and \(|rr\rangle \) does not attend in the system evolution of two atoms. The initial-state-specified fidelity of the SWAP gate smoothly increases to \(F=0.999\) with slighter oscillations.

Figure 4
figure 4

(a) Initial-state-specified fidelity of the SWAP gate at the finial time versus \({\bar{\Omega}}_{\mathrm{0m}}\). \(T=4\pi /{\bar{\Omega}}_{\mathrm{0m}}\) and \(\Omega _{\mathrm{0m}}={\bar{\Omega}}_{\mathrm{0m}}\) for the case of the constant pulse, while \(T=8\pi /{\bar{\Omega}}_{\mathrm{0m}}\) for the case of soft quantum control. (b) Initial-state-specified fidelity and populations of related states with evolution of time. \({\bar{\Omega}}_{\mathrm{0m}}/2\pi =2\text{ MHz}\) and other parameters are the same as those in Fig. 3(b)

Full size image

4 Discussion

4.1 Average fidelity and insensitivity to atomic decay

The initial-state-specified fidelity is an efficient way to investigate the evolution of related state involved in dominant dynamics but is not sufficient to estimate completely the performance of a quantum gate that should work well on an arbitrary initial state. To this end, it is supposed to introduce the idea of average fidelity to verify the initial-state randomicity for executing \({\hat{U}}_{\mathrm{SWAP}}\). Here wo adopt Nielsen’s trace-preserving-quantum-operator-based average fidelity defined as [69]

$$ \bar{F}(\varepsilon , \hat{U}_{\mathrm{SWAP}})= \frac{\sum_{j=1}^{16} \operatorname{tr} [\hat{U}_{\mathrm{SWAP}} \hat{u}_{j}^{\dagger} \hat{U}_{\mathrm{SWAP}}^{\dagger} \varepsilon (\hat{u}_{j} ) ]+l^{2}}{l^{2}(l+1)}, $$
(8)

with \(l=4\) for a two-qubit gate. \(\hat{u}_{j}=\bigotimes_{k}^{2}{\hat{\sigma}}_{k}\) denotes a tensor of Pauli matrices \({\hat{\sigma}}_{k}\in \{\hat{I}, \hat{\sigma}^{x}, \hat{\sigma}^{y}, \hat{\sigma}^{z}\}\) on computational states \(\{|0\rangle ,~|1\rangle \}\). \(\varepsilon (\hat{u}_{j})\) is a trace-preserving quantum operation with the input operator \(\hat{u}_{j}\), which can be obtained through solving the master equation

$$ {\dot{\rho}}(t)=i\bigl[{\rho}(t),\hat{H}_{12}\bigr] -\sum_{j=1}^{2}\sum _{k=0}^{2} \frac{\gamma _{k}}{2} \bigl[\hat{ \mathcal{L}}_{k}^{j\dagger } \hat{\mathcal{L}}_{k}^{j}{ \rho}(t)-2\hat{\mathcal{L}}_{k}^{j}{\rho}(t) \hat{ \mathcal{L}}_{k}^{j\dagger }+{\rho}(t)\hat{\mathcal{L}}_{k}^{j\dagger } \hat{\mathcal{L}}_{k}^{j} \bigr], $$
(9)

with \({\rho}(t)\) being the density operator. The Lindblad operator defined by \(\hat{\mathcal{L}}_{k}^{j}\equiv |k\rangle _{j}\langle r|\) describes the atomic decay path from the Rydberg state \(|r\rangle \) to the ground state \(|k\rangle \), for which we add an additional ground state \(|2\rangle _{j}\) denoting the decay path from \(|r\rangle \) to other ground Zeeman magnetic sublevels instead of \(|0\rangle _{j}\) and \(|1\rangle _{j}\). For convenience, here we assume that the atomic decay rates from the Rydberg state \(|r\rangle =|70S_{1/2}\rangle \) of 87Rb atoms into eight ground states are equivalent, so we have \(\gamma _{0}=\gamma _{1}=1/8\tau \) and \(\gamma _{2}=3/4\tau \) where τ is defined as the lifetime of \(|r\rangle =|70S_{1/2}\rangle \). Based on current experimental techniques [44, 56, 57, 70, 71], Rydberg atoms can be cooled to an order of T∼10 μK, and the Rydberg state \(|r\rangle =|70S_{1/2}\rangle \) has an effective lifetime τ∼ 400 μs at a cryogenic temperature of T∼10 μK [11, 34, 72–75].

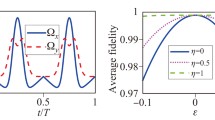
In Fig. 5(a), we show the numerical calculation (without considering atomic decay) of the average fidelity for implementing \({\hat{U}}_{\mathrm{SWAP}}\) in both cases of constant pulse and the soft quantum control, where average fidelity lines in the two cases both reach over 0.998 finally with the same gate time, identifying the validity of implementing \({\hat{U}}_{\mathrm{SWAP}}\) for an arbitrary initial state. Furthermore, it is noted that with the same gate time, the case of soft quantum control shows a smoother average fidelity curve in the end, remaining near unity for a longer while. More importantly, different from the case of constant pulse where the Rydberg excitation process sustains throughout the whole evolution, in the case of soft quantum control the evolution duration that involves the Rydberg excitation [see the highlighted area in Fig. 5(a)] covers only a half of the whole gate duration, which will mitigate the damage of atomic decay to the gate performance. Concretely, when considering atomic decay, to see the damage of atomic decay to the gate performance, we plot in Fig. 5(b) the effect of lifetime of the Rydberg state on the initial-state-specified fidelity of implementing the SWAP gate at the corresponding gate time in both cases of constant pulse and the soft quantum control, where the initial-state-specified fidelity is defined by \(F(t)=\langle \Psi _{i}|{\hat{U}}_{\mathrm{SWAP}}^{\dagger}\rho (t){\hat{U}}_{ \mathrm{SWAP}}|\Psi _{i}\rangle \) with \(\rho (t)\) being obtained by the master equation in Eq. (9) and \(|\Psi _{i}\rangle =(|01\rangle +|11\rangle )/\sqrt {2}\) being the initial state. Obviously, the final fidelity of performing the SWAP gate in the case of soft quantum control is always higher than that in the case of constant pulse, but overall both of the two cases are insensitive to atomic decay because even though the lifetime of the Rydberg state is \(\tau =50~{\mu\mathrm{s}}\) the fidelity in both cases is over 0.994. For a Rydberg atom that can be cooled to T∼10 μK, the lifetime of the Rydberg state \(|r\rangle =|70S_{1/2}\rangle \) is τ∼ 400 μs, and the fidelity in both cases is over 0.997 with considering atomic decay. The insensitivity of the present SWAP scheme to the atomic decay is much stronger than that of the SWAP schemes in Refs. [52, 53], which is attributed to the undegraded fast dynamics and also the suppression of the doubly-excited Rydberg pair state.

Figure 5
figure 5

(a) Without considering atomic decay, evolution of the average fidelity for implementing \({\hat{U}}_{\text{SWAP}}\) in both cases of constant pulse (\(\Omega _{\mathrm{0m}}/2\pi =1\text{ MHz}\)) and the soft quantum control (\({ \bar{\Omega}}_{\mathrm{0m}}/2\pi =2\text{ MHz}\)). (b) When considering atomic decay, final initial-state-specified fidelity versus lifetime of the Rydberg state in both cases

Full size image

4.2 Enhanced robustness against deviations in interatomic interaction

In addition to atomic decay, the SWAP schemes in Refs. [52, 53] are also very sensitive to the interatomic separation as well as interaction strength, because the doubly-excited Rydberg pair state \(|rr\rangle \) attends the evolution of two atoms. However, in practice it is very difficult to strictly fix the interatomic separation because of imperfections in cooling and trapping atoms. We can describe the interatomic separation by a quasi one-dimensional Gaussian probability distribution with the mean (ideal) being \(d=\sqrt[6]{C_{6}/V}\) and the standard deviation being marked as \(\sigma _{d}\) [57]. In Fig. 6, we simulate effect of the standard deviations of the interatomic separation on the initial-state-specified fidelity of implementing the SWAP gate in both cases. Different from the SWAP gate schemes in Refs. [52, 53] being extremely sensitive to the interatomic separation deviation where even \(\sigma _{d}=2\text{ nm}\) will decrease the fidelity to below 0.9, the final fidelity of the present SWAP scheme in the case of soft quantum control is over 0.9 even when \(\sigma _{d}=10\text{ nm}\), which verifies that the robustness of the SWAP gate against deviations in interatomic separation is significantly enhanced. More intuitively, we define a relative deviation \(\delta _{V}\) that changes the ideal interaction strength between two atoms into \(V[1+\operatorname{rand}(\delta _{V})]\). \(\operatorname{rand}(\delta _{V})\) is used to create a number of random numbers within \([-\delta _{V},~\delta _{V}]\). Then in Fig. 7 we show effect of relative deviation in V on the initial-state-specified fidelity of implementing the SWAP gate in both cases, which clearly illustrates that in the case of soft quantum control the effect of \(\delta _{V}\) on the SWAP gate is slighter. With \(\delta _{V}<0.5\) the final fidelity can be over 0.98, indicating great improvement of robustness against deviations in interatomic interaction over that in Refs. [52, 53].

Figure 6
figure 6

Effect of deviations in the separation between two atoms on the initial-state-specified fidelity of implementing the SWAP gate in both cases. Each point denotes the average of 201 results without considering atomic decay

Full size image
Figure 7
figure 7

Effect of deviations in the interaction strength between two atoms on the initial-state-specified fidelity of implementing the SWAP gate in both cases. Each point denotes the average of 201 results without considering atomic decay

Full size image

4.3 Potential applications of the SWAP gate on Rydberg atoms

Although it is proved that the platform of Rydberg atoms possesses the excellent scalability [76] and arbitrary atomic structures may be assembled with a sufficient number of atoms [77–79], it is still a tough nut to crack for efficiently entangling two atoms that are separated remotely in the atomic array, because the interaction between two Rydberg atoms are dependent of distance between sites. Here we show some certain potential applications of the proposed SWAP gate for avoiding the interaction between remote sites.

For an application in quantum computation, we consider the five-qubit error-correcting code proposed by DiVincenzo and Shor [80]. In this kind of error-correcting code, it is needed to execute CNOT operations between the (target) ancilla qubit and each one of the five systematic (control) qubits, which would be hard to realize without crosstalk in a platform of Rydberg atoms because of an unavailable structure of atomic layout. However, referred to the scheme proposed by Schuch and Siewert [46], we can implement the five-qubit error-correcting code on the platform of Rydberg atoms with only the nearest-neighbor interactions by combining the CNOT and SWAP gates (see Ref. [46] for details). Accordingly, the proposed SWAP gate can facilitate quantum computation on Rydberg atoms by rendering implementations of some certain error-correcting codes. For entanglement swapping and quantum repeater, we consider the widely studied one-dimensional array of Rydberg atoms, where the direct generation of entanglement between a pair of next-nearest-neighbor atoms is difficult while the generation of the nearest-neighbor atomic entanglement is straightforward [44, 56, 57]. Assuming that the four atoms, labeled by A, B, C, and D, respectively, are assembled in order in a one-dimensional array, and the atoms A and B (C and D) are generated in the Bell state \((|00\rangle +|11\rangle )/\sqrt {2}\). Apparently, after conducting the SWAP gate on the atoms B and C, the state of the four atoms will change from \((|00\rangle _{AB}+|11\rangle _{AB})\otimes (|00\rangle _{CD}+|11 \rangle _{CD})/2\) to \((|00\rangle _{AC}+|11\rangle _{AC})\otimes (|00\rangle _{BD}+|11 \rangle _{BD})/2\), which shows a operation of entanglement swapping between atoms B and C. In a similar way, when only atoms A and B are generated in entanglement initially, through executing sequential SWAP gates between atoms B and C, C and D, D and E, … , one can entangle the atom A with a remote atom, which denotes the implementation of a quantum repeater.

5 Conclusion

We have proposed a superior mechanism for implementing the SWAP gate on ground-state manifolds of two Rydberg atoms, which shows the undegraded first-order dynamics and enhanced robustness to atomic decay and deviations in interaction strength between two atoms, compared to existing schemes. By elaborately engineering amplitude modulation of lasers driving ground-Rydberg state transitions, we figure out the effective dynamics involving constructive interference of maintaining the single-excitation states but destructive interference of suppressing the double-excitation state, which not only reduces damages of atomic decay to the gate fidelity but also enhances robustness against deviations in interatomic interaction strength due to the absence of the double-excitation state in the evolution of two atoms. In addition, the use of soft quantum control in manipulating the SWAP transformation makes the parameters satisfy the rotating-wave approximation better. The present mechanism of implementing a SWAP gate shows a method of engineering fast dynamics and enhancing stability of Rydberg-atom systems, and to some certain degree may promote ones to demonstrate high-fidelity transformations and to explore peculiar dynamics in Rydberg-atom systems.