1 Introduction

Optomechanical system usually consists of the electromagnetic cavity and the mechanical oscillator coupled by radiation pressure [1–3]. In the past decades, both linear and quadratic optomechanical coupling have been under extensive exploration, where the cavity resonance frequency linearly and quadratically depends on the displacement of the mechanical oscillator, respectively. In particular, tremendous progresses have been made in optomechanical systems, such as ground state cooling of the mechanical oscillator [4, 5], optomechanical squeezing of light and mechanical motion [6–9], quantum entanglement between mechanical oscillators [10, 11]. Furthermore, the optical response of the optomechanical system can exhibit some interesting phenomena by driving the cavity under different conditions, including optomechanically induced transparency (OMIT) [12–19], optomechanically induced amplification (OMIA) [20, 21], and Fano resonance [22, 23]. OMIT is the analog of electromagnetically induced transparency (EIT) [24, 25], which results from the destructive interference between different excitation pathways in atomic vapors and various solid-state systems [26–29]. Recently, different types of OMIT, such as nonlinear OMIT [30–32], two-color OMIT [33], vector OMIT [34], reversed OMIT [35–37], and nonreciprocal OMIT [38, 39], have been extensively explored. Besides the nonreciprocal OMIT [39], the spinning optomechanical system also provides a platform to study quantum effects such as nonreciprocal photon blockade [40] and nonreciprocal optomechanical entanglement [41]. Closely related to EIT, the Fano resonance with asymmetric line shape was first explained by Ugo Fano in terms of the interference of a narrow discrete resonance with a broad spectral line or continuum [42, 43]. These phenomena can have potential applications in slow light [44, 45], optical switching [46], sensing [47], and so on.

In this work, we study the controllable optical response of a multimode optomechanical system with quadratic coupling, where two movable membranes are placed in the middle of an optical cavity with two fixed mirrors. Note that quadratic coupling has been experimentally realized in a Fabry–Pérot cavity containing a SiN membrane [48, 49] or a cloud of ultracold atoms [50, 51], a tunable photonic crystal optomechanical cavity [52], and a microsphere-nanostring system [53]. Theoretical works have shown that quadratic coupling can be exploited to investigate mechanical squeezing [54, 55], photon blockade and phonon blockade [56–59], quantum nondemolition measurement of phonons [60], quantum phase transition [61], a highly sensitive mass sensor [62], two-phonon OMIT [63], and Fano resonance [64]. Different from the linearly coupled optomechanical systems, the underlying physical mechanism in quadratically coupled optomechanical systems involves a two-phonon process [63], where the square of the displacement of the mechanical oscillator affects the response of the system. Advantages of quadratic over linear coupling include quantum nondemolition readout of a membrane’s energy eigenstate [48, 49], more persistent entanglement and higher spectral nonlinearity [65], and so on. If two or more mechanical oscillators are involved, the multimode quadratic coupling optomechanical system can exhibit multiple transparency windows [66–68].

In addition, more complex interference effect occurs in optomechanical systems if the mechanical oscillator can be excited directly, which results in more interesting response property [69–76]. Zhai et al. proposed that mechanical driving field can serve as a switch of photon blockade and photon-induced tunneling [77]. In experiments, mechanical driving field has been exploited to realize electro-optomechanically induced transparency [78], cascaded optical transparency [79], phase-sensitive parametric amplifier [80], injection locking [81], and virtual exceptional points [82]. Recently, optomechanically induced opacity and amplification of two-phonon higher-order sidebands have been studied in a quadratically coupled optomechanical system with mechanical driving [83, 84]. It is pointed out that mechanical driving in the quadratically coupled system can be realized by parametrically modulating the spring constant of the membrane at twice the membrane’s resonance frequency with an integrated electrical interface [80–83, 85, 86], which generates the mechanical coherence via the two-phonon process. Here we discuss the optical response properties of a multimode quadratically coupled optomechanical system to a weak probe field in the presence of a strong optical control field and two weak mechanical driving fields. We show that this system can exhibit a series of unique phenomena by tuning the optical control field and mechanical driving fields, including optomechanically induced transparency, single and double Fano resonances, and selective amplification of the weak probe field. Our results may find potential applications in optical switching based on multimode optomechanical systems.

2 Model and theory

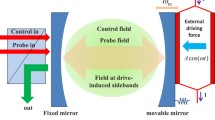
We consider the optomechanical system schematically shown in Fig. 1, where two movable membranes with finite reflectivity \(R_{k}\) (\(k=1,2\)) are placed in an optical cavity with two fixed mirrors. The cavity is driven by a strong control field with amplitude \(\varepsilon _{c}\), frequency \(\omega _{c}\), and phase \(\phi _{c}\) and detected by a weak probe field with amplitude \(\varepsilon _{p}\), frequency \(\omega _{p}\), and phase \(\phi _{p}\). Moreover, two weak coherent mechanical driving fields with amplitude \(\varepsilon _{k}\), frequency \(\Omega _{k}\), and phase \(\phi _{k}\) are, respectively, applied to excite the two membranes. When the membranes locate at the antinodes of the intracavity standing wave, the cavity field is coupled to the square of the position of the membrane with the quadratic optomechanical coupling strength \(g_{k}=\frac{8\pi ^{2} c}{\lambda ^{2}L}\sqrt{\frac{R_{k}}{1-R_{k}}}\), where c is the speed of light in a vacuum, λ is the wavelength of the control field, and L is the length of the cavity. The Hamiltonian of the multimode optomechanical system is given by

$$ H=\hbar \omega _{0} a^{\dagger }a+\sum _{k=1}^{2} \biggl( \frac{p_{k}^{2}}{2m_{k}}+ \frac{1}{2}m_{k}\omega _{k}^{2}q_{k}^{2} \biggr)+\sum_{k=1}^{2}\hbar g_{k} a^{\dagger }a q_{k}^{2}+H_{ \mathrm{dr}}, $$
(1)

where \(a^{\dagger }\) (a) is the creation (annihilation) operator of the cavity field with resonance frequency \(\omega _{0}\), while \(p_{k}\) and \(q_{k}\) are the momentum and position operators of the kth membrane with effective mass \(m_{k}\) and resonance frequency \(\omega _{k}\). Therefore, the first and second terms in Eq. (1) represent the energy of the cavity and mechanical modes, respectively, and the third term corresponds to the quadratic coupling between the cavity and mechanical modes. \(H_{\mathrm{dr}}\) denotes the interaction between the driving fields and the optomechanical system, which takes the form

$$\begin{aligned} H_{\mathrm{dr}} =&i\hbar \varepsilon _{c} \bigl(a^{\dagger }e^{-i \omega _{c} t-i\phi _{c}}-a e^{i\omega _{c} t+i\phi _{c}} \bigr)+i \hbar \varepsilon _{p} \bigl(a^{\dagger }e^{-i\omega _{p} t-i\phi _{p}}-a e^{i\omega _{p} t+i\phi _{p}} \bigr) \\ &{}+\sum_{k=1}^{2}i\hbar \varepsilon _{k} \bigl[\bigl(b_{k}^{\dagger } \bigr)^{2}e^{-i \Omega _{k}t-i\phi _{k}} -b_{k}^{2}e^{i\Omega _{k} t+i\phi _{k}} \bigr]. \end{aligned}$$
(2)

The first and second terms in Eq. (2) describe the interaction between the cavity and the strong control field and the weak probe field. The amplitudes \(\varepsilon _{c,p}\) are related to their respective powers \(P_{c,p}\) by the relation \(\varepsilon _{c,p}=\sqrt{\kappa _{e} P_{c,p}/\hbar \omega _{c,p}}\), where \(\kappa _{e}\) is the external decay rate of the cavity given by \(\kappa _{e}=\eta _{c}\kappa \) with κ being the total decay rate. The coupling parameter \(\eta _{c}\) can be continuously adjusted, and we choose \(\eta _{c}=0.5\) throughout this work. The last term describes the coherent mechanical driving of the two membranes. The creation (annihilation) operator \(b_{k}^{\dagger }\) (\(b_{k}\)) of the membrane is defined as \(b_{k}=(b_{k}^{\dagger })^{\dagger }=\sqrt{m_{k}\omega _{k}/(2\hbar )}[q_{k}+ip_{k}/(m_{k} \omega _{k})]\).

Figure 1
figure 1

Schematic diagram of the multimode optomechanical mechanical system. The two movable membranes can be treated as mechanical modes with annihilation operators \(b_{1}\) and \(b_{2}\), which are quadratically coupled to the common cavity mode a. The cavity is driven by a control (probe) field with amplitude \(\varepsilon _{c}(\varepsilon _{p})\), frequency \(\omega _{c}(\omega _{p})\), and phase \(\phi _{c}(\phi _{p})\). In addition, the two membranes are excited by two weak coherent mechanical driving fields with amplitudes \(\varepsilon _{1,2}\), frequency \(\Omega =\omega _{p}-\omega _{c}\), and phases \(\phi _{1,2}\)

Full size image

In the rotating frame at the frequency \(\omega _{c}\) of the control field, the system Hamiltonian can be rewritten as

$$\begin{aligned} H =&\hbar \Delta _{c} a^{\dagger }a+\sum _{k=1}^{2} \biggl( \frac{p_{k}^{2}}{2m_{k}}+ \frac{1}{2}m_{k}\omega _{k}^{2}q_{k}^{2} \biggr)+\sum_{k=1}^{2}\hbar g_{k} a^{\dagger }a q_{k}^{2}+i\hbar \varepsilon _{c} \bigl(a^{\dagger }-a \bigr) \\ &{}+i\hbar \varepsilon _{p} \bigl(a^{\dagger }e^{-i\Omega t-i\phi _{pc}}-a e^{i\Omega t+i\phi _{pc}} \bigr) \\ &{} +\sum_{k=1}^{2}i \frac{m_{k}\omega _{k}}{2}\varepsilon _{k} \biggl[ \biggl(q_{k}-i \frac{p_{k}}{m_{k}\omega _{k}} \biggr)^{2}e^{-i\Omega t-i \phi _{k}} - \biggl(q_{k}+i\frac{p_{k}}{m_{k}\omega _{k}} \biggr)^{2}e^{i \Omega t+i\phi _{k}} \biggr], \end{aligned}$$
(3)

where \(\Delta _{c}=\omega _{0}-\omega _{c}\), \(\Omega =\omega _{p}-\omega _{c}\), \(\phi _{pc}=\phi _{p}-\phi _{c}\), and we have assumed that \(\Omega _{1}=\Omega _{2}=\Omega \).

The time evolution of the system operators can be derived by applying the Heisenberg equation of motion and adding the damping and input noise terms phenomenologically, which yield

$$\begin{aligned}& \frac{da}{dt} = -\bigl[\kappa /2+i\bigl(\Delta _{c}+g_{1} q_{1}^{2}+g_{2} q_{2}^{2} \bigr)\bigr]a+ \varepsilon _{c}+\varepsilon _{p} e^{-i\Omega t-i\phi _{pc}}+\sqrt{ \kappa }a_{\mathrm{in}}, \end{aligned}$$
(4)
$$\begin{aligned}& \frac{dq_{k}}{dt} = \frac{p_{k}}{m_{k}}+q_{k}\varepsilon _{k}\bigl(e^{-i \Omega t-i\phi _{k}}+e^{i\Omega t+i\phi _{k}}\bigr)-i \frac{p_{k}}{m_{k}\omega _{k}}\varepsilon _{k}\bigl(e^{-i\Omega t-i\phi _{k}}-e^{i \Omega t+i\phi _{k}} \bigr), \end{aligned}$$
(5)
$$\begin{aligned}& \begin{aligned}[b] \frac{dp_{k}}{dt} =& {-}m_{k}\omega _{k}^{2} q_{k}-2\hbar g_{k} a^{ \dagger }a q_{k}-\gamma _{k} p_{k}-i m_{k}\omega _{k} q_{k} \varepsilon _{k}\bigl(e^{-i\Omega t-i\phi _{k}}-e^{i\Omega t+i\phi _{k}}\bigr) \\ &{}-p_{k}\varepsilon _{k}\bigl(e^{-i\Omega t-i\phi _{k}}+e^{i\Omega t+i \phi _{k}} \bigr)+\xi , \end{aligned} \end{aligned}$$
(6)

where \(a_{\mathrm{in}}\) is the input vacuum noise entering the cavity with zero mean value and ξ is the Brownian stochastic force acting on the membrane with zero mean value. Neglecting the weak probe field and mechanical driving field, the expectation values of the system operators at the steady state can be derived by setting the time derivatives in Eqs. (4)–(6) to zero, which are given by

$$ a_{s}= \frac{\varepsilon _{c}}{\kappa /2+i(\Delta _{c}+g_{1} \langle q_{1}^{2}\rangle _{s} +g_{2}\langle q_{2}^{2}\rangle _{s})},\qquad q_{ks}=0,\qquad p_{ks}=0. $$
(7)

Equation (7) shows that the steady-state solutions of the momentum and position of the membranes equal to zero, and the cavity field depends on the square of the position of the membranes at the steady state, which involves a two-phonon process. Consequently, we turn to calculate the time evolution of the expectation values of the operators a, \(q_{k}^{2}\equiv Q_{k}\), \(p_{k}^{2}\equiv P_{k}\), and \(q_{k} p_{k}+p_{k} q_{k}\equiv X_{k}\). Using the factorization assumption \(\langle abc\rangle =\langle a\rangle \langle b\rangle \langle c \rangle \) for the relevant operators, we can obtain

$$\begin{aligned}& \frac{d}{dt}\langle a\rangle = - \biggl[\frac{\kappa }{2}+i\bigl( \Delta _{c}+ig_{1} \langle Q_{1}\rangle +ig_{2} \langle Q_{2}\rangle \bigr) \biggr]\langle a \rangle +\varepsilon _{c}+\varepsilon _{p} e^{-i\Omega t-i\phi _{pc}}, \end{aligned}$$
(8)
$$\begin{aligned}& \begin{aligned}[b] \frac{d}{dt}\langle Q_{k}\rangle ={}& \frac{1}{m_{k}} \langle X_{k} \rangle +2\varepsilon _{k} \bigl(e^{-i\Omega t-i\phi _{k}}+e^{i \Omega t+i\phi _{k}} \bigr)\langle Q_{k} \rangle \\ &{}-\frac{i}{m_{k}\omega _{k}}\varepsilon _{k} \bigl(e^{-i\Omega t-i \phi _{k}}-e^{i\Omega t+i\phi _{k}} \bigr)\langle X_{k}\rangle , \end{aligned} \end{aligned}$$
(9)
$$\begin{aligned}& \begin{aligned}[b] \frac{d}{dt}\langle P_{k}\rangle ={}& {-} \bigl(m_{k} \omega _{k}^{2}+2 \hbar g_{k} \bigl\langle a^{\dagger }\bigr\rangle \langle a\rangle \bigr) \langle X_{k} \rangle -2\gamma _{k} \langle P_{k}\rangle +\gamma _{k}(1+2n_{k})m_{k} \hbar \omega _{k} \\ &{} -2\varepsilon _{k} \bigl(e^{-i\Omega t-i\phi _{k}}+e^{i\Omega t+i \phi _{k}} \bigr)\langle P_{k}\rangle -im_{k}\omega _{k}\varepsilon _{k} \bigl(e^{-i\Omega t-i\phi _{k}}-e^{i\Omega t+i\phi _{k}} \bigr) \langle X_{k}\rangle , \end{aligned} \end{aligned}$$
(10)
$$\begin{aligned}& \begin{aligned}[b] \frac{d}{dt}\langle X_{k}\rangle ={}& \frac{2}{m_{k}} \langle P_{k} \rangle -2\bigl(m_{k}\omega _{k}^{2}+2\hbar g_{k}\bigl\langle a^{\dagger }\bigr\rangle \langle a\rangle \bigr)\langle Q_{k} \rangle -\gamma _{k}\langle X_{k} \rangle \\ &{} -2i \biggl(m_{k}\omega _{k}\langle Q_{k} \rangle + \frac{1}{m_{k}\omega _{k}}\langle P_{k}\rangle \biggr) \varepsilon _{k} \bigl(e^{-i\Omega t-i\phi _{k}}-e^{i\Omega t+i\phi _{k}} \bigr). \end{aligned} \end{aligned}$$
(11)

The term \(\gamma _{k}(1+2n_{k})m_{k}\hbar \omega _{k}\) in Eq. (10) arises from the coupling of the membrane to the thermal environment, where \(n_{k}=[e^{\frac{\hbar \omega _{k}}{k_{B} T}}-1]^{-1}\) is the mean phonon occupation number of the membrane at the temperature T and \(k_{B}\) is the Boltzmann’s constant. In this work, both the optical probe field and the mechanical driving field are much weaker than the strong control field, thus Eqs. (8)–(11) can be solved by writing each expectation value as the sum of a steady-state solution and a small fluctuation, i.e.,

$$ \langle O\rangle =O_{s}+O_{+}e^{-i\Omega t}+O_{-}e^{i\Omega t}, $$
(12)

where O represents any of these quantities a, \(Q_{k}\), \(P_{k}\), and \(X_{k}\). The steady-state solutions \(O_{s}\) are determined by the strong control field and are given by

$$ a_{s}=\frac{\varepsilon _{c}}{\beta },\qquad P_{ks}=(1+2n_{k}) \frac{\hbar m_{k}\omega _{k}}{2},\qquad Q_{ks}= \frac{P_{ks}}{m_{k}^{2}\omega _{k}^{2}(1+\alpha _{k})},\qquad X_{ks}=0 $$
(13)

with \(\Delta =\Delta _{c}+g_{1} Q_{1s}+g_{2}Q_{2s}\), \(\alpha _{k}=\frac{2\hbar g_{k}|a_{s}|^{2}}{m_{k}\omega _{k}^{2}}\), \(\beta =\kappa /2+i\Delta \). Upon substituting Eq. (12) into Eqs. (8)–(11) and equating the coefficients of \(e^{0}\), \(e^{i\Omega t}\), \(e^{-i\Omega t}\), we can obtain

$$\begin{aligned} a_{+}= &\frac{L_{1} L_{2}-ig_{1} a_{s} R_{1}L_{2}-ig_{2}a_{s}R_{2}L_{1}}{L_{1}L_{2}(\beta -i\Omega )+ig_{1}a_{s}M_{1}L_{2}+ig_{2}a_{s}M_{2}L_{1}} \varepsilon _{p} e^{-i\phi _{pc}} \\ &{}- \frac{ig_{1}a_{s}N_{1}L_{2}}{L_{1}L_{2}(\beta -i\Omega )+ ig_{1}a_{s}M_{1}L_{2}+ig_{2}a_{s}M_{2}L_{1}} \varepsilon _{1} e^{-i\phi _{1}} \\ &{}- \frac{ig_{2}a_{s}N_{2}L_{1}}{L_{1}L_{2}(\beta -i\Omega )+ ig_{1}a_{s}M_{1}L_{2}+ig_{2}a_{s}M_{2}L_{1}} \varepsilon _{2} e^{-i\phi _{2}}, \end{aligned}$$
(14)

where

$$\begin{aligned}& L_{k}=-i\Omega m_{k}(\gamma _{k}-i \Omega )+2m_{k}\omega _{k}^{2}(1+ \alpha _{k})- \frac{2i\Omega m_{k}\omega _{k}^{2}(1+\alpha _{k})}{2\gamma _{k}-i\Omega }, \\ & M_{k}=- \frac{2g_{k}\hbar ^{2}a_{s}^{*}(1+2n_{k})}{m_{k}\omega _{k}(1+\alpha _{k})}+ \frac{2g_{k}\hbar ^{2} a_{s}(1+2n_{k})}{m_{k}\omega _{k}(1+\alpha _{k})} \frac{\beta -i\Omega }{\beta ^{*}-i\Omega }, \\ & N_{k}= \frac{\hbar (\gamma _{k}-i\Omega )(1+2n_{k})}{\omega _{k}(1+\alpha _{k})}- \frac{i\hbar (1+2n_{k})}{1+\alpha _{k}} -i\hbar (1+2n_{k}), \\ & R_{k}=- \frac{2g_{k}\hbar ^{2}a_{k}(1+2n_{k})}{(\beta ^{*}-i\Omega )m_{k}\omega _{k}(1+\alpha _{k})}, \end{aligned}$$
(15)

with \(k=1,2\).

The output field of the optical cavity can be derived according to the input-output relation [87]

$$ a_{\mathrm{out}}+\varepsilon _{c}+\varepsilon _{p} e^{-i\Omega t-i \phi _{pc}}=\kappa _{e}\langle a\rangle . $$
(16)

In order to investigate the optical response of the system to the probe field, we define the corresponding quadratures of the output field oscillating at the frequency \(\omega _{p}\) of the probe field as \(\varepsilon _{T}=\kappa _{e} a_{+}/(\varepsilon _{p} e^{-i\phi _{pc}})\) [69]. The real and imaginary parts of \(\varepsilon _{T}\) represent the absorptive and dispersive behavior of the system to the probe field. In addition, the transmission coefficient at the frequency \(\omega _{p}\) can be derived as

$$ t_{p}= \frac{\kappa _{e} a_{+}-\varepsilon _{p} e^{-i\phi _{pc}}}{\varepsilon _{p} e^{-i\phi _{pc}}}= \varepsilon _{T}-1=t_{1}+t_{2}, $$
(17)

where

$$\begin{aligned}& t_{1}= \frac{L_{1} L_{2}-ig_{1} a_{s} R_{1}L_{2}-ig_{2}a_{s}R_{2}L_{1}}{L_{1}L_{2}(\beta -i\Omega )+ig_{1}a_{s}M_{1}L_{2}+ig_{2}a_{s}M_{2}L_{1}} \kappa _{e}-1, \end{aligned}$$
(18)
$$\begin{aligned}& \begin{aligned}[b] t_{2}= {}& {-} \frac{ig_{1}a_{s}N_{1}L_{2}}{L_{1}L_{2}(\beta -i\Omega )+ig_{1}a_{s}M_{1}L_{2}+ig_{2}a_{s}M_{2}L_{1}} \kappa _{e}r_{1} e^{-i\Phi _{1}} \\ &{} - \frac{ig_{2}a_{s}N_{2}L_{1}}{L_{1}L_{2}(\beta -i\Omega )+ig_{1}a_{s}M_{1}L_{2}+ig_{2}a_{s}M_{2}L_{1}} \kappa _{e} r_{2} e^{-i\Phi _{2}}, \end{aligned} \end{aligned}$$
(19)

with the amplitude ratio \(r_{1,2}=\varepsilon _{1,2}/\varepsilon _{p}\), and phase difference \(\Phi _{1,2}=\phi _{1,2}-\phi _{pc}\). Here \(t_{1}\) is the contribution from the probe and control field, which results in the phenomena of OMIT and Fano resonance. The two terms in \(t_{2}\) represent, respectively, the contributions from the phonon-photon processes involving the mechanical driving on the two membranes [83], which can lead to the amplification or suppression of the probe field. Interference effect between \(t_{1}\) and \(t_{2}\) determines the transmission (absorption) spectrum of the probe field, where the phase differences \(\Phi _{1}\) and \(\Phi _{2}\) play an important role.

3 Results and discussion

In this section, we numerically study the controllable optical response of the system using the above analytical expressions and the experimentally realizable parameters. The parameters are chosen from the recent experimental [48] and theoretical works [63]: the length of the cavity \(L=6.7\text{ cm}\), and the cavity decay rate \(\kappa =2\pi \times 10^{4}\text{ Hz}\); the parameters of the membranes are \(\omega _{1}=\omega _{2}=\omega _{m}=2\pi \times 10^{5}\text{ Hz}\), \(\gamma _{1}=\gamma _{2}=20\text{ Hz}\), \(m_{1}=m_{2}=10^{-9}\text{ g}\), and \(R_{1}=R_{2}=0.45\). Here we have assumed that the two membranes are the same, and we will study the case that the two membranes are nondegenerate in the following. In addition, the wavelength of the control field \(\lambda =\frac{2\pi c}{\omega _{c}}= 532\text{ nm}\) and the temperature of the environment \(T=90\mbox{ K}\).

We first consider the simple case that the two membranes are the same. The phenomenon of OMIT has been observed in the probe transmission spectrum [13], and thus we plot the power transmission coefficient \(|t_{p}|^{2}\) versus the normalized detuning \(\Omega /\omega _{m}\) for different values of the mechanical driving fields in Fig. 2. Under the condition of two-phonon resonance, i.e., \(\Delta =2\omega _{m}\), Fig. 2(a) shows that the transmission spectrum can exhibit the phenomenon of OMIT around \(\Omega =2\omega _{m}\) if \(r_{1}=r_{2}=0\). The underlying mechanism of the OMIT can be explained as a result of the radiation pressure force at the beat frequency Ω between the probe and control photons. The membranes can vibrate coherently under the action of the radiation pressure, which in turn generates the Stokes- and anti-Stokes scattering of light from the strong control field via the two-phonon process. At \(\Delta =2\omega _{m}\), the highly off-resonant Stokes scattering at frequency \(\omega _{c}-2\omega _{m}\) is suppressed and only anti-Stokes scattering at frequency \(\omega _{c}+2\omega _{m}\) builds up inside the cavity. However, if the incident probe field is nearly resonant with the cavity field, destructive interference between the probe field and the anti-Stokes field can suppress the build-up of an intracavity probe field, which results in a transparency window in the transmission spectrum. Such a two-phonon OMIT has been extensively investigated in recent works by discussing the absorption \(\operatorname{Re} ( \varepsilon _{T})\) [63, 66, 67]. Moreover, the transmission spectrum can be further modified by the additional mechanical driving fields. If only one membrane is excited by a coherent mechanical driving field (\(r_{1}=10^{-5}\)), the transparency window in Fig. 2(a) becomes a transmission peak with \(|t_{p}|^{2}\approx 2.4\) for \(\Phi _{1}=0\), as shown in Fig. 2(b). Therefore, the weak probe field can be amplified due to the additional mechanical driving field, which can be explained by the interference effect as follows. In the simultaneous presence of a strong control field, a weak probe field, and a weak coherent mechanical driving field, the energy level of the system can form a closed-loop transition structure, giving rise to the phase-dependent optical response properties [69–75]. At \(\Phi _{1}=0\), constructive interference between \(t_{1}\) and the first term in \(t_{2}\) results in the amplification of the probe field [75]. If the phase difference \(\Phi _{1}\) is tuned to be π, Fig. 2(c) shows that destructive interference between \(t_{1}\) and \(t_{2}\) results in the strong suppression of transmission with \(|t_{p}|^{2}\approx 0.04\) around \(\Omega /\omega _{m}=2\). The interference effect in this system becomes more complicated when both the membranes are excited directly. At \(r_{1}=r_{2}=10^{-5}\) and \(\Phi _{1}=\Phi _{2}=0\), the peak transmission coefficient at \(\Omega /\omega _{m}\approx 2.0029\) is further enhanced to be \(|t_{p}|^{2}\approx 5.3\) because the two terms in \(t_{2}\) interfere constructively. If \(\Phi _{1}=0\) but \(\Phi _{2}=\pi \), the two terms in \(t_{2}\) interfere destructively, and the inset of Fig. 2(d) shows that the peak transmission coefficient around \(\Omega /\omega _{m}=2\) is almost equal to that in Fig. 2(a). Consequently, the optical response of this system can be controlled more flexibly when the mechanical driving field is modulated independently.

Figure 2
figure 2

The power transmission coefficient \(|t_{p}|^{2}\) as functions of the normalized detuning \(\Omega /\omega _{m}\) for different values of the mechanical driving fields. Other parameters are \(\lambda =532\text{ nm}\), \(L=6.7\text{ cm}\), \(\kappa =2\pi \times 10^{4}\text{ Hz}\), \(\eta _{c}=0.5\), \(\omega _{1}=\omega _{2}=\omega _{m}=2\pi \times 10^{5}\text{ Hz}\), \(\gamma _{1}=\gamma _{2}=20\text{ Hz}\), \(m_{1}=m_{2}=10^{-9}\text{ g}\), \(R_{1}=R_{2}=0.45\), \(T=90\) K, \(P_{c}=90~\mu \mathrm{W}\), and \(\Delta =2\omega _{m}\)

Full size image

In order to see the effect of phase difference more clearly, we plot the power transmission coefficient \(|t_{p}|^{2}\) at \(\Omega =2.0029\omega _{m}\) as functions of \(\Phi _{1}/\pi \) and \(\Phi _{2}/\pi \) in Fig. 3. It is shown that the transmission coefficient \(|t_{p}|^{2}\) reaches the maximum around \(\Phi _{1}=\Phi _{2}=0\) with peak value \(|t_{p}|^{2}\approx 5.3\), and the minimum value is obtained around \((\Phi _{1}=-0.75\pi ,\Phi _{2}=0.75\pi )\) and \((\Phi _{1}=0.75\pi ,\Phi _{2}=-0.75\pi )\) with \(|t_{p}|^{2}\approx 0\). This phase dependent phenomenon arises from the interference effect in that we consider \(\omega _{1}=\omega _{2}=\omega _{m}\), \(\Omega _{1}=\Omega _{2}=\Omega \) and \(r_{1}=r_{2}\) here. Moreover, the contour line with \(|t_{p}|^{2}=1\) forms a “circular runway”. The transmitted probe field can be amplified inside the contour line, otherwise it will be attenuated.

Figure 3
figure 3

Contour plot of the power transmission coefficient \(|t_{p}|^{2}\) at \(\Omega =2.0029\omega _{m}\) versus the phase difference \(\Phi _{1}/\pi \) and \(\Phi _{2}/\pi \). The other parameters are the same as those in Fig. 2 except \(r_{1}=r_{2}=10^{-5}\)

Full size image

We have shown that a symmetric peak locates around \(\Omega /\omega _{m}=2\) in the transmission spectrum under the two-phonon resonance condition. If the cavity-control field detuning \(\Delta \neq 2\omega _{m}\), asymmetric Fano line shape can be observed [64, 68]. Similar to previous works about Fano resonance in optomechanical systems [22, 23, 64, 68, 76], we also study the absorptive behavior \(\operatorname{Re} (\varepsilon _{T})\) of the output probe field. At small coupling parameter \(\eta _{c}\ll 1\), we can obtain \(|t_{p}|\simeq 1-\operatorname{Re}(\varepsilon _{T})\) and \(\arg (t_{p})\simeq -\operatorname{Im}(\varepsilon _{T})\) [69]. Therefore, both the transmission \(|t_{p}|^{2}\) and absorption \(\operatorname{Re} (\varepsilon _{T})\) can reveal the same phenomena of the system. At \(\Delta =1.9\omega _{m}\), Fig. 4 plots the absorption \(\operatorname{Re} ( \varepsilon _{T})\) of the output probe field versus the normalized detuning \(\Omega /\omega _{m}\) when one membrane is excited with different phases. In the absence of the mechanical driving field, the top panel in Fig. 4 shows that the absorption spectrum can exhibit an asymmetric Fano line shape around \(\Omega /\omega _{m}=2\) and a broad absorption peak around \(\Omega /\omega _{m}=1.9\). The asymmetric Fano line shape results from the destructive interference between the anti-Stokes field and the probe field at frequency \(\omega _{p}=\omega _{c}+2\omega _{m}\), where the anti-Stokes field is not resonant with the cavity frequency \(\omega _{0}\). The broad absorption peak at \(\Omega /\omega _{m}=1.9\) is due to the resonant absorption of the probe photons by the cavity. When the mechanical driving field is turned on, the absorption spectrum can be modified, depending on the phase difference. At \(r_{1}=10^{-5}\) and \(\Phi _{1}=0\), the minimum absorption \(\operatorname{Re} ( \varepsilon _{T})\) in the vicinity of \(\Omega /\omega _{2}=2\) is negative, which indicates the amplification of the probe field. A transition between amplification and absorption occurs when the normalized detuning \(\Omega /\omega _{m}\) increases. At fixed amplitude ratio \(r_{1}\), Fig. 4 shows that the asymmetric Fano line shape around \(\Omega /\omega _{m}=2\) can be modulated effectively for various phase difference \(\Phi _{1}\), where the interference effect is evident. However, the absorption spectrum in other parameter regime almost keeps the same.

Figure 4
figure 4

The absorption \(\operatorname{Re} (\varepsilon _{T})\) of the output probe field as a function of the normalized detuning \(\Omega /\omega _{m}\) for different values of the mechanical driving field. The other parameters are the same as those in Fig. 2 except \(\Delta =1.9\omega _{m}\) and \(r_{2}=0\)

Full size image

We have assumed that the resonance frequencies of the two membranes are the same in the above, but it is possible to tune the resonance frequency independently, which enables us to control the optical response of the system more flexibly. For \(\omega _{1}=2\pi \times 10^{5}\text{ Hz}\) and \(\omega _{2}=2\pi \times 0.94\times 10^{5}\text{ Hz}\), we plot the absorption \(\operatorname{Re} (\varepsilon _{T})\) of the output probe field as a function of the normalized detuning \(\Omega /\omega _{1}\) in Fig. 5 with \(\Delta =2\omega _{1}\). In this case, the condition of two-phonon resonance is only satisfied for the membrane with resonance frequency \(\omega _{1}\). In the absence of the mechanical driving field, the absorption spectrum in Fig. 5(a) exhibits a symmetric absorption dip around \(\Omega /\omega _{1}=2\), which indicates the appearance of optomechanically induced transparency (OMIT), and an asymmetric Fano line shape near \(\Omega /\omega _{1}=2\omega _{2}/\omega _{1}=1.88\). OMIT and Fano line shape result from the destructive interference between the probe field and the generated anti-Stokes fields at frequency \(\omega _{c}+2\omega _{1}\) and \(\omega _{c}+2\omega _{2}\), respectively. When both the mechanical driving fields are switched on with fixed amplitudes and various phases, the absorption spectra can be modified, as shown in Figs. 5(b)–5(d). At \(\Phi _{1}=0\) and \(\Phi _{2}=0.5\pi \), the absorption peak around \(\Omega /\omega _{1}=1.88\) becomes larger than 1, which indicates the enhanced absorption due to the mechanical driving field. However, the absorption dip around \(\Omega /\omega _{1}=2\) becomes negative, which corresponds to the amplification of the probe field. By tuning the phase differences \(\Phi _{1}\) and \(\Phi _{2}\) independently, we can see from Figs. 5(c)–5(d) that the two resonances around \(\Omega /\omega _{1}=1.88\) and \(\Omega /\omega _{1}=2\) switch between the enhanced absorption and amplification. Therefore, the output probe field can be selectively amplified by tuning the mechanical driving fields. Different from the case that \(\omega _{1}=\omega _{2}=\omega _{m}\), Fig. 5 demonstrates that the absorption curves around \(\Omega /\omega _{1}=1.88\) and \(\Omega /\omega _{1}=2\) are controlled independently by tuning the phase differences. The two mechanical driving fields cannot interfere with each other since the frequency difference \(|\omega _{1}-\omega _{2}|\) is much larger than the linewidth of the absorption peaks (dips) around \(\Omega /\omega _{1}=1.88\) and \(\Omega /\omega _{1}=2\).

Figure 5
figure 5

The absorption \(\operatorname{Re} (\varepsilon _{T})\) of the output probe field versus the normalized detuning \(\Omega /\omega _{1}\) for different values of the mechanical driving fields. The other parameters are the same as those in Fig. 2 except \(\omega _{1}=2\pi \times 10^{5}\text{ Hz}\), \(\omega _{2}=2\pi \times 0.94\times 10^{5}\text{ Hz}\), and \(\Delta =2\omega _{1}\). In Figs. 5(c)–(d), we choose \(r_{1}=r_{2}=10^{-5}\)

Full size image

When the cavity-control field detuning is tuned to be \(\Delta =\omega _{1}+\omega _{2}\) with \(\omega _{1}=2\pi \times 10^{5}\text{ Hz}\) and \(\omega _{2}=2\pi \times 0.8\times 10^{5}\text{ Hz}\), the absorption \(\operatorname{Re} ( \varepsilon _{T})\) of the output probe field exhibits a broad absorption peak in the center and two sideband peaks (dips). Figures 6(b) and 6(c) are the enlargement of the two sideband peaks around \(\Omega /\omega _{1}=1.6\) and \(\Omega /\omega _{1}=2\), in which the red solid curves correspond to the asymmetric Fano line shapes for \(r_{1}=r_{2}=0\). In this case, both the generated anti-Stokes fields at frequencies \(\omega _{c}+2\omega _{1}\) and \(\omega _{c}+2\omega _{2}\) are not resonant with the cavity frequency. The Fano resonance around \(\Omega /\omega _{1}=2\) is caused by interference effect between the probe field and the anti-Stokes field at frequency \(\omega _{c}+2\omega _{1}\), while the Fano resonance around \(\Omega /\omega _{1}=1.6\) is due to the interference effect at frequency \(\omega _{c}+2\omega _{2}\). Therefore, the phenomena of a single OMIT and a single Fano resonance in Fig. 5 can be switched to double Fano resonances by modulating the cavity-control field detuning Δ. Moreover, the Fano line shapes can be modified by the mechanical driving fields. At \(\Phi _{1}=\Phi _{2}=0.5\pi \), the peak value around \(\Omega /\omega _{1}=1.6\) becomes larger than 1 that is an indication of enhanced absorption, but the absorption peak near \(\Omega /\omega _{1}=2\) becomes an absorption dip with negative value of \(\operatorname{Re} (\varepsilon _{T})\). The double Fano resonance is reversed if \(\Phi _{1}=\Phi _{2}=1.5\pi \) compared with \(\Phi _{1}=\Phi _{2}=0.5\pi \).

Figure 6
figure 6

The absorption \(\operatorname{Re} (\varepsilon _{T})\) of the output probe field as a function of the normalized detuning \(\Omega /\omega _{1}\) for different values of the mechanical driving fields. Figure 6(b) and 6(c) are the enlarged images of Fig. 6(a) around \(\Omega /\omega _{1}=1.6\) and \(\Omega /\omega _{1}=2.0\), respectively. The other parameters are the same as those in Fig. 5 except \(\omega _{2}=2\pi \times 0.8\times 10^{5}\text{ Hz}\) and \(\Delta =2\omega _{m}=\omega _{1}+\omega _{2}\). The dashed and dash-dotted curves correspond to \(r_{1}=r_{2}=10^{-5}\)

Full size image

Finally, we study the effect of the amplitude of the mechanical driving field on the transmission spectrum. Figure 7(a) plots the power transmission coefficient \(|t_{p}|^{2}\) versus the normalized detuning \(\Omega /\omega _{1}\) for \(r_{1}=0,0.5\times 10^{-5},1.0\times 10^{-5},1.5\times 10^{-5}\), and \(2\times 10^{-5}\), respectively. Here we keep \(\Phi _{1}=1.5\pi \), \(r_{2}=10^{-5}\), \(\Phi _{2}=0.5\pi \) fixed. For \(r_{1}=0\), the transmission coefficient \(|t_{p}|^{2}<1\) at \(\Omega /\omega _{1}\approx 2\) but \(|t_{p}|^{2}>1\) at \(\Omega /\omega _{1}\approx 1.6\). For \(r_{1}=0.5\times 10^{-5}\), the minimum value of \(|t_{p}|^{2}\) becomes smaller due to the interference effect induced by the mechanical driving field. When the amplitude ratio \(r_{1}\) is increased to 10−5, the minimum transmission coefficient \(|t_{p}|^{2}\) near \(\Omega /\omega _{1}=2\) becomes larger. At higher value of \(r_{1}\), the transmission dip is switched to a transmission peak with \(|t_{p}|^{2}>1\). Meanwhile, the transmission peak around \(\Omega /\omega _{1}\approx 1.6\), which is determined by the interference effect at frequency \(\omega _{c}+2\omega _{2}\), keeps almost the same when the amplitude ratio \(r_{1}\) increases. In Fig. 7(b), the transmission coefficient \(|t_{p}|^{2}\) at \(\Omega =2.00362\omega _{1}\) is plotted as a function of the amplitude ratio \(r_{1}\) for various values of phase difference \(\Phi _{1}\). At \(\Phi _{1}=1.5\pi \), the transmission coefficient \(|t_{p}|^{2}\) decreases from an initial value to zero when the amplitude ratio \(r_{1}\) increases. With further increasing the amplitude ratio \(r_{1}\), the transmission coefficient \(|t_{p}|^{2}\) starts to increase again and can be larger than 1. This phenomenon can be well explained in terms of the complicated interference effect induced by the mechanical driving field [75]. In addition, the phase-dependent effect can be seen from the curves for \(\Phi _{1}=0\) and \(\Phi _{1}=0.5\pi \), where the transmission coefficient \(|t_{p}|^{2}\) increases monotonically with the enhancement of the amplitude ratio \(r_{1}\).

Figure 7
figure 7

(a) The power transmission coefficient \(|t_{p}|^{2}\) as functions of the normalized detuning \(\Omega /\omega _{1}\) for different values of the amplitude ratio \(r_{1}\) with \(\Phi _{1}=1.5\pi \). (b) The transmission coefficient \(|t_{p}|^{2}\) at \(\Omega =2.00362\omega _{1}\) versus the amplitude ratio \(r_{1}\) with \(\Phi _{1}=1.5\pi ,0\), and 0.5π, respectively. The other parameters are the same as those in Fig. 6 except \(r_{2}=10^{-5}\) and \(\Phi _{2}=0.5\pi \)

Full size image

4 Conclusion

In conclusion, we have studied the controllable optical response of a multimode optomechanical system with quadratic coupling, where two movable membranes are placed in an optical cavity with two fixed mirrors. The response of the system to a weak probe field is investigated when the cavity is driven by a strong control field and the membranes are, respectively, excited by weak coherent mechanical driving fields. If the two membranes have the same resonance frequency, a single optomechanically induced transparency window occurs in the transmission spectrum under the condition of two-phonon resonance, which can be further modified by the two mechanical driving fields. When the condition of two-phonon resonance is not satisfied, the absorption spectrum can exhibit a single asymmetric Fano line shape. It is shown that the switch between the amplification and enhanced absorption of the probe field can be realized by tuning the phases of the mechanical driving fields. If the frequencies of the two membranes are different, by tuning the cavity-control field detuning, the absorption spectrum can exhibit the phenomenon of a single OMIT and a single Fano line shape or the phenomenon of double Fano line shapes, which results from the interference effect between the probe field and the two generated anti-Stokes fields. Moreover, the line shapes around the two frequencies of the anti-Stokes fields can be controlled independently by the phases and amplitudes of the two mechanical driving fields.