1 Introduction

The topic of gravitational collapse and black hole formation in general relativity dates back to the seminal papers of Oppenheimer et al. [1, 2]. Although the literature has thereafter grown immensely [3], many technical and conceptual difficulties remain unsolved. One thing we can safely claim is that gravity will come into play strongly whenever a given amount of matter is localised within a sufficiently small volume. This is the idea in Thorne’s hoop conjecture [4]: A black hole forms when the impact parameter b of two colliding objects is shorter than the Schwarzschild radius of the system, that is for Footnote 1

$$\begin{aligned} b \lesssim 2\,\ell _{\textrm{p}}\,\frac{E}{m_{\textrm{p}}} \equiv r_{\textrm{H}}, \end{aligned}$$
(1.1)

where E is total energy in the centre-mass frame. The conjecture, which has been checked in a variety of situations, was formulated initially having in mind black holes of astrophysical size [5,6,7], for which the very concept of a classical background metric and related horizon structure should be reasonably safe.

The appearance of a classical horizon is relatively easy to understand in a spherically symmetric space-time. We can write a general spherically symmetric metric \(g_{\mu \nu }\) as

$$\begin{aligned} \textrm{d}s^2 = g_{ij}\,\textrm{d}x^i\,\textrm{d}x^j + r^2(x^i)\left( \textrm{d}\theta ^2+\sin ^2\theta \,\textrm{d}\phi ^2\right) , \end{aligned}$$
(1.2)

where r is the areal coordinate and \(x^i=(x^1,x^2)\) are coordinates on surfaces where the angles \(\theta\) and \(\phi\) are constant. The location of a trapping horizon, a surface where the escape velocity equals the speed of light, is then determined by the equation [8]

$$\begin{aligned} 0 = g^{ij}\,\nabla _i r\,\nabla _j r = 1-\frac{2\,M}{r}, \end{aligned}$$
(1.3)

where \(\nabla _i r\) is the covector perpendicular to surfaces of constant area \(\mathcal {A}=4\,\pi \,r^2\). The function \(M=\ell _{\textrm{p}}\,m/m_{\textrm{p}}\) is the active gravitational (or Misner–Sharp) mass, representing the total energy enclosed within a sphere of radius r. For example, if we set \(x^1=t\) and \(x^2=r\), the function m is explicitly given by the integral of the classical matter density \(\rho =\rho (x^i)\) weighted by the flat metric volume measure,

$$\begin{aligned} m(t,r) = 4\,\pi \int _0^r \rho (t, \bar{r})\,\bar{r}^2\,\textrm{d}\bar{r}, \end{aligned}$$
(1.4)

as if the space inside the sphere were flat. Of course, it is in general very difficult to follow the dynamics of a given matter distribution and verify the existence of surfaces satisfying Eq. (1.3), but we can say an horizon exists if there are values of r such that \(r_{\textrm{H}}=2\,M(t,r)>r\), which is a mathematical reformulation of the hoop conjecture (1.1).

Whether the above condition on the Misner–Sharp mass, or the hoop conjecture, can also be trusted for sources with energy around the Planck size or much smaller, however, becomes questionable. In fact, for elementary particles we know for an experimental fact that quantum effects may not be neglected [9], as it also follows from a very simple argument. Consider a spin-less point-like source of mass m, whose Schwarzschild radius is given by \(r_{\textrm{H}}\) in Eq. (1.1) with \(E=m\). For such a particle, the Heisenberg principle of quantum mechanics introduces an uncertainty in its spatial localisation, typically of the order of the Compton–de Broglie length,

$$\begin{aligned} \lambda _m \simeq \ell _{\textrm{p}}\,\frac{m_{\textrm{p}}}{m}. \end{aligned}$$
(1.5)

Assuming quantum physics is a more refined description of reality, the clash of the two lengths, \(r_{\textrm{H}}\) and \(\lambda _m\), implies that the former only makes sense if it is larger than the latter,

$$\begin{aligned} r_{\textrm{H}}\gtrsim \lambda _m \quad \Rightarrow \quad m \gtrsim m_{\textrm{p}}\, \end{aligned}$$
(1.6)

or \(M\gtrsim \ell _{\textrm{p}}\). Note that this argument employs the flat space Compton length (1.5), and it is likely that the particle’s self-gravity will affect it. However, it is still reasonable to assume the condition (1.6) holds as an order of magnitude estimate and that black holes can only exist with mass (much) larger than the Planck scale.

The above argument immediately brings us to face a deeply conceptual challenge: how can we describe a system containing both quantum mechanical objects (like the elementary particles) and classical horizons? Moreover, since matter constituents are properly described by quantum physics, how can we reliably describe the formation of horizons inside collapsing matter? As a necessary tool to address these questions, we shall define a wavefunction for the horizon that can be associated with any localised quantum mechanical particle. This definition will also allow us to put on quantitative grounds the condition (1.6) that distinguishes black holes from regular particles.

2 Horizon wavefunction

Let us first formulate the construction and then explain it with an example. We shall only consider quantum mechanical states representing objects which are both localised in space and at rest in the chosen reference frame. The reasons for such restrictions should be physically obvious, since localisation is part of the idea behind the hoop conjecture, and we want to avoid the irrelevant complications due to the relative motion of the source. The particle is consequently described by a wavefunction \(\psi _{\textrm{S}}\in L^2(\mathbb {R}^3)\), which can be decomposed into energy eigenstates,

$$\begin{aligned} \left| \psi _{\textrm{S}}\right\rangle = \sum _E\,C(E)\,\left| \psi _E\right\rangle , \end{aligned}$$
(2.1)

where the sum represents the spectral decomposition in Hamiltonian eigenmodes,

$$\begin{aligned} \hat{H}\,\left| \psi _E\right\rangle =E\,\left| \psi _E\right\rangle , \end{aligned}$$
(2.2)

and H can be specified depending on the model we wish to consider. If we further assume the wavefunction is spherically symmetric, all we need is to recall the expression of the Schwarzschild radius in Eq. (1.1), which can be inverted to obtain

$$\begin{aligned} E = m_{\textrm{p}}\,\frac{r_{\textrm{H}}}{2\,\ell _{\textrm{p}}}. \end{aligned}$$
(2.3)

We then define the (unnormalised) “horizon wavefunction” as

$$\begin{aligned} \tilde{\psi }_{\textrm{H}}(r_{\textrm{H}}) = C\left( m_{\textrm{p}}\,{r_{\textrm{H}}}/{2\,\ell _{\textrm{p}}}\right) . \end{aligned}$$
(2.4)

whose normalisation is fixed by assuming the norm

$$\begin{aligned} \langle \, \psi _{\textrm{H}} \mid \phi _{\textrm{H}}\,\rangle = 4\,\pi \,\int _0^\infty \psi _{\textrm{H}}^*(r_{\textrm{H}})\,\phi _{\textrm{H}}(r_{\textrm{H}})\,r_{\textrm{H}}^2\,\textrm{d}r_{\textrm{H}}. \end{aligned}$$
(2.5)

We interpret the normalised wavefunction \(\psi _{\textrm{H}}\) simply as yielding the probability that we would detect a horizon of areal radius \(r=r_{\textrm{H}}\) associated with the particle in the quantum state \(\psi _{\textrm{S}}\). Such a horizon is necessarily “fuzzy”, like is the position of the particle itself.

Having defined the \(\psi _{\textrm{H}}\) associated with a given \(\psi _{\textrm{S}}\), the probability density that the particle lies inside its own horizon of radius \(r=r_{\textrm{H}}\) will be given by

$$\begin{aligned} P_<(r<r_{\textrm{H}}) = P_{\textrm{S}}(r<r_{\textrm{H}})\,P_{\textrm{H}}(r_{\textrm{H}}), \end{aligned}$$
(2.6)

where

$$\begin{aligned} P_{\textrm{S}}(r<r_{\textrm{H}}) = 4\,\pi \,\int _0^{r_{\textrm{H}}} |\psi _{\textrm{S}}(r)|^2\,r^2\,\textrm{d}r \end{aligned}$$
(2.7)

is the probability that the particle is inside a sphere of radius \(r=r_{\textrm{H}}\), and

$$\begin{aligned} P_{\textrm{H}}(r_{\textrm{H}}) = 4\,\pi \,r_{\textrm{H}}^2\,|\psi _{\textrm{H}}(r_{\textrm{H}})|^2 \end{aligned}$$
(2.8)

is the probability density that the horizon is located on the sphere of radius \(r=r_{\textrm{H}}\). Finally, the probability that the particle described by the wavefunction \(\psi _{\textrm{S}}\) is a black hole will be obtained by integrating (2.6) over all possible values of the radius, namely

$$\begin{aligned} P_{\textrm{BH}} = \int _0^\infty P_<(r<r_{\textrm{H}})\,\textrm{d}r_{\textrm{H}}. \end{aligned}$$
(2.9)

3 Massive particle

The above construction can be exemplified by describing a massive particle at rest in the origin of the reference frame with the spherically symmetric Gaussian wavefunction

$$\begin{aligned} \psi _{\textrm{S}}(r) = \frac{e^{-\frac{r^2}{2\,\ell ^2}}}{\ell ^{3/2}\,\pi ^{3/4}}, \end{aligned}$$
(3.1)

corresponding to the momentum space wavefunction

$$\begin{aligned} \psi _{\textrm{S}}(p) = \frac{e^{-\frac{p^2}{2\,\Delta ^2}}}{\Delta ^{3/2}\,\pi ^{3/4}}, \, \end{aligned}$$
(3.2)

where \(p^2=\textbf{p}\cdot \textbf{p}\) and \(\Delta =\hbar /\ell =m_{\textrm{p}}\,\ell _{\textrm{p}}/\ell\). For the energy of the particle, we simply assume the relativistic mass-shell relation in flat space, \(E^2=p^2+m^2\), and, upon inverting the expression of the Schwarzschild radius (1.1), we obtain the horizon wavefunction

$$\begin{aligned} \psi _H(r_{\textrm{H}}) = \frac{\ell ^{3/2}\,e^{-\frac{\ell ^2\,r_{\textrm{H}}^2}{8\,\ell _{\textrm{p}}^4}}}{2^{3/2}\,\pi ^{3/4}\,\ell _{\textrm{p}}^3}. \end{aligned}$$
(3.3)

Note that, since \(\langle \, \hat{r}^2\,\rangle \simeq \ell ^2\) and \(\langle \, \hat{R}_{\textrm{H}}^2\,\rangle \simeq \ell _{\textrm{p}}^4/\ell ^2\), we expect the particle will be inside its own horizon if \(\langle \, \hat{r}^2\,\rangle \ll \langle \, \hat{R}_{\textrm{H}}^2\,\rangle\), which precisely yields the condition (1.6) if \(\ell \simeq \lambda _m\). In fact, the probability density (2.6) can now be explicitly computed,

$$\begin{aligned} P_<(r<r_{\textrm{H}}) = \frac{\ell ^3\,r_{\textrm{H}}^2}{2\,\sqrt{\pi }\,\ell _{\textrm{p}}^6}\, e^{-\frac{\ell ^2\,r_{\textrm{H}}^2}{4\,\ell _{\textrm{p}}^4}} \left[ \textrm{Erf}\left( \frac{r_{\textrm{H}}}{\ell }\right) - \frac{2\,r_{\textrm{H}}}{\sqrt{\pi }\,\ell }\, e^{-\frac{r_{\textrm{H}}^2}{\ell ^2}} \right] , \end{aligned}$$
(3.4)

from which the probability (2.9) for the particle to be a black hole is obtained as

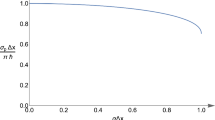
$$\begin{aligned} P_{\textrm{BH}}(\ell ) = \frac{2}{\pi }\left[ \arctan \left( 2\,\frac{\ell _{\textrm{p}}^2}{\ell ^2}\right) + 2\,\frac{\ell ^2\,(4-\ell ^4/\ell _{\textrm{p}}^4)}{\ell _{\textrm{p}}^2\,(4+\ell ^4/\ell _{\textrm{p}}^4)^2} \right] . \end{aligned}$$
(3.5)

In Fig. 1, we show the probability density (3.4) that the particle is inside its own horizon, for the two cases \(\ell =\ell _{\textrm{p}}\) and \(\ell =2\,\ell _{\textrm{p}}\), and the probability (3.5) that the particle is a black hole as a function of the Gaussian width \(\ell\). From the plot of \(P_{\textrm{BH}}\), it appears pretty obvious that the particle is most likely a black hole, \(P_{\textrm{BH}}\simeq 1\), if \(\ell \lesssim \ell _{\textrm{p}}\). Assuming \(\ell =\lambda _m=\ell _{\textrm{p}}\,m_{\textrm{p}}/m\), we have thus derived the same condition (1.6), from a totally quantum mechanical picture.

Fig. 1
figure 1

Left panel: probability density that particle is inside horizon of radius \(r_{\textrm{H}}\), for \(\ell =\ell _{\textrm{p}}\) (solid line) and for \(\ell =2\,\ell _{\textrm{p}}\) (dashed line). Right panel: probability that particle of width \(\ell\) is a black hole

Full size image

4 Concluding remarks

Of course, the above construction could be further refined. For example, one could employ dispersion relations \(E=E(p)\) derived from quantum field theory in curved space-time, and a better definition of what a localised state in the latter context should probably be employed as well.Footnote 2 Regardless of such improvements, the usefulness of our construction should already be fairly clear, in that it allows us to deal with very general sources, and to do so in a quantitative fashion. For example, one could review the issue of quantum black holes [11, 12] in light of the above formalism, as well as finally tackle the description of black hole formation and dynamical horizons [8] in the gravitational collapse of truly quantum matter [9, 13].