1 Introduction

The most accurate mathematical representations of natural phenomena often hinge on differential equations, encompassing both linear and nonlinear formulations. Nonlinear systems, in particular, frequently yield such equations during the modeling process, nearly all fields of contemporary science, spanning from plasma physics, atomic physics, and solid-state physics to astronomy, mathematics, biology, and chemistry, engage in investigations concerning these nonlinear evolution equations. In this article, we delve into the examination of the \((2+1)\)-dimensional HSI equation, augmented by the incorporation of four additional second-order derivative terms:

$$\begin{aligned} \begin{aligned}&H_{\varpi \varpi \varpi \iota }+3(H_{\varpi }H_{\varpi \iota }+H_{\iota }H_{\varpi \varpi }) +{\Delta _{6}}H_{\iota \iota }+{\Delta _{1}}H_{\upsilon \iota }+{\Delta _{5}}H_{\upsilon \upsilon }+{\Delta _{4}}H_{\varpi \iota }+ {\Delta _{3}}H_{\varpi \upsilon }+{\Delta _{2}}H_{\varpi \varpi }= 0. \end{aligned} \end{aligned}$$
(1)

The equation discussed above is recognized as the completely generalized Hirota–Satsuma–Ito (cgHSI) Eq. [1], as it encompasses every second-order dissipative-type element. The cgHSI equation serves as a model for shallow water waves, delineating the amplitude of these waves through the function H, which relies on the components \(\varpi\), \(\upsilon\), and \(\iota\). It is expressed using partial derivatives concerning the spatial components \(\varpi\) and \(\upsilon\), as well as the temporal component \(\iota\). The equation incorporates free parameters denoted by \(\Delta _1\), \(\Delta _2\), \(\Delta _3\), \(\Delta _4\), \(\Delta _5\), and \(\Delta _6\). Shallow water equations of motion are employed to depict the horizontal structure of an atmosphere and the dynamics of shallow water waves, portraying the behavior of an incompressible fluid under the influences of rotational and gravitational accelerations.

Several significant advancements have been achieved in the research of the (2+1)-generalized shallow water equation and its variants. Notably, our fully generalized shallow water model stands out uniquely in the realm of research publications. We have noticed a plethora of studies delineating distinct wave structures under the same model name. In Gao and Tian [2], the (2+1)-dimensional generalized shallow water wave equation is shown using the technique of the generalized tanh method with symbolic computation, exhibiting the structure that follows:

$$\begin{aligned} H_{\upsilon \iota }+H_{\varpi \varpi \upsilon }-3H_{\varpi \varpi }H_{\upsilon }-3H_{\varpi }H_{\varpi \upsilon }=0. \end{aligned}$$

In this research paper [3], precise solutions and conserved vectors of the two-dimensional generalized shallow water wave equation, characterized by the subsequent structure, are elucidated:

$$\begin{aligned} H_{\iota \varpi }+\Delta _{1}H_{\upsilon }H_{\varpi \varpi }+2\Delta _{1}H_{\varpi }H_{\varpi \upsilon }+\Delta _{2}H_{\varpi \upsilon }+\Delta _{3}H_{\varpi \varpi \varpi \upsilon }=0. \end{aligned}$$

Here, \(\Delta _{1}\) and \(\Delta _{2}\) are seen as something that isn’t zero, regardless of whether it is positive or negative. The periodic wave solution for the generalized shallow water wave equation [4] is obtained using the improved Jacobi elliptic function method with the following structure:

$$\begin{aligned} H_{\varpi \varpi \varpi \iota }+\Delta _{1}H_{\varpi }H_{\varpi \iota }+\Delta _{2}H_{\iota }H_{\varpi \varpi }-H_{\varpi \iota }-\Delta _{3}H_{\varpi \varpi }=0, \end{aligned}$$

where \(\Delta _{1},\Delta _{2},\Delta _{3}\)   are arbitrary nonzero constants. By employing the homogeneous balance method, an auto-Bäcklund transformation for the generalized shallow water wave equation [5] is derived with the following structure:

$$\begin{aligned} H_{\varpi \varpi \varpi \iota }+\Delta _{1}H_{\varpi }H_{\varpi \iota }+\Delta _{2}H_{\iota }H_{\varpi \varpi }-H_{\varpi \iota }-H_{\varpi \varpi }=0. \end{aligned}$$

In this equation, \(\Delta _{1}\) and \(\Delta _{2}\) represent arbitrary nonzero constants. In the cited work [6], the authors delve into \((2 + 1)\)-dimensional generalized Hirota–Satsuma–Ito equations, providing insights into Lie symmetry analysis, invariant solutions, and dynamics of soliton solutions for the following model:

$$\begin{aligned}{} & {} v_{\iota }+H_{\varpi \varpi \iota }+3(Hw)_{\varpi }+\Delta _{1}H_{\varpi }=0, \\{} & {} H_{\upsilon }=v_{\varpi }, H_{\iota }=w_{\varpi }. \end{aligned}$$

Here, H is a physical field. v and w indicators of potentials of field derivatives physical field. Alongside this, \(\varpi\) and \(\upsilon\) refer to dimensions of space, whereas \(\iota\) is the other time variable. Abundant exact interaction solutions, such as lump-soliton, lump-kink, and lump-periodic solutions, are computed for the \((2 + 1)\)-dimensional Hirota–Satsuma–Ito equation described [7], following this model:

$$\begin{aligned} H_{\iota }=H_{\varpi \varpi \iota }+3HH_{\iota }-3H_{\varpi }v_{\iota }-H_{\varpi },~~v_\varpi =H. \end{aligned}$$

Research into shallow-water wave phenomena within a (2+1)-dimensional Hirota–Satsuma–Ito system has led to investigations on X-type soliton, resonant Y-type soliton, and hybrid solutions [8]:

$$\begin{aligned} H_{\iota }=H_{\varpi \iota }+3HH_{\iota }-3H_{\varpi }v_{\iota }-H_{\varpi },~~v_{\varpi }=-H. \end{aligned}$$

Researchers in different disciplines have investigated various techniques for solving PDE, many of which produce the solitary wave solution. Effective strategies for addressing these nonlinear differential problems include the extended direct algebraic method [9], the generalized \(\textrm{exp}(-\phi (\zeta ))\) expansion technique [10], the symmetry method [11], the tanh-coth function method [12], the sine-cosine technique [13], the exp-function method [14], the new extended auxiliary equation method [15], the new Jacobi elliptic functions method [16], the new extended generalized Kudryashov scheme [17], the residual power series method [18]. In addition, approximate analytical and numerical methods such as the homotopy analysis method (HAM) [19], the Adomian decomposition method (ADM) [20], the variational iteration method (VIM) [21], and the variational homotopy perturbation method (VHPM) [22].

One of the most appropriate analytical approaches to reduce the complexity of nonlinear partial differential equations (PDE), proposed by Norwegian mathematician Marcus Sophus Lie (1842–1899), is the symmetry method [23]. The centerpiece of the Lie symmetry method is the existence of transformation which makes solutions to the differential equation we consider, fixed points. Lie vector fields are found through this technique for what is under discussion in differential equations to be invariant. The overlying group of symmetry is the basis for the solution with an invariant group or similarity to the PDE. As a result of improving methods of continuous Lie groups study, bifurcation theory, control theory, classical mechanics, and relativity have been given new tools that helped in establishing the role of symmetry in different branches of science [24].

The principle of conservation states that the amount of a system of physical entities does not decrease as time goes on, thus, it is conserved. For physical systems that are governed by the laws of motion, the equations of motion are usually derived from conservation laws such as the principle of conservation of momentum. The collection may also preserve other physical quantities that are worth knowing about the physical process controlling the motion. On top of that, the conservation law knowledge will be useful for solving methods, for instance, conservative numerical methods that assume the shape of conservation law [25].

Noether was first to point out this crucial and defining characteristic in 1918 and she propounded the Noether theorem which is a mathematical explanation of this relationship between symmetry and conservation laws [26]. Subsequently, numerous researchers have endeavored to devise novel approaches for determining conservation laws [27]. Addressing a major limitation of this finding the absence of a Lagrangian Ibragimov extended the Noether theorem [28]. Researchers commonly employ the concept of nonlinear self-adjointness and the formulation of local conservation laws to establish conservation laws for differential equations lacking a classical Lagrangian. A selection of their works is presented in [29, 30]. In this study, through meticulous analysis of the Lie group and new auxiliary equation groups associated with the model under investigation, we have generated various patterns of solitary wave solutions.

  The structure of the paper is outlined as follows: Section (2) introduces the foundational concepts of Lagrangian and nonlinear self-adjointness.  Section 3 conducts a Lie analysis to identify the symmetries of Eq. (1) and employs the new auxiliary equation method to determine the traveling wave structure of Eq. (1). Additionally, this section offers a graphical representation of some pertinent solutions of Eq. (1). Section 4 is dedicated to nonlinear self-adjointness analysis and the computation of conserved vectors for Eq. (1). Finally, concluding remarks are provided, summarizing the research findings and bringing closure to the paper.

2 Preliminaries

Suppose a system of n PDEs of pth order is defined as:

$$\begin{aligned} G_{\gamma }=G_{\gamma }(\varpi ,H,H_{1},H_{2},...,H_{p})=0,~~~~~\gamma =1,2,3,...,n, \end{aligned}$$
(2)

where n and q represent dependent and independent variables respectively, and \(H_{1}, H_{2}, \dots , H_{n}\) denote the first, second, up to the nth order partial derivatives of H. The total differential operator corresponding to \(\varpi ^{k}\) is:

$$\begin{aligned} A_{k}={\partial _{\varpi ^{k}}+{H^\gamma _k}{\partial _{H^\gamma }}}+H^\gamma _{kl}\ {\partial _{ H^\gamma _{l}}}+H^\gamma _{klm} {\partial _{ H^\gamma _{lm}}}+..., ~~~~ k=1,2,...q, \end{aligned}$$
(3)

where \(\partial _{\varpi ^{k}}=\frac{\partial }{\partial \varpi ^{k}}\), \({\partial _{H^\gamma }}=\frac{\partial }{\partial {H^\gamma }}\), \({\partial _{ H^\gamma _{l}}}=\frac{\partial }{\partial H^\gamma _{l}}\), \({\partial _{H^\gamma _{lm}}}=\frac{\partial }{\partial H^\gamma _{lm}}.\)

2.1 Formal Lagrangian

The formal Lagrangian for Eq. (2) can be defined as follows:

$$\begin{aligned} S=\sum _{\beta =1}^{n} {h^{\beta } S_\beta }. \end{aligned}$$
(4)

S is known as the formal Lagrangian, where \(h=(h^1,h^2,...,h^n)\) represents the dependent variables. 

The adjoint formula turns into this:

$$\begin{aligned} G^{*}_\gamma (\varpi ,H,h,H_1,h_1,H_2,h_2,H_2,....,H_{P},h_p)=\frac{\delta (S)}{\delta H^\gamma }=0. \end{aligned}$$
(5)

The variational derivative is defined as:

$$\begin{aligned} \frac{\delta }{\delta {H^\gamma }}={\partial _ H^\gamma }+\sum _{g=1}^{\infty } (-1)^{g}A_{k_{1}}...A_{k_{g}}{\partial _{H^\gamma _{k_{1}...k_{g}}}},~~~ \gamma =1,2,3,....,n. \end{aligned}$$
(6)

2.2 Nonlinear self-adjointness

Definition 1

Equation (1) is said to be strictly self-adjoint if the equation obtained by substituting \(\Upsilon =H\) from its adjoint equation is identical to the original equation Eq. (2):

$$\begin{aligned} \left. G^{*}_\gamma \right| _{\Upsilon =H}=\Upsilon (\varpi ,H,...)G_{\gamma }. \ \end{aligned}$$

Definition 2

The equation expressed in Eq. (1) is said to be quasi-self-adjoint if, upon substituting \(\Upsilon =\omega (H)\), where \(\omega (H)\ne 0\), from its adjoint equation, the resulting equation is identical to the one in Eq. (2):

$$\begin{aligned} \left. G^{*}_\gamma \right| _{\Upsilon =\omega (H)}=\Upsilon (\varpi ,H,...)G_{\gamma }. \ \end{aligned}$$

Definition 3

Equation (1) is said to be weak self-adjoint if the equation generated by substituting \(\Upsilon =\omega (\varpi , H)\), where \(\omega\) is a nontrivial function, \(\omega _H \ne 0\), and \({\omega }_{\varpi }\ne 0\), from its adjoint equation is identical to Eq. (2):

$$\begin{aligned} \left. G^{*}_\gamma \right| _{\Upsilon =\omega (\varpi ,H)}=\Upsilon (\varpi ,H,...)G_{\gamma }. \ \end{aligned}$$

Definition 4

Equation (1) is said to be nonlinearly self-adjoint if the equation obtained by substituting \(\Upsilon =\omega (\varpi , H)\), where \(\omega (\varpi , H)\) is a nonzero function of \(\varpi\) and H, from its adjoint equation is identical to Eq. (2):

$$\begin{aligned} \left. G^{*}_\gamma \right| _{\Upsilon =\omega (\varpi ,H)}=\Upsilon (\varpi ,H,...)G_{\gamma }. \ \end{aligned}$$

3 Lie analysis

Definition 5

The following is an outline of the infinitesimal generator M prolongation:

$$\begin{aligned} \begin{aligned} M^{s}=\,\,&\epsilon ^{k}(\varpi ,\upsilon ,\iota ,H){\partial \varpi _{k}}+\vartheta _{k}(\varpi ,\upsilon ,\iota ,H_{1}){\partial H_{k}} +..+\vartheta _{k_1..k_s}(\varpi ,\upsilon ,\iota ,H_{1},..,H_{s}){\partial H_{k_1..k_s}}. \end{aligned} \end{aligned}$$

In this instance, \(\vartheta _{s}\) can be shown as follows:

$$\begin{aligned} \begin{aligned} \vartheta ^{\gamma }_{k}=\,\,&A_{k}(\psi ^{\gamma })-H^{\gamma }_{l}A_{k}(\epsilon ^{l}),\\ \vartheta ^{\gamma }_{kl}=\,\,&A_{l}(\vartheta ^{\gamma }_{k})-H^{\gamma }_{kr}A_{l}(\epsilon ^{r}),\\ {}&. \\ {}&. \\ {}&. \\ \vartheta ^{\gamma }_{k_{1}....k_{s}}=\,\,&A_{k_{s}}(\vartheta ^{\gamma }_{k_{1}....k_{s-1}})-H^{\gamma }_{rk_{1}...k_{s-1}}A_{k_{s-1}} A_{k_{s}}(\epsilon ^{l}), \end{aligned} \end{aligned}$$

since, the total differential operator given in Eq. (3) is shown by \(A_{k_{s}}\).

3.1 Infinitesimal generators

The one-parameter Lie group corresponds to the form’s infinitesimal transformation [31]:

$$\begin{aligned} \begin{aligned} {\bar{\varpi }}=\,\,&\varpi +\varepsilon \epsilon ^{1}+O(\varepsilon ^2), \\ {\bar{\upsilon }}=\,\,&\upsilon +\varepsilon \epsilon ^{2}+O(\varepsilon ^2), \\ {\bar{\iota }}=\,\,&\iota +\varepsilon \epsilon ^{3}+O(\varepsilon ^2), \\ {\bar{H}}=\,\,&H+\varepsilon \vartheta +O(\varepsilon ^2),\\ \end{aligned} \end{aligned}$$

where \(\epsilon ^{1},~\epsilon ^{2},~\epsilon ^{3}\), and \(\vartheta\) represent independent and dependent variables of infinitesimal transformation, respectively. The vector field for Eq. (1) can be shown as the fifth prolongation of M:

$$\begin{aligned} \begin{aligned} M=\,\,&\epsilon ^{1}(\varpi ,\upsilon ,\iota ,H){\partial _ \varpi }+&\epsilon ^{2}(\varpi ,\upsilon ,\iota ,H){\partial _ \upsilon }+\epsilon ^{3}(\varpi ,\upsilon ,\iota ,H){\partial _ \iota }+\vartheta (\varpi ,\upsilon ,\iota ,H){\partial _ H}.~ \end{aligned} \end{aligned}$$

The invariance form for M in Eq. (1) becomes:

$$\begin{aligned} M^{[4]}\bigg (H_{\varpi \varpi \varpi \iota }+3H_{\varpi }H_{\varpi \iota }+3H_{\iota }H_{\varpi \varpi } +{\Delta _{6}}H_{\iota \iota }+{\Delta _{1}}H_{\upsilon \iota }+{\Delta _{5}}H_{\upsilon \upsilon }+{\Delta _{4}}H_{\varpi \iota }+ {\Delta _{3}}H_{\varpi \upsilon }+{\Delta _{2}}H_{\varpi \varpi }\bigg )|_{Eq. (\text {1})} =0,\\ \end{aligned}$$

where the fourth prolongation, \(M^{[4]}\), can be constructed in the following manner:

$$\begin{aligned} \begin{aligned} M^{[4]}&=M+\vartheta ^{\varpi }{\partial _{ H_{\varpi }}}+\vartheta ^{\upsilon }{\partial _{ H_{\upsilon }}}+\vartheta ^{\varpi \varpi }{\partial _{ H_{\varpi \varpi }}}+\vartheta ^{\varpi \upsilon }{\partial _{ H_{\varpi \upsilon }}}+\vartheta ^{\varpi \varpi \varpi }{\partial _{ H_{\varpi \varpi \varpi }}}+\vartheta ^{\upsilon \upsilon \upsilon }{\partial _{ H_{\upsilon \upsilon \upsilon }}}\\&\qquad +\vartheta ^{\varpi \varpi \iota }{\partial _{ H_{\varpi \varpi \iota }}}+ \vartheta ^{\varpi \varpi \upsilon }{\partial _{ H_{\varpi \varpi \upsilon }} + \vartheta ^{\varpi \varpi \varpi \varpi \upsilon }{\partial _{ H_{\varpi \varpi \varpi \varpi \upsilon }}}}.~ \end{aligned} \end{aligned}$$

The Lie algebra of Eq. (1) is six-dimensional:

$$\begin{aligned} \begin{aligned} M_{1}&={\partial _{\varpi }},~~~~~ M_{2}={\partial _{\iota }},~~~~~ M_{3}={\partial _{\upsilon }},~~~~~ M_{4}={\partial _{H}},~~~~~ M_{5}=\upsilon {\partial _{\varpi }},~~~~~ \\ M_{6}&={\frac{(y_{1}) {\partial _{H}}}{z_{1}}+\frac{(y_{2}){\partial _{\iota }}}{z_{1}}+\frac{(y_{3}) ({\partial _{\varpi }})}{z_{1}}+\frac{(y_{4})(\partial _{\upsilon })}{z_{1}}}, \end{aligned} \end{aligned}$$
(7)

where \(y_{1}=-4\iota \Delta _2\Delta _5+\iota \Delta ^2_{3}+\varpi \Delta _1\Delta _3-2\varpi \Delta _4\Delta _5-3H\Delta _5\),  \(y_{2}=9\Delta _5\iota\),  \(y_{3}=3\varpi \Delta _5+3\upsilon \Delta _3,\) \(y_{4}=9\Delta _5\upsilon\),  \(z_{1}=\Delta _1\Delta _3-2\Delta _4\Delta _5.\)

Table 1 Commutator table
Full size table

where \(\varepsilon \ll 1\) is a fundamental parameter in Table 1a and 1b.

3.2 Symmetry group

In this phase, we will employ the Lie symmetry groups from the associated symmetries to produce some precise novel responses [32]. As, we take:

$$\begin{aligned} J_{i}:(\varpi ,\upsilon ,\iota ,H)\rightarrow & {} ({\bar{\varpi }},{\bar{\upsilon }},{\bar{\iota }},{\bar{H}}),~J_{i}~ {\text {for}}~ 1\le i \le 6, \\ \frac{d}{d\varepsilon }({\bar{\varpi }},{\bar{\upsilon }},{\bar{\iota }},{\bar{H}})=\,\,& {} \Lambda ({\bar{\varpi }},{\bar{\upsilon }},{\bar{\iota }},{\bar{H}})~{\text {with}}~~~({\bar{\varpi }},{\bar{\upsilon }},{\bar{\iota }},{\bar{H}})|_{\varepsilon =0}=(\varpi ,\upsilon ,\iota ,H), \end{aligned}$$

where the parameter \(\varepsilon\) is extremely tiny. Consider:

$$\begin{aligned} \Lambda =\epsilon ^{1} H_{\varpi }+\epsilon ^{2} H_{\upsilon }+\epsilon ^{3} H_{\iota }+\vartheta H, \end{aligned}$$

with the use of the infinitesimal generators \(\vartheta\), \(\epsilon ^{1}\), \(\epsilon ^{2}\), and \(\epsilon ^{3}\). We acquire the subsequent:

$$\begin{aligned} \begin{aligned} J_{1}:(\varpi ,\upsilon ,\iota ,H) \rightarrow&(\varpi +\varepsilon ,\upsilon ,\iota ,H),\\ J_{2}:(\varpi ,\upsilon ,\iota ,H) \rightarrow&(\varpi ,\upsilon ,\iota +\varepsilon ,H),\\ J_{3}:(\varpi ,\upsilon ,\iota ,H)\rightarrow&(\varpi ,\upsilon +\varepsilon ,\iota ,H),\\ J_{4}:(\varpi ,\upsilon ,\iota ,H) \rightarrow&(\varpi ,\upsilon ,\iota ,H+{\varepsilon }),\\ J_{5}:(\varpi ,\upsilon ,\iota ,H) \rightarrow&(\varpi +\varepsilon \upsilon ,\upsilon ,\iota ,H),\\ J_{6}:(\varpi ,\upsilon ,\iota ,H) \rightarrow&(\varpi {e^{z_{2}\varepsilon }},\upsilon {e^{z_{3}\varepsilon }},\iota {e^{z_{3}\varepsilon }},H+R_{1}). \end{aligned} \end{aligned}$$
(8)

where \(R_{1}=\frac{(4\iota {\Delta _2}{\Delta _5}{e^{z_3{\varepsilon }}}-\iota {\Delta ^{2}_{3}}{e^{z_{3}\varepsilon }-2{\Delta _{3}\Delta _{1}\varpi {e^{z_{2}\varepsilon }}}}+4\varpi {\Delta _4}{\Delta _5}{e^{z_2}\varepsilon }-{e^{-z_{2}\varepsilon }}(4\varepsilon {\Delta _2}{\Delta _5}-\iota \Delta ^2_{3}-2\varpi \Delta _{1}\Delta _{3}+4\varpi \Delta _{1}\Delta _{3}+4\varpi \Delta _{4}\Delta _{5}+12\,H\Delta _{5}))}{12\Delta _5},\) \(z_{2}={\frac{3\Delta _{5}}{z_{1}}},z_{3}={\frac{9\Delta _{5}}{z_{1}}}\).  While \(J_{1}\), \(J_{2}\), and \(J_{3}\) represent the time interpretation, and invariance of space, respectively, in Eq. (8). The new solution \(H_{i}\) should be obtained using \(J_{i}\)where \(1 \le i \le 6\), and we have a known solution form \(H=f(\varpi ,\upsilon ,\iota )\):

$$\begin{aligned} \begin{aligned} H_{1}=\,\,&f_{1}(\varpi -\varepsilon ,\upsilon ,\iota ),\\ H_{2}=\,\,&f_{2}(\varpi ,\upsilon ,\iota -\varepsilon ),\\ H_{3}=\,\,&f_{3}(\varpi ,\upsilon -\varepsilon ,\iota ),\\ H_{4}=\,\,&e^{-\varepsilon }f_{4} (\varpi ,\upsilon ,\iota ),\\ H_{5}=\,\,&f_{5} (\varpi ,\upsilon -\varepsilon \upsilon ,\iota ),\\ H_{6}=\,\,&e^{-\varepsilon }f_{6}((\varpi {e^{-z_{2}\varepsilon }},\upsilon {e^{-z_{3}\varepsilon }},\iota {e^{-z_{3}\varepsilon }})-R_{2}). \end{aligned} \end{aligned}$$

where \(R_{2}=\frac{(4\iota {\Delta _2}{\Delta _5}{e^{z_3{\varepsilon }}}-\iota {\Delta ^{2}_{3}}{e^{z_{3}\varepsilon }-2{\Delta _{3}\Delta _{1}\varpi {e^{z_{2}\varepsilon }}}}+4\varpi {\Delta _4}{\Delta _5}{e^{z_2}\varepsilon }-{e^{-z_{2}\varepsilon }}(4\varepsilon {\Delta _2}{\Delta _5}-\iota \Delta ^2_{3}-2\varpi \Delta _{1}\Delta _{3}+4\varpi \Delta _{1}\Delta _{3}+4\varpi \Delta _{4}\Delta _{5}))}{12\Delta _5}.\)

3.3 Optimal system

\(M=\{M_{1}, M_{2}, M_{3}, M_{4}\}\) generates an abelian subalgebra, as shown in Table 1a and b. Consequently, the one-dimensional optimal system [33] is as follows:

3.3.1 Unary class

$$\begin{aligned} {\mathbb {Z}}_{1a}=<M_{1}>,~ {\mathbb {Z}}_{1b}=<M_{2}>,~ {\mathbb {Z}}_{1c}=<M_{3}>,~ {\mathbb {Z}}_{1d}=<M_{4}>,~ {\mathbb {Z}}_{1e}=<M_{5}>,~ {\mathbb {Z}}_{1f}=<M_{6}>. \end{aligned}$$

3.3.2 Binary class

$$\begin{aligned} \begin{aligned} {\mathbb {Z}}_{2a}=\,\,& {} lt;M_{1}+c_{1}M_{2}>,~ {\mathbb {Z}}_{2b}=<M_{1}+c_{2}M_{3}>,~ {\mathbb {Z}}_{2c}=<M_{1}+c_{3}M_{4}>,~ {\mathbb {Z}}_{2d}=<M_{1}+c_{4}M_{5}>,~\\ {\mathbb {Z}}_{2d}=\,\,& {} lt;M_{1}+c_{5}M_{6}>, {\mathbb {Z}}_{2e}=<M_{2}+c_{6}M_{3}>,~ {\mathbb {Z}}_{2f}=<M_{2}+c_{7}M_{4}>,~ {\mathbb {Z}}_{2g}=<M_{2}+c_{8}M_{5}>,~\\ {\mathbb {Z}}_{2h}=\,\,& {} lt;M_{2}+c_{9}M_{6}>,~ {\mathbb {Z}}_{2i}=<M_{3}+c_{10}M_{4}>,~ {\mathbb {Z}}_{2j}=<M_{3}+c_{11}M_{5}>,~ {\mathbb {Z}}_{2k}=<M_{3}+c_{12}M_{6}>,~\\ {\mathbb {Z}}_{2l}=\,\,& {} lt;M_{4}+c_{13}M_{5}>,~ {\mathbb {Z}}_{2m}=<M_{4}+c_{14}M_{6}>,~ {\mathbb {Z}}_{2n}= <M_{5}+c_{15}M_{6}>. \end{aligned} \end{aligned}$$

3.3.3 Ternary class

$$\begin{aligned} \begin{aligned} {\mathbb {Z}}_{3a}=\,\,& {} lt;M_{1}+aM_{2}+bM_{3}>,~ {\mathbb {Z}}_{3b}=<M_{1}+a_{1}M_{2}+b_{1}M_{4}>,~ {\mathbb {Z}}_{3c}=<M_{1}+a_{2}M_{2}+b_{2}M_{5}>,~\\ {\mathbb {Z}}_{3d}=\,\,& {} lt; M_{1}+a_{3}M_{2}+b_{3}M_{6}>,~ {\mathbb {Z}}_{3e}=< M_{2}+a_{4}M_{3}+b_{4}M_{4}>,~ {\mathbb {Z}}_{3f}=<M_{2}+a_{5}M_{3}+b_{5}M_{5}>,~\\ {\mathbb {Z}}_{3g}=\,\,& {} lt; M_{2}+a_{6}M_{3}+b_{6}M_{6}>,~ {\mathbb {Z}}_{3h}=< M_{3}+a_{7}M_{4}+b_{7}M_{5}>,~ {\mathbb {Z}}_{3i}=<M_{3}+a_{8}M_{4}+b_{8}M_{6}>,~\\ {\mathbb {Z}}_{3j}&=<M_{4}+a_{9}M_{5}+b_{9}M_{36}>. \end{aligned} \end{aligned}$$

3.3.4 Combination of all classes

$$\begin{aligned} \begin{aligned} {\mathbb {Z}}_{4}=<M_{1}+d_{1}M_{2}+d_{2} M_{3}+d_{3} M_{4}>. \end{aligned} \end{aligned}$$

We calculate similarity variables which are used to calculate all obtainable similarity reductions for Eq. (1).

3.4 Reducing similarity through unary class

Case 1: The Lagrange structure corresponding to the vector field \({\mathbb {Z}}_{1a}=<{\partial _{\varpi }}>\) is shown as follows:

$$\begin{aligned} \frac{\textrm{d}\varpi }{1}=\frac{\textrm{d}\upsilon }{0}=\frac{\textrm{d}\iota }{0}=\frac{\textrm{d}H}{0}. \end{aligned}$$

Utilizing the shown details, we ascertain the form of the similarity function and similarity variables:

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=R(Y,T),~~~\text {where}~~ Y=\upsilon ,~~T=\iota ,~~ \end{aligned}$$
(9)

by substituting Eq. (9) into Eq. (1), we derive the reduced (1 + 1)-dimensional nonlinear PDE expressed as:

$$\begin{aligned} \Delta _{6}R_{TT}+\Delta _{1}R_{YT}+\Delta _{5}R_{YY}=0. \end{aligned}$$
(10)

From Eq. (10), we obtain the subsequent explicit solution for Eq. (1):

$$\begin{aligned} R(Y,T)=G_{1}\Bigg (\frac{-Y{\sqrt{\Delta ^2_{1}-4\Delta _{5}\Delta _{6}}}-2T\Delta _{5}+Y\Delta _{1}}{2\Delta _{5}}\bigg )+G_{2}\Bigg (\frac{Y{\sqrt{\Delta ^2_{1}-4\Delta _{5}\Delta _{6}}}+2T\Delta _{5}-Y\Delta _{1}}{2\Delta _{5}}\bigg ), \end{aligned}$$
(11)

by reintroducing Eq. (11) into Eq. (9), we arrive at the solution for Eq. (1):

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=G_{1}\Bigg (\frac{-\upsilon {\sqrt{\Delta ^2_{1}-4\Delta _{5}\Delta _{6}}}-2\iota \Delta _{5}+\upsilon \Delta _{1}}{2\Delta _{5}}\bigg )+G_{2}\Bigg (\frac{\upsilon {\sqrt{\Delta ^2_{1}-4\Delta _{5}\Delta _{6}}}+2\iota \Delta _{5}-\upsilon \Delta _{1}}{2\Delta _{5}}\bigg ). \end{aligned}$$

Case 2: The Lagrange configuration corresponding to the vector field \({\mathbb {Z}}_{1b}=<{\partial _{\iota }}>\) is provided as follows:

$$\begin{aligned} \frac{\textrm{d}\varpi }{0}=\frac{\textrm{d}\upsilon }{0}=\frac{\textrm{d}\iota }{1}=\frac{\textrm{d}H}{0}. \end{aligned}$$

With the provided information, we derive the similarity function and similarity variables in this manner:

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=R(X,Y),~~~\text {where} ~~X=\varpi ,~~Y=\upsilon , \end{aligned}$$
(12)

 by substituting Eq. (12)  into Eq. (1), we derive the reduced \((1 + 1)-\)dimensional nonlinear PDE shown as:

$$\begin{aligned} \Delta _{5}R_{YY}+\Delta _{3}R_{YX}+\Delta _{2}R_{XX}=0. \end{aligned}$$
(13)

From Eq. (13), we obtain the subsequent explicit solution for Eq. (1):

$$\begin{aligned} R(Y,T)=G_{3}\Bigg (\frac{-X{\sqrt{\Delta ^2_{3}-4\Delta _{5}\Delta _{2}}}-2Y\Delta _{2}+X\Delta _{3}}{2\Delta _{2}}\bigg )+G_{4}\Bigg (\frac{X{\sqrt{\Delta ^2_{3}-4\Delta _{5}\Delta _{2}}}+2Y\Delta _{2}-X\Delta _{3}}{2\Delta _{2}}\bigg ), \end{aligned}$$
(14)

by reintroducing Eq. (14) into Eq. (12), we arrive at the solution for Eq. (1):

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=G_{3}\Bigg (\frac{-\varpi {\sqrt{\Delta ^2_{3}-4\Delta _{5}\Delta _{2}}}-2\upsilon \Delta _{2}+\varpi \Delta _{3}}{2\Delta _{2}}\bigg )+G_{4}\Bigg (\frac{\varpi {\sqrt{\Delta ^2_{3}-4\Delta _{5}\Delta _{2}}}+2\upsilon \Delta _{2}-\varpi \Delta _{3}}{2\Delta _{2}}\bigg ). \end{aligned}$$

Case 3:  The Lagrange framework corresponding to the vector field \({\mathbb {Z}}_{1c}=<{\partial _{\upsilon }}>\) is shown as follows:

$$\begin{aligned} \frac{\textrm{d}\varpi }{0}=\frac{\textrm{d}\upsilon }{1}=\frac{\textrm{d}\iota }{0}=\frac{\textrm{d}H}{0}. \end{aligned}$$

Utilizing the provided data, we ascertain the structure of the similarity function and similarity variables:

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=R(X,T),~~~\text {where} ~~X=\varpi ,~~T=\iota , \end{aligned}$$
(15)

by substituting Eq. (15) into Eq. (1), we derive the reduced \((1 + 1)-\)dimensional nonlinear PDE expressed as:

$$\begin{aligned} R_{XXXT}+3R_{X}R_{XT}+3R_{T}R_{XX}+\Delta _{6}R_{TT}+\Delta _{4}R_{XT}+\Delta _{2}R_{XX}=0. \end{aligned}$$
(16)

From Eq. (16), we obtain the subsequent explicit solution for Eq. (1):

$$\begin{aligned} R(Y,T)=2p_{2}\textrm{Tan}h\bigg (\frac{p_{2}T(4p^{2}_{2}-\Delta _{4}+{\sqrt{16p^{4}_{2}+8p^{2}_{2}\Delta _{4}-4\Delta _{2}\Delta _{6}+\Delta ^{2}_{4}}})}{2\Delta _{6}}+Xp_{2}+p_{1}\bigg ). \end{aligned}$$
(17)

By reintroducing Eq. (17) into Eq. (15), we arrive at the solution for Eq. (1):

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=2p_{2}\textrm{Tan}h\bigg (\frac{c_{2}\iota (4p^{2}_{2}-\Delta _{4}+{\sqrt{16c^{4}_{2}+8p^{2}_{2}\Delta _{4}-4\Delta _{2}\Delta _{6}+\Delta ^{2}_{4}}})}{2\Delta _{6}}+\varpi {p_{2}}+p_{1}\bigg ). \end{aligned}$$

Case 4:  The Lagrange organized corresponding to the vector field \({\mathbb {Z}}_{1d}=<{\partial _{H}}>\) is shown as follows:

$$\begin{aligned} \frac{\textrm{d}\varpi }{0}=\frac{\textrm{d}\upsilon }{0}=\frac{\textrm{d}\iota }{0}=\frac{\textrm{d}H}{1}. \end{aligned}$$

We determine the similarity function and similarity variables in the following manner using the provided information:

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=R(X,Y),~~~\text {where} ~~X=\varpi ,~~Y=\upsilon , \end{aligned}$$
(18)

by substituting Eq. (18)  into Eq. (1), we derive the reduced \((1 + 1)\)-dimensional PDE shown as:

$$\begin{aligned} \Delta _{5}R_{YY}+\Delta _{3}R_{YX}+\Delta _{2}R_{XX}=0. \end{aligned}$$
(19)

From Eq. (19),we obtain the subsequent explicit solution for Eq. (1):

$$\begin{aligned} R(X,Y)=G_{5}\Bigg (\frac{-X{\sqrt{\Delta ^2_{3}-4\Delta _{5}\Delta _{2}}}-2Y\Delta _{2}+X\Delta _{3}}{2\Delta _{2}}\bigg )+G_{6}\Bigg (\frac{X{\sqrt{\Delta ^2_{3}-4\Delta _{5}\Delta _{2}}}+2Y\Delta _{2}-X\Delta _{3}}{2\Delta _{2}}\bigg ), \end{aligned}$$
(20)

by reintroducing Eq. (20) into Eq. (18), we arrive at the solution for Eq. (1):

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=G_{5}\Bigg (\frac{-\varpi {\sqrt{\Delta ^2_{3}-4\Delta _{5}\Delta _{2}}}-2\upsilon \Delta _{2}+\varpi \Delta _{3}}{2\Delta _{2}}\bigg )+G_{6}\Bigg (\frac{\varpi {\sqrt{\Delta ^2_{3}-4\Delta _{5}\Delta _{2}}}+2\upsilon \Delta _{2}-\varpi \Delta _{3}}{2\Delta _{2}}\bigg ). \end{aligned}$$

3.5 Reducing similarity utilizing binary class

Case 5: The Lagrange structure corresponding to the vector field \({\mathbb {Z}}_{2a}=<{\partial _{\varpi }}+c_{1}\partial _{\iota }>\) is shown as follows:

$$\begin{aligned} \frac{\textrm{d}\varpi }{1}=\frac{\textrm{d}\upsilon }{0}=\frac{\textrm{d}\iota }{c_{1}}=\frac{\textrm{d}H}{0}. \end{aligned}$$

We construct the similarity function and similarity variables in the following approach using our supplied information:

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=R(\eta ),~~~\eta =\iota -c_{1}\varpi . \end{aligned}$$
(21)

Upon substituting the similarity variables Eq. (21) into Eq. (1), we arrive at the subsequent ODE:

$$\begin{aligned} -c_{1}^3 R^{\prime \prime \prime }+3c_{1}^2 (R^{\prime })^2+( \Delta _6-c_{1}\Delta _4+c_{1}^2 \Delta _2)R^{\prime }=0. \end{aligned}$$
(22)

Case 6:  The Lagrange foundation corresponding to the vector field \({\mathbb {Z}}_{2b}=<{\partial _{\varpi }}+c_{2}\partial _{\upsilon }>\) is shown as follows:

$$\begin{aligned} \frac{\textrm{d}\varpi }{1}=\frac{\textrm{d}\upsilon }{c_2}=\frac{\textrm{d}\iota }{0}=\frac{\textrm{d}H}{0}. \end{aligned}$$

We estimate the similarity function and similarity variables in the following approach using our supplied information:

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=R(\eta ),~~~\eta =\upsilon -c_{2}\varpi , \end{aligned}$$
(23)

from Eq. (23), we obtain the subsequent explicit solution for Eq. (1):

$$\begin{aligned} R(\eta )=g_{1}+\eta {g_{2}}. \end{aligned}$$
(24)

Putting Eq. (24) into Eq. (23), we arrive at the solution for Eq. (1):

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=g_{1}+(\upsilon -c_{2}\varpi ){g_{2}}. \end{aligned}$$

3.6 Reducing similarity through ternary class

Case 7:  The Lagrange order corresponding to the vector field \({\mathbb {Z}}_{3a}=<{\partial _{\varpi }}+a\partial _{\iota }+b\partial _{\upsilon }>\) is shown as follows:

$$\begin{aligned} \frac{\textrm{d}\varpi }{1}=\frac{\textrm{d}\iota }{a}=\frac{\textrm{d}\upsilon }{b}=\frac{\textrm{d}H}{0}. \end{aligned}$$

We generate the similarity function and similarity variables in the following approach using the included information:

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=R(\eta ),~~~\eta =\varpi -a\iota -b\upsilon . \end{aligned}$$
(25)

The subsequent ODE is obtained by inserting similarity variables Eq. (25) into Eq. (1):

$$\begin{aligned} -aR^{\prime \prime \prime \prime }-6aR^{\prime }R^{\prime \prime }+(\Delta _{6}a^{2}+ab\Delta _{1}+b^{2}\Delta _{5}-a\Delta _{4}-b\Delta _{3}+\Delta _{2})R^{\prime \prime }=0. \end{aligned}$$
(26)

After integrating Eq. (26) and taking the constant of integration equal to zero, we can get:

$$\begin{aligned} aR^{\prime \prime \prime }+3a(R^{\prime })^{2}-(\Delta _{6}a^{2}+ab\Delta _{1}+b^{2}\Delta _{5}-a\Delta _{4}-b\Delta _{3}+\Delta _{2})R^{\prime }=0. \end{aligned}$$
(27)

3.7 Reducing similarity utilizing Combination of all classes

Case 8: The Lagrange structure corresponding to the vector field \({\mathbb {Z}}_{4}=<{\partial _{\varpi }}+d_{1}\partial _{\iota }+d_{2}\partial _{\upsilon }+d_{3}\partial _{H}>\) is shown as follows:

$$\begin{aligned} \frac{\textrm{d}\varpi }{1}=\frac{\textrm{d}\iota }{d_{1}}=\frac{\textrm{d}\upsilon }{d_{2}}=\frac{\textrm{d}H}{d_{3}}. \end{aligned}$$

We compute the similarity function and similarity variables in a specific manner using the shown information:

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=d_{3}\varpi -R(\eta ),~~~\eta =d_{2}\iota -d_{1}\upsilon , \end{aligned}$$
(28)

from Eq. (28), we obtain the subsequent explicit solution for Eq. (1):

$$\begin{aligned} R(\eta )=h_{1}+\eta {h_{2}}. \end{aligned}$$
(29)

By reintroducing Eq. (29) into Eq. (28), we arrive at the solution for Eq. (1):

$$\begin{aligned} H(\varpi ,\upsilon ,\iota )=d_{3}\varpi -h_{1}-(d_{2}\iota -d_{1}\upsilon ){h_{2}}. \end{aligned}$$
(30)

Remark

 In this section, we have determined the similarity function and similarity variables for \({\mathbb {Z}}_{1a}\), \({\mathbb {Z}}_{1b}\), \({\mathbb {Z}}_{1c}\), \({\mathbb {Z}}_{1d}\), \({\mathbb {Z}}_{2a}\), \({\mathbb {Z}}_{2b}\), \({\mathbb {Z}}_{3a}\), and \({\mathbb {Z}}_{4}\). Although the similarity function and variables for other cases are also computable, we have chosen to exclude them here for the sake of brevity.

3.7.1 Traveling wave solutions from Eq. (27)

In this section, we aim to determine the traveling wave structures of Eq. (1) using Eq. (27) through a novel extended direct algebraic method. By equating the linear term \(R^{\prime \prime \prime }\) in Eq. (27) and the nonlinear term \((R^{\prime })^2\) in Eq. (27), we arrive at a solution structured as follows:

$$\begin{aligned} R(\eta )=r_{0}+r_{1}g(\eta ). \end{aligned}$$
(31)

Suppose \(g(\eta )\) represents the solution of the subsequent equation:

$$\begin{aligned} g^{\prime }(\eta )=ln({\rho })(\Theta _{1}+\Theta _{2} g(\eta )+\Theta _{3} g^{2}(\eta )), \end{aligned}$$
(32)

by substituting Eqs. (31) and (32) into (27) and then equating the coefficients of powers of \(g({\eta })\), we deduce the subsequent system of algebraic equations:

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} (g(\eta ))^{0}:~&{}3{\Theta _{1}}{r_{1}}^2{ln(\rho )}^2{\Theta _{1}}^2-{r_{1}}{\Delta _{2}}{ln(\rho )}{\Theta _{1}}-{\Theta _{1}}{\Theta _{2}}{r_{1}}{\Delta _{1}}{ln(\rho )}{\Theta _{1}}+{\Theta _{1}}{r_{1}}{ln(\rho )}^3{\Theta _{2}}^2{\Theta _{1}}+2{\Theta _{1}}\\ &{}{r_{1}}{ln(\rho )}^3{\Theta _{3}}{\Theta _{1}}^2-{\Theta _{1}}^2{r_{1}}{\Delta _{6}}{ln(\rho )}{\Theta _{1}}-{\Theta _{2}}^2{r_{1}}{\Delta _{5}}{ln(\rho )}{\Theta _{1}}+{\Theta _{1}}{r_{1}}{\Delta _{4}}{ln(\rho )}{\Theta _{1}}+{\Theta _{2}}{r_{1}}\\ &{}{\Delta _{3}}{ln(\rho )}{\Theta _{1}} = 0,\\ (g(\eta ))^{1}:~&{}{\Theta _{1}}{r_{1}}{ln(\rho )}^3{\Theta _{2}}^3-{r_{1}}{\Delta _{2}}{ln(\rho )}{\Theta _{2}}+{\Theta _{1}}{r_{1}}{\Delta _{4}}{ln(\rho )}{\Theta _{2}}+{\Theta _{2}}{r_{1}}{\Delta _{3}}{ln(\rho )}{\Theta _{2}}-{\Theta _{1}}^2{r_{1}}{\Delta _{6}}\\ &{}{ln(\rho )}{\Theta _{2}}+6{\Theta _{1}}{r_{1}}^2{ln(\rho )}^2{\Theta _{1}}{\Theta _{2}}-{\Theta _{2}}^2{r_{1}}{\Delta _{5}}{ln(\rho )}{\Theta _{2}}+8{\Theta _{1}}{r_{1}}{ln(\rho )}^3{\Theta _{3}}{\Theta _{1}}{\Theta _{2}}-{\Theta _{1}}{\Theta _{2}}\\ &{}{r_{1}}{\Delta _{1}}{ln(\rho )}{\Theta _{2}} = 0,\\ (g(\eta ))^{2}:~&{}3{\Theta _{1}}{r_{1}}^2{ln(\rho )}^2{\Theta _{2}}^2-{r_{1}}{\Delta _{2}}{ln(\rho )}{\Theta _{3}}-{\Theta _{1}}^2{r_{1}}{\Delta _{6}}{ln(\rho )}{\Theta _{3}}+6{\Theta _{1}}{r_{1}}^2{ln(\rho )}^2{\Theta _{1}}{\Theta _{3}}-{\Theta _{2}}^2\\ &{}{r_{1}}{\Delta _{5}}{ln(\rho )}{\Theta _{3}}+{\Theta _{1}}{r_{1}}{\Delta _{4}}{ln(\rho )} {\Theta _{3}}+{\Theta _{2}}{r_{1}}{\Delta _{3}}{ln(\rho )}{\Theta _{3}}+8{\Theta _{1}}{r_{1}}{ln(\rho )}^3{\Theta _{3}}^2{\Theta _{1}}+7{\Theta _{1}}{r_{1}}\\ &{}{ln(\rho )}^3{\Theta _{3}}{\Theta _{2}}^2-{\Theta _{1}}{\Theta _{2}}{r_{1}}{\Delta _{1}}{ln(\rho )}{\Theta _{3}} = 0,\\ (g(\eta ))^{3}:~&{} 6{\Theta _{1}}{r_{1}}^2{ln(\rho )}^2{\Theta _{2}}{\Theta _{3}}+12{\Theta _{1}}{r_{1}}{ln(\rho )}^3{\Theta _{3}}^2{\Theta _{2}} = 0,\\ (g(\eta ))^{4}:~&{} 6{\Theta _{1}}{r_{1}}{ln(\rho )}^3{\Theta _{3}}^3+3{\Theta _{1}}{r_{1}}^2{ln(\rho )}^2{\Theta _{3}}^2 = 0. \end{aligned} \end{array} \right. \ \end{aligned}$$
(33)

After solving the described system with maple to find \(r_{0}\), \(r_{1}\), and a, we derive the subsequent sets of solutions:

$$\begin{aligned} r_{0}=\,\,& {} {r_{0}},~~ r_{1}={-2}\Theta _{3}\ln ({\rho }),~~~a=\frac{-{\mathfrak {B}}+{\sqrt{P}+\Delta _{4}}}{2\Delta _{6}}, \\ {\mathfrak {B}}=\,\,& {} 16{\Theta _{1}}^{2}\Theta _{{3}}^{2}{ln(\rho )}^{4}-8{\Theta _{1}}\Theta _{{2}}^{2}\Theta _{{3}}{ln(\rho )}^{4}+\Theta _{{2}}^{4}{ln(\rho )}^{4}+8{\Theta _{1}}\Theta _{{3}}{ln(\rho )}^{2}\Theta _{{2}}\Delta _{_{1}}-2\Theta _{{2}}^{2}{ln(\rho )}^{2}\Theta _{{2}}\Delta _{_{1}} \\{} & {} -8{\Theta _{1}}\Theta _{{3}}{ln(\rho )}^{2}\Delta _{_{4}}+2\Theta _{{2}}^{2} {ln(\rho )}^{2}\Delta _{_{4}}+\Theta _{{2}}^{2}\Delta _{_{1}}^{2}-4\Theta _{{2}}^{2}\Delta _{_{5}}\Delta _{_{6}}-2\Theta _{{2}}\Delta _{_{1}}\Delta _{_{4}}+4\Theta _{{2}}\Delta _{_{3}}\Delta _{_{6}}-4\Delta _{_{2}}\Delta _{_{6}}. \\ {P}=\,\,& {} 16{\Theta _{1}}^{2}\Theta _{{3}}^{2}{ln(\rho )}^{4}-8{\Theta _{1}}\Theta _{{2}}^{2}\Theta _{{3}}{ln(\rho )}^{4}+\Theta _{{2}}^{4}{ln(\rho )}^{4}+8{\Theta _{1}}\Theta _{{3}}{ln(\rho )}^{2}\Theta _{{2}}\Delta _{_{1}}-2\Theta _{{2}}^{2}{ln(\rho )}^{2}\Theta _{{2}}\Delta _{_{1}} \\{} & {} -8{\Theta _{1}}{\Theta _{{3}}}{ln(\rho )}^{2}\Delta _{_{4}}+2\Theta _{{2}}^{2}{ln(\rho )}^{2}\Delta _{_{4}}+\Theta _{{2}}^{2}\Delta _{_{1}}^{2}-4\Theta _{{2}}^{2}\Delta _{_{5}}\Delta _{_{6}}-2\Theta _{{2}}\Delta _{_{1}}\Delta _{_{4}}+4\Theta _{{2}}\Delta _{_{3}}\Delta _{_{6}}-4\Delta _{_{2}}\Delta _{_{6}}, \end{aligned}$$

where \(\rho \ne 0,1\), and \(\Theta _{1},\Theta _{2},\) \(\Theta _{3}\),and \(r_{0}\) are constants. By making the assumption \(\Pi =\Theta ^{2}_{2}- 4 {\Theta _{1}\Theta _{3}}\), the solutions of Eq. (32) can be shown as follows:

Family 1. When \(\Pi < 0\) and \(\Theta _{3} \ne 0\), then:

$$\begin{aligned} \begin{aligned} H_{1}(\varpi ,\upsilon ,\iota )&={r_{0}}{-{\textrm{ln}(\rho )}}\left[ -\Theta _{2}+\sqrt{-\Pi }\tan _{{\rho }}(\frac{\sqrt{-\Pi }}{2}{\eta })\right] ,\\ \\ H_{2}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}-\sqrt{-\Pi }\cot _{{\rho }}(\frac{\sqrt{-\Pi }}{2}{\eta })\right] ,\\ \\ H_{3}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}+\sqrt{-\Pi }(\tan _{{\rho }}(\sqrt{-\Pi }{\eta }) \pm \sqrt{rs}\sec _{{\rho }}(\sqrt{-\Pi }{\eta }))\right] ,\\ \\ H_{4}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}-\sqrt{-\Pi }(\cot _{{\rho }}(\sqrt{-\Pi }{\eta }) \pm \sqrt{rs}\csc _{{\rho }}(\sqrt{-\Pi }{\eta }))\right] ,\\ \\ H_{5}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}+\frac{\sqrt{-\Pi }}{2}\left( \tan _{{\rho }}\left( \frac{\sqrt{-\Pi }}{4}{\eta }\right) -\cot _{{\rho }}\left( \frac{\sqrt{-\Pi }}{4}{\eta }\right) \right) \right] . \end{aligned} \end{aligned}$$

Family 2. When \(\Pi > 0\) and \(\Theta _{3} \ne 0\), then:

$$\begin{aligned} \begin{aligned} H_{6}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}-\sqrt{\Pi }\tanh _{{\rho }}(\frac{\sqrt{\Pi }}{2}{\eta })\right] ,\\ \\ H_{7}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}-\sqrt{\Pi }\coth _{{\rho }}(\frac{\sqrt{\Pi }}{2}{\eta })\right] ,\\ \\ H_{8}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}-\sqrt{\Pi }(\tanh _{{\rho }}(\sqrt{\Pi }{\eta }) \pm \iota \sqrt{rs}~\textrm{sech} \,_{{\rho }}(\sqrt{\Pi }{\eta }))\right] ,\\ \\ H_{9}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}-\sqrt{\Pi }(\coth _{{\rho }}(\sqrt{\Pi }{\eta }) \pm \sqrt{rs}~\textrm{csch} \,_{{\rho }}(\sqrt{\Pi }{\eta }))\right] ,\\ \\ H_{10}(\varpi ,\upsilon ,\iota )&={r_{0}}-{\textrm{ln}(\rho )}\left[ -\Theta _{2}-\frac{\sqrt{\Pi }}{2}\left( \tanh _{{\rho }}\left( \frac{\sqrt{\Pi }}{4}{\eta }\right) +\coth _{{\rho }}\left( \frac{\sqrt{\Pi }}{4}{\eta }\right) \right) \right] . \end{aligned} \end{aligned}$$

Family 3. When \(\Theta _{3}\Theta _{1} > 0\) and \(\Theta _{2}=0\), then:

$$\begin{aligned} \begin{aligned} H_{11}(\varpi ,\upsilon ,\iota )&={r_{0}}-2\Theta _{3}\sqrt{\Theta _{3}\Theta _{1}} {\textrm{ln}(\rho )}\tan _{{\rho }}(\sqrt{\Theta _{3}\Theta _{1}}{\eta }),\\ \\ H_{12}(\varpi ,\upsilon ,\iota )&={r_{0}}+2\Theta _{3}\sqrt{\Theta _{3}\Theta _{1}} {\textrm{ln}(\rho )}\cot _{{\rho }}(\sqrt{\Theta _{3}\Theta _{1}}{\eta }),\\ \\ H_{13}(\varpi ,\upsilon ,\iota )&={r_{0}}-2\Theta _{3}\sqrt{\Theta _{3}\Theta _{1}}{{\textrm{ln}(\rho )}}[\tan _{{\rho }}(2\sqrt{\Theta _{3}\Theta _{1}}{\eta }) \pm \sqrt{rs}\sec _{{\rho }}(2\sqrt{\Theta _{3}\Theta _{1}}{\eta })],\\ \\ H_{14}(\varpi ,\upsilon ,\iota )&={r_{0}}+2\Theta _{3}\sqrt{\Theta _{3}\Theta _{1}}{\textrm{ln}(\rho )}[\cot _{{\rho }}(2\sqrt{\Theta _{3}\Theta _{1}}{\eta }) \pm \sqrt{rs}\csc _{{\rho }}(2\sqrt{\Theta _{3}\Theta _{1}}{\eta })],\\ \\ H_{15}(\varpi ,\upsilon ,\iota )&={r_{0}}-\Theta _{3}\sqrt{\Theta _{3}\Theta _{1}}{\textrm{ln}(\rho )}\left[ \tan _{{\rho }}\left( \frac{\sqrt{\Theta _{3}\Theta _{1}}}{2}{\eta }\right) -\cot _{{\rho }}\left( \frac{\sqrt{\Theta _{3}\Theta _{1}}}{2}{\eta }\right) \right] . \end{aligned} \end{aligned}$$

Family 4. When \(\Theta _{3}\Theta _{1} < 0\) and \(\Theta _{2}=0\), then:

$$\begin{aligned} \begin{aligned} H_{16}(\varpi ,\upsilon ,\iota )&={r_{0}}-\sqrt{-\Theta _{3}\Theta _{1}} {-{\Theta _{3}}\textrm{ln}(\rho )}\tanh _{{\rho }}(\sqrt{-\Theta _{3}\Theta _{1}}{\eta }),\\ \\ H_{17}(\varpi ,\upsilon ,\iota )&={r_{0}}-\sqrt{-\Theta _{3}\Theta _{1}} {-{\Theta _{3}}\textrm{ln}(\rho )}\coth _{{\rho }}(\sqrt{-\Theta _{3}\Theta _{1}}{\eta }),\\ \\ H_{18}(\varpi ,\upsilon ,\iota )&={r_{0}}-\sqrt{-\Theta _{3}\Theta _{1}}{-{\Theta _{3}}\textrm{ln}(\rho )}\left[ \tanh _{{\rho }}(2\sqrt{-\Theta _{3}\Theta _{1}}{\eta }) \pm \iota \sqrt{rs}~\textrm{sech} \,_{{\rho }}(2\sqrt{-\Theta _{3}\Theta _{1}}{\eta })\right] ,\\ \\ H_{19}(\varpi ,\upsilon ,\iota )&={r_{0}}-\sqrt{-\Theta _{3}\Theta _{1}}{-{\Theta _{3}}\textrm{ln}(\rho )}\left[ \coth _{{\rho }}(2\sqrt{-\Theta _{3}\Theta _{1}}{\eta }) \pm \sqrt{rs}~\textrm{csch} \,_{{\rho }}(2\sqrt{-\Theta _{3}\Theta _{1}}{\eta })\right] ,\\ \\ H_{20}(\varpi ,\upsilon ,\iota )&={r_{0}}-\frac{1}{2\Theta _{3}}\sqrt{-\Theta _{3}\Theta _{1}}{-{\Theta _{3}}\textrm{ln}(\rho )}\left[ \tanh _{{\rho }}\left( \frac{\sqrt{-\Theta _{3}\Theta _{1}}}{2}{\eta }\right) +\coth _{{\rho }}\left( \frac{\sqrt{-\Theta _{3}\Theta _{1}}}{2}{\eta }\right) \right] . \end{aligned} \end{aligned}$$

Family 5. When \(\Theta _{2}=0\) and \(\Theta _{3}=\Theta _{1}\), then:

$$\begin{aligned} \begin{aligned} H_{21}(\varpi ,\upsilon ,\iota )&={r_{0}} -2{{\Theta _{1}}\textrm{ln}(\rho )}\tan _{{\rho }}(\Theta _{1}{\eta }),\\ \\ H_{22}(\varpi ,\upsilon ,\iota )&={r_{0}}+2{\Theta _{1}}{\textrm{ln}(\rho )}\cot _{{\rho }}(\Theta _{1}{\eta }),\\ \\ H_{23}(\varpi ,\upsilon ,\iota )&={r_{0}}{-2{\Theta _{1}}\textrm{ln}(\rho )}[\tan _{{\rho }}(2\Theta _{1}{\eta }) \pm \sqrt{rs}\sec _{{\rho }}(2\Theta _{1}{\eta })],\\ \\ H_{24}(\varpi ,\upsilon ,\iota )&={r_{0}} {H+2{\Theta _{1}}\textrm{ln}(\rho )}[\cot _{{\rho }}(2\Theta _{1}{\eta }) \pm \sqrt{rs}\csc _{{\rho }}(2\Theta _{1}{\eta })],\\ \\ H_{25}(\varpi ,\upsilon ,\iota )&={r_{0}} {-{\Theta _{1}}\textrm{ln}(\rho )}\left[ \tan _{{\rho }}\left( \frac{\Theta _{1}}{2}{\eta }\right) -\cot _{{\rho }}\left( \frac{\Theta _{1}}{2}{\eta }\right) \right] . \end{aligned} \end{aligned}$$

Family 6. When \(\Theta _{2}=0\) and \(\Theta _{3}=-\Theta _{1}\), then:

$$\begin{aligned} \begin{aligned} H_{26}(\varpi ,\upsilon ,\iota )&={r_{0}}{-2{\Theta _{1}}\textrm{ln}(\rho )}\tanh _{{\rho }}(\Theta _{1}{\eta }),\\ \\ H_{27}(\varpi ,\upsilon ,\iota )&={r_{0}} {-2{\Theta _{1}}\textrm{ln}(\rho )}\coth _{{\rho }}(\Theta _{1}{\eta }),\\ \\ H_{28}(\varpi ,\upsilon ,\iota )&={r_{0}} {-2{\Theta _{1}}\textrm{ln}(\rho )}[\tanh _{{\rho }}(2\Theta _{1}{\eta }) \pm \iota \sqrt{rs}~\textrm{sech} \,_{{\rho }}(2\Theta _{1}{\eta })],\\ \\ H_{29}(\varpi ,\upsilon ,\iota )&={r_{0}} {-2{\Theta _{1}}\textrm{ln}(\rho )}[\coth _{{\rho }}(2\Theta _{1}{\eta }) \pm \sqrt{rs}~\textrm{csch} \,_{{\rho }}(2\Theta _{1}{\eta })],\\ \\ H_{30}(\varpi ,\upsilon ,\iota )&={r_{0}}-\Theta _{1} {\textrm{ln}(\rho )}\left[ \tanh _{{\rho }}\left( \frac{\Theta _{1}}{2}{\eta }\right) +\coth _{{\rho }}\left( \frac{\Theta _{1}}{2}{\eta }\right) \right] . \end{aligned} \end{aligned}$$

Family 7. When \(\Theta _{2}^{2}=4\Theta _{3}\Theta _{1}\), then:

$$\begin{aligned} \begin{aligned} H_{31}(\varpi ,\upsilon ,\iota )={r_{0}}-\frac{2\Theta _{3}\Theta _{1} d(\sqrt{4\Theta _{3}\Theta _{1}}{\eta }\ln ({\rho })+2)}{4\Theta _{3}\Theta _{1}{\eta }}. \end{aligned} \end{aligned}$$

Family 8. When \(\Theta _{2}=\lambda\), \(\Theta _{1}=m\lambda ~(m\ne 0)\) and \(\Theta _{3}=0\), then:

$$\begin{aligned} \begin{aligned} H_{32}(\varpi ,\upsilon ,\iota )={r_{0}}. \end{aligned} \end{aligned}$$

we get the trivial solution.

Family 9. When \(\Theta _{2}=\Theta _{3}=0\), then:

$$\begin{aligned} \begin{aligned} H_{33}(\varpi ,\upsilon ,\iota )={r_{0}}. \end{aligned} \end{aligned}$$

we get a trivial solution.

Family 10. When \(\Theta _{2}=\Theta _{1}=0\), then:

$$\begin{aligned} \begin{aligned} H_{34}(\varpi ,\upsilon ,\iota )={r_{0}}-\frac{d}{{\eta }}. \end{aligned} \end{aligned}$$

Family 11. When \(\Theta _{1}=0\) and \(\Theta _{2}\ne 0\), then:

$$\begin{aligned} \begin{aligned} H_{35}(\varpi ,\upsilon ,\iota )&={r_{0}}+\frac{2u {{\Theta _{3}}ln(\rho )}}{[\cosh _{{\rho }}(\Theta _{2}{\eta })-\sinh _{{\rho }}(\Theta _{2}{\eta })+r]}.\\ H_{36}(\varpi ,\upsilon ,\iota )&={r_{0}}+\frac{{2{\Theta _{3}}ln(\rho )}[\cosh _{{\rho }}(\Theta _{2}{\eta })+\sinh _{{\rho }}(\Theta _{2}{\eta })]}{[\cosh _{{\rho }}(\Theta _{2}{\eta })+\sinh _{{\rho }}(\Theta _{2}{\eta })+s]}. \end{aligned} \end{aligned}$$

Family 12. When \(\Theta _{2}=\lambda\), \(\Theta _{3}=m\lambda ~(m\ne 0)\) and \(\Theta _{1}=0\), then:

$$\begin{aligned} \begin{aligned} H_{37}(\varpi ,\upsilon ,\iota )={r_{0}} {-{\Theta _{3}}ln(\rho )}\frac{r{\rho }^{\lambda {\eta }}}{s-mr{\rho }^{\lambda {\eta }}}. \end{aligned} \end{aligned}$$

In this context, we introduce the hyperbolic and trigonometric functions as follows:

$$\begin{aligned} \begin{aligned} \sinh _{{\rho }}({\eta })&=\frac{u{\rho }^{{\eta }}-s{\rho }^{-{\eta }}}{2},~~~\cosh _{{\rho }}({\eta })=\frac{u{\rho }^{{\eta }}+s{\rho }^{-{\eta }}}{2},~~~\tanh _{{\rho }}({\eta })=\frac{u{\rho }^{{\eta }}-s{\rho }^{-{\eta }}}{u{\rho }^{{\eta }}+s{\rho }^{-{\eta }}},~~~\coth _{{\rho }}({\eta })=\frac{u{\rho }^{{\eta }}+s{\rho }^{-{\eta }}}{u{\rho }^{{\eta }}-s{\rho }^{-{\eta }}},\\ \\ \textrm{csch} \,_{{\rho }}({\eta })&=\frac{2}{u{\rho }^{{\eta }}-s{\rho }^{-{\eta }}},~~~\textrm{sech} \,_{{\rho }}({\eta })=\frac{2}{u{\rho }^{{\eta }}+s{\rho }^{-{\eta }}},~~~\sin _{{\rho }}({\eta })=\frac{u{\rho }^{\iota {\eta }}-s{\rho }^{-\iota {\eta }}}{2\iota },~~~\cos _{{\rho }}({\eta })=\frac{u{\rho }^{\iota {\eta }}+s{\rho }^{-\iota {\eta }}}{2},\\ \\ \tan _{{\rho }}({\eta })&=-\iota \frac{u{\rho }^{\iota {\eta }}-s{\rho }^{-\iota {\eta }}}{u{\rho }^{\iota {\eta }}+s{\rho }^{-\iota {\eta }}},~~~\cot _{{\rho }}({\eta })=\iota \frac{u{\rho }^{\iota {\eta }}+s{\rho }^{-\iota {\eta }}}{u{\rho }^{\iota {\eta }}-s{\rho }^{-\iota {\eta }}},~~~\csc _{{\rho }}({\eta })=\frac{2\iota }{u{\rho }^{\iota {\eta }}-s{\rho }^{-\iota {\eta }}},~~~\textrm{sech} \,_{{\rho }}({\eta })=\frac{2}{u{\rho }^{\iota {\eta }}+s{\rho }^{-\iota {\eta }}}, \end{aligned} \end{aligned}$$

The constants u and s, which are also referred to as the deformation parameters.

3.8 Graphical behavior

In this section, we utilize graphical representations to gain insights into some of the solutions. We illustrate the 2D and 3D graphical behavior of traveling wave solutions by varying the involved parameters.

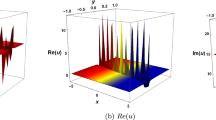
  • Fig. 1a depicts the three-dimensional graphical behavior of \(H_{1}(\varpi ,\upsilon ,\iota )\) for the parameter values \(r_{0}=-1, \Theta _{2}=2, b=1, \rho =e, a=1,\) and \(c=1\), describing an anti-kink type solution.

  • Fig. 1b exhibits the two-dimensional graphical behavior of \(H_{1}(\varpi ,\upsilon ,\iota )\) across different values of \(\varpi\) (specifically \(\varpi = -3,-1,0,2,5\)), within a finite domain of \(-10 \le t \le 10\).

  • Fig. 2a presents the three-dimensional graphical behavior of \(H_{8}(\varpi ,\upsilon ,\iota )\) for the parameter values \(r_{0}=-4,\Theta _{2}=5, b=5, r=1, s=1,\rho =e, a=1,\) and \(c=2\).

  • Fig. 2b displays the two-dimensional graphical behavior of \(H_{8}(\varpi ,\upsilon ,\iota )\) for varying \(\varpi\) (specifically \(\varpi = -3,-1,0,2,5\)), within a finite domain of \(-10 \le t \le 10\).

  • Fig. 3a demonstrates the three-dimensional graphical behavior of \(H_{10}(\varpi ,\upsilon ,\iota )\) for the parameter values \(r_{0}=-5,\Theta _{2}=6, b=2, \rho =e, a=1,\) and \(c=1\), portraying a dark–bright singular type solution.

  • Fig. 3b illustrates the two-dimensional graphical behavior of \(H_{10}(\varpi ,\upsilon ,\iota )\) for varying \(\varpi\) (specifically \(\varpi = -3,-1,5\)), within a finite domain of \(-30 \le t \le 30\).

  • Fig. 4a showcases the three-dimensional graphical behavior of \(H_{16}(\varpi ,\upsilon ,\iota )\) for the parameter values \(r_{0}=2,\Theta _{1}=-1,\Theta _{3}=1, \rho =e\). \(H_{16}(\varpi ,\upsilon ,\iota )\) describing kink type solution.

  • Fig. 4b displays the two-dimensional graphical behavior of \(H_{16}(\varpi ,\upsilon ,\iota )\) for varying \(\varpi\) (specifically \(\varpi = -10,-5,0,2,8\)) within a finite domain of \(-20 \le t \le 20\).

Fig. 1
figure 1

Graphical representation of \(H_{1}(\varpi ,\upsilon ,\iota )\) for \(r_{0}=-1,~ \Theta _{2}=2,~b=1,~\rho =e, a=1,\) and c=1

Full size image
Fig. 2
figure 2

Graphical depiction of \(H_{8}(\varpi ,\upsilon ,\iota )\) for \(r_{0}=-4,~\Theta _{2}=5, b=5,~r=1,~s=1,~\rho =e,~a=1,\) and \(c=2\)

Full size image
Fig. 3
figure 3

Graphical portrayal of \(H_{10}(\varpi ,\upsilon ,\iota )\) is shown for \(r_{0}=-5,~\Theta _{2}=6,~b=2,~\rho =e,~a=1,\) and \(c=1\)

Full size image
Fig. 4
figure 4

Graphical description of \(H_{16}(\varpi ,\upsilon ,\iota )\) for \(r_{0}=2,\Theta _{1}=-1,\Theta _{3}=1,\) and \(\rho =e.\) \(H_{16}(\varpi ,\upsilon ,\iota )\) shows the kink shape

Full size image

4 Conservation laws

4.1 Non-local conservation laws

We will elucidate the classification of Eq. (1) using the concept of nonlinear self-adjointness, a fundamental aspect of our analysis. The formal Lagrangian \({\mathcal {S}}\) [34], serves as a cornerstone in this classification process:

$$\begin{aligned} S=\Upsilon (\varpi ,\upsilon ,\iota )( H_{\varpi \varpi \varpi \iota }+3H_{\varpi }H_{\varpi \iota }+3H_{\iota }H_{\varpi \varpi } +{\Delta _{6}}H_{\iota \iota }+{\Delta _{1}}H_{\upsilon \iota }+{\Delta _{5}}H_{\upsilon \upsilon }+{\Delta _{4}}H_{\varpi \iota }+{\Delta _{3}}H_{\varpi \upsilon }+{\Delta _{2}}H_{\varpi \varpi }). \end{aligned}$$
(34)

The action integral can be shown as:

$$\begin{aligned} \int _{0}^{\mu }\int _{\mu _{1}}\int _{\mu _{2}}{\mathcal {S}}(\varpi ,\upsilon ,\iota ,H_{\varpi },H_{\upsilon },H_{\iota },H_{\varpi \varpi },H_{\upsilon \upsilon },H_{\iota \iota },H_{\varpi \iota },H_{\upsilon \iota },H_{\varpi \upsilon },H_{\varpi \varpi \varpi \iota })d\varpi d\upsilon d\iota . \end{aligned}$$

Now, we apply the Euler-Lagrange operator to Eq. (34). We obtain:

$$\begin{aligned} \begin{aligned}&A_{\varpi }^{3}A_{\iota }[\Upsilon ]-3A_{\varpi }[{\Upsilon }H_{\varpi \iota }]-3A\varpi A_{\iota }[\Upsilon H_{\varpi }]+3A_{\iota }[cH_{\varpi \varpi }]+3A^2_{\varpi }[{\Upsilon }H_{\iota }]+\Delta _6 A^{2}{\iota }[\Upsilon ]\\&\quad +\Delta _1A_{\upsilon }A_{\iota }[\Upsilon ]+\Delta _{5}A^2_{\upsilon }+\Delta _4A_{\upsilon }A_{\iota }[\Upsilon ]+\Delta _{3} A_{\varpi }A_{\upsilon }[\Upsilon ]+\Delta _{2}A^2_{\varpi }[\Upsilon ]=0. \end{aligned} \end{aligned}$$
(35)

The total derivative  \(A_\varpi\), \(A_{\upsilon }\) and \(A_\iota\) can be defined as:

$$\begin{aligned} A_{\varpi }=\,\,& {} {\partial _{\varpi }+{H^\gamma _\varpi }{\partial _{H^\gamma }}}+H^\gamma _{\varpi {l}}{\partial _{H^\gamma _{l}}}+H^\gamma _{\varpi {lm}}{\partial _{H^\gamma _{lm}}}+..., \\ A_{\iota }=\,\,& {} {\partial _{\iota }+{H^\gamma _\iota }{\partial _{H^\gamma }}}+H^\gamma _{\iota {l}}{\partial _{H^\gamma _{l}}}+H^\gamma _{\iota {lm}} {\partial _{H^\gamma _{lm}}}+..., \\ A_{\upsilon }=\,\,& {} {\partial _{\upsilon }+{H^\gamma _\upsilon }{\partial _{H^\gamma }}}+H^\gamma _{\upsilon {l}}{\partial _{H^\gamma _{l}}}+H^\gamma _{\upsilon lm} {\partial _{ H^\gamma _{lm}}}+..., \end{aligned}$$

with \(\Upsilon =\Upsilon (\varpi ,\upsilon ,\iota )\) and \(H=H(\varpi ,\upsilon ,\iota )\), we proceed to calculate \(A_\varpi\), \(A_{\upsilon }\) and \(A_\iota\) in Eq. (35), yielding:

$$\begin{aligned} \Delta _{1}{\Upsilon }_{\iota \upsilon }+\Delta _{2}{\Upsilon }_{\varpi \varpi }+\Delta _{3}{\Upsilon }_{\varpi \upsilon }+\Delta _{4}{\Upsilon }_{\iota \varpi }+\Delta _{5}{\Upsilon }_{\upsilon \upsilon }+\Delta _{6}{\Upsilon }_{\iota \iota }+3{\Upsilon }_{\varpi \varpi }H_{\iota }+3{\Upsilon }_{\iota \varpi }H_{\varpi }+6H_{\iota \varpi }{\Upsilon }_{\varpi }+{\Upsilon }_{\varpi \varpi \varpi \iota }=0. \end{aligned}$$

Through utilizing the given definitions (1–4) and carrying out the standard computations, we can propose the subsequent theorem:

Theorem 1

Equqtion (1) is neither nonlinear self-adjoint, nor quasi self-adjoint, nor weakly self-adjoint. However, Eq. (1) is strictly self-adjoint for \(v=\Upsilon (\varpi ,\upsilon ,\iota ,H)\)where \(\Upsilon\) can be shown as:

$$\begin{aligned} \Upsilon (\varpi ,\upsilon ,\iota ,H)=f(\iota +\upsilon ,H)+g(\iota -\upsilon ,H). \end{aligned}$$

The functions \(f(\iota +\upsilon , H)\) and \(g(\iota -\upsilon , H)\) are unrestricted and can be chosen arbitrarily.

Theorem 2

Considering the form of infinitesimal symmetry:

$$\begin{aligned} M=\epsilon ^{k}(\varpi ,H,H_1,H_2,...)\partial _{\varpi ^k}+\vartheta (\varpi ,H,H_1,H_2,...) {\partial _ H}, \end{aligned}$$

with formal Lagrangian S, conserved vectors for Eq. (2) are:

$$\begin{aligned} \begin{aligned} \nu ^{k}&=\epsilon ^{k}{\mathcal {S}}+B^{\gamma }_{k}[({\partial _{ H^{\gamma }_{k}}}{\mathcal {S}})-A_{l}({\partial _{ H^{\gamma }_{kl}}}{\mathcal {S}})+A_{l}A_{m}({\partial _{ H^{\gamma }_{klm}}}{\mathcal {S}})-...]+A_{l}(B^{\gamma }_k)[({\partial _{ H^{\gamma }_{kl}}}{\mathcal {S}})\\&\qquad -A_{m}({\partial _{ H^{\gamma }_{klm}}}{\mathcal {S}})+...]+A_{l}A_{m}(B^{\gamma }_k)[({\partial _{ H^{\gamma }_{klm}}}{\mathcal {S}})-...], \end{aligned} \end{aligned}$$

where B is known as a Lie characteristic function that can be calculated as:

$$\begin{aligned} B^{\gamma } =\psi ^{\gamma }-\epsilon ^{l} H^\gamma _{l}. \end{aligned}$$

Theorem 3

The conserved vectors for Eq. (1) must satisfy the subsequent expression:

$$\begin{aligned}{}[A_{\varpi }(\nu ^{\varpi })+A_{\upsilon }(\nu ^{\upsilon })+A_{\iota }(\nu ^{\iota })]_{Eq.~(\text {1})} =0, \end{aligned}$$

where \(\nu ^{\varpi }\), \(\nu ^{\upsilon }\), \(\nu ^{\iota }\), \(\varpi\), \(\upsilon\), \(\iota\), \(H(\varpi ,\upsilon ,\iota )\) are conserved vectors, independent variables, and dependent variable, respectively.

$$\begin{aligned} {\bar{M}}+A_{\varpi }(\epsilon ^{1})K+A_{\upsilon }(\epsilon ^{2})K+A_{\iota }(\epsilon ^{3})K=B\frac{\delta }{\delta H}+ A_{\varpi }(\nu ^{\varpi })+A_{\upsilon }(\nu ^{\upsilon })+A_{\iota }(\nu ^{\iota }), \end{aligned}$$

where K, \(\frac{\delta }{\delta H}\), \(\nu ^{\varpi }\), \(\nu ^{\upsilon }\), \(\nu ^{\iota }\) are identity operator, variational derivative and conserved vectors, respectively. \({\bar{M}}\) is described as:

$$\begin{aligned} \begin{aligned} {\bar{M}}&=\epsilon ^{1}{\partial _\varpi }+\epsilon ^{2}{\partial _{\upsilon }}+\epsilon ^{3}{\partial \iota }+\vartheta {\partial _{H}}+\vartheta ^{\varpi }{\partial _{H_{\varpi }}}+\vartheta ^{\upsilon }{\partial _{H_{\upsilon }}}+\vartheta ^{\iota }{\partial _{H_{\iota }}}+\vartheta ^{\varpi \varpi }{\partial _{H_{\varpi \varpi }}}\\&\qquad +\vartheta ^{\upsilon \upsilon }{\partial _{H_{\upsilon \upsilon }}}+\vartheta ^{\iota \iota }{\partial _{ H_{\iota \iota }}} +\vartheta ^{\varpi \upsilon }{\partial _{ H_{\varpi \upsilon }}}+\vartheta ^{\varpi \iota }{\partial _{H_{\varpi \iota }}}+\vartheta ^{\upsilon \iota }{\partial _ {H_{\upsilon \iota }}}+\vartheta ^{\varpi \varpi \varpi \iota }{\partial _{ H_{\varpi \varpi \varpi \iota }}}~, \end{aligned} \end{aligned}$$

and Lie characteristic function are represented by B, which has a particular expression to describe it:

$$\begin{aligned} B=\vartheta -\epsilon ^{1}H^{\varpi }_1-\epsilon ^{2}H^{\upsilon }_{2}-\epsilon ^{3}H^{\iota }_{3}. \end{aligned}$$

The expression as follows can be used to produce the conserved vectors \(\nu ^{k}\):

$$\begin{aligned} \begin{aligned} \nu ^{k}&=\epsilon ^{k}{\mathcal {S}}+B^{\gamma }_{k}[({\partial _{ H^{\gamma }_{k}}}{\mathcal {S}})-A_{l}({\partial _{ H^{\gamma }_{kl}}}{\mathcal {S}})+A_{l}A_{m}({\partial _{ H^{\gamma }_{klm}}}{\mathcal {S}})-.....]+A_{l}(B^{\gamma }_k)[({\partial _{ H^{\gamma }_{kl}}}{\mathcal {S}})\\&\qquad -A_{m}({\partial _{ H^{\gamma }_{klm}}}{\mathcal {S}})+....]+A_{l}A_{m}(B^{\gamma }_k)[({\partial _{ H^{\gamma }_{klm}}}{\mathcal {S}})-....], ~ \end{aligned} \end{aligned}$$
(36)

where \(\epsilon ^{\varpi }=\epsilon ^{1},~\epsilon ^{\upsilon }=\epsilon ^2,~\epsilon ^{\iota }=\epsilon ^{3}~and~\gamma =1,2,3,...6~.\) The subsequent form of the corresponding characteristic functions for operators \(M_{i} (i=1,2,3,..,6)\):

$$\begin{aligned} \begin{aligned} B^\gamma _{1}&=-H_{\varpi },~~~B^\gamma _{2}=-H_{\upsilon },~~~B^\gamma _{3}=-H_{\iota },~~~B^\gamma _{4}=1,~~~B^\gamma _{5}=-\upsilon ,\\ B^\gamma _{6}&=(-4\iota \Delta _2\Delta _5+\iota \Delta ^2_{3}+\varpi \Delta _1\Delta _3-2\varpi \Delta _4\Delta _5-3H\Delta _5)-\left( \frac{H_{3}\varpi \Delta _5+3\upsilon \Delta _3\varpi }{\Delta _1\Delta _3-2\Delta _4\Delta _5}\right) -\left( \frac{9H_{\upsilon }\Delta _5\upsilon }{\Delta _1\Delta _3-2\Delta _4\Delta _5}\right) \\&\qquad -\left( \frac{9H_{\iota }\Delta _5\iota }{\Delta _1\Delta _3-2\Delta _4\Delta _5}\right) . \end{aligned} \end{aligned}$$
(37)

Substitute Eqs. (34) and (37) into Eq. (36). We acquired:

$$\begin{aligned} \begin{aligned} \nu ^{\varpi }&=\epsilon ^{\varpi }{\mathcal {S}}+(B^\gamma _{i})\bigg [({\partial _{H_{\varpi }}}{{\mathcal {S}}}) -A_{\varpi }({\partial _{H_{\varpi \varpi }}}{{\mathcal {S}}})- A_{\upsilon }({\partial _{H_{\varpi \upsilon }}}{{\mathcal {S}}})-A_{\iota }({\partial _{H_{\varpi \iota }}}{{\mathcal {S}}}) -A_{\varpi }A_{\varpi }A_{\iota }({\partial _{H_{\varpi \varpi \varpi \iota }}}{{\mathcal {S}}})\\&\qquad -A_{\varpi }A_{\iota }A_{\varpi }({\partial _{H_{\varpi \varpi \iota \varpi }}}{\mathcal {S}})-A_{\iota }A_{\varpi }A_{\varpi }({\partial _{H_{\varpi \iota \varpi \varpi }}}{\mathcal {S}})\bigg ]+A_{\varpi }(B^\gamma _{i})\bigg [({\partial _{H_{\varpi \varpi }}}{\mathcal {S}})+A_{\varpi }A_{\iota }({\partial _{H_{\varpi \varpi \varpi \iota }}}{\mathcal {S}})\\&\qquad +A_{\iota } A_{\varpi }({\partial _{H_{\varpi \varpi \iota \varpi }}}{{\mathcal {S}}})\bigg ] +A_{\upsilon }(B^\gamma _{i})\bigg [({\partial _{H_{\varpi \upsilon }}}{{\mathcal {S}}})\bigg ] +A_{\iota }(B^\gamma _{i})\bigg [({\partial _{H_{\varpi \iota }}}{{\mathcal {S}}})+A_{\varpi } A_{\varpi }({\partial _{H_{\varpi \iota \varpi \varpi }}}{{\mathcal {S}}})\bigg ]-A_{\varpi }A_{\varpi }(B_{i})\bigg [A_{\iota }({\partial _{H_{\varpi \varpi \varpi \iota }}}{\mathcal {S}})\bigg ]\\&\qquad -A_{\varpi }A_{\iota }(B^\gamma _{i})\bigg [A_{\varpi }({\partial _{H_{\varpi \varpi \iota \varpi }}}{\mathcal {S}})\bigg ] -A_{\iota }A_{\varpi }(B_{i})\bigg [A_{\varpi }({\partial _{H_{\varpi \iota \varpi \varpi }}}{\mathcal {S}})\bigg ] +A_{\varpi }A_{\varpi }A_{\iota }(B^\gamma _{i}) \bigg [({\partial _{H_{\varpi \varpi \varpi \iota }}}{\mathcal {S}})\bigg ]\\&\qquad +A_{\varpi }A_{\iota }A_{\varpi }(B^\gamma _{i})\bigg [({\partial _{H_{\varpi \varpi \iota \varpi }}}{\mathcal {S}})\bigg ]+A_{\iota }A_{\varpi }A_{\varpi }(B^\gamma _{i})\bigg [({\partial _{H_{\varpi \iota \varpi \varpi }}}{\mathcal {S}})\bigg ],\\ \nu ^{\upsilon }&=\epsilon ^{\upsilon }({\mathcal {S}})+(B^\gamma _{i})\bigg [-A_{\varpi }({\partial _{ H_{\upsilon \varpi }}}{\mathcal {S}})-A_{\upsilon } ({\partial _{H_{\upsilon \upsilon }}{\mathcal {S}}})-A_{\iota }({\partial _{H_{\upsilon \iota }}}{\mathcal {S}})\bigg ] +A_{\varpi }(B^\gamma _{i}) \bigg [({\partial _{H_{\upsilon \varpi }}}{\mathcal {S}})\bigg ]\\&\qquad +A_{\upsilon }(B^\gamma _{i}) \bigg [({\partial _{H_{\upsilon \upsilon }}}{\mathcal {S}})\bigg ]+A_{\iota }(B^\gamma _{i})\bigg [({\partial _{H_{\upsilon \iota }}}{\mathcal {S}})\bigg ],\\ \nu ^{\iota }&=\epsilon ^{\iota }{\mathcal {S}}+(B^\gamma _{i})\bigg [({\partial _{ H_{\iota }}{\mathcal {S}}})-A_{\varpi }({\partial _ {H_{\iota \varpi } }}{\mathcal {S}})- A_{\upsilon }({\partial _{H_{\iota \upsilon }}}{\mathcal {S}})-A_{\iota } ({\partial _{H_{\iota \iota }}}{\mathcal {S}})-A^{3}_{\varpi } ({\partial _ {H_{\iota \varpi \varpi \varpi }}}{\mathcal {S}})\bigg ]\\&\qquad +A_{\varpi }(B^\gamma _{i}) \bigg [({\partial _{H_{\iota \varpi }}}{\mathcal {S}})+A^{2}_{\varpi }({\partial _{H_{\iota \varpi \varpi \varpi }}}{\mathcal {S}})\bigg ]+A_{\upsilon }(W_{i})\Bigg [({\partial _{H_{\iota \upsilon }}}{\mathcal {S}})\Bigg ] +A_{\iota }(B^\gamma _{i})\Bigg [({\partial _{H_{\iota \iota }}}{\mathcal {S}})\Bigg ] -A^{2}_{\varpi }(B^\gamma _{i})\Bigg [A_{\varpi }({\partial _{H_{\iota \varpi \varpi \varpi }}}{\mathcal {S}})\Bigg ]\\&\qquad +A^{3}_{\varpi }(B^\gamma _{i})\Bigg [({\partial _{ H_{\iota \varpi \varpi \varpi }}}{\mathcal {S}})\Bigg ], \end{aligned} \end{aligned}$$

where  \(i=1,2,3,4,5,6.\)

Family 1: For \(M_{1}\), we have \(B^\gamma _{1} =-H_{\varpi }\) and \(\epsilon ^{\varpi }= 1\),we get:

$$\begin{aligned} \begin{aligned} \nu ^{\iota }&=\Delta _{3}H_{\varpi \varpi }\Upsilon _{\iota }+H_{\varpi \iota }\Upsilon _{\upsilon } -H_{\varpi }\Upsilon _{\upsilon \iota }+H_{\varpi \varpi \iota }\Upsilon _{\iota }~, \\ \nu ^{\varpi }&={\mathcal {S}}-H_{\varpi }[-\Delta _{4}H_{\varpi \varpi \upsilon }{\Upsilon }+\Upsilon _{\upsilon \iota }+\Delta _{1}\Upsilon _{\varpi \varpi \varpi \upsilon }-4\Upsilon _{\upsilon }+\Delta _{4}H_{\varpi }\Upsilon _{\varpi \upsilon } +4\Upsilon _{\varpi \varpi }H_{\upsilon }]+H_{\varpi \iota }\Upsilon _{\upsilon }\\&\qquad -H_{\varpi \varpi }[\Delta _{2}\Upsilon _{\varpi \upsilon }-\Upsilon _{\iota }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi } -\Delta _{1}{\Upsilon }H_{\varpi \upsilon }-4\Upsilon _{\upsilon }H_{\upsilon }]-H_{\varpi \upsilon }[\Delta _{1}{\Upsilon }H_{\varpi \varpi }]-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }~, \\ \nu ^{\upsilon }&=-H_{\varpi }[4H_{\varpi \varpi \varpi }\psi -\Delta _{1}\Upsilon _{\upsilon }H_{\varpi \varpi }-\Delta _{1}{\Upsilon }H_{\varpi \varpi \upsilon }+\Upsilon _{\varpi \varpi \varpi \upsilon }+ \Delta _{4}H_{\varpi \varpi }\Upsilon _{\upsilon } +\Delta _{4}H_{\varpi }H_{\varpi \upsilon }\\&\qquad +\Delta _{4}H_{\varpi \upsilon }\Upsilon _{\upsilon }+{\Upsilon }H_{\varpi \varpi \upsilon } -\Upsilon _{\upsilon \upsilon }]\Delta _{1}-H_{\varpi \varpi }[-\Upsilon _{\varpi \varpi \upsilon } -\Delta _{4}{\Upsilon }H_{\varpi \upsilon }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }+\Upsilon _{\upsilon }]\\&\qquad -H_{\varpi \upsilon }[-\Upsilon _{\varpi \varpi \varpi }+ \Delta _{1}{\Upsilon }H_{\varpi \varpi }-\Delta _{1}\Delta _{4}{\Upsilon }H_{\varpi \varpi } -\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }+\Upsilon _{\upsilon }]-\Delta _{4}{\Upsilon }H_{\varpi }\cdot \end{aligned} \end{aligned}$$

Family 2: For \(M_{2}\), we have \(B^\gamma _{2} =-H_{\iota }\) and \(\epsilon ^{\iota }= 1\), we acquired:

$$\begin{aligned} \begin{aligned} \nu ^{\iota }&={\mathcal {S}}-H_{\iota }\Upsilon _{\upsilon \iota }+H_{\iota \iota }\Upsilon _{\upsilon }+H_{\varpi \iota }\Upsilon _{\iota }+H_{\varpi \iota \iota }\Upsilon _{\iota }~, \\ \nu ^{\varpi }&=-H_{\iota }[-4H_{\varpi \varpi \upsilon }{\Upsilon }+\Upsilon _{\upsilon \iota }+\Upsilon _{\varpi \varpi \varpi \upsilon }-4\Delta _{2}H_{\varpi \varpi }\Upsilon _{\upsilon }+\Delta _{4}H_{\varpi }\Upsilon _{\varpi \upsilon } +4\Upsilon _{\varpi \varpi }H_{\upsilon }]+H_{\iota \iota }\Upsilon _{\upsilon }\\&\qquad -H_{\varpi \iota }[\Delta _{3}\Delta _{2}\Upsilon _{\varpi \upsilon }-\Upsilon _{\iota }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi } -\Delta _{1}{\Upsilon }H_{\varpi \upsilon }-4\Upsilon _{\upsilon }H_{\upsilon }]-{\Upsilon }\Delta _{2}H_{\varpi }H_{\varpi \upsilon \iota }{\Upsilon }H_{\varpi \iota \iota }\\&\qquad -\Delta _{4}H_{\upsilon \iota }[4{\Upsilon }H_{\varpi \varpi }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }-\Delta _{4}(\Upsilon _{\varpi \varpi \varpi }\Delta _{2}H_{\varpi \varpi \upsilon } +3\upsilon _{HH}\Delta _{2}H_{\varpi \upsilon }+3\Upsilon _{\upsilon }H_{\varpi \upsilon })],\\ \nu ^{\upsilon }&=-H_{\iota }[4H_{\varpi \varpi \varpi }\psi -\Delta _{1}\Upsilon _{\upsilon }H_{\varpi \varpi }-\Delta _{1}{\Upsilon }H_{\varpi \varpi \upsilon }+\Upsilon _{\varpi \varpi \varpi \upsilon }+ \Delta _{4}H_{\varpi \varpi }\Upsilon _{\upsilon } +\Delta _{4}H_{\varpi }H_{\varpi \upsilon }\\&\qquad +\Delta _{4}H_{\varpi \upsilon }\Upsilon _{\upsilon }+{\Upsilon }H_{\varpi \varpi \upsilon }-\Upsilon _{\upsilon \upsilon }]-H_{\varpi \iota }[-\Upsilon _{\varpi \varpi \upsilon }-\Delta _{4}{\Upsilon }H_{\varpi \upsilon }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }+\Upsilon _{\upsilon }]\\&\qquad -H_{t\upsilon }[-\Upsilon _{\varpi \varpi \varpi }-{\Upsilon }H_{\varpi \upsilon \iota }+ \Delta _{1}{\Upsilon }H_{\varpi \varpi }-\Delta _{4}{\Upsilon }H_{\varpi \varpi }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }+\Upsilon _{\upsilon }]-\Delta _{4}{\Upsilon }H_{\varpi }\\&\qquad H_{\varpi \upsilon \iota }-\Upsilon _{\upsilon \upsilon }-\Upsilon _{\upsilon }H_{\varpi \varpi \upsilon \iota }\cdot \end{aligned} \end{aligned}$$

Family 3: For \(M_{3}\), we have \(B^\gamma _{3} =-H_{\upsilon }\) and \(\epsilon ^{\upsilon }= 1\), we obtained:

$$\begin{aligned} \begin{aligned} \nu ^{\iota }=\,\,&H_{\upsilon \iota }\Upsilon _{\upsilon }+H_{\varpi \upsilon }\Upsilon _{\iota }-H_{\upsilon }\Upsilon _{\upsilon \iota }+H_{\varpi \iota \upsilon }\Upsilon _{\iota }~, \\ \nu ^{\varpi }=\,\,&H_{\upsilon }[-4H_{\varpi \varpi \upsilon }{\Upsilon }+\Upsilon _{\upsilon \iota }+\Upsilon _{\varpi \varpi \varpi \upsilon }-4H_{\varpi \varpi }\Upsilon _{\upsilon }+\Delta _{4}H_{\varpi }\Upsilon _{\varpi \upsilon } +4\Upsilon _{\varpi \varpi }H_{\upsilon }]+H_{\iota \upsilon }\Upsilon _{\upsilon }\\ {}&+H_{\varpi \upsilon }[\Delta _{3}\Upsilon _{\varpi \upsilon }-\Upsilon _{\iota }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi } +\Delta _{1}{\Upsilon }H_{\varpi \upsilon }-4\Upsilon _{\upsilon }H_{\upsilon }]-4{\Upsilon }H_{\upsilon }H_{\varpi \upsilon }+\Upsilon _{\upsilon }-{\Upsilon }H_{\varpi \upsilon \iota }\\ {}&-H_{\upsilon \upsilon }[4{\Upsilon }H_{\varpi \varpi }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }-\Delta _{4}(\Upsilon _{\varpi \varpi \varpi }+3\Upsilon _{\upsilon }H_{\varpi \varpi \upsilon }+\Upsilon _{\upsilon }H_{\varpi \varpi \varpi \upsilon })]\\ {}&-\Delta _{4}{\Upsilon }H_{\varpi }H_{\varpi \upsilon \upsilon }, \\ \nu ^{\upsilon }=\,\,&{\mathcal {S}}-H_{\upsilon }[4H_{\varpi \varpi \varpi }\psi -\Delta _{1}\Upsilon _{\upsilon }H_{\varpi \varpi }-\Delta _{1}{\Upsilon }H_{\varpi \varpi \upsilon }+ \Delta _{4}H_{\varpi \varpi }\Upsilon _{\upsilon } +\Delta _{4}H_{\varpi }H_{\varpi \upsilon }+\Delta _{4}H_{\varpi \upsilon }\Upsilon _{\upsilon }\\ {}&+{\Upsilon }H_{\varpi \varpi \upsilon }-\Upsilon _{\upsilon \upsilon }]-H_{\varpi \upsilon }[-\Upsilon _{\varpi \varpi \upsilon }-\Delta _{4}{\Upsilon }H_{\varpi \upsilon }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }+\Upsilon _{\upsilon }]-H_{\upsilon \upsilon }[-\Upsilon _{\varpi \varpi \varpi }\\ {}&+ \Delta _{1}{\Upsilon }H_{\varpi \varpi }-\Delta _{4}{\Upsilon }H_{\varpi \varpi }-\Delta _{4}\Upsilon _{\upsilon }H_{\varpi }+\Upsilon _{\upsilon }]-\Delta _{4}{\Upsilon }H_{\varpi } H_{\varpi \upsilon \upsilon }-\Upsilon _{\upsilon \upsilon }-\Upsilon _{\upsilon }H_{\varpi \varpi \upsilon }, \end{aligned} \end{aligned}$$

where \(\Upsilon (\varpi ,\upsilon ,\iota ,H)=f(\iota +\upsilon ,H)+g(\iota -\upsilon ,H).\)

In this section, we have rigorously computed the conservation laws for \(B^\gamma _{1}\). It is noteworthy that the conservation laws for \(B^\gamma _{2}\), \(B^\gamma _{3}\), \(B^\gamma _{4}\), \(B^\gamma _{5}\), and \(B^\gamma _{6}\) are also computable, although they have been omitted from our discussion for brevity.

4.2 Local conservation laws

4.2.1 Multiplier approach

\({Step 1:}\) Let us consider a multiplier of the form:

$$\begin{aligned} \pi ^{\sigma }=\pi ^{\sigma }(\varpi ,H,H_1,H_2,...,H_r). \end{aligned}$$

The condition \(r \le p\) is crucial for obtaining the conserved vectors of Eq. (2).

\({Step 2:}\) These vectors must satisfy the condition \(\nu =(\nu ^1,\nu ^2,\nu ^3,...\nu ^q)\)where q is the number of independent vectors:

$$\begin{aligned} \pi ^{\sigma }(E_\sigma )=A_k(\nu ^{k}). \end{aligned}$$
(38)

\({Step 3:}\) We derive the subsequent determining system from the variational derivative of Eq. (38):

$$\begin{aligned} \frac{\delta }{\delta H^\gamma }[ \pi ^{\sigma }(E_\sigma )]=0, \end{aligned}$$
(39)

and solving Eq. (39) provides the required multipliers.

4.3 Conserved vectors for Eq. (1)

In this section, we harness the multiplier technique to establish the conservation laws for Eq. (1), a pivotal step in our analysis. The determining equation governing the multiplier \(\pi (\varpi ,\upsilon ,\iota , H)\), as shown from Eq. (39), is pivotal for this purpose:

$$\begin{aligned} \begin{aligned}&\frac{\delta }{\delta {H}^{\gamma }}[{\pi }(H_{\varpi \varpi \varpi \iota }+3H_{\varpi }H_{\varpi \iota }+3H_{\iota }H_{\varpi \varpi }+{\Delta _{6}}H_{\iota \iota }+{\Delta _{1}}H_{\upsilon \iota }+{\Delta _{5}}H_{\upsilon \upsilon }+{\Delta _{4}}H_{\varpi \iota } +{\Delta _{3}}H_{\varpi \upsilon }+{\Delta _{2}}H_{\varpi \varpi })]= 0, \end{aligned} \end{aligned}$$
(40)

where the total derivative  \(A_\varpi\),  \(A_\iota\),  and \(A_\upsilon\) are defined as:

$$\begin{aligned} A_{\varpi }=\,\,& {} {\partial _{\varpi }+{H^\gamma _\varpi }{\partial _{H^\gamma }}}+H^\gamma _{\varpi {l}}{\partial _{H^\gamma _{l}}}+H^\gamma _{\varpi {lm}}{\partial _{H^\gamma _{lm}}}+..., \\ A_{\iota }=\,\,& {} {\partial _{\iota }+{H^\gamma _\iota }{\partial _{H^\gamma }}}+H^\gamma _{\iota {l}}{\partial _{H^\gamma _{l}}}+H^\gamma _{\iota {lm}} {\partial _{H^\gamma _{lm}}}+..., \\ A_{\upsilon }=\,\,& {} {\partial _{\upsilon }+{H^\gamma _\upsilon }{\partial _{H^\gamma }}}+H^\gamma _{\upsilon {l}}{\partial _{H^\gamma _{l}}}+H^\gamma _{\upsilon lm} {\partial _{ H^\gamma _{lm}}}+...\cdot \end{aligned}$$

Through rigorous evaluation of Eq. (40) and meticulous further calculations, we derive the following two multipliers:

$$\begin{aligned} \begin{aligned} \pi _{1}({\varpi ,\upsilon ,\iota ,H})={F}, ~~~~\pi _{2}({\varpi ,\upsilon ,\iota ,H})={G}, \end{aligned} \end{aligned}$$
(41)

where

$$\begin{aligned} F=F\left( \frac{-\upsilon {\sqrt{\Delta ^{2}_{1}-4\Delta _{5}\Delta _{6}}-2\iota \Delta _{5}+\upsilon \Delta _{1}}}{2\Delta _{5}}\right) ~~~ G=G\left( \frac{\upsilon {\sqrt{\Delta ^{2}_{1}-4\Delta _{5}\Delta _{6}}+2\iota \Delta _{5}-\upsilon \Delta _{1}}}{2\Delta _{5}}\right) . \end{aligned}$$

The conserved vectors are obtained from Eq. (41) and Eq. (38).

Case 1: The conservation laws for Eq. (1) involve three components of conserved vectors, denoted as \(\nu ^{\iota }\), \(\nu ^{\varpi },\) and \(\nu ^{\upsilon }\). These conservation laws can be expressed in terms of  \(\pi _{1}({\varpi ,\upsilon ,\iota ,H})=F:\)

$$\begin{aligned} \begin{aligned} \nu _{1}^{\iota }=\,\,&{\frac{3}{2}}H{F}H_{\varpi \varpi }+{\frac{3}{2}}{H^{2}_{\varpi }}{H^{2}_{\varpi }}{F}-H{F^{\prime }}{\Delta _{6}}+{H_{\iota }}{F}{\Delta _{6}}+{H_{\varpi }}{F}{\Delta _{4}}+{H_{\upsilon }}{F}{\Delta _{1}}+{H_{\varpi \varpi \varpi }}{F},\\ {\nu _{1}^{\varpi }}=\,\,&-{\frac{3}{2}}F{H_{\iota \varpi }}-{\frac{3}{2}}{F^{\prime }}H{H_{\varpi }}+{\frac{3}{2}}{H_{\varpi }}F{H_{\iota }}-H{F^{\prime }}{\Delta _{4}}+{H_{\varpi }}F{\Delta _{2}}+{H_{\upsilon }}F{\Delta _{3}}-{H_{\varpi \varpi }}{F^{\prime }},\\ \nu _{1}^{\upsilon } =\,\,&-{\frac{1}{2}}H{F^{\prime }}{\Delta _{1}}+H{F^{\prime }}\sqrt{{\Delta _{1}}^2-4{\Delta _{5}}{\Delta _{6}}}+H_{\upsilon }F{\Delta _{5}}.\\ \end{aligned} \end{aligned}$$

Case 2: The conservation laws pertaining to \(\pi ^{2}(\varpi ,\upsilon ,\iota ,H)=G\) can be shown as follows:

$$\begin{aligned} \begin{aligned} \nu _{2}^{\iota } =\,\,&{\frac{3}{2}}H{G}{H{\varpi \varpi }}+{\frac{3}{2}}{H^{2}_{\varpi }}{G}-H{G^{\prime }}{\Delta _{6}}+H_{\iota }{G}{\Delta _{6}}+{H_{\varpi }}{G}{\Delta _{4}}+{H_{\upsilon }}{G}{\Delta _{1}}+{H{\varpi \varpi }}\varpi {G},\\ \nu _{2}^{\varpi } =\,\,&-{\frac{3}{2}}H{G}{H_{\iota \varpi }}-{\frac{3}{2}}{G^{\prime }}H{H_{\varpi }}+{\frac{3}{2}}{H_{\varpi }}{G}H_{\iota }-H{G^{\prime }}{\Delta _{4}}+{H_{\varpi }}{G}{\Delta _{2}}+{H_{\upsilon }}{\Delta _{3}}{G}-{H{\varpi \varpi }}{G^{\prime }},\\ \nu _{3}^{\upsilon } =\,\,&-{\frac{1}{2}}H{G^{\prime }}{\Delta _{1}}-H{\frac{\sqrt{{\Delta _{1}}^2-4{\Delta _{5}}{\Delta _{6}}}}{2}}{G^{\prime }}+{H_{\upsilon }}{G}{\Delta _{5}}. \end{aligned} \end{aligned}$$

Here, it is imperative to underscore that the functions F and G are regarded as arbitrary, with \(F^{\prime }\) and \(G^{\prime }\) denoting their respective first-order explicit derivatives. It is crucial to emphasize that the self-adjointness approach consistently yields a greater number of conservation laws compared to the multiplier approach. Each symmetry identified through the self-adjointness method contributes distinct conservation laws for the model under examination. Local conservation laws describe conservation locally at each point, while nonlocal conservation laws describe conservation over an extended region.

5 Conclusions

In conclusion, this study delved into the completely generalized Hirota–Satsuma–Ito (cgHSI) equation through Lie analysis, aiming to achieve several objectives: deriving one-dimensional conjugacy classes using Lie point symmetries for the abelian algebra of the Lie group, leading to model reductions with similarity variables. Various techniques were employed to obtain new solitary wave solutions and exact explicit solutions of the equation, including the use of hyperbolic, trigonometric, and rational functions. Additionally, a hybrid method combining the Lie symmetry method with the extended direct algebraic method was employed to rigorously analyze exact and soliton solutions. Conservation laws for the equation were also computed, and their classification was achieved using nonlinear self-adjointness theory. Interestingly, a greater number of conservation laws were obtained using nonlinear self-adjointness compared to the multiplier approach. Overall, the results of this study enhance our understanding of the Hirota–Satsuma–Ito equation and pave the way for future research in the field. The newly discovered exact solutions hold promise for applications across various fields, providing valuable insights for mathematicians and physicists and driving further exploration of nonlinear models. Avenues for future research could include further exploration into bifurcation analysis, chaos theory applications, and conducting sensitivity analysis on the model under consideration. These directions could provide deeper insights into the dynamics and robustness of the model, enhancing its applicability and understanding within the field.