Constraining photon trajectories in black hole shadows

Abstract

We examine the shadow cast by a Kerr black hole, focusing on constraints on photons corresponding to different shadow boundaries. The photons are related to different orbital ranges and impact parameter values, creating a map of the shadow boundaries. Our analysis fixes also the conditions under which it is possible to observe an “imprint” of the black hole (outer) ergosurface and (outer) ergoregion on the Kerr black hole shadow boundary. The counter-rotating case resulted strongly constrained with respect to the co-rotating case, constituting a remarkable and significant difference where the counter-rotating component associated with the shadow boundary is strongly distinct from the co-rotating one. However, in this framework, even the co-rotating photons imply restrictions on conditions on the spins and planes, which are bounded by limiting values. We believe the results found here, being a tracer for the central black hole, can constitute new templates for the ongoing observations.

1 Introduction

The first image of the black hole (BH) shadow was released by the Event Horizon Telescope (EHT) Collaboration¹ in 2019, first results concerning the detection of an event horizon of a super-massive black hole (SMBH) at the center of a neighboring elliptical Messier 87 (M87) galaxy were announced in [1,2,3,4,5,6]. The corresponding linear-polarimetric EHT images of the center of M87 were presented in [7]. In [8] the resolved polarization structures (and Atacama Large Millimeter/submillimeter Array observation (ALMA)) have been compared to theoretical models. (A new sharper image of the M87 BH has been released, in 2023 created with PRIMO algorithm [9]). In 2022 the EHT Collaboration has been able to observe the shadow cast by the SMBH Sagittarius A* (SgrA*) in the center of our galaxy² [10,11,12,13,14,15]. The EHT observations, providing immediate evidences of an event horizon presence, constitute a consistent advance in astronomy having made also possible to focus on physical phenomena in the close proximity of the BH. (The BH shadow could be related to complex astrophysical phenomena, typically accretion disks and related jets orbiting close to the horizon³.)

We expect that it will be possible to observe even more refined and clearer details from the astronomical observations in near future (see [22]). There is a continuous improvement (and updating) of the SMBH M87* image, through new analyses and simulations. Advancements and new data analysis techniques can allow a more clear observation and description of the BH environment and more refined analyses will be able to clearly discern the presence and structure of different photon orbits, as predicted by the theory. In [23], for example, the M87* images from EHT collaboration has been re-analyzed, using a series of kinetic plasma simulations, predicting the images during the outbursts characterizing M87*. It was found that, following magnetic-field instabilities, radio-wave hot spots (connected to closed magnetic structures-plasmoids-of the BH magnetosphere) may appear as rotating around the BH shadow on an orbit three times larger than the BH size. In [24], revisiting the past observations, it has been claimed to have spotted the sharp light ring around M87*—see also [9, 19, 25,26,27,28]. (The ring was predicted by general relativistic magnetohydrodynamical (GRMHD) simulations in the near horizon region of M87*). This new analysis also provides evidence of a rotating jet ejected from the BH region [27] and [9, 24, 25, 27,28,29,30,31]. A recent analysis of EHT data sharpened the view of the glowing gas around the BH. The new image was reconstructed using the PRIMO algorithm, [9]; new observations, obtained combined data from radio telescopes Global Millimetre VLBI Array, ALMA, and the Greenland Telescope, have shown the ring-like accretion structure in M87 connecting the BH plasma jet to the BH and the accretion matter[22].

BHs shadows have been studied analytically in numerous studies [32,33,34,35]. The standard notion of the BH shadow defines rather the silhouette (shadow boundary) than shadow due to definition of the dark region in radiating screen in situation where the BH is located before the screen and the distant observer [32, 36]. The boundary of the shadow is constituted by unstable photon (spherical and circular) orbits [32, 36,37,38,39,40,41,42,43], whereas the shadow itself is the dark region bounded by shadow boundary. From methodological view-point, in general the BH shadow boundary is found considering photons coming from all the points at infinity. The observer is located at infinity, and the BH has a well defined and fixed inclination angle⁴. Photons on unstable orbits can reach the far away observer after perturbation. The photons moving towards the BH could be trapped in unstable spherical orbits, or they can be captured by BH gravitational field producing the central dark region (shadow), or they could escape to infinity, being detected by the distant observer if in line of sight. However, the observed shadow boundary can be substantially modified by properties of the orbiting matter and even by properties of photons radiated by the orbiting matter, depending on properties of the region of the light distribution and its source. Possible source of the light can be the accretion disk orbiting the central BH. In these conditions, the photons could interact with the accreting plasma affecting therefore the photons distribution and the intensity. The shadow in this case has been also extensively studied for example in [44,45,46,47,48,49,50].

The shape and size of a BH shadow boundary depend in particular on the BH parameters. Hence observations of the shadow boundary not only provide compelling BH evidence, but also an estimation on the BH parameters. In order to fit astronomical observations, several observables were constructed using special points on the shadow boundary in the celestial coordinates (see [29]). These new observables should carry information on the central spinning BH and different orbiting structures. In this work we study some aspects of the BH shadows boundary analyzing photon spherical orbits in orbital ranges associated to accretion process. In our analysis we solve the equations for the null geodesics constituting the shadow boundary, fixing constraints on the photons impact parameter $\ell$ or the radius $r=$constant. In this way we individuate points on the BHs shadow profiles correspondent to the fixed constraints on $\ell$ or r, investigated for all values of the BH spin parameter. We consider photons co-rotating and counter-rotating motion (determined by $\ell$). We also explore the effects of frame dragging on the shadow boundary, investigating the possibility to observe an “imprint” of the outer ergoregion and the outer ergosurface on the shadows boundary, by examining the photon spherical orbits in the outer ergoregion and on the outer ergosurface.

The structure of this article is as follows. In Sect. 2 we introduce the spacetime metric. Constants of motion and geodesics equations are summarized in Sect. 2.1. Black hole shadows are introduced in Sect. 3. Shadows analysis is in Sect. 4. We investigate shadows for specific impact parameter in Sect. 4.1, while in Sect. 4.8 solutions are analysed for fixed r related to particular spherical orbital ranges. In Sect. 4.14 photons spherically orbiting on the outer ergosurface, and in the outer ergoregion are investigated. Concluding remarks are in Sect. 5. In Appendix 1 there are further notes on the Kerr spacetime geodesic structure. In Appendix 1 various aspects of the analysis have been further detailed.

2 The spacetime metric

In the Boyer-Lindquist (BL) coordinates $\{t,r,\theta ,\phi \}$,⁵ the Kerr spacetime line element reads

$$\begin{aligned}{} & {} ds^2=-\left( 1-\frac{2Mr}{\Sigma }\right) dt^2+\frac{\Sigma }{\Delta }dr^2+\Sigma d\theta ^2+\left[ (r^2+a^2)+\frac{2M r a^2}{\Sigma }\sin ^2\theta \right] \sin ^2\theta d\phi ^2 -\frac{4rMa}{\Sigma } \sin ^2\theta dt d\phi , \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \hbox {where}\quad \Delta \equiv a^2+r^2-2 rM\quad \hbox {and}\quad \Sigma \equiv a^2 (1-\sin ^2\theta )+r^2. \end{aligned}$$

(2)

Parameter $a=J/M\ge 0$ is the metric spin, where total angular momentum is J and the gravitational mass parameter is M. A Kerr BH is defined by the condition $a\in [0,M]$. The extreme Kerr BH has dimensionless spin $a/M=1$. The non-rotating case $a=0$ is the Schwarzschild BH solution. (The Kerr naked singularities (NSs) have $a>M$.)

The BH horizons are

$$\begin{aligned} r_-\le r_+,\quad \hbox {where} \quad r_{\pm }\equiv M\pm \sqrt{M^2-a^2}. \end{aligned}$$

(3)

The outer ergoregion of the spacetime is $]r_+,r_{\epsilon }^+ ]$, where the outer ergosurface $r_{\epsilon }^+$ is

$$\begin{aligned} r_{\epsilon }^{+}\equiv M+\sqrt{M^2- a^2 (1-\sigma )}\quad \hbox {with}\quad \sigma \equiv \sin ^2\theta \in [0,1], \end{aligned}$$

(4)

and there is $r_{\epsilon }^+=2M$ in the equatorial plane ($\sigma =1$), and $r_+<r_{\epsilon }^+$ on $\theta \ne 0$.

In the following, we will use dimensionless units with $M=1$ (where $r\rightarrow r/M$ and $a\rightarrow a/M$).

2.1 Geodesics equations and constants of motion

The equatorial plane is the symmetry plane for the metric, and the constant r orbits on this plane are circular. The geodesic equations in Kerr spacetime are fully separable. There are four constants of motion. For convenience we summarize the (Carter) equations of motion as follows (see [51]):

$$\begin{aligned} \dot{t}= \frac{1}{\Sigma }\left[ \frac{P \left( a^2+r^2\right) }{\Delta }-{a \left[ a \mathcal {E}\sigma -\mathcal {L}\right] }\right] ,\, \dot{r}= \pm \frac{\sqrt{R}}{\Sigma };\,\dot{\theta }=\pm \frac{\sqrt{T}}{\Sigma }, \dot{\phi }= {} \frac{1}{\Sigma }\left[ \frac{a P}{\Delta }-\left[ {a \mathcal {E}-\frac{\mathcal {L}}{\sigma }}\right] \right] ; \end{aligned}$$

(5)

for $p^a=dx^a/d \tau \equiv u^a\equiv \{ \dot{t},\dot{r},\dot{\theta },\dot{\phi }\}$, the geodesic tangent four-vector, where $\tau$ is an affine parameter, normalized so that $p^ap_a=-\mu ^2$, and $\mu$ is the rest mass of the test particle where a null geodesics has $\mu =0$,⁶ and

$$\begin{aligned} P\equiv \mathcal {E}\left( a^2+r^2\right) -a \mathcal {L},\, R\equiv P^2-\Delta \left[ (\mathcal {L}-a \mathcal {E})^2+\mu ^2 r^2+\mathcal {Q}\right] ,\, T\equiv \mathcal {Q}- (\cos \theta )^2 \left[ a^2 \left( \mu ^2-\mathcal {E}^2\right) +\left( \frac{\mathcal {L}^2}{\sigma }\right) \right] , \end{aligned}$$

(6)

where $\mathcal {Q}$ is the Carter constant of motion. Quantities $(\mathcal {E}, \mathcal {L})$ are constants of geodesic motions

$$\begin{aligned} \mathcal {E}=-(g_{t\phi } \dot{\phi }+g_{tt} \dot{t}),\quad \mathcal {L}=g_{\phi \phi } \dot{\phi }+g_{t\phi } \dot{t}, \end{aligned}$$

(7)

defined from the Kerr geometry rotational Killing field $\xi _{\phi }\equiv \partial _{\phi }$, and the Killing field $\xi _{t}\equiv \partial _{t}$ representing the stationarity of the background.

The constant $\mathcal {L}$ in Eq. 7 may be interpreted as the axial component of the angular momentum of a test particle following timelike geodesics. Constant $\mathcal {E}$ represents the energy of the test particle related to the static observers at infinity⁷. We introduce also the specific angular momentum (called also impact parameter)

$$\begin{aligned} \ell \equiv \frac{\mathcal {L}}{\mathcal {E}}=-\frac{g_{\phi \phi }u^\phi +g_{\phi t} u^t }{g_{tt} u^t +g_{\phi t} u^\phi }, \end{aligned}$$

(8)

With $a>0$, the fluids and particles counter-rotation (co-rotation) is defined by $\ell a<0$ ($\ell a>0$).

Static observers, having four-velocity $\dot{\theta }=\dot{r}=\dot{\phi }=0$, cannot exist inside the ergoregion. Whereas, trajectories $\dot{r}\ge 0$, including photons crossing the outer ergosurface and escaping outside in the region $r\ge r_{\epsilon }^+$ are possible.

3 Shadows

In this section we discuss the concept of BH shadows, introducing the quantities $(q,\ell )$ (constants of motion), the celestial coordinates $(\alpha ,\beta )$ and we discuss the constraints adopted in our analysis.

Focusing on the null geodesic equations (5), the boundary of the BH shadow is determined by the (unstable) photon orbits defined by:

$$\begin{aligned} R=\partial _r R=0,\quad \partial _r^2R>0, \end{aligned}$$

(9)

hereafter refereed as set $(\mathfrak {R})$ of equations, within constraints provided by the set⁸ of Eq. 5.

We introduce the motion constants q and $\ell$ (impact parameter)

$$\begin{aligned} \ell \equiv \frac{\mathcal {L}}{\mathcal {E}},\quad q\equiv \frac{\mathcal {Q}}{\mathcal {E}^2}. \end{aligned}$$

(10)

Following [32] we assume the observer is located at infinity (i.e, at very large distance in practical calculation), introducing the celestial coordinates⁹$\alpha$ and $\beta$ for the null geodesics

$$\begin{aligned}{} & {} \alpha =-\frac{\ell }{\sqrt{\sigma }},\, \beta =\pm \sqrt{q-q_c} \nonumber \\{} & {} \hbox {for}\quad \sigma \ne 0\quad \hbox {and}\quad q\ge q_c,\quad \hbox {where}\quad q_{c}\equiv \frac{(1-\sigma ) \left( \ell ^2-\ell _c^2 \right) }{\sigma },\quad \ell _c^2\equiv a^2 \sigma . \end{aligned}$$

(11)

The shadow boundary is, at fixed spin a and angle $\sigma$, a closed curve in the plane $\alpha -\beta$, and its points correspond to constant r, (solutions of $(\mathfrak {R})$), q and parameter,¹⁰$\ell$.

In this work we study the solutions $(r,q,\ell )$, corresponding to the points $(\alpha ,\beta )$ of the shadow boundary, then analysing the variation of $(r,q,\ell )$ with $(a,\sigma )$. In order to do this, r and $\ell$ are set in ranges defined by some boundary values. We then proceed by solving system $(\mathfrak {R})$ for the boundary r and $\ell$ values, obtaining, for fixed radius r, the solutions $(\alpha ,\beta ,\ell ,q)$ and, for fixed parameter $\ell$, solutions $(\alpha ,\beta ,r,q)$, then analyzed for all values of a and $\sigma$. Ultimately, we obtain the parts of the shadow boundary associated to the fixed constraints, and therefore a shadow boundary map (in dependence on the selected ranges of values for $\ell$ or r for all possible values of $(a,\sigma )$). Below we discuss the limit values for r and $\ell$.

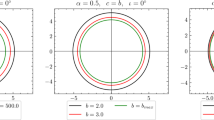
In Sect. 4.14 we solve system $\mathfrak {(R)}$ for fixed $r\in ]r_+,r_{\epsilon }^+]$. Solutions are unstable spherical photon orbits located in the outer ergoregion and on the outer ergosurface. The frame-dragging effects on the BH shadow profile are explored also studying the solutions of the equations $\mathfrak {(R)}$ for $\dot{\phi }=0$, i.e. for null geodesics, with $\ell <0$, on an inversion surface [55]. An inversion surface is a closed surface, defined by condition $\dot{\phi }=0$ on the geodesics, embedding a Kerr BH, and located out of the Kerr BH outer ergosurface, which can be seen as effect of the Kerr spacetime frame-dragging—Fig. 1. We use the notation $\textrm{Q}_{\mathbf{\mathrm{T}}}$ for any quantity $\textrm{Q}$ considered at the inversion point, where within the condition $\dot{\phi }=0$, there is $\ell =\ell _{\mathbf{\mathrm{T}}}\equiv \left. -\frac{g_{t\phi }}{g_{tt}}\right| _{\mathbf{\mathrm{T}}}$.

For the other limiting values, we will consider radii $\{r_\gamma ^\pm ,r_{mbo}^{\pm },r_{mso}^{\pm }\}$ and, for the parameter $\ell$, the functions $\{\ell _{mso}^\pm ,\ell _{mbo}^\pm ,\ell _{\gamma }^\pm \}$, defined in Appendix 1 for co-rotating $(-)$ and counter-rotating $(+)$ motion. (There is $\textrm{Q}_\bullet$ for any quantity $\textrm{Q}$ evaluated at $r_\bullet$.) Radii $r_\gamma ^\pm (a)$ are photon circular orbits on the equatorial plane.¹¹ They are solutions of $\mathfrak {(R)}$ for $\sigma =1$ ($q=0$) and $\ell =\ell _\gamma ^\pm (a)$ respectively. Radii $r_{mbo}^{\pm }$ are the marginal circular bound orbits, and radii $r_{mso}^{\pm }$ are marginal stable circular orbits for time-like particles on the equatorial plane, having $\ell = \ell _{mbo}^\pm$ and $\ell = \ell _{mso}^\pm$ respectively [36]. Therefore, radii $\{r_{mbo}^{\pm },r_{mso}^{\pm }\}$ cannot be solutions of $\mathfrak {(R)}$ with $\ell ^\pm \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm \}$ respectively, $q=0$ and $\sigma =1$. However, here we solve $\mathfrak {(R)}$ on the spherical surfaces defined by radii $\{r_{mbo}^{\pm },r_{mso}^{\pm },r_\gamma ^\pm \}$, examining the unstable photons circular orbits (solutions of $\mathfrak {(R)}$) on $r=\{r_{mbo}^{\pm },r_{mso}^{\pm },r_\gamma ^\pm \}$ for a general angle $\sigma$ and constants¹²$(\ell ,q)$. Similarly, we find solutions of $\mathfrak {(R)}$ for spherical photon orbits with parameter $\ell ^\pm \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm ,\ell _{\gamma }^\pm \}$ at a general radius r, a general angle $\sigma$ and constant¹³q.

The spherical surfaces $\{r_{mbo}^{\pm },r_{mso}^{\pm },r_\gamma ^\pm \}$ can provide an immediate astrophysical context in relation to the structures orbiting around the BH¹⁴. In fact, the accretion disk inner edge (cusp) orbiting on the BH equatorial plane is located in region $r\in ]r_{mbo}^\pm ,r_{mso}^\pm ]$¹⁵ of the equatorial plane, and therefore, close to $\sigma =1$, the inner region of an axially symmetric counter-rotating or co-rotating accretion torus is in the spherical shell $]r_{mbo}^\pm ,r_{mso}^\pm ]$ respectively. The inner orbital shell, $[r_{\gamma }^\pm , r_{mbo}^\pm ]$, covers on the equatorial plane the cusps of the open (hydrodynamical) toroidal structures corresponding to matter funnels along the BH rotational axis, which are generally associated to geometrically thick accretion tori [60,61,62,63,64,65,66,67].

In geometrically thin disks, the flows, freely falling from the cusps can be considered leaving the marginally stable circular orbit with $\ell =\ell _{mso}^\pm$, and more in general with ${\mp }\ell ^\pm \in ]{\mp }\ell _{mbo}^\pm ,{\mp }\ell _{mso}^\pm ]$ from $]r_{mbo}^\pm ,r_{mso}^\pm ]$ (or ${\mp }\ell ^\pm \in {[}{\mp }\ell _{mbo}^\pm ,{\mp }\ell _{\gamma }^\pm [$ according to the cusp location in $]r_{\gamma }^\pm , r_{mbo}^\pm ]$ for the open configurations). These momenta also fix the range of location of the accretion disk center, defined as the maximum pressure point in the disks—see Appendix 1.

Fig. 1

Left panel: inversion surfaces sections, for $\ell _{mso}^+$ (plain) and $\ell _{mbo}^+$ (dashed), $\ell _{\gamma }^+$ (dotted-dashed). It is $r= \sqrt{y^2+z^2}$ and $\theta =\arccos ({z}/r)$. Right panel: counter-rotating photon orbits (yellow curves) to the BH (black region). Inversion point $r_{{\mathbf{\mathrm{T}}}}$ is the deep-purple curve. It is $\{z=r \cos \theta ,y=r \sin \theta \sin \phi ,x=r \sin \theta \cos \phi \}$. Gray region is the outer ergosurface, light-purple region is $r< r_{\mathbf{\mathrm{T}}}(\sigma _{\mathbf{\mathrm{T}}})$

Hence, in Sect. 4.1 we investigate the solutions of $(\mathfrak {R})$, for $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm ,\ell _{\gamma }^\pm ,\ell _{\mathbf{\mathrm{T}}}\}$, in terms of orbit r, constant q, angle $\sigma$, and coordinates $(\alpha ,\beta )$. In Sect. 4.8 we examine the solutions of $(\mathfrak {R})$, for $r=\{r_{\gamma }^\pm ,r_{mbo}^\pm ,r_{mso}^\pm \}$, and in the spherical shells $r\in [r_{mbo}^\pm ,r_{mso}^\pm ]$, $r\in [r_{\gamma }^\pm ,r_{mbo}^\pm ]$, in terms of parameter $\ell$ and $(q,\sigma ,\alpha ,\beta )$.

4 Shadows analysis

4.1 Parameters $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm ,\ell _{\gamma }^\pm ,\ell _{{\mathbf{\mathrm{T}}}}\}$

In general for BHs with spin¹⁶$a\in ]0,a_g[$, spherical photon orbits, solutions of system $\mathfrak {(R)}$ with $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm \}$, are on radius $r=r_\lambda \ne \{r_{mso}^\pm ,r_{mbo}^\pm \}$ with motion constant $q=q_\lambda \ge 0$, where

$$\begin{aligned}{} & {} a_g(\ell )\equiv \frac{4 \ell }{\ell ^2+4}=-\frac{4 \alpha \sqrt{\sigma }}{\alpha ^2 \sigma +4}\quad \hbox {and}\quad q_\lambda \equiv \frac{r \left[ a^2 (r+2)-4 a \ell +r^3-(r-2) \ell ^2\right] }{\Delta },\quad r_{\lambda }\equiv \frac{3-a (a+\ell )}{\root 3 \of {3} \root 3 \of {\lambda }}+\frac{\root 3 \of {\lambda }}{3^{2/3}}+1 \end{aligned}$$

(12)

where $\lambda \equiv \frac{1}{6} \sqrt{\left[ 54(1- a^2)\right] ^2+108 [a (a+\ell )-3]^3}+9(1- a^2)$ Figs. 2, 3. Functions $(q_\lambda ,r_\lambda )$ will be further constrained when evaluated for $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm \}$, as we discuss in details below. In Appendix 2, various aspects of the analysis have been further detailed.

First, by using the condition $T\ge 0$ (and $\dot{t}>0$), we find that for $a\in ]0,1]$ there is $\sigma \in [\sigma _\lambda ,1]$ and, for the Schwarzschild BH, solutions exist for $\sigma \in [\sigma _\ell ,1]$, where $\sigma _\ell$ and $\sigma _\lambda$ are

$$\begin{aligned}\sigma _{\ell }\equiv \frac{\ell ^2}{q+\ell ^2},\quad \sigma _{\lambda }\equiv \frac{q+\ell ^2-a^2 \left[ \sqrt{\frac{\left( q+\ell ^2\right) ^2}{a^4} +\frac{2 \left( q-\ell ^2\right) }{a^2}+1}-1\right] }{2 a^2}. \end{aligned}$$

(13)

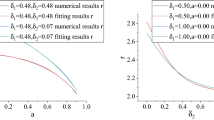
Therefore, $\sigma$ is bottom bounded by a value $\sigma _\ell$ or $\sigma _\lambda$, depending on the BH spin and the Carter constant. The limiting angle $\sigma _\lambda$ is shown in Fig. 4 for $\ell \in \{\ell _{mso}^\pm , \ell _{mbo}^\pm \}$ for BHs with spin $a\in [0,1]$. It is clear how $\sigma _\lambda$ changes for the co-rotating and counter-rotating case, and for slowly spinning and fast spinning BHs for value $\ell =\ell _{mso}^\pm$. Solutions $r_\lambda$, for $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm ,\ell _{\gamma }^\pm ,\ell _{\mathbf{\mathrm{T}}}\}$, are shown in Fig. 3 together with radii $\{r_{mso}^\pm ,r_{mbo}^\pm ,r_{\gamma }^\pm ,r_{\mathbf{\mathrm{T}}}\}$. Solutions $(\sigma _\lambda ,q_\lambda )$, relative to the cases $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm ,\ell _{\gamma }^\pm ,\ell _{\mathbf{\mathrm{T}}}\}$, are shown in Figs. 2 and 4. In Fig. 2 left panel we also show the celestial coordinate $\alpha$ as function of the BH dimensionless spin a, for $\sigma =1$, evaluated on the parameter $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm ,\ell _{\gamma }^\pm \}$.

Fig. 2

For $\ell \gtrless 0$ there is $\alpha \lessgtr 0$ respectively, and solutions $(-\alpha )$ are not represented. Quantity $q_\lambda$ is in Eq. 12, spin $a_q$ is in Eq. 17. Right panel is a close up view of the center panel

Fig. 3

Radius $r_\lambda$ (solid curves) and $r_{\mathbf{\mathrm{T}}}$ (right panel: dotted-dashed curves) are plotted for $\ell \in \{\ell _\gamma ^\pm ,\ell _{mbo}^\pm ,\ell _{mso}^\pm \}$ (cyan, blue,darker-blue) together with the radii $\{r_\gamma ^\pm ,r_{mbo}^\pm ,r_{mso}^\pm \}$ (dashed curves). Spin $a_{\lambda }^-$ is in Eq. 38. Left panel is a close-up view of the center panel

Fig. 4

Quantity $\sigma _\lambda$ of Eq. 13 for $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm \}$. Left panel is a close-up view of the right panel. Maximum value $(a_\sigma , \sigma _\sigma )$ is in Eq. 38

Parameter $\ell =\ell _{mso}^-$

The case $\ell =\ell _{mso}^-$ is illustrated in Fig. 5, where we show the first results of the analysis for this constraint by giving the constrained $\beta$ as a function of the spin a for all possible $\sigma$ (left upper panel), and as function of the angle $\sigma$ for each BH spin a (central upper panel), and finally as function of the celestial coordinate $\alpha$ for $\sigma \in [0,1]$ and for different a, as signed on the curves. Each point of a curve is for a different $\sigma$. These panels provide immediate information on the parts of shadow boundary correspondent to null geodesics with $\ell =\ell _{mso}^-$ for different $(\sigma , a)$. Lower panels summarize the results for this constraint, by relating the coordinates $(\beta ,\alpha )$ to (r, q), in the entire range of possible a and $\sigma$.

Thus, as clear also from Fig. 5, photons with $\ell =\ell _{mso}^-$ can be observed for large latitudes, i.e. $\sigma \gtrapprox 0.53$. The coordinate $\beta$ (in magnitude) increases with $\sigma$ and decreases with a for $\sigma <\sigma _\sigma$ and $a<a_\sigma$ (where $a_{\sigma }\equiv 0.98217$, and $\sigma _{\sigma }\equiv 0.563773$—see Fig. 4).

Considering $\beta$ for different a and $\sigma$, it is clear that difference appears for large latitude angles, i.e. $\sigma >\sigma _\sigma$, and small $\sigma \in [0.53,\sigma _\sigma ]$. Angle $\sigma _\sigma$ (and spin $a=a_\sigma$) is a critical value where there can be $\beta =0$. With $\sigma >\sigma _\sigma$ and $a>a_\sigma$, solutions appear for small values of $(\beta ,\alpha )$ in magnitude. The external regions of the plane $\alpha -\beta$, correspondent to the larger values of $(\beta ,\alpha )$ in magnitude, distinguish slower from faster spinning BHs, and the smaller $(\sigma \approx 0.56)$ from larger latitudinal angles.

Fig. 5

Case $\ell =\ell _{mso}^-$. Upper panels: each point of a solid curve is for a different $\sigma$. Dotted-dashed lines are for different $\sigma$ signed on the curves. Each point of a dotted-dashed curve is for a different spin a. Bottom panels: each point of a curve is for a different $\sigma$

From Figs. 2 and 3 we see that $r_\lambda$ and $q_\lambda$ are constant for fixed a and different $\alpha$ (and confirmed also by Fig. 5). The radius $r\in [1,3]$ and parameter q decrease with the BH dimensionless spin and the $\beta$ in magnitude and q ranges decrease with the BH spin. The celestial coordinate $\alpha$ is negative, since $\ell >0$. As shown in Figs. 2 and 5 the magnitude $\alpha$ decreases with a and q, increases with r and the range of $\alpha$ values increases with r and decreases with a.

Parameter $\ell =\ell _{mso}^+$

Photons with $\ell =\ell _{mso}^+$ are considered in Fig. 6. It is clear how $|\beta |$ increases with the BH spin and the angle $\sigma >0.479$. For $\sigma >0.55$ there is $|\beta |>0$. For this constraint, small values of $(\alpha ,\beta )$ (in magnitude), i.e. the inner regions of the $\alpha -\beta$ plane, characterize slowly spinning BHs. From Fig. 8 lower panels (and Fig. 2 it is clear as r and q are constant for different $(\sigma ,\beta ,\alpha )$. The radius $r_\lambda$ and the quantity $q_\lambda$ are larger then in for $\ell =\ell _{mso}^-$, increasing with the BH spin. The range of values of the celestial coordinate $\beta$ increases with (r, a). On the other hand, the range of values for the $\alpha$ coordinate increases with (r, a, q).

Fig. 6

Analysis of the $\ell =\ell _{mso}^+$ case. (For further details see Fig. 5)

Fig. 7

Case $\ell =\ell _{mbo}^+$. (For further details see Fig. 5)

Fig. 8

Case $\ell =\ell _{mbo}^-$. (For further details see Fig. 5)

Parameter $\ell =\ell _{mbo}^+$

Figure 7 present the results for $\ell =\ell _{mbo}^+$. Coordinate $|\beta |$ increases with the angle $\sigma >0.55$ and the BH spin a. For $\sigma \gg 0.58$ there is $|\beta |>0$. Smaller values of $(\alpha ,\beta )$ (in magnitude), coincident with the inner regions of the $\alpha -\beta$ plane, identify the slowly spinning BHs. $|\beta |$ also increases with (a, r, q), according to Fig. 7. Quantities r and q increase with a.

Parameter $\ell =\ell _{mbo}^-$

The case $\ell =\ell _{mbo}^-$ is in Fig. 8. Celestial coordinate $|\beta |$ decreases with spin and increases with $\sigma >0.593$. These curves for fast spinning BHs can be observed in the inner regions of the $\alpha -\beta$ plane. The coordinate $|\alpha |$, the range of $\alpha$ values and (r, q) decrease (in magnitude) with the spin.

Parameter $\ell =\ell _{\gamma }^\pm$

For $\ell =\ell _{\gamma }^\pm$ there are the photon circular orbits $r_{\gamma }^\pm$, on the equatorial plane, where $q=0$ and $\sigma =1$.

Fig. 9

Analysis for $\ell =\ell _{\mathbf{\mathrm{T}}}$. Upper panels: each point of the solid curve is for a different angle $\sigma _{\mathbf{\mathrm{T}}}$. Each point of a dotted-dashed curve is for a different a. As $\ell _{\mathbf{\mathrm{T}}}<0$, there is $\alpha >0$, the analysis is for $(\beta>0,\alpha >0)$. Bottom left panel: each point of a curve is for a different radius $r_{\mathbf{\mathrm{T}}}$. Bottom right panel: each point of each curve is for a different angle $\sigma _{\mathbf{\mathrm{T}}}$

Fig. 10

Analysis for $\ell =\ell _{\mathbf{\mathrm{T}}}$. Left and center panels: each point of a curve is for a different $\sigma _{\mathbf{\mathrm{T}}}$. Right panel: each point of a curve is for a different radius $r_{\mathbf{\mathrm{T}}}$

Fig. 11

Analysis for $\ell =\ell _{\mathbf{\mathrm{T}}}$. Left panel: each point of a curve is for a different $\ell _{\mathbf{\mathrm{T}}}$. Center panel: each point of a curve is a different $\sigma _{\mathbf{\mathrm{T}}}$. Right panel: each point of a curve is a different radius $r_{\mathbf{\mathrm{T}}}$. For further details see also caption of Fig. 10

Fig. 12

Analysis for $\ell =\ell _{\mathbf{\mathrm{T}}}$ Left panel: each point is for a different $\ell _{\mathbf{\mathrm{T}}}$. Middle panel: each point of a curve is for a different angle $\sigma _{\mathbf{\mathrm{T}}}$. Right panel: each point of a curve is for a different radius $r_{\mathbf{\mathrm{T}}}$. For further details see also caption of Fig. 10

Fig. 13

Cases $\ell =\{\ell _{mbo}^\pm ,\ell _{mso}^\pm \}$. Left panel: merging of Figs. 5, 6, 7 and 8 right panels. Dotted-dashed lines are for spin $a\in [0,1]$ and for different angles $\sigma$. (Each point of a fixed curve is for a different spin a). Solid lines are for $\sigma \in [0,1]$ and for different spin. (Each point of each curve is for a different angle $\sigma$). Right panel: each point of each curve is for a different angle $\sigma$)

Parameter $\ell =\ell _{\mathbf{\mathrm{T}}}$

The case of photons from the inversion surfaces, analyzed assuming $\ell =\ell _{\mathbf{\mathrm{T}}}$, is shown in Fig. 9 where $\beta (\alpha )$ for this impact parameter is shown at different $\sigma$ and spin on the inversion surface, and the celestial coordinate $\beta$ is then related to $(r_{\mathbf{\mathrm{T}}}, \sigma _{\mathbf{\mathrm{T}}})$. Fig. 10 relate $\alpha$ to $(q,r_{\mathbf{\mathrm{T}}},\sigma _{\mathbf{\mathrm{T}}})$, while $(r_{\mathbf{\mathrm{T}}},\sigma _{\mathbf{\mathrm{T}}},q,\ell )$ are analyzed in Figs. 11 and 12. Within this constraint we consider $q\ge 0$, and $\dot{\phi }=0$ for the inversion points i.e.

$$\begin{aligned} \mathcal {F}_{\mathbf{\mathrm{T}}}\equiv a^2 (\sigma -1) \ell -2 a r \sigma -(r-2) r \ell =0. \end{aligned}$$

(14)

There is $\alpha >0$ since $\ell _{\mathbf{\mathrm{T}}}<0$, and in Fig. 9 we restricted the analysis to $(\beta>0,\alpha >0)$. Note that for $\ell =\ell _{\mathbf{\mathrm{T}}}$ function $\beta (\alpha )$ is strongly distinct from the case $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm \}$—see also Fig. 3.

For fixed $\alpha$, where $4.8\lessapprox |\beta | \lessapprox 5.2$, the celestial coordinate $\beta (\alpha )$ decreases (in magnitude) with the BH spin. $|\beta |$ increases linearly with $r_{\mathbf{\mathrm{T}}}>2.5$, decreases with a for fixed $(\alpha ,\sigma _{\mathbf{\mathrm{T}}},q)$, and it increases with $\sigma _{\mathbf{\mathrm{T}}}$ and q (smaller values of q characterize fast spinning BHs). Considering Figs. 10, 11 and 12 for $\ell =\ell _{\mathbf{\mathrm{T}}}$, quantity q, where $22\lessapprox q\lessapprox 27$, increases with $|\alpha |<2$. The coordinate $\beta$ is maximum for $|\beta |\approx 5.196$ where $(r_{\mathbf{\mathrm{T}}}=3, q=27)$ for $a=1$ and $\sigma _{\mathbf{\mathrm{T}}}=1$. For $\sigma _{\mathbf{\mathrm{T}}}\approx 0$ there is $(r_{\mathbf{\mathrm{T}}}=2.41421, |\beta |=4.82843)$, there is $q= 22.31$ for $\sigma _{\mathbf{\mathrm{T}}}\approx 0$ and $a=1$.

Celestial coordinate $|\alpha |$ increases with q. Then, $|\alpha |$ (and $\alpha$ range) increases with a and $\sigma _{\mathbf{\mathrm{T}}}$. Quantity q decreases in general with a and increases with $\sigma _{\mathbf{\mathrm{T}}}$. Radius r increases with $(|\alpha |,\sigma _{\mathbf{\mathrm{T}}},q)$. However $r_{\mathbf{\mathrm{T}}}$ decreases with a only for the limiting value $\sigma _{\mathbf{\mathrm{T}}}\lessapprox 0.63$ (related to the inversion surfaces maximum [55]).

Final remarks on the cases $\ell =\{\ell _{mbo}^\pm ,\ell _{mso}^\pm ,\ell _{\mathbf{\mathrm{T}}}\}$

Figure 13, merging of Figs. 5, 6, 7, 8 upper right panels, show cases $\ell =\{\ell _{mbo}^\pm ,\ell _{mso}^\pm \}$. The shadow boundary regions correspondent to the inversion surfaces are completely distinct from the cases correspondent to $\ell =\{\ell _{mbo}^\pm ,\ell _{mso}^\pm \}$. Furthermore, despite there is $\ell _{\mathbf{\mathrm{T}}}<0$, the shadows parts in the fast spinning BHs correspond to smaller values of $|\beta |$ (and larger range of $|\alpha |$).

Comparing profiles of Figs. 5, 6, 7 and 8 upper right panels and Figs. 9 and 13, it can be seen that in general, orbits for $\ell = \ell _{\mathbf{\mathrm{T}}}$ are located approximately at the central region of the shadow boundary, $\ell _{mbo}^\pm$ is more external (larger values of $\alpha$ in magnitude), $\ell _{mso}^\pm$ is more internal.

Analysis of $\sigma _\lambda$ in Fig. 4 shows that, for $\ell =\ell _{mso}^-$, the angle $\sigma _\lambda$ increases with the BH spin a to the maximum value at $a=a_\sigma$. For $\ell =\{\ell _{mso}^+,\ell _{mbo}^+\}$, the angle $\sigma _\lambda$ decreases with a and, for $\ell =\ell _{mbo}^-$, increases with a. There is

$$\begin{aligned} \sigma _\lambda (\ell _{mbo}^-)>\sigma _\lambda (\ell _{mbo}^+)>\sigma _\lambda (\ell _{mso}^-)>\sigma _\lambda (\ell _{mso}^+), \end{aligned}$$

(15)

and in general $\sigma _\lambda \gtrapprox 0.479$.

From Fig. 2 it is noted that for $\sigma =1$ coordinate $\alpha$ decreases (in magnitude) with the BH spin for the co-rotating cases and increases with spin for the counter-rotating case; there is

$$\begin{aligned} -\alpha _\lambda (\ell _{mso}^-)>-\alpha _\lambda (\ell _{mbo}^-)>-\alpha _\lambda (\ell _{\gamma }^-)\quad \hbox {and}\quad \alpha _\lambda (\ell _{\gamma }^+)>\alpha _\lambda (\ell _{mbo}^+)>\alpha _\lambda (\ell _{mso}^+). \end{aligned}$$

(16)

On the other hand, $q_\lambda$ increases with a for the counter-rotating cases and decreases with a in the co-rotating cases; there is

$$\begin{aligned} & \hbox {for}\quad a>a_q:\quad q_\lambda (\ell _{mso}^+)>q_\lambda (\ell _{mbo}^+)>q_\lambda (\ell _{mso}^-)>q_\lambda (\ell _{mbo}^-),\quad \hbox {where}\quad a_q\equiv 0.153054, \nonumber \\{} &\quad {} \hbox {for}\quad a\in [0,a_q[:\quad q_\lambda (\ell _{mso}^+)>q_\lambda (\ell _{mso}^-)>q_\lambda (\ell _{mbo}^+)>q_\lambda (\ell _{mbo}^-), \end{aligned}$$

(17)

see Fig. 2. From Fig. 3 (and Fig. 7) it is clear that $r_\lambda$ decreases with the BH spin for the co-rotating cases and it increases with the BH spin for the counter-rotating case. For $\ell \in \{\ell _{mbo}^+,\ell _{mso}^+\}$ there is $r_\lambda \in [r_{\gamma }^+,r_{\mathbf{\mathrm{T}}}(\sigma =1)]$. However for $\ell =\ell _{mso}^-$ there is:

$$\begin{aligned} \hbox {for}\quad a<a_{\lambda }^-:\quad r_\lambda \in [r_{\gamma }^-,r_{mbo}^-], \quad \hbox {and for}\quad a>a_{\lambda }^-:\quad r_\lambda \in [r_{mbo}^-,r_{mso}^-]. \end{aligned}$$

(18)

From Fig. 13, showing the superimposition of the Figs. 5, 6, 7 and 8-right panels, it is possible to note that the BH spin is capable to distinguish the cases $\{\ell _{mbo}^\pm ,\ell _{mso}^{\pm }\}$. For the static case ($a=0$) the shadow boundary parts are very close and practically indistinguishable. The static case separates the co-rotating case (spread on the more internal and smaller region of the boundary-smaller values of $(|\alpha |,|\beta |)$) and the counter-rotating case (on a more external-larger values of $(|\alpha |,|\beta |)$) for different angles $\sigma$.

For an extreme Kerr BH there is

$$\begin{aligned} C_\beta (\ell _{mbo}^+)>C_\beta (\ell _{mso}^+)>C_\beta (\ell _{mso}^-)>C_\beta (\ell _{mso}^-), \end{aligned}$$

(19)

where $C_\beta (\ell _{u})>C_\beta (\ell _{v})$ indicates that the curve $C_\beta (\ell _{u})$ for a momentum $\ell _u$ is more external (on the shadow boundary as in the Fig. 13 than the curve $C_\beta (\ell _{v})$ for a momentum $\ell _u$, for different angles $\sigma$. Each curve has been evaluated for $\sigma \in [0,1]$. Celestial coordinate $|\beta |$ increases generally for fixed $\alpha$ with the BH spin for the counter-rotating case and decreases with the BH spin for co-rotating case; $\alpha$ in magnitude increases for fixed $\beta$ with the BH spin and the magnitude of $\ell ^+$ for the counter-rotating case, viceversa, $\alpha$ in magnitude decreases for fixed $\beta$ with the BH spin and the $\ell ^-$ for the co-rotating case. Whereby the co-rotating and counter-rotating cases are sharply distinct and distinguishable for each angle.

Note, from Fig. 3 it is clear how in the co-rotating case $r_\lambda$ can cross the outer ergosurface for fast spinning BHs (depending on the angle $\sigma$). We will focus on this special case in Sec.4.14.

In general, considering $r_\lambda$ as function of a, there is $r_\lambda ^+>r_\lambda ^-$ for the counter-rotating and co-rotating cases. In the co-rotating case the radius $r_\lambda ^-$ decreases with the BH spin and there is $r\approx 3$ at $a\approx 0$. Viceversa $r_\lambda ^+$ increases with the BH spin from $r\approx 3$ at $a\approx 0$ to $r\approx 4$ for $a\approx 1$. There is $r_\lambda ^+(\ell _*^+)>r_{\mathbf{\mathrm{T}}}$ for $\ell _*^+\in \{\ell _{mbo}^+,\ell _{mso}^+\}$ (see also Fig. 3) for any angle $\sigma$. Therefore photons from these inversion surfaces cannot be observed from the BH shadow boundary. However, as proved in this analysis, photons with $-\ell ^+=-\ell _{mso}^+$ can be part of the BH shadow boundary. Furthermore, there is

$$\begin{aligned} r_\lambda ^+(\ell _{\gamma }^+)>r_\lambda ^+(\ell _{mbo}^+)>r_\lambda ^+(\ell _{mso}^+)>r_\lambda ^-(\ell _{mso}^-)> r_\lambda ^-(\ell _{mbo}^-)>r_\lambda ^-(\ell _{\gamma }^-). \end{aligned}$$

(20)

In Sect. 4.8 we analyze in additional details shadows from $r_\lambda \in \{r_{mbo}^-,r_{mso}^-\}$.

4.2 Assuming $r\in \{r_{mbo}^-,r_{mso}^-\}$

In general, photons spherical orbits, solutions of system $\mathfrak {(R)}$ with $r_\lambda \in \{r_{mso}^\pm ,r_{mbo}^\pm \}$, are for an impact parameter $\ell \ne \{\ell _{mso}^\pm ,\ell _{mbo}^\pm \}$ and constant $q=q_\lambda \ge 0$. (The radius $r_\lambda$ for $\ell \in \{\ell _{\gamma }^\pm ,\ell _{mbo}^\pm ,\ell _{mso}^\pm \}$ is compared in Fig. 3 to the radii of the geodesic structures $r\in \{r_{\gamma }^\pm ,r_{mbo}^\pm ,r_{mso}^\pm \}$.) In this section we assume $r_\lambda \in [r_{mbo}^\pm ,r_{mso}^\pm ]$ and $r_\lambda \in [r_{\gamma }^\pm ,r_{mbo}^\pm ]$.

We will show that solutions of $(\mathfrak {R})$ for $r_\lambda \in [r_{mbo}^\pm ,r_{mso}^\pm ]$ and $r_\lambda \in [r_{\gamma }^\pm ,r_{mbo}^\pm ]$ are strongly differentiated. No solutions have been found for $r\in \{r_{mbo}^+, r_{mso}^+\}$, and we focus our study for $r\in \{r_{mbo}^-, r_{mso}^-\}$.

Fig. 14

Case $r=r_{mso}^-$. Each point of a curve is for a different $\sigma$. Upper left panel: each point of a curve is for a different a

Case $r= r_{mso}^-$

From Fig. 14 we see the situation for $r= r_{mso}^-$. There are solutions for co-rotating $(\ell >0)$ and counter-rotating $(\ell <0)$ photon orbits. Coordinate $\alpha$ is larger and positive for the counter-rotating case for $a\ge 0.66$. Coordinate $|\beta |$ is larger for $a\approx 0.85$, and a minimum occurs for $a=1$. $|\beta |$ is greater for $\ell$ small in magnitude, and it increases with q.

Case $r= r_{mbo}^-$

The case $r=r_{mbo}^-$ is shown in Fig. 15 and it is qualitatively similar to the case $r=r_{mso}^-$.

Fig. 15

Case $r=r_{mbo}^-$. (For further details see also caption of Fig. 14)

In the spherical shells $[r_{mbo}^\pm ,r_{mso}^\pm ]$

In general, it can be $r_\lambda \in [r_{mbo}^\pm ,r_{mso}^\pm ]$ for some ranges of values of the impact parameter $\ell$, and we study the general solutions: (a) $r_\lambda \in [r_{mbo}^+,r_{mso}^+]$, for $\ell <0$ and (b) $r_\lambda \in [r_{mbo}^-,r_{mso}^-]$ for $\ell >0$. It is convenient to consider the solution $\ell _\lambda$ of the equation $r=r_\lambda (\ell )$, leading to the impact parameter

$$\begin{aligned} \ell _\lambda \equiv \frac{a^2 (r+1)+(r-3) r^2}{a(1-r)}: r_\lambda (\ell )=r, \end{aligned}$$

(21)

showed in Fig. 16 for different BH spin, with respect to the Kerr spacetime geodesic structure. Below we comment our results focusing first on the co-rotating case and we close this section with the analysis of the counter-rotating photons.

The co-rotating case

Momentum $\ell _\lambda >0$ is shown (for $\sigma \in [0,1]$) in Fig. 16, with the limiting spins

$$\begin{aligned} a_{mso}^*\equiv 0.8528: \ell _\lambda (r_{mso}^-)=0,\quad a_{mbo}^*\equiv 0.516: \ell _\lambda (r_{mbo}^-)=0. \end{aligned}$$

(22)

Assuming $\ell >0$, there is $r_\lambda =r_{mso}^-$ for $a>a_{mso}^*$, and $r_\lambda =r_{mbo}^-$ for $a>a_{mbo}^*$, therefore in general $r\in [r_{mbo}^-,r_{mso}^-]$ only for $a>a_{mbo}^*$ (where $\sigma \in [0,1]$), where further constraints should be applied, considering the full set of equations (5).

From Fig. 3 it can be seen that $r_{\lambda }(\ell _{mso}^-)\in [r_{mbo}^-,r_{mso}^-]$ for $a>a_\lambda ^-$.

More specifically, considering Fig. 16 there is

$$\begin{aligned}{} & {} \hbox {for}\quad a\in [0,a_\lambda ^-[:\quad \ell _{\gamma }^-=\ell _\lambda (r_{\gamma }^-)>\ell _{mbo}^->\ell _{mso}^->\ell _\lambda (r_{mbo}^-)>\ell _\lambda (r_{mso}^-), \nonumber \\{} & {} \hbox {for}\quad a>a_\lambda ^-:\quad \ell _{\gamma }^-=\ell _\lambda (r_{\gamma }^-)>\ell _{mbo}^->\ell _\lambda (r_{mbo}^-)>\ell _{mso}^->\ell _\lambda (r_{mso}^-), \end{aligned}$$

(23)

for all $\sigma \in [0,1]$. Hence, for $\ell >0$, there is $r_\lambda \in [r_{mbo}^-,r_{mso}^-]$, with a momentum $\ell$ smaller then $\ell _{mso}^-$ for $a\in [0,a_\lambda ^-[$. For $a>a_\lambda ^-$ there is $r_\lambda \in [r_{mbo}^-,r_{mso}^-]$, close to $r_{mbo}^-$. (Radius $r_\lambda$ is located in the ergoregion for sufficiently large spins.). Finally, according to the analysis of Fig.17 left panel, there is

$$\begin{aligned} C_\beta (r_{mbo}^-)>C_\beta (r_{mso}^-),\quad \hbox {for}\quad \sigma =1 \end{aligned}$$

(24)

in the plane $\alpha -\beta$, in the sense that the curve correspondent to $r=r_{mbo}^-$ is more external then the curve for $r=r_{mso}^-$. As there is $\sigma =1$, and therefore $\beta =\sqrt{q}$, solutions at $q=0$ are only the curves $r=r_{\gamma }^-$.

From Fig. 17-right panel, we see that for fixed spin $a=1$, radii $r_{mso}^-$ and $r_{mbo}^-$ are inside the outer ergoregion, and there are no solutions for a spin $a<a_{min}$ where, for $r_{mso}^-$, there is $a_{min}\approx 0.86$ (according to limit $a=a_{mso}^\lambda \equiv 0.7851: r_{\lambda }(\ell _{mso}^-)=r_{\epsilon }^+$), for $r_{mbo}^-$ there is $a_{min}=0.66$, for $r_{\epsilon }^+$ there is $a_{min}=0.73$. Coordinate $|\beta |$ increases with $\sigma$. For large BH spins, curves for $r_{mso}^-$ and $r_{mbo}^-$ cross the ergosurface. (It is interesting to note that the ergosurfaces curves cross at different spins.). At fixed $r=r_{mso}^-$, the $\beta$ variation with $\alpha$ distinguishes different BH spins. (In this analysis we selected the cases $\ell >0$, therefore focusing on $\alpha <0$). In this case, however, there is:

$$\begin{aligned} C_\beta (r_{mbo}^-)<C_\beta (r_{mso}^-),\quad \hbox {for}\quad a\approx 1. \end{aligned}$$

(25)

Figure 17-left panel shows $\beta (\alpha )$ for all BH (dimensionless) spins $a\in [0,1]$, for fixed orbits $r\in \{r_{\epsilon }^+,r_{\gamma }^\pm ,r_{mso}^-,r_{mbo}^-,r_{{\mathbf{\mathrm{T}}}},(r_{\gamma }^+-0.1)\}$ on the equatorial plane. Curves exist only for a spin $a>a_{min}$, in agreement also with the analysis of Figs. 14 and 15, where there is

$$\begin{aligned} \hbox {for}\quad \sigma{} & {} =1:\quad a_{\min }(r_{\gamma }^-)\approx 0,\quad a_{\min }(r_{mbo}^-)=0.52,\quad a_{\min }(r_{mso}^-)=0.853, \nonumber \\{} & {} \hspace{3cm} a_{\min }(r_{\gamma }^+)\approx 0,\quad a_{\min }(r_{{\mathbf{\mathrm{T}}}})\approx 0,\quad a_{\min }(r_{\epsilon }^+)=0.71, \end{aligned}$$

(26)

Figure 17. Note, $a_{\min }(r_{mbo}^-)$ corresponds to solution $a_{mbo}^*$, and $a_{\min }(r_{mso}^-)$ to the limiting spin $a_{mso}^*$ and $a_{\min }(r_{\epsilon }^+)$ to $a_{\gamma }^\epsilon : r_{\gamma }^-=r_{\epsilon }^+(\sigma =1)$. Finally, solutions with $\ell \in [\ell _{mbo}^-,\ell _{\gamma }^-]$ or $r_\lambda \in \{r_{mbo}^-,r_{\gamma }^-\}$ are also possible—see Fig. 17.

In conclusion, the analysis on the co-rotating case shows that there are constraints on the spin and on the angle $\sigma$ for the shadow boundary. The second condition explored here sees $r_\lambda$ located in the orbital range for the accretion disk inner edge (or for cusps closer to the BH), addressed for larger poloidal angles and on the equatorial plane (where $q =0$ only in the case of the photon circular orbit on the equatorial plane). In any case, there can be orbits on the outer ergosurface and in the outer ergoregion for fast spinning BHs—see Fig. 3 and discussion in Sect.4.14. However, this analysis proves that for any $\sigma \in [0,1]$ there is (with small impact parameter) a bottom limit, $(a_{min},\sigma _{min})$, for the BH spin and the $\sigma$ coordinate according to Eqs. 22 and 26.

This implies that the contribution to the shadow boundary from co-rotating photons in the ranges considered here are constrained, especially for smaller $\sigma$ and BH spins. Finally, we conclude by stressing that these orbital spherical shells can be in the BH ergoregion¹⁷ and in Sect. 4.14 we shall focus on shadows boundary from photons orbiting the outer ergosurface and the outer ergoregion.

The counter-rotating case

In the counter-rotating case the situation is strongly different. As clear from the analysis of Figs. 2, 4, 6 and 7 there are solutions for $\ell \in \{\ell _{mso}^+,\ell _{mbo}^+\}$.

Considering Fig. 16 we find that

$$\begin{aligned} -\ell _\lambda (r_{mso}^+)>-\ell _{\lambda }(r_{mbo}^+)>-\ell _{\lambda }(r_{\gamma }^+)= -\ell _{\gamma }^+>-\ell _{mbo}^+>-\ell _{mso}^+. \end{aligned}$$

(27)

However, further inspection on the photons trajectories constraints informs that there are no counter-rotating solutions for $r>r_{\gamma }^+$.

Fig. 16

Shadows from the inner edge (Sect. 4.8). $\ell _\lambda$ is in Eq. 21. Left (right) panel shows the situation for the co-rotating (counter-rotating) case, center panel is a close-up view of the left panel

Fig. 17

Shadows from the inner edge (Sect. 4.8). Left panel: there are no solutions for $r=\{r_{mso}^+,r_{mbo}^+\}$). Each point of a curve is for a spin a. $a_{min}$ is the smallest BH spin a solution exists, different for each fixed radius r. Right panel: each point of a curve is for a angle $\sigma$. (It is $\ell >0$ ($\alpha <0$) for $\{r_{mso}^-,r_{mbo}^-,r_{\gamma }^-\}$ and $\ell <0$ ($\alpha >0$) for $\{r_{mso}^+,r_{mbo}^+,r_{\gamma }^+\}$). (Solutions $(-\alpha )$ are not represented)

More generally, there is no solution $r_\lambda >r_{\gamma }^+$ for $\ell <0$ (for any $\sigma$).

On the other hand, there is $r_\lambda <r_{\gamma }^+$ for $\ell \in \{\ell _{mso}^+,\ell _{mbo}^+\}$ that is, in this range of $\ell$ radius $r_\lambda$ cannot be in the range for accretion disks inner edge on the equatorial plane.

Radius $r_{\mathbf{\mathrm{T}}}<r_{\gamma }^+$ is shown, at any $\sigma$, in Fig. 3. Figure 17-left panel shows $\beta (\alpha )$ for all $a\in [0,1]$ and for fixed orbits $r\in \{r_{\epsilon }^+,r_{\gamma }^\pm ,r_{mso}^-,r_{mbo}^-,r_{{\mathbf{\mathrm{T}}}},(r_{\gamma }^+-0.1)\}$ on the equatorial plane (also for the counter-rotating orbits there is a bottom boundary $(a_{min},\sigma _{min})$ for the BH spin and $\sigma$). If there is $\sigma =1$, and therefore $\beta =\sqrt{q}$, solutions at $q=0$ are only the orbits $r=r_{\gamma }^+$. Figure 17 shows that on the equatorial plane the shadow from the inversion point, i.e. $r=r_{\mathbf{\mathrm{T}}}$, is almost constant in $\alpha$ for different spins $a\in [a_{min} (r_{\mathbf{\mathrm{T}}}),1]$. It is also clear how the variation with spin for the curves $\beta (\alpha )$ is opposite for $r_{\gamma }^-$ and $r_{\gamma }^+$, and for $r_\epsilon ^+$ and $\{r_{mso}^-,r_{mbo}^-,r_{\mathbf{\mathrm{T}}},(r_{\gamma }^+-0.1)\}$ as $\beta$ is greater for the fast spinning BHs and $|\alpha |$ is large for small spin. In the counter-rotating case, $|\beta |$ increases with decreasing r—Fig. 17.

The analysis of Fig. 16 confirms the constrains on the specific angular momentum raising questions on the observability of the counter-rotating case as defined in this framework.

4.3 Shadows from the outer ergoregion

Fig. 18

Left panel: solutions $(\sigma ,a): r_\lambda (\ell _*)=r_{\epsilon }^+$, $r_\lambda$ is in Eq.12 and $\ell _*\in \{\ell _{mso}^-,\ell _{mbo}^-,\ell _{\gamma }^-\}$. For $\sigma =1$ there is $r_\lambda (r_*)=r_\epsilon ^+$ in the geometries with $a_*\in \{a_{mso}^\lambda ,a_{mbo}^\lambda ,a_{\gamma }^\lambda \}$ in Eq. 29. Center (right) panel: solutions $\sigma (a)$ of $r_{\gamma }^-=r_{\epsilon }^+(r_x)$, $r_{mbo}^-=r_{\epsilon }^+(r_x)$, $r_{mso}^-=r_{\epsilon }^+(r_x)$

Fig. 19

Case $r=r_{\epsilon }^+$. Each point of a curve is for a different $\sigma$. Upper left panel: each point of a curve is for a different a

Fig. 20

Case $r=r_x\in ]r_+,r_\epsilon ^+]$ of Eq. 28. (For further details see also Fig. 19)

There can be stable, bound and unstable co-rotating circular orbits in the outer ergoregion of the fast spinning Kerr BHs. On the other hand, the inner edge of a co-rotating torus, are possible inside the ergoregion for large BHs spins [69]. In this section we consider the possibility that the outer ergoregion (and the outer ergosurface) will be “imprinted” in the shadow boundary, i.e. here we analyze solutions of the equations $(\mathfrak {R})$ for $r\in ]r_+,r_\epsilon ^+]$. First, from the analysis of Fig. 3 it is clear, how (depending on the angle $\sigma$) in the co-rotating case, radius $r_\lambda$ can cross the outer ergosurface for large BH spins.

Figure 17 shows the shadow profiles from fixed orbits $r\in \{r_{\epsilon }^+,r_{\gamma }^\pm ,r_{mso}^-,r_{mbo}^-,r_{{\mathbf{\mathrm{T}}}},(r_{\gamma }^+-0.1)\}$, on the equatorial plane $\sigma =1$ for all BH spins $a\in [0,1]$. (No counter-rotating solutions have been found for $r>r_{\gamma }^+$, and in particular for $r\in [ r_{mso}^+,r_{mbo}^+]$).

The curve $\beta (\alpha )$, correspondent to the photons orbit coincident with the outer ergosurface ($r=r_\epsilon ^+$), crosses the curve $\beta (\alpha )$ for fixed $r\in \{r_{mso}^-,r_{mbo}^-\}$ for determined values of $\alpha$ correspondent in general to different BH spins (each point of the curve represents a different spin, from a maximum $a=1$, marked with a blue point, to a minimum $a_{min}$, different for each curve $\beta (\alpha )$ for fixed orbit r and marked with a red point). There is $a\in [a_{min} (r_\epsilon ^+),1]$ where $a_{min} (r_\epsilon ^+)=0.71$. Therefore, there is $r_{\epsilon }^+\in [r_{mbo}^-,r_{mso}^-]$ only for some ranges of BH spins (in agreement with the analysis of Fig. 3). From Fig. 17 it is easy to see that, as there is $\sigma =1$ and therefore $\beta =\sqrt{q}$, solutions at $q=0$ are only the curves $r=r_{\gamma }^\pm$.

Therefore we set, at different angles $\sigma \in [0,1]$, the condition $r=r_x\in ]r_+,r_{\epsilon }^+[$ and $r=r_\epsilon ^+$ respectively, where

$$\begin{aligned} r_x\equiv \frac{r_\epsilon ^+-r_+}{5}+r_+. \end{aligned}$$

(28)

In Fig. 19 the shadow boundary is shown for $r=r_\epsilon ^+$, for different a and $\sigma$. The plots illustrate the dependence of the constrained coordinates $\beta$ and $\alpha$ from parameters $\ell$ and q, and the curves $\ell (q)$ for $r=r_\epsilon ^+$. The analysis of Fig. 19 is reproduced in Fig. 20 for $r=r_x$. In Figs. 19 and 20, as $\ell >0$ on $r=r_\epsilon ^+$ and $r=r_x$, there is $\alpha <0$, here we restricted the analysis to $(\beta >0,\alpha <0)$.

From the outer ergosurface

Here we consider the case $r=r_\epsilon ^+$.

From Fig. 18 left panel we see the solutions $(\sigma ,a): r_\lambda (\ell _*)=r_{\epsilon }^+$, for $\sigma \in [0,1]$, and $\ell _*\in \{\ell _{mso}^-,\ell _{mbo}^-,\ell _{\gamma }^-\}$. For $\sigma =1$ there is $r_\lambda (\ell _*)=r_\epsilon ^+$ in the geometries with $a\ge a_*$ where $a_*\in \{a_{mso}^\lambda ,a_{mbo}^\lambda ,a_{\gamma }^\lambda \}$ defined as follows

$$\begin{aligned} \hbox {for}\quad \sigma =1:\quad a_{mso}^\lambda \equiv 0.7851: r_{\lambda }(\ell _{mso}^-)=r_{\epsilon }^+,\quad a_{mbo}^\lambda \equiv 0.76: r_{\lambda }(\ell _{mbo}^-)=r_{\epsilon }^+,\quad a_{\gamma }^\lambda \equiv 0.7071: r_{\lambda }(\ell _{\gamma }^-)=r_{\epsilon }^+, \end{aligned}$$

(29)

radius $r_\lambda (\ell _*)$ for $\ell _*\in \{\ell _{mso}^-,\ell _{mbo}^-,\ell _{\gamma }^-\}$ is in the outer ergoregion in the geometries with BH spins $a\ge a_*$ where $a_*\in \{a_{mso}^\lambda ,a_{mbo}^\lambda ,a_{\gamma }^\lambda \}$ respectively, see Fig. 18.

In Fig. 18 center and right panel we show the solutions $\sigma (a)$ of the equations $r_{*}=\{r_{\epsilon }^+,r_x\}$, where $r_*\in \{r_{\gamma }^-,r_{mbo}^-,r_{mso}^-\}$. It is convenient to introduce the spins

$$\begin{aligned} a_{mbo}^\epsilon \equiv 0.828427: r_{mbo}^-=r_{\epsilon }^+(\sigma =1),\quad a_{\gamma }^\epsilon \equiv 0.707107: r_{\gamma }^-=r_{\epsilon }^+(\sigma =1),\quad a_{mso}^\epsilon \equiv 0.942809: r_{mso}^-=r_{\epsilon }^+(\sigma =1), \end{aligned}$$

(30)

similarly spins $\{a_{\gamma }^x,a_{mbo}^x,a_{mso}^x\}$ are defined by $r_{*}=r_x(\sigma =1)$—see Fig. 18. Note, in general $\{a_{mso}^\lambda ,a_{mbo}^\lambda ,a_{\gamma }^\lambda \}$ do not coincide with spins $\{a_{mso}^\epsilon ,a_{mbo}^\epsilon ,a_{\gamma }^\epsilon \}$ (both defined for $\sigma =1$) in Eq.30. However, there is $a_{\gamma }^\lambda =a_{\gamma }^\epsilon$.

Results of this analysis are shown in Figs. 19 and 20: we note that the coordinate $|\beta |$ decreases with $\ell$ and $|\alpha |<3.5$, and increases with $q\lessapprox 16$. At fixed $\alpha$, it decreases with a and increases with $\sigma$. Quantity q decreases with $\alpha$ in magnitude, $|\alpha |$ increases with $\ell$ and decreases with q.

From the outer ergoregion

A qualitatively similar situation occurs for a point $r=r_x$, located inside the outer ergoregion—Fig. 20 but with some notable differences with respect to the orbits from the outer ergosurface. In Fig. 21 there are the shadows boundaries for different $(a,\sigma )$ for $\ell =\{\ell _{mbo}^\pm ,\ell _{mso}^\pm ,\ell _{\mathbf{\mathrm{T}}}\}$ and $r=\{r_\epsilon ^+,r_x\}$, (merging of Figs. 5, 6, 7, 8 and 13 upper right panles). The analysis in Fig. 21 allows to clarify how the situation for photons orbiting in the ergoregion, at $r_\lambda =r_x$, appears different as compared to $r_\lambda =r_\epsilon ^+$. At $a=1$, the curve $\beta (\alpha )$ at $r_\lambda = r_\epsilon ^+$ is more external than the curve at $r_\lambda = r_x$ (in agreement with the situation for the other curves $\beta (\alpha )$).

However,differences appear with the variation of the BH spin at fixed radius $r_\lambda$. For $r_\lambda =r_\epsilon ^+$, the curve moves inward with increasing of the BH spin, viceversa the curve corresponding to the orbits at $r_\lambda =r_x$ moves inward with decreasing of the BH spin in contrast with the other curves for the co-rotating orbits. (We remind that $r_x$ is a function of $(a,\sigma )$). This divergence appears also from the comparison of Fig. 19 and 20, also for the curve $\beta (\alpha )$ at different BH spin for a fixed angle.

Therefore, orbits in the outer ergosurface and the outer ergoregion are possible for BH spin $a>a_{min}$ and $\sigma \in [\sigma _{min},1]$, where the $\sigma$ are explored in Fig. 17 and the limits for a general $\ell$ are in Figs. 18, 19 and 20. In general $|\beta |$ is greatest for $\sigma =1$.

Fig. 21

Cases $\ell =\{\ell _{mbo}^\pm ,\ell _{mso}^\pm ,\ell _{\mathbf{\mathrm{T}}}\}$ and $r=\{r_\epsilon ^+,r_x\}$, merging of Figs. 6, 7, 8 and 13. Each point of a curve is for a different value of $\sigma$

Figures 22 and 23 show the location of the photons considered in this analysis (cases $\ell =\{\ell _{mbo}^\pm ,\ell _{mso}^\pm ,\ell _{\mathbf{\mathrm{T}}}\}$ and $r=\{r_\epsilon ^+,r_x\}$) on the BH shadow boundary, for selected values of $(a,\sigma )$, complementing the analysis of Sect.4.1.

Fig. 22

Boundary of the BH shadows. Dashed blue vertical lines are $\ell =\ell _{\mathbf{\mathrm{T}}}$. Vertical orange, purple and cyan lines are $\ell \in \{\ell _{mbo}^\pm ,\ell _{\gamma }^\pm ,\ell _{mso}^\pm \}$ respectively. (Pink solid, pink dotted-dashed, red, green) lines are for $r=\{r_\epsilon ^+,r_x,r_{mbo}^-,r=r_{mso}^-\}$. ($(-\alpha )$ for simplicity have been omitted here)

Fig. 23

A close view of the case ($a\approx 1$,$\sigma =0.71$) in Fig. 22

Figure 21 show cases $\ell =\{\ell _{mbo}^\pm ,\ell _{mso}^\pm ,\ell _{\mathbf{\mathrm{T}}}\}$ and $r=\{r_\epsilon ^+,r_x\}$. Curves at $\{\ell _{mbo}^-,\ell _{mso}^-\}$ are inside the outer ergoregion. There is

$$\begin{aligned} C_\beta (a=0.72,r_\epsilon ^+)< C_\beta (a=1,r_\epsilon ^+)< C_\beta (a=1,r_x)<C_\beta (a=0.97,r_x)<C_\beta (a=1,\ell _{mso}^-)<C_\beta (a=1,\ell _{mbo}^-) \end{aligned}$$

(31)

where $C_\beta (\textbf{Y})>C_\beta (\textbf{Z})$ indicates that the curve $C_\beta (\textbf{Y})$ for a parameter set $\textbf{Y}$ is more external (on the shadow boundary as in the Fig. 21) than the curve $C_\beta (\textbf{Z})$ for the set of parameters $\textbf{Z}$, for different $\sigma \in [0,1]$.

Therefore, at fixed spin, the curve of the plane $\alpha -\beta$, from orbits from the outer ergosurface, is more external than the curve correspondent to photon orbits $r_x$ inside the ergoregion. On the outer ergosurface, as for the other cases with fixed $\ell >0$, the largest BH spins correspond to innermost curves of the plane $\alpha -\beta$. Viceversa, in agreement with the analysis in Fig. 20, inside the ergoregion (on the orbit $r_x$), the fast spinning BHs correspond to outer curves in the $\alpha -\beta$ plane.

5 Discussion and conclusions

Co-rotating and counter-rotating null geodesics, solutions of set $(\mathfrak {R})$ in Eq. 9 have been constrained by their impact parameter $\ell$ or radii r, and related to particular parts of the shadow boundary. Hence, as results we obtained a map, for all $(\sigma ,a)$, of regions on the shadows boundaries, correspondent to photon spherical orbits with $\ell \in \{\ell _{\mathbf{\mathrm{T}}}(a),\ell _{mso}^\pm (a),\ell _{mbo}^\pm (a),\ell _{\gamma }^\pm (a)\}$, or with radius r in the outer ergoregion, $r\in ]r_+,r_\epsilon ^+]$, in the spherical shells and on the spherical surfaces defined by the radii $r=\{r_{mso}^\pm ,r_{mbo}^\pm ,r_{\gamma }^\pm \}$. Results are illustrated in Fig. 22 (for fixed angle $\sigma$ and spin a), in Fig. 21 and Figs. 5, 6, 7, 8, 13—upper right panels (for all angles $\sigma$ and spin a).

Note, fixing $(a,\sigma )$, solutions of $(\mathfrak {R})$ with fixed $\ell$ or r, are a set of points on the shadow boundary represented by the vertical lines in the plane $\alpha -\beta$ of Fig. 22.

On the other hand, solving $(\mathfrak {R})$ with constraints on $\ell$ or r, at fixed a and for all $\sigma \in [0,1]$, provides curves of the $\alpha -\beta$ plane, made of points of the shadow boundaries relative to the constrained null spherical geodesics, for all values of $\sigma$. The results of this analysis are shown in Figs. 13, 21, and as solid curves of Fig. 5, 6, 7 and 8 upper right panels. In these plots each solid curve corresponds to a fixed spin, and each point of each solid curve is for fixed $\sigma$. Dotted-dashed lines are for a fixed $\sigma$, and each point of a dotted-dashed line is for a different spin. Then $(\alpha ,\beta )$ have been then directly related, for each constraint, to the quantities $(a,\sigma ,r,\ell ,q)$ in Figs. 10, 11 and 12 and Figs. 5, 6, 7, 8, 13.

Findings for photons spherical orbits in the outer ergoregion are shown in Figs. 19, 20, 21 and discussed in Sect.4.14. The possibility to observe the emission from the outer ergosurface and from the inside the outer ergoregion is limited for BH spin $a>a_{min}$ as from a angle $\sigma \in [\sigma _{min},1]$ (in general $|\beta |$ is greater for $\sigma =1$) where $(a_{min},\sigma _{min})$ have been discussed in Sect. 4.14 see also Fig. 22.

In general there are solutions for parameters $\ell \in \{\ell _{mso}^+,\ell _{mbo}^+,\ell _{\gamma }^+,\ell _{{\mathbf{\mathrm{T}}}}\}$—see for example Figs. 6, 7, while no solutions have been found for $r\in \{r_{mbo}^+, r_{mso}^+\}$—Sect. 4.8.

Figures 13 and 21 summarize results showing the difference between the co-rotating and counter-rotating photon orbits considered within the different constraints, at different $(a,\sigma )$.

Results for $\ell =\ell _{mso}^-$ are in Fig. 5, solutions are $\sigma \gtrapprox 0.53$ and $\beta$ (in magnitude) increases with $\sigma$ and decreases with a for $\sigma <\sigma _\sigma$ and $a<a_\sigma$—Fig. 4). Differently for $\sigma >\sigma _\sigma$, and $\sigma \in [0.53,\sigma _\sigma ]$. With $(\sigma>\sigma _\sigma , a>a_\sigma )$, solutions appear for small values of $(\beta ,\alpha )$ in magnitude, distinguishing slower from faster spinning BHs, and the smaller $(\sigma \approx 0.56)$ from larger $\sigma$.

Photons with $\ell =\ell _{mso}^+$ are considered in Fig. 6. Inner regions of the $\alpha -\beta$ plane, characterize slowly spinning BHs. $|\beta |$ increases with the BH spin and the angle $\sigma >0.479$. For $\sigma >0.55$ there is $|\beta |>0$. The case $\ell =\ell _{mbo}^-$ is in Fig. 8 and the results for $\ell =\ell _{mbo}^+$ are for Fig. 7. ($\ell =\ell _{\gamma }^\pm$ correspond to photon circular orbits $r_{\gamma }^\pm$, on the equatorial plane($q=0$)). The case of photons from the inversion surfaces, is shown in Figs. 9, 10, 11 and 12. Solutions of $(\mathfrak {R})$ for $r_\lambda \in [r_{mbo}^\pm ,r_{mso}^\pm ]$ and $r_\lambda \in [r_{\gamma }^\pm ,r_{mbo}^\pm ]$ are strongly differentiated and there are no solutions have been found for $r\in \{r_{mbo}^+, r_{mso}^+\}$. The case $r=r_{mbo}^-$ is shown in Fig. 15. Case $r= r_{mso}^-$ is in Fig. 14 for co-rotating and counter-rotating photon orbits. Orbits in the shell $r_\lambda \in [r_{mbo}^+,r_{mso}^+]$ are studied for $\ell <0$ and $\ell >0$ for $r_\lambda \in [r_{mbo}^-,r_{mso}^-]$ only for $a>a_{mbo}^*$, in fact we found solutions on $r_\lambda =r_{mso}^-$ for $a>a_{mso}^*$, and on $r_\lambda =r_{mbo}^-$ for $a>a_{mbo}^*$. On the other hand, from Fig. 3 it can be seen that $r_{\lambda }(\ell _{mso}^-)\in [r_{mbo}^-,r_{mso}^-]$ for $a>a_\lambda ^-$. As clear from the analysis of Figs. 4, 2, 6 and 7, there are solutions for $\ell \in \{\ell _{mso}^+,\ell _{mbo}^+\}$. There are no counter-rotating solutions for $r>r_{\gamma }^+$.

The poles $(\sigma \approx 0)$ and the ergoregion of a Kerr BH, explored in this work, are regions where it would be possible to trace important information on the spacetime structure for these BHs and the processes involving fields and matter constituting the astrophysical BH embedding environment. We stress that realistic BH shadows can depend on properties of the region of the light distribution and its source, as the accretion disks, with photons interacting with the accreting plasma. BH shadow may also be affected by physical processes involving the accreting disk inner edge¹⁸.

We expect that the regions highlighted here will be distinctly recognizable in future observational enhancement. EHT Collaboration has already compared numerical torus models directly to observations in several comprehensive analyses, performing GRMHD models fit with the observations¹⁹, for example in [5, 14]. For this reason there is no fixing accretion or accretion disk model. In this sense our analysis can be adaptable to and complement the constraints imposed by the specific numerical or analytical model of accretion disks.

Appendices

Appendix 1: Co-rotating and counter-rotating geodesic structure

The marginally stable co-rotating $(-)$ and counter-rotating $(+)$ radius is

$$\begin{aligned} r_{mso}^{\mp } \equiv Z_2+3 {\mp }\sqrt{(3-Z_1) (Z_1+2 Z_2+3)}, \end{aligned}$$

(32)

where

$$\begin{aligned} Z_1\equiv \left( \root 3 \of {1-a}+\root 3 \of {a+1}\right) \root 3 \of {1-a^2}+1,\quad Z_2\equiv \sqrt{3 a^2+\left( \left( \root 3 \of {1-a}+\root 3 \of {a+1}\right) \root 3 \of {1-a^2}+1\right) ^2}. \end{aligned}$$

(33)

The marginally bounded radius is

$$\begin{aligned} r_{mbo}^\pm \equiv \pm a+2 \sqrt{1\pm a}+2. \end{aligned}$$

(34)

The photons circular counter-rotating and co-rotating orbits on the equatorial plane are

$$\begin{aligned} r_{\gamma }^+ \equiv 4 \cos ^2\left( \frac{1}{6} \arccos \left( 2 a^2-1\right) \right) ,\quad r_{\gamma }^- \equiv 2 \left[ \sin \left( \frac{1}{3} \arcsin \left( 1-2 a^2\right) \right) +1\right] . \end{aligned}$$

(35)

There is $\ell _{mso}^\pm \equiv \ell ^\pm (r_{mso}^\pm )$, $\ell _{mbo}^\pm \equiv \ell ^\pm (r_{mbo}^\pm )$ and $\ell _{\gamma }^\pm \equiv \ell ^\pm (r_{\gamma }^\pm )$ respectively, where, considering Eq. 8, there is

$$\begin{aligned} \ell ^{\mp }(r)=\frac{a^3{\mp }\sqrt{r^3 \left( a^2+(r-2) r\right) ^2}-a (4-3 r) r}{a^2-(r-2)^2 r}. \end{aligned}$$

(36)

The location of the tori centers, $r_{center}^\pm$, is constrained by the fluids specific angular momentum $\ell$, according to the radii $r_{(mbo)}^{\pm }$ and $r_{(\gamma )}^{\pm }$, defined by the relations:

$$\begin{aligned}{} & {} r_{\mathrm {(mbo)}}^{\pm }:\;\ell ^{\pm }(r_{\textrm{mbo}}^{\pm })= \ell ^{\pm }(r_{\mathrm {(mbo)}}^{\pm })\equiv \mathbf {\ell _{\textrm{mbo}}^{\pm }},\quad r_{(\gamma )}^{\pm }: \ell ^{\pm }(r_{\gamma }^{\pm })= \ell ^{\pm }(r_{(\gamma )}^{\pm })\equiv \ell _{\gamma }^{\pm } \quad \hbox {where} \nonumber \\ {}{} & {} r_{\gamma }^{\pm }<r_{\textrm{mbo}}^{\pm }<r_{\textrm{mso}}^{\pm }< r_{\mathrm {(mbo)}}^{\pm }< r_{(\gamma )}^{\pm } \end{aligned}$$

(37)

respectively. On the equatorial plane, accretion tori cusps are in $\in ]r^{\pm }_{mbo},r^{\pm }_{mso}]$, with center in $r^{\pm }_{center}\in ]r^{\pm }_{mso},r^{\pm }_{(mbo)}]$. Toroids with ${\mp }\ell ^{\pm }\equiv [{\mp } \ell _{mbo}^{\pm },{\mp }\ell _{\gamma }^{\pm }[$ (the cusp is located in $]r_{\gamma }^{\pm },r_{mbo}^{\pm }]$), have center in $r_{center}^{\pm }\in ]r_{(mbo)}^{\pm },r_{(\gamma )}^{\pm }]$. Toroids with ${\mp } \ell ^{\pm }\ge {\mp }\ell _{\gamma }^{\pm }$, have centers $r^{\pm }_{center}>r_{(\gamma )}^{\pm }$ [109, 110].

Appendix 2: On solutions of $(\mathfrak {R})$

Here we consider again solutions of $(\mathfrak {R})$ for $\ell \in \{\ell _{mso}^\pm ,\ell _{mbo}^\pm ,\ell _{\gamma }^\pm \}$. In order to clarify aspects of the shadow boundaries in dependence on the parameter $\ell$, spin a and coordinates $(r,\sigma )$ it is convenient to introduce the following quantities:

$$\begin{aligned} a_{mso}^-\equiv 0.839825,\quad a_\lambda ^- \equiv 0.93259, \quad a_{\sigma }\equiv 0.98217,\quad \sigma _{\sigma }\equiv 0.563773,\quad \sigma _0\equiv 0.148148, \end{aligned}$$

(38)

(see Fig. 4) and spin function $a_C$:

$$\begin{aligned}{} & {} a_C\equiv \frac{3 \left( \lambda _C^{2/3}-1\right) }{\root 3 \of {\lambda _C}}-\ell ,\quad \hbox {where}\quad \lambda _C\equiv \ell +\sqrt{\ell ^2+1}, \end{aligned}$$

(39)

Fig. 24

Spin $a_g(\ell )$ of Eq. 39 expression of the BH horizons as function of the BH horizons angular momentum. Spin function $a_C$ is in Eq. 39

see Fig. 24. Quantities in Eqs. 38 and 39, bound the constrained solutions of equations $(\mathfrak {R})$ we discuss below.

Case: $\ell =\ell _{mso}^-$

We consider $\ell \in [\ell _{mso}^-(a=1),\ell _{mso}^-(a=0)]$²⁰. There is then $r=3$ for $a=0$.

Whereas, for $a\in ]0,a_g(\ell )[$, there is $r=r_\lambda$ and $q= q_\lambda$, with $q_\lambda \in ]q_\lambda (a=1),q_\lambda (a=0)[$²¹ see Fig. 2. There is $a_g(\ell _{mso}^-)\in [a_{mso}^-,1]$, constraining the photons orbit depending on the central BH spin-mass ratio—Fig. 24. Therefore, there is

$$\begin{aligned}{} & {} \hbox {for}\quad a=0:\quad \sigma \in [ \sigma _{\ell },1],\quad \hbox {where}\quad \sigma _{\ell }(\ell _{mso}^-) \in [0.5,1], \nonumber \\{} & {} \hbox {for}\quad a\in ]0,1]: \sigma \in [\sigma _\lambda ,1], \quad \hbox {where}\quad \sigma _\lambda \in [\sigma _\lambda (a=0),\sigma _\sigma ], \quad \hbox {and}\quad \sigma _\lambda (a=0)=0.5, \end{aligned}$$

(40)

where $\sigma _\sigma$ is a maximum at $a=a_\sigma$—see Fig. 2. There is²²

$$\begin{aligned} q=q_\lambda :\quad \ell \in [\ell _{mso}^-(a=1),\ell _{mso}^-(a=0)],\quad (a\in ]0,a_g[, r=r_\lambda );\quad (a\in ]a_g,1], r=r_C),\quad \hbox {where}\quad r_C\equiv \sqrt{a (\ell - a)}. \end{aligned}$$

(41)

Similarly, using the constraint $T\ge 0$, for $a\in ]0,1]$ the solution can be written as

$$\begin{aligned} r=r_{\lambda },\quad q=q_{\lambda }: \quad (a=a_C, \sigma =1);\quad (a\in ]0,a_C[, \sigma \in [\sigma _C,1]); \end{aligned}$$

(43)

where $\sigma _C$ is a zero of the polynomial $\sum _{i=0}^6 x_i \sigma _C^i=0$, with coefficients

$$\begin{aligned}{} & {} x_0\equiv \left( a^2-1\right) \ell ^6,\nonumber \\{} & {} x_1\equiv \ell ^4 \left[ 27-a^2 \left( a^2-4 a \ell +\ell ^2+30\right) \right] , \nonumber \\{} & {} x_2\equiv a \ell ^2 \left[ -4 \left( a^4+27\right) \ell +96 a^3-4 a^2 \ell ^3+\left( 7 a^2+33\right) a \ell ^2\right] , \nonumber \\{} & {} x_3\equiv 2a^2[a^2(-32 a^2+4 a \ell ^3-3 \ell ^4)-3 \left( a^4+22 a^2-27\right) \ell ^2],\nonumber \\{} & {} x_4=\frac{a^2}{\ell ^2}x_2, \quad x_5=\frac{a^4}{\ell ^4}x_1, \quad x_6=\frac{a^6}{\ell ^6}x_0, \end{aligned}$$

(44)

There is $\sigma _C(\ell _\bullet )= \sigma _\lambda (\ell _\bullet ,q_\lambda (\ell _\bullet ))$ where $\ell _\bullet =\{\ell _{mso}^-,\ell _{mbo}^-\}$ (note for $\ell _\bullet =\ell _{\gamma }^\pm$ there is $\sigma _C=\sigma _\lambda =1$).

Case: $\ell =\ell _{mso}^+$

For $\ell =\ell _{mso}^+$ there is $r=r_\lambda$ and $q=q_\lambda$ for $a\in [0,1]$. There is $\ell \in [\ell _{mso}^+(a=1),\ell _{mso}^+(a=0) ]$²³, and $q_\lambda \in [q_\lambda (a=0),q_\lambda (a=1)]$,²⁴ where

$$\begin{aligned}{} & {} \hbox {for}\quad a=0:\quad \sigma \in [\sigma _\ell ,1]; \quad \hbox {and for}\quad a\in ]0,1]: \sigma \in [\sigma _\lambda ,1],\quad \hbox {where}\quad \sigma _\lambda \in [\sigma _\lambda (a=1),\sigma _\lambda (a=0)], \end{aligned}$$

(45)

with $\sigma _\lambda (a=0)=0.5$ and $\sigma _\lambda (a=1)=0.477$—Fig. 2.

Case: $\ell =\ell _{mbo}^+$

For $\ell \in [\ell _{mbo}^+(a=0),\ell _{mbo}^+(a=1)]$²⁵, for $a\in [0,1]$, there is $r=r_\lambda$ and $q=q_\lambda$, where $q_\lambda \in [q_\lambda (a=0),q_\lambda (a=1)]$.²⁶

Condition $T\ge 0$ implies that:

$$\begin{aligned}{} & {} \hbox {for}\quad a=0:\quad \sigma \in [\sigma _\ell ,1], \nonumber \\{} & {} \hbox {for}\quad a\in ]0,1]:\quad \sigma \in [\sigma _\lambda ,1],\quad \hbox { where}\quad \sigma _\lambda \in [\sigma _\lambda (a=1),\sigma _\lambda (a=0)], \end{aligned}$$

(46)

with $\{\sigma _\lambda (a=0)=0.591797, \sigma _\lambda (a=1)=0.554998\}$—Fig. 2.

Case: $\ell =\ell _{mbo}^-$

We consider the case $\ell =\ell _{mbo}^- \in [\ell _{mbo}^- (a=1),\ell _{mbo}^- (a=0)]$²⁷ for $a\in [0,1]$. There is $q=q_\lambda$ and $r=r_\lambda$ where $q\in [q_\lambda (a=1),q_\lambda (a=0)]$.²⁸

Condition $T\ge 0$ implies that

$$\begin{aligned}{} & {} \hbox {for}\quad a=0:\quad \sigma \in [\sigma _\ell ,1], \nonumber \\{} & {} \hbox {for}\quad a\in ]0,1]:\quad \sigma \in [\sigma _\lambda ,1],\quad \hbox { where }\quad \sigma _\lambda \in [\sigma _\lambda (a=0),\sigma _\lambda , (a=1)] \end{aligned}$$

(47)

with $\{ \sigma _\lambda (a=0)=0.59256, \sigma _\lambda (a=1)=0.76391\}$.

There is $q_\lambda \in [q_\lambda (a=1),q_\lambda (a=0)]$, where $\{q_\lambda (a=1)=1,q_\lambda (a=0)=11\}$.

More in details there is

$$\begin{aligned}{} & {} q=q_{\lambda }\quad \hbox {for} \nonumber \\{} & {} \ell =\ell _{mbo}^-(a=1): \quad (a=0, \sigma \in [\sigma _s, 1], r=3); \quad (a\in ]0,1[, \sigma \in [\sigma _C,1], r=r_{\lambda })); \quad \hbox {where}\quad \sigma _s\equiv \frac{4}{27}, \nonumber \\{} & {} \ell \in ]\ell _{mbo}^-(a=1),\ell _{mbo}^-(a=0)]:\quad (a=0,\sigma \in [ \sigma _f, 1], r=3);\nonumber \\{} &\quad (a\in ]0,a_C[, \sigma \in [\sigma _C,1], r=r_{\lambda });\quad (a=a_C, \sigma =1, r=r_{\lambda }),\quad \hbox {where}\quad \sigma _f\equiv \frac{\ell ^2}{27}. \end{aligned}$$

(48)

Case $\ell =\ell _{\gamma }^\pm$

For $\ell =\ell _{\gamma }^\pm$ there are the photon circular orbits $r_{\gamma }^\pm$, where $q=0$ and $\sigma =1$.