1 Introduction

Differential equations represent many physical processes arising in a vast range of science. The equations are of special importance in modern scientific research and mathematical modelling. Advection usually dominates diffusion in various transport processes represented by physical problems having a hyperbolic nature. Researchers have widely focused on establishing numerical methods that produce stable responses to the physical environment of the advection-dominated behaviour. Involving the reaction of the physical environment leads to spending extra effort, and the advection-dominant case is considered as the case of perturbative behaviour of the physical region.

Frequently, problems of many physical behaviours could be reduced to the solution of a mathematical model of advection–diffusion-reaction processes. Since they are more realistic, partial differential equations (PDEs) are particularly important. The PDEs model physical, chemical, economic and biological processes almost perfectly. To shed light on the subject, one may suggest various branches of physics, mathematical biology, traffic flow and so on as examples of such applied areas. However, more realistic PDEs usually have two challenging aspects; namely, the first one is nonlinearity and the second one is a singular perturbation. Moreover, most of such realistic PDEs do not own an analytical solution; or if the given PDE possesses an analytical solution it is time-consuming to find this solution. Therefore, numerical treatments for such models involving both nonlinearity and singular perturbation are of special importance. A singularly perturbative problem can be remembered to be a parameter/parameters-dependent problem in such a manner that solutions to the problem behave consistently for very small values of the parameter. Singularly perturbed differential equations are encountered in many branches of applied sciences.

When a discretization approach is used for a problem involving a parameter, the parameter affects the behaviour of the approach. For singularly perturbative behaviours represented by the model equation, traditional numerical methods usually give rise to discretization which is of serious limitations when the parameter is too small. That is why this article is interested in a wavelet method that is expected to capture the perturbative behaviour even for tiny values of the parameter. An important review of singularly perturbed PDEs was carried out by [3]. A guiding article on the singularly perturbative problems can be found in [4]. Although singularly perturbed differential equations were studied in detail in the literature, at present, many things are still available to be investigated in the corresponding ground.

The present paper mainly proposes an effective method for solving one of the well-known singularly perturbed nonlinear PDEs, namely the SPGBHE. The SPGBHE is stated as

$$\begin{aligned} u_t+\alpha u^\delta u_x-\epsilon u_{xx}= \beta u (1-u^\delta ) (u^\delta -\gamma ) \end{aligned}$$
(1.1)

where \(0 \le x \le 1\) and \(0 \le t\). Here \(\alpha , \beta , \delta , \gamma\) and \(\epsilon\) are parameters such that \(\epsilon >0\), \(\beta \ge 0\), \(\delta >0\), \(\gamma \in (0,1)\).

This equation describes advection-convection, diffusion effects and reaction mechanisms generally, and it also includes a singularly perturbative behaviour led by the parameter \(\epsilon\) in front of the term \(u_{xx}\). The parameter \(\epsilon\) is known as viscosity and \(1/\epsilon\) sometimes is called Reynolds number. Viscosity is a notion in fluid dynamics that is characterizing the strength of a liquid against fluidity. Therefore, the SPGBHE is of special importance in the study of viscous fluids or the study of Newtonian fluids with high Reynolds numbers.

The SPGBHE is important not only in fluid dynamics but also in various disciplines of science and engineering. By considering \(\delta =1\) and \(\beta =0\), Eq. (1.1) reduces to the well-known Burgers equation, which is important in shock wave studies. It is known that the shock waves are generated due to a balance between the sharp behaviour of the convection process and the smoothing effect of the diffusion process in the model. In that sense, the Burgers equation is of nonlinear behaviour represented by an equilibrated relation between convection and diffusion phenomena. Equation (1.1) gives the Huxley equation, for the choices of \(\alpha =0\) and \(\delta =1\), describing the propagation of some pulses in nerves. When \(\epsilon =1\), Eq. (1.1) leads to the GBH equation; and with the initial condition (IC)

$$\begin{aligned} u(x,0)=\left( \frac{\gamma }{2}+\frac{\gamma }{2}\tanh (a_1x) \right) ^{1/\delta } \end{aligned}$$
(1.2)

and boundary conditions (BCs)

$$\begin{aligned} u(0,t)= & {} \left( \frac{\gamma }{2}+\frac{\gamma }{2}\tanh (-a_1a_2t) \right) ^{1/\delta } \end{aligned}$$
(1.3)
$$\begin{aligned} u(1,t)= & {} \left( \frac{\gamma }{2}+\frac{\gamma }{2}\tanh (a_1 (1-a_2 t)) \right) ^{1/\delta } \end{aligned}$$
(1.4)

Equation (1.1) is of the following continuous solution

$$\begin{aligned} u(x,t)=\left( \frac{\gamma }{2}+\frac{\gamma }{2}\tanh (a_1(x-a_2t)) \right) ^{1/\delta } \end{aligned}$$
(1.5)

where

$$\begin{aligned} a_1&=\frac{-\alpha \delta +\delta \sqrt{\alpha ^2+4\beta (1+\delta )}}{4(1+\delta )} \\ a_2&= \frac{\alpha \gamma }{1+\delta }-\frac{(1+\delta -\gamma )(-\alpha +\sqrt{\alpha ^2+4\beta (1+\delta )})}{2(1+\delta )}. \end{aligned}$$

The GBH equation was solved via a meshless method with the use of radial basis functions [5], a quadrature technique [6], a high-order difference method [7], a version of the Chebyshev spectral collocation method[8], a wavelet method [9], a 2N-order difference method [10]. Moreover, some analytical solutions of the GBH equation were found in [11,12,13] and [14].

When \(\epsilon < 1\), Eq. (1.1) does not have an exact solution, particularly, if \(\epsilon \ll 1\) the conventional methods usually fail to catch the behaviour of the problem. In such cases, the importance of finding a numerical solution comes out. Recently, an operator splitting method was utilized to solve the SPGBHE [15]. An error analysis through the properties of Sobolev spaces was also given in [15]. Variational iteration method [16], a lattice Boltzmann model [17], a three-step Taylor-Galerkin method [18], homotopy analysis method [19] and a finite difference scheme including a time semi-discretization and space quasi-linearization [20] were utilized to solve the SPGBHE.

In the literature, wavelet methods were used to solve such nonlinear PDEs because of their multi-resolution properties [21, 22]. Besides, the convergence theorem for the Haar wavelet method based on the approach introduced in [21] was proved in [1]. Majak et.al. developed the higher order Haar wavelet method (HOHWM) and the order of convergence of the upgraded method is shown to be four in [28]. The HOHWM was utilized to derive the numerical solutions of the Burgers’ equation, the Korteweg-de Vries equation including the modified one, and the sine-Gordon equation [29]. The mentioned method is also used to get static responses of a buckling beam [30, 31].

In light of previous works, we have applied Haar wavelets to a singularly perturbed nonlinear PDE, namely SPGBHE. To achieve this, we have needed a time discretization and integrals of Haar wavelets. To understand this study, the tiny section below about Haar wavelets will suffice, but enthusiasts may start with [23, 24] and [25].

This paper investigates solutions of the SPGBHE by utilizing Haar wavelets, tracking the way in [21]. As far as the authors of the current paper know, the present methods have some difficulties in handling nonlinearity and singular perturbation at the same time. This factor pushes us to use a wavelet method to catch singularly perturbative behaviours represented by nonlinear PDEs (Fig. 1).

2 Haar wavelets

Haar wavelets are the earliest family of wavelets. The scaling function of the Haar family is

$$\begin{aligned} \phi (x)={\left\{ \begin{array}{ll} 1, &{} x \in [0,1].\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
(2.1)

and the wavelet function of Haar family is

$$\begin{aligned} \psi (x)={\left\{ \begin{array}{ll} +1, &{} 0\le x \le 1/2.\\ -1, &{} 1/2 \le x \le 1. \\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
(2.2)
Fig. 1
figure 1

Haar scaling function (left) and wavelet function (right)

Full size image

Then the set of wavelet functions \(\{\psi _{j,k}\}_{j,k\in {\mathbb {Z}}}\) is a basis for \(L^2({\mathbb {R}})\). Here \(\psi _{j,k}(x)=2^{j/2}\psi (2^jx-k)\). For the sake of brevity, the wavelet functions can be written as

$$\begin{aligned} h_i(x)=\psi _{j,k}(x)=2^{j/2}\psi (2^jx-k) \end{aligned}$$
(2.3)

where \(j\in {\mathbb {N}}\), \(k\in {\mathbb {Z}}\) and \(i=2^j+k+1\). Particularly, setting \(j=k=0\) we can obtain \(h_2(x)=\psi (x)\). Here, notice also that \(h_1(x)\) stands for the scaling function \(\phi (x)\). Since Haar functions are piecewise constants, integrals of them can be obtained as

$$\begin{aligned} p_{i,1}(x)&=\int _0^xh_i(x)dx, \end{aligned}$$
(2.4)
$$\begin{aligned} p_{i,k}(x)&=\int _0^xp_{i,k-1}(x)dx \end{aligned}$$
(2.5)

In this study, we need only \(p_{i,1}(x)\) and \(p_{i,2}(x)\).

3 Numerical treatment of the SPGBHE

As far as PDEs are concerned, there exist many different articles in the literature connecting Haar wavelets and PDEs. But being the simplest wavelet family, Haar wavelets have the main drawback: Haar wavelets are discontinuous functions, and hence, cannot be used directly to solve partial differential Eqs. [22, 26, 27]. To utilize Haar wavelets, in the study of PDEs, consideration of interpolating splines is to give one way in regularizing Haar wavelets [27] and the second way is to find Haar series expansion of the highest derivative of the unknown function that is appearing in the equation rather than the function itself [21]. In the present paper, we expand \(u_{xxt}(x,t)\) into Haar series i.e.

$$\begin{aligned} u_{xxt}(x,t)=\sum _{k=1}^{2^{J+1}}c_kh_k(x) \end{aligned}$$
(3.1)

where J stands for the level of resolution. By integrating (3.1) once and twice with respect to time t and space x, the coming expressions can be produced

$$\begin{aligned} u_{xx}(x,t)= & {} (t-t_s)\sum _{k=1}^{2^{J+1}}c_kh_k(x)+u_{xx}(x,t_s) \end{aligned}$$
(3.2)
$$\begin{aligned} u_x(x,t)= & {} (t-t_s)\sum _{k=1}^{2^{J+1}}c_kp_{k,1}(x)+u_x(x,t_s)-u_x(0,t_s)+u_x(0,t) \end{aligned}$$
(3.3)
$$\begin{aligned} u(x,t)= & {} (t-t_s)\sum _{k=1}^{2^{J+1}}c_kp_{k,2}(x)+u(x,t_s)-u(0,t_s)+x \left( u_x(0,t_s)-u_x(0,t) \right) +u(0,t) \end{aligned}$$
(3.4)
$$\begin{aligned} u_t(x,t)= & {} \sum _{k=1}^{2^{J+1}}c_kp_{k,2}(x)+xu_{xt}(0,t)+u_t(0,t) \end{aligned}$$
(3.5)

Then using additional conditions \(u(x,0)=f(x)\) and \(u(0,t)=g_0(t)\) and \(u(1,t)=g_1(t)\), one can find that

$$\begin{aligned} u(0,t_s)=g_0(t_s), u(1,t_s)=g_1(t_s), u_t(0,t_s)=g_0'(t_s), u_t(1,t_s)=g_1'(t_s) \end{aligned}$$
(3.6)

Moreover, using Eqs. (3.4) and (3.5), we can obtain

$$\begin{aligned} u_x(0,t)-u_x(0,t_s)= & {} -(t-t_s)\sum _{k=1}^{2^{J+1}}c_kp_{k,2}(1)+g_1(t)-g_1(t_s)+g_0(t_s)-g_0(t) \end{aligned}$$
(3.7)
$$\begin{aligned} u_{xt}(0,t)= & {} -\sum _{k=1}^{2^{J+1}}c_kp_{k,2}(1)-g_0'(t)+g_1'(t) \end{aligned}$$
(3.8)

If Eqs. (3.7) and (3.8) are used in Eqs. (3.2) and (3.3); and the obtained equations are discritized as \(x\rightarrow x_l\) and \(t\rightarrow t_{s+1}\), then we have the following equations

$$\begin{aligned} u_{xx}(x_l,t_{s+1})=(t_{s+1}-t_s) \sum _{k=1}^{2^{J+1}}c_kh_k(x_l)+u_{xx}(x_l,t_s) \end{aligned}$$
(3.9)
$$\begin{aligned} u_x(x_l,t_{s+1})=\,&(t_{s+1}-t_s) \sum _{k=1}^{2^{J+1}}c_kp_{k,1}(x_l)-(t_{s+1}-t_s)\sum _{k=1}^{2^{J+1}}c_kp_{k,2}(1) \nonumber \\&+u_x(x_l,t_s)+g_1(t_{s+1})-g_1(t_s)+g_0(t_s)-g_0(t_{s+1}) \end{aligned}$$
(3.10)
$$\begin{aligned} u(x_l,t_{s+1})&= (t_{s+1}-t_s) \sum _{k=1}^{2^{J+1}}c_kp_{k,2}(x_l)+u(x_l,t_s)+g_0(t_{s+1})-g_0(t_s) \nonumber \\&-x_l \left( (t_{s+1}-t_s) \sum _{k=1}^{2^{J+1}}c_kp_{k,2}(1)-g_1(t_{s+1})+g_1(t_s)-g_0(t_s)+g_0(t_{s+1}) \right) \end{aligned}$$
(3.11)
$$\begin{aligned} u_t(x_l,t_{s+1})= \sum _{k=1}^{2^{J+1}}c_kp_{k,2}(x_l)-x_l \left( \sum _{k=1}^{2^{J+1}}c_kp_{k,2}(1)-g_1'(t_{s+1}) +g_0'(t_{s+1}) \right) +g_0'(t_{s+1}) \end{aligned}$$
(3.12)

where \(x_l=(l-0.5)/2^{J+1}\), \(l=1,2,\dots ,2^{J+1}\). Then plugging (3.9)-(3.12) into (1.1), we can find \(u(x,t_{s+1})\) iteratively by time marching. Throughout the calculations, the time step was considered to be 0.001. To illustrate the relative error (RE) of the computed solution we use the following relative error formula

$$\begin{aligned} RE=\sqrt{\frac{\sum _{k=1}^{2^{J+1}-1} |u(x_{l+1},t_{s+1})-u(x_l,t_{s+1})|^2}{\sum _{k=1}^{2^{J+1}}|u(x_l,t_{s+1})|^2 }} \end{aligned}$$
(3.13)

The convergence theorem for the Haar wavelet method was proved in [1] and the order of convergence of the method is computed to be two. Also, following the methodology in [2], the numerical rate of convergence of the present method could be depicted as two.

4 Numerical illustrations

In most applications of wavelet theory, the error is proportional to \(O(2^{-J})\). Therefore, when the density of the mesh, i.e., J, increases, the error diminishes rapidly. Moreover, the rate of convergence of the Haar wavelet method has been proven to be two in the literature [1]. In the following examples, we can observe this truth experimentally. On the other hand, when both the effects of nonlinearity and singular perturbation are dominant, the method may suffer from high errors, and there are some numerical jumps in the errors. The reason for this loss of accuracy can be explained by the accumulation of errors that have come out during iterations. Another reason for this situation can be the cumulative error in the application of Newton’s method, which is considered to solve the derived nonlinear system. In all circumstances, we do not need any linearization in the present method, and we observe a fast decay in the propagation of error. Hence, a trend of decrease in the relative errors can be observed in the tables when the elapsed time becomes large.

Example

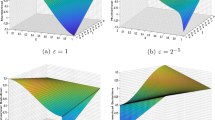
Take the model \(u_t+u^\delta u_x-\epsilon u_{xx}=(1-u^\delta )(u^\delta -0.5)u\) under BCs \(u(0,t)=u(1,t)=0, 0\le t \le T\) and IC \(u(x,0)=\sin (\pi x), 0\le x \le 1\). As seen from Table 1, the REs have been presented at \(t=0.9\) for variation of the parameters \(\delta , \epsilon\) and for various resolutions J (Figs. 2, 3, 4).

Table 1 REs for Example 1 at \(t=0.9\) for various values of \(\delta\), \(\epsilon\) and J
Full size table
Fig. 2
figure 2

x vs u(x, t) graphs for Example 1 with \(J=3\) and \(t=0.1\) (upper left), \(J=3\) and \(t=0.9\) (upper right), \(J=3\) and \(\epsilon =2^{-1}\) (bottom left), \(J=4\) and \(\epsilon =2^{-6}\) (bottom right)

Full size image
Fig. 3
figure 3

3D graph (left) and contour plot (right) of u(x, t) for Example 1 with \(J=3\) and \(\epsilon =2^{-6}\)

Full size image
Fig. 4
figure 4

REs for Example 1 with various levels of resolution and \(\delta =1/2\)

Full size image

Example

\(u_t+u^\delta u_x=\epsilon u_{xx}\) under homogeneous Dirichlet BCs \(u(0,t)=u(1,t)=0, 0\le t \le T\) and IC \(u(x,0)=x(1-x^2), 0\le x\le 1\). In terms of the REs, effects of the advection and diffusion processes have been observed both qualitatively and quantitatively in Table  2 and Figs. 5, 6 at t=0.9 with various values of the parameters \(\delta\), \(\epsilon\) and J. Simultaneous effects of the viscosity and resolution on the solution have been exhibited in Fig. 7. When the diffusion is non-dominant, the steep behaviour of the physical process has properly been seen in the figures.

Table 2 REs for Example 2 at \(t=0.9\) for various values of \(\delta\), \(\epsilon\) and J
Full size table
Fig. 5
figure 5

3D graph (left) and contour plot (right) of u(x, t) for Example 2 with \(J=3\) and \(\epsilon =2^{-9}\)

Full size image
Fig. 6
figure 6

x vs u(x, t) graphs for Example 2 with \(J=5\) and \(t=0.1\) (upper left), \(J=5\) and \(t=1.5\) (upper right), \(J=3\) and \(\epsilon =2^{-3}\) (bottom left), \(J=5\) and \(\epsilon =2^{-12}\) (bottom right)

Full size image
Fig. 7
figure 7

REs for Example 2 with various levels of resolution and \(\delta =2\)

Full size image

Example

Selection of \(\epsilon =1\) and \(\alpha =0\) in Equation (1.1) leads to the GH equation. Tables  3-4 give absolute errors (AEs) and REs for variation of the parameters x, t, \(J=3\), \(\alpha\), \(\beta\) and \(\delta\). The exact and the Haar wavelet solutions have been compared in Table 3. Effects of the resolution J has been exhibited quantitatively in Tables 5 and 6. Also, the current results and the CFD6 results in [7] have been compared. Even when we have used relatively large time steps (\(\Delta t=10^{-3}\)) and relatively low resolution (\(J=3\)), the obtained solutions have been found to be slightly more precise than the solutions of [7].

Table 3 AEs and REs for Example 3 with various values of x, t when \(\epsilon =1\), \(J=3\), \(\alpha =0\), \(\beta =1\), \(\gamma =0.001\) and \(\delta =1\)
Full size table
Table 4 AEs and REs for Example 3 with various values of x, t when \(\epsilon =1\), \(J=3\), \(\alpha =1\), \(\beta =1\), \(\gamma =0.001\) and \(\delta =1\)
Full size table
Table 5 AEs for Example 3 with various values of x, t, J when \(\epsilon =1\), \(\alpha =1\), \(\beta =1\), \(\gamma =0.001\) and \(\delta =1\)
Full size table
Table 6 REs for Example 3 with various values of x, t, J when \(\epsilon =1\), \(\alpha =1\), \(\beta =1\), \(\gamma =0.001\) and \(\delta =1\)
Full size table

5 Conclusions and recommendations

This article has explored the utility of wavelet theory based on multi-resolution properties in capturing the behaviour of singularly perturbative processes represented by the SPGBHE. Thus, exploiting the multi-resolution properties of wavelets, the steep behaviour of the model equation has also been observed more clearly. In this context, quite accurate numerical behaviour of the model has been held back even for relatively high Reynolds numbers and at severe nonlinearities. This has been achieved by using relatively large time steps at considerably low-resolution levels. For future research, other wavelet families may deserve to be put in use to produce the behaviour of various singularly perturbed nonlinear processes.