1 Introduction

The currently favored cosmological model is built upon the hot Big Bang with an early inflationary period, followed by expansion over the ensuing 14 billion years. The present-day universe is dominated by two components: dark matter which makes up \(\sim 30\%\) of the total energy density, and dark energy which comprises \(\sim 70\%\). The expansion of the universe is described with the Hubble parameter \(H(t)={\dot{a}}/a\), where a is a scale factor and dot is the derivative with respect to time. Units of the Hubble parameter are kilometers per second per megaparsec, and this number indicates the expansion rate of the universe at any point in its history.

The present-day value of the Hubble parameter—the Hubble constant \(H_0\) — has had a rich and eventful history. It was originally measured by Edwin Hubble in 1929 [1] based on galaxy-velocity data collected by Vesto Slipher. Hubble himself famously massively overestimated the Hubble constant, obtaining \(H_0\sim 500\,\mathrm{km\ s^{-1}Mpc^{-1}}\). At face value, this implied the age of the universe of \(t_0\simeq 1/H_0\simeq 2\,\textrm{Gyr}\), which was already then in conflict with observations (being younger than the age of Earth!). Despite the in-retrospect obviously wrong value of \(H_0\), Hubble’s 1929 paper is crucially important because it correctly surmised that the relation between recession velocity and distance is linear—a hallmark of expanding space. In fact, every expanding space, not just our universe, can be characterized by a “Hubble constant” that encodes the rate of its expansion.

The measured value of \(H_0\) was subsequently reduced with better observations and better control over the systematic errors. For many decades, thereafter (roughly 1950-1990), the favored \(H_0\) values varied between \(50\,\mathrm{km\ s^{-1}Mpc^{-1}}\) (favored by astronomer Allan Sandage [e.g., 2]) and \(100\,\mathrm{km\ s^{-1}Mpc^{-1}}\) (favored by Gérard de Vaucouleurs [e.g., 3]). The large variation between various measurements was due to the presence of systematic errors in these measurements and inferences. This impasse was mercifully resolved starting in the 1990s when new, more precise measurements using the Hubble Space Telescope obtained \(H_0\simeq 70\,\mathrm{km\ s^{-1}Mpc^{-1}}\) [4], roughly halfway between these two hotly contested values.

However, recent measurements of the Hubble constant revealed a new discrepancy between measurements obtained by two methods, leading to the Hubble tension. Measurements by means of the so-called distance ladder (where distances to nearby galaxies are measured and compared to their recession velocities) reveal \(H_0=(73.0\pm 1.0)\,\mathrm{km\ s^{-1}Mpc^{-1}}\), while inferences from the cosmic microwave background give \(H_0=(67.4\pm 0.5)\,\mathrm{km\ s^{-1}Mpc^{-1}}\). While they look similar in the historical context, the two measurements are discrepant due to their small corresponding measurement errors. In these proceedings, we describe these two measurements of the Hubble constant, mention several more promising methods, comment on theoretical explanations, and finally explain why a large cosmic underdensity (in which we might possibly live) cannot explain the Hubble tension.

2 Hubble tension

Two precise and physically very different types of measurements currently appear to be in tension. We now describe these two measurements.

2.1 Distance-ladder measurements

The local measurement of \(H_0\) relies on a so-called “distance ladder” to measure distances to (relatively) nearby galaxies. In this technique that is a workhorse of traditional cosmology, distances to more nearby objects are used to calibrate distances to a more distant set of objects, and so on. For example:

  • Parallax (apparent change in position on the sky due to Earth’s motion around the Sun) is used to get distances to very nearby Cepheids (variable stars) and calibrate the Cepheid period-luminosity relation (the relation between a Cepheid’s pulsation period and its luminosity).

  • With the period-luminosity relation in hand, a measurement of Cepheid’s period will give its luminosity L. Then, given the measurement of flux f from the Cepheid and the relation \(f=L/(4\pi d^2)\), we can determine the distance d to the Cepheid.

  • Some galaxies hosting Cepheids are also hosts to type Ia supernovae (SNIa) — standardizable candles which all have a similar luminosity L. Cepheids in SNIa-hosting galaxies can then be used to determine the distance to SNIa in those same galaxies, thus establishing the “anchor” to SNIa distances. Effectively, those Cepheids help determine the unique luminosity L of (all, in the standard-candle limit) SNIa.

The measurements of the distance to SNIa can determine the Hubble constant. This is because

$$\begin{aligned} d\simeq \frac{cz}{H_0}+O(z^2), \end{aligned}$$
(1)

where c is the speed of light and z s the redshift of the supernova. Therefore, absolute distances to individual SNIa that are the result of the distance-ladder procedure described above, combined with their redshifts which can be directly measured from the positions of spectral lines, provide a measurement of the Hubble constant. The \(O(z^2)\) term in Eq. (1) involves other cosmological parameters such as the matter density relative to critical \(\Omega _M\), but this term is typically negligible because only low-z supernovae (\(z\lesssim 0.15\)) are used to constrain \(H_0\). [Nevertheless, one could equally use all available SNIa, going out to \(z\gtrsim 1\), and constraint \(H_0\) along with other cosmological parameters in a joint analysis [5].]

Distance-ladder measurements of the Hubble constant have led to the increasingly precise measurements [6,7,8,9], culminating recently in [10]

$$\begin{aligned} { H_0^{\textrm{loc}}= (73.04 \pm 1.04) \,\mathrm{km\ s^{-1}Mpc^{-1}}}. \end{aligned}$$
(2)

These papers have carried out a very detailed analysis of the possible systematic errors, folding those errors into the total error budget that is captured in Eq. (2). The SNIa analysis, based on the same data but different statistical techniques, was independently done by Ref. [11] who found consistent results.

There are other distance-ladder based methods that have been producing increasingly accurate constraints on \(H_0\). These include the Tip of the Red Giant Branch (TRGB) method, which makes use of a sharp discontinuity in the red giant branch luminosity function at a fixed magnitude to effectively provide a standard candle for distance measurements. Other methods include surface brightness fluctuations and water masers; they are all briefly reviewed in e.g. Freedman and Madore [12]. Here, we shall just remark that none of these methods has yet the statistical power and the control of the systematics to provide a decisive measurement of \(H_0\) and/or resolve the Hubble tension, although the TRGB method in particular does have a potential do so in the near future.

2.2 CMB measurements

Alternative measurements of the Hubble constant come from the cosmic microwave background (CMB). Here, one uses the fact that the angular power spectrum of temperature fluctuations just happens to be very sensitive to the value of the Hubble constant. A slightly more detailed way to understand this measurement is that the CMB determines the position of acoustic peaks very accurately,

$$\begin{aligned} \ell _{\mathrm{1st\, peak}}\simeq \frac{\pi }{\theta _{\mathrm{1st\, peak}}} = \pi \frac{r_{\textrm{dec}}}{r_s}, \end{aligned}$$
(3)

where \(\ell _{\mathrm{1st\, peak}}\) and \(\theta _{\mathrm{1st\, peak}}\) are respectively the multipole and angle location of the first acoustic peak, and \(r_{\textrm{dec}}\equiv r(z_{\textrm{dec}})\) is the comoving distance to the time of decoupling (of photons and baryons), and \(r_s\) is the sound horizon (the distance that sound perturbation can travel from the Big Bang to the time of decoupling). The peak locations can be determined to a fabulously good accuracy from the CMB data; the Planck experiment reports a \(0.03\%\) accuracy for what we call \(\ell _{\mathrm{1st\, peak}}\). The sound horizon \(r_s\) is moreover determined very well by morphology of the acoustic peaks (their absolute and relative heights); Planck reports a \(0.4\%\) accuracy in it and this measurement is largely independent of the information encoded in peak locations. With measurements of \(\ell _{\mathrm{1st\, peak}}\) and \(r_s\) in hand, we can determine the distance to recombination \(r(z_{\textrm{dec}})\) which, in the \(\Lambda \)CDM cosmological model, is

$$\begin{aligned} r_{\textrm{dec}} = \frac{1}{H_0}\int _0^{z_{\textrm{dec}}} \frac{dz}{\sqrt{\Omega _M(1+z)^3+1-\Omega _M}}. \end{aligned}$$
(4)

Given that the physical matter density \(\Omega _M h^2\) is determined from the morphology of the CMB peaks, it can be used in combination with the effective measurement of \(r_{\textrm{dec}}\) to determine the Hubble constant \(H_0\).

The current CMB measurement is given by Planck [13]

$$\begin{aligned} H_0= (67.36 \pm 0.54) \,\mathrm{km\ s^{-1}Mpc^{-1}}. \end{aligned}$$
(5)

Similar but slightly less precise results have been obtained by a combination of WMAP and ACT data: \(H_0=(67.6\pm 1.1)\,\mathrm{km\ s^{-1}Mpc^{-1}}\) [14]. These constraints are all significantly smaller than the locally measured value in Eq. (2). With recent measurements, the discrepancy between Planck and the distance-ladder measurements has exceeded 5\(\sigma \) (see the review in Ref. [15]).

2.3 Other measurements

It is also interesting to consider that other cosmological data may weigh in on the Hubble constant. In particular, the combination of galaxy clustering (from, say, Dark Energy Survey), baryon acoustic oscillations (from, say, the BOSS survey), and big-bang nucleosynthesis (which pins down the baryon density \(\Omega _Bh^2\)) can pin down \(H_0\) independently of either the distance ladder or the CMB. The analysis that combines precisely these probes, carried out by the DES team, is \(H_0= 67.4^{+1.1}_{-1.2} \,\mathrm{km\ s^{-1}Mpc^{-1}}\) [16]. Similar results has been obtained by combining the eBOSS galaxy-clustering data with the baryon density from big-bang nucleosynthesis; that result is \( H_0= (67.35\pm 0.97) \,\mathrm{km\ s^{-1}Mpc^{-1}}\) [17] or else \(H_0=(67.6\pm 1.1)\,\mathrm{km\ s^{-1}Mpc^{-1}}\) [18]. All of these measurements indicate a slower rate of expansion, in agreement with Planck but with somewhat larger error bars.

Strong gravitational lensing also independently constrains the Hubble constant. The idea is that measurements of time delays in images in muliply-imaged lensing systems depends on the Hubble constant. The constraints are not yet competitive to weigh in on the tension (\(H_0= 73.3^{+1.7}_{-1.8} \,\mathrm{km\ s^{-1}Mpc^{-1}}\) [19]), but will be more precise in the near future, with more multiply-imaged systems and better control of the systematics.

Finally, inspiral events (merging black holes or neutron stars), which serve as “standard sirens” by providing an absolute measurement of the luminosity distance. An independent measurement of the redshift to the host galaxy then enables the determination of the Hubble constant: for nearby inspiral events (so when \(z\ll 1\)), \(H_0\simeq cz/d\) where z is redshift and d is distance to the host galaxy. Standard sirens already provide constraints on \(H_0\) [20], but these constraints are currently weak because only one gravitational-wave event with the electromagnetic counterpart – so, where the host galaxy’s redshift is available—has been observed. In the future, tight constraints from standard sirens are expected [e.g., 21]. The gravitational wave measurements of \(H_0\) are particularly important, as some of them will be at low redshift, thus potentially validating the low-z result from SNIa, and thus complements most other measurements (CMB, baryon acoustic oscillations, strong lensing) which probe higher redshifts.

2.4 Searching for the explanation

Hubble tension has generated a huge interest in cosmology, as it may well be a harbinger of new physics—or, at the very least, unexpectedly large systematic errors in either of the two principal measurements. Many explanations have been put forth—a review in Ref. [22] lists more than 1,000 papers on this — but none have yet proven to be compelling.

Particularly active have been the attempts to use dark energy to explain the tension (see [23] for a review). Here, the idea is to introduce a component of early dark energy at \(z\lesssim z_{\textrm{dec}}\simeq 1000\) and with energy density \(\rho _{\textrm{EDE}}/\rho _{\textrm{TOT}}\simeq 0.05\) (at that epoch). Early dark energy decreases the sound horizon at that epoch. As can be seen from Eqs. (3) and (4), this decrease in \(r_s\) must be accompanied by an increase in \(H_0\) in order to preserve the measured locations of the peak \(\ell _{\mathrm{1st\, peak}}\). Hence \(H_0\) would increase from \(H_0\simeq 67\,\mathrm{km\ s^{-1}Mpc^{-1}}\) to presumably \(H_0\simeq 73\,\mathrm{km\ s^{-1}Mpc^{-1}}\), thus agreeing with the distance-ladder result. However, the early dark energy models tend to be quite fine-tuned and contain several free parameters (or other equivalent choices), and have not yet established themselves as a compelling resolution to the \(H_0\) tension.

As the tremendous activity on the front of trying to explain Hubble tension with theory has unfolded, one thing has become clear: no easy explanations have presented themselves. Most of the theoretical explanations try to change the global \(H_0\) from \(\sim 67\,\mathrm{km\ s^{-1}Mpc^{-1}}\) to \(\sim 73\,\mathrm{km\ s^{-1}Mpc^{-1}}\). While doing so, they have to preserve the excellent fit to CMB, baryon acoustic oscillation, and other cosmological data which—in an unmodified, standard cosmological model—favor \(H_0\sim 67\,\mathrm{km\ s^{-1}Mpc^{-1}}\). Even in reasonably successful proposed models explanations, it has proven difficult to raise the Hubble constant all the way to \(\sim 73\,\mathrm{km\ s^{-1}Mpc^{-1}}\) (rather than halfway there, to \(\sim 70\,\mathrm{km\ s^{-1}Mpc^{-1}}\)) while at the same time improving the goodness of fit to the data to justify the new parameter(s) of the theoretical-model explanation in question.

It is likely that Hubble tension will be either resolved or statistically strengthened with upcoming data from a variety of astrophysical and cosmological observations. Observations from the James Webb Space Telescope will extend the quality and quantity of data required for the distance-ladder determinations of \(H_0\), namely Cepheids, type Ia supernovae, TRGB, and other probes (for a review, see Ref. [12]). New measurements of the CMB anisotropy from South Pole Telescope, Atacama Cosmology Telescope, Simons Observatory, and eventually CMB-S4 experiment, will determine the Hubble constant independently of Planck and with even better precision. Finally cosmological observations of galaxy clustering, especially that from the Dark Energy Spectroscopic Instrument (DESI), will provide distance measurements which, when combined with priors on the baryon abundance (e.g. [17]), will provide extremely tight constraints on the Hubble constant that are comparable in precision to those from the CMB.

3 It’s not a void!

We now review the simplest explanation for the Hubble tension — the effect of sample variance (often called “cosmic variance” in cosmology) or, equivalently, the possibility that we live in a void. This explanation goes as follows. There are underdensities and overdensities in space. If we live in an underdensity, then the locally measured Hubble constant, \(H_0^{\textrm{loc}}\), will be higher than the global Hubble constant, as less mass in the void implies a higher expansion rate. This would imply a possible mismatch between \(H_0^{\textrm{loc}}\) and the global, “true” \(H_0\).

The effect can be quantified in slightly more detail as follows. In an underdense region, the expansion rate is indeed higher than the mean (and vice versa in an overdense region) [24,25,26,27,28,29,30,31,32,33]. Namely, the relation between the deviation in \(H_0\) and the local density contrast \(\delta \) is

$$\begin{aligned} \frac{\Delta H_0}{H_0} =-\frac{1}{3} \delta f(\Omega _M) \Theta (\delta , \Omega _M), \end{aligned}$$
(6)

where \(f(\Omega _M)\simeq \Omega _M(a)^{0.55}\) is the growth rate of density perturbations (see Ref. [34] for a review), and \(\Theta =1-O(\delta )\) is a small non-linear correction. Therefore, an underdensity with \(\delta <0\) will automatically lead to a higher measured local expansion rate, that is, \(\Delta H_0>0\). The effect of an under/overdensity described here is qualitatively guaranteed, as sample variance is definitely a factor in all local measurements that we make. Is it possible that sample variance provides a sufficiently large effect to explain the Hubble tension?

The answer is resoundingly negative. The effect of sample variance on the local measurements of \(H_0\) had been studied analytically by multiple authors [35,36,37,38], and was definitively confirmed by numerical simulations of the local measurements [39]. These results indicate that it is extremely unlikely that we live in a void that is sufficiently large in size and deep (devoid of galaxies) to explain the Hubble tension.

Here we recapitulate the results of Wu & Huterer [39]. In that work, we used the public release of the Dark Sky simulationsFootnote 1 [40]. Specifically, we used the largest volume ds14_a with \(1.07\times 10^{12}\) (\(10240^3\)) particles within a volume of \((8 \,h^{-1}\textrm{Gpc})^3\). The cosmological parameters correspond to a standard flat \(\Lambda \)CDM model and are consistent with Planck and other probes. The N-body simulation was performed using the adaptive tree code 2HOT[41], and the dark matter halos were identified using the halo finder Rockstar[42]. The data are accessible online using yt[43]. We used dark matter halos with virial mass \(M_{\textrm{vir}}> 10^{12.3}\, \textrm{M}_{\odot} \) (35 particles).

Fig. 1
figure 1

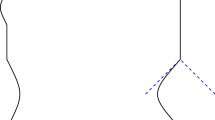
Sketch of the procedure in Ref. [39]. We divide the DarkSky simulation volume into 512 subvolumes, and place an observer at the center of each. In each subvolume, we also orient the global coordinates of the observed SNIa (now shown in this sketch), and find the closest dark-matter halo (in some mass range) to each SNIa. We then use the known properties of that halo—its distance from the observer and its peculiar velocity—as proxies for those in SNIa, in order to get an estimate of the Hubble constant (see Eq. (7)

Full size image

We divided this \((8\,h^{-1}\textrm{Gpc})^3\) volume into 512 subvolumes of \((1\,h^{-1}\textrm{Gpc})^3\). We then chose the halo with virial mass \(M_{\textrm{vir}}\in [10^{12.3}, 10^{12.4}]\, \textrm{M}_{\odot} \) that is closest to the center of each subvolume as our observer. This choice simulates 512 separate observers located on Milky Way mass halos, each with a separate subvolume of the large-scale structure out to the distance of interest (\(z_{\textrm{max}}= 0.15\)). For the host halos of SNIa, we also used Milky Way mass halos with \(M_{\textrm{vir}}\in [10^{12.3}, 10^{12.4}]\, \textrm{M}_{\odot} \), and we have explicitly checked that this choice leads to the same results as using all halos above \(10^{12.3}\, \textrm{M}_{\odot} \).

Given the DarkSky simulation output, our procedure goes as follows (see also Fig. 1):

  1. 1.

    Divide the whole DarkSky box into 512 subvolumes as mentioned above; each halo in every subvolume, in some mass range, is a possible host of a SNIa.

  2. 2.

    Select the orientation of the overall SNIa sky coordinates from with respect to the subvolume.

  3. 3.

    Assign each of the SNIa (given its spatial coordinates) to the closest halo in the subvolume.

  4. 4.

    Calculate the \(H_0^{\textrm{loc}}\) from the radial velocity of these SNIa hosts using the relation

    $$\begin{aligned} H_0 r + v_r = H_0^{\textrm{loc}}r. \end{aligned}$$
    (7)

    where \(H_0\) is the global Hubble constant (assumed from the outset), r and \(v_r\) are the comoving distance to, and the peculiar velocity of, the halo that hosts a SNIa, and \(H_0^{\textrm{loc}}\) is that individual halo’s inferred local Hubble constant. [The actual analysis is a little more complicated; see [39] for details.]

  5. 5.

    Go to step 2., repeat the measurements for many different orientations, and obtain the histogram of \(\Delta H_0^{\textrm{loc}}\) of different orientations from a single subvolume.

  6. 6.

    Go to step 1., repeat the measurements for multiple, non-overlapping subvolumes, and obtain the distribution of \(\Delta H_0^{\textrm{loc}}\) from all subvolumes and all orientations.

The procedure outlined above corresponds to some 1.5 million (512 subvolumes times \(\sim 3000\) SNIa coordinate system orientations in each subvolume) simulations of inferring the Hubble constant from local (\(0.023<z<0.15\)) SNIa. It also assumes the structure typical of a \(\Lambda \)CDM universe.

Fig. 2
figure 2

Sample variance in \(\Delta H_0^{\textrm{loc}}\) from the simulations of Wu & Huterer [39], compared to the Planck and distance-ladder (“Riess” in the plot) error bars (and assuming Planck’s \(H_0\) is the true global value). The blue histogram shows 3240 rotations of SNIa coordinate system from 512 subvolumes in the Dark Sky simulations, corresponding to \(\sim \)1.5 million SN-to-halo coordinate system configurations. The green histogram shows the results of a particularly underdense subvolume with a high \(\Delta H_0^{\textrm{loc}}\) at the 2-\(\sigma \) level relative to all subvolumes. Note that the sample variance in \(H_0^{\textrm{loc}}\) is much smaller than the difference between R16 and P16 measurements. Adopted from Ref. [39]

Full size image

The final results of this analysis are shown in Fig. 2. It shows that the sample variance in \(H_0\) measurements is much smaller than the amount that would explain the Hubble tension. For example, even a void that is low at the \(\sim 2\sigma \) level relative to the mean (green histogram) would lead to the locally measured Hubble constant, \(H_0^{\textrm{loc}}\), that is only slightly larger than the mean value, assumed here to correspond to Planck’s \(H_0\simeq 67\,\mathrm{km\ s^{-1}Mpc^{-1}}\). We have in fact been able to measure the standard deviation of the measured Hubble constant very precisely,

$$\begin{aligned} \sigma _{\mathrm{sample\, variance}}=0.31\,\mathrm{km\ s^{-1}Mpc^{-1}}. \end{aligned}$$
(8)

In other words, \(|H_0^{\textrm{Planck}}-H_0^{\textrm{loc}}|/\sigma _{\mathrm{sample\, variance}}\simeq 20\). Therefore, sample variance is about 20 times too small to explain the Hubble tension.

Why does sample variance of local measurements with SNIa give such a small effect? The answer is in the fact that the SNIa that are used in the analysis are not quite “local”, the volume they span goes out to \(z=0.15\) (corresponding to distances of about \(\sim 500\,h^{-1}\textrm{Mpc}\)), and is actually quite large. Averaged over such large volumes, overdensities and underdensities are not very pronounced, and the variations in the “locally” determined Hubble constant are correspondingly small.

This result, and the related ones cited above, put a nail in the coffin of the sample-variance explanations for the Hubble tension. Because the sample-variance (or, void) explanation was arguably the simplest one, it leads to an exciting situation that the true explanation, whatever it is, is likely to only be more “exotic” and, overall, more unexpected.

4 Conclusions

In these proceedings, we have reviewed the status of Hubble tension. We briefly reviewed measurements by two principal probes of \(H_0\) — cosmic microwave background anisotropies, and the distance ladder that includes type Ia supernovae. We have also mentioned some promising complementary probes, such as the combination of baryon acoustic oscillations and big-bang nucleosynthesis, time delays between images observed in strongly lensed systems, and gravitational standard sirens.

We pointed out that there is a huge number of proposed theoretical explanations. These explanations attempt to introduce new models (or new ingredients in the currently favored cosmological model with dark matter and dark energy) in order to effectively raise the value of \(H_0\simeq 67\,\mathrm{km\ s^{-1}Mpc^{-1}}\) measured by the CMB and make it closer to the locally observed value of \(H_0^{\textrm{loc}}\simeq 73\,\mathrm{km\ s^{-1}Mpc^{-1}}\). Thus far, these theoretical explanations have had limited success, mainly due to the fact that they appear finely tuned and not particularly motivated or favored by independent measurements in cosmology.

We have described in more detail the author’s own work [39] on using numerical simulation to study whether sample variance is the cause of the Hubble tension. In this scenario, we live in a locally underdense region and, as a consequence, locally measure a higher expansion rate than the global mean \(H_0\). We sharply stress-tested this scenario by placing observers in an N-body simulation and directly “measuring” what variation in the Hubble constant the observer would see, depending on their location. The conclusion is that the observed variation in the locally measured Hubble constant is much too small—by a factor of \(\sim 20\)—in order to explain the Hubble tension. Therefore, presence of a large void definitely cannot explain the Hubble tension.

Hubble tension remains the foremost development on the frontiers of cosmology. When explained or understood it will, at the very minimum, reveal a large and unexpected systematic error in data or observations. Alternatively, and more excitingly, it will point to a non-trivial extension of the standard cosmological model. Stay tuned!