Skip to main content
SpringerLink
Log in

Non-Fickian transport of sodium chloride in inter-river land: experiment validation and fractional derivative modeling

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

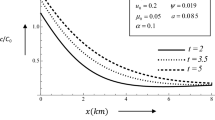
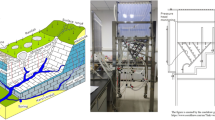
River–groundwater interactions, accompanied by solute transport, are one of the most important contemporary challenges. Non-Fickian diffusion behavior has been extensively documented for solute transport in groundwater or river, but less in river–groundwater system. This paper confirms the existence of anomalous diffusion in the river–groundwater system by experiments and then accurately describes the solute transport process by fractional derivative model, especially for the long-time power law tailing characteristic. Laboratory experiment in inter-river land sample shows that the time fractional advection–dispersion equation, which has a parameter (time index \(\alpha\)) defining memory function and other basic transport parameters (velocity v and dispersion coefficient D) with the different hydrogeologic significances, provides a prominent improvement in simulating non-Fickian diffusion behavior compared with the classical advection–dispersion equation. Analysis results indicate that low flow rates reduce mass exchange between the mobile and immobile domains, resulting in late-time heavy tailing phenomenon. In a word, this study provides a new approach to improve our understanding on solute transport in the interfluve with river–groundwater interactions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability Statement

This manuscript has associated data in a data repository. [Authors’ comment: All experimental data were conducted in Hefei University of Technology (China). Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.]

References

  1. N. Su, P.N. Nelson, S. Connor, The distributed-order fractional diffusion-wave equation of groundwater flow: theory and application to pumping and slug tests. J. Hydrol. 529(10), 1262–1273 (2015). https://doi.org/10.1016/j.jhydrol.2015.09.033

    Article  ADS  Google Scholar 

  2. P. Brunner, R. Therrien, P. Renard, C.T. Simmons, H.H. Franssen, Advances in understanding river-groundwater interactions: river-groundwater interactions. Rev. Geophys. 55(3), 818–854 (2017). https://doi.org/10.1002/2017RG000556

    Article  ADS  Google Scholar 

  3. D. Lapworth, N. Baran, M. Stuart, R. Ward, Emerging organic contaminants in groundwater: a review of sources, fate and occurrence. Environ. Pollut. 163, 287–303 (2012). https://doi.org/10.1016/j.envpol.2011.12.034

    Article  Google Scholar 

  4. D.W. Meals, S.A. Dressing, T.E. Davenport, Lag time in water quality response to best management practices: a review. J. Environ. Qual. 39(1), 85–96 (2010). https://doi.org/10.2134/jeq2009.0108

    Article  Google Scholar 

  5. W.W. Woessner, Stream and fluvial plain ground water interactions: rescaling hydrogeologic thought. Groundwater 38(3), 423–429 (2000). https://doi.org/10.1111/j.1745-6584.2000.tb00228.x

    Article  Google Scholar 

  6. L. Lambs, Interactions between groundwater and surface water at river banks and the confluence of rivers. J. Hydrol. 288(3), 312–326 (2004). https://doi.org/10.1016/j.jhydrol.2003.10.013

    Article  ADS  Google Scholar 

  7. B. Bijeljic, A. Raeini, P. Mostaghimi, M.J. Blunt, Predictions of non-fickian solute transport in different classes of porous media using direct simulation on pore-scale images. Phys. Rev. E 87(1), 013011 (2013). https://doi.org/10.1103/PhysRevE.87.013011

    Article  ADS  Google Scholar 

  8. B. Berkowitz, G. Kosakowski, G. Margolin, H. Scher, Application of continuous time random walk theory to tracer test measurements in fractured and heterogeneous porous media. Groundwater 39(4), 593–604 (2001). https://doi.org/10.1111/j.1745-6584.2001.tb02347.x

    Article  Google Scholar 

  9. R. Haggerty, S.M. Gorelick, Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 31(10), 2383–2400 (1995). https://doi.org/10.1029/95WR10583

    Article  ADS  Google Scholar 

  10. R. Schumer, D.A. Benson, M.M. Meerschaert, B. Baeumer, Fractal mobile/immobile solute transport. Water Resour. Res. 39(10), 1296–1307 (2003). https://doi.org/10.1029/2003WR002141

    Article  ADS  Google Scholar 

  11. A.J. Valocchi, Validity of the local equilibrium assumption for modeling sorbing solute transport through homogeneous soils. Water Resour. Res. 21(6), 808–820 (1985). https://doi.org/10.1029/WR021i006p00808

    Article  ADS  Google Scholar 

  12. R. Therrien, E. Sudicky, Three-dimensional analysis of variably-saturated flow and solute transport in discretely-fractured porous media. J. Contam. Hydrol. 23(1–2), 1–44 (1996). https://doi.org/10.1016/0169-7722(95)00088-7

    Article  ADS  Google Scholar 

  13. B. Lu, Y. Zhang, C. Zheng, C.T. Green, C. O’Neill, H.G. Sun, J. Qian, Comparison of time nonlocal transport models for characterizing non-fickian transport: from mathematical interpretation to laboratory application. Water 10(6), 778 (2018). https://doi.org/10.3390/w10060778

    Article  ADS  Google Scholar 

  14. B. Berkowitz, A. Cortis, M. Dentz, H. Scher, Modeling non-fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 44(2), RG2003 (2006). https://doi.org/10.1029/2005RG000178

    Article  ADS  Google Scholar 

  15. B. Lu, X. Liu, P. Dong, G.R. Tick, C. Zheng, Y. Zhang, M. Mahmood-UI-Hassan, H. Bai, E. Lamy, Quantifying fate and transport of nitrate in saturated soil systems using fractional derivative model. Appl. Math. Model. 81, 279–295 (2020). https://doi.org/10.1016/j.apm.2019.12.005

    Article  MathSciNet  MATH  Google Scholar 

  16. M.H. Puckett, Y. Zhang, B. Lu, Y. Lu, H.G. Sun, C. Zheng, W. Wei, Application of fractional differential equation to interpret the dynamics of dissolved heavy-metal uptake in streams at a wide range of scales. Eur. Phys. J. Plus 134(8), 377 (2019). https://doi.org/10.1140/epjp/i2019-12897-1

    Article  Google Scholar 

  17. Y. Zhang, R.L. Martin, D. Chen, B. Baeumer, H.G. Sun, L. Chen, A subordinated advection model for uniform bed load transport from local to regional scales. J. Geophys. Res. Earth Surf. 119(12), 2711–2729 (2014). https://doi.org/10.1002/2014JF003145

    Article  ADS  Google Scholar 

  18. Y. Zhang, L. Chen, D.M. Reeves, H.G. Sun, A fractional-order tempered-stable continuity model to capture surface water runoff. J. Vib. Control 22(8), 1993–2003 (2016). https://doi.org/10.1177/1077546314557554

    Article  MathSciNet  Google Scholar 

  19. N. Su, P.N. Nelson, S. Connor, The distributed-order fractional diffusion-wave equation of groundwater flow: theory and application to pumping and slug tests. J. Hydrol. 529, 1262–1273 (2015). https://doi.org/10.1016/j.jhydrol.2015.09.033

    Article  ADS  Google Scholar 

  20. J. Qian, H. Zhan, W. Zhao, F. Sun, Experimental study of turbulent unconfined groundwater flow in a single fracture. J. Hydrol. 311(1–4), 134–142 (2005). https://doi.org/10.1016/j.jhydrol.2005.01.013

    Article  ADS  Google Scholar 

  21. D. Nielsen, J. Biggar, Miscible displacement: Iii. theoretical considerations. Soil Sci. Soc. Am. J. 26(3), 216–221 (1962). https://doi.org/10.2136/sssaj1962.03615995002600030010x

    Article  ADS  Google Scholar 

  22. M. Caputo, Linear models of dissipation whose q is almost frequency independent-ii. Geophys. J. Int. 13(5), 529–539 (1967). https://doi.org/10.1111/j.1365-246X.1967.tb02303.x

    Article  ADS  Google Scholar 

  23. Y. Zhang, M.M. Meerschaert, B. Baeumer, Particle tracking for time-fractional diffusion. Phys. Rev. E 78(3), 036705 (2008). https://doi.org/10.1103/PhysRevE.78.036705

    Article  ADS  Google Scholar 

  24. D.A. Murio, Implicit finite difference approximation for time fractional diffusion equations. Comput. Math. Appl. 56(4), 1138–1145 (2008). https://doi.org/10.1016/j.camwa.2008.02.015

    Article  MathSciNet  MATH  Google Scholar 

  25. W. Deng, Finite element method for the space and time fractional fokker-planck equation. SIAM J. Numer. Anal. 47(1), 204–226 (2009). https://doi.org/10.1137/080714130

    Article  MathSciNet  MATH  Google Scholar 

  26. F. Liu, P. Zhuang, I. Turner, K. Burrage, V. Anh, A new fractional finite volume method for solving the fractional diffusion equation. Appl. Math. Model. 38(15–16), 3871–3878 (2014). https://doi.org/10.1016/j.apm.2013.10.007

    Article  MathSciNet  MATH  Google Scholar 

  27. K. Diethelm, N.J. Ford, A.D. Freed, A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29(1), 3–22 (2002). https://doi.org/10.1023/A:1016592219341

    Article  MathSciNet  MATH  Google Scholar 

  28. I. Ahmad, H. Ahmad, P. Thounthong, Y.M. Chu, C. Cesarano, Solution of multi-term time-fractional pde models arising in mathematical biology and physics by local meshless method. Symmetry 12(7), 1195 (2020). https://doi.org/10.3390/sym12071195

    Article  ADS  Google Scholar 

  29. H. Sheng, Y. Li, Y. Chen, Application of numerical inverse laplace transform algorithms in fractional calculus. J. Franklin Inst. 348(2), 315–330 (2011). https://doi.org/10.1016/j.jfranklin.2010.11.009

    Article  MathSciNet  MATH  Google Scholar 

  30. J. Valsa, L. Brančik, Approximate formulae for numerical inversion of laplace transforms. Int. J. Numer. Model. Electron. Netw. Devices Fields 11(3), 153–166 (1998). https://doi.org/10.1002/(SICI)1099-1204(199805/06)11:33.0.CO;2-C

    Article  MATH  Google Scholar 

  31. C.J. Willmott, K. Matsuura, Advantages of the mean absolute error (mae) over the root mean square error (rmse) in assessing average model performance. Climate Res. 30(1), 79–82 (2005). https://doi.org/10.3354/cr030079

    Article  ADS  Google Scholar 

  32. D.R. Legates, G.J. McCabe Jr., Evaluating the use of “goodness-of-fit’’ measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 35(1), 233–241 (1999). https://doi.org/10.1029/1998WR900018

    Article  ADS  Google Scholar 

  33. Y. Zhang, H.G. Sun, C. Zheng, Lagrangian solver for vector fractional diffusion in bounded anisotropic aquifers: development and application. Fract. Calculus Appl. Anal. 22(6), 1607–1640 (2019). https://doi.org/10.1515/fca-2019-0083

    Article  MathSciNet  MATH  Google Scholar 

  34. J.F. Pickens, G.E. Grisak, Scale-dependent dispersion in a stratified granular aquifer. Water Resour. Res. 17(4), 1191–1211 (1981). https://doi.org/10.1029/WR017i004p01191

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This research was funded by the National Natural Science Foundation of China, grant numbers U2267218, 11972148 and 41831289, the Natural Science Foundation of Jiangsu Province, Grant Number BK20190024, Key R &D Program of Anhui Province, Grant Number 201904a07020071.

Author information

Authors and Affiliations

  1. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, College of Mechanics and Materials, Hohai University, Nanjing, Jiangsu, 210098, China

    Yi Xu & HongGuang Sun

  2. School of Resources and Environmental Engineering, Hefei University of Technology, Hefei, 230009, China

    Chuantai Qiao & Jiazhong Qian

Authors
  1. Yi Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. HongGuang Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chuantai Qiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jiazhong Qian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to HongGuang Sun.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, Y., Sun, H., Qiao, C. et al. Non-Fickian transport of sodium chloride in inter-river land: experiment validation and fractional derivative modeling. Eur. Phys. J. Plus 137, 1275 (2022). https://doi.org/10.1140/epjp/s13360-022-03498-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-022-03498-6

Search

Navigation