1 Introduction

The onset of thermal convection in horizontal layers of fluids, uniformly heated from below, was studied for the first time by Henri Bénard in 1900 via experiments and, later, was analytically investigated by Lord Rayleigh. In particular, a “threshold phenomenon” was observed: Lord Rayleigh introduced a dimensionless parameter—the Rayleigh number \({\mathcal {R}}\), depending on the physical features of the layer and of the fluid and on the gravity acceleration—and established that the thermal convection arises when \({\mathcal {R}}\) overcomes a certain threshold \({\mathcal {R}}_c\). From a mathematical point of view, the critical value \({\mathcal {R}}_c\) is determined via the instability analysis of the thermal conduction solution. Concerning the linear instability analysis, requiring that all the eigenvalues of the linear operator have negative real part, one can determine a threshold \({\mathcal {R}}_L\) such that condition \({\mathcal {R}}> {\mathcal {R}}_L\) implies instability of the thermal conduction solution and, consequently, the onset of thermal convection. Concerning the nonlinear stability analysis, introducing a suitable norm and choosing properly a Lyapunov functional, one needs to determine the conditions for which this functional is decreasing along the solutions of the nonlinear system, these conditions give rise to the nonlinear threshold \({\mathcal {R}}_N(\le {\mathcal {R}}_L)\) such that the condition \({\mathcal {R}}<{\mathcal {R}}_N\) implies stability, i.e. if \({\mathcal {R}}<{\mathcal {R}}_N\) convection cannot occur. In order to have useful results for the applications, the challenge is to find a norm for which \({\mathcal {R}}_N={\mathcal {R}}_L\). Furthermore, in many applications, the thermal convection can arise via steady or oscillatory motions and convection is named steady or oscillatory convection, respectively.

The determination of the critical value \({\mathcal {R}}_c\) is a challenging task that attracted the interest of many researchers—in the past as nowadays—due to the many phenomena of the real world involving thermal convection in either clear fluids (see [1,2,3,4] and the references therein) or in fluids saturating porous media (materials composed of a solid skeleton containing interconnected voids through which a fluid can flow). The onset of convection in porous media was widely studied in the literature taking into account various effects, such as uniform rotation of the layer [5,6,7], the influence of an external transverse magnetic field on an electrically conducting fluid [8,9,10,11,12,13], the presence of nanoparticles in the saturating fluid [14, 15] or the presence of one or more chemicals dissolved in the fluid [16,17,18,19], the combined effects of uniform rotation and the presence of a chemical [20,21,22]. Recently, the attention of many scientists is moving toward bi-disperse porous media.

Definition 1.1

A bi-disperse porous medium (BDPM) is a double porosity material composed of clusters of large particles that are agglomerations of small particles and the solid matrix is characterized by two types of pores: There are macropores between the clusters and micropores within them, the macropores are referred to as f-phase (meaning “fractured phase”), while the remainder of the structure is referred to as p-phase (meaning “porous phase”) [23, 24].

In the following, we will denote by \(\varphi\) the porosity associated with the macropores—the ratio of the volume of the macropores to the total volume—and by \(\epsilon\) the porosity associated to the micropores—the ratio of the volume of the micropores to the volume of the porous body which remains once the macropores are removed. The earliest refined model describing the onset of convection in a bi-disperse porous medium is attributable to Nield and Kuznetsov in [24,25,26], in those papers the authors introduced a mathematical model which employs different velocities \(\mathbf{v}^f\) and \(\mathbf{v}^p\) in the macropores and in the micropores, different pressures \(p^f\) and \(p^p\) and different temperatures \(T^f\) and \(T^p\).

Through numerical simulations applied to a bi-disperse porous medium consisting of blocks of porous material which are themselves composed of smaller microblocks, Imani and Hooman in [27] showed that, when the macropores are relatively large compared to the micropores, it is possible to assume that the temperature of the solid skeleton matches those of the fluid in the macro- and micropores, so there is local thermal equilibrium. The single temperature model, i.e. with the assumption \(T^f=T^p=T\), may be sufficient to represent many real situations (see for instance [28,29,30], and the governing equations describing the evolutionary behaviour of the thermal conduction solution in a horizontal layer of single temperature BDPM were introduced by Gentile and Straughan in [31]. Dual porosity materials have a large number of practical applications in industrial field (in order to design heat pipes and computer chips [32], to understanding landslides or for the treatment of nuclear waste), in geophysics (the stockpiled pieces of coal are dual porosity media [33], biological and medical field (brain and bones are natural examples of dual porosity materials). Moreover, it was demonstrated by Nield and Kuznetsov in [24] that convection occurs at higher Rayleigh numbers in a dual porosity material with respect to an equivalent single porosity one, so the heat transfer due to the convective fluid motion is delayed, for this reason dual porosity materials are better suited for insulation problems and thermal management problem (such as cooling of data centers). Since bi-disperse porous media offer much more possibilities to design man-made materials then single porosity media [34,35,36], heat transfer problems in a rotating BDPM find many engineering or industrial applications. Rotating bi-disperse porous media were analysed under various assumptions by Capone et al. in [28, 29, 37,38,39,40]: for instance, in [39] Capone et al. analysed the influence of vertical rotation on the onset of convection in a single temperature BDPM, according to Darcy’s law, while [37] deals with the inertia effect on the onset of convection in a horizontal rotating layer of anisotropic bi-disperse porous medium. In particular, while in [39] it was proved the validity of the principle of exchange of stabilities—so convection can arise only via steady motions—and the coincidence between linear instability threshold and nonlinear stability threshold was obtained, in [37], since inertia term and uniform rotation of the layer have been simultaneously taken into account, the onset of convection can set in through stationary or oscillatory motions, and the critical values of the Rayleigh number for the onset of steady and oscillatory convection were determined. To obtain the results even more useful in applications involving, for instance, food and chemical processes, solidification and centrifugal casting of metals, rotating machineries, petroleum industry, biomechanics and geophysical problems, the presence of one or more chemicals (salts) dissolved in the fluid has been largely analysed either in rotating clear fluids [3] or in rotating single porosity media [17, 22]. The analysis of double diffusive convection requires to suppose that there is a salt dissolved in the fluid, so one considers simultaneous temperature and salt gradients, i.e. simultaneous mass diffusion and thermal diffusion in a liquid mixture. From a mathematical point of view, the competing effects of heating from below (that has a destabilizing effect on the conduction solution) and of rotation and salting from below (that both have a stabilizing effect) are challenging to analyse, since rotation and salt concentration give rise to a skewsymmetric part in the linear operator of the governing equations. Double diffusive bi-dispersive convection was studied by Straughan in [41, 42], by Challoob et al. in [43] under generalized boundary conditions, while Badday and Harfash in [33, 44] deal with bi-dispersive double diffusive convection, taking into account chemical reaction effects. However, in the present paper we focus our attention to double diffusive convection in a uniformly rotating single temperature bi-disperse porous material.

Unlike the diffusion of heat, the diffusion of salt can take place only through the fluid phase, so there are two physical effects to consider: the Soret effect, i.e. the mass flux created by a temperature gradient, and the Dufour effect, i.e. the energy flux induced by a concentration gradient, but, according to the experimental results, the Dufour effect plays a minor role in comparison with the Soret effect when a binary liquid mixture saturating a porous medium is considered (see [45] and the references therein).

As defined in [46], the Soret effect, also known as thermodiffusion, is the mass diffusion in a liquid mixture when a temperature gradient exists and is constantly maintained across the multicomponent mixture, causing all species to move. In response to a gradual and continuous migration of all particles from the hot side to the cold side, following the direction of the heat flow, a concentration gradient starts to develop within the mixture, which slows down the migration of the species to the cold side and causes some of the particles to move on the opposite direction. The contrast between thermal and concentration forces causes the rearrangement of the species until the final steady state. Some applications of the Soret effect are optimum oil recovery from hydrocarbon reservoirs, fabrication of semiconductor devices in molten metal and semiconductor mixtures, separation of species such as polymers, manipulation of macromolecules such as DNA [46].

The plan of the article is as follows. In Sect. 2 the mathematical model and the associated perturbation equations are introduced. In Sect. 3 we perform linear instability analysis of the thermal conduction solution and prove that if \(\epsilon _1 Le \le 1\) the strong principle of exchange of stabilities holds. As described in [1], states of marginal stability—which separates the stable state from the unstable one - can be stationary or oscillatory. If the amplitude of a generic perturbation grow (or is damped) aperiodically, the transition from stability to instability takes place via a marginal state via a steady pattern of motions. If the perturbations are characterized by oscillations of increasing (or decreasing) amplitude, instability occurs through oscillatory motions. If instability arises via stationary motions, the principle of exchange of stabilities holds and the instability sets in as stationary secondary flow. If oscillatory motions prevail, then one has overstability. Hence, in Sects. 3.1 and 3.2 we determine the critical Rayleigh numbers for the onset of steady and oscillatory convection, respectively. In Sect. 3.3 some mathematical aspects shared by the stationary and the oscillatory instability thresholds are discussed. In Sect. 4 the differential constraint approach is utilized to derive the global nonlinear instability threshold and we found that there are regions of subcritical instabilities. In Sect. 5 we perform some numerical simulations in order to analyse the behaviour of the instability thresholds with respect to fundamental physical parameters. The paper ends with a concluding section that summarizes all the obtained results.

2 Mathematical model

Let us consider a reference frame Oxyz with fundamental unit vectors \(\mathbf{i},\mathbf{j},\mathbf{k}\) (\(\mathbf{k}\) pointing vertically upward) and a plane layer \(L={\mathbb {R}}^2 \times [0,d]\) of saturated bi-disperse porous medium that is uniformly and simultaneously heated and salted from below and that is filled by an incompressible Newtonian fluid. Furthermore, we confine ourselves to the case of a single temperature bi-disperse porous material, so there is thermal equilibrium between the f-phase and the p-phase, i.e. \(T^f=T^p=T\). The layer L rotates about the vertical axis with constant angular velocity \(\Omega \mathbf{k}\), and hence, Darcy’s model is extended in order to include Coriolis forces in the momentum equations in the macropores and in the micropores. Moreover, a Boussinesq approximation is applied and the density in the buoyancy force has a linear dependence on temperature and concentration:

$$\begin{aligned} \varrho =\varrho _F [1-\alpha (T-T_0) + \alpha _C (C-C_0)], \end{aligned}$$

\(\alpha\) and \(\alpha _C\) being the thermal and chemical expansion coefficients, respectively. The governing equations for the onset of thermal convection in a uniformly rotating bi-disperse porous medium heated and salted from below, taking into account the Soret effect, are (cf. [39, 41]

$$\begin{aligned} {\left\{ \begin{array}{ll} - \dfrac{\mu }{K_f} \mathbf{v}^f - \zeta (\mathbf{v}^f -\mathbf{v}^p) - \nabla p^f + \varrho _F \alpha g T \mathbf{k} - \varrho _F \alpha _C g C \mathbf{k} - \dfrac{2 \varrho _F \Omega }{\varphi } \mathbf{k} \times \mathbf{v}^f = \mathbf{0}, \\ - \dfrac{\mu }{K_p} \mathbf{v}^p - \zeta (\mathbf{v}^p - \mathbf{v}^f) - \nabla p^p + \varrho _F \alpha g T \mathbf{k} - \varrho _F \alpha _C g C \mathbf{k} - \dfrac{2 \varrho _F \Omega }{\epsilon } \mathbf{k} \times \mathbf{v}^p = \mathbf{0}, \\ \nabla \cdot \mathbf{v}^f = 0, \\ \nabla \cdot \mathbf{v}^p = 0, \\ (\varrho c)_m \dfrac{\partial T}{\partial t} + (\varrho c)_F (\mathbf{v}^f + \mathbf{v}^p) \cdot \nabla T = k_m \Delta T, \\ \epsilon _1 \dfrac{\partial C}{\partial t} + (\mathbf{v}^f + \mathbf{v}^p) \cdot \nabla C = \epsilon _2 \Delta C + S \Delta T, \end{array}\right. } \end{aligned}$$
(1)

where \(p^f\) and \(p^p\) are the reduced pressures, i.e.

$$p^{s} = P^{s} - \frac{{\varrho _{F} }}{2}\left| {{\boldsymbol{\Omega }} \times {\mathbf{x}}} \right|^{2} \quad s = f,p$$

\(\mathbf{x}=(x,y,z)\), \(\mathbf{v}^s\) = seepage velocity for \(s=\{f,p\}\), T = temperature field, C = concentration field, \(\zeta\) = interaction coefficient between the f-phase and the p-phase, \(\mathbf{g}=-g \mathbf{k}\) = gravity, \(\mu\) = fluid viscosity, \(\varrho _F\) = reference constant density, \(K_s\) = permeability for \(s=\{f,p\}\), c = specific heat, \(k_m\) = thermal conductivity, \(k_s\) = thermal conductivity for \(s=\{f,p\}\), \(k^s_C\) = salt diffusivity for \(s=\{f,p\}\), \(S=\varphi S_T^f + \epsilon (1-\varphi ) S_T^p\), \(S_T^s\) = Soret coefficient for \(s=\{f,p\}\),

$$\begin{aligned} (\varrho c)_{m} & = (1 - \varphi )(1 - \epsilon )(\varrho c)_{{{\text{sol}}}} + \varphi (\varrho c)_{f} + \epsilon (1 - \varphi )(\varrho c)_{p} , \\ k_{m} & = (1 - \varphi )(1 - \epsilon )k_{{{\text{sol}}}} + \varphi k_{f} + \epsilon (1 - \varphi )k_{p} , \\ \epsilon _{1} & = \varphi + \epsilon (1 - \varphi ),\;\epsilon _{2} = \varphi k_{C}^{f} + \epsilon (1 - \varphi )k_{C}^{p} , \\ \end{aligned}$$

where the subscript sol is referred to the solid skeleton. Let us point out that in the case of single temperature BDPM, since macropores and micropores are saturated by the same fluid, we expect that [47] \((\varrho c)_f=(\varrho c)_p=(\varrho c)_F\), hence \((\varrho c)_m=(1-\varphi )(1-\epsilon )(\varrho c)_{sol}+[\varphi +\epsilon (1-\varphi )](\varrho c)_F\). The boundary conditions associated with (1) are

$$\begin{aligned} \mathbf{v}^s \cdot \mathbf{n} = 0 \ \text {on} \ z=0,d, \ \text {for} \ s=\{f,p\} \\ T=T_L \ \text {on} \ z=0, \quad T=T_U \ \text {on} \ z=d, \\ C=C_L \ \text {on} \ z=0, \quad C=C_U \ \text {on} \ z=d \end{aligned}$$
(2)

where \(\mathbf{n}\) is the unit outward normal to the impermeable horizontal planes delimiting the layer. Moreover, since the layer of BDPM is heated and salted from below, we assume \(T_L>T_U\) and \(C_L>C_U\). System (1)–(2) admits the stationary conduction solution

$$\begin{aligned} \begin{array}{l} \mathbf{{\overline{v}}}^f=0, \ \mathbf{{\overline{v}}}^p=0, \ {\overline{T}}=- \beta z + T_L, \ {\overline{C}}=- \beta _C z + C_L, \\ \dfrac{1}{\varrho _F} {\overline{p}}^s(z)= g(-\alpha \beta +\alpha _C \beta _C) \dfrac{z^2}{2} + g (\alpha T_L - \alpha _C C_L) z + {\overline{p}}^s(0), \ \text {with} \ s=\{f,p\} \end{array} \end{aligned}$$

where \(\beta =\dfrac{T_L-T_U}{d}\) is the temperature gradient, \(\beta _C=\dfrac{C_L-C_U}{d}\) is the concentration gradient and \({\bar{p}}^s(0)\) are assigned constants, for \(s=\{f,p\}\). Introducing a perturbation \(\{ \mathbf{u}^f, \mathbf{u}^p, \theta , \gamma , \pi ^f, \pi ^p \}\) to the steady solution, with \(\mathbf{u}^f=(u^f,v^f,w^f)\) and \(\mathbf{u}^p=(u^p,v^p,w^p)\), the arising perturbation equations are

$$\begin{aligned} {\left\{ \begin{array}{ll} - \dfrac{\mu }{K_f} \mathbf{u}^f - \zeta (\mathbf{u}^f - \mathbf{u}^p) - \nabla \pi ^f + \varrho _F \alpha g \theta \mathbf{k} - \varrho _F \alpha _C g \gamma \mathbf{k}- \dfrac{2 \varrho _F \Omega }{\varphi } \mathbf{k} \times \mathbf{u}^f = \mathbf{0}, \\ - \dfrac{\mu }{K_p} \mathbf{u}^p - \zeta (\mathbf{u}^p - \mathbf{u}^f)- \nabla \pi ^p + \varrho _F \alpha g \theta \mathbf{k} - \varrho _F \alpha _C g \gamma \mathbf{k} - \dfrac{2 \varrho _F \Omega }{\epsilon } \mathbf{k} \times \mathbf{u}^p = \mathbf{0}, \\ \nabla \cdot \mathbf{u}^f = 0, \\ \nabla \cdot \mathbf{u}^p = 0, \\ (\varrho c)_m \dfrac{\partial \theta }{\partial t} + (\varrho c)_F (\mathbf{u}^f + \mathbf{u}^p) \cdot \nabla \theta = (\varrho c)_f (w^f+w^p) \beta + k_m \Delta \theta , \\ \epsilon _1 \dfrac{\partial \gamma }{\partial t} + (\mathbf{u}^f + \mathbf{u}^p) \cdot \nabla \gamma = (w^f+w^p) \beta _C + \epsilon _2 \Delta \gamma + S \Delta \theta . \end{array}\right. } \end{aligned}$$
(3)

Let us introduce the following non-dimensional parameters:

$$\begin{aligned} \begin{array}{l} \mathbf{x}^{*} = \dfrac{\mathbf{x}}{d}, \ t^{*}=\dfrac{t}{t^{\#}}, \ \theta ^{*} = \dfrac{\theta }{T^{\#}}, \ \gamma ^{*} = \dfrac{\gamma }{C^{\#}} \\ \\ \mathbf{u}^{s*} = \dfrac{\mathbf{u}^s}{U}, \ \pi ^{s*} = \dfrac{\pi ^s}{P^{\#}}, \ \text {for} \ s=\{ f,p \} \\ \\ \eta =\dfrac{\varphi }{\epsilon }, \ \xi =\dfrac{K_f \zeta }{\mu }, \ K_r=\dfrac{K_f}{K_p}, \ A=\dfrac{(\varrho c)_m}{(\varrho c)_F} \end{array} \end{aligned}$$

where the scales are given by

$$\begin{aligned} U=\frac{k_m}{(\varrho c)_F d}, \ t^{\#} = \frac{d^2 (\varrho c)_m}{k_m}, \ P^{\#} = \frac{k_m \mu }{(\varrho c)_F K_f}, \ T^{\#} = \frac{\beta d^2 U (\varrho c)_F}{k_m}, \ C^{\#} = \frac{\beta _C U d^2}{\epsilon _2}, \end{aligned}$$

and let us define the Lewis number Le, the non-dimensional Soret number \({\mathcal {S}}\), the Taylor number \({\mathcal {T}}\), the Rayleigh number \({\mathcal {R}}\) and the Rayleigh number for the salt field \({\mathcal {C}}\), respectively, given by

$$\begin{aligned} \begin{array}{l} \mathrm{Le}=\dfrac{k_m}{\epsilon _2 (\varrho c)_m}, \quad {\mathcal {S}}=\dfrac{S T^{\#}}{\epsilon _2 C^{\#}}, \quad {\mathcal {T}} = \dfrac{2 \varrho _F \Omega K_f}{\varphi \mu }, \\ \\ {\mathcal {R}}= \dfrac{\beta d^2 (\varrho c)_F \varrho _F \alpha g K_f}{\mu k_m}, \quad {\mathcal {C}}= \dfrac{K_f \varrho _F \alpha _C g \beta _C d^2}{\mu \epsilon _2}. \end{array} \end{aligned}$$

The dimensionless equations describing the evolutionary behaviour of the perturbation fields, dropping all the asterisks, are

$$\begin{aligned} {\left\{ \begin{array}{ll} - \mathbf{u}^f - \xi (\mathbf{u}^f - \mathbf{u}^p) - \nabla \pi ^f + {\mathcal {R}}\theta \mathbf{k} - {\mathcal {C}}\gamma \mathbf{k} - {\mathcal {T}} \mathbf{k} \times \mathbf{u}^f = \mathbf{0}, \\ - K_r \mathbf{u}^p - \xi (\mathbf{u}^p - \mathbf{u}^f) - \nabla \pi ^p + {\mathcal {R}}\theta \mathbf{k} - {\mathcal {C}}\gamma \mathbf{k} - \eta {\mathcal {T}} \mathbf{k} \times \mathbf{u}^p = \mathbf{0}, \\ \nabla \cdot \mathbf{u}^f = 0, \\ \nabla \cdot \mathbf{u}^p = 0, \\ \dfrac{\partial \theta }{\partial t} + (\mathbf{u}^f + \mathbf{u}^p) \cdot \nabla \theta = w^f+w^p + \Delta \theta , \\ \epsilon _1 \mathrm{Le} \dfrac{\partial \gamma }{\partial t} + A \, \mathrm{Le} (\mathbf{u}^f + \mathbf{u}^p) \cdot \nabla \gamma = w^f+w^p + \Delta \gamma + {\mathcal {S}}\Delta \theta . \end{array}\right. } \end{aligned}$$
(4)

The initial conditions and the boundary conditions appended to system 4 are

$$\begin{aligned} \mathbf{u}^s(\mathbf{x},0)=\mathbf{u}^s_0(\mathbf{x}), \quad \pi ^s(\mathbf{x},0)=\pi ^s_0(\mathbf{x}), \quad \theta (\mathbf{x},0)=\theta _0(\mathbf{x}), \quad \gamma (\mathbf{x},0)=\gamma _0(\mathbf{x}) \end{aligned}$$

with \(\nabla \cdot \mathbf{u}^s_0=0\), for \(s=\{f,p\}\), and

$$\begin{aligned} w^f=w^p=\theta =\gamma =0 \quad \text {on} \ z=0,1, \end{aligned}$$
(5)

respectively.

Remark 2.1

With the aim to perform the stability analysis of the conduction solution to system (1)–(2), so of the null solution to (4)–(5), let us denote by

$$\begin{aligned} V=\left [ 0,\frac{2 \pi }{l} \right ] \times \left [ 0,\frac{2 \pi }{m} \right ] \times [0,1] \end{aligned}$$

the periodicity cell, let us assume that \(\forall f \in \{\nabla \pi ^s,u^s,v^s,w^s,\theta ,\gamma \}\) for \(s=\{f,p\}\), \(f \in W^{2,2}(V) \ \forall t \in {\mathbb {R}}^{+}\), and that f is a periodic function in the x and y directions of period \(2 \pi / l\) and \(2 \pi / m\), respectively.

3 Linear instability analysis

In order to study the linear instability of the thermal conduction solution, let us consider the linear version of system (4) and seek for a solution \(\mathbf{u}^f, \mathbf{u}^p, \pi ^f, \pi ^p, \theta , \gamma\) with time dependence like \(e^{\sigma t}\), with \(\sigma \in {\mathbb {C}}\), so we get

$$\begin{aligned} {\left\{ \begin{array}{ll} - \mathbf{u}^f - \xi (\mathbf{u}^f - \mathbf{u}^p) - \nabla \pi ^f + {\mathcal {R}}\theta \mathbf{k} - {\mathcal {C}}\gamma \mathbf{k} - {\mathcal {T}} \mathbf{k} \times \mathbf{u}^f = \mathbf{0}, \\ - K_r \mathbf{u}^p - \xi (\mathbf{u}^p - \mathbf{u}^f) - \nabla \pi ^p + {\mathcal {R}}\theta \mathbf{k} - {\mathcal {C}}\gamma \mathbf{k} - \eta {\mathcal {T}} \mathbf{k} \times \mathbf{u}^p = \mathbf{0}, \\ \nabla \cdot \mathbf{u}^f = 0, \\ \nabla \cdot \mathbf{u}^p = 0, \\ \sigma \theta = w^f+w^p + \Delta \theta , \\ \epsilon _1 \mathrm{Le} \, \sigma \, \gamma = w^f+w^p + \Delta \gamma + {\mathcal {S}}\Delta \theta . \end{array}\right. } \end{aligned}$$
(6)

Setting

$$\begin{aligned} \omega ^s_3=(\nabla \times \mathbf{u}^s) \cdot \mathbf{k},\,\, s=\{f,p\}, \end{aligned}$$

and taking the third component of curl of (6)\(_1\) and (6)\(_2\), we get

$$\begin{aligned} {\left\{ \begin{gathered} (\xi +1) \omega _3^f - \xi \omega _3^p = {\mathcal {T}} \dfrac{\partial w^f}{\partial z}, \\ (\xi +K_r) \omega _3^p - \xi \omega _3^f = \eta {\mathcal {T}} \dfrac{\partial w^p}{\partial z}, \end{gathered}\right. } \end{aligned}$$
(7)

i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega _3^f = \Gamma ^{-1} {\mathcal {T}} \Bigl [ (\xi +K_r) \dfrac{\partial w^f}{\partial z} + \eta \xi \dfrac{\partial w^p}{\partial z} \Bigr ], \\ \omega _3^p = \Gamma ^{-1} {\mathcal {T}} \Bigl [ \xi \dfrac{\partial w^f}{\partial z} + \eta (\xi +1) \dfrac{\partial w^p}{\partial z} \Bigr ], \end{array}\right. } \end{aligned}$$
(8)

where \(\Gamma =\xi +\xi K_r+K_r\). Now, substituting the derivative with respect to z of (8) in the third component of double curl of (6)\(_1\) and (6)\(_2\), that is

$$\begin{aligned} {\left\{ \begin{array}{ll} (1+\xi ) \Delta w^f - \xi \Delta w^p - {\mathcal {R}}\Delta _1 \theta + {\mathcal {C}}\Delta _1 \gamma + {\mathcal {T}} \dfrac{\partial \omega _3^f}{\partial z} = 0, \\ (K_r+\xi ) \Delta w^p - \xi \Delta w^f - {\mathcal {R}}\Delta _1 \theta + {\mathcal {C}}\Delta _1 \gamma + \eta {\mathcal {T}} \dfrac{\partial \omega _3^p}{\partial z} = 0, \end{array}\right. } \end{aligned}$$
(9)

where \(\Delta _1=\partial ^2/\partial x^2 + \partial ^2/\partial y^2\) is the horizontal Laplacian, we finally get the following boundary value problem in \(w^f, w^p, \theta , \gamma\)

$$\begin{aligned} {\left\{ \begin{array}{ll} \!\! (1+\xi ) \Delta w^f \!\!-\! \xi \Delta w^p \!\!-\! {\mathcal {R}}\Delta _1 \theta \!+\! {\mathcal {C}}\Delta _1 \gamma \!+\! \Gamma ^{-1} {\mathcal {T}}^2 \Bigl [ (\xi \!+\! K_r) \dfrac{\partial ^2 w^f}{\partial z^2} \!\!+\! \eta \xi \dfrac{\partial ^2 w^p}{\partial z^2} \Bigr ] \!\!=\! 0, \\[2mm] \!\! (K_r+\xi ) \Delta w^p \!\!-\! \xi \Delta w^f \!\!-\! {\mathcal {R}}\Delta _1 \theta \!+\! {\mathcal {C}}\Delta _1 \gamma \!+\! \Gamma ^{-1} \eta {\mathcal {T}}^2 \Bigl [ \xi \dfrac{\partial ^2 w^f}{\partial z^2} \!\!+\! \eta (\xi \!+\! 1) \dfrac{\partial ^2 w^p}{\partial z^2} \Bigr ] \!\!=\! 0, \\ \sigma \theta = w^f+w^p + \Delta \theta , \\ \epsilon _1 \mathrm{Le} \, \sigma \, \gamma = w^f+w^p + \Delta \gamma + {\mathcal {S}}\Delta \theta . \end{array}\right. } \end{aligned}$$
(10)

According to boundary conditions (5) and to the periodicity of the perturbations fields, being \(\{ \sin (n \pi z) \}_{n \in {\mathbb {N}}}\) a complete orthogonal system for \(L^2([0,1])\), we employ normal modes solutions in (10):

$$\begin{aligned} w^f&= \sum _{n=1}^{\infty } W^f_{0n} \sin (n \pi z) e^{i(lx+my)}, \\ w^p&= \sum _{n=1}^{\infty } W^p_{0n} \sin (n \pi z) e^{i(lx+my)}, \\ \theta&= \sum _{n=1}^{\infty } \Theta _{0n} \sin (n \pi z) e^{i(lx+my)}, \\ \gamma&= \sum _{n=1}^{\infty } \Gamma _{0n} \sin (n \pi z) e^{i(lx+my)}, \end{aligned}$$
(11)

where \(W^f_{0n}, W^p_{0n}, \Theta _{0n}, \Gamma _{0n}\) are real constants. Consequently we get

$$\begin{aligned} \left\{ \begin{aligned}&\Bigl [ (1+\xi ) \Lambda _n + \Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 (\xi +K_r) \Bigr ] W^f_{0n} + \Bigl [ - \xi \Lambda _n + \Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \eta \xi \Bigr ] W^p_{0n} \\&\qquad \qquad - {\mathcal {R}}a^2 \Theta _{0n} + {\mathcal {C}}a^2 \Gamma _{0n} =0, \\&\Bigl [ - \xi \Lambda _n +\Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \eta \xi \Bigr ] W^f_{0n} + \Bigl [ (K_r+\xi ) \Lambda _n + \Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \eta ^2 (\xi +1) \Bigr ] W^p_{0n} \\&\qquad \qquad - {\mathcal {R}}a^2 \Theta _{0n} + {\mathcal {C}}a^2 \Gamma _{0n} =0, \\&W^f_{0n}+W^p_{0n}-(\Lambda _n + \sigma ) \Theta _{0n}=0, \\&W^f_{0n}+W^p_{0n}-(\Lambda _n + \epsilon _1 \mathrm{Le} \sigma ) \Gamma _{0n} - {\mathcal {S}}\Lambda _n \Theta _{0n}=0. \end{aligned} \right. \end{aligned}$$
(12)

\(a^2=l^2+m^2\) being the wavenumber and \(\Lambda _n=n^2 \pi ^2+a^2\). Setting

$$\begin{aligned} H_1&=(1+\xi ) \Lambda _n + \Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 (\xi +K_r), \\ H_2&=- \xi \Lambda _n +\Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \eta \xi \\ H_3&=(K_r+\xi ) \Lambda _n + \Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \eta ^2 (\xi +1) \end{aligned}$$

and requiring the determinant of (12) to be zero, we obtain

$$\begin{aligned}&\sigma ^2 \epsilon _1 \mathrm{Le} (H_1 H_3-H_2^2)+\sigma [\Lambda _n (H_1 H_3-H_2^2)(1+\epsilon _1 \mathrm{Le}) +(H_1-2H_2+H_3)a^2({\mathcal {C}}-{\mathcal {R}}\epsilon _1 \mathrm{Le}) ] \\&\quad + \Lambda _n^2 (H_1 H_3-H_2^2)-a^2 \Lambda _n (H_1-2H_2+H_3) [{\mathcal {R}}-{\mathcal {C}}(1-{\mathcal {S}})]=0, \end{aligned}$$
(13)

hence

$$\begin{aligned} {\mathcal {R}}\!=\! \dfrac{(\Lambda _n \!+\! \sigma )(\Lambda _n \!+\!\epsilon _1 \mathrm{Le} \sigma )(H_1 H_3\!-\!H_2^2)\!+\!a^2[\Lambda _n {\mathcal {C}}(1\!-\!{\mathcal {S}}) \!+\! \sigma {\mathcal {C}}](H_1\!-\!2 H_2\!+\!H_3)}{a^2(H_1-2 H_2+H_3)(\Lambda _n+\epsilon _1 \mathrm{Le} \sigma )} \!\! \end{aligned}$$
(14)

Theorem 3.1

Condition \(\epsilon _1 \mathrm{Le} \le 1\) implies the validity of the strong form of the Principle of exchange of stabilities and, in this case, convection can arise only via stationary motions.

Proof

Both roots of (13) are real if

$$\begin{aligned}&[\Lambda _n (H_1 H_3-H_2^2)(1+\epsilon _1 \mathrm{Le})+(H_1-2H_2+H_3)a^2({\mathcal {C}}-{\mathcal {R}}\epsilon _1 \mathrm{Le}) ]^2- \\&\quad 4\epsilon _1 \mathrm{Le} (H_1 H_3\!-\!H_2^2)\{ \Lambda _n^2 (H_1 H_3\!-\!H_2^2)\!-\!a^2 \Lambda _n (H_1\!-\!2H_2\!+\!H_3) [{\mathcal {R}}\!-\!{\mathcal {C}}(1\!-\!{\mathcal {S}})] \} \! \ge \! 0 \end{aligned}$$
(15)

i.e.

$$\begin{aligned}&\Lambda _n^2 (H_1 H_3-H_2^2)^2 (1-\epsilon _1 \mathrm{Le})^2+({\mathcal {C}}-\epsilon _1 \mathrm{Le} {\mathcal {R}})^2 (H_1-2H_2+H_3)^2a^4+ \\&\quad 2 (H_1-2H_2+H_3)(H_1 H_3-H_2^2)a^2 \Lambda _n [(1-\epsilon _1 \mathrm{Le}) (\epsilon _1 \mathrm{Le} {\mathcal {R}}+{\mathcal {C}})+2 {\mathcal {S}}{\mathcal {C}}\epsilon _1 \mathrm{Le}] \ge 0 \end{aligned}$$
(16)

that is surely satisfied if \(\epsilon _1 \mathrm{Le} \le 1\), since

$$\begin{aligned} H_1-2 H_2+ H_3 =\,&\Lambda _n (1+K_r+4 \xi )+\Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 [K_r+\eta ^2 +\xi (\eta -1)^2] \\ H_1 H_3-H_2^2 =\,&\Gamma \Lambda _n^2+\Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \Lambda _n [\eta ^2(\xi +1)^2+2 \eta \xi ^2 + (\xi +K_r)^2] \\&+\Gamma ^{-1} {\mathcal {T}}^4 n^4 \pi ^4 \eta ^2 \end{aligned}$$
(17)

are positive. Therefore

$$\begin{aligned} \epsilon _1 \mathrm{Le} \le 1 \ \Rightarrow \ \sigma \in {\mathbb {R}}. \end{aligned}$$
(18)

\(\hfill\square\)

3.1 Steady convection threshold

When convective instability occurs via steady motions, the marginal state is characterized by \(\sigma =0\), so from (14) we derive the critical Rayleigh number for the onset of stationary convection:

$$\begin{aligned} {\mathcal {R}}_S=\min _{(n,a^2)} \dfrac{\Lambda _n}{a^2} \dfrac{\Gamma \Lambda _n^2+\Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \Lambda _n {\mathcal {A}}+\Gamma ^{-1} {\mathcal {T}}^4 n^4 \pi ^4 \eta ^2}{\Lambda _n (1\!+\!K_r\!+\!4 \xi )\!+\! \Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 [K_r\!+\!\eta ^2 \!+\! \xi (\eta -1)^2]} \!+\! {\mathcal {C}}(1\!-\!{\mathcal {S}}), \end{aligned}$$
(19)

where \({\mathcal {A}}=\eta ^2(\xi +1)^2+2 \eta \xi ^2 + (\xi +K_r)^2\). The minimum with respect to \(n \in {\mathbb {N}}\) is attained at \(n=1\), so the steady critical Rayleigh number is given by

$$\begin{aligned} {\mathcal {R}}_S= f(a^2_c) + {\mathcal {C}}(1-{\mathcal {S}}) \end{aligned}$$
(20)

where

$$\begin{aligned} f(a^2_c) = \min _{a^2 \in {\mathbb {R}}^{+}} \dfrac{\Lambda _1}{a^2} \dfrac{\Gamma \Lambda _1^2+\Gamma ^{-1} {\mathcal {T}}^2 \pi ^2 \Lambda _1 {\mathcal {A}}+\Gamma ^{-1} {\mathcal {T}}^4 \pi ^4 \eta ^2}{\Lambda _1 (1+K_r+4 \xi )+\Gamma ^{-1} {\mathcal {T}}^2 \pi ^2 [K_r+\eta ^2 +\xi (\eta -1)^2]} . \end{aligned}$$
(21)

Moreover, the minimum (21) is attained at the positive solution of the fourth-order algebraic equations \(s(x)=0\), with \(x=a^2\) and

$$\begin{aligned} s(x)=h_1 x^4 + h_2 x^3 +h_3 x^2+h_4 x+h_5, \end{aligned}$$

where

$$\begin{aligned} h_1=&\Gamma (1+K_r+4 \xi ), \\ h_5 =&\!-\! \pi ^8 c_1 \cdot c_2. \end{aligned}$$

and

$$\begin{aligned} c_1&= 1 \!+\! K_r \!+\! 4 \xi \!+\! \Gamma ^{-1} K_r {\mathcal {T}}^2 \!+\! \Gamma ^{-1} {\mathcal {T}}^2 [\eta ^2 \!+\! \xi (\eta \!-\! 1)^2], \\ c_2&= \Gamma \!+\! \Gamma ^{-1} {\mathcal {T}}^2 [2 \xi ^2 \eta \!+\! \eta ^2 (1 \!+\! \xi )^2 \!+\! (K_r \!+\! \xi )^2 \!+\! {\mathcal {T}}^2 \eta ^2]. \end{aligned}$$

For that matter, the equation \(s(x)=0\) admits at least one positive root since

$$\begin{aligned} s(0)=h_5<0 \quad \text {and} \quad \lim _{x \rightarrow \infty } s(x)=+\infty . \end{aligned}$$

Let us finally point out that in the absence of rotation (i.e. for \({\mathcal {T}} \rightarrow 0\)) from (19) we recover the stationary threshold found in [41], while confining ourselves to the case of a single component fluid (i.e. for \({\mathcal {C}}\rightarrow 0\)), (19) coincides with the instability threshold found in [39]. When the Soret effect is neglected (i.e. for \({\mathcal {S}}\rightarrow 0\)), one obtains that \({\mathcal {R}}_S= f(a^2_c) + {\mathcal {C}}\).

3.2 Oscillatory convection threshold

In order to determine the instability threshold for the onset of oscillatory convection, the growth rate of the system \(\sigma\) needs to be purely imaginary, hence let us consider \(\sigma =i \sigma _1\), with \(\sigma _1 \in R-\{ 0 \}\), so (14) becomes

$$\begin{aligned} {\mathcal {R}}= \mathrm{Re}({\mathcal {R}}) + i \ \mathrm{Im}({\mathcal {R}}) \, . \end{aligned}$$
(22)

whit

$$\begin{aligned} \mathrm{Re}({\mathcal {R}}) &=\dfrac{\Lambda _n (H_1 H_3 \!-\! H_2^2)}{a^2 (H_1 \!-\! 2 H_2 \!+\! H_3)} \!+\! \dfrac{{\mathcal {C}}(1-{\mathcal {S}}) \Lambda _n^2 \!+\! \epsilon _1 \mathrm{Le} \sigma _1^2 {\mathcal {C}}}{\Lambda _n^2 \!+\! (\epsilon _1 \mathrm{Le} \sigma _1)^2} \\[3mm] \mathrm{Im}({\mathcal {R}}) &=\sigma _1 \Bigl [ \dfrac{H_1 H_3 \!-\! H_2^2}{a^2(H_1 \!-\! 2 H_2+H_3)} \!+\! \dfrac{\Lambda _n {\mathcal {C}}\!-\! \Lambda _n \epsilon _1 \mathrm{Le} {\mathcal {C}}(1 \!-\! {\mathcal {S}})}{\Lambda _n^2 \!+\!(\epsilon _1 \mathrm{Le} \sigma _1)^2} \Bigr ] \end{aligned}$$
(23)

Imposing the imaginary part \(Im({\mathcal {R}})\) of (22) to vanish, we get

$$\begin{aligned} (H_1 H_3 \!-\! H_2^2) [\Lambda _n^2 \!+\! (\epsilon _1 \mathrm{Le} \sigma _1)^2] \!+\! a^2(H_1\!-\!2H_2\!+\!H_3)\Lambda _n {\mathcal {C}}(1\!-\!\epsilon _1 \mathrm{Le} \!+\! \epsilon _1 \mathrm{Le} {\mathcal {S}}) \!=\! 0. \end{aligned}$$
(24)

Hence, necessary conditions for the onset of oscillatory convection are

$$\begin{aligned}&\epsilon _1 \mathrm{Le} >1, \\&\Lambda _n^2 (H_1 H_3 -H_2^2) + a^2 (H_1-2H_2+H_3) \Lambda _n {\mathcal {C}}(1-\epsilon _1 \mathrm{Le} +\epsilon _1 \mathrm{Le} {\mathcal {S}})<0. \end{aligned}$$
(25)

Consequently, the critical Rayleigh number for the onset of oscillatory convection is

$$\begin{aligned} {\mathcal {R}}_O \!=\! \min _{(n,a^2)} \!\! \dfrac{\Lambda _n}{a^2} \dfrac{\Gamma \Lambda _n^2 \!+\! \Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \Lambda _n {\mathcal {A}}\!+\!\Gamma ^{-1} {\mathcal {T}}^4 n^4 \pi ^4 \eta ^2}{\Lambda _n (1\!+\!K_r\!+\!4 \xi )\!+\!\Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 [K_r\!+\!\eta ^2 \!+\!\xi (\eta \!-\!1)^2]} {\mathcal {B}} + \dfrac{{\mathcal {C}}}{\epsilon _1 \mathrm{Le}} \end{aligned}$$
(26)

where \({\mathcal {B}}=\Bigl (1\!+\!\dfrac{1}{\epsilon _1 \mathrm{Le}} \Bigr )\), while the frequency of the oscillations is given by

$$\begin{aligned} \sigma _1^2= \dfrac{a^2 (H_1-2H_2+H_3) \Lambda _n {\mathcal {C}}(\epsilon _1 \mathrm{Le} -1 -\epsilon _1 \mathrm{Le} {\mathcal {S}})-\Lambda _n^2 (H_1 H_3 -H_2^2)}{(\epsilon _1 \mathrm{Le})^2 (H_1 H_3-H_2^2)}. \end{aligned}$$
(27)

Since the minimum of (26) with respect to \(n \in {\mathbb {N}}\) is attained at \(n=1\), the oscillatory critical Rayleigh number is given by

$$\begin{aligned} {\mathcal {R}}_O = f(a^2_c) \Bigl (1+\dfrac{1}{\epsilon _1 \mathrm{Le}} \Bigr )+ \dfrac{{\mathcal {C}}}{\epsilon _1 \mathrm{Le}} \, , \end{aligned}$$
(28)

or, equivalently,

$$\begin{aligned} {\mathcal {R}}_O={\mathcal {R}}_S \left(1+\dfrac{1}{\epsilon _1 \mathrm{Le}} \right)+{\mathcal {C}}\left[ {\mathcal {S}}\left(1+\dfrac{1}{\epsilon _1 \mathrm{Le}} \right)-1 \right], \end{aligned}$$
(29)

hence, while the oscillatory Rayleigh number given by (28) does not depend on the Soret number \({\mathcal {S}}\), i.e. the Soret effect does not directly affect the oscillatory instability threshold, from (29) one gets

$$\begin{aligned} {\mathcal {S}}> \dfrac{\epsilon _1 \mathrm{Le}}{\epsilon _1 \mathrm{Le} +1} \quad \Rightarrow \quad {\mathcal {R}}_O>{\mathcal {R}}_S \end{aligned}$$
(30)

and convection arises through stationary motions. As shown for the stationary threshold, in the absence of rotation from (26) we recover the same oscillatory instability threshold found in [41]. Let us remark that when a binary mixture and the Soret effect are considered, convection can arise via steady or oscillatory motions, while the principle of exchange of stabilities was proved for the single component case, so, in that case, oscillatory convection cannot occur (see [39].

3.3 Remarks

Since

$$\begin{aligned} \dfrac{\partial {\mathcal {R}}_S}{\partial {\mathcal {C}}}>0 \quad \text {and} \quad \dfrac{\partial {\mathcal {R}}_O}{\partial {\mathcal {C}}}>0, \end{aligned}$$

the chemical component dissolved at the bottom of the layer has a stabilizing effect on the onset of convection, i.e. it delays the onset of convection through both stationary and oscillatory motions. Moreover,

$$\begin{aligned} \dfrac{\partial {\mathcal {R}}_S}{\partial {\mathcal {T}}^2}>0 \quad \text {and} \quad \dfrac{\partial {\mathcal {R}}_O}{\partial {\mathcal {T}}^2}>0, \end{aligned}$$

this means that rotation has a stabilizing effect on the onset of both steady and oscillatory convection. As one is expected, both the rotation and the dissolved solute act to stop heat transfer and fluid motion through convection. From (20) and (28) one obtains

$$\begin{aligned} {\mathcal {R}}_O>{\mathcal {R}}_S \quad \Leftrightarrow \quad f(a^2_c) > {\mathcal {C}}\left[\epsilon _{1} {\mathrm{Le}} (1-{\mathcal {S}})-1\right], \end{aligned}$$
(31)

that is a necessary and sufficient condition for the onset of stationary convection. Moreover, the steady and oscillatory instability thresholds (20) and (28) are straight lines in the \(({\mathcal {C}},{\mathcal {R}})\) plane, so for increasing \({\mathcal {C}}\) there is a transition from steady to oscillatory convection in correspondence of the intersection point

$$\begin{aligned} {\mathcal {C}}^{*} = \dfrac{f(a^2_c)}{\epsilon _1 \mathrm{Le}( 1-{\mathcal {S}}) -1} \ . \end{aligned}$$
(32)

4 Nonlinear stability

Let us consider the nonlinear system (10)\(_{1,2}\) and (4)\(_{5,6}\)

$$\begin{aligned} \left\{ \begin{aligned}&\!(1\!+\!\xi ) \Delta w^f \!-\! \xi \Delta w^p \!-\! {\mathcal {R}}\Delta _1 \theta \!+\! {\mathcal {C}}\Delta _1 \gamma \!+\! \Gamma ^{-1} {\mathcal {T}}^2 \Bigl [ (\xi \!+\! K_r) \dfrac{\partial ^2 w^f}{\partial z^2} \!+\! \eta \xi \dfrac{\partial ^2 w^p}{\partial z^2} \Bigr ] \!\!=\! 0, \\&\!(K_r\!+\!\xi ) \Delta w^p \!-\! \xi \Delta w^f \!-\! {\mathcal {R}}\Delta _1 \theta \!+\! {\mathcal {C}}\Delta _1 \gamma \!+\! \Gamma ^{-1} \eta {\mathcal {T}}^2 \Bigl [ \xi \dfrac{\partial ^2 w^f}{\partial z^2} \!+\! \eta (\xi \!+\!1) \dfrac{\partial ^2 w^p}{\partial z^2} \Bigr ] \!\!=\! 0, \\&\dfrac{\partial \theta }{\partial t} + (\mathbf{u}^f+\mathbf{u}^p) \cdot \nabla \theta = w^f+w^p + \Delta \theta , \\&\epsilon _1 \mathrm{Le} \, \dfrac{\partial \gamma }{\partial t} +A \, \mathrm{Le} (\mathbf{u}^f+\mathbf{u}^p) \cdot \nabla \gamma = w^f+w^p + \Delta \gamma + {\mathcal {S}}\Delta \theta . \end{aligned} \right. \end{aligned}$$
(33)

The threshold for the nonlinear stability of the conduction solution will be determined employing the differential constraint approach [18]. Therefore, denoting by \((\cdot ,\cdot )\) and \(\Vert \cdot \Vert\) inner product and norm on the Hilbert space \(L^2(V)\), respectively, let us set

$$\begin{aligned} E(t) = \dfrac{1}{2} \Vert \theta \Vert ^2 + \epsilon _1 \mathrm{Le} \dfrac{\mu }{2} \Vert \gamma \Vert ^2, \end{aligned}$$
(34)
$$\begin{aligned} I(t) = (w^f+w^p,\theta ) + \mu (w^f+w^p,\gamma ) +\mu {\mathcal {S}}(\Delta \theta , \gamma ), \quad D(t) = \Vert \nabla \theta \Vert ^2 + \mu \Vert \nabla \gamma \Vert ^2, \end{aligned}$$

where \(\mu\) is a positive coupling parameter to be chosen. Retaining (33)\(_{1,2}\) as constraints, integrating over the periodicity cell Eq. 33)\(_3\) multiplied by \(\theta\) and Eq. (33)\(_4\) multiplied by \(\gamma\), adding the resulting equations one gets

$$\begin{aligned} \frac{dE}{dt} = I-D \le D \left( m-1 \right) , \end{aligned}$$
(35)

where

$$\begin{aligned} m = \max _{{\mathcal {H}}^{*}} \frac{I}{D} \end{aligned}$$
(36)

and

$$\begin{aligned} {\mathcal {H}}^{*}& = \{(w^f,w^p,\theta ,\gamma ) \in (H^1)^4 \mid w^f=w^p=\theta =\gamma =0 \ \text {on} \ z=0,1; \text {periodic in} \ x,y \\&\text {with periods} \ 2 \pi /l, 2 \pi /m;D<\infty ; \text {verifying} \ (33)_{1,2} \} \end{aligned}$$

is the space of kinematically admissible solutions. Let us introduce the Lagrange multipliers \(\lambda ^{'}(\mathbf{x})\) and \(\lambda ^{''}(\mathbf{x})\), hence, the maximum problem (36) is equivalent to

$$\begin{aligned} m = \hbox{max} _{{\mathcal {H}}} \frac{I + \int _V \lambda ^{\prime} f_1 \ dV + \int _V \lambda ^{''} f_2 \ dV }{D}, \end{aligned}$$
(37)

where

$$\begin{aligned} f_1 &=M_1 w^f + M_2 w^p -{\mathcal {R}}\Delta _1 \theta + {\mathcal {C}}\Delta _1 \gamma , \quad f_2=M_2 w^f + M_3 w^p -{\mathcal {R}}\Delta _1 \theta + {\mathcal {C}}\Delta _1 \gamma , \\ {\mathcal {H}} &= \{(w^f,w^p,\theta ,\gamma ) \in (H^1)^4 \mid w^f=w^p=\theta =\gamma =0 \ \text {on} \ z=0,1; \text {periodic in} \ x,y \\&\quad \text {with periods} \ 2 \pi /l, 2 \pi /m, \ \text {respectively};D< \infty \}, \end{aligned}$$

and the following operators were defined:

$$\begin{aligned}&M_1 \equiv (1+\xi ) \Delta + \Gamma ^{-1} {\mathcal {T}}^2 (\xi +K_r)\partial _{zz}, \\ &M_2 \equiv -\xi \Delta + \Gamma ^{-1} {\mathcal {T}}^2 \eta \xi \partial _{zz}, \\ &M_3 \equiv (K_r+\xi ) \Delta + \Gamma ^{-1} {\mathcal {T}}^2 \eta ^2 (\xi +1)\partial _{zz}. \end{aligned}$$

Theorem 4.1

Condition \(m<1\) guarantees the global, nonlinear stability of the stationary conduction solution with respect to the \(E-norm\).

Proof

By virtue of Poincaré inequality, one obtains that \(D \ge \pi ^2 \Vert \theta \Vert ^2 + \mu \pi ^2 \Vert \gamma \Vert ^2\), hence, if \(m<1\) from (35) it follows

$$\begin{aligned} {\dot{E}}(t) \le D \left( m-1 \right) \le \pi ^2 {\hat{\alpha }} (m-1) E(t), \quad \Longrightarrow \quad E(t) \le E(0) \exp (\pi ^2 {\hat{\alpha }} (m-1) t), \end{aligned}$$
(38)

with \({\hat{\alpha }}=\min (1,1/\epsilon _1 \mathrm{Le})\), i.e. condition \(m<1\) implies \(E(t) \rightarrow 0\) at least exponentially. Moreover, multiplying (4)\(_1\) by \(\mathbf{u}^f\) and (4)\(_2\) by \(\mathbf{u}^p\), one gets

$$\begin{aligned} (1+\xi ) \Vert \mathbf{u}^f \Vert ^2 - \xi (\mathbf{u}^f,\mathbf{u}^p)&= {\mathcal {R}}(\theta ,w^f)-{\mathcal {C}}(\gamma ,w^f), \\ (K_r+\xi ) \Vert \mathbf{u}^p \Vert ^2 - \xi (\mathbf{u}^f,\mathbf{u}^p)&= {\mathcal {R}}(\theta ,w^p)-{\mathcal {C}}(\gamma ,w^p), \end{aligned}$$
(39)

hence, by virtue of Cauchy–Schwarz inequality,

$$\begin{aligned} (1+\xi ) \Vert \mathbf{u}^f \Vert -\xi \Vert \mathbf{u}^p \Vert&\le \Vert {\mathcal {R}}\theta - {\mathcal {C}}\gamma \Vert , \\ (K_r+\xi ) \Vert \mathbf{u}^p \Vert -\xi \Vert \mathbf{u}^f \Vert&\le \Vert {\mathcal {R}}\theta - {\mathcal {C}}\gamma \Vert . \end{aligned}$$
(40)

Adding (40)\(_1\) and (40)\(_2\) one finally obtains

$$\begin{aligned} \Vert \mathbf{u}^f \Vert + K_r \Vert \mathbf{u}^p \Vert \le 2 \Vert {\mathcal {R}}\theta - {\mathcal {C}}\gamma \Vert , \end{aligned}$$
(41)

i.e. if \(m<1\) the seepage velocities \(\mathbf{u}^f\) and \(\mathbf{u}^p\) exponentially go to zero, hence, the global, nonlinear stability of the conduction solution with respect to the \(E-\)norm is guaranteed. \(\hfill\square\)

Remark 4.1

If \({\mathcal {R}}_E\) is the critical value of the Rayleigh number such that \(m=1\), condition \(m<1\) is equivalent to condition \({\mathcal {R}}<{\mathcal {R}}_E\).

The Euler–Lagrange equations associated with (37) are

$$\begin{aligned} {\left\{ \begin{array}{ll} M_1 w^f + M_2 w^p -{\mathcal {R}}\Delta _1 \theta + {\mathcal {C}}\Delta _1 \gamma =0, \\ M_2 w^f + M_3 w^p -{\mathcal {R}}\Delta _1 \theta + {\mathcal {C}}\Delta _1 \gamma =0, \\ \theta + \mu \gamma + M_1 \lambda ^{'} + M_2 \lambda ^{''} =0, \\ \theta + \mu \gamma + M_2 \lambda ^{'} + M_3 \lambda ^{''} =0, \\ w^f+w^p +\mu {\mathcal {S}}\Delta \gamma - {\mathcal {R}}(\Delta _1 \lambda ^{'} + \Delta _1 \lambda ^{''} ) + 2 \Delta \theta =0, \\ \mu (w^f+w^p) +\mu {\mathcal {S}}\Delta \theta +{\mathcal {C}}(\Delta _1 \lambda ^{'} + \Delta _1 \lambda ^{''} ) + 2 \mu \Delta \gamma =0, \end{array}\right. } \end{aligned}$$
(42)

Employing normal modes representation in (42):

$$\begin{aligned} w^f_n&= W^f_{0n} \sin (n \pi z) e^{i(lx+my)}, \\ w^p_n&= W^p_{0n} \sin (n \pi z) e^{i(lx+my)}, \\ \theta _n&= \Theta _{0n} \sin (n \pi z) e^{i(lx+my)}, \\ \gamma _n&= \Gamma _{0n} \sin (n \pi z) e^{i(lx+my)}, \\ \lambda ^{'}_n&= \lambda _{0n}^{'} \sin (n \pi z) e^{i(lx+my)}, \\ \lambda ^{''}_n&= \lambda _{0n}^{''} \sin (n \pi z) e^{i(lx+my)}, \end{aligned}$$
(43)

the global nonlinear stability threshold with respect to the \(E-\)norm is found requiring zero determinant for the system

$$\begin{aligned} {\left\{ \begin{array}{ll} H_1 W_{0n}^f + H_2 W_{0n}^p -{\mathcal {R}}a^2 \Theta _{0n} + {\mathcal {C}}a^2 \Gamma _{0n} =0, \\ H_2 W_{0n}^f + H_3 W_{0n}^p -{\mathcal {R}}a^2 \Theta _{0n} + {\mathcal {C}}a^2 \Gamma _{0n} =0, \\ \Theta _{0n} + \mu \Gamma _{0n} - H_1 \lambda _{0n}^{'} - H_2 \lambda _{0n}^{''} =0, \\ \Theta _{0n} + \mu \Gamma _{0n} - H_2 \lambda _{0n}^{'} - H_3 \lambda _{0n}^{''} =0, \\ W_{0n}^f+W_{0n}^p - \mu {\mathcal {S}}\Lambda _n \Gamma _{0n} + {\mathcal {R}}a^2 ( \lambda _{0n}^{'} + \lambda _{0n}^{''} ) -2 \Lambda _n \Theta _{0n} =0, \\ \mu (W_{0n}^f+W_{0n}^p) - \mu {\mathcal {S}}\Lambda _n \Theta _{0n} - {\mathcal {C}}a^2 (\lambda _{0n}^{'} +\lambda _{0n}^{''} ) - 2 \mu \Lambda _n \Gamma _{0n} =0, \end{array}\right. } \end{aligned}$$
(44)

\(a^2=l^2+m^2\) being the wavenumber, while \(\Lambda _n=a^2+n^2 \pi ^2\). Hence, one obtains the stability condition

$$\begin{aligned} {\mathcal {R}}<{\mathcal {R}}_E \end{aligned}$$
(45)

where the critical nonlinear Rayleigh number is found to be

$$\begin{aligned} {\mathcal {R}}_E =\max _{\mu } \min _{n,a^2} \! \dfrac{2 \sqrt{(H_1 H_3 \!-\! H_2^2) \Lambda _n X } \sqrt{1 \!+\! \mu (1\!-\!{\mathcal {S}})} \!+\! \mu {\mathcal {S}}\Lambda _n (H_1 H_3 \!-\! H_2^2) \!-\! Y }{\mu a^2 (H_1-2 H_2 +H_3)} \end{aligned}$$
(46)

where \(X= {\mathcal {C}}a^2 (H_1-2 H_2 +H_3) + \Lambda _n (H_1 H_3 - H_2^2)\) and \(Y= {\mathcal {C}}a^2 (H_1-2 H_2 +H_3) + 2 \Lambda _n (H_1 H_3 - H_2^2)\). The maximum of (46) with respect to \(\mu\) is attained at

$$\begin{aligned} \mu _c=\dfrac{{\mathcal {C}}a^2 (H_1-2 H_2 +H_3)}{\Lambda _n (H_1 H_3 - H_2^2) (1-{\mathcal {S}})} \end{aligned}$$

consequently

$$\begin{aligned} {\mathcal {R}}_E = \min _{n,a^2} \dfrac{\Lambda _n}{a^2} \dfrac{\Gamma \Lambda _n^2+\Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 \Lambda _n {\mathcal {A}} +\Gamma ^{-1} {\mathcal {T}}^4 n^4 \pi ^4 \eta ^2}{\Lambda _n (1+K_r+4 \xi )+\Gamma ^{-1} {\mathcal {T}}^2 n^2 \pi ^2 [K_r+\eta ^2 +\xi (\eta -1)^2]}. \end{aligned}$$
(47)

In conclusion, we obtained that \({\mathcal {R}}_E=f(a_c^2)\) and

$$\begin{aligned} {\mathcal {R}}_E < \min ({\mathcal {R}}_S,{\mathcal {R}}_O), \end{aligned}$$

therefore, there are regions of possible subcritical instabilities. However, for \({\mathcal {S}}\rightarrow 1\) the coincidence between the stationary threshold \({\mathcal {R}}_S\) and the global nonlinear threshold \({\mathcal {R}}_E\) is achieved, even though the dependence of the instability thresholds on the concentration field is lost. Let us observe that the nonlinear stability threshold \({\mathcal {R}}_E\) coincides with the stability threshold obtained when the Soret effect is not taken into account, therefore, if \({\mathcal {R}}<{\mathcal {R}}_E\), the thermal conduction solution is unconditionally stable, regardless of what value \({\mathcal {C}}\) has and no matter of whether the Soret effect is taken into account or not, hence, the global nonlinear stability threshold obtained by the energy (34) is affected only by rotation and the stabilizing effect of the concentration gradient on the onset of convection is not achieved. Let us remark that condition (31) becomes

$$\begin{aligned} {\mathcal {R}}_O>{\mathcal {R}}_S \quad \Leftrightarrow \quad {\mathcal {R}}_E > {\mathcal {C}}\left[\epsilon _{1} {\mathrm{Le}} (1-{\mathcal {S}})-1\right], \end{aligned}$$
(48)

5 Numerical simulations

The purpose of this section is to numerically investigate the asymptotic behaviour of steady and oscillatory thresholds (20) and (28) with respect to the meaningful parameters of the model. Since our thresholds are consistent with those ones found in [41], let us fix \(\{\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924 \}\) in the following simulations.

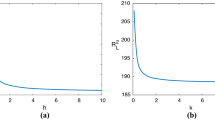
For high concentrations of the dissolved chemical component, convection sets in through oscillatory motions, indeed in Fig. 1a the linear dependence of the Rayleigh number on the chemical Rayleigh number is depicted, and, for the chosen set of parameters, the critical value of the concentration Rayleigh number for which there is a switch from stationary to oscillatory convection is \({\mathcal {C}}^{*} =4.0839\).

In Table 1(a) and (b) the stabilizing effect of rotation on the onset of convection is displayed, for low salt concentration - cfr. 1(a) - and for high salt concentration - cfr. 1(b).

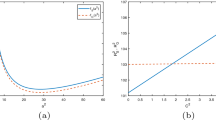
Table 2 and Fig.1b show the stabilizing effect of salt concentration on the onset of convection and, in particular, as \({\mathcal {C}}\) increases, the increasing of \({\mathcal {R}}_O\) is slower than the increasing of \({\mathcal {R}}_S\) and, as already observed, for \({\mathcal {C}}^*=4.0839\) there is the switch from steady to oscillatory convection. While the Soret effect does not directly affect the oscillatory instability threshold, as already pointed out, its increasing leads to a decreasing of the thermal critical stationary Rayleigh number, so the Soret effect has a inhibiting effect on the onset of stationary convection (see Table 3 and Fig. 2b).

On the other hand, \(\epsilon _1 Le\) does not directly affect the steady instability threshold but has a destabilizing effect on the onset of oscillatory convection (see Fig. 2a).

The condition (31) gives us a prediction of the type of motions through which convection will arise and it is tested in Table 4, in particular Table 4(a), shows that for \(\epsilon _1 \mathrm{Le} \le 1\) the necessary conditions for the onset of oscillatory convection are not satisfied, so convection can arise only via stationary motions.

In Fig. 3a, b the steady and oscillatory thresholds and the global nonlinear threshold are depicted for quoted values of the Soret number, in particular for \({\mathcal {S}}=1\) the coincidence between \({\mathcal {R}}_E\) and \({\mathcal {R}}_S\) is depicted in (3)b.

Table 1 Critical steady and oscillatory Rayleigh numbers and critical wavenumber at low concentration (\({\mathcal {C}}=1\)) (a) and at high concentration (\({\mathcal {C}}=5\)) (b) for quoted values of the Taylor number \({\mathcal {T}}^2\). Table a: \(\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924, {\mathcal {S}}=0.5 , {\mathcal {C}}=1\). Table b: \(\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924, {\mathcal {S}}=0.5, {\mathcal {C}}=5\)
Full size table
Table 2 Critical steady and oscillatory Rayleigh numbers as functions of the concentration Rayleigh number. \(\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924, {\mathcal {T}}^2=10, {\mathcal {S}}=0.5\). \(a^2_c=32.5315\)
Full size table
Table 3 Steady instability thresholds at low concentration (\({\mathcal {C}}=1\)) (a) and at high concentration (\({\mathcal {C}}=5\)) (b) and for quoted values of the Soret number \({\mathcal {S}}\) (b). Table a: \(\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924, {\mathcal {T}}^2=10 , {\mathcal {C}}=1\). Table b: \(\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924, {\mathcal {T}}^2=10, {\mathcal {C}}=5\).In the first case, \({\mathcal {R}}_O=112.0982\), in the second one, \({\mathcal {R}}_O=112.1697\), while \(a^2_c=32.5315\)
Full size table
Table 4 (a) Oscillatory thresholds at quoted values of \(\epsilon _1 \mathrm{Le}\), while \({\mathcal {C}}=4, {\mathcal {S}}=0.5\). For these values, the critical steady Rayleigh number is \({\mathcal {R}}_S = 112.1114\). (b) Steady and oscillatory thresholds at quoted values of the chemical Rayleigh number \({\mathcal {C}}\), while \(\epsilon _1 \mathrm{Le} = 55.924, {\mathcal {S}}=0.5\). The other physical parameters are fixed as \(\xi =0.1, K_r=1.5, \eta =1.5, {\mathcal {T}}^2=10\), and, for this set of parameters, the critical wavenumber is \(a^2_c=32.5315\), while \(f(a_c^2)=110.1114\)
Full size table
Fig. 1
figure 1

a Critical steady and oscillatory Rayleigh numbers plotted as functions of the concentration Rayleigh number. b Steady and oscillatory thresholds for quoted values of the concentration Rayleigh number. The other parameters are fixed as \(\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924, {\mathcal {T}}^2=10, {\mathcal {S}}=0.5\)

Full size image
Fig. 2
figure 2

a Oscillatory thresholds for quoted values of \(\epsilon _1 \mathrm{Le}\) for \(\xi =0.1, K_r=1.5, \eta =1.5, {\mathcal {C}}=5, {\mathcal {T}}^2=10, {\mathcal {S}}=0.5\). b Stationary thresholds for quoted values of the Soret number \({\mathcal {S}}\) for \(\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924, {\mathcal {T}}^2=10, {\mathcal {C}}=5\)

Full size image
Fig. 3
figure 3

The steady and oscillatory thresholds and the global nonlinear threshold are plotted for quoted values of the Soret number. The other parameters are fixed as \(\xi =0.1, K_r=1.5, \eta =1.5, \epsilon _1 \mathrm{Le} =55.924, {\mathcal {T}}^2=10, {\mathcal {C}}=5\)

Full size image

6 Conclusions

In the present paper the onset of convection in a bi-disperse porous layer, filled by an incompressible fluid mixture, that uniformly rotates about a vertical axis and that is simultaneously heated and salted from below, was studied. Taking into account the Soret effect, via linear instability analysis it was determined that convection can set in via stationary or oscillatory motions and that the critical thermal Rayleigh numbers for the onset of convection and the concentration Rayleigh number have a linear dependence on each other. Moreover, both rotation and salt concentration have a stabilizing effect on the onset of steady and oscillatory convection. Through differential constraint approach, the global nonlinear stability threshold was determined and it was found that regions of possible subcritical instabilities are present. Numerical simulations were performed in order to test the theoretical proven results.