Global dynamics and evolution for the Szekeres system with nonzero cosmological constant term

Abstract

The Szekeres system with cosmological constant term describes the evolution of the kinematic quantities for Einstein field equations in ${\mathbb {R}}^4$. In this study, we investigate the behavior of trajectories in the presence of cosmological constant. It has been shown that the Szekeres system is a Hamiltonian dynamical system. It admits at least two conservation laws, h and $I_{0}$ which indicate the integrability of the Hamiltonian system. We solve the Hamilton–Jacobi equation, and we reduce the Szekeres system from ${\mathbb {R}}^4$ to an equivalent system defined in ${\mathbb {R}}^2$. Global dynamics are studied where we find that there exists an attractor in the finite regime only for positive valued cosmological constant and $I_0<-2 .08$. Otherwise, trajectories reach infinity. For $I_ {0}>0$ the origin of trajectories in ${\mathbb {R}}^2$ is also at infinity. Finally, we investigate the evolution of physical properties by using dimensionless variables different from that of Hubble-normalization conducing to a dynamical system in ${\mathbb {R}}^5$. We see that the attractor at the finite regime in ${\mathbb {R}}^5$ is related with the de Sitter universe for a positive cosmological constant.

Appendix A: Szekeres system with \(\Lambda =0\)

Fig. 20

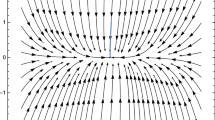
Phase-space portraits for Szekeres associated to system (A1), (A2) for different values of the free parameters $I_{0}$ and h and zero value for the cosmological constant, i.e. $\Lambda =0$. Figures of the first row are in the local variables $\left( x,y\right)$, while figures of the second row are for the compactified variables $\left( X,Y\right)$

In this “Appendix” we discuss about the global dynamics for Szekeres system with $\Lambda =0$. Such analysis has been published before for other set of variables in [26]. However, for the completeness of our analysis we summarize the main results in the following lines. The dynamical system (57), (58) for $\Lambda =0$ reads

$$\begin{aligned} {\dot{x}}&=-\sqrt{3}y\left( 3I_{0}y+6\right) , \end{aligned}$$

(A1)

$$\begin{aligned} {\dot{y}}&=-\sqrt{3}\left( x\left( y^{3}-3\right) +3hy^{2}\right) . \end{aligned}$$

(A2)

The latter dynamical system in the finite regime admits the stationary points $P_{0}^{\left( \Lambda =0\right) }=\left( 0,0\right)$ and $P_{1}^{\left( \Lambda =0\right) }=\left( \frac{4h}{I_{0}^{2}},-\frac{2}{I_{0}}\right)$ which exist for $I_{0}\ne 0$ and it is physically accepted when $I_{0}<0,$ because $y\ge 0.$ The eigenvalues of the linearized system around point $P_{0}^{\left( \Lambda =0\right) }$ are $-6\sqrt{3}$ and $3\sqrt{3}$, which means that the point is saddle. Similarly, for point $P_{1}^{\left( \Lambda =0\right) }$ we derive the eigenvalues $6\sqrt{3}$ and $3\sqrt{3}$ which means that $P_{1}^{\left( \Lambda =0\right) }$ is a source. Thus, do not exists stationary point at the finite regime. As far as the analysis at infinity is concerned, we can easily conclude from the results of Sect. 4 that results for $\Lambda <0$ and $I_{0}<0$ apply also when $\Lambda =0$ and $I_{0}<0$. Therefore, the trajectories can end at infinity, while they are originated at infinity or the source point $P_{1}^{\left( \Lambda =0\right) }$.

In Fig. 20 phase-space portraits for the Szekeres system with zero cosmological constant terms for different values of the free variables are presented. We observe that the trajectories of the dynamical systems end at infinity.