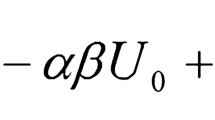Skip to main content
SpringerLink
Log in

Evaluation of specific heat capacity and speed of sound of fluids by using the quantum correction to second virial coefficient with Kihara potential

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

In this work, an analytical formula for the quantum corrections to second virial coefficient over Kihara potential is proposed to evaluate correct and precision the specific heat capacities and speed of sound of fluids by using analytical expression. Also, analytical formulae are presented for the first and second derivatives of the quantum corrections to second virial coefficient. As an example, the suggested approach has been applied to \({\text{Xe}},\;{\text{Ne}},\;{\text{Ar}},\;{\text{N}}_{2} ,\;{\text{H}}_{2} ,\;{\text{CO}}_{2} ,\;{\text{CF}}_{4} ,\;{\text{C}}_{{6}} {\text{H}}_{6} \), n–C4H10, and n–C5H12 fluids for the evaluation of the quantum corrections to second virial coefficient with Kihara potential, specific heat capacity, and speed of sound as a function of temperature and pressure. The analytical formula leads to a rapid and correct evaluation and enables fluids precision calculations of thermodynamic properties (entropy, enthalpy, and internal energy) even in complex molecules due to the Kihara potential. Agreement of the obtained results with the available literature data demonstrates that the proposed formulae are accurate and effective.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Data Availability Statement

The data used to support the findings of this study are included within the article. This manuscript has associated data in a data repository. [Authors’ comment: All data availabled in this manuscript are included upon request by contacting with the corresponding author.]

References

  1. H.E. Dillon, S.G.A. Penoncello, A fundamental equation for calculation of the thermodynamic properties of ethanol. Int. J. Thermophys. 25, 321–335 (2004)

    Article  ADS  Google Scholar 

  2. I. Polishuk, Generalized cubic equation of state adjusted to the virial coefficients of real gases and its prediction of auxiliary thermodynamic properties. Industrial. Eng. Chem. Res. 48, 10708–10717 (2009)

    Article  Google Scholar 

  3. C. Guder, W.A. Wagner, Reference equation of state for the thermodynamic properties of Sulfur Hexafluoride (SF6) for temperatures from the melting line 625 K and pressures up to 150 MPa. J. Phys. Chem. Ref. Data 38, 33–94 (2009)

    Article  ADS  Google Scholar 

  4. E. Somuncu, B.A. Mamedov, Developing the evaluation method of heat capacity and speed of sound of real gases using fourth virial coefficient over Lennard-Jones (12–6) potential. Eur. Phys. J. Plus 135, 454 (2020)

    Article  Google Scholar 

  5. H. Cacan, B.A. Mamedov, The comparative analytical evaluation of quantum corrections to the second virial coefficient with Morse potential and its applications to real systems. J. Chem. Thermodyn. 138, 147–150 (2019)

    Article  Google Scholar 

  6. D.A. McQuarine, J.D. Simon, Phys. Chem.: A Mol. Approach (1997)

  7. D.A. McQuarrie, Statistical mechanics, HarperRow (1973)

  8. I. Nagata, Kihara potential and Lennard-Jones and Devonshire equation of state of liquids and dense gases. Can. J. Chemistry 4(1) (1966)

  9. J.P. O’connell, J.M. Haile, Thermodynamics Fundamentals of Applications (Cambridge University Press, UK, 2005)

    Book  Google Scholar 

  10. T. Kihara, The second virial coefficient of non-spherical molecules. J. Phys. Soc. Jpn 6(5), 289–296 (1951)

    Article  ADS  MathSciNet  Google Scholar 

  11. E. Somuncu et al., A comparative evaluation of speed of sound and specific heat capacities of gases by using the quantum mechanical and classical second virial coefficients. J. Math. Chem. 57, 1935–1948 (2019)

    Article  MathSciNet  Google Scholar 

  12. M.E. Boyd, Quantum corrections to the second virial coefficient for the Lennard-Jones (m-6) potential. J. Res. Natl. Bureau Stands Sect. A 75A, 57–95 (1971)

    Article  Google Scholar 

  13. E.M. Costa, N.H.T. Lemes, M.O. Alves, Quantum second virial coefficient calculation for the 4He dimer on a recent potential. J. Braz. Chem. Soc. 24, 363–368 (2013)

    Article  Google Scholar 

  14. G.K. Schenter, The development of effective classical potentials and the quantum statistical mechanical second virial coefficient of water. J. Chem. Phys. 117, 6573–6581 (2002)

    Article  ADS  Google Scholar 

  15. G. Garberoglio, A.H. Harvey, Path-integral calculation of the third virial coefficient of quantum gases at low temperatures. Natl. Inst. Stand. Technol. 1–13 (2011)

  16. H.B. Ghassib, A.S. Sandouqa, B.R. Joudeh, S.M. Mosameh, Predicting the borderline between the classical and quantum regimes in 4He gas from the second virial coefficient. Can. J. Phys. 92(9), 997–1001 (2014)

    Article  ADS  Google Scholar 

  17. T. Kwon et al., The estimation of the second virial coefficients of He and N2 based on neural network potentials with quantum mechanical calculations. Chem. Phys. 548, 111231 (2021)

    Article  ADS  Google Scholar 

  18. O. T. Al-Obeidat, Second virial coefficient of CH4 vapor in 5 mK-10000 K temperature range in quantum and classical regimes. Acta Phys. Pol. A 139(2), (2021)

  19. K.W. Suh, T.S. Storvick, Second virial coefficients of nonspherical polar gases. J. Phys. Chem. 71, 1450–1456 (1967)

    Article  Google Scholar 

  20. L.S. Tee, S. Gotoh, W.E. Stewart, Molecular parameters for normal fluids. Lennard-Jones 12–6 potential. I&EC Fundam. 5, 363–367 (1966)

    Article  Google Scholar 

  21. P.K. Clayton, Second virial coefficient of nonpolar gases using the Kihara potential. J. Chem. Edu. 60, 1063–1062 (1983)

    Article  Google Scholar 

  22. J.O. Hirschfelder, C.F. Curtiss, R.B. Bird, Molecular Theory of Gases and Liquids (Wiley, New Jersey, 1954)

    MATH  Google Scholar 

  23. I.G. Kaplan, Intermolecular Interactions: Physical Picture. Computational Methods and Model Potentials (Wiley, New Jersey, 2006)

    Book  Google Scholar 

  24. M. Abramowitz, I.A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (Dover, New York, 1972)

    MATH  Google Scholar 

  25. I.S. Gradshteyn, I.M. Ryzhik, Tables of Integrals, Series and Products (Academic, London, 1965)

    Google Scholar 

  26. H.J.M. Hanley, G.E. Childs, The viscosity and thermal conductivity coefficients of dilute neon, krypton, and xenon. NBS Tech. Note 352, 23 (1967)

    Google Scholar 

  27. S. Sinehbaghizadeh, Thermodynamic modelling phase boundary of hydrogen hydrate in the presence of cyclopentane as a promising mechanism for hydrogen storage 4th international conferences on recent innovations in Chem. Chem. Eng. (2017)

  28. A.E. Sherwood, J.M. Prausnitz, Intermolecular potential functions and the second and third virial coefficients. J. Chem. Phys. 41, 429 (1964)

    Article  ADS  Google Scholar 

  29. J.M. Prausnitz, R.N. Lichtenthaler, E.G. de Azevedo, Fugacities in Gas Mixtures. Molecular Thermodynamics of Fluid-Phase Equilibria (Prentice-Hall, New Jersey, 1999)

    Google Scholar 

  30. J. De Boer, A. Michels, Contribution to the quantum-mechanical theory of the equation of state and the law of corresponding states Determination of the law of force of helium. Physica 10, 945–957 (1938)

    Article  Google Scholar 

  31. N. Corbin, W.J. Meath, A.R. Allnatt, Second virial coefficients, including quantum corrections, for nitrogen using model potentials. Mol. Phys. 53, 225–232 (1984)

    Article  ADS  Google Scholar 

  32. CEARUN, NASA. https://cearun.grc.nasa.gov

  33. J.J. Hurly et al., The viscosity of seven gases measured with a greenspan viscometer. Int. J. Thermophys. 24(6), 1441 (2003)

    Article  ADS  Google Scholar 

  34. R.D. Goodwin, Benzene thermophysical properties from 279 to 900 K at pressures to 1000 bar. J. Phys. Chem. Ref. Data 17(4), 1541–1636 (1988)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Medical Services and Technology, Ulubey Vocational High School, Usak University, Usak, Turkey

    Elif Somuncu

  2. Department of Physics, Faculty of Arts and Sciences, Gaziosmanpaşa University, Tokat, Turkey

    Bahtiyar A. Mamedov

Authors
  1. Elif Somuncu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bahtiyar A. Mamedov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Elif Somuncu.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (DOCX 144 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Somuncu, E., Mamedov, B.A. Evaluation of specific heat capacity and speed of sound of fluids by using the quantum correction to second virial coefficient with Kihara potential. Eur. Phys. J. Plus 137, 298 (2022). https://doi.org/10.1140/epjp/s13360-022-02503-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-022-02503-2

Search

Navigation