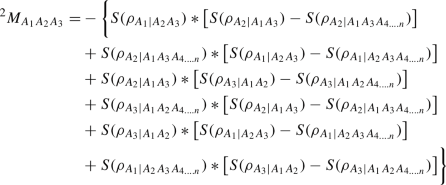A geometrical representation of entanglement

Abstract

We introduce a novel geometrical approach to characterize entanglement relations in large quantum systems. Our approach is inspired by Schumacher’s singlet state triangle inequality, which used an entropy-based distance to capture the strange properties of entanglement using geometry-based inequalities. Schumacher uses classical entropy and can only describe the geometry of bipartite states. We extend his approach by using von Neumann entropy to create an entanglement monotone that can be generalized for higher-dimensional systems. We achieve this by utilizing recent definitions for entropic areas, volumes, and higher-dimensional volumes for multipartite quantum systems. This enables us to differentiate systems with high quantum correlation from systems with low quantum correlation and differentiate between different types of multipartite entanglement. It also enable us to describe some of the strange properties of quantum entanglement using simple geometrical inequalities. Our geometrization of entanglement provides new insight into quantum entanglement. Perhaps by constructing well-motivated geometrical structures (e.g., relations among areas, volumes, etc.), a set of trivial geometrical inequalities can reveal some of the complex properties of higher-dimensional entanglement in multipartite systems. We provide numerous illustrative applications of this approach, and in particular to a random sample of a thousand density matrices.

Appendix

In this section, we will present the proves for our proposed claims in the manuscript.

1.1 Appendix A

For any density matrix $\rho _{ABC}$, the convoluted metric $M_{AB}$ may be seen as a pseudo-metric. That is to say:

• 1.1 $M_{AB} = M_{BA}$

• 1.2 $M_{AB} \ge 0\ \hbox {and is equal to}\ 0\$iff $\rho _{ABC}=\rho _{AB} \otimes \rho _C$.

• 1.3 $M_{AB} + M_{BC} \ge M_{AC}$

Proof

• 1.1 In Eq.4, A and B are interchangeable.

• 1.2 We know from strong subadditivity of quantum entropy (SSA) inequality [41] that for tripartite separable density matrix

  $$\begin{aligned} S(\rho _{ABC})\le S(\rho _{AC})+S(\rho _{BC})-S(\rho _{C}) \end{aligned}$$

  (28)

  One can write this inequality in two different ways

  $$\begin{aligned} S(\rho _{ABC})\le S(\rho _{AC})+S(\rho _{AB})-S(\rho _{A}) \end{aligned}$$

  (29)
  $$\begin{aligned} S(\rho _{ABC})\le S(\rho _{BC})+S(\rho _{AB})-S(\rho _{B}) \end{aligned}$$

  (30)

  Now by summing up these inequalities, one will reach to

  $$\begin{aligned} S(\rho _{ABC})+ S(\rho _{ABC})\le S(\rho _{BC})+S(\rho _{AB})-S(\rho _{B})+S(\rho _{AC})+S(\rho _{AB})-S(\rho _{A}) \end{aligned}$$

  (31)

  This will lead to

  $$\begin{aligned} \big [S(\rho _{ABC})-S(\rho _{BC})\big ]+ \big [S(\rho _{ABC})-S(\rho _{AC})\big ] \le S(\rho _{AB})-S(\rho _{B})+S(\rho _{AB})-S(\rho _{A}) \end{aligned}$$

  (32)

  which is equal to

  $$\begin{aligned} \widetilde{D}_{AB} \le D_{AB}; \end{aligned}$$

  (33)

  hence, $M_{AB}$ is

  $$\begin{aligned} 0\le D_{AB}-\widetilde{D}_{AB}= M_{AB}. \end{aligned}$$

  (34)

  Furthermore, $M_{AB}$ is zero if and only if $\rho _{ABC}=\rho _{AB} \otimes \rho _C$. Since

  $$\begin{aligned} S(ABC)=&S(AB)+S(C) \nonumber \\ S(AC)=&S(A)+S(C) \nonumber \\ S(BC)=&S(B)+S(C) \end{aligned}$$

  (35)

  for $\rho _{ABC}=\rho _{AB} \otimes \rho _C$ and plugging in 35 in Eq. 4 will make $M_{AB}=0$.

• 1.3 For triangle inequality, we start with definition of $M_{AB}$

  $$\begin{aligned}&M_{AB}= S(\rho _{A|B})+S(\rho _{B|A})-S(\rho _{A|BC})-S(\rho _{B|AC}) \end{aligned}$$

  (36)
  $$\begin{aligned}&M_{AB}=2S(\rho _{AB})-2S(\rho _{ABC})+S(\rho _{BC})+S(\rho _{AC})-S(\rho _A)-S(\rho _B) \end{aligned}$$

  (37)

  Now plugging in the definition into

  $$\begin{aligned} M_{AB}+M_{BC}\ge M_{AC} \end{aligned}$$

  (38)

  and after canceling the terms, we have

  $$\begin{aligned} 2S(\rho _{AB})-2S(\rho _{ABC})+2S(\rho _{BC})-2S(\rho _B) \ge 0 . \end{aligned}$$

  (39)

  This is strong subadditivity equation [41]

  $$\begin{aligned} S(\rho _{AB})+S(\rho _{BC}) \ge S(\rho _{ABC})+S(\rho _B) \end{aligned}$$

  (40)

  and is true for any arbitrary density matrix.$\square$

For n-partite systems to show $M_{12}$ is a metric, one just needs to adjust $\rho _{3}$ to $\rho _{3...n}$.

1.2 Appendix B

Given $\rho _{ABX}$, the convoluted metric $M_{AB}$ is an entanglement monotone for detecting separability between the registers AB and X satisfies the following properties:

• 2.1 $M_{AB}$ is invariant under local and global isometries

• 2.2 $M_{AB}$ is non-increasing under LOCC

• 2.3 $M_{AB}$ is convex.

Proof

If we write the $M_{AB}$ in terms of conditional mutual information

$$\begin{aligned} M_{AB} =&-2S(ABC) + 2S(AB) + S(AC) + S(BC) -S(A) - S(B) \nonumber \\ =&[S(AB) + S(AC) -S(ABC) - S(A)] + [S(AB) + S(BC) -S(ABC) - S(B)] \nonumber \\ =&I(B:C|A) + I(A:C|B) \end{aligned}$$

(41)

• 2.1 von Neumann entropy is invariant under unitary operation; therefore, $M_{AB}$ is invariant under unitary operation.

• 2.2 Conditional mutual information is non-increasing under LOCC [22]; therefore, $M_{AB}$ is non-increasing under LOCC.

• 2.3 Conditional mutual information is convex [22]; therefore, $M_{AB}$ is convex since the sum of two convex functions is also convex.

$\square$

1.3 Appendix C

Given $\rho _{A_1...A_n}$, the $^2M_{A_iA_jA_k}$ satisfies the following properties:

• 3.1 is invariant under local and global isometries

• 3.2 is convex.

• 3.3 is non-increasing under LOCC.

Proof

• 3.1 The von Neumann entropy is invariant under unitary operation; therefore, $^2M_{A_i A-j A_k}$ is invariant under unitary operation.

• 3.2 By adding and subtracting the terms

  $$\begin{aligned}&S(\rho _{A_1|A_2A_3})*S(\rho _{A_2|A_1A_3A_{4 ....n}}) \end{aligned}$$

  (42)
  $$\begin{aligned}&S(\rho _{A_2|A_1A_3})*S(\rho _{A_3|A_1A_2A_{4 ....n}}) \end{aligned}$$

  (43)
  $$\begin{aligned}&S(\rho _{A_3|A_1A_2})*S(\rho _{A_1|A_2A_3A_{4 ....n}}) \end{aligned}$$

  (44)

  To $^2M_{A_1A_2A_3}$ make it equal to

  

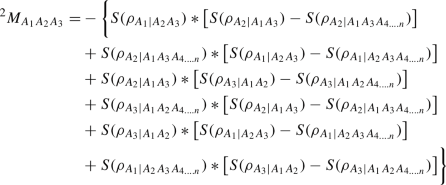  (45)

  Then we rewrite this as

  $$\begin{aligned} ^2M_{A_1A_2A_3}=&-\big [S(\rho _{A_1|A_2A_3})+S(\rho _{A_3|A_1A_2A_{4 ....n}})\big ]*\big [S(\rho _{A_2|A_1A_3})-S(\rho _{A_2|A_1A_3A_{4 ....n}})\big ]\nonumber \\&- \big [S(\rho _{A_3|A_1A_2})+S(\rho _{A_2|A_1A_3A_{4 ....n}})\big ]*\big [S(\rho _{A_1|A_2A_3})-S(\rho _{A_1|A_2A_3A_{4 ....n}})\big ] \nonumber \\&- \big [S(\rho _{A_2|A_1A_3})+S(\rho _{A_1|A_2A_3A_{4 ....n}})\big ]*\big [S(\rho _{A_3|A_1A_2})-S(\rho _{A_3|A_1A_2A_{4 ....n}})\big ] \end{aligned}$$

  (46)

  One can express this in terms of conditional mutual information as

  $$\begin{aligned} ^2M_{A_1A_2A_3}=&\big [I(A_1;A_2A_3)+I(A_3;A_1A_2A_{4 ....n})-S(A_1)-S(A_3)\big ]*\big [I(A_2;A_{4 ....n}|A_1A_3)\big ]\nonumber \\&+ \big [I(A_3;A_1A_2)+I(A_2;A_1A_3A_{4 ....n})-S(A_3)-S(A_2)\big ]*\big [I(A_1;A_{4 ....n}|A_2A_3)\big ] \nonumber \\&+ \big [I(A_2;A_1A_3)+I(A_1;A_2A_3A_{4 ....n})-S(A_1)-S(A_2)\big ]*\big [I(A_3;A_{4 ....n}|A_1A_3)\big ] \end{aligned}$$

  (47)

  Now since we know subsystems $A_iA_jA_k$ is separable from the rest of the system $^2M_{A_iA_jA_k}$ will equal to zero due to $I(A_i;A_{4 ....n}|A_jA_k)=0$.

• 3.3 To prove that $^2M_{A_1A_2A_3}$ is non-increasing under LOCC, we have to use the proposition by [22]

Proposition 1

A convex function f does not increase under LOCC if and only if

• a) f is invariant under local unitary operators

• b) if f satisfies

  $$\begin{aligned} f\left( \sum _i p_i \rho _{AB}^i\otimes |i\rangle x \langle i| \right) =\sum _i p_if(\rho _{AB}^i). \end{aligned}$$

  (48)

Since $^2M_{A_1A_2A_3}$ satisfies both of these, then it is non-increasing under LOCC.

1.4 Appendix D

Given $\rho _{A_1...A_n}$, the $E(\rho )$ satisfies the following properties:

• 6.1 $E(\rho )$ is invariant under local and global isometries;

• 6.2 $E(\rho )$ is non-increasing under LOCC; and

• 6.3 $E(\rho )$ is convex.

Proof

• 1. $E(\rho )$ is invariant under local unitary operators due to $^mM_{A_i...A_m}$ being invariant under local unitary operators.

• 2. From our previous discussions, we know that $^mM_{A_i...A_m}$ are non-increasing under LOCC, and we know that sum of non-increasing terms will also be non-increasing under LOCC. Then $E(\rho )$ is non-increasing under LOCC.

1.5 Appendix E

For a given state $\rho _{AB}$, squashed entanglement is given by

$$\begin{aligned} E_{sq}(\rho _{AB}) = \frac{1}{2} inf I(A : B|E), \end{aligned}$$

(49)

with

$$\begin{aligned} I(A:B|E)=S(AE)+S(BE)-S(ABE)-S(E). \end{aligned}$$

(50)

It is obvious from the equation above that $I(A:B|E)= I(B:A|E)$. We have stated that if C is separable from AB our method will give answer similar to squashed entanglement, this is because the degree of entanglement of A and B in this case will equal to entanglement of the $\rho _{AC}$ part with $\rho _{B}$, or the $\rho _{BC}$ part with$\rho _{C}$. In appendix B, we have shown that

$$\begin{aligned} M_{AB}&= -2S(ABC) + 2S(AB) + S(AC) + S(BC) -S(A) - S(B) \\&= [S(AB) + S(AC) -S(ABC) - S(A)] + [S(AB) + S(BC) -S(ABC) - S(B)] \\&= I(B:C|A) + I(A:C|B). \end{aligned}$$

If we write this for either $M_{AC}$ or $M_{BC}$ after applying our convex roof method, we will simply get a constant number multiplied by Eq. 49, which means $M_{AC}$ multiplied by value of squashed entanglement. The motivation we choose to mention getting result similar to squashed entanglement is the reason we compare it to squashed entanglement is simply because, similar to squashed entanglement our function look at entanglement of A and B from point of view of register C.