Frequency control of cross-ply magnetostrictive viscoelastic plates resting on Kerr-type elastic medium

Abstract

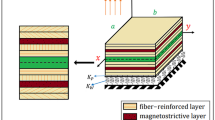
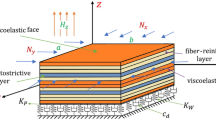
In the present study, a higher-order shear deformation plate theory with hyperbolic shape function is used to analyze vibration suppression of a novel design of a cross-ply composite plate that contains a homogenous core and viscoelastic faces and is embedded in three-parameter Kerr’s foundation. Two magnetostrictive actuating layers and simple velocity feedback control are employed for vibration control of the sandwich plate. Kelvin–Voigt viscoelastic relation is utilized to model faces of the viscoelastic material. The system of the governing equations is formulated utilizing Hamilton’s principle and using Navier’s approach to solve the system analytically. Comprehensive parametric studies are carried out to assess influences of the magnitude of the feedback control gain, magnetostrictive layer location, thickness ratio, aspect ratio, viscoelastic layer thickness-to-core thickness ratio, magnetostrictive layer thickness-to-core thickness ratio, half wave numbers, orientations of the viscoelastic layer’s fiber, and foundation on the vibration suppression characteristics of plates. The present results show that the combination of the passive and active strategies for vibration damping of the structures can develop control systems of the structural applications excellently. Further, the use of the Kerr-type foundation model can improve the vibration suppression characteristics.

Appendices

Appendix 1

The coefficients $\overline{Q}_{ij}^{\left( r \right)}$ and $\overline{q}_{ij}$ that appeared in Eqs. (7)–(9) are expanded as

$$ \overline{Q}_{11}^{\left( r \right)} = Q_{11}^{\left( r \right)} \cos^{4} \theta^{\left( r \right)} + 2\left( {Q_{12}^{\left( r \right)} + 2Q_{66}^{\left( r \right)} } \right)\cos^{2} \theta^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} + Q_{22}^{\left( r \right)} \sin^{4} \theta^{\left( r \right)} , $$

$$ \overline{Q}_{12}^{\left( r \right)} = \left( {Q_{11}^{\left( r \right)} + Q_{22}^{\left( r \right)} - 4Q_{66}^{\left( r \right)} } \right)\cos^{2} \theta^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} + Q_{12}^{\left( r \right)} \left( {\sin^{4} \theta^{\left( r \right)} + \cos^{4} \theta^{\left( r \right)} } \right), $$

$$ \overline{Q}_{22}^{\left( r \right)} = Q_{11}^{\left( r \right)} \sin^{4} \theta^{\left( r \right)} + 2\left( {Q_{12}^{\left( r \right)} + 2Q_{66}^{\left( r \right)} } \right)\cos^{2} \theta^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} + Q_{22}^{\left( r \right)} \cos^{4} \theta^{\left( r \right)} , $$

$$ \overline{Q}_{44}^{\left( r \right)} = Q_{44}^{\left( r \right)} \cos^{2} \theta^{\left( r \right)} + Q_{55}^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} , $$

$$ \overline{Q}_{55}^{\left( r \right)} = Q_{55}^{\left( r \right)} \cos^{2} \theta^{\left( r \right)} + Q_{44}^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} , $$

$$ \overline{Q}_{66}^{\left( r \right)} = \left( {Q_{11}^{\left( r \right)} + Q_{22}^{\left( r \right)} - 2Q_{12}^{\left( r \right)} - 2Q_{66}^{\left( r \right)} } \right)\sin^{2} \theta^{\left( r \right)} \cos^{2} \theta^{\left( r \right)} + Q_{66}^{\left( r \right)} \left( {\sin^{4} \theta^{\left( r \right)} + \cos^{4} \theta^{\left( r \right)} } \right), $$

$$ Q_{11}^{\left( r \right)} = \frac{{E_{1} \left( {1 - {\upnu }_{23}^{\left( r \right)} {\upnu }_{32}^{\left( r \right)} } \right)}}{\Delta },{\quad}Q_{12}^{\left( r \right)} = \frac{{E_{1} \left( {{\upnu }_{21}^{\left( r \right)} + {\upnu }_{31}^{\left( r \right)} {\upnu }_{23}^{\left( r \right)} } \right)}}{\Delta }, \quad Q_{22}^{\left( r \right)} = \frac{{E_{2} \left( {1 - {\upnu }_{13}^{\left( r \right)} {\upnu }_{31}^{\left( r \right)} } \right)}}{\Delta }, $$

$$ Q_{44}^{\left( r \right)} = G_{23}^{\left( r \right)} ,{\quad}Q_{55}^{\left( r \right)} = G_{13}^{\left( r \right)} ,{\quad}Q_{66}^{\left( r \right)} = G_{12}^{\left( r \right)} , $$

$$\Delta = 1 - {{\nu }}_{21}^{\left( r \right)}{\rm{\nu }}_{12}^{\left( r \right)} - {{\nu }}_{23}^{\left( r \right)}{\nu }_{32}^{\left( r \right)} - {{\nu }}_{13}^{\left( r \right)}{\rm{\nu }}_{31}^{\left( r \right)}- 2{\rm{\nu }}_{21}^{\left( r \right)}{\nu}_{13}^{\left( r \right)}{{\nu }}_{32}^{\left( r \right)},$$

$${\nu}_{21}^{\left( r \right)} = \frac{{{\nu}_{12}^{\left( r \right)}E_{22}^{\left( r \right)}}}{{E_1^{\left( r \right)}}}, \quad {\nu}_{31}^{\left( r \right)} = \frac{{{\nu }_{13}^{\left( r \right)}E_3^{\left( r \right)}}}{{E_1^{\left( r \right)}}},\quad {\nu }_{32}^{\left( r \right)} = \frac{{{\nu }_{23}^{\left( r \right)}E_3^{\left( r \right)}}}{{E_2^{\left( r \right)}}},$$

$$ \overline{q}_{31} = q_{31} \cos^{2} \theta + q_{32} \sin^{2} \theta , \quad \overline{q}_{32} = q_{32} \cos^{2} \theta + q_{31} \sin^{2} \theta , $$

$$ \overline{q}_{14} = \left( {q_{15} - q_{24} } \right)\sin \theta \cos \theta , \quad \overline{q}_{24} = q_{24} \cos^{2} \theta + q_{15} \sin^{2} \theta , $$

$$ \overline{q}_{15} = q_{15} \cos^{2} \theta + q_{24} \sin^{2} \theta , \quad \overline{q}_{25} = \left( {q_{15} - q_{24} } \right)\sin \theta \cos \theta , $$

$$ \overline{q}_{36} = \left( {q_{31} - q_{32} } \right)\sin \theta \cos \theta , $$

where ${E}_{i}$, ${v}_{ij}$ and ${G}_{ij}$ refer to Young’s moduli, Poisson’s ratios, and shear moduli, respectively. The coefficients ${q}_{ij}$ denote the magnetostrictive modules.

Appendix 2

The coefficients $\hat{S}_{ij}$, $\hat{M}_{ij}$ and $\hat{C}_{ij}$ ($i = 1, 2, 3$) that appeared in Eq. (31) are expanded as the following:

$$\begin{aligned} \hat{S}_{11} &= \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {D_{11} \left( {\frac{n\pi }{a}} \right)^{4} + D_{22} \left( {\frac{m\pi }{b}} \right)^{4} + \left( {2D_{12} + 4D_{66} } \right)\left( {\frac{n\pi }{a}} \right)^{2} \left( {\frac{m\pi }{b}} \right)^{2} } \right]\\ & \quad+ \frac{{K_{P} K_{u} }}{{K_{l} + K_{u} }}\left( {\frac{n\pi }{a}} \right)^{2} + \frac{{K_{P} K_{u} }}{{K_{l} + K_{u} }}\left( {\frac{m\pi }{b}} \right)^{2} + \frac{{K_{l} K_{u} }}{{K_{l} + K_{u} }},\end{aligned}$$

$$ \hat{S}_{12} = - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{11}^{1} \left( {\frac{n\pi }{a}} \right)^{3} + \left( {E_{21}^{1} + 2E_{66}^{1} } \right)\frac{n\pi }{a}\left( {\frac{m\pi }{b}} \right)^{2} } \right], $$

$$ \hat{S}_{13} = - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{22}^{1} \left( {\frac{m\pi }{b}} \right)^{3} + \left( {E_{12}^{1} + 2E_{66}^{1} } \right)\left( {\frac{n\pi }{a}} \right)^{2} \frac{m\pi }{b}} \right], $$

$$ \hat{S}_{22} = \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{11}^{3} \left( {\frac{n\pi }{a}} \right)^{2} + E_{66}^{3} \left( {\frac{m\pi }{b}} \right)^{2} + E_{55}^{3} } \right], $$

$$ \hat{S}_{23} = \hat{S}_{23} = \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {\left( {E_{12}^{3} + E_{66}^{3} } \right)\frac{n\pi }{a}\frac{m\pi }{b}} \right], $$

$$ \hat{S}_{33} = \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{66}^{2} \left( {\frac{n\pi }{a}} \right)^{2} + E_{22}^{3} \left( {\frac{m\pi }{b}} \right)^{2} + E_{44}^{3} } \right], $$

$$ \hat{M}_{11} = - \beta_{31} \left( {\frac{n\pi }{a}} \right)^{2} - \beta_{32} \left( {\frac{m\pi }{b}} \right)^{2} ,\quad \hat{M}_{21} = \gamma_{31} \frac{n\pi }{a},\quad \hat{M}_{31} = \gamma_{32} \frac{m\pi }{b}, $$

$$ \hat{M}_{12} = \hat{M}_{13} = \hat{M}_{22} = \hat{M}_{23} = \hat{M}_{32} = \hat{M}_{33} = 0, $$

$$ \hat{C}_{11} = I_{2} \left[ {\left( {\frac{n\pi }{a}} \right)^{2} + \left( {\frac{m\pi }{b}} \right)^{2} } \right] + I_{0} ,{\quad}\hat{C}_{12} = - I_{e} \frac{n\pi }{a},{\quad}\hat{C}_{13} = - I_{e} \frac{m\pi }{b}, $$

$$ \hat{C}_{22} = I_{e}^{2} ,\quad \hat{C}_{23} = 0,{\quad}\hat{C}_{33} = I_{e}^{2} . $$