1 Introduction

Phase factors play a significant role in quantum mechanics (QM). Broadly speaking, they can be classified into different classes depending on their physical origin and features [1]. Among these, dynamic and geometric phases are certainly the most common examples one faces with when working in the realm of quantum theory. As suggested by their names, while the former take into account the time evolution of a system, the latter—which are the focus of the present analysis—are influenced by the change of the n-tuple of parameters \(\mathbf{R} (t)=(R_1(t),\dots ,R_n(t))\) appearing in the Hamiltonian. In the space spanned by \(\mathbf{R} \), as t grows the system traces a path, and the geometric phase only depends on this path, regardless of how long the system takes to go from the starting to the arrival point [1]. This result was firstly achieved by Berry in the context of adiabatic transformations [2] and then generalized by Aharonov and Anandan [3] to the case of cyclic quantum evolutions.

One of the most eloquent manifestations of geometric phases occurs in the Aharonov–Bohm (AB) effect [4], which predicts that an electrically charged particle is affected by an electromagnetic potential, despite being confined to a region in which both the magnetic and electric fields are vanishing. The first evidence of such a phenomenon was found out one year later its theoretical prediction [5] and confirmed with a higher degree of precision in subsequent laboratory tests [6]. As a matter of fact, we mention that a dual effect was also discovered for neutral particles with a non-vanishing magnetic moment (Aharonov–Casher (AC) effect [7]), for the case of a gravitational field instead of the electromagnetic one (Colella, Overhauser and Werner (COW) effect) [8, 9] and in the presence of two pulses of light sent in opposite directions around a rotating ring interferometer (Sagnac effect [10]).

In the standard analysis of AB, AC and Sagnac phenomena, gravity effects are usually neglected, as they give contributions below current experimental sensitivity. In spite of these technical aspects, their study may be non-trivial at the theoretical level, since it allows for a direct investigation of the influence of gravity on quantum mechanical systems. In the absence of a consistent theory which describes the quantum and gravity worlds on the same footing, this represents an important step toward the understanding of how such a unified framework should appear when applied to well-known QM phenomena.

As usually done in the literature, a natural way to embed gravitational effects in QM is by generalizing the Heisenberg uncertainty relation so as to account for the emergence of a minimal uncertainty in position at Planck scale [11], which thus appears as a gravity-induced UV correctionFootnote 1. In the seminal papers on the generalized uncertainty principle (GUP), deformations of the uncertainty relations stem from the attempt of explaining the divergences appearing in quantum field theory (QFT) without invoking an ad hoc cut-off in the momentum space [12, 13]. In this context, considerations from string theory [14,15,16,17] and gedanken experiments on micro-black holes [18] have converged to the following proposal for the (one-dimensional) non-relativistic GUP:

$$\begin{aligned} \sigma _{{\hat{X}}}\sigma _{\hat{P}_x}\ge \frac{\hbar }{2}\left( 1+\beta \, f(\sigma _{\hat{P}_x}^2)\right) , \end{aligned}$$
(1)

where \(\sigma _{{\hat{X}}}\), \(\sigma _{\hat{P}_x}\) are the uncertainties on position and momentum operators, respectively, \(\beta \) is the dimensionless deformation parameter (which is usually assumed to be of order one in the most common quantum gravity formulations) and \(\ell _p\) denotes the Planck length. For various choices of \(f(\sigma _{\hat{P}_x}^2)\), Eq. (1) finds applications in a number of contexts, ranging from black-hole physics [18,19,20,21,22,23,24,25,26,27,28], to non-commutative geometry [29,30,31] and QFT [32,33,34,35,36,37,38,39] (for an overview, see Ref. [40]). Clearly, in all of these scenarios, the standard QM results are recovered for \(\beta f(\sigma _{\hat{P}_x}^2)\ll 1\).

Starting from the outlined picture, in this work we analyze the effects induced by modifications of the commutation relations on the Aharonov–Bohm, Aharonov–Casher, COW and Sagnac phase shifts within two different GUP frameworks. The first one was used in Ref. [11] to reveal the universality of the quantum gravity influence on almost any system with a well-defined Hamiltonian and is characterized by the only redefinition of the physical (high-energy) momentum. On the other hand, the second model arises from a relativistic covariant generalization of Eq. (1) and also predicts the non-commutativity of spacetime coordinates [41, 42]. Apart from understanding how UV gravity effects manifest themselves in well-established QM interferometry phenomena, the obtained GUP-corrected expressions allow us to impose bounds on the deformation parameters that might be tested experimentally in the future.

The paper is organized as follows: in Sect. 2, we set the stage to discuss GUP effects on QM geometric phases. Section 3 is devoted to the study of the Aharonov–Bohm experiment; in particular, we review the standard derivation of the AB phase shift and generalize the outcome to the GUP framework. The same analysis is performed for the Aharonov–Casher, COW and Sagnac effects in Sect. 4. A summary of the results and a discussion about future perspectives are presented in Sect. 5.

2 Geometric phases in quantum mechanics with a minimal length

In what follows, we consider two different generalizations of the Heisenberg uncertainty principle. In order to figure out how GUP corrections affect QM geometric phases, we first write down the modified Schrödinger equation and then apply it to a set of interferometry experiments.

2.1 First framework

Let us start by showing how to deal with the perturbation induced by a weak external potential V to the Schrödinger equation in the presence of a minimal position uncertainty [43, 44]. In this regard, we note that, for mirror symmetric states (i.e., states with \(\langle {\hat{P}}_x\rangle =0\)), the GUP (1) with \(f(\sigma _{\hat{P}_x}^2)=\ell _p^2\,\sigma _{\hat{P}_x}^2/\hbar ^2\) is equivalent to the (one-dimensional) non-relativistic deformed commutator [45]

$$\begin{aligned} \left[ \hat{X},\hat{P}_x\right] =i\hbar \left( 1+\beta \,\ell _p^2\,\frac{\hat{P}_x^2}{\hbar ^2}\right) . \end{aligned}$$
(2)

For our purposes, we need to generalize the above relation to three dimensions. Assuming rotational isotropy, the most general deformation reads [46, 47]

$$\begin{aligned} \left[ \hat{X}^j,\hat{P}^k\right] =i\hbar \left( \delta ^{jk}+\beta \,\ell _p^2\,\frac{\hat{P}^2}{\hbar ^2}\delta ^{jk}+\beta '\,\ell _p^2\,\frac{\hat{P}^j\hat{P}^k}{\hbar ^2}\right) , \end{aligned}$$
(3)

to the lowest order in the positive dimensionless parameters \(\beta \) and \(\beta '\) and with \(j,k=\{1,2,3\}\).

We shall consider the particular case \(\beta '=2\beta \): this is a preferred choice, since it does not affect the usual hypothesis of commutativity of coordinates [11, 46, 47]. A possible way to realize the above algebra is to define the physical (high-energy) operators \(\hat{\mathbf{X }}\) and \(\hat{\mathbf{P }}\) as

$$\begin{aligned} \hat{X}^j=\hat{x}^j\,, \quad \hat{P}^k=\hat{p}^k\left( 1+\beta \,\ell _p^2\,\frac{\hat{p}^2}{\hbar ^2}\right) , \end{aligned}$$
(4)

where \(\hat{p}^2=\sum _{k=1}^3 {\hat{p}}^k\,{\hat{p}}^k\) and we have denoted by \(\hat{\mathbf{x }}\) and \(\hat{\mathbf{p }}\) the auxiliary (low-energy) position and momentum operators satisfying the canonical commutator \([{\hat{x}}^j, {\hat{p}}^k]=i\hbar \,\delta ^{jk}\). Clearly, since \({\hat{p}}^k\) has the standard representation \({\hat{p}}^k=-i\hbar \,\partial /\partial x^k\), we have

$$\begin{aligned} \hat{P}^k=-i\hbar \left( 1-\beta \,\ell _p^2\nabla ^2\right) \frac{\partial }{\partial x^k}\,. \end{aligned}$$
(5)

Now, by use of Eq. (4), the Schrödinger equation for a particle of mass m is modified with the addition of a fourth-order derivative term, namely [48]

$$\begin{aligned} \left[ -\frac{\hbar ^2}{2m}\nabla ^2+\frac{\beta \,\ell _p^2\hbar ^2}{m}\nabla ^2\,\nabla ^2+V\right] \psi =i\hbar \,\partial _t\psi \,. \end{aligned}$$
(6)

As usual, for a free-particle (i.e., \(V=0\)), we can speculate the solution to be of the form

$$\begin{aligned} \psi _0(t,\mathbf{x} )=\exp \Big [-\frac{i}{\hbar }\left( {E_0t-\mathbf{p} _0\cdot \mathbf{x} }\right) \Big ], \end{aligned}$$
(7)

with \(E_0\) and \(\mathbf{p} _0\) being the free energy and momentum, respectively. Substitution of Eq. (7) into (6) leads to the following modified dispersion relation:

$$\begin{aligned} E_0\,=\,E^{(QM)}\,+\,E_\beta \,, \end{aligned}$$
(8)

where the quantum mechanical kinetic energy \(E^{(QM)}\) and the GUP-induced correction \(E_\beta \) are defined as

$$\begin{aligned} E^{(QM)}\,=\,\frac{{p_0}^2}{2m}\,,\quad E_\beta \,=\,\frac{\beta \,\ell _p^2\,}{m\hbar ^2}\,p_0^4\,, \end{aligned}$$
(9)

and we have used the notation \(p_0\equiv |\mathbf{p} _0|\). Clearly, in the limit \(\sqrt{\beta }\,\ell _p\,p_0/\hbar \rightarrow 0\), the standard energy-momentum relation for a free particle is recovered.

Now, since we want to study the case of a stationary phase shifter, we suppose that the perturbation induced by the external potential V modifies the solution (7) in such a way that the energy spectrum remains unaffected, i.e., \(E= E_0\), but the wave function changes according toFootnote 2 [43, 44, 49]

$$\begin{aligned} \psi (t,\mathbf{x} )=\psi _0(t,\mathbf{x} )\,\xi (\mathbf{x} )\,, \end{aligned}$$
(10)

with \(\xi \) to be determined. Following Ref. [43, 44], we require \(\psi (t,\mathbf{x} )\) to satisfy the semiclassical condition

$$\begin{aligned} |\varvec{\nabla }\xi |\ll \frac{p_0}{\hbar }\,\xi \,, \end{aligned}$$
(11)

and hence higher-order derivatives of the function \(\xi \) can be safely neglected. By using this approximation and plugging Eq. (10) into (6), we are led to

$$\begin{aligned} \left[ \frac{p_0^2}{2m}\left( 1+2\,\beta \,\ell _p^2\,\frac{p_0^2}{\hbar ^2}\right) -\frac{i\hbar }{m}\left( 1+4\,\beta \,\ell _p^2\,\frac{p_0^2}{\hbar ^2}\right) \mathbf{p} _0\cdot \varvec{\nabla }\right] \xi \approx \left( E-V\right) \xi \,. \end{aligned}$$
(12)

However, since \(E=E_0\), the above equation can be rearranged as

$$\begin{aligned} \mathbf{p} _0\cdot \varvec{\nabla }\xi \approx -\left( 1-4\,\beta \,\ell _p^2\,\frac{p_0^2}{\hbar ^2}\right) \frac{im}{\hbar }V\xi \,, \end{aligned}$$
(13)

where we have used the dispersion relation (8). If we denote the distance measured along the direction of \(\mathbf{p} _0\) by s, we have

$$\begin{aligned} \frac{1}{\xi }\frac{\partial \xi }{\partial s}\approx -\left( 1-4\,\beta \,\ell _p^2\,\frac{p_0^2}{\hbar ^2}\right) \frac{im}{\hbar \,p_0}V\,. \end{aligned}$$
(14)

Therefore, by observing that \(p_0/m=\mathrm{d}s/\mathrm{d}t\) and separating out the correction induced by the GUP, we obtain

$$\begin{aligned} \xi =\xi ^{(QM)}\,\xi _{\beta }\,, \end{aligned}$$
(15)

where

$$\begin{aligned} \xi ^{(QM)}\,=\,\exp \Big [{-\frac{i}{\hbar } \oint V\,\mathrm{d}t}\,\Big ]\,,\,\,\,\,\, \xi _\beta \,=\,\exp \Big [\,\frac{4\,i\,\beta \,\ell _p^2\,p_0^2}{\hbar ^3}\,\oint V\,\mathrm{d}t\,\Big ]\,, \end{aligned}$$
(16)

and the integration has to be performed on a closed path.

At this point, it is more convenient to cast Eq. (15) in terms of the variation of the momentum \(\delta \mathbf{p} \) due to the external potential. As remarked above, a stationary phase shifter is represented by a potential V which changes the momentum due to the energy conservation [43, 44], i.e.,

$$\begin{aligned} \frac{\left( \mathbf{p} _0+\delta \mathbf{p} \right) ^2}{2m}\left[ 1+2\,\beta \,\ell _p^2\frac{\left( \mathbf{p} _0+\delta \mathbf{p} \right) ^2}{\hbar ^2}\right] +V=E= E_0\,. \end{aligned}$$
(17)

Thus, to the leading order in \(\delta \mathbf{p} \), we have

$$\begin{aligned} \left( 1+4\,\beta \,\ell _p^2\,\frac{p_0^2}{\hbar ^2}\right) \mathbf{p} _0\cdot \delta \mathbf{p} \approx -mV\,, \end{aligned}$$
(18)

which impliesFootnote 3

$$\begin{aligned} -\oint V\mathrm{d}t\approx \left( 1+4\,\beta \,\ell _p^2\,\frac{p_0^2}{\hbar ^2}\right) \oint \delta \mathbf{p} \cdot d\mathbf{s} \,. \end{aligned}$$
(19)

Now, by replacing Eq. (19) into (16) and keeping up to \(\mathcal {O}(\beta )\), we obtain

$$\begin{aligned} \xi ^{(QM)}\,=\,\exp \Big [i\varDelta g^{(QM)}\Big ]\,,\quad \,\, \xi _\beta \,=\,1\,, \end{aligned}$$
(20)

whereFootnote 4

$$\begin{aligned} \varDelta g^{(QM)}\,=\,\frac{1}{\hbar }\oint \delta \mathbf{p} \cdot \mathrm{d}{} \mathbf{s} \,, \end{aligned}$$
(21)

is the quantum mechanical phase shift of the interference pattern.

From Eq. (20), it follows that the deformation (3) with \(\beta '=2\beta \) has no effect at all on interferometry phenomena, unless the QM phase shift explicitly depends on the momentum of the test particle. In this case, indeed, the GUP enters the result via the redefinition (4) of the physical momentum. We stress that the same GUP independence of the QM phase shift is peripherally discussed in Ref. [11] for the Aharonov–Bohm effect only. Here, such a result has been derived via a different approach and for a wider class of interferometry examples.

2.2 Second framework

For the following analysis, we are mainly inspired by Refs. [41, 42], where a relativistic covariant generalization of the usual GUP is formulated. In particular, by using the Minkowski metric with the mostly positive signature \(\eta ^{\mu \nu }=\{-,+,+,+\}\) \((\mu ,\nu =\{0,1,2,3\})\) and denoting by \(m_p=\hbar /c\,\ell _p\) the Planck mass, we consider the deformed commutator

$$\begin{aligned} \left[ \hat{X}^\mu ,\hat{P}^\nu \right] =i\hbar \left[ 1+\left( \varepsilon -\alpha \right) \frac{\hat{P}^\rho \hat{P}_\rho }{m_p^2c^2}\right] \eta ^{\mu \nu }+i\hbar \left( \chi +2\,\varepsilon \right) \frac{\hat{P}^\mu \hat{P}^\nu }{m_p^2c^2}\,, \end{aligned}$$
(22)

where \(\varepsilon , \alpha \) and \(\chi \) are positive dimensionless parameters. Notice that, by restricting to the spatial components and expressing the Planck mass in terms of the Planck length, the above equation reads

$$\begin{aligned} \left[ \hat{X}^j,\hat{P}^k\right] =i\hbar \left[ 1+\left( \varepsilon -\alpha \right) \frac{\ell ^2_p}{\hbar ^2}\left( -{\frac{\hat{E}^2}{c^2}+|\hat{\mathbf{P }}|^2}\right) \right] \delta ^{jk}+i\hbar \left( \chi +2\,\varepsilon \right) \frac{\ell _p^2}{\hbar ^2}{\hat{P}^j\hat{P}^k}\,, \end{aligned}$$
(23)

where we have explicitly written the product \(\hat{P}^\rho \hat{P}_\rho \) in terms of the energy and three-momentum operators, respectively. It is now straightforward to show that, in the non-relativistic limit \(c\rightarrow \infty \), the obtained GUP exactly mimics Eq. (3), provided that we identify \(\beta =\varepsilon -\alpha \) and \(\beta '=\chi +2\varepsilon \).

Following Ref. [42], we shall henceforth assume that \(\chi =0\) (in order not to break the isotropy of spacetime) and \(\varepsilon =\alpha \) (which leads to an unmodified Poincaré algebra). It is worth observing that, with such a setting, it is no longer feasible to map the first GUP framework into the second one even in the non-relativistic limit,Footnote 5 since for the latter we now have \(\beta =0\) and \(\beta '=2\varepsilon \). To corroborate this, one can show that the deformed algebra (22) leads to a non-commutative spacetime \(\left[ \hat{X}^\mu ,\hat{X}^\nu \right] \ne 0\), contrary to the first GUP scenario. Consequently, both the physical position and momentum operators must now be rewritten according to [42]

$$\begin{aligned} \hat{X}^\mu =\left( 1-\alpha \,\frac{\hat{p}^\rho \hat{p}_\rho }{m_p^2c^2}\right) \hat{x}^\mu \,, \qquad \hat{P}^\mu =\left( 1+\alpha \,\frac{\hat{p}^\rho \hat{p}_\rho }{m_p^2c^2}\right) \hat{p}^\mu \,. \end{aligned}$$
(24)

Next, to compare the two GUP frameworks introduced above, let us consider the deformed Klein-Gordon (KG) equation

$$\begin{aligned} \hat{P}^\mu \hat{P}_\mu =-m^2c^2\,, \end{aligned}$$
(25)

and perform the standard expansion according to which the rest mass is the dominant contribution. In so doing, an easy way to embed the GUP corrections is to solve Eq. (25) with respect to the low-energy momentum \(\hat{p}^\mu \). To the leading order in \(\alpha \), we get [42]

$$\begin{aligned} \hat{p}^\mu \hat{p}_\mu \equiv -M^2c^2= -m^2c^2\left( 1+2\alpha \frac{m^2}{m_p^2}\right) , \end{aligned}$$
(26)

from which it arises that GUP effects amount to an effective reparameterization of the mass such that

$$\begin{aligned} m\rightarrow M=m\left( 1+\alpha \,\frac{m^2}{m_p^2}\right) . \end{aligned}$$
(27)

As discussed in Ref. [42], by using this procedure one discards two solutions of the fourth-order KG equation, which, however, would introduce very small corrections and can thus be neglected.

In order to derive the Schrödinger equation with GUP corrections, let us now expand Eq. (26) to the fourth order in \(\hat{\mathbf{p }}\), obtaining

$$\begin{aligned} \left[ Mc^2-\frac{\hbar ^2}{2M}\nabla ^2-\frac{\hbar ^4}{8M^3c^2}\nabla ^2\nabla ^2+V\right] \psi \,=\,i\hbar \,\partial _t\psi \,, \end{aligned}$$
(28)

which consists of the rest mass, the relativistic kinetic energy and GUP corrections. Here, \(\nabla \) must be intended as a derivative acting on the auxiliary variable \(\mathbf{x} \). Therefore, although the reparameterization of the mass does not modify the KG equation, in this case GUP corrections affect the kinetic energy, as well as the related relativistic term [42]. In the next section, we will show that such corrections give rise to potentially measurable effects in interferometry experiments.

At this stage, it should be noted that even though Eq. (28) admits a solution formally similar to Eqs. (20)–(21), the effects of the GUP (22) significantly differ from the ones induced by the deformation (3). Indeed, due to Eq. (24), whenever the resulting phase shift depends on the mass and/or the physical length of the system, we have to implement the mass reparameterization (27) along with the substitution [42]

$$\begin{aligned} \ell \rightarrow L\left( 1-\alpha \frac{m^2}{m_p^2}\right) , \end{aligned}$$
(29)

which follows from the fact that Eq. (28) is written in terms of the low-energy position operator rather than the high-energy one (here, L is the effective physical dimension of the system, while \(\ell \) the auxiliary variable). Clearly, this prescription is absent within the first GUP framework (see Eq. (4)).

Before turning to the discussion of concrete applications, we observe that the different predictions of the two GUP models presented above are not attributable to the relativistic character of Eq. (22). Indeed, for the interferometry phenomena we shall consider below, one can show that the GUP relativistic corrections in Eq. (28) do not enter at all the calculation of the phase shift. Alternatively, one can make a more straightforward comparison by considering the non-relativistic limit \(c\rightarrow \infty \) of Eq. (28) and omitting the rest energy term. To prove this, we start from rewriting Eq. (28) as

$$\begin{aligned} \left[ -\left( 1-\alpha \frac{m^2}{m_p^2}\right) \frac{\hbar ^2}{2m}\nabla ^2+V\right] \psi \,=\,i\hbar \,\partial _t\psi \,. \end{aligned}$$
(30)

Here, we have used Eq. (27) and we have considered only the leading term in \(\alpha m^2/m_p^2\). Clearly, in the absence of an external potential (i.e., \(V=0\)), the free energy reads

$$\begin{aligned} E_0=E^{(QM)}+E_\alpha =\frac{p_0^2}{2m}\left( 1-\alpha \frac{m^2}{m_p^2}\right) \,, \end{aligned}$$
(31)

where all the information about the relativistic GUP is encoded in \(E_\alpha \), as also argued in Ref. [42]. Now, starting from Eqs. (30) and (31) and retracing all the steps performed for the stationary phase shifter in the first GUP framework, one arrives at

$$\begin{aligned} \mathbf{p} _0\cdot \varvec{\nabla }\xi =-\left( 1+\alpha \frac{m^2}{m_p^2}\right) \frac{im}{\hbar }V\xi \,, \end{aligned}$$
(32)

where we have used the same notation of Eq. (10).

By requiring energy conservation as in Eq. (17), one can show that the same relations as in Eqs. (20) and (21) are obtained. Therefore, it follows that the different predictions between the first and the second GUP frameworks are due to the spatial non-commutativity arising in the latter, which in turn is a consequence of the particular choice for \(\beta \) and \(\beta '\).

3 Aharonov–Bohm effect

The Aharonov–Bohm effect shows how a quantum system made up of charged particles can be affected by the electromagnetic potentials even when both the electric and magnetic fields are vanishing in the region where particles propagate [4]. For the sake of simplicity, here we will deal only with the magnetic AB effect. We will perform the full reasoning for this example only, since for the other phenomena the considerations turn out to be very similar.

Fig. 1
figure 1

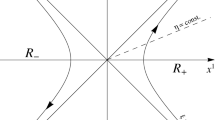
Scheme of Aharonov–Bohm effect on the equatorial plane (i.e., \(\theta =\pi /2\)). Here, we are assuming to look at the experimental setup from above. Charged particles are emitted from the source on the left side of the apparatus. After being split into two components, the beam coherently recombines on the screen on the right side, giving rise to an interference pattern (blue line) which is shifted of the factor \(\varDelta g^{(QM)}\) when the magnetic field \(\mathbf{B} \) is turned on (red line)

Full size image

Let us consider a beam of charged particles with mass m and charge q separated into two components by a beam splitter (see Fig. 1). An infinitely long solenoid of radius d is located between two beams, which travel along different paths and coherently recombine on a screen, giving rise to the interference pattern. Clearly, although this setup is characterized by a non-vanishing value of the magnetic field \(\mathbf{B} \) only inside the solenoid (\(r<d\)), the magnetic vector potential \(\mathbf{A} \) is nonzero even for \(r>d\). By resorting to the Coulomb gauge \(\varvec{\nabla }\cdot \mathbf{A} =0\), its expression reads

$$\begin{aligned} \mathbf{A} =\frac{Bd^2}{2r}{\hat{\varphi }}\,, \end{aligned}$$
(33)

where \(\mathbf{B} =\varvec{\nabla }\times \mathbf{A} \), \(B=|\mathbf{B} |\) and \({\hat{\varphi }}\) is the azimuthal vector related to the angle \(\varphi \) (see figure). Without loss of generality, we assume that the apparatus lies in the equatorial plane (i.e., the polar angle \(\theta \) is chosen to be \(\theta =\pi /2\)).

By performing the minimal coupling procedure of the low-energy momentum \(\mathbf{p} \) with the potential \(\mathbf{A} \), the Schrödinger equation in the above framework takes the well-known formFootnote 6

$$\begin{aligned} \hat{H}\psi =\left[ \frac{1}{2m}\left( -i\hbar \varvec{\nabla }-q\mathbf{A} \right) ^2 \right] \psi =i\hbar \,\partial _t\psi \,. \end{aligned}$$
(34)

In the language of Sect. 2, it is clear that the shift induced by the potential \(\mathbf{A} \) on the momentum of the particles is nothing but \(\delta \mathbf{p} =-q\mathbf{A} \). Therefore, by using Eq. (21), one can readily derive the QM phase shift acquired by the two beams when recombining on the screen, which is

$$\begin{aligned} \varDelta g^{(QM)}\,\equiv \,g_{(2)}-g_{(1)}\,=\,-\frac{q\pi Bd^2}{\hbar }\,, \end{aligned}$$
(35)

where

$$\begin{aligned} g_{(I)}=-\frac{q}{\hbar }\int _{(I)}{} \mathbf{A} \cdot d\mathbf{s} \,, \end{aligned}$$
(36)

and the index \(I=1,2\) refers to the two paths in Fig. 1.

Now, since the QM phase shift does not depend on the momentum of the test particle, it follows that the first GUP framework does not affect the standard Aharonov–Bohm prediction (see the discussion at the end of Sect. 2.1), consistently with the result of Ref. [11].

Vice versa, in order to derive the corrections induced by the GUP (22), let us observe that Eq. (35) depends on the area enclosed by the paths of the two beams. Following the prescription of Sect. 2.2, we then employ Eq. (29) to read off the physical dimensions D of the radius of the solenoid, obtaining

$$\begin{aligned} \varDelta g=\varDelta g^{(QM)}+\varDelta g_\alpha =-\frac{q\pi BD^2}{\hbar }\left( 1-2\,\alpha \frac{m^2}{m_p^2}\right) , \end{aligned}$$
(37)

where we have denoted by \(\varDelta g_\alpha \) the GUP correction. Therefore, gravity effects in the guise of the deformed commutator (22) contribute to further shift the AB interference pattern, as shown in Fig. 2. Clearly, as long as the quantity \(\alpha \,m^2/m_p^2\) is negligible (that is, for masses far away from the Planck scale), the additional term goes to zero and the standard formula for AB interferometry measurements is recovered [43, 44].

Fig. 2
figure 2

Phase shift of the AB interference pattern. The GUP interference fringes (green line) are further shifted of the factor \(\varDelta g_{\alpha }\) with respect to the QM prediction \(\varDelta g^{(QM)}\) (the blue and red lines have the same meaning as in Fig. 1). Note that \(\varDelta g^{(QM)}\) and \(\varDelta g_{\alpha }\) are not in scale

Full size image

Now, the obtained \(\alpha \)-dependent expression of \(\varDelta g\) allows us to infer an upper bound on the GUP parameter on the basis of simple experimental considerations. To the best of our knowledge, indeed, the AB phase shift is measured in current interferometry experiments with an error of about \(11\%\) [6, 54]. Since GUP gravity effects are well below current experimental sensitivity, we can obtain a bound on the parameter \(\alpha \) by fitting the ratio \(\left| \varDelta g_\alpha /\varDelta g^{(QM)}\right| \) into the accuracy bound of the experiments to test the AB effect. In so doing, we obtain

$$\begin{aligned} \left| \frac{\varDelta g_\alpha }{\varDelta g^{(QM)}}\right| \lesssim 10^{-1}\,\Longrightarrow \,\alpha \lesssim 10^{-1}\frac{m_p^2}{2\,m^2}\,. \end{aligned}$$
(38)

If we consider electrons as test particles, then we have

$$\begin{aligned} \alpha \lesssim 10^{43}\,, \end{aligned}$$
(39)

which is very close to the bound derived in Ref. [42] within different frameworks.

4 Other applications

To explore the possibility of finding more stringent constraints on the GUP parameters, let us now extend the previous analysis to other well-understood QM interferometry effects, such as the Aharonov–Casher, COW and Sagnac effects.

4.1 Aharonov–Casher effect

The Aharonov–Casher effect [7] is the analogue of the AB effect for neutral particles. Specifically, it arises whenever a neutral particle with non-vanishing magnetic moment \(\varvec{\mu }\) travels around a charged wire. In this framework, the geometric phase turns out to be non-vanishing since the electric field \(\mathbf{E} \) generated by the wire induces a variation of the particle momentum according to [7, 54]

$$\begin{aligned} \mathbf{p} _0\rightarrow \mathbf{p} _0+\varvec{\mu }\times \mathbf{E} \,, \end{aligned}$$
(40)

from which we derive \(\delta \mathbf{p} =\varvec{\mu }\times \mathbf{E} \). If the wire is sufficiently long, the electric field in cylindrical coordinates can be approximately written as

$$\begin{aligned} \mathbf{E} \approx \frac{\lambda }{2\pi \epsilon _0 r}\hat{r}\,, \end{aligned}$$
(41)

where \(\lambda \) is the linear charge density of the wire, whereas the particle is displaced in such a way that \(\varvec{\mu }=\mu \hat{z}\).

By resorting to Eq. (21), one can show that the phase shift for a test particle moving around the line charge is

$$\begin{aligned} \varDelta g^{(QM)}\,=\,\frac{\mu \lambda }{\epsilon _0\hbar }\,. \end{aligned}$$
(42)

Clearly, similarly to the Aharonov–Bohm effect, \(\varDelta g^{(QM)}\) will be insensitive to the first GUP model, since it does not depend on the momentum of the particle.

Conversely, the corrected phase shift within the second GUP framework takes the form

$$\begin{aligned} \varDelta g=\varDelta g^{(QM)}+\varDelta g_\alpha =\frac{\mu \varLambda }{\epsilon _0\hbar }\left( 1+\,\alpha \frac{m^2}{m_p^2}\right) , \end{aligned}$$
(43)

where we have used Eq. (29) to make the dependence of the linear charge density on the physical length of the wire explicit.

Following the same reasoning as in Sect. 3, we can now extract a constraint on the deformation parameter in relation to the precision with which laboratory tests of the AC effect are carried out. According to the available data [54, 55] the most accurate measurements of the AC phase shift are characterized by an error of about \(24\%\). If we consider neutrons as test particles, we get

$$\begin{aligned} \alpha \lesssim 10^{37}\,, \end{aligned}$$
(44)

which improves of several orders the previous bound.

4.2 COW effect

In 1974, Overhauser and Colella proposed to detect the QM phase shift caused by the interaction of particles with the classical Earth’s Newtonian potential \(V=m\phi \) by devising a specific laboratory test [8]. The idea was to perform neutron interferometry between coherently split beams traveling at different heights and, thus, with different velocities. A year later its theoretical prediction, such an effect was experimentally verified [9], providing one of the first examples of how gravity appears in the realm of quantum theory.

With reference to the setting depicted above, it is possible to derive the COW phase shift as a function of the surface S enclosed by the arms of the interferometer and the gap \(\delta \mathbf{p} =\mathbf{p} _0-\mathbf{p} _u\) between the momenta of the lower and upper beams. On the basis of straightforward considerations on the energy conservation, we obtain [56]

$$\begin{aligned} \varDelta g^{(QM)}=\frac{m^2g\,S}{\hbar \,p_0}\,, \end{aligned}$$
(45)

which explicitly depends on the momentum \(p_0\) of the test particle. As a consequence, in this case both the GUPs (3) and (22) will induce non-trivial corrections on the QM phase shift. In particular, for the first deformation, GUP effects can be estimated by expressing the low-energy momentum \(p_0\) in terms of the physical one P through Eq. (4). To the leading order in \(\beta \), we have

$$\begin{aligned} \varDelta g \,=\, \varDelta g^{(QM)}+\varDelta g_\beta \,=\, \frac{m^2g\,S}{\hbar \,P}\left( 1+\beta \ell _p^2\frac{P^2}{\hbar ^2}\right) . \end{aligned}$$
(46)

Now, since the COW experiment deals with neutrons, the available data are the same as the ones considered for the AC effect, the only difference being the estimated error on the measurements of the phase shift, which is of the order of \(1\%\) [54]. Then, for typical velocity \(v_n\simeq 10^3\,\text {m/s}\) of neutrons involved in interferometry tests, by estimating the bound as seen in Eq. (38) we get the following constraint on \(\beta \):

$$\begin{aligned} \beta \lesssim 10^{47}\, \end{aligned}$$
(47)

which is of the same order as other constraints derived from both gravitational and condensed matter experiments [30, 57].

Let us now turn our attention to the second GUP framework. By taking into account Eq. (24) and the redefinitions (27)–(29) of the physical mass and spatial dimensions of the system, we are led to

$$\begin{aligned} \varDelta g=\frac{m^2g\,\varSigma }{\hbar \,P}\left( 1-\,\alpha \frac{m^2}{m_p^2}\right) , \end{aligned}$$
(48)

where \(\varSigma \) is the rescaled surface enclosed by the interferometer. From this equation, it follows that

$$\begin{aligned} \alpha \lesssim 10^{36}\,, \end{aligned}$$
(49)

which is the most stringent bound on this parameter to the best of our knowledge.

4.3 Sagnac effect

Soon after the discovery by Colella, Overhauser and Werner, Page observed that the rotation of the Earth could induce corrections to the phase shift elicited by the Earth’s Newtonian potential of the same order as the COW term [10]. Since a similar effect had previously been analyzed by Sagnac in the context of the interferometry between light signals around a rotating ring, this phenomenon is commonly regarded as the counterpart of the Sagnac effect for matter waves.

Following Refs. [43, 44, 54], it can be shown that the variation of the momentum between two beams propagating in opposite directions along the arms of a rotating interferometer is

$$\begin{aligned} \delta \mathbf{p} =m\varvec{\omega }\times \mathbf{r} \,, \end{aligned}$$
(50)

where \(\varvec{\omega }\) is the angular velocity of the apparatus. In a setup in which the angular motion traces a circle, we can set \(\varvec{\omega }=\omega \hat{z}\) in cylindrical coordinates. Accordingly, the result of the integral in Eq. (21) gives

$$\begin{aligned} \varDelta g^{(QM)}\,=\,\frac{2m\omega S}{\hbar }\,, \end{aligned}$$
(51)

with S being the surface enclosed by the path.

By implementing the prescriptions (27)-(29), straightforward calculations lead to the following GUP-corrected phase shift:

$$\begin{aligned} \varDelta g=\varDelta g^{(QM)}+\varDelta g_\alpha =\frac{2m\omega \varSigma }{\hbar }\left( 1-\alpha \frac{m^2}{m_p^2}\right) , \end{aligned}$$
(52)

where we have denoted by \(\varSigma \) the rescaled area of the surface bounded by the interferometer, as before.

In Ref. [58], it is possible to find the technical specifications of an experiment aimed at detecting the Sagnac effect by use of an electron biprism interferometer rotating on a turntable. By observing that the experimental error for this test is about \(30\%\) [54], we infer for \(\alpha \)

$$\begin{aligned} \alpha \lesssim 10^{44}\,. \end{aligned}$$
(53)

In the next section, we summarize the constraints on the GUP parameters derived in the previous examples and discuss how they can in principle be improved.

5 Conclusions and discussion

We have analyzed the effects of two GUPs with a minimal uncertainty in position on some well-known interferometry phenomena, such as the Aharonov–Bohm, Aharonov–Casher, COW and Sagnac effects. By using a properly modified Schrödinger equation, we have computed the lowest-order correction to the phase shift of the interference pattern. For the first GUP model, which predicts a redefinition of the high-energy momentum alone, we have shown that a non-trivial correction only appears in the COW experiment, as the characteristic QM phase shift explicitly depends on the momentum of the test particle. Conversely, within the second GUP framework, we have found that the non-commutativity of spacetime coordinates along with the reparameterization of both the mass and momentum result in GUP-corrected phase shifts for all the considered phenomena.

As remarked in Ref. [11], these GUP corrections can be interpreted in two complementary ways: from the phenomenological point of view, one can say that they are too much small and, thus, out of reach of current experiments. Notwithstanding this, at the theoretical level their role may be highly non-trivial, since they could pave the way to analyze how gravity influences quantum mechanical systems when approaching Planck scale. From the latter perspective, the above analysis provides us with the possibility to predict upper bounds on the GUP deformations parameters. The obtained values are summarized in the following table:

Table 1 Estimated constraints on the GUP parameters
Full size table

We note that although the bound derived on \(\beta \) does not improve the constraints already existing in the literature [30], the one on \(\alpha \) is of several order smaller than the values found in Ref. [42] in different physical scenarios. Furthermore, the advantage of our approach is that it is based on interferometry measurements, which are getting more and more refined in recent years in various contexts and by use of varied techniques [59,60,61,62,63]. This may allow for a direct test of our predictions via future high-precision interferometry experiments. Hopefully, more accurate measurements of the phase shifts should either be able to test these predictions or further improve the above constraints.

Clearly, in order to better understand the scale on which quantum gravity effects should start to become relevant, the GUP framework must be further analyzed to infer the exact value of the deformation parameters. Given that GUP physics is largely heuristic, one should keep any scenario open, including the possibility that these parameters are dynamical functions (rather than constants), as proposed in Ref. [64] to preserve the black hole complementarity principle. Waiting for definitive answers from experiments, more work is inevitably required at theoretical level in order to search for viable frameworks where distinctive signatures of quantum gravity effects do arise. Interferometry, for instance, may be one of this.