Coupled free vibration analysis of functionally graded shaft-disk system by differential quadrature finite element method

Abstract

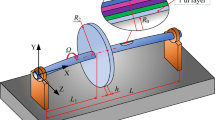
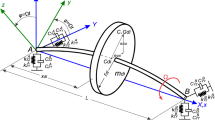
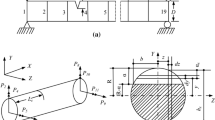
The purpose of this paper is to investigate coupling vibration characteristics of the flexible functionally graded material (FGM) shaft-disk coupling system with variable thickness disk. The mathematical model of the shaft-disk system is based on the first-order shear deformation theory, combined with the Voigt model and the four-parameter power-law distribution. The energy expression is discretized by the differential quadrature finite element method, and furthermore the differential equation of the shaft-disk system is derived. In order to verify the convergence and calculation accuracy of the current model, a series of numerical examples are introduced. In addition, the influence of geometrical and material parameters on vibration results is discussed, while the boundary conditions and the cross-sectional shape of the disk are considered. It can be seen that the variation of the FGM parameters will affect the vibration characteristics within a certain range, while the frequency parameter with different disk cross-sectional shapes is different in sensitivity to parameter changes. The parametric analysis can provide reference for the determination of structure and material parameters.

Graphic abstract

Appendix A

Differential quadrature is based on the numerical analysis method to transform the differential equation describing the boundary value problem into a set of algebraic equations in order to achieve the purpose of rapid solution.

For one-dimensional problems, let the one-dimensional function f(x) of the independent variable x be continuous and differentiable on the interval [− 1, 1]. Taking N different nodes in the interval, the first derivative of the function in xi can be expressed as:

$$ \begin{aligned} \left. {\frac{{{\text{d}}f(x)}}{{{\text{dx}}}}} \right|_{i} & = {\mathbf{A}}^{(1)} \,{\mathbf{f}},i = 1,2, \ldots ,N, \\ {\mathbf{A}}^{(1)} & = \left[ {\begin{array}{*{20}l} {A_{11}^{(1)} } & {A_{12}^{(1)} } & \ldots & {A_{1N}^{(1)} } \\ {A_{21}^{(1)} } & {A_{22}^{(1)} } & \ldots & {A_{2N}^{(1)} } \\ \ldots & \ldots & \ddots & \ldots \\ {A_{N1}^{(1)} } & {A_{N2}^{(1)} } & \ldots & {A_{NN}^{(1)} } \\ \end{array} } \right], \\ {\mathbf{f}} & = \left[ {\begin{array}{*{20}l} {f_{1} } & {f_{2} } & \cdots & {f_{N} } \\ \end{array} } \right]^{{\text{T}}} \\ \end{aligned} $$

(A.1)

where A⁽¹⁾ is a first-order weighting coefficient matrix with dimension N × N composed of first-order weighting coefficients A(1) ij, i, j = 1, 2, …, N, the superscript “(1)” indicates that the function takes the first derivative, and f is the unit displacement column vector. In this paper, Lagrange polynomials are used as the interpolation basis functions, and the elements of matrix A⁽¹⁾ in Eq. (A.1) can be expressed as

$$ A_{ij}^{(1)} = \frac{{\prod\nolimits_{k = 1,k \ne i}^{N} {(x_{i} - x_{k} )} }}{{(x_{i} - x_{j} )\prod\nolimits_{k = 1,k \ne j}^{N} {(x_{j} - x_{k} )} }},\,A_{ii}^{{({1})}} = - \sum\limits_{j = 1,j \ne i}^{N} {A_{ij}^{{({1})}} } . $$

(A.2)

Similar to the differential processing, the nodes are divided in the integration interval of [− 1, 1], and then the function is integrated by the numerical integration method:

$$ \int_{ - 1}^{1} {f\left( x \right)} {\text{d}}x = {\mathbf{Cf}},\,{\mathbf{C}} = {\text{diag}}(C_{1} \, C_{2} \, \ldots \, C_{N} ) $$

(A.3)

in which C is an element in the matrix of integral weight coefficients and f is a column vector of unit displacement. The weight coefficient can be solved by the Gauss quadrature method:

$$ \begin{aligned} C_{1} & = C_{n} = \frac{2}{n(n - 1)}, \, \\ \, C_{j} & = \frac{2}{{n(n - 1)\left[ {P_{n - 1} (\xi_{j} )} \right]^{2} }} \, (j \ne 1,n) \\ \end{aligned} $$

(A.4)

where P_n(ξ_j), j = 1, 2, …, n − 1, are Legendre polynomials of order n and P_n−1(ξ_j) is the (j − 1)th zero of the first derivative.

In order to adapt to the solution of different length shaft elements, the weight coefficient matrix is modified:

$$ {\mathbf{A}}_{1}^{(1)} { = }\frac{2}{{L_{S}^{e} }}{\mathbf{A}}^{\left( 1 \right)} ;{\mathbf{C}}_{1} = \frac{{L_{S}^{e} }}{2}{\mathbf{C}} $$

(A.5)

where Le S indicates the length of the shaft unit.

For two-dimensional problems, a two-dimensional function g(x, y), whose independent variables are x, y and their value range is [− 1, 1], is supposed. M and N nodes in the x and y directions are divided, respectively, and the first derivative of the function with respect to x and y at node (x_i, y_j) is

$$ \begin{aligned} \left. {\frac{\partial g}{{\partial x}}} \right|_{ij} & = {\mathbf{A}}_{02}^{(1)} {\mathbf{g}},\left. {\frac{\partial g}{{\partial y}}} \right|_{ij} = {\mathbf{B}}_{02}^{(1)} {\mathbf{g}},\left. {\frac{{\partial^{2} g}}{\partial x\partial y}} \right|_{ij} = {\mathbf{A}}_{02}^{(1)} {\mathbf{B}}_{02}^{(1)} {\mathbf{g}} \\ {\mathbf{A}}_{02}^{(1)} & = \left[ {\begin{array}{*{20}l} {{\mathbf{A}}_{01}^{(1)} } &\quad \quad 0 &\quad \ldots &\quad 0 \\ 0 &\quad {{\mathbf{A}}_{01}^{(1)} } &\quad \ldots &\quad 0 \\ \ldots &\quad\ldots &\quad \ddots &\quad \ldots \\ 0 &\quad 0 &\quad \ldots &\quad {{\mathbf{A}}_{01}^{(1)} } \\ \end{array} } \right], \\ {\mathbf{B}}_{02}^{(1)} & = \left[ {\begin{array}{*{20}l} {{\mathbf{B}}_{11}^{(1)} } &\quad {{\mathbf{B}}_{12}^{(1)} } &\quad \ldots &\quad {{\mathbf{B}}_{1N}^{(1)} } \\ {{\mathbf{B}}_{21}^{(1)} } &\quad {{\mathbf{B}}_{22}^{(1)} } &\quad \ldots &\quad {{\mathbf{B}}_{2N}^{(1)} } \\ \ldots &\quad \ldots &\quad \ddots &\quad \ldots \\ {{\mathbf{B}}_{N1}^{(1)} } &\quad {{\mathbf{B}}_{N2}^{(1)} } &\quad \ldots &\quad {{\mathbf{B}}_{NN}^{(1)} } \\ \end{array} } \right], \\ {\mathbf{B}}_{ij}^{(1)} & = \left[ {\begin{array}{*{20}l} {{\mathbf{A}}_{ij}^{(1)} } &\quad 0 &\quad \ldots &\quad 0 \\ 0 &\quad {{\mathbf{A}}_{ij}^{(1)} } &\quad \ldots &\quad 0 \\ \ldots &\quad \ldots &\quad \ddots &\quad \ldots \\ 0 &\quad 0 &\quad \ldots &\quad {{\mathbf{A}}_{ij}^{(1)} } \\ \end{array} } \right], \\ {\mathbf{g}} & = \left[ {\begin{array}{*{20}l} {g_{11} } &\quad \ldots &\quad {g_{M1} } &\quad {g_{12} } &\quad \ldots &\quad {g_{M2} } &\quad \ldots &\quad {g_{1N} } &\quad \ldots &\quad {g_{MN} } \\ \end{array} } \right]^{{\text{T}}} \\ \end{aligned} $$

(A.6)

in which the matrix A(1) 02 is the weight coefficient matrix in Eq. (A.6) and matrix B(1) ij is the diagonal matrix shown in the equation.

Similarly, the two-dimensional integral weight coefficient matrix can be expressed as follows:

$$ \begin{aligned} & \int_{{{ - }1}}^{1} {\int_{ - 1}^{1} {g\left( {x,y} \right)} {\text{d}}x{\text{d}}y = \sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{N} {C_{i} C_{j} g\left( {x,y} \right)} } ,} \\ & {\mathbf{C}}_{02} = {\text{diag}}(\begin{array}{*{20}l} {C_{1} C_{1} } & \ldots & {C_{M} C_{1} } & {C_{1} C_{2} } & \ldots & {C_{M} C_{2} } & \ldots & {C_{M} C_{N} } \\ \end{array} ) \\ \end{aligned}. $$

(A.7)

It is worth noting that these matrices are obtained when the interval between x and y is [− 1, 1], so the solution range needs to be transformed in practical applications.